 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田のおもしろ数学566〜条件付き不等式の証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a\gt 0,b\gt 0,c\gt 0,abc=1$のとき、
$\dfrac{a}{ab+1}+\dfrac{b}{bc+1}+\dfrac{c}{ca+1} \geqq \dfrac{3}{2}$
を証明して下さい。
この動画を見る
$a\gt 0,b\gt 0,c\gt 0,abc=1$のとき、
$\dfrac{a}{ab+1}+\dfrac{b}{bc+1}+\dfrac{c}{ca+1} \geqq \dfrac{3}{2}$
を証明して下さい。
福田の数学〜早稲田大学2025教育学部第2問〜組合せと確率の基本的な性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
$n$を自然数とする。
$1$から$n$mでの数字がもれなく一つずつ記入された
$n$枚の赤色のカードと$1$から$n$までの数字がもれなく
一つずつ記入された$n$枚の白色のカードがある。
この$2n$枚のカードの中から同時に$2$枚を取り出し、
カードに記入された数字を確認した後にもとに戻す、
という試行を$2$回行う。次の問いに答えよ。
(1)$1$回目に取り出した$2$枚のカードに記入された
数字が同じであり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した$2$枚の
カードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(2)$1$回目に取り出した$2$枚のカードに記入された
数字が異なり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した
$2$枚のカードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(3)$1$回目に取り出した$2$枚のカードに記入された数字と
$2$回目に取り出した$2$枚のカードに記入された
数字の間に共通の数字が存在する確率を
$n$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{2}$
$n$を自然数とする。
$1$から$n$mでの数字がもれなく一つずつ記入された
$n$枚の赤色のカードと$1$から$n$までの数字がもれなく
一つずつ記入された$n$枚の白色のカードがある。
この$2n$枚のカードの中から同時に$2$枚を取り出し、
カードに記入された数字を確認した後にもとに戻す、
という試行を$2$回行う。次の問いに答えよ。
(1)$1$回目に取り出した$2$枚のカードに記入された
数字が同じであり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した$2$枚の
カードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(2)$1$回目に取り出した$2$枚のカードに記入された
数字が異なり、かつ$1$回目に取り出した$2$枚の
カードに記入された数字と$2$回目に取り出した
$2$枚のカードに記入された数字の間に共通の数字が
存在しない取り出し方の総数を$n$を用いて表せ。
(3)$1$回目に取り出した$2$枚のカードに記入された数字と
$2$回目に取り出した$2$枚のカードに記入された
数字の間に共通の数字が存在する確率を
$n$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
福田のおもしろ数学565〜Nesbittの不等式の証明
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a\gt 0,b\gt 0,c \gt 0$のとき
$\dfrac{c}{a+b}+\dfrac{a}{b+c}+\dfrac{b}{c+a} \geqq \dfrac{3}{2}$
を証明して下さい。
この動画を見る
$a\gt 0,b\gt 0,c \gt 0$のとき
$\dfrac{c}{a+b}+\dfrac{a}{b+c}+\dfrac{b}{c+a} \geqq \dfrac{3}{2}$
を証明して下さい。
福田の数学〜早稲田大学2025教育学部第1問(4)〜2変数関数の最大

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(4)$4$つの辺$AB,BC,CD,DA$の長さが$1$である
四面体$ABCD$を考える。
そのような四面体の体積の最大値を求めよ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{1}$
(4)$4$つの辺$AB,BC,CD,DA$の長さが$1$である
四面体$ABCD$を考える。
そのような四面体の体積の最大値を求めよ。
$2025$年早稲田大学教育学部過去問題
福田のおもしろ数学564〜1分チャレンジ!数値計算

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\dfrac{2025^3+2024^3+3\cdot 2025\cdot 2024-1}{2026^2+2025^2+1}$
を計算して下さい。
この動画を見る
$\dfrac{2025^3+2024^3+3\cdot 2025\cdot 2024-1}{2026^2+2025^2+1}$
を計算して下さい。
福田の数学〜早稲田大学2025教育学部第1問(3)〜5角柱の10個の点から同一平面上にある4点を選ぶ確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(3)底面が正五角形である$5$角柱の頂点から相異なる
$4$点を選ぶとき、
$4$点が同一平面上にある確率を求めよ。
ただし、$4$点の選び方は同様に確からしいとする。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{1}$
(3)底面が正五角形である$5$角柱の頂点から相異なる
$4$点を選ぶとき、
$4$点が同一平面上にある確率を求めよ。
ただし、$4$点の選び方は同様に確からしいとする。
$2025$年早稲田大学教育学部過去問題
福田のおもしろ数学563〜不定方程式の整数解

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$101x+102y+103z=2025$
を満たす正の整数の組$(x,y,z)$
をすべて求めて下さい。
この動画を見る
$101x+102y+103z=2025$
を満たす正の整数の組$(x,y,z)$
をすべて求めて下さい。
福田の数学〜早稲田大学2025教育学部第1問(2)〜三角形の外心と垂心と点の回転

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2)座標平面上の$3$点
$A(1,0),B(0,-1),C(-1,1)$を
頂点とする三角形$ABC$を考える。
三角形$ABC$をその外心を中心として反時計回りに
$\dfrac{\pi}{3}$だけ回転することで得られる三角形の
垂心の座標を求めよ。
なお、三角形の$3$頂点から対辺または
その延長に下ろした$3$本の垂線は一点で交わり、
その交点を三角形の垂心という。
$2025$年早稲田大学教育学部第1問過去問題
この動画を見る
$\boxed{1}$
(2)座標平面上の$3$点
$A(1,0),B(0,-1),C(-1,1)$を
頂点とする三角形$ABC$を考える。
三角形$ABC$をその外心を中心として反時計回りに
$\dfrac{\pi}{3}$だけ回転することで得られる三角形の
垂心の座標を求めよ。
なお、三角形の$3$頂点から対辺または
その延長に下ろした$3$本の垂線は一点で交わり、
その交点を三角形の垂心という。
$2025$年早稲田大学教育学部第1問過去問題
福田のおもしろ数学562〜連立漸化式で定まる数列に関する証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\{a_k\},\{b_k\}$が$a_0=b_0=0$,
$a_{k+1}=b_k,b_{k+1}=\dfrac{a_k b_k+a_k+1}{b_k+1}$
で定義されている。
$a_{2024}+b_{2024}\geqq 88$
であることを証明して下さい。
この動画を見る
数列$\{a_k\},\{b_k\}$が$a_0=b_0=0$,
$a_{k+1}=b_k,b_{k+1}=\dfrac{a_k b_k+a_k+1}{b_k+1}$
で定義されている。
$a_{2024}+b_{2024}\geqq 88$
であることを証明して下さい。
福田の数学〜早稲田大学2025教育学部第1問(1)〜シグマ計算

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)$k$を自然数とする。次の数
$-1^2+2^2-3^2+4^2-5^2+6^2- \cdots -(2k-1)^2+(2k)^2$
を$k$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{1}$
(1)$k$を自然数とする。次の数
$-1^2+2^2-3^2+4^2-5^2+6^2- \cdots -(2k-1)^2+(2k)^2$
を$k$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
福田のおもしろ数学561〜三角形の3つの内角を度数法で表したときの論証その2

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
三角形の$3$つの内角を度数表で測ったものを
$x,y,z$とする。次を証明して下さい。
$\dfrac{x}{y},\dfrac{y}{z},\dfrac{z}{x}$のうち、
ちょうど$1$つだけ有理数
$\Rightarrow x,y,z$はすべて無理数
この動画を見る
三角形の$3$つの内角を度数表で測ったものを
$x,y,z$とする。次を証明して下さい。
$\dfrac{x}{y},\dfrac{y}{z},\dfrac{z}{x}$のうち、
ちょうど$1$つだけ有理数
$\Rightarrow x,y,z$はすべて無理数
福田の数学〜東京慈恵会医科大学2025医学部第4問〜複素数の絶対値の取りうる値の範囲

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$z$は実数ではない複素数で、
$z+\dfrac{1}{z-1}$が正の実数となるものとする。
このとき、
$ \left \vert \dfrac{1}{z-1}-\dfrac{z- \overline{z}}{2}+1 \right \vert $がとりうる値の
範囲を求めよ。
ただし、$\overline{z}$は$z$に共役な複素数とする。
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{4}$
$z$は実数ではない複素数で、
$z+\dfrac{1}{z-1}$が正の実数となるものとする。
このとき、
$ \left \vert \dfrac{1}{z-1}-\dfrac{z- \overline{z}}{2}+1 \right \vert $がとりうる値の
範囲を求めよ。
ただし、$\overline{z}$は$z$に共役な複素数とする。
$2025$年東京慈恵会医科大学医学部過去問題
福田のおもしろ数学560〜三角形の3つの内角を度数法で表したときの論証

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
三角形の$3$つの内角を度数法で測ったものを
$x,y,z$とする。次を証明して下さい。
$\dfrac{x}{y},\dfrac{y}{z},\dfrac{z}{x}$がすべて有理数
$\Rightarrow x,y,z$はすべて有理数
この動画を見る
三角形の$3$つの内角を度数法で測ったものを
$x,y,z$とする。次を証明して下さい。
$\dfrac{x}{y},\dfrac{y}{z},\dfrac{z}{x}$がすべて有理数
$\Rightarrow x,y,z$はすべて有理数
福田の数学〜東京慈恵会医科大学2025医学部第3問〜双曲線が表す領域と素数の性質

単元:
#数A#大学入試過去問(数学)#平面上の曲線#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
自然数$p$は$2$以上の定数とする。
$xy$平面上で不等式$x^2-py^2 \geqq -1$の表す領域
を$D$とする。
自然数$r$は、円$(x-p)^2+y^2=r$が領域$D$に
含まれるような最大のものとするとき、
次の問いに答えよ。
(1)$r$を$p$を用いて表せ。
(2) (1)のもとで、関係式$(x-p)^2+y^2=r$をみたす
互いに異なる素数の組$(x,y,p)$のうち、
$p$の値が最小となるものを求めよ。
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{3}$
自然数$p$は$2$以上の定数とする。
$xy$平面上で不等式$x^2-py^2 \geqq -1$の表す領域
を$D$とする。
自然数$r$は、円$(x-p)^2+y^2=r$が領域$D$に
含まれるような最大のものとするとき、
次の問いに答えよ。
(1)$r$を$p$を用いて表せ。
(2) (1)のもとで、関係式$(x-p)^2+y^2=r$をみたす
互いに異なる素数の組$(x,y,p)$のうち、
$p$の値が最小となるものを求めよ。
$2025$年東京慈恵会医科大学医学部過去問題
福田のおもしろ数学559〜3Xnのタイルを2つの図形で覆うことができるためのnの条件
単元:
#数A#図形の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
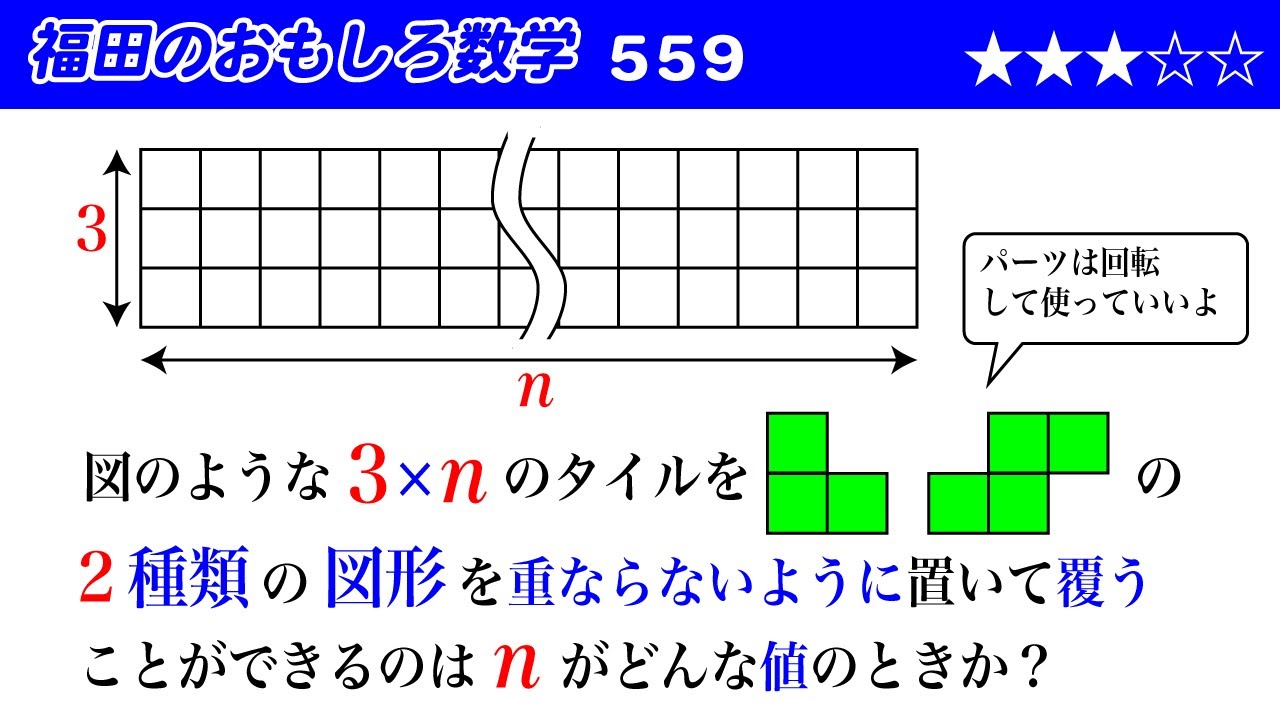
図のような$3\times n$のタイルを(動画を参照)の
$2$種類の図形を重ならないように置いて覆う
ことができるのは$n$がどんな値のときか?
図は動画内参照
この動画を見る
図のような$3\times n$のタイルを(動画を参照)の
$2$種類の図形を重ならないように置いて覆う
ことができるのは$n$がどんな値のときか?
図は動画内参照
福田の数学〜東京慈恵会医科大学2025医学部第2問〜定積分と不等式の証明

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
次の問いに答えよ。ただし、対数は自然対数とする。
(1)$3$以上の自然数$n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{2\log(n+1)}\leqq \displaystyle \int_{0}^{1} \dfrac{x}{\log(x+n)} dx \leqq \dfrac{1}{2\log n}$
(2)不定積分$\displaystyle \int \dfrac{1}{x(log x)^2} dx$ を求めよ。
(3)$m \geqq n$をみたす$3$以上の自然数$m,n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{\log n}-\dfrac{1}{\log(m+1)}\leqq \displaystyle \sum_{k=n}^{m} \dfrac{2}{k \log k} \displaystyle \int_{0}^{1} \dfrac{1}{\log(x+k)} dx \leqq \dfrac{1}{\log(n-1)} -\dfrac{1}{\log m}$
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{2}$
次の問いに答えよ。ただし、対数は自然対数とする。
(1)$3$以上の自然数$n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{2\log(n+1)}\leqq \displaystyle \int_{0}^{1} \dfrac{x}{\log(x+n)} dx \leqq \dfrac{1}{2\log n}$
(2)不定積分$\displaystyle \int \dfrac{1}{x(log x)^2} dx$ を求めよ。
(3)$m \geqq n$をみたす$3$以上の自然数$m,n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{\log n}-\dfrac{1}{\log(m+1)}\leqq \displaystyle \sum_{k=n}^{m} \dfrac{2}{k \log k} \displaystyle \int_{0}^{1} \dfrac{1}{\log(x+k)} dx \leqq \dfrac{1}{\log(n-1)} -\dfrac{1}{\log m}$
$2025$年東京慈恵会医科大学医学部過去問題
福田のおもしろ数学558〜長方形を面積の等しい5個の長方形に分割すると合同な長方形が含まれている証明

単元:
#数A#図形の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
ある長方形を面積の等しい$5$個の長方形に
分割する。
このとき、少なくとも$2$個は
合同であることを証明せよ。
この動画を見る
ある長方形を面積の等しい$5$個の長方形に
分割する。
このとき、少なくとも$2$個は
合同であることを証明せよ。
福田の数学〜東京慈恵会医科大学2025医学部第1問〜さいころの目の積の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
$1$個のさいころを$3$回続けて投げるとき、
$k$回目に出る目を$X_k (k-1,2,3)$とする。
このとき、
積$X_1 X_2 X_3$が$10$の倍数になる確率は$\boxed{ア}$、
和$X_1+X_2,X_2+X_3,X_3+X_1$が、
いずれも$6$の倍数にならない確率は$\boxed{イ}$である。
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{1}$
$1$個のさいころを$3$回続けて投げるとき、
$k$回目に出る目を$X_k (k-1,2,3)$とする。
このとき、
積$X_1 X_2 X_3$が$10$の倍数になる確率は$\boxed{ア}$、
和$X_1+X_2,X_2+X_3,X_3+X_1$が、
いずれも$6$の倍数にならない確率は$\boxed{イ}$である。
$2025$年東京慈恵会医科大学医学部過去問題
福田のおもしろ数学557〜AがBを割り切ることを証明

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
自然数$a,b,c$が次の性質を満たしている。
$a^b$は$b^a$を割り切る。
$b^c$は$c^b$を割り切る。
このとき、$a^c$は$c^a$を割り切ることを
証明して下さい。
この動画を見る
自然数$a,b,c$が次の性質を満たしている。
$a^b$は$b^a$を割り切る。
$b^c$は$c^b$を割り切る。
このとき、$a^c$は$c^a$を割り切ることを
証明して下さい。
福田の数学〜早稲田大学2025社会科学部第3問〜三角関数の最大最小と三角方程式の解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#三角関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$\theta$の関数
$f(\theta)=\cos 2\theta-\sqrt3 \sin 2\theta+4\cos\dfrac{\theta}{2}\left(\sin\dfrac{\theta}{2}-\sqrt3 \cos\dfrac{\theta}{2}\right)+2\sqrt3$
を考える。
ただし、$0\leqq \theta \leqq \pi$とする。次の問いに答えよ。
(1)$k=\sin\theta-\sqrt3 \cos \theta$とおくとき、
$f(\theta)$を$k$の関数で表せ。
(2)$f(\theta)$の最大値、最小値を求めよ。
また、そのときの$\theta$の値を求めよ。
(3) (1)の$k$に対して、$\theta$の方程式
$f(\theta)=ak$の解の個数を求めよ。
ただし、定数$a$は$0\lt a \leqq 3$とする。
$2025$年早稲田大学社会科学部過去問題
この動画を見る
$\boxed{3}$
$\theta$の関数
$f(\theta)=\cos 2\theta-\sqrt3 \sin 2\theta+4\cos\dfrac{\theta}{2}\left(\sin\dfrac{\theta}{2}-\sqrt3 \cos\dfrac{\theta}{2}\right)+2\sqrt3$
を考える。
ただし、$0\leqq \theta \leqq \pi$とする。次の問いに答えよ。
(1)$k=\sin\theta-\sqrt3 \cos \theta$とおくとき、
$f(\theta)$を$k$の関数で表せ。
(2)$f(\theta)$の最大値、最小値を求めよ。
また、そのときの$\theta$の値を求めよ。
(3) (1)の$k$に対して、$\theta$の方程式
$f(\theta)=ak$の解の個数を求めよ。
ただし、定数$a$は$0\lt a \leqq 3$とする。
$2025$年早稲田大学社会科学部過去問題
福田のおもしろ数学556〜直角三角形の内接円の接点が斜辺を分ける長さと面積
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
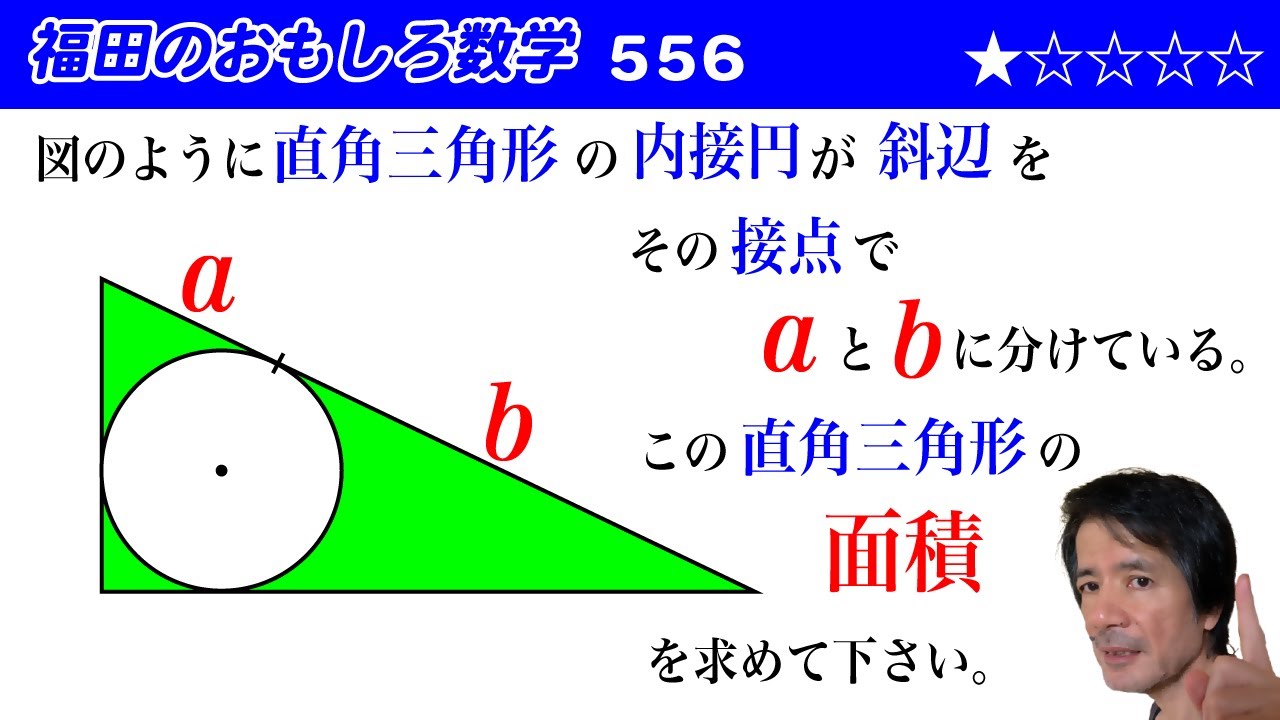
図のような直角三角形の内接円が斜辺を
その接点で$a$と$b$に分けている。
この直角三角形の面積を求めて下さい。
図は動画内参照
この動画を見る
図のような直角三角形の内接円が斜辺を
その接点で$a$と$b$に分けている。
この直角三角形の面積を求めて下さい。
図は動画内参照
福田の数学〜早稲田大学2025社会科学部第2問〜階差数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
数列$\{a_n\}$の階差数列を$\{b_n\}$、すなわち
$b_n=a_{n+1}-a_n \quad (n=1,2,3,\cdots)$
とする。次の問いに答えよ。
(1)$a_n=-\dfrac{1}{n}$のとき、
$b_n$を$n$の式で表す。
(2)$b_n=\dfrac{1}{n(n+1)}$のとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
(3)数列$\{b_n\}$が以下を満たすとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
b_1=1 \\
b_n=n(n+1) \quad (n\geqq 2)
\end{array}
\right.
\end{eqnarray}$
$2025$念早稲田大学社会科学部過去問題
この動画を見る
$\boxed{2}$
数列$\{a_n\}$の階差数列を$\{b_n\}$、すなわち
$b_n=a_{n+1}-a_n \quad (n=1,2,3,\cdots)$
とする。次の問いに答えよ。
(1)$a_n=-\dfrac{1}{n}$のとき、
$b_n$を$n$の式で表す。
(2)$b_n=\dfrac{1}{n(n+1)}$のとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
(3)数列$\{b_n\}$が以下を満たすとき、
$a_n$を$n$の式で表せ。ただし、$a_1=1$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
b_1=1 \\
b_n=n(n+1) \quad (n\geqq 2)
\end{array}
\right.
\end{eqnarray}$
$2025$念早稲田大学社会科学部過去問題
福田のおもしろ数学555〜連立方程式に解が存在するかどうかの検証

単元:
#連立方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a,b,c$は異なる実数であり
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
ax=b \\
bx=c \\\
cx=a
\end{array}
\right.
\end{eqnarray}$
が解をもつような$(a,b,c)$は存在するか。
この動画を見る
$a,b,c$は異なる実数であり
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
ax=b \\
bx=c \\\
cx=a
\end{array}
\right.
\end{eqnarray}$
が解をもつような$(a,b,c)$は存在するか。
福田の数学〜早稲田大学2025社会科学部第1問〜n^pの1の位

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
自然数$n,p$に対して、$n^p$の$1$の位の数を
$f_p(n)$で表す。次の問いに答えよ。
(1)$f_2(n)$の取りうる値をすべて求めよ。
(2)$f_5(n)-f_1(n)$の値を求めよ。
(3)$f_{100}(n)$の取りうる値をすべて求めよ。
$2025$年早稲田大学社会科学部過去問題
この動画を見る
$\boxed{1}$
自然数$n,p$に対して、$n^p$の$1$の位の数を
$f_p(n)$で表す。次の問いに答えよ。
(1)$f_2(n)$の取りうる値をすべて求めよ。
(2)$f_5(n)-f_1(n)$の値を求めよ。
(3)$f_{100}(n)$の取りうる値をすべて求めよ。
$2025$年早稲田大学社会科学部過去問題
福田のおもしろ数学554〜nのn乗根の最大と最小

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_1=1,a_n=\sqrt[n]{n} \quad (n\geqq 2)$
で定める数列$\{a_n\}$について
(1)$n\geqq 3$のとき$\dfrac{a_{n+1}}{a_n} \lt 1$を示せ。
(2)この数列の最大の項と
最小の項を求めよ。
この動画を見る
$a_1=1,a_n=\sqrt[n]{n} \quad (n\geqq 2)$
で定める数列$\{a_n\}$について
(1)$n\geqq 3$のとき$\dfrac{a_{n+1}}{a_n} \lt 1$を示せ。
(2)この数列の最大の項と
最小の項を求めよ。
福田の数学〜早稲田大学2025人間科学部第5問〜接線と面積
単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
曲線$C:y=\cos x\left(0\leqq x \leqq \dfrac{\pi}{2}\right)$上の点
$(\theta,\cos\theta)$における接線を$l$とする。
(1)$\theta=\dfrac{\pi}{4}$のとき、接線$l$と
$x$軸との交点の座標は$\left(\dfrac{\pi+\boxed{二}}{\boxed{ヌ}},0\right)$である。
(2)曲線$C$と接線$l$、および$x$軸によって
囲まれた部分の面積が$1$であるとき、
$\sin\theta=\boxed{ネ}-\sqrt{\boxed{ノ}}$である。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{5}$
曲線$C:y=\cos x\left(0\leqq x \leqq \dfrac{\pi}{2}\right)$上の点
$(\theta,\cos\theta)$における接線を$l$とする。
(1)$\theta=\dfrac{\pi}{4}$のとき、接線$l$と
$x$軸との交点の座標は$\left(\dfrac{\pi+\boxed{二}}{\boxed{ヌ}},0\right)$である。
(2)曲線$C$と接線$l$、および$x$軸によって
囲まれた部分の面積が$1$であるとき、
$\sin\theta=\boxed{ネ}-\sqrt{\boxed{ノ}}$である。
$2025$年早稲田大学人間科学部過去問題
福田のおもしろ数学553〜部分分数分解を工夫してやろう
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
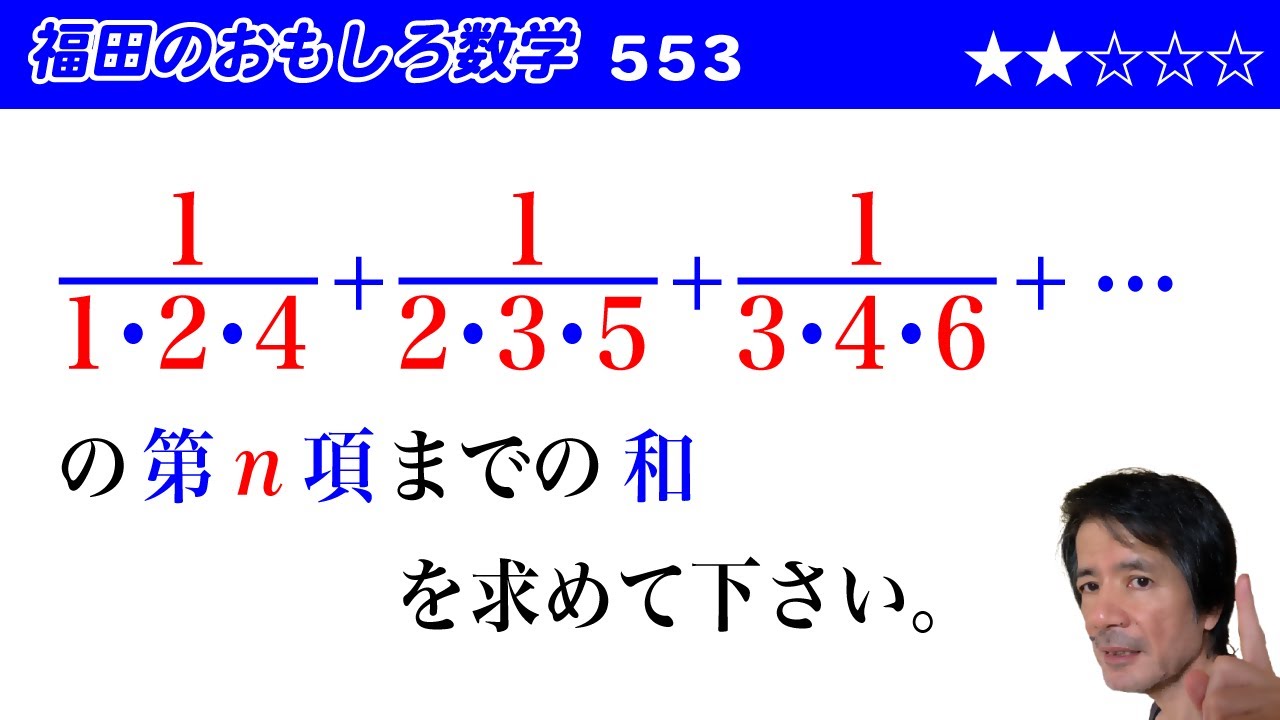
$\dfrac{1}{1\cdot 2 \cdot 4}+\dfrac{1}{2\cdot 3 \cdot 5}+\dfrac{1}{3\cdot 4 \cdot 6}+\cdots$
の第$n$項までの和を求めて下さい。
この動画を見る
$\dfrac{1}{1\cdot 2 \cdot 4}+\dfrac{1}{2\cdot 3 \cdot 5}+\dfrac{1}{3\cdot 4 \cdot 6}+\cdots$
の第$n$項までの和を求めて下さい。
福田の数学〜早稲田大学2025人間科学部第4問〜3次方程式の解が直角三角形を作る条件

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$k$を実数の定数となる。
$z$についての方程式
$z^3-5z^2+kz-5=0$の$3$つの解は
複素数平面上で斜辺$2$の直角三角形の頂点となる。
このとき、$k=\boxed{ト}$であり、
この直角三角形の面積は$\boxed{ナ}$である。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{4}$
$k$を実数の定数となる。
$z$についての方程式
$z^3-5z^2+kz-5=0$の$3$つの解は
複素数平面上で斜辺$2$の直角三角形の頂点となる。
このとき、$k=\boxed{ト}$であり、
この直角三角形の面積は$\boxed{ナ}$である。
$2025$年早稲田大学人間科学部過去問題
福田のおもしろ数学552〜(−1)のi乗はいくら?

福田の数学〜早稲田大学2025人間科学部第3問〜外心と内心の位置ベクトル
単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
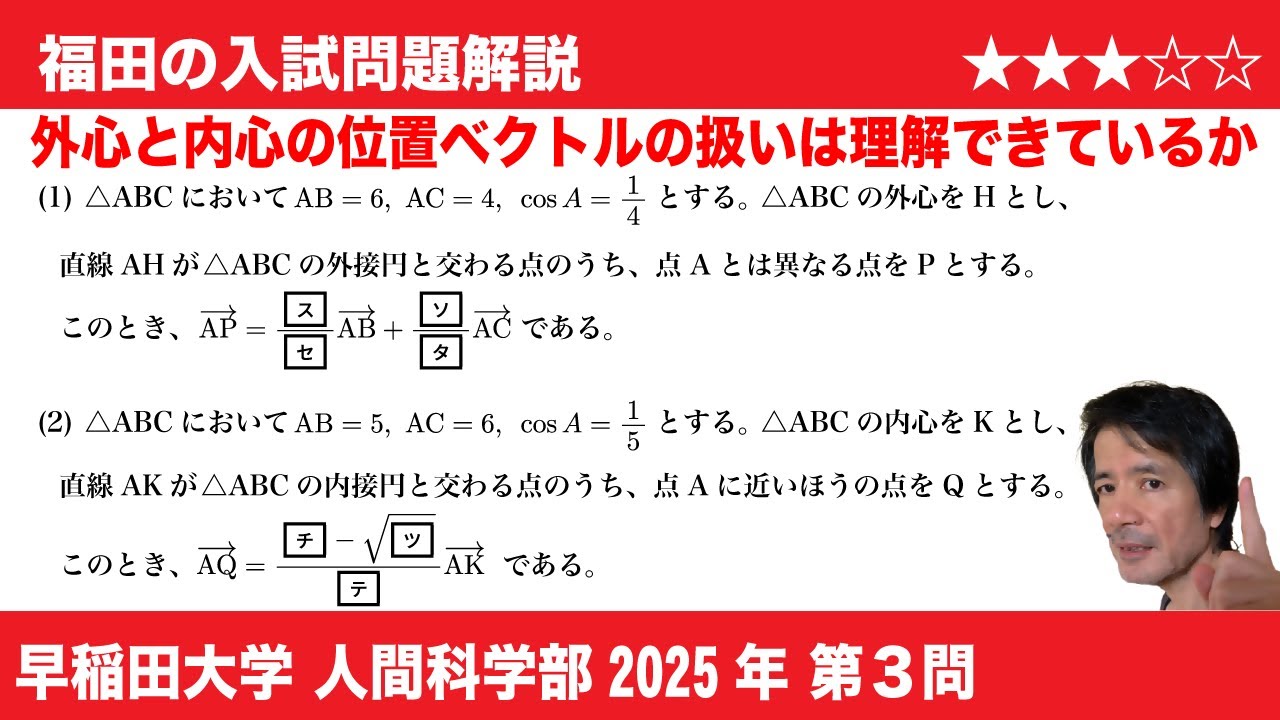
$\boxed{3}$
(1)$\triangle ABC$において$AB=6,AC=4,$
$\cos A=\dfrac{1}{4}$とする。
$\triangle ABC$の外心を$H$とし、直線$AH$が
$\triangle ABC$の外接円と交わる点のうち、
点$A$とは異なる点を$P$とする。
このとき、$\overrightarrow{AP}=\dfrac{\boxed{ス}}{\boxed{セ}}\overrightarrow{AB}+\dfrac{\boxed{ソ}}{\boxed{タ}}\overrightarrow{AC}$である。
(2)$\triangle ABC$において$AB=5,AC=6,$
$\cos A=\dfrac{1}{5}$とする。
$\triangle ABC$の内心を$K$とし、
直線$AK$が$\triangle ABC$の内接円と
交わる点のうち、点$A$に近いほうの点を
$Q$とする。
このとき、$\overrightarrow{AQ}=\dfrac{\boxed{チ}-\sqrt{\boxed{ツ}}}{\boxed{テ}}\overrightarrow{AK}$である。
$2025$年早稲田大学人間科学部過去問題
この動画を見る
$\boxed{3}$
(1)$\triangle ABC$において$AB=6,AC=4,$
$\cos A=\dfrac{1}{4}$とする。
$\triangle ABC$の外心を$H$とし、直線$AH$が
$\triangle ABC$の外接円と交わる点のうち、
点$A$とは異なる点を$P$とする。
このとき、$\overrightarrow{AP}=\dfrac{\boxed{ス}}{\boxed{セ}}\overrightarrow{AB}+\dfrac{\boxed{ソ}}{\boxed{タ}}\overrightarrow{AC}$である。
(2)$\triangle ABC$において$AB=5,AC=6,$
$\cos A=\dfrac{1}{5}$とする。
$\triangle ABC$の内心を$K$とし、
直線$AK$が$\triangle ABC$の内接円と
交わる点のうち、点$A$に近いほうの点を
$Q$とする。
このとき、$\overrightarrow{AQ}=\dfrac{\boxed{チ}-\sqrt{\boxed{ツ}}}{\boxed{テ}}\overrightarrow{AK}$である。
$2025$年早稲田大学人間科学部過去問題



