ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
大学入試問題#740「解き方色々」 東京医科大学(2024) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-2}^{1} (x+2)(x-1)^7 dx$
出典：2024年東京医科大学 入試問題
この動画を見る
$\displaystyle \int_{-2}^{1} (x+2)(x-1)^7 dx$
出典：2024年東京医科大学 入試問題
東京都立大学 2023年 #定積分 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京都立大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2\pi} 2\theta\ \sin^2\theta\ d\theta$
出典：2023年東京都立大学
この動画を見る
$\displaystyle \int_{0}^{2\pi} 2\theta\ \sin^2\theta\ d\theta$
出典：2023年東京都立大学
大学入試問題#739「このタイプ、定期的に難関大学で出題されてる」 早稲田大学国際教養学部(2005)三角関数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\sin\ x+\sin\ y=\displaystyle \frac{2}{3},\ \cos\ x\ \cos\ y=\displaystyle \frac{1}{2}$のとき、
$\sin\ x\sin\ y,\ \sin\displaystyle \frac{x+y}{2}$の値を求めよ。
出典：2005年早稲田大学国際教養学部 入試問題
この動画を見る
$\sin\ x+\sin\ y=\displaystyle \frac{2}{3},\ \cos\ x\ \cos\ y=\displaystyle \frac{1}{2}$のとき、
$\sin\ x\sin\ y,\ \sin\displaystyle \frac{x+y}{2}$の値を求めよ。
出典：2005年早稲田大学国際教養学部 入試問題
大学入試問題#738「これはガチ良問！」 藤田医科大学(2024) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-5}^{7} \sqrt{ x^4+2x^3-3x^2-4x+4 }\ dx$
出典：2024年藤田医科大学 入試問題
この動画を見る
$\displaystyle \int_{-5}^{7} \sqrt{ x^4+2x^3-3x^2-4x+4 }\ dx$
出典：2024年藤田医科大学 入試問題
大学入試問題#737「もはや三角関数の問題」 早稲田大学人間科学部(2001)定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\sin\ 15^{ \circ }}^{\cos\ 15^{ \circ }} (3x^2-1) dx$
出典：2001年早稲田大学人間科学部 入試問題
この動画を見る
$\displaystyle \int_{\sin\ 15^{ \circ }}^{\cos\ 15^{ \circ }} (3x^2-1) dx$
出典：2001年早稲田大学人間科学部 入試問題
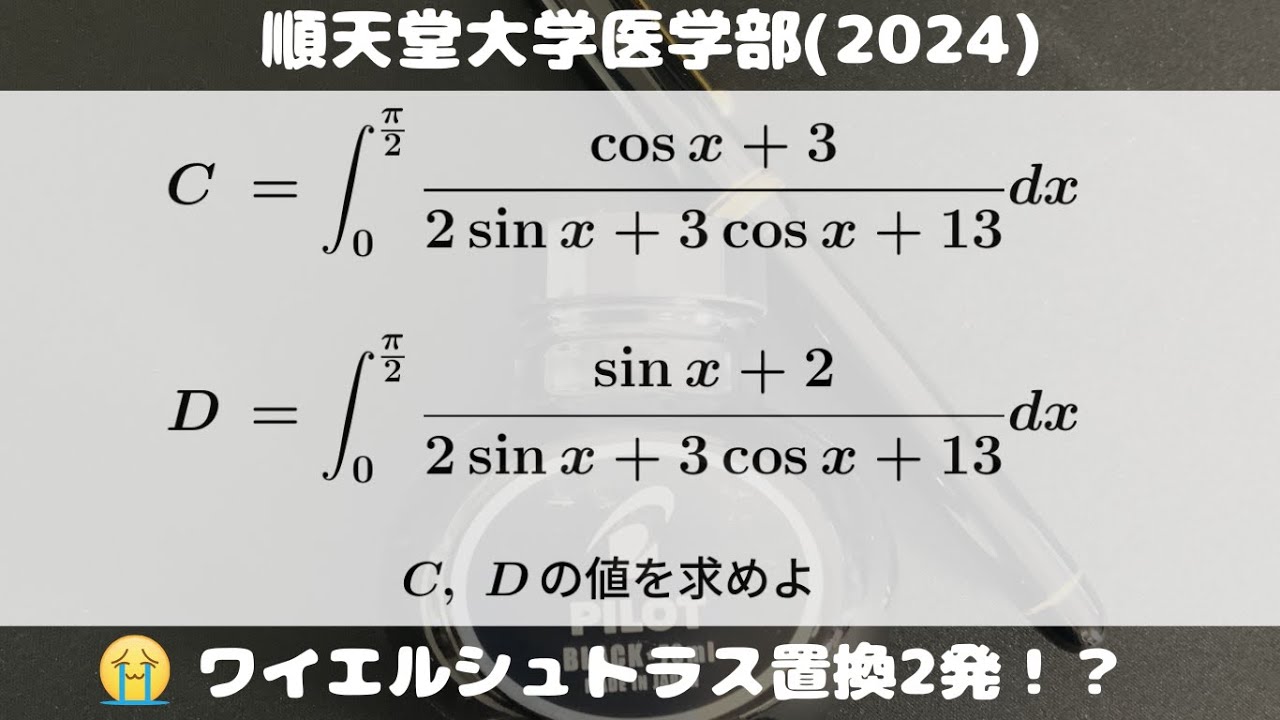
大学入試問題#736「茶番積分」 順天堂大学医学部(2024) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#順天堂大学
指導講師：
ますただ
問題文全文(内容文)：
$C=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos\ x+3}{2\sin\ x+3\cos\ x+13} dx$
$D=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x+2}{2\sin\ x+3\cos\ x+13} dx$
$C,D$の値を求めよ。
出典：2024年順天堂大学医学部 入試問題
この動画を見る
$C=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\cos\ x+3}{2\sin\ x+3\cos\ x+13} dx$
$D=\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin\ x+2}{2\sin\ x+3\cos\ x+13} dx$
$C,D$の値を求めよ。
出典：2024年順天堂大学医学部 入試問題
大学入試問題#735「因数分解だからと舐めプ厳禁」 関西医科大学(2016)因数分解
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$x(x+9)(x-4)(x-13)+2016$を因数分解せよ
出典：2016年関西医科大学 入試問題
この動画を見る
$x(x+9)(x-4)(x-13)+2016$を因数分解せよ
出典：2016年関西医科大学 入試問題
大学入試問題#734「落とせん！！」 東海大学医学部(2004) 不定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{2x+1}{x(x-1)^2}dx$
出典：2004年東海大学医学部 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{2x+1}{x(x-1)^2}dx$
出典：2004年東海大学医学部 入試問題
大学入試問題#733「教科書の章末問題」 東海大学医学部(2021) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{\sqrt{ \sqrt{ e }-1 }}^{\sqrt{ e^2-1 }} \displaystyle \frac{x\ log(log(x^2+1))}{x^2+1} dx$
出典：2021年東海大学医学部 入試問題
この動画を見る
$\displaystyle \int_{\sqrt{ \sqrt{ e }-1 }}^{\sqrt{ e^2-1 }} \displaystyle \frac{x\ log(log(x^2+1))}{x^2+1} dx$
出典：2021年東海大学医学部 入試問題
大学入試問題#732「まあ面白い良問！」 早稲田大学人間科学部(2022) 級数
単元：
#関数と極限#数列の極限#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
自然数$n$に対して、
$S_n=\displaystyle \int_{e^{n-1}}^{e^n} \displaystyle \frac{\sin(\pi\ log\ x)}{x^2} dx$とする。
さらに $T=\displaystyle \sum_{n=1}^\infty S_n$とする。
以下の問いに答えよ。
（1）$S_1$を求めよ。
（2）$\displaystyle \frac{S_{n+1}}{S_n}$を求めよ。
（3）$T$を求めよ。
出典：2022年早稲田大学人間科学部 入試問題
この動画を見る
自然数$n$に対して、
$S_n=\displaystyle \int_{e^{n-1}}^{e^n} \displaystyle \frac{\sin(\pi\ log\ x)}{x^2} dx$とする。
さらに $T=\displaystyle \sum_{n=1}^\infty S_n$とする。
以下の問いに答えよ。
（1）$S_1$を求めよ。
（2）$\displaystyle \frac{S_{n+1}}{S_n}$を求めよ。
（3）$T$を求めよ。
出典：2022年早稲田大学人間科学部 入試問題
大学入試問題#731「手を動かす前に読みをいれる」 東京慈恵会医科大学(2004) 定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\theta$は$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$かつ$\tan\theta=2$を満たすとする。
$\displaystyle \int_{\frac{\pi}{4}}^{\theta} \displaystyle \frac{dx}{\sin^4x}$
出典：2004年東京慈恵医科大学 入試問題
この動画を見る
$\theta$は$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$かつ$\tan\theta=2$を満たすとする。
$\displaystyle \int_{\frac{\pi}{4}}^{\theta} \displaystyle \frac{dx}{\sin^4x}$
出典：2004年東京慈恵医科大学 入試問題
楕円の性質 by にっし~Diaryさん #Shorts
単元：
#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
曲線$C:3x^2+4y^2=12$がある。
次の問いに答えよ。
（1）
点$P(1-\sqrt{ 3 },(3+\sqrt{ 3 }/2))$から曲線$C$に2本の接線が引ける。
2つの接点の座標を求めよ。
（2）
原点を$O$とする。
（1）の2つの接点のうち、$x$座標が小さいものから順番に点$A,$点$B$とするとき、曲線$C$と直線$OA$、直線$OB$で囲まれた図形$D$の面積を求めよ。
（3）
（2）の図形$D$を$x$軸を中心に一回転してできる立体の体積$V$を求めよ。
この動画を見る
曲線$C:3x^2+4y^2=12$がある。
次の問いに答えよ。
（1）
点$P(1-\sqrt{ 3 },(3+\sqrt{ 3 }/2))$から曲線$C$に2本の接線が引ける。
2つの接点の座標を求めよ。
（2）
原点を$O$とする。
（1）の2つの接点のうち、$x$座標が小さいものから順番に点$A,$点$B$とするとき、曲線$C$と直線$OA$、直線$OB$で囲まれた図形$D$の面積を求めよ。
（3）
（2）の図形$D$を$x$軸を中心に一回転してできる立体の体積$V$を求めよ。
大学入試問題#730「総和と間違えそう」 早稲田大学商学部(2011) 個数の処理
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$n$を正の整数とする。
$10^n$の正の約数すべての積の値を求めよ。
出典：2011年早稲田大学商学部 入試問題
この動画を見る
$n$を正の整数とする。
$10^n$の正の約数すべての積の値を求めよ。
出典：2011年早稲田大学商学部 入試問題
大学入試問題#729「医学部なら落とせん」 関西医科大学(2021) 整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$x^2-|x|y+y^2=3$を満たす整数の組$(x,y)$をすべて求めよ。
出典：2021年関西医科大学 入試問題
この動画を見る
$x^2-|x|y+y^2=3$を満たす整数の組$(x,y)$をすべて求めよ。
出典：2021年関西医科大学 入試問題
数列 by ハルハルさん すげー解答: 英語orドイツ語さん #Shorts
単元：
#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
ますただ
問題文全文(内容文)：
$a_1=0$
$a_{n+1}=(a_n+4)(a_n+10)$
この動画を見る
$a_1=0$
$a_{n+1}=(a_n+4)(a_n+10)$
大学入試問題#728「たぶん良問」 早稲田大学商学部(2014) 積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
任意の実数$x$に対して、
$\displaystyle \int_{0}^{x} f(t) dt-3\displaystyle \int_{-x}^{0} f(t) dt=x^3$を満たす関数$f(x)$を求めよ
出典：2014年早稲田大学商学部 入試問題
この動画を見る
任意の実数$x$に対して、
$\displaystyle \int_{0}^{x} f(t) dt-3\displaystyle \int_{-x}^{0} f(t) dt=x^3$を満たす関数$f(x)$を求めよ
出典：2014年早稲田大学商学部 入試問題
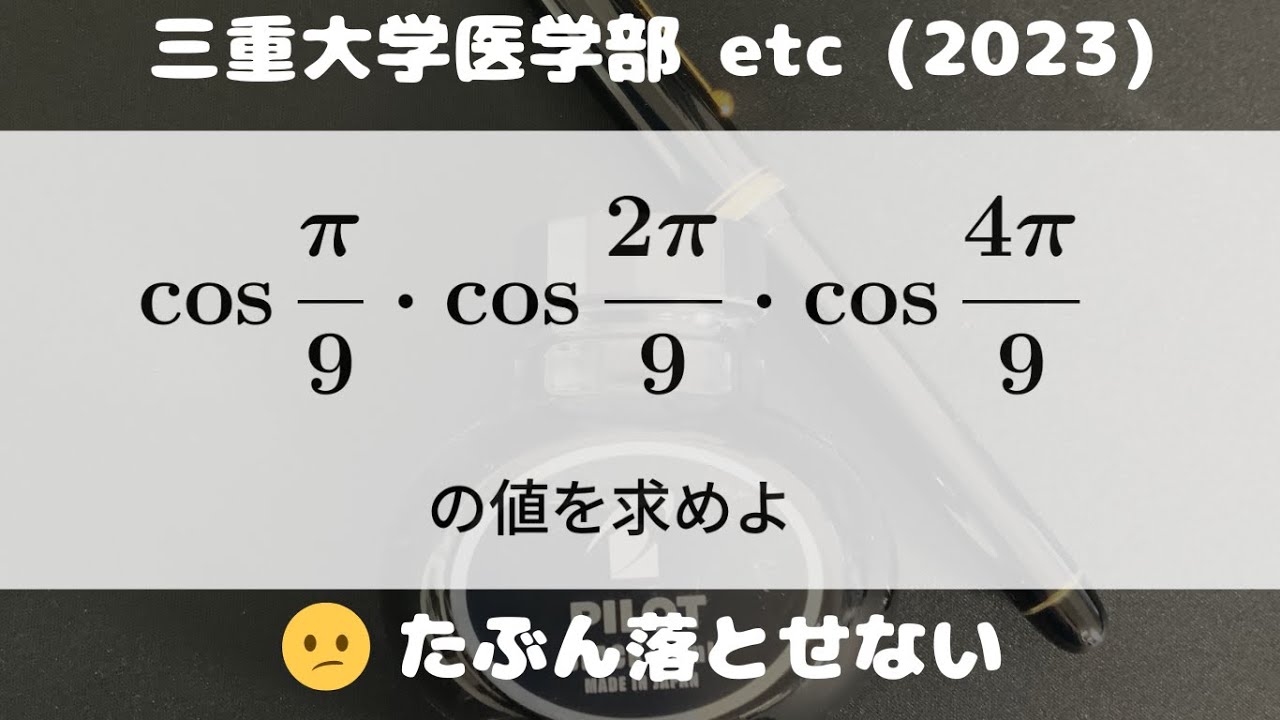
大学入試問題#727 三重大学医学部etc (2023) 三角関数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学
指導講師：
ますただ
問題文全文(内容文)：
$\cos\displaystyle \frac{\pi}{9}・\cos\displaystyle \frac{2\pi}{9}・\cos\displaystyle \frac{4\pi}{9}$の値を求めよ
出典：2023年三重大学医学部 入試問題
この動画を見る
$\cos\displaystyle \frac{\pi}{9}・\cos\displaystyle \frac{2\pi}{9}・\cos\displaystyle \frac{4\pi}{9}$の値を求めよ
出典：2023年三重大学医学部 入試問題
大学入試問題#726「一橋レベルでこれは落とせん」 一橋大学(2021)積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)$は微分可能かつ導関数が連続な関数とする。
$f(0)=0$であるとき、
$\displaystyle \frac{d}{dx}(\displaystyle \int_{0}^{x} e^{-t}f(x-t)dt)=\displaystyle \int_{0}^{x} e^{-t}f'(x-t)dt$ を示せ
出典：2021年一橋大学後期 入試問題
この動画を見る
$f(x)$は微分可能かつ導関数が連続な関数とする。
$f(0)=0$であるとき、
$\displaystyle \frac{d}{dx}(\displaystyle \int_{0}^{x} e^{-t}f(x-t)dt)=\displaystyle \int_{0}^{x} e^{-t}f'(x-t)dt$ を示せ
出典：2021年一橋大学後期 入試問題
関西大学 2011
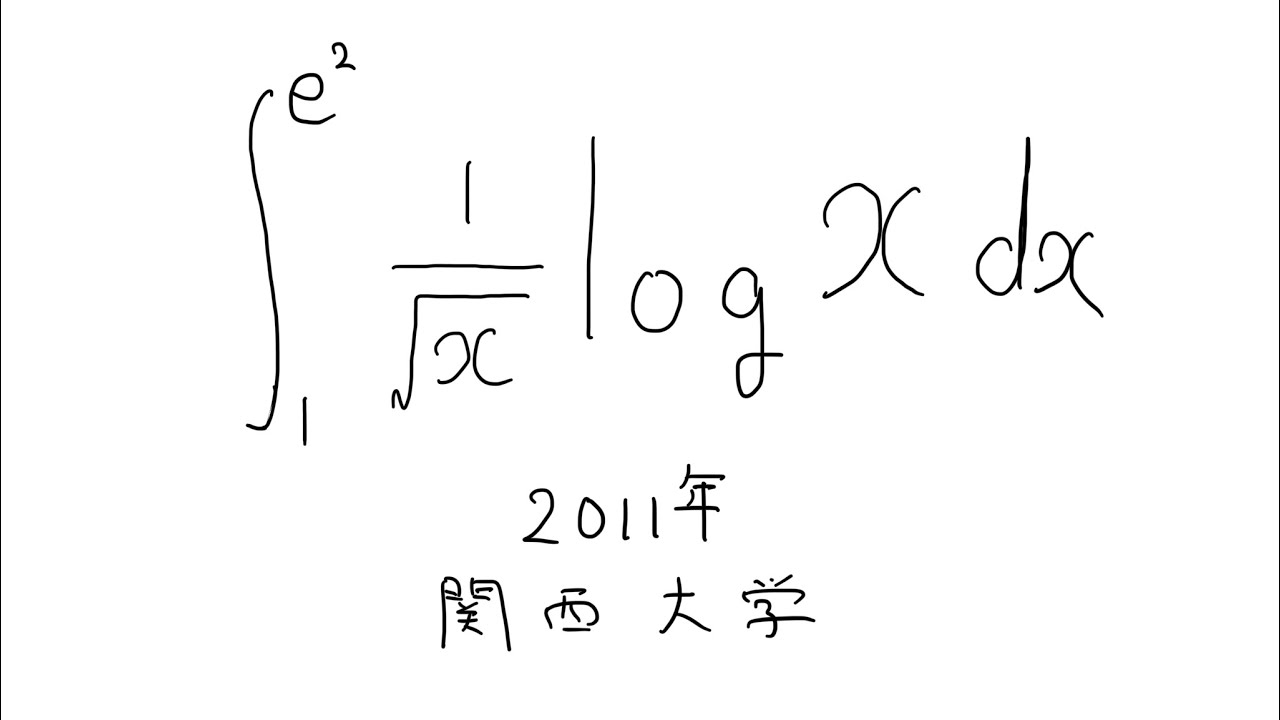
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{e^2} \displaystyle \frac{1}{\sqrt{ x }} log_x\ dx$
出典：2011年関西大学
この動画を見る
$\displaystyle \int_{1}^{e^2} \displaystyle \frac{1}{\sqrt{ x }} log_x\ dx$
出典：2011年関西大学
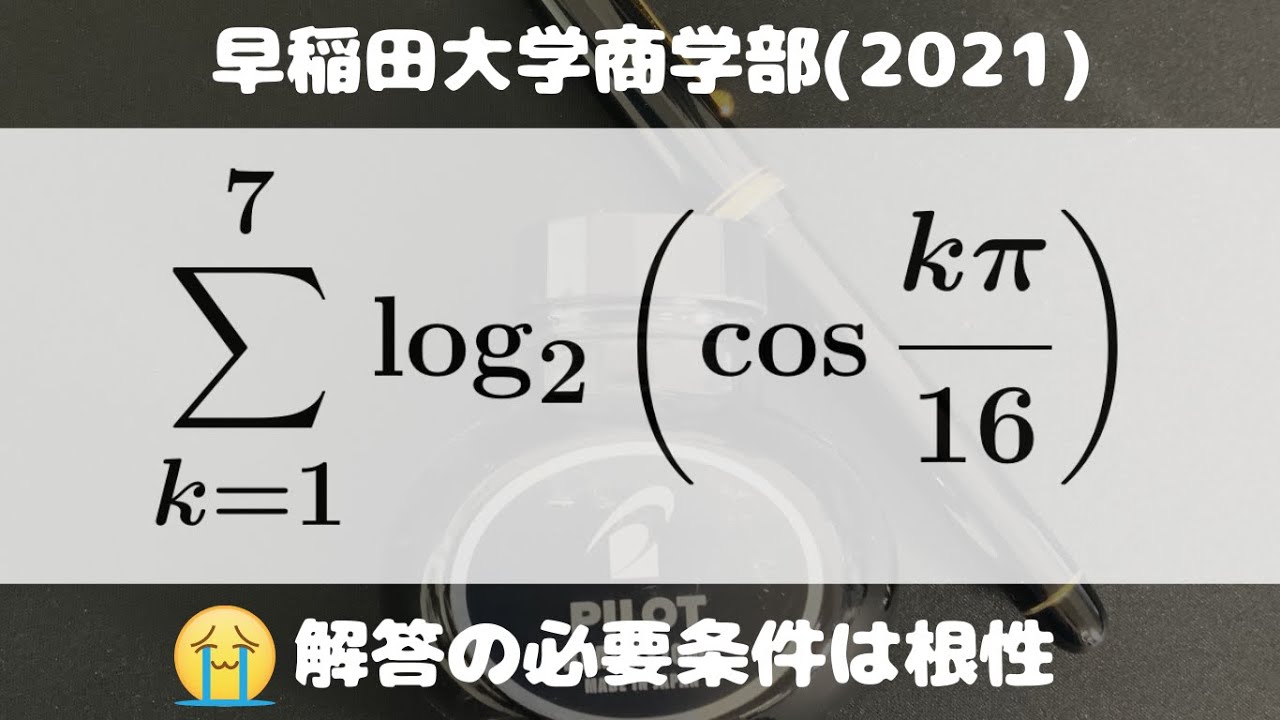
大学入試問題#725「計算ミスだけ注意」 早稲田商学部(2015) 対数と三角関数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \sum_{k=1}^7 log_2(\cos\displaystyle \frac{k\pi}{16})$
出典：2021年早稲田大学商学部 入試問題
この動画を見る
$\displaystyle \sum_{k=1}^7 log_2(\cos\displaystyle \frac{k\pi}{16})$
出典：2021年早稲田大学商学部 入試問題
大学入試問題#724「教科書の例題」 千葉大学(2023) 積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=x^2+\displaystyle \int_{-1}^{2} (xf(t)-t)dt$を満たす関数$f(x)$を求めよ
出典：2023年千葉大学 入試問題
この動画を見る
$f(x)=x^2+\displaystyle \int_{-1}^{2} (xf(t)-t)dt$を満たす関数$f(x)$を求めよ
出典：2023年千葉大学 入試問題
大学入試問題#723「いつもとタイプが違う」 一橋大学(2023)整数問題
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ m }+\sqrt{ n }=\sqrt{ 2023 }$を満たす自然数の組$(m,n)$の個数を求めよ。
出典：2023年一橋大学後期 入試問題
この動画を見る
$\sqrt{ m }+\sqrt{ n }=\sqrt{ 2023 }$を満たす自然数の組$(m,n)$の個数を求めよ。
出典：2023年一橋大学後期 入試問題
大学入試問題#722「これはミスれん！」 千葉大学(2023)定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{a}^{b} (x-a)^3(x-b) dx$
ただし、$a,b$は定数とする
出典：2023年千葉大学
この動画を見る
$\displaystyle \int_{a}^{b} (x-a)^3(x-b) dx$
ただし、$a,b$は定数とする
出典：2023年千葉大学
関西医科大学 2011 極限
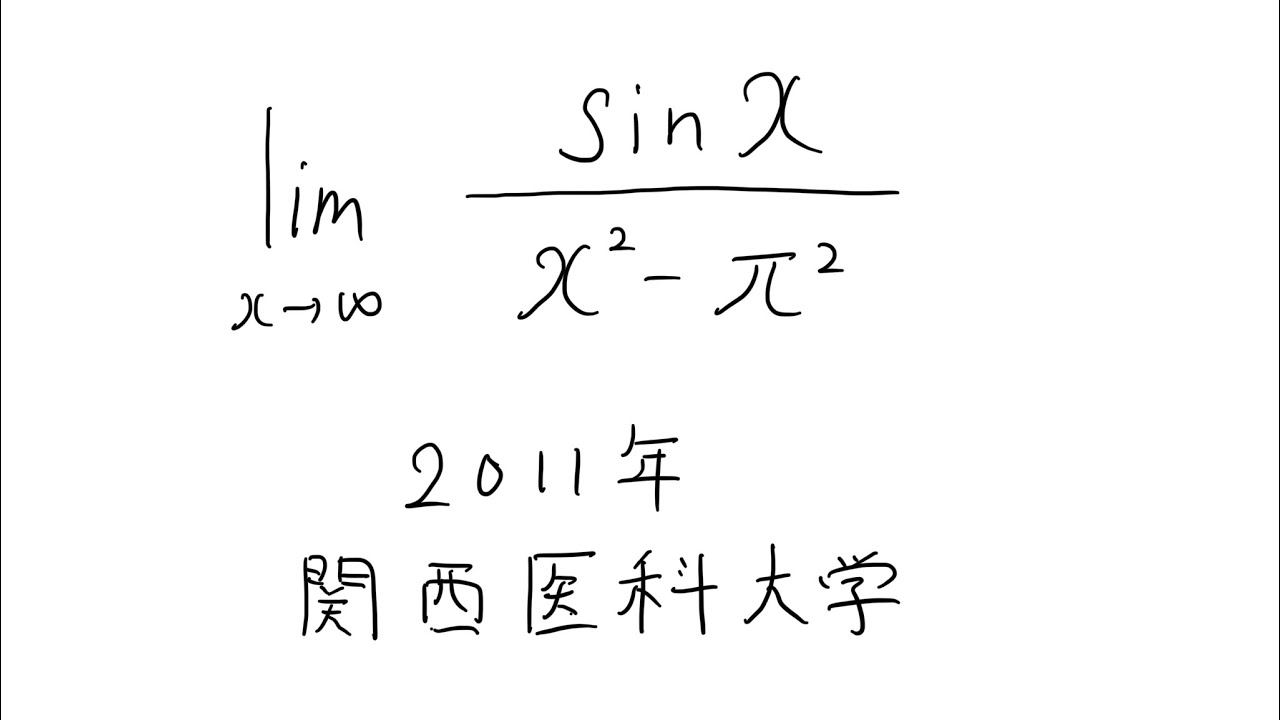
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to \pi } \displaystyle \frac{\sin\ x}{x^2-\pi^2}$
出典：2011年関西医科大学
この動画を見る
$\displaystyle \lim_{ x \to \pi } \displaystyle \frac{\sin\ x}{x^2-\pi^2}$
出典：2011年関西医科大学
大学入試問題#721「落ち着いて計算」 早稲田商学部(2012) 積分方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
定数関数でない関数$f(x)$が
$f(x)=x^2-\displaystyle \int_{0}^{1}(f(t)+x)^2 dt$を満たすとき$f(x)$を求めよ。
出典：2012年早稲田大学商学部 入試問題
この動画を見る
定数関数でない関数$f(x)$が
$f(x)=x^2-\displaystyle \int_{0}^{1}(f(t)+x)^2 dt$を満たすとき$f(x)$を求めよ。
出典：2012年早稲田大学商学部 入試問題
大学入試問題#720「正面突破はしんどい？」 電気通信大学(2023) y軸回転体
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#東京電機大学
指導講師：
ますただ
問題文全文(内容文)：
$0 \leq x \leq 1$で定まる関数
$f(x)=\sqrt{ 1-x^2 }+\displaystyle \frac{x}{2}-1$において、$y=f(x)$と$x$軸で囲まれた部分を、$y$軸の周りに1回転して得られる体積$V$を求めよ。
出典：2023年電気通信大学 入試問題
この動画を見る
$0 \leq x \leq 1$で定まる関数
$f(x)=\sqrt{ 1-x^2 }+\displaystyle \frac{x}{2}-1$において、$y=f(x)$と$x$軸で囲まれた部分を、$y$軸の周りに1回転して得られる体積$V$を求めよ。
出典：2023年電気通信大学 入試問題
大学入試問題#719「これは落としたくない」 早稲田大学商学部(2005) 3次方程式
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
3次方程式
$x^3-px^2+11x-q=0$が3つの連続する正の整数を解とするとき、$p,q$の値を求めよ。
出典：2005年早稲田大学商学部 入試問題
この動画を見る
3次方程式
$x^3-px^2+11x-q=0$が3つの連続する正の整数を解とするとき、$p,q$の値を求めよ。
出典：2005年早稲田大学商学部 入試問題
大学入試問題#718「理系の偏差値63ではきつい」 早稲田商学部(2011) 微積の応用
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=\displaystyle \int_{0}^{1} |t^2-x^2|dt$の最小値を求めよ。
出典：2011年早稲田大学商学部 入試問題
この動画を見る
$f(x)=\displaystyle \int_{0}^{1} |t^2-x^2|dt$の最小値を求めよ。
出典：2011年早稲田大学商学部 入試問題
昭和大学医学部 2018年 区分求積法 #Shorts
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n (\displaystyle \frac{\sqrt{ n }}{n+k})^2$
出典：2018年昭和大学医学部
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n (\displaystyle \frac{\sqrt{ n }}{n+k})^2$
出典：2018年昭和大学医学部
大学入試問題#717「これはよく考えられた問題だな～～」 早稲田商学部(2012) 対数
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$log_3\ x-\displaystyle \frac{1}{log_9\ x}=(-1)^x$を満たす正の整数$x$の値を求めよ。
出典：2012年早稲田大学商学部 入試問題
この動画を見る
$log_3\ x-\displaystyle \frac{1}{log_9\ x}=(-1)^x$を満たす正の整数$x$の値を求めよ。
出典：2012年早稲田大学商学部 入試問題