ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
大学入試問題をベースに数学の動画を作成しています。大学過去問を多数解説しています。
頻繁に更新していますので是非ご視聴ください！
職業：数学者
職歴：高校非常勤（院生時代）、高専、大学 准教授
趣味：
①将棋 棋力は将棋ウォーズ４段、将棋倶楽部２４はR２０００前後（小学校５，６年のころに頑張ってました）
②麻雀 アカウントは消えましたが、無課金で天鵬で７段まで上がりました。
③ソフトテニス 中学から大学まで、１０年間部活でやっていました。大学時代は４年になってもリーグにでていました。
大学入試問題#260 慶應義塾大学 改 (2011) #定積分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2}8(x+1)\sqrt{ 4x+1 }\ dx$を計算せよ。
出典：2011年慶應義塾大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2}8(x+1)\sqrt{ 4x+1 }\ dx$を計算せよ。
出典：2011年慶應義塾大学 入試問題
大学入試問題#259 島根大学(2012) #微分
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学
指導講師：
ますただ
問題文全文(内容文)：
$f(x)=|x|\sin\ x$の$x=0$における微分可能性を調べよ。
出典：2012年島根大学 入試問題
この動画を見る
$f(x)=|x|\sin\ x$の$x=0$における微分可能性を調べよ。
出典：2012年島根大学 入試問題
大学入試問題#258 東京理科大学(2011) #定積分 #面積
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$y-\tan\ x(0 \leqq x \lt \displaystyle \frac{\pi}{2})$
$y-\cos\ x(0 \leqq x \leqq \displaystyle \frac{\pi}{2})$
$x$軸で囲まれた部分の面積を求めよ。
出典：2011年東京理科大学 入試問題
この動画を見る
$y-\tan\ x(0 \leqq x \lt \displaystyle \frac{\pi}{2})$
$y-\cos\ x(0 \leqq x \leqq \displaystyle \frac{\pi}{2})$
$x$軸で囲まれた部分の面積を求めよ。
出典：2011年東京理科大学 入試問題
AkiyaMathさんと学ぶ積分計算 Level 1 #定積分
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-\frac{1}{2}}^{\frac{3}{2}}\displaystyle \frac{dx}{x^3-3x+2}$を計算せよ
この動画を見る
$\displaystyle \int_{-\frac{1}{2}}^{\frac{3}{2}}\displaystyle \frac{dx}{x^3-3x+2}$を計算せよ
大学入試問題#257 東京理科大学(2011) #極限 #区分求積法
単元：
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{k}{n^2}log(\displaystyle \frac{n+k}{n})$を求めよ。
出典：2011年東京理科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{k}{n^2}log(\displaystyle \frac{n+k}{n})$を求めよ。
出典：2011年東京理科大学 入試問題
【誘導あり：概要欄】大学入試問題#256 神戸大学2012 #極限 #はさみうちの定理
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
（1）
$2 \leqq k$：自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
（2）
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典：2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
（1）
$2 \leqq k$：自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
（2）
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典：2012年神戸大学 入試問題
ハルハル様の作成問題③ #複素数
単元：
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$z$：複素数
$a$：実数
$2Z^2+3|Z|Z=a$を解け
この動画を見る
$z$：複素数
$a$：実数
$2Z^2+3|Z|Z=a$を解け
大学入試問題#254 神戸大学2012 #定積分
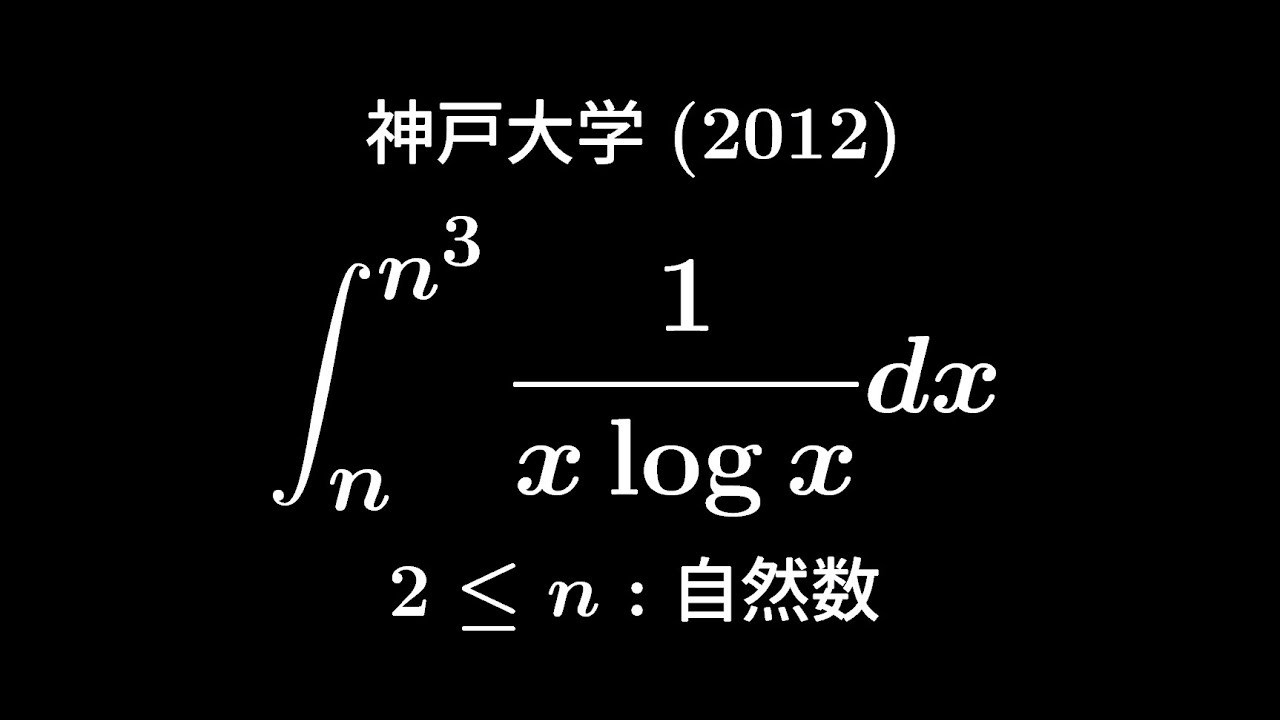
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典：2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典：2012年神戸大学 入試問題
大学入試問題#253 青山学院大学(2011) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典：2011年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典：2011年青山学院大学 入試問題
大学入試問題#252 茨城大学(2012) #定積分
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典：2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典：2012年茨城大学 入試問題
大学入試問題#251 新潟大学(2012) #相加相乗平均
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学
指導講師：
ますただ
問題文全文(内容文)：
$a,b,c,d$：正の実数
$\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[ 4 ]{ abcd }$を示せ
出典：2012年新潟大学 入試問題
この動画を見る
$a,b,c,d$：正の実数
$\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[ 4 ]{ abcd }$を示せ
出典：2012年新潟大学 入試問題
大学入試問題#250 福井大学(2012) #定積分
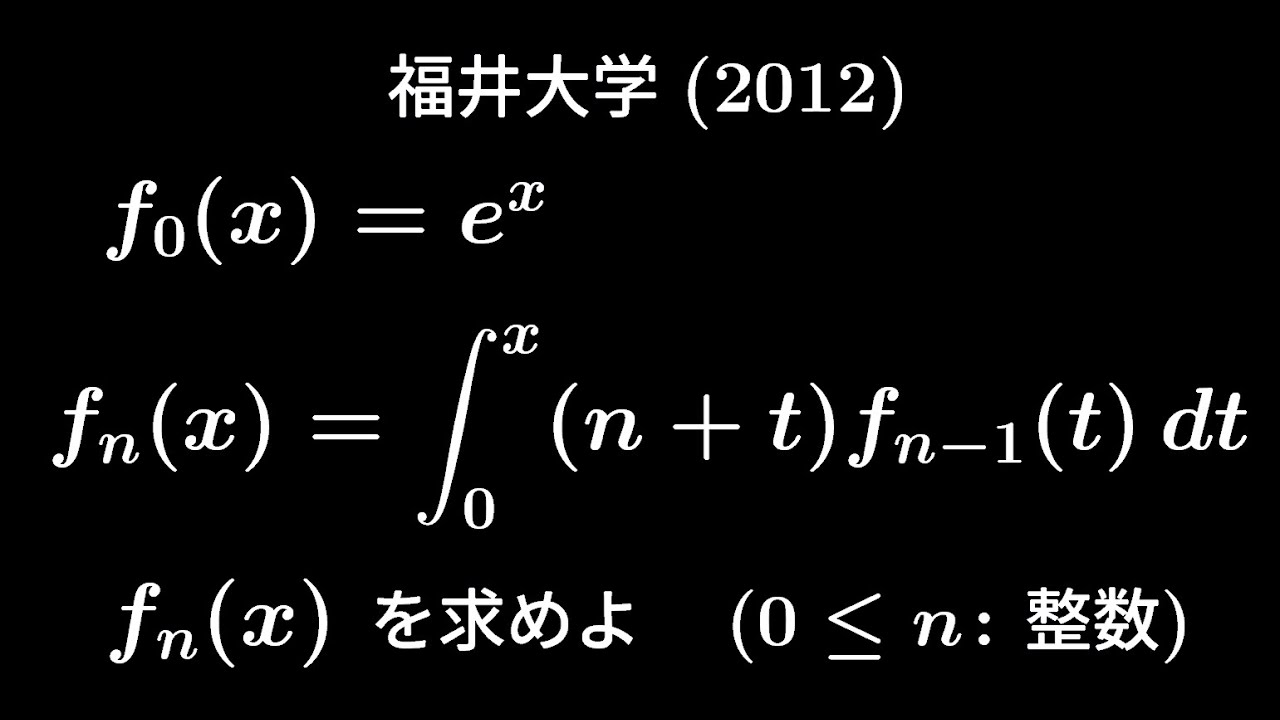
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#数列#漸化式#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
（ⅰ）$f_0(x)=e^x$
（ⅱ）$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典：2012年福井大学 入試問題
この動画を見る
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
（ⅰ）$f_0(x)=e^x$
（ⅱ）$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典：2012年福井大学 入試問題
AkiyaMath様の作成問題① 初コラボ #整数問題 #3次方程式の応用
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$k$：整数
3次方程式
$4x^3-(k+3)x+2k+1=0$の解になる2以上の有理数の総和を求めよ。
この動画を見る
$k$：整数
3次方程式
$4x^3-(k+3)x+2k+1=0$の解になる2以上の有理数の総和を求めよ。
大学入試問題#249 早稲田大学(2014) #定積分
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典：2014年早稲田大学 入試問題
この動画を見る
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典：2014年早稲田大学 入試問題
大学入試問題#248 慶應義塾大学(2014) #方程式
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x,y,z:0$でない整数
$\displaystyle \frac{1}{xy}+\displaystyle \frac{1}{yz}+\displaystyle \frac{1}{zx}=\displaystyle \frac{1}{xy+yz+zx}$
$2^{x+1}=\displaystyle \frac{5^{2y}}{10^{z+1}}$
をみたすとき$x,y,z$の値を求めよ。
出典：2014年慶應義塾大学 入試問題
この動画を見る
$x,y,z:0$でない整数
$\displaystyle \frac{1}{xy}+\displaystyle \frac{1}{yz}+\displaystyle \frac{1}{zx}=\displaystyle \frac{1}{xy+yz+zx}$
$2^{x+1}=\displaystyle \frac{5^{2y}}{10^{z+1}}$
をみたすとき$x,y,z$の値を求めよ。
出典：2014年慶應義塾大学 入試問題
大学入試問題#247 明治大学(2014) #極限
単元：
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ h \to 0 }\displaystyle \frac{log(1+5h+6h^2)}{h}$を求めよ。
出典：2014年明治大学 入試問題
この動画を見る
$\displaystyle \lim_{ h \to 0 }\displaystyle \frac{log(1+5h+6h^2)}{h}$を求めよ。
出典：2014年明治大学 入試問題
大学入試問題#246 津田塾大学(2014) #極限
単元：
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#津田塾大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{x(e^{3x}-1)}{1-\cos\ x}$を求めよ。
出典：2014年津田塾大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{x(e^{3x}-1)}{1-\cos\ x}$を求めよ。
出典：2014年津田塾大学 入試問題
大学入試問題#245 津田塾大学2014 #三角関数 基本的な問題ですが、数IIの範囲で解ける良問だと思いました。
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#津田塾大学
指導講師：
ますただ
問題文全文(内容文)：
$0 \leqq \theta \leqq 2\pi$
$\sin^3\theta+\cos^3\theta$の最大値、最小値を求めよ。
出典：2014年津田塾大学 入試問題
この動画を見る
$0 \leqq \theta \leqq 2\pi$
$\sin^3\theta+\cos^3\theta$の最大値、最小値を求めよ。
出典：2014年津田塾大学 入試問題
大学入試問題#244 南山大学(2014) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#南山大学
指導講師：
ますただ
問題文全文(内容文)：
$a$：正の定数
$\displaystyle \int_{-a}^{a}\displaystyle \frac{|x|e^x}{(1+e^x)^2}dx$を計算せよ
出典：2014年南山大学 入試問題
この動画を見る
$a$：正の定数
$\displaystyle \int_{-a}^{a}\displaystyle \frac{|x|e^x}{(1+e^x)^2}dx$を計算せよ
出典：2014年南山大学 入試問題
大学入試問題#243 慶應義塾大学(2014) #3次方程式の性質
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$k$：実数
$x^3-kx+1=0$は実数の重解とそれと異なる実数解をもつ
このとき$k$の値を求めよ。
出典：2014年慶應義塾大学 入試問題
この動画を見る
$k$：実数
$x^3-kx+1=0$は実数の重解とそれと異なる実数解をもつ
このとき$k$の値を求めよ。
出典：2014年慶應義塾大学 入試問題
大学入試問題#242 神戸大学(2015) 改 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ \sin\ x}{\cos^2x}$dxを計算せよ。
出典：2015年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ \sin\ x}{\cos^2x}$dxを計算せよ。
出典：2015年神戸大学 入試問題
大学入試問題#241 早稲田大学(2014) #指数
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
関数$f(x)=(27^x+\displaystyle \frac{1}{27^x})-5(9^x+\displaystyle \frac{1}{9^x})$
$-5(3^x+\displaystyle \frac{1}{3^x})+1$の最小値と、そのときの$x$の値を求めよ。
出典：2014年早稲田大学 入試問題
この動画を見る
関数$f(x)=(27^x+\displaystyle \frac{1}{27^x})-5(9^x+\displaystyle \frac{1}{9^x})$
$-5(3^x+\displaystyle \frac{1}{3^x})+1$の最小値と、そのときの$x$の値を求めよ。
出典：2014年早稲田大学 入試問題
大学入試問題#240 防衛医科大学(2020) #曲線の長さ
単元：
#大学入試過去問(数学)#微分とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師：
ますただ
問題文全文(内容文)：
$0 \leqq t \leqq \pi$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=3\cos\ t-\cos\ 3t \\
y=3\sin\ t-\sin\ 3t
\end{array}
\right.
\end{eqnarray}$
で表される曲線の長さを求めよ。
出典：2020年防衛医科大学 入試問題
この動画を見る
$0 \leqq t \leqq \pi$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=3\cos\ t-\cos\ 3t \\
y=3\sin\ t-\sin\ 3t
\end{array}
\right.
\end{eqnarray}$
で表される曲線の長さを求めよ。
出典：2020年防衛医科大学 入試問題
大学入試問題#239 弘前大学(2012) #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{1}^{3}(x-\displaystyle \frac{1}{x})(log\ x)^2dx$を計算せよ。
出典：2012年
この動画を見る
$\displaystyle \int_{1}^{3}(x-\displaystyle \frac{1}{x})(log\ x)^2dx$を計算せよ。
出典：2012年
【誘導有：概要欄】大学入試問題#238 首都大学東京(2012) #定積分
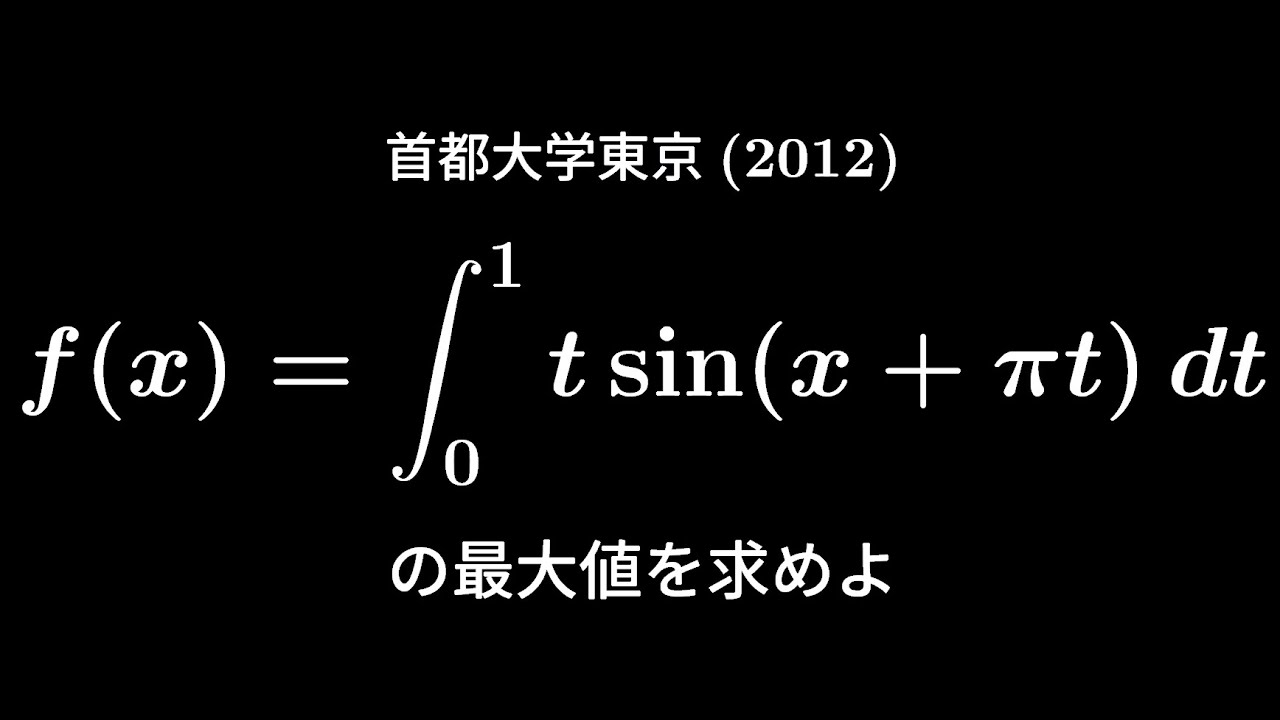
単元：
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
（1）
実数$x$に対して定積分$f(x)=\displaystyle \int_{0}^{1}t\ \sin(x+\pi t)dt$を求めよ。
（2）
関数$f(x)$の最大値を求めよ。
出典：2012年首都大学東京 入試問題
この動画を見る
（1）
実数$x$に対して定積分$f(x)=\displaystyle \int_{0}^{1}t\ \sin(x+\pi t)dt$を求めよ。
（2）
関数$f(x)$の最大値を求めよ。
出典：2012年首都大学東京 入試問題
大学入試問題#237 岡山県立大学(2020) #数学的帰納法
単元：
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B#岡山県立大学
指導講師：
ますただ
問題文全文(内容文)：
$(1+2+3+・・・+n)^2=1^3+2^3+3^3+・・・+n^3$が成り立つことを示せ。
$n$：自然数
2020年岡山県立大学 入試問題
この動画を見る
$(1+2+3+・・・+n)^2=1^3+2^3+3^3+・・・+n^3$が成り立つことを示せ。
$n$：自然数
2020年岡山県立大学 入試問題
大学入試問題#236 茨城大学(2012) 改 #不定積分
単元：
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int \displaystyle \frac{1}{x^2}(1+\displaystyle \frac{2}{x})^4dx$を計算せよ。
出典：2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x^2}(1+\displaystyle \frac{2}{x})^4dx$を計算せよ。
出典：2012年茨城大学 入試問題
大学入試問題#236 富山県立大学(2012) #背理法
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#富山県立大学
指導講師：
ますただ
問題文全文(内容文)：
$x^3-x^2+2x-1=0$の実数解は無理数であることを背理法を用いて示せ
出典：2012年富山県立大学 入試問題
この動画を見る
$x^3-x^2+2x-1=0$の実数解は無理数であることを背理法を用いて示せ
出典：2012年富山県立大学 入試問題
大学入試問題#235 自治医科大学(2014) 複素数
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#自治医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\omega=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$のとき
$\omega^{20}+\omega^{19}+\omega^8+\omega^6+\omega^4+\omega^3$の値を求めよ。
出典：2012年自治医科大学 入試問題
この動画を見る
$\omega=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$のとき
$\omega^{20}+\omega^{19}+\omega^8+\omega^6+\omega^4+\omega^3$の値を求めよ。
出典：2012年自治医科大学 入試問題
大学入試問題#234 東京理科大学 #定積分
単元：
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\frac{3}{4}\pi}\sqrt{ 1-\cos\ 4x }\ dx$
出典：2012年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{3}{4}\pi}\sqrt{ 1-\cos\ 4x }\ dx$
出典：2012年東京理科大学 入試問題