 ますただ
ますただ
 ますただ
ますただ
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
#山梨大学2013#定積分#ますただ
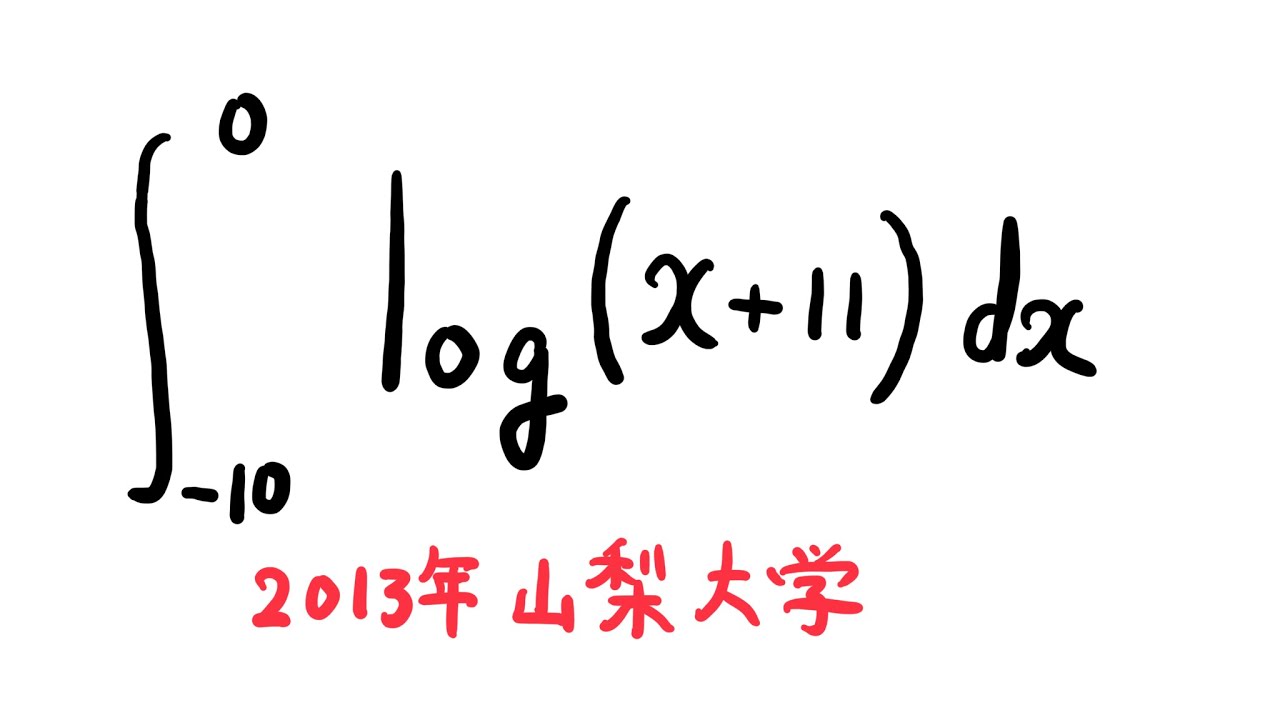
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-10}^{0} log(x+11)$ $dx$
出典:2013年山梨大学
この動画を見る
$\displaystyle \int_{-10}^{0} log(x+11)$ $dx$
出典:2013年山梨大学
#青山学院大学#定積分#ますただ
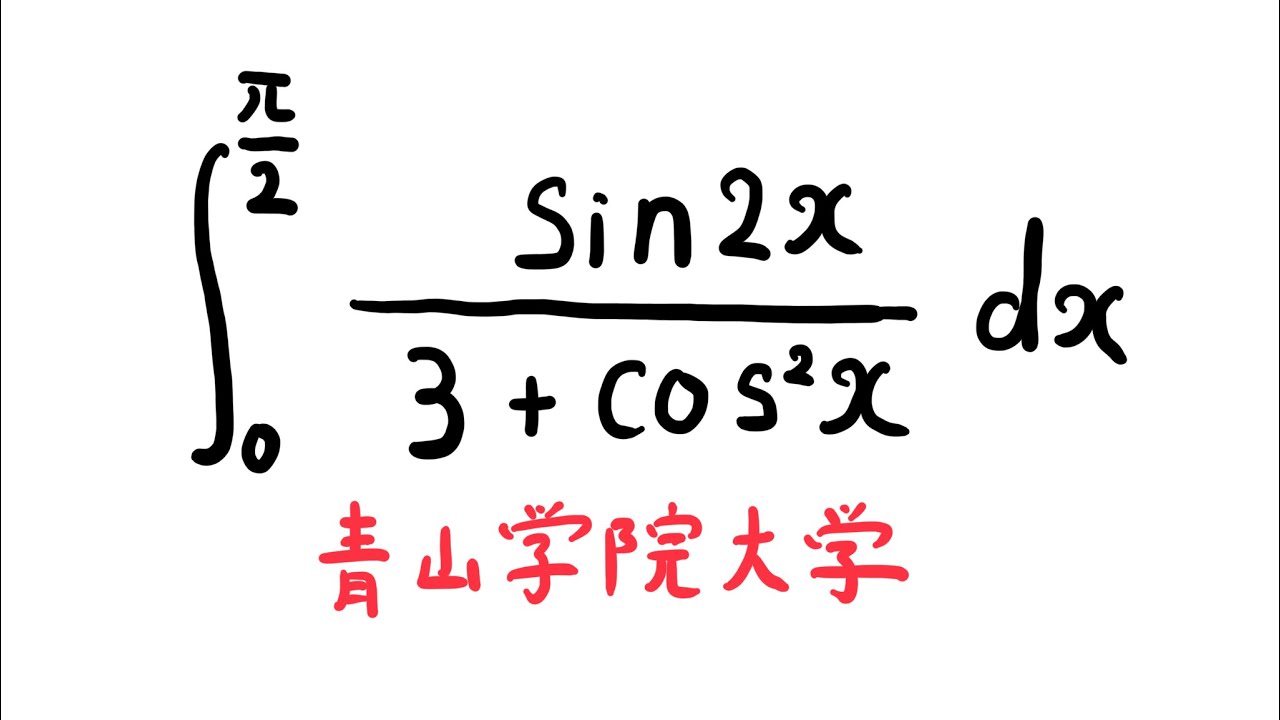
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin2x}{3+\cos^2x} dx$
出典:青山学院大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin2x}{3+\cos^2x} dx$
出典:青山学院大学
2024年6月28日
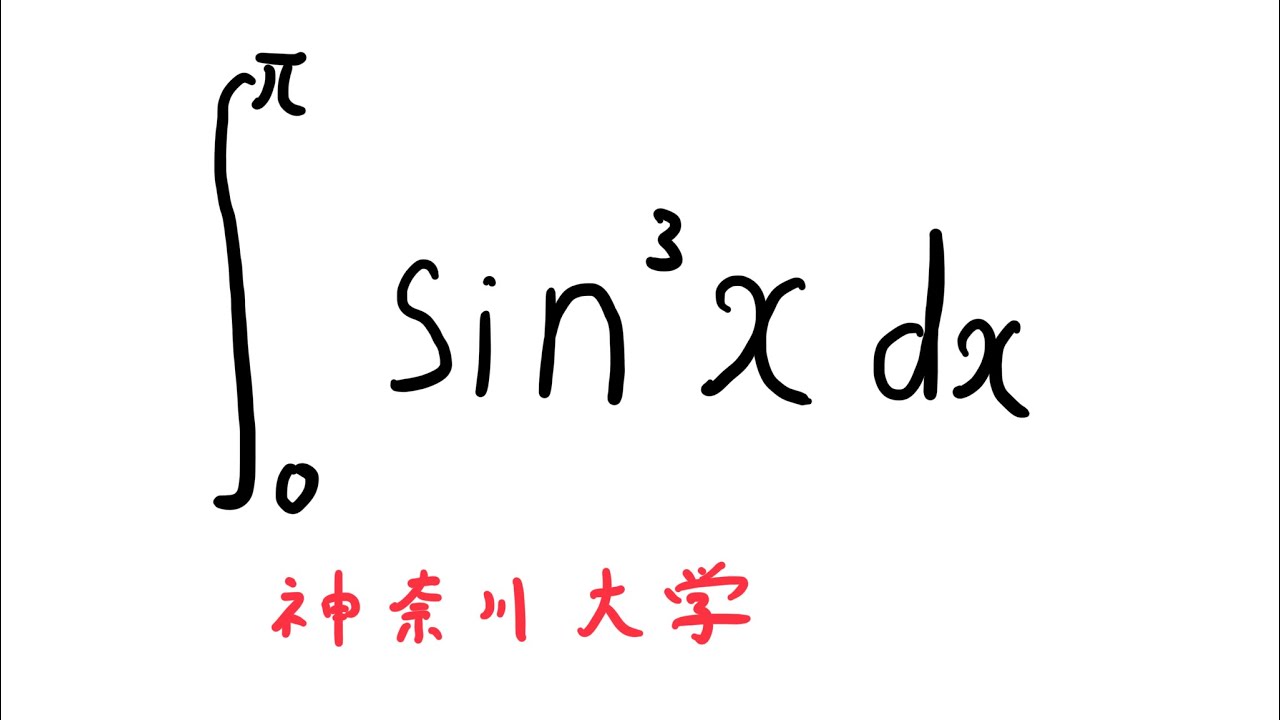
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神奈川大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} \sin^3x$ $dx$
出典:神奈川大学
この動画を見る
$\displaystyle \int_{0}^{\pi} \sin^3x$ $dx$
出典:神奈川大学
大学入試問題#880「基本の基本!」 #聖マリアンナ医科大学(2021) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#聖マリアンナ医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n,\sqrt{ n^2+2021 }$がともに自然数のとき、$n$の値をすべて求めよ。
$2021=43\times47$を利用してよい
出典:2021年聖マリアンナ医科大学
この動画を見る
$n,\sqrt{ n^2+2021 }$がともに自然数のとき、$n$の値をすべて求めよ。
$2021=43\times47$を利用してよい
出典:2021年聖マリアンナ医科大学
#玉川大学#不定積分#ますただ
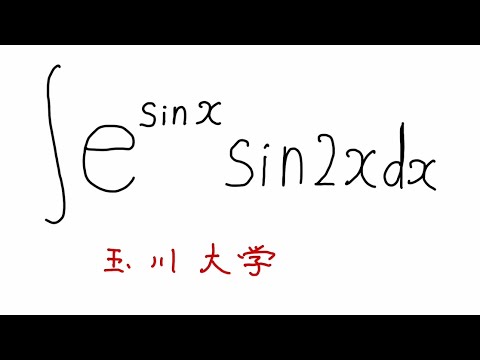
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け
$\displaystyle \int e^{\sin x} \sin2x$ $dx$
出典:玉川大学
この動画を見る
以下の不定積分を解け
$\displaystyle \int e^{\sin x} \sin2x$ $dx$
出典:玉川大学
#信州大学 #不定積分
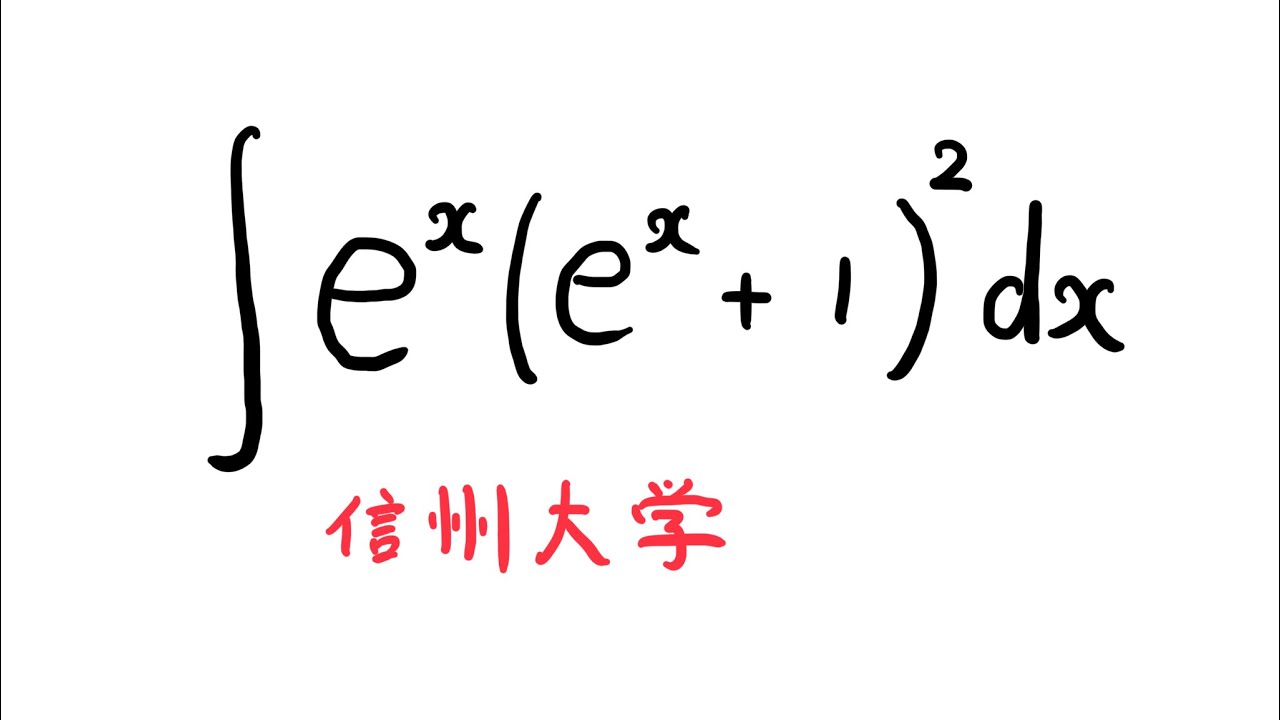
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け
$\displaystyle \int e^x(e^x+1)^2 dx$
出典:信州大学
この動画を見る
以下の不定積分を解け
$\displaystyle \int e^x(e^x+1)^2 dx$
出典:信州大学
#高知工科大学2020 #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高知工科大学
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{1}^{\sqrt{ e }} \displaystyle \frac{(log x)^3}{x} dx$
出典:2020年高知工科大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{1}^{\sqrt{ e }} \displaystyle \frac{(log x)^3}{x} dx$
出典:2020年高知工科大学
#藤田保健衛生大学2012 #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$a \gt 0,b \gt 0$
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{\{ax+b(1-x\}^2)} dx$
出典:2010年藤田保健衛生大学
この動画を見る
以下の定積分を解け。
$a \gt 0,b \gt 0$
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{\{ax+b(1-x\}^2)} dx$
出典:2010年藤田保健衛生大学
大学入試問題#873「コメント欄が賑わいそう」 #東京理科大学(2022) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{4} \displaystyle \frac{2}{(x+1)(x+2)(x+3)} dx$
出典:2022年東京理科大学 大学入試問題
この動画を見る
$\displaystyle \int_{0}^{4} \displaystyle \frac{2}{(x+1)(x+2)(x+3)} dx$
出典:2022年東京理科大学 大学入試問題
#自治医科大学2015 #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \{\sqrt{ (n+2)(n+3) }-\sqrt{ (n-2)(n-3) }\}$
出典:2015年自治医科大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \{\sqrt{ (n+2)(n+3) }-\sqrt{ (n-2)(n-3) }\}$
出典:2015年自治医科大学
#関西学院大学2012 #不定積分
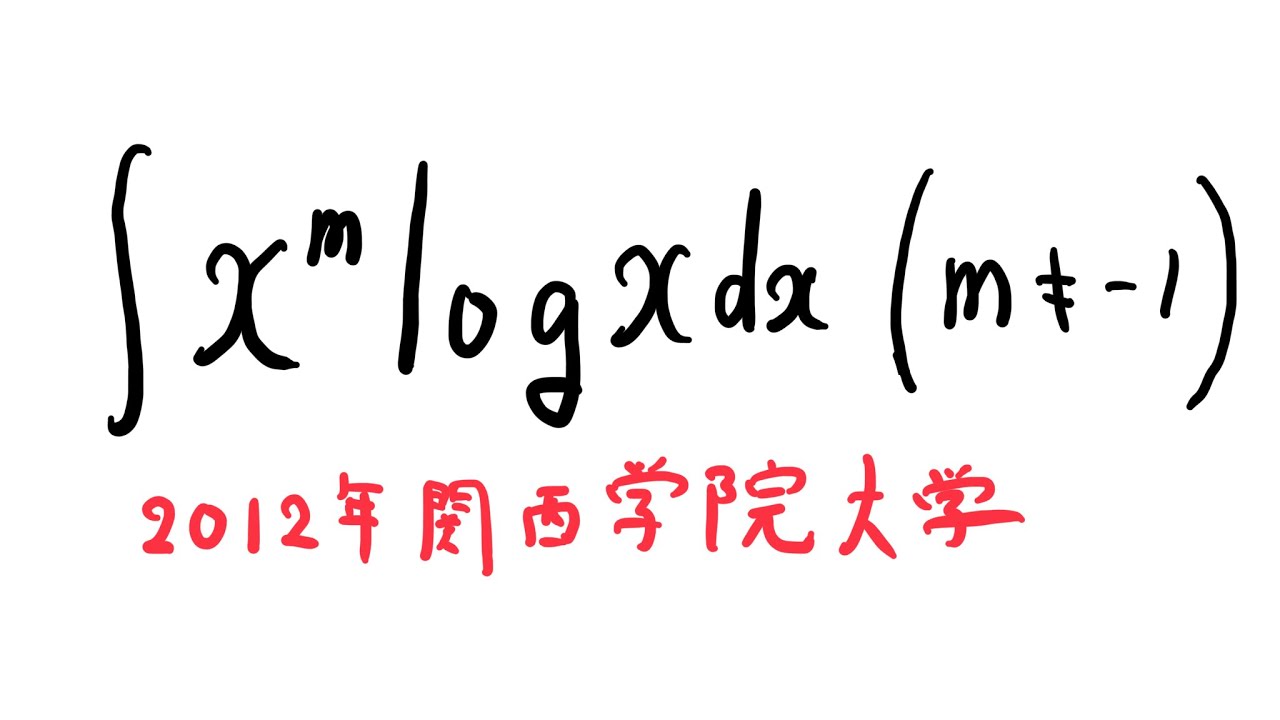
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x^m log$ $x$ $dx(m \neq -1)$
出典:2012年関西学院大学
この動画を見る
$\displaystyle \int x^m log$ $x$ $dx(m \neq -1)$
出典:2012年関西学院大学
#関西大学2012 #三角関数
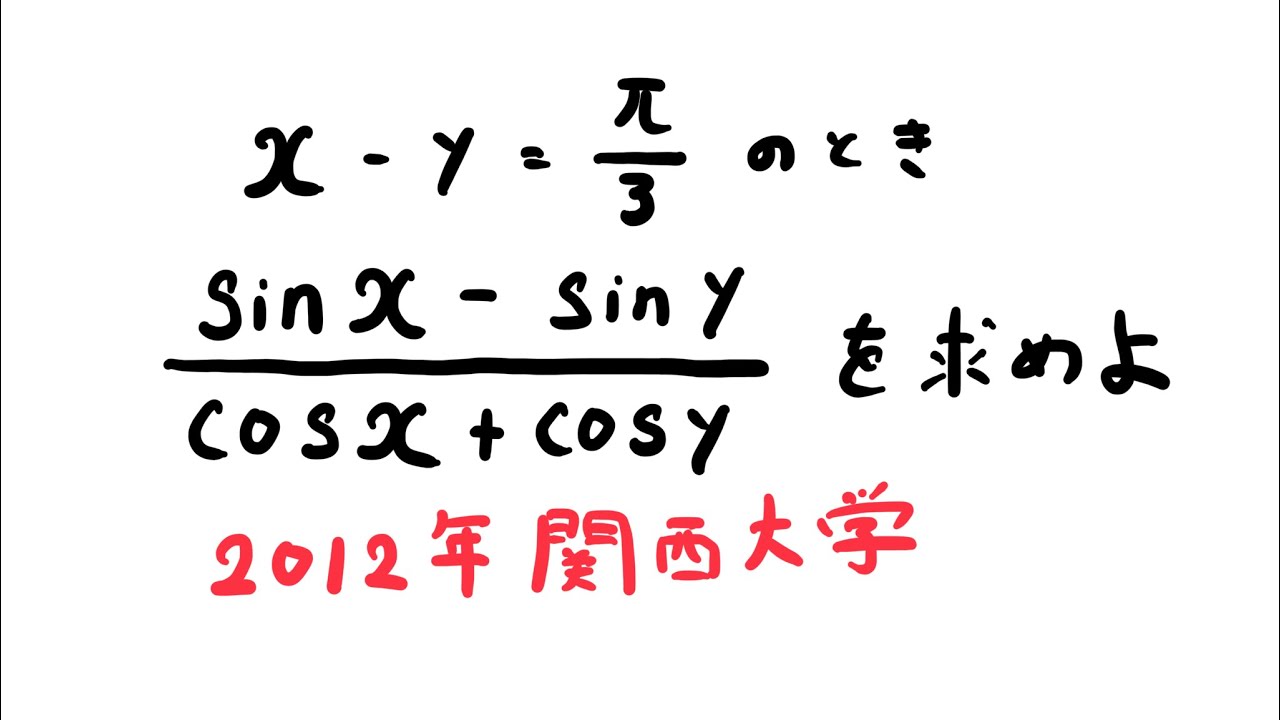
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ますただ
問題文全文(内容文):
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin x-\sin y}{\cos x+\cos y}$を求めよ。
出典:2012年関西大学
この動画を見る
$x-y=\displaystyle \frac{\pi}{3}$のとき
$\displaystyle \frac{\sin x-\sin y}{\cos x+\cos y}$を求めよ。
出典:2012年関西大学
大学入試問題#872「受験生は一度は解くべき」 #東北大学医学部AO(2019) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a$を実数とする。
次の極限を求めよ。
$\displaystyle \lim_{ n \to \infty } (1+a^{2n})^{\frac{1}{n}}$
出典:2019年東北大学医学部AO
この動画を見る
$a$を実数とする。
次の極限を求めよ。
$\displaystyle \lim_{ n \to \infty } (1+a^{2n})^{\frac{1}{n}}$
出典:2019年東北大学医学部AO
#青山学院大2019 #定積分
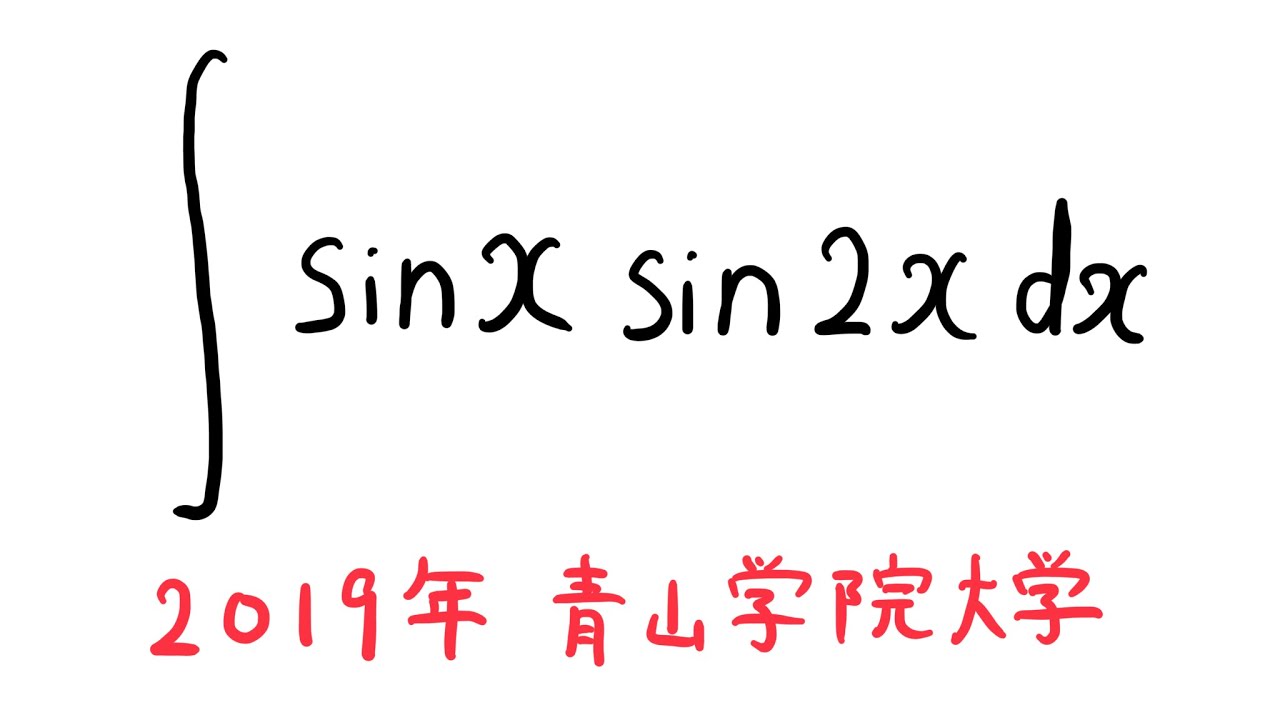
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \sin x \sin 2x$ $dx$
出典:2019年青山学院大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \sin x \sin 2x$ $dx$
出典:2019年青山学院大学
大学入試問題#871「初手が大事な基本問題」 #日本工業大学(2023) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{2x^2-x+2}{x^3+x} dx$
出典:2023年日本工業大学
この動画を見る
$\displaystyle \int_{1}^{\sqrt{ 3 }} \displaystyle \frac{2x^2-x+2}{x^3+x} dx$
出典:2023年日本工業大学
#自治医科大(2015) #定積分 #Shorts

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{35}{2}\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^7x$ $dx$
出典:2015年自治医科大学
この動画を見る
$\displaystyle \frac{35}{2}\displaystyle \int_{0}^{\frac{\pi}{2}} \sin^7x$ $dx$
出典:2015年自治医科大学
#青山学院大学(2006) #定積分 #Shorts
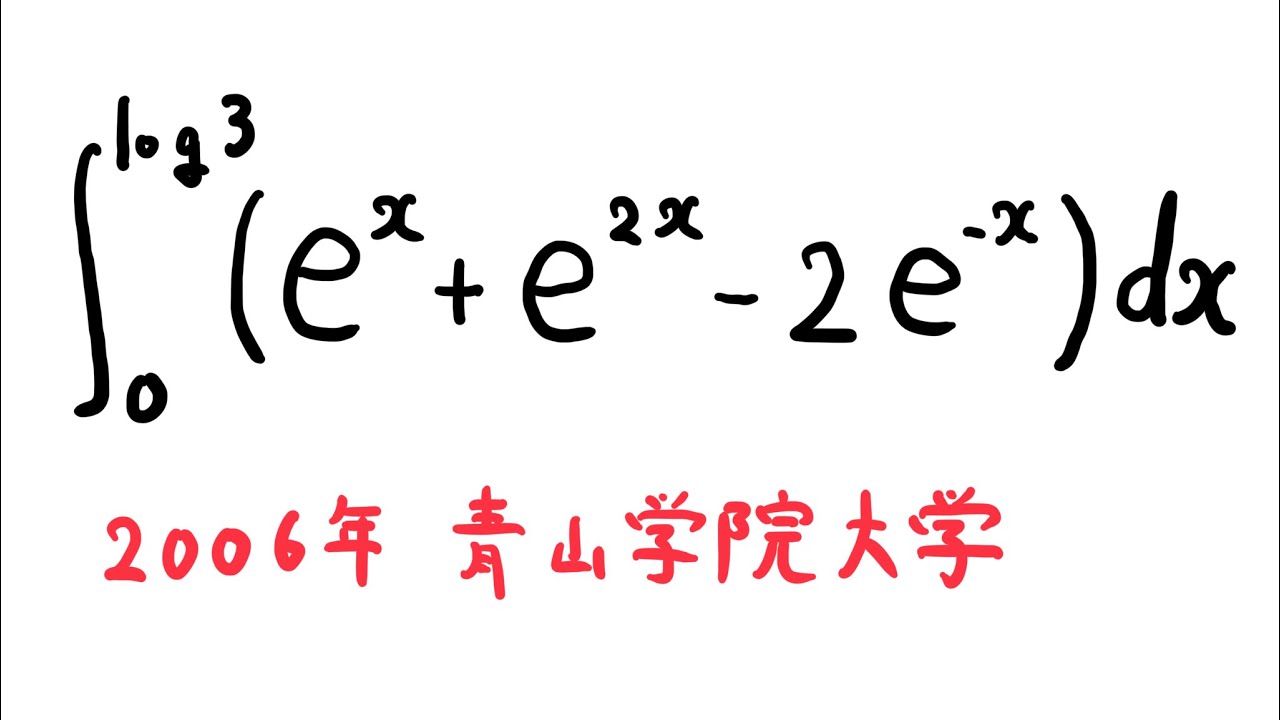
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log3} (e^x+e^{2x}-2e^{-x}) dx$
出典:2006年青山学院大学
この動画を見る
$\displaystyle \int_{0}^{log3} (e^x+e^{2x}-2e^{-x}) dx$
出典:2006年青山学院大学
大学入試問題#870「基本問題」 #東北大学医学部AO(2019) #数列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$S_n=2a_n+3n$を満たす数列$\{a_n\}$の一般項$a_n$を求めよ。
出典:2019年東北大学医学部AO
この動画を見る
$S_n=2a_n+3n$を満たす数列$\{a_n\}$の一般項$a_n$を求めよ。
出典:2019年東北大学医学部AO
大学入試問題#868「ヒントがあれば、どうってことない」 #埼玉医科大学(2010) #式変形

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉医科大学
指導講師:
ますただ
問題文全文(内容文):
$a \leq b \leq c$とする。
$\sqrt{ 10+\sqrt{ 24 }+\sqrt{ 40 }+\sqrt{ 60 } }=\sqrt{ a }+\sqrt{ b }+\sqrt{ c }=$であるとき、$a,b,c$の値を求めよ。
出典:2010年埼玉医科大学
この動画を見る
$a \leq b \leq c$とする。
$\sqrt{ 10+\sqrt{ 24 }+\sqrt{ 40 }+\sqrt{ 60 } }=\sqrt{ a }+\sqrt{ b }+\sqrt{ c }=$であるとき、$a,b,c$の値を求めよ。
出典:2010年埼玉医科大学
#68数学検定1級1次「答えはめっちゃスッキリ」 #定積分

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{ 1 } \displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}$ $dx$
出典:数検1級1次
この動画を見る
$\displaystyle \int_{-1}^{ 1 } \displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}$ $dx$
出典:数検1級1次
大学入試問題#867「これは、過去1番の難問かも」 #産業医科大学(2012) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ 1-2\sin 2x+3\cos^2x }$ $dx$
出典:2012年産業医科大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ 1-2\sin 2x+3\cos^2x }$ $dx$
出典:2012年産業医科大学
大学入試問題#866「まあ、なんとかなるわな」 #東京女子医科大学(2005) #式変形

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$(1-\sqrt[ 3 ]{ 2 }+\sqrt[ 3 ]{ 4 })^8$を計算せよ
出典:2005年東京女子医科大学
この動画を見る
$(1-\sqrt[ 3 ]{ 2 }+\sqrt[ 3 ]{ 4 })^8$を計算せよ
出典:2005年東京女子医科大学
大学入試問題#865「中学生の問題か!?」 #岩手医科大学(2008) #方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x-1)(y-1)=9 \\
x+y-\sqrt{ x^2+xy+y^2 }=1
\end{array}
\right.
\end{eqnarray}$を解け。
出典:2008年岩手医科大学
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x-1)(y-1)=9 \\
x+y-\sqrt{ x^2+xy+y^2 }=1
\end{array}
\right.
\end{eqnarray}$を解け。
出典:2008年岩手医科大学
大学入試問題#864「基本に忠実に」 #宮崎大学(2013) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{e^{4x}}{e^{2x}+2} dx$
出典:2013年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{e^{4x}}{e^{2x}+2} dx$
出典:2013年宮崎大学 入試問題
#67数学検定1級1次「こんな問題で時間使いたくない」 #因数分解

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師:
ますただ
問題文全文(内容文):
$xy(x^2-y^2)+yz(y^2-z^2)+zx(z^2-x^2)$を因数分解せよ
出典:数検1級1次
この動画を見る
$xy(x^2-y^2)+yz(y^2-z^2)+zx(z^2-x^2)$を因数分解せよ
出典:数検1級1次
#66数学検定1級1次過去問「怖いのは計算ミスのみ」 #式変形

単元:
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師:
ますただ
問題文全文(内容文):
$(1-\sqrt[ 3 ]{ 2 }+\sqrt[ 3 ]{ 4 })^3$を簡単にせよ
出典:数検1級1次
この動画を見る
$(1-\sqrt[ 3 ]{ 2 }+\sqrt[ 3 ]{ 4 })^3$を簡単にせよ
出典:数検1級1次
大学入試問題#863「ごちゃごちゃしとる」 #産業医科大学(2012) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \{\sqrt[ 3 ]{ (n^3-n^2)^2 }-2n\sqrt[ 3 ]{ n^3-n^2 }+n^2$
出典:2012年産業医科大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \{\sqrt[ 3 ]{ (n^3-n^2)^2 }-2n\sqrt[ 3 ]{ n^3-n^2 }+n^2$
出典:2012年産業医科大学
大学入試問題#862「一言、よくある良問」 #横浜国立大学 #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} x^3\sqrt{ 4-x^2 } dx$
出典:横浜国立大学
この動画を見る
$\displaystyle \int_{0}^{2} x^3\sqrt{ 4-x^2 } dx$
出典:横浜国立大学
大学入試問題#861「初見では苦しいか!?」 #学習院大学(2017) 視聴者の僚太さんの紹介

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#学習院大学
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0,b \gt 0$
$\displaystyle \lim_{ x \to \infty } x \sin(\sqrt{ a^2x^2+b }-ax)$
出典:2017年学習大学
この動画を見る
$a \gt 0,b \gt 0$
$\displaystyle \lim_{ x \to \infty } x \sin(\sqrt{ a^2x^2+b }-ax)$
出典:2017年学習大学
視聴者の僚太さんの難易度高めの積分です。大事な感覚が盛り込まれてます。

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#大学入試解答速報
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^2}{(1+x^2)\sqrt{ 1+x^2 }}$
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2}{(1+x^2)\sqrt{ 1+x^2 }}$



