鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
法政大 確率
単元：
#数A#場合の数と確率#確率#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023年 法政大学過去問
サイコロ4つを同時に投げる。
出た目の積が300の倍数となる確率
この動画を見る
2023年 法政大学過去問
サイコロ4つを同時に投げる。
出た目の積が300の倍数となる確率
法政大 確率
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#法政大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023法政大過去問
サイコロを３つ同時に投げる。出た目の積が300の倍数となる確率を求めよ.
この動画を見る
2023法政大過去問
サイコロを３つ同時に投げる。出た目の積が300の倍数となる確率を求めよ.
約数の基本問題
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#大阪医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
大阪医科薬(看)
600の正の約数のうち偶数であるものの総和を求めよ.
この動画を見る
大阪医科薬(看)
600の正の約数のうち偶数であるものの総和を求めよ.
整数の基本問題
因数分解
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
因数分解(整数係数)\\
x^4-2x^2-20x-24
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
因数分解(整数係数)\\
x^4-2x^2-20x-24
\end{eqnarray}
$
対数の性質
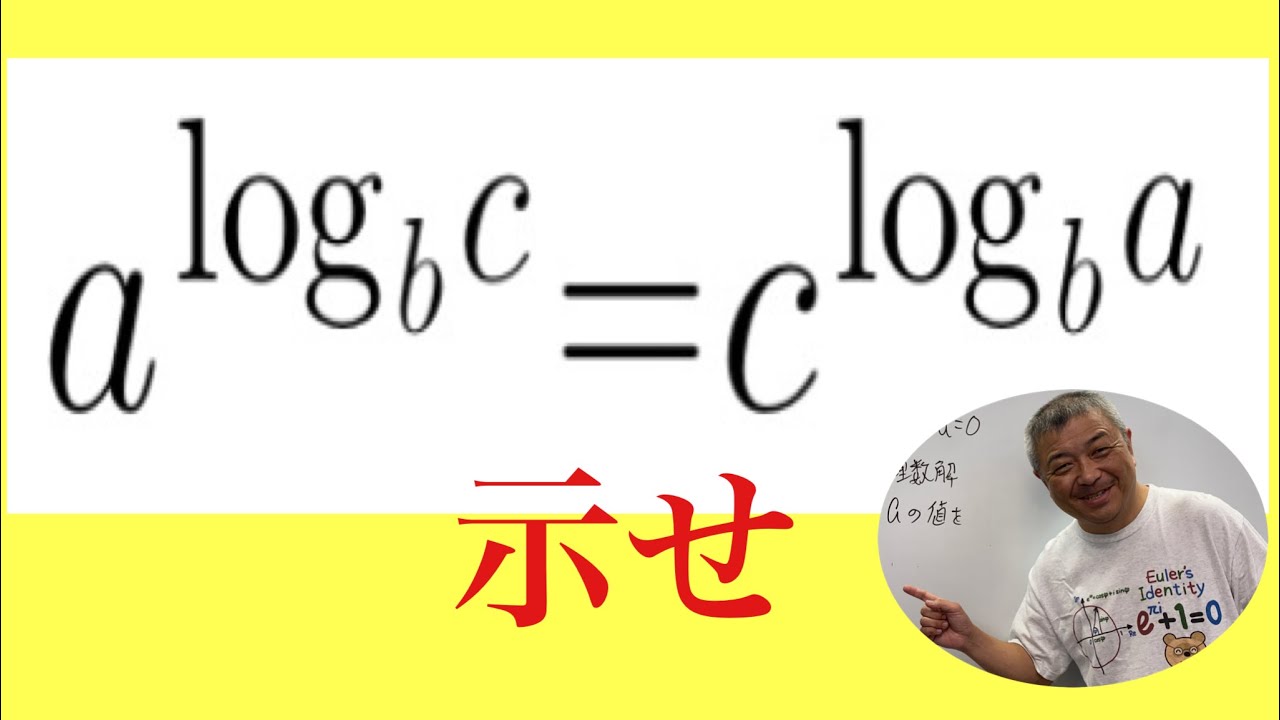
指数・対数の基本問題
単元：
#数Ⅱ#指数関数と対数関数#指数関数#対数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
&&3^a=7^b=441\\
&&\frac{ab}{a+b} = ?
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&3^a=7^b=441\\
&&\frac{ab}{a+b} = ?
\end{eqnarray}
$
指数方程式
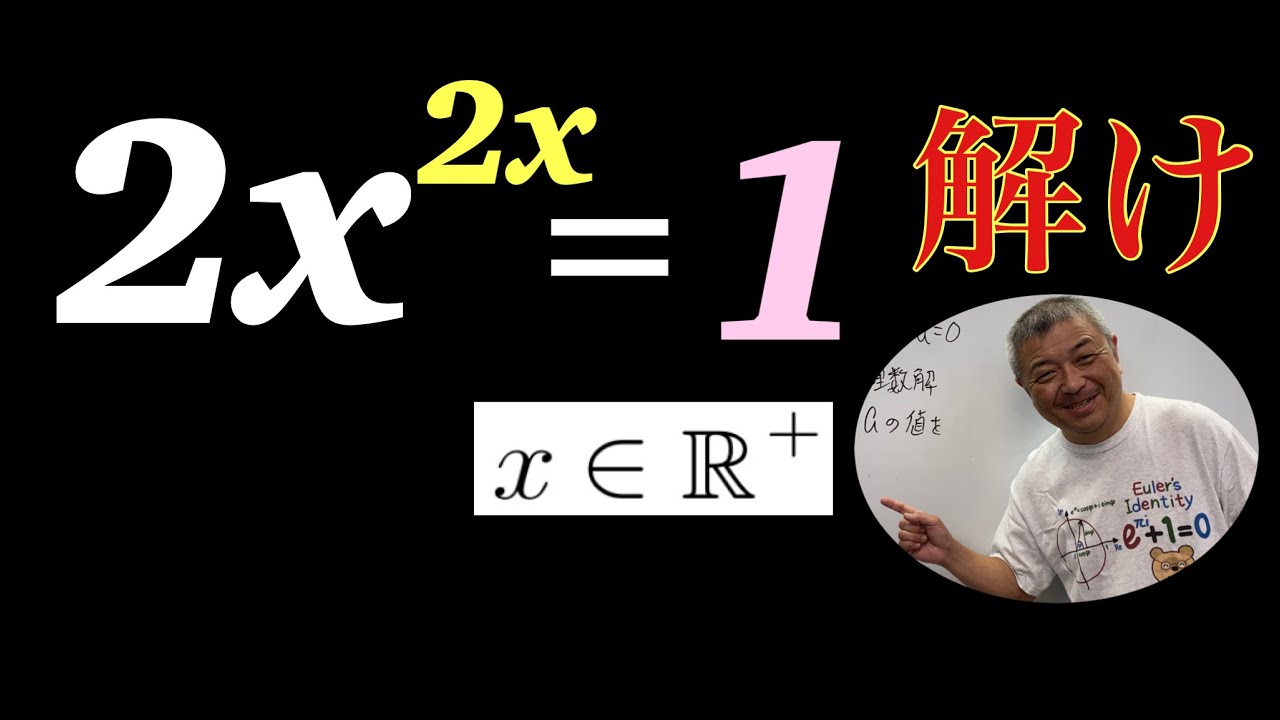
単元：
#数Ⅱ#指数関数と対数関数#指数関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
&&解け\\
&&x＞0\\
&&2x^{2x}=1
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&解け\\
&&x＞0\\
&&2x^{2x}=1
\end{eqnarray}
$
１０進数に変換せずに答えを出そう！
単元：
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
11111(7)を6進法で表せ
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
11111(7)を6進法で表せ
\end{eqnarray}
$
整数の基本問題 島根大
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$z^2-z$が6で割り切れるようなすべての奇数$z$を整数$n$を用いて表せ.
島根大過去問
この動画を見る
$z^2-z$が6で割り切れるようなすべての奇数$z$を整数$n$を用いて表せ.
島根大過去問
山口大 １の十乗根の問題
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
&&2023山口大\\
&&2Z^4+(1-\sqrt{5})Z^2+2=0\\
&&①Z^{10}=1 を示せ\\
&&②Z+Z^3+Z^5+Z^7+Z^9の値\\
&&③\cos\frac{\pi}{5}\cos\frac{2\pi}{5} = \frac{1}{4}を示せ
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&2023山口大\\
&&2Z^4+(1-\sqrt{5})Z^2+2=0\\
&&①Z^{10}=1 を示せ\\
&&②Z+Z^3+Z^5+Z^7+Z^9の値\\
&&③\cos\frac{\pi}{5}\cos\frac{2\pi}{5} = \frac{1}{4}を示せ
\end{eqnarray}
$
４次方程式の解と係数の関係 答えがあっていればなんでもいいか！山口大
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
&&2023山口大\\
&&x^4-6x^2+25=0の4つの解をp,q,r,s\\
&&①p^3+q^3+r^3+s^3\\
&&②p^3q^3+p^3r^3+p^3s^3+q^3r^3+q^3s^3+r^3s^3
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&2023山口大\\
&&x^4-6x^2+25=0の4つの解をp,q,r,s\\
&&①p^3+q^3+r^3+s^3\\
&&②p^3q^3+p^3r^3+p^3s^3+q^3r^3+q^3s^3+r^3s^3
\end{eqnarray}
$
愚直にやるかすっきりやるか・整式の剰余
単元：
#剰余の定理・因数定理・組み立て除法と高次方程式
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
&&x^{2022}を(x^2+x+1)^2で割った余り
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&x^{2022}を(x^2+x+1)^2で割った余り
\end{eqnarray}
$
横浜市立（医・理）
単元：
#複素数平面#複素数平面#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023横浜市立(医・理)
$
\\
Z^4=Z^2-1をみたす\\
Z^{40}+2Z^{10}+\frac{1}{Z^{20}}
$
この動画を見る
2023横浜市立(医・理)
$
\\
Z^4=Z^2-1をみたす\\
Z^{40}+2Z^{10}+\frac{1}{Z^{20}}
$
対数の基本
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023横浜市立(医・理)
$
\\
2^{log_49}の値
$
この動画を見る
2023横浜市立(医・理)
$
\\
2^{log_49}の値
$
複素数の計算
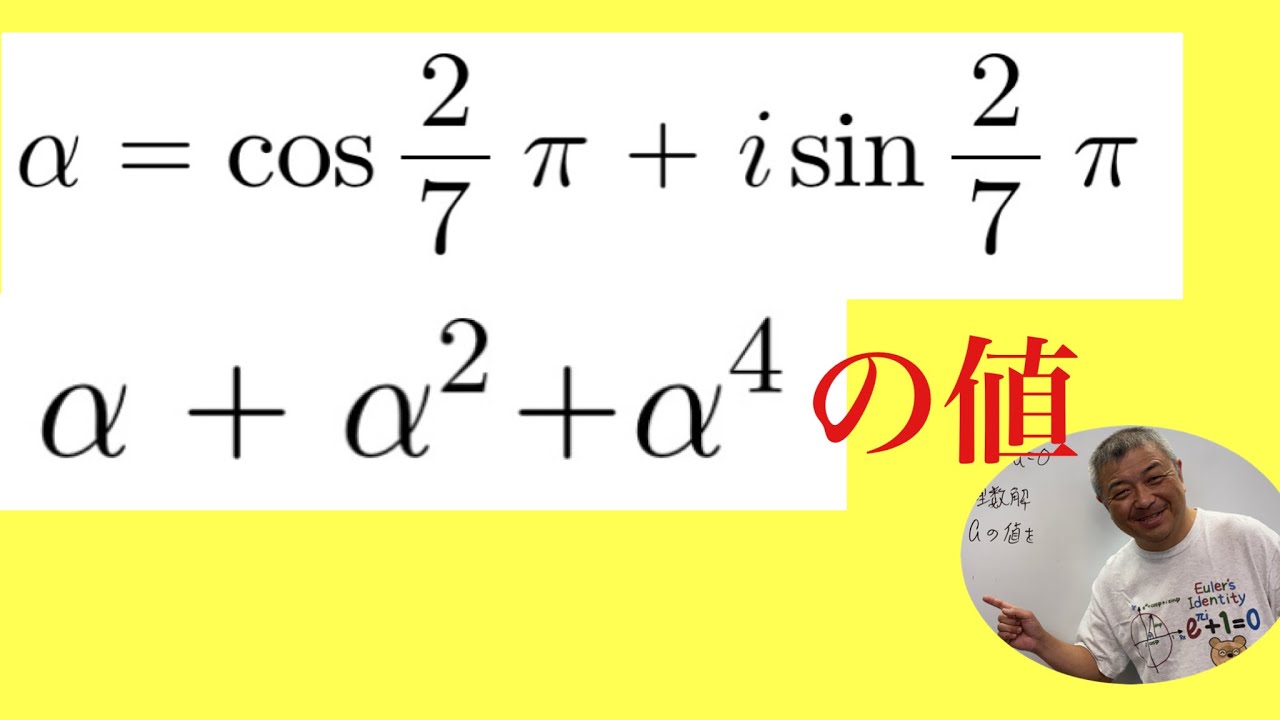
単元：
#複素数と方程式
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
\begin{eqnarray}
&&α=\cos\frac{2}{7}\pi+i\sin\frac{2}{7}\pi\\
&&α+α^2+α^4の値
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
&&α=\cos\frac{2}{7}\pi+i\sin\frac{2}{7}\pi\\
&&α+α^2+α^4の値
\end{eqnarray}
$
絶妙な係数
単元：
#大学入試過去問(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x,y,z$自然数とする.
\begin{eqnarray}
\left\{
\begin{array}{l}
7x^2 - 3y^2+4z^2 = 8 \\
16x^2 - 7y^2+9z^2 = -3
\end{array}
\right.
\end{eqnarray}
この動画を見る
$x,y,z$自然数とする.
\begin{eqnarray}
\left\{
\begin{array}{l}
7x^2 - 3y^2+4z^2 = 8 \\
16x^2 - 7y^2+9z^2 = -3
\end{array}
\right.
\end{eqnarray}
ただの計算問題
単元：
#大学入試過去問(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
計算せよ
$
\\
(\frac{1+\sqrt{13}}{2})^7+(\frac{1
-\sqrt{13}}{2})^7
$
この動画を見る
計算せよ
$
\\
(\frac{1+\sqrt{13}}{2})^7+(\frac{1
-\sqrt{13}}{2})^7
$
整式の剰余 あれでもいけるか？上智大
東京学芸大
単元：
#学校別大学入試過去問解説(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023東京学芸大学過去問題
①$log x\lt \sqrt x$を示し,$\displaystyle \lim_{x\to\infty}\dfrac{\log x}{x}$を求めよ.
②$m^n=n^m$を満たす自然数$m,n(m\lt n)$をすべて求めよ.
この動画を見る
2023東京学芸大学過去問題
①$log x\lt \sqrt x$を示し,$\displaystyle \lim_{x\to\infty}\dfrac{\log x}{x}$を求めよ.
②$m^n=n^m$を満たす自然数$m,n(m\lt n)$をすべて求めよ.
奈良教育大 あまりの問題
東京医科大 約数
単元：
#学校別大学入試過去問解説(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2019東京医科大学過去問題
1008の正の約数n個を大きい順に並べた数列
$
\begin{eqnarray}
\\
&&a_1,a_2,\cdots,a_n\\
&&S(x) = \sum_{k=1}^{n}a_k^x\\
&&次の値\\
&&①S_{(0)} ②S_{(-1)} ③\frac{S_{(2)}} {S_{(1)}}
\end{eqnarray}
$
この動画を見る
2019東京医科大学過去問題
1008の正の約数n個を大きい順に並べた数列
$
\begin{eqnarray}
\\
&&a_1,a_2,\cdots,a_n\\
&&S(x) = \sum_{k=1}^{n}a_k^x\\
&&次の値\\
&&①S_{(0)} ②S_{(-1)} ③\frac{S_{(2)}} {S_{(1)}}
\end{eqnarray}
$
整数問題
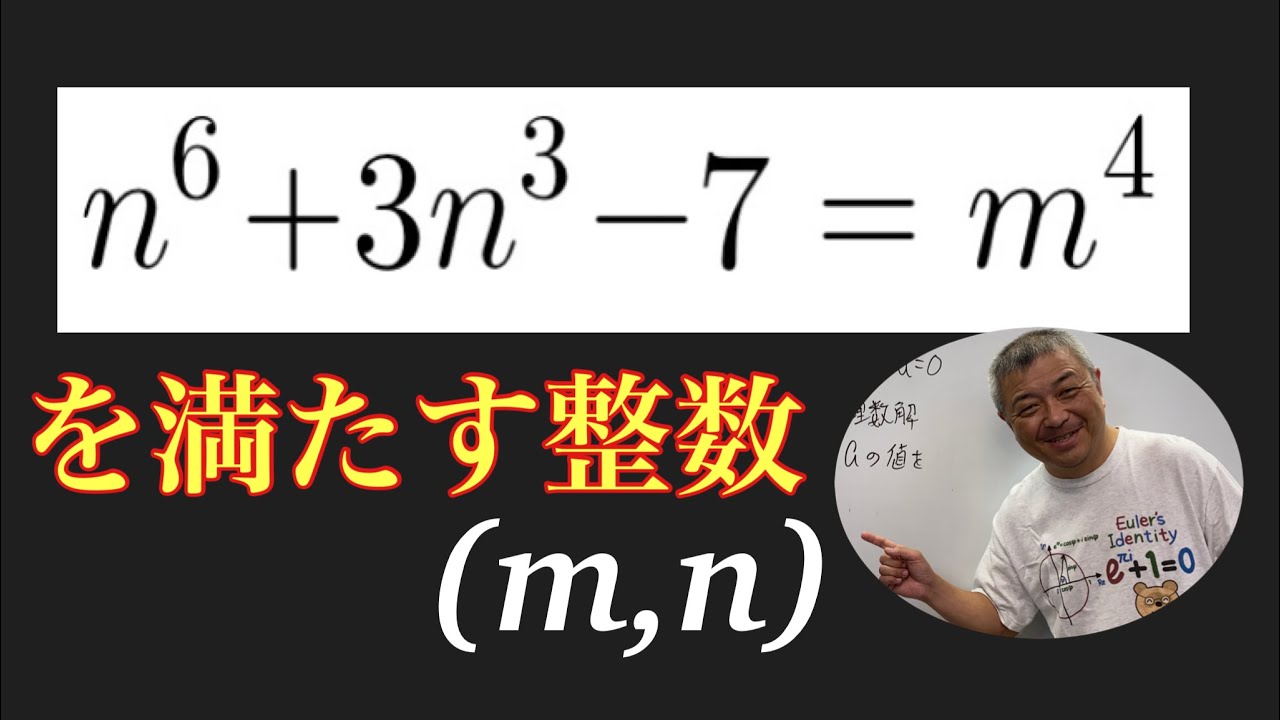
単元：
#整数の性質#ユークリッド互除法と不定方程式・Ｎ進法#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$n^6+3n^3-7 = m^4\\を満たす整数(m,n)$
この動画を見る
$n^6+3n^3-7 = m^4\\を満たす整数(m,n)$
東京医科大 ４次方程式
単元：
#解と判別式・解と係数の関係
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2021東京医科大学過去問題
$x^4+11x^3+31x^2+11x+1=0$の4つの解を,$\alpha,\beta,\gamma,\delta$とする.
下の値を求めよ.
①$\dfrac{1}{\alpha}+\dfrac{1}{\beta}+\dfrac{1}{\gamma}+\dfrac{1}{\delta}$
②$\alpha^2+\beta^2+\gamma^2+\delta^2$
③$\alpha^3+\beta^3+\gamma^3+\delta^3$
この動画を見る
2021東京医科大学過去問題
$x^4+11x^3+31x^2+11x+1=0$の4つの解を,$\alpha,\beta,\gamma,\delta$とする.
下の値を求めよ.
①$\dfrac{1}{\alpha}+\dfrac{1}{\beta}+\dfrac{1}{\gamma}+\dfrac{1}{\delta}$
②$\alpha^2+\beta^2+\gamma^2+\delta^2$
③$\alpha^3+\beta^3+\gamma^3+\delta^3$
神様の順列 記述式だけど答えだけでいいんじゃね？
単元：
#場合の数と確率
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023茨城大学過去問題
赤玉4個白玉5個入った袋から1個ずつ順に3個とり出す(もどさない)
3個目が白である確率
この動画を見る
2023茨城大学過去問題
赤玉4個白玉5個入った袋から1個ずつ順に3個とり出す(もどさない)
3個目が白である確率
そりゃー漸化式でも出せるよね
単元：
#数列
指導講師：
鈴木貫太郎
問題文全文(内容文)：
n人を3つのグループに分ける場合の数を$a_{n}$通りとする
$a_{n+1}$と$a_{n}$の関係を式で表せ
$a_{n}$を求めよ$(n \geqq 3)$
この動画を見る
n人を3つのグループに分ける場合の数を$a_{n}$通りとする
$a_{n+1}$と$a_{n}$の関係を式で表せ
$a_{n}$を求めよ$(n \geqq 3)$
場合の数、具体的に求める？一般的に求める？
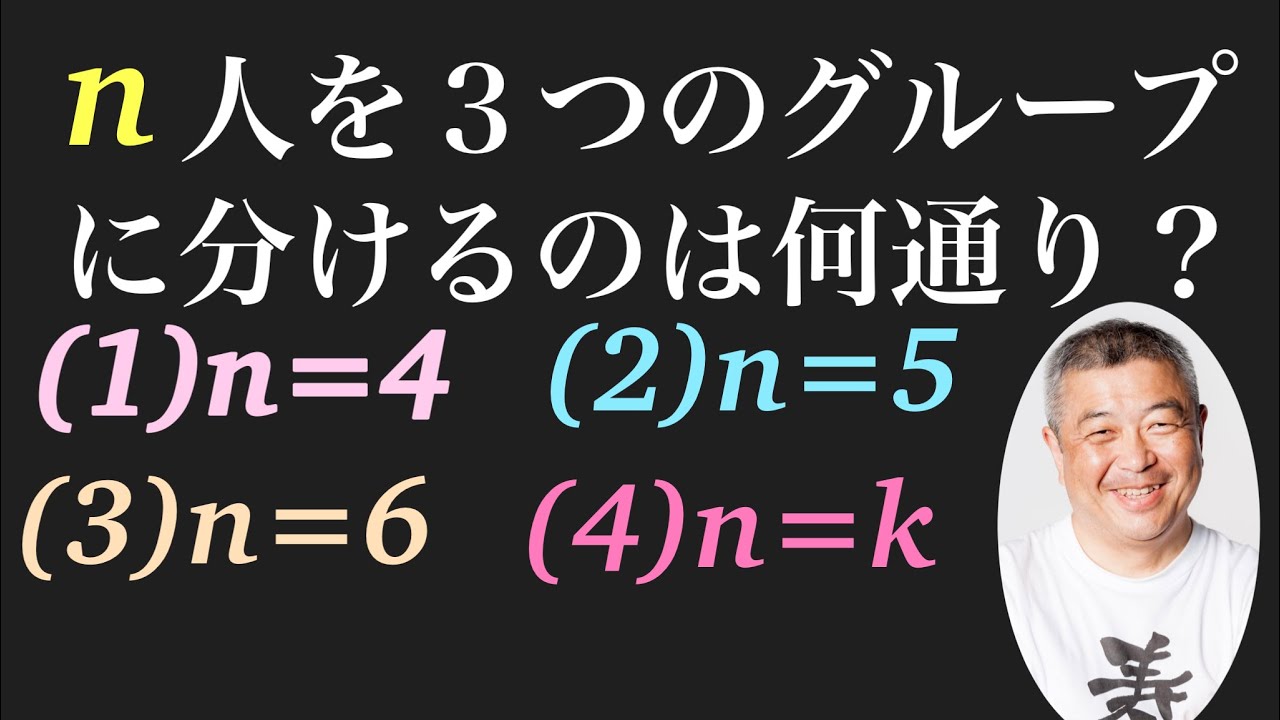
単元：
#場合の数と確率
指導講師：
鈴木貫太郎
問題文全文(内容文)：
n人を3つのグループに分ける。それぞれ何通りか？
・0人は不可
・グループに名前はない
・個人は区別する
(1)n=4
(2)n=5
(3)n=6
(4)n=k
この動画を見る
n人を3つのグループに分ける。それぞれ何通りか？
・0人は不可
・グループに名前はない
・個人は区別する
(1)n=4
(2)n=5
(3)n=6
(4)n=k
茨城大 漸化式ぐらい自由に解かせてくれ
単元：
#数列#学校別大学入試過去問解説(数学)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023茨城大学過去問題
一般項$a_{n}$を求めよ
$3a_{n}=S_{n}+n^2-2n+1$
$S_n=\displaystyle\sum_{k=1}^{n}a_{k}$
この動画を見る
2023茨城大学過去問題
一般項$a_{n}$を求めよ
$3a_{n}=S_{n}+n^2-2n+1$
$S_n=\displaystyle\sum_{k=1}^{n}a_{k}$
信州大（医）整数問題の基本
単元：
#整数の性質#信州大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2023信州大学過去問題
3つの自然数P,P+10,P+20がすべて素数となるようなPがただ1つ存在することを示せ
この動画を見る
2023信州大学過去問題
3つの自然数P,P+10,P+20がすべて素数となるようなPがただ1つ存在することを示せ
あれを使ってスッキリ解こう❗️信州大
