 青山学院大学
青山学院大学
 青山学院大学
青山学院大学
福田の数学〜青山学院大学2025理工学部第5問〜鋭角三角形の条件と垂心の位置ベクトル

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#数C#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{5}$
$\triangle OAB$は鋭角三角形であり、
$\vert \overrightarrow{OA}\vert=4,\vert \overrightarrow{OB}\vert=3$
を満たしている。
$\overrightarrow{OA}\cdot \overrightarrow{OB}=k$とおくとき、以下の問いに答えよ。
(1)$k$のとり得る値の範囲を求めよ。
上で与えた$\triangle OAB$の頂点$A,B$から
それぞれの対辺に下ろした$2$本の垂線の交点
を$H$とし、辺$AB$を$2:1$に内分する点を$C$とする。
(2)$\overrightarrow{OH}$を$\overrightarrow{OA},\overrightarrow{OB}$および$k$を用いて表せ。
(3)$3$点$O,H,C$が同一直線上にあるとき、
$k$の値と$\dfrac{OH}{OC}$を求めよ。
$2025$年青山学院大学理工学部過去問題
この動画を見る
$\boxed{5}$
$\triangle OAB$は鋭角三角形であり、
$\vert \overrightarrow{OA}\vert=4,\vert \overrightarrow{OB}\vert=3$
を満たしている。
$\overrightarrow{OA}\cdot \overrightarrow{OB}=k$とおくとき、以下の問いに答えよ。
(1)$k$のとり得る値の範囲を求めよ。
上で与えた$\triangle OAB$の頂点$A,B$から
それぞれの対辺に下ろした$2$本の垂線の交点
を$H$とし、辺$AB$を$2:1$に内分する点を$C$とする。
(2)$\overrightarrow{OH}$を$\overrightarrow{OA},\overrightarrow{OB}$および$k$を用いて表せ。
(3)$3$点$O,H,C$が同一直線上にあるとき、
$k$の値と$\dfrac{OH}{OC}$を求めよ。
$2025$年青山学院大学理工学部過去問題
福田の数学〜青山学院大学2025理工学部第4問〜折れ線の長さの和が4となる点の軌跡と面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$xy$平面上に$2$つの定点$A(-1,0),B(1,0)$がある。
線分$AB$上の点$P$に対して、
$xy$平面上の点$Q$は以下の条件$(a),(b)$を
満たすとする。
$(a)$$P$と$Q$の$x$座標は等しく、
$Q$の$y$座標は正である。
$(b)$$AP+PQ+QB=4$
このとき、以下の問いに答えよ。
ただし、線分は両方の端点を含むものとする。
(1)$P$の座標を$(s,0)$とするとき、
$Q$の座標を$s$を用いて表せ。
(2)$P$が線分$AB$上を$A$から$B$まで動くとき、
$Q$の軌跡を$xy$平面上に図示せよ。
(3)$P$が線分$AB$上を$A$から$B$まで動くとき、
線分$PQ$が通過する範囲の面積を求めよ。
$2025$年青山学院大学理工学部過去問題
この動画を見る
$\boxed{4}$
$xy$平面上に$2$つの定点$A(-1,0),B(1,0)$がある。
線分$AB$上の点$P$に対して、
$xy$平面上の点$Q$は以下の条件$(a),(b)$を
満たすとする。
$(a)$$P$と$Q$の$x$座標は等しく、
$Q$の$y$座標は正である。
$(b)$$AP+PQ+QB=4$
このとき、以下の問いに答えよ。
ただし、線分は両方の端点を含むものとする。
(1)$P$の座標を$(s,0)$とするとき、
$Q$の座標を$s$を用いて表せ。
(2)$P$が線分$AB$上を$A$から$B$まで動くとき、
$Q$の軌跡を$xy$平面上に図示せよ。
(3)$P$が線分$AB$上を$A$から$B$まで動くとき、
線分$PQ$が通過する範囲の面積を求めよ。
$2025$年青山学院大学理工学部過去問題
福田の数学〜青山学院大学2025理工学部第3問〜三角関数のグラフと面積

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$f(x)=\cos^3 x+\sin^3 x,g(x)=\sin x$とする。
(1)$0\leqq x \leqq \pi$において、
曲線$y=f(x)$の概形を描け。
ただし、凹凸は調べなくてよい。
(2)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$の共有点の座標を求めよ。
(3)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$で囲まれた図形の
面積$S$を求めよ。
$2025$年青山学院大学理工学部過去問題
この動画を見る
$\boxed{3}$
$f(x)=\cos^3 x+\sin^3 x,g(x)=\sin x$とする。
(1)$0\leqq x \leqq \pi$において、
曲線$y=f(x)$の概形を描け。
ただし、凹凸は調べなくてよい。
(2)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$の共有点の座標を求めよ。
(3)$0\leqq x \leqq \pi$において、
$2$曲線$y=f(x),y=g(x)$で囲まれた図形の
面積$S$を求めよ。
$2025$年青山学院大学理工学部過去問題
福田の数学〜青山学院大学2025理工学部第2問〜虚数係数の2次方程式の解と正方形の頂点
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
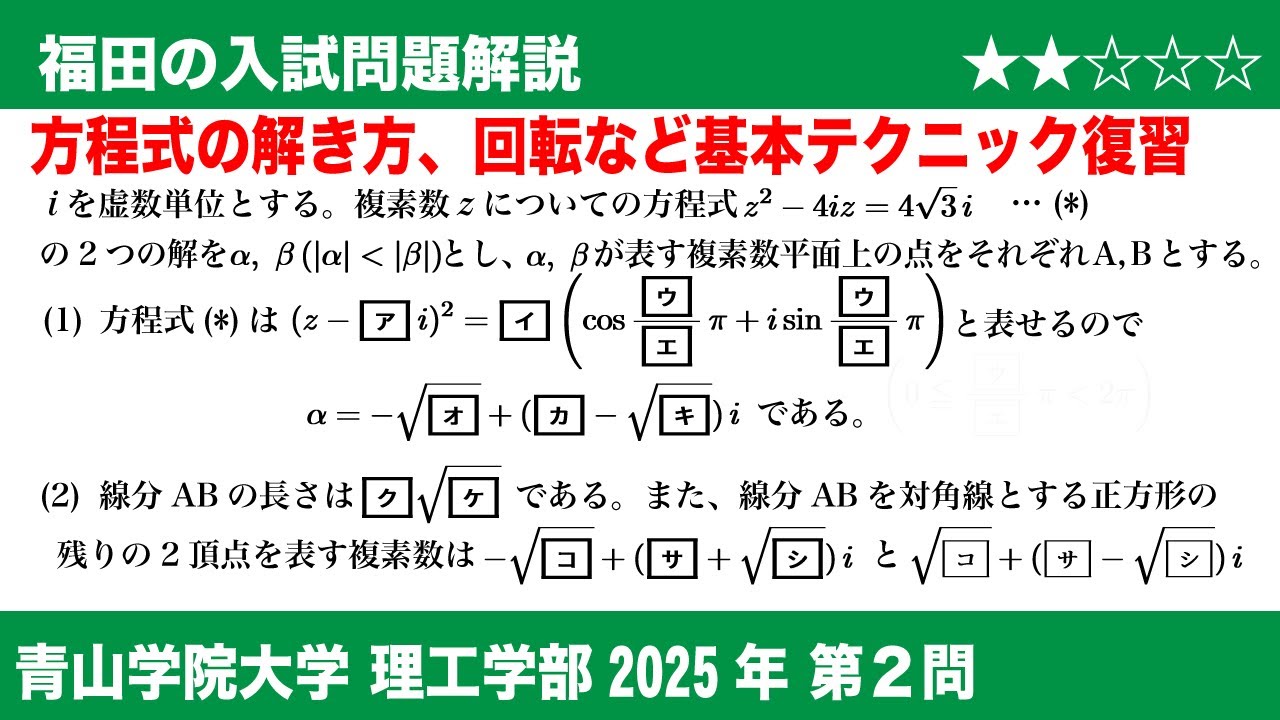
$\boxed{2}$
$i$を虚数単位とする。
複素数$z$についての方程式
$z^2-4iz=4\sqrt3 i \ \cdots (*)$
の$2$つの解を$\alpha,\beta(\vert \alpha \vert \lt \vert \beta \vert )$とし、
$\alpha,\beta$が表す複素数平面上の点を
それぞれ$A,B$とする。
(1)方程式$(*)$は
$(z-\boxed{ア}i)^2=\boxed{イ} \left(\cos \dfrac{\boxed{ウ}}{\boxed{エ}}\pi+i\sin\dfrac{\boxed{ウ}}{\boxed{エ}}\pi\right) \qquad \left(0\leqq \dfrac{\boxed{ウ}}{\boxed{エ}}\pi \lt 2\pi \right)$
と表せるので
$\alpha=-\sqrt{\boxed{オ}}+\left(\boxed{カ}-\sqrt{\boxed{キ}}\right)i$である。
(2)線分$AB$の長さは$\boxed{ク}\sqrt{\boxed{ケ}}$である。
また、線分$AB$を対角線とする正方形の
残りの$2$頂点を表す複素数は
$-\sqrt{\boxed{コ}}+\left(\boxed{サ}+\sqrt{\boxed{シ}}\right)i$と
$\sqrt{\boxed{コ}}-\left(\boxed{サ}+\sqrt{\boxed{シ}}\right)i$である。
$2025$年青山学院大学理工学部過去問題
この動画を見る
$\boxed{2}$
$i$を虚数単位とする。
複素数$z$についての方程式
$z^2-4iz=4\sqrt3 i \ \cdots (*)$
の$2$つの解を$\alpha,\beta(\vert \alpha \vert \lt \vert \beta \vert )$とし、
$\alpha,\beta$が表す複素数平面上の点を
それぞれ$A,B$とする。
(1)方程式$(*)$は
$(z-\boxed{ア}i)^2=\boxed{イ} \left(\cos \dfrac{\boxed{ウ}}{\boxed{エ}}\pi+i\sin\dfrac{\boxed{ウ}}{\boxed{エ}}\pi\right) \qquad \left(0\leqq \dfrac{\boxed{ウ}}{\boxed{エ}}\pi \lt 2\pi \right)$
と表せるので
$\alpha=-\sqrt{\boxed{オ}}+\left(\boxed{カ}-\sqrt{\boxed{キ}}\right)i$である。
(2)線分$AB$の長さは$\boxed{ク}\sqrt{\boxed{ケ}}$である。
また、線分$AB$を対角線とする正方形の
残りの$2$頂点を表す複素数は
$-\sqrt{\boxed{コ}}+\left(\boxed{サ}+\sqrt{\boxed{シ}}\right)i$と
$\sqrt{\boxed{コ}}-\left(\boxed{サ}+\sqrt{\boxed{シ}}\right)i$である。
$2025$年青山学院大学理工学部過去問題
福田の数学〜青山学院大学2025理工学部第1問〜さいころの目によって平面上を動く点に関する確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
$1$個のさいころを$4$回続けて投げる
反復試行において、
さいころの出る目を順に$X_1,X_2,X_3,X_4$として、
$xy$平面上の$4$点$P_1,P_2,P_3,P_4$を
以下のように定める。
$1$.原点$O$から$x$軸の正の向きに$X_1$だけ進んだ位置に
ある点を$P_1$とする。
$2$.$P_1$から$y$軸の正の向きに$X_2$だけ進んだ位置に
ある点を$P_2$とする。
$3$.$P_2$から$x$軸の負の向きに$X_3$だけ進んだ位置に
ある点を$P_3$とする。
$4$.$P_3$から$y$軸の負の向きに$X_4$だけ進んだ位置に
ある点を$P_4$とする。
例えば、さいころの出た目が順に$3,2,5,5$ならば
$P_1,P_2,P_3,P_4$の座標はそれぞれ
$(3,0),(3,2),(-2,2),(-2,-3)$となる。
(1)$P_4$が$O$と一致する確率は$\dfrac{\boxed{ア}}{\boxed{イウ}}$である。
(2)線分$OP_1$と線分$P_3P_4$が共有点をもつ確率は
$\dfrac{\boxed{エオ}}{\boxed{カキク}}$である。
ただし、線分は両方の端点を含むものとする。
(3)$P_4$の座標が$(3,3)$である確率は
$\dfrac{\boxed{ケ}}{\boxed{コサシ}}$である。
この動画を見る
$\boxed{1}$
$1$個のさいころを$4$回続けて投げる
反復試行において、
さいころの出る目を順に$X_1,X_2,X_3,X_4$として、
$xy$平面上の$4$点$P_1,P_2,P_3,P_4$を
以下のように定める。
$1$.原点$O$から$x$軸の正の向きに$X_1$だけ進んだ位置に
ある点を$P_1$とする。
$2$.$P_1$から$y$軸の正の向きに$X_2$だけ進んだ位置に
ある点を$P_2$とする。
$3$.$P_2$から$x$軸の負の向きに$X_3$だけ進んだ位置に
ある点を$P_3$とする。
$4$.$P_3$から$y$軸の負の向きに$X_4$だけ進んだ位置に
ある点を$P_4$とする。
例えば、さいころの出た目が順に$3,2,5,5$ならば
$P_1,P_2,P_3,P_4$の座標はそれぞれ
$(3,0),(3,2),(-2,2),(-2,-3)$となる。
(1)$P_4$が$O$と一致する確率は$\dfrac{\boxed{ア}}{\boxed{イウ}}$である。
(2)線分$OP_1$と線分$P_3P_4$が共有点をもつ確率は
$\dfrac{\boxed{エオ}}{\boxed{カキク}}$である。
ただし、線分は両方の端点を含むものとする。
(3)$P_4$の座標が$(3,3)$である確率は
$\dfrac{\boxed{ケ}}{\boxed{コサシ}}$である。
福田の数学〜青山学院大学2024理工学部第3問〜2次方程式の解の条件と領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$p,qを実数の定数とし、xについての2次方程式$
$x^2+px+q=0 \cdots (\ast)$
を考える。2次方程式$(\ast)$が異なる2つの実数解$\alpha,\beta(\alpha\lt\beta)$をもち、かつ$\alpha,\beta$が
$\displaystyle \frac{\alpha}{2}\leqq\beta\leqq2\alpha$
を満たすとき、以下の問いに答えよ。
(1)点$(p,q)$のとりうる範囲を座標平面上に図示せよ。
(2)$\alpha,\beta$がさらに
$(\alpha+1)(\beta+1)\leqq 3$
を満たすとする。このとき、pの値が最小となるような$(p,q)$を求めよ。
(3)(2)で求めた$(p,q)$に対して、2次方程式$(\ast)$の解$\alpha,\beta$を求めよ。
この動画を見る
$p,qを実数の定数とし、xについての2次方程式$
$x^2+px+q=0 \cdots (\ast)$
を考える。2次方程式$(\ast)$が異なる2つの実数解$\alpha,\beta(\alpha\lt\beta)$をもち、かつ$\alpha,\beta$が
$\displaystyle \frac{\alpha}{2}\leqq\beta\leqq2\alpha$
を満たすとき、以下の問いに答えよ。
(1)点$(p,q)$のとりうる範囲を座標平面上に図示せよ。
(2)$\alpha,\beta$がさらに
$(\alpha+1)(\beta+1)\leqq 3$
を満たすとする。このとき、pの値が最小となるような$(p,q)$を求めよ。
(3)(2)で求めた$(p,q)$に対して、2次方程式$(\ast)$の解$\alpha,\beta$を求めよ。
福田の数学〜青山学院大学2024理工学部第2問〜法線と面積と回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\tan{x}$とする。また、曲線
$\displaystyle C:y=f(x)(-\frac{\pi}{2}\lt x\lt \frac{\pi}{2})$
上の点$(\displaystyle \frac{\pi}{6},f(\frac{\pi}{6}))$における法線を$\ell$とする。
(1)法線$\ell$の方程式は$\displaystyle y=\frac{\fbox{アイ}}{\fbox{ウ}}x+\frac{\fbox{エ}}{\fbox{オ}}\pi+\frac{\sqrt{\fbox{カ}}}{\fbox{キ}}である。$
(2)曲線$C$と$x$軸および法線$\ell$で囲まれた図形の面積は
$\log{a}+b(a=\frac{\fbox{ク}\sqrt{\fbox{ケ}}}{\fbox{コ}},b=\frac{\fbox{サ}}{\fbox{シ}})$
この動画を見る
$f(x)=\tan{x}$とする。また、曲線
$\displaystyle C:y=f(x)(-\frac{\pi}{2}\lt x\lt \frac{\pi}{2})$
上の点$(\displaystyle \frac{\pi}{6},f(\frac{\pi}{6}))$における法線を$\ell$とする。
(1)法線$\ell$の方程式は$\displaystyle y=\frac{\fbox{アイ}}{\fbox{ウ}}x+\frac{\fbox{エ}}{\fbox{オ}}\pi+\frac{\sqrt{\fbox{カ}}}{\fbox{キ}}である。$
(2)曲線$C$と$x$軸および法線$\ell$で囲まれた図形の面積は
$\log{a}+b(a=\frac{\fbox{ク}\sqrt{\fbox{ケ}}}{\fbox{コ}},b=\frac{\fbox{サ}}{\fbox{シ}})$
#青山学院大学2023#定積分_30#元高校教員

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos3x\cos\displaystyle \frac{x}{3} dx$
出典:2023年 青山学院大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \cos3x\cos\displaystyle \frac{x}{3} dx$
出典:2023年 青山学院大学
#青山学院大学2023#定積分_26#元高校教員
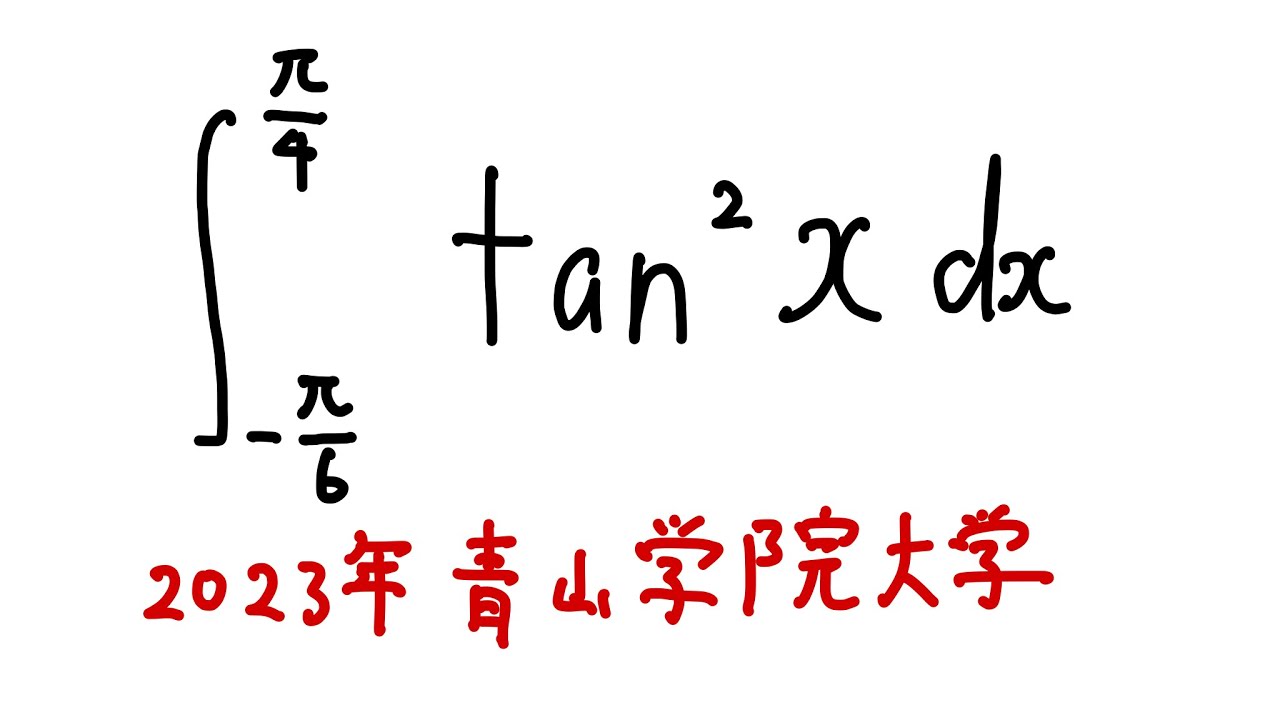
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{4}} \tan^2x dx$
出典:2023年青山学院大学
この動画を見る
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{4}} \tan^2x dx$
出典:2023年青山学院大学
#青山学院大学#不定積分#ますただ
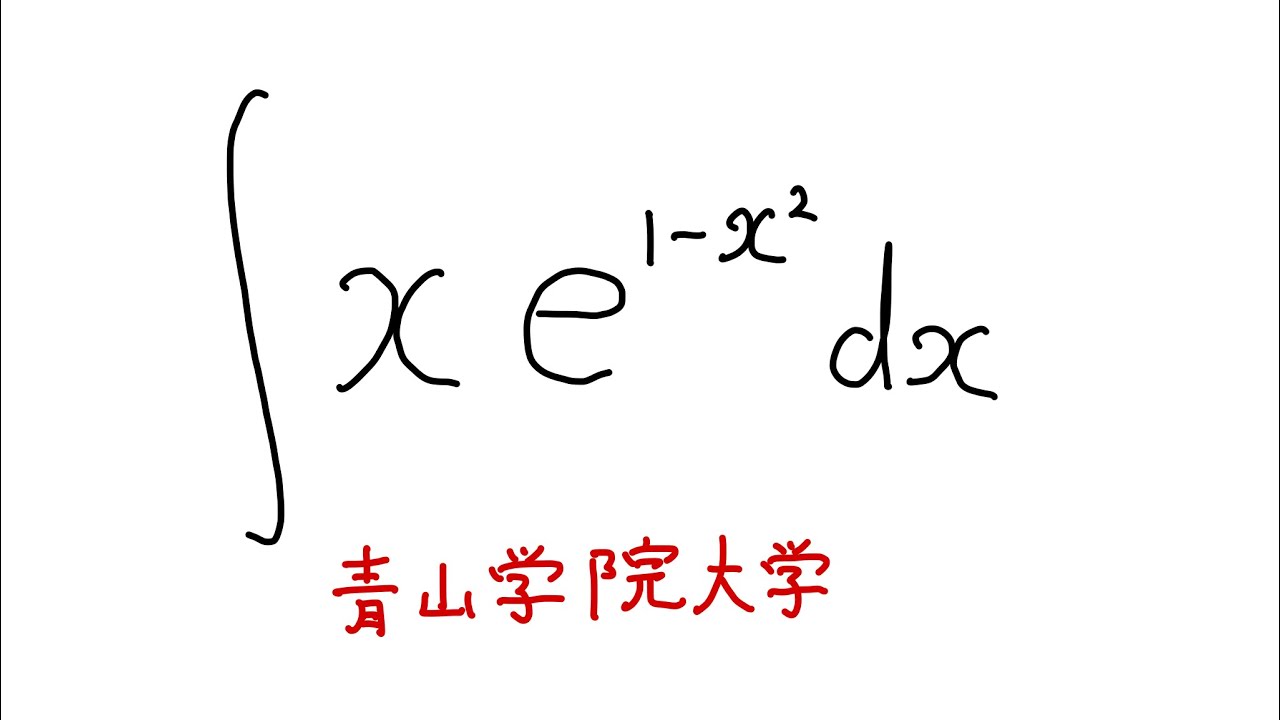
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int xe^{1-x^2}dx$
出典:青山学院大学
この動画を見る
$\displaystyle \int xe^{1-x^2}dx$
出典:青山学院大学
#青山学院大学#定積分#ますただ
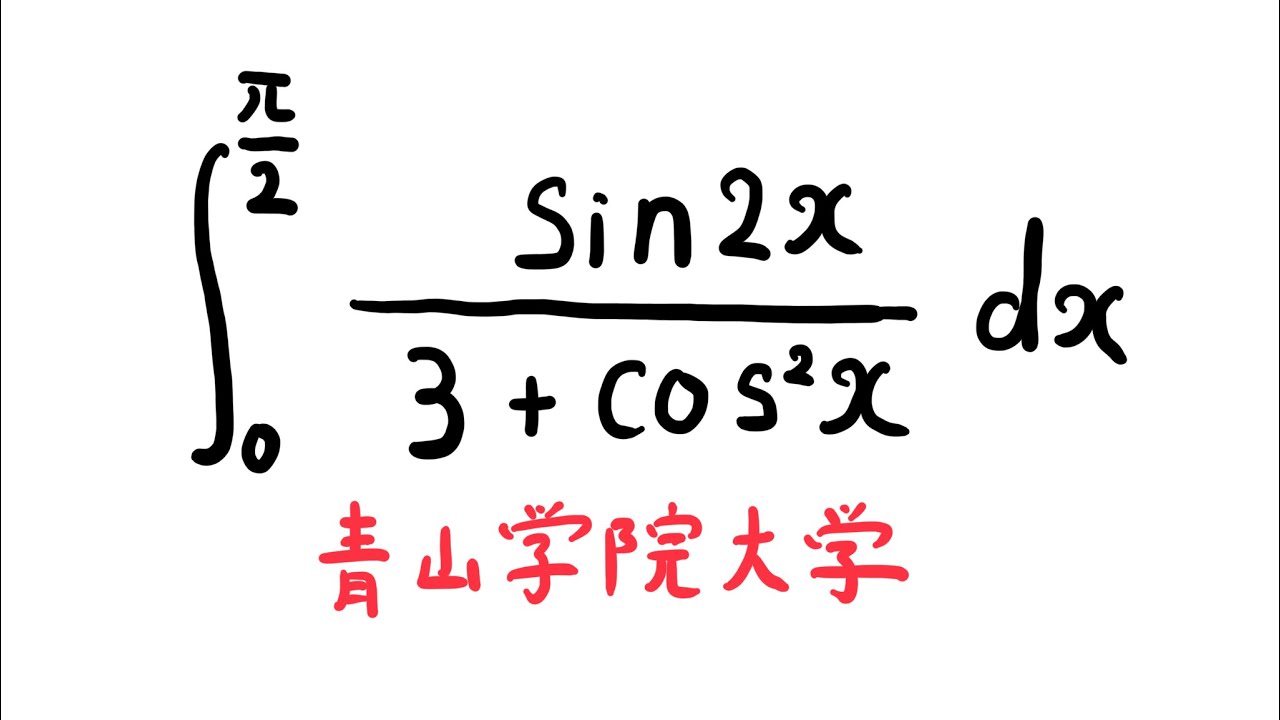
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin2x}{3+\cos^2x} dx$
出典:青山学院大学
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} \displaystyle \frac{\sin2x}{3+\cos^2x} dx$
出典:青山学院大学
#青山学院大2019 #定積分
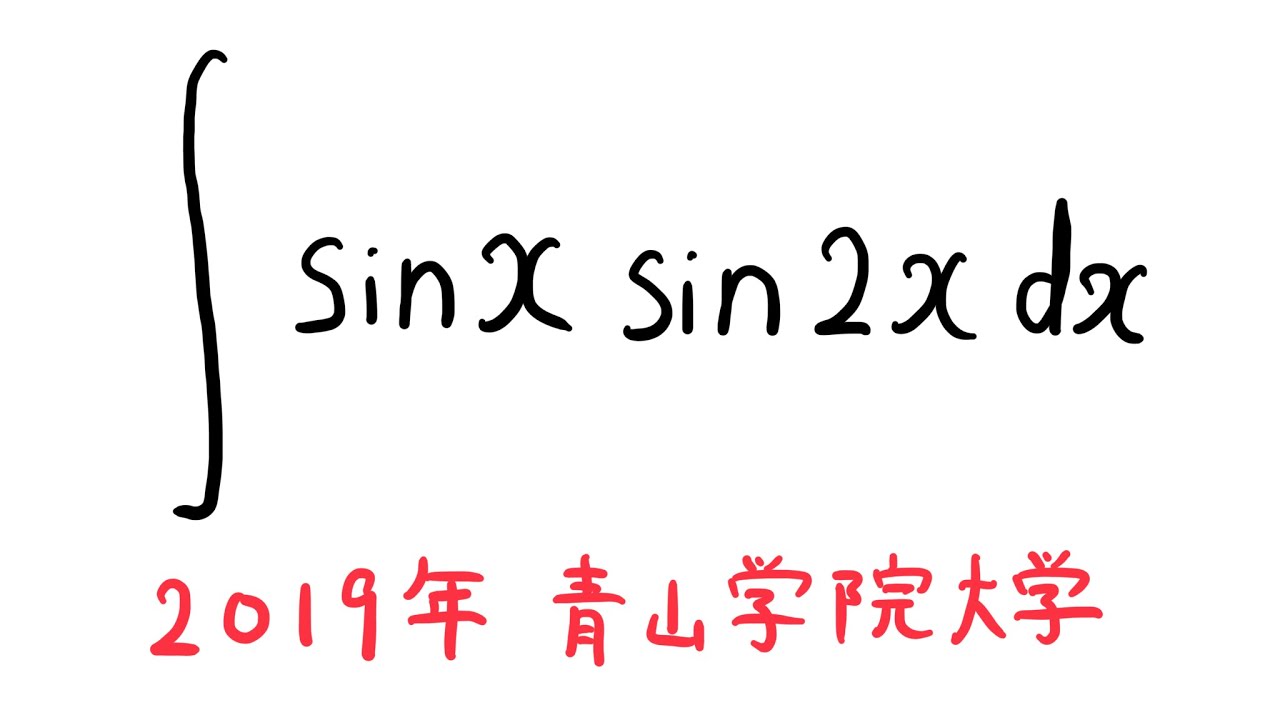
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \sin x \sin 2x$ $dx$
出典:2019年青山学院大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \sin x \sin 2x$ $dx$
出典:2019年青山学院大学
#青山学院大学(2006) #定積分 #Shorts
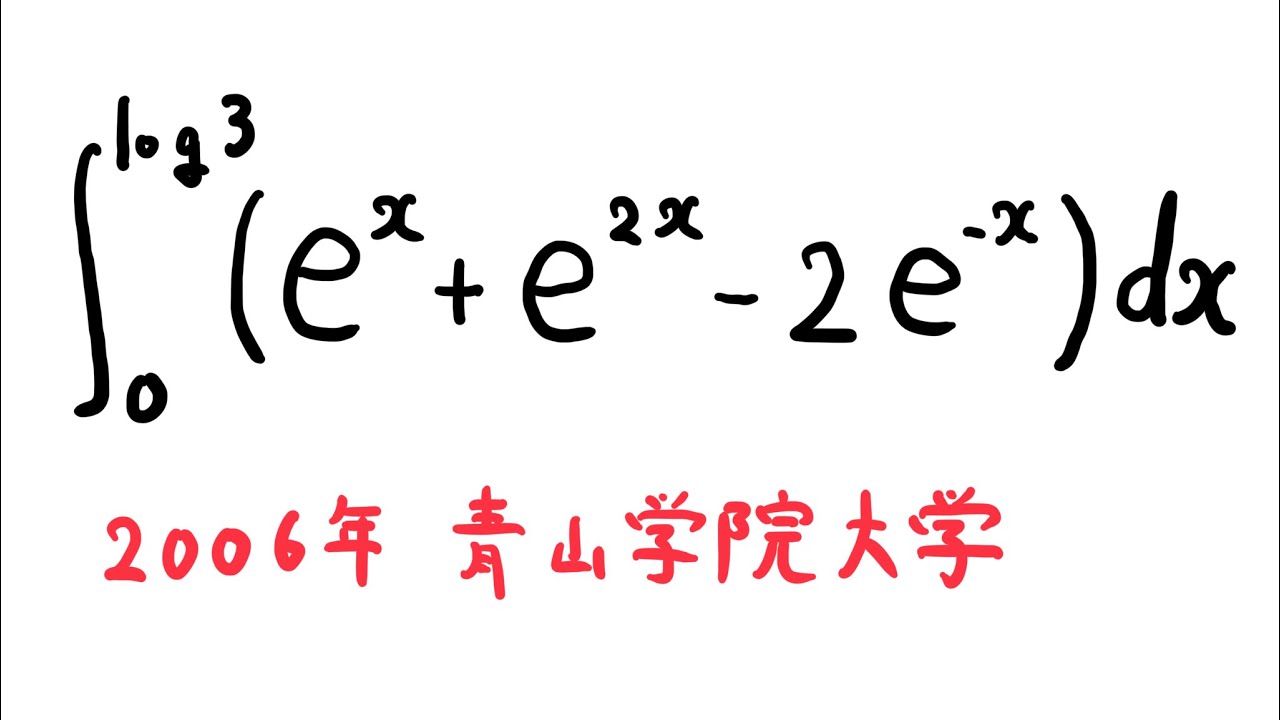
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log3} (e^x+e^{2x}-2e^{-x}) dx$
出典:2006年青山学院大学
この動画を見る
$\displaystyle \int_{0}^{log3} (e^x+e^{2x}-2e^{-x}) dx$
出典:2006年青山学院大学
大学入試問題#847「もうネタ切れ寸前」 #青山学院大学(2006) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \{log(4-x^2)+2\} dx$
出典:2006年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \{log(4-x^2)+2\} dx$
出典:2006年青山学院大学 入試問題
大学入試問題#779「コメントするなら普通の問題」 青山学院大学(2021) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\sqrt{ n^2+2n+16 }$ が整数となるような整数$n$をすべて求めよ
出典:2021年青山学院大学
この動画を見る
$\sqrt{ n^2+2n+16 }$ が整数となるような整数$n$をすべて求めよ
出典:2021年青山学院大学
大学入試問題#773「綺麗な良問」 青山学院大学(2019) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
素数$p.q$および自然数$n$に対し
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{pq}=\displaystyle \frac{1}{n}$
が成り立つような$(p,q,n)$の組をすべて求めよ
出典:2019年青山学院大学
この動画を見る
素数$p.q$および自然数$n$に対し
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{pq}=\displaystyle \frac{1}{n}$
が成り立つような$(p,q,n)$の組をすべて求めよ
出典:2019年青山学院大学
大学入試問題#714「The basic integral problem」 青山学院大(2021) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{5} \displaystyle \frac{dx}{(x+3)\sqrt{ x+1 }}$
出典:2021年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{5} \displaystyle \frac{dx}{(x+3)\sqrt{ x+1 }}$
出典:2021年青山学院大学 入試問題
大学入試問題#654「特に工夫はなし」 青山学院大学(2012) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} (x^2+2x+3)log(x+1) dx$
出典:2012年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2} (x^2+2x+3)log(x+1) dx$
出典:2012年青山学院大学 入試問題
大学入試問題#649「慌てない慌てない」 青山学院大(2006) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} x(1+x^2\sin\displaystyle \frac{\pi\ x}{2}) dx$
出典:2006年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} x(1+x^2\sin\displaystyle \frac{\pi\ x}{2}) dx$
出典:2006年青山学院大学 入試問題
大学入試問題#644 青山学院大(2022) #積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$
$f(x)=\displaystyle \int_{1}^{e} log(xt)f(t) \ dt+x$のとき$f(x)$を求めよ
出典:2022年青山学院大学 入試問題
この動画を見る
$x \gt 0$
$f(x)=\displaystyle \int_{1}^{e} log(xt)f(t) \ dt+x$のとき$f(x)$を求めよ
出典:2022年青山学院大学 入試問題
福田の数学〜青山学院大学2023年理工学部第5問〜定積分で定義された数列と極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ $a_n$=$\displaystyle\frac{1}{n!}\int_1^e(\log x)^ndx$ ($n$=1,2,3,...)とおく。
(1)$a_1$を求めよ。
(2)不等式0≦$a_n$≦$\frac{e-1}{n!}$ が成り立つことを示せ。
(3)$n$≧2のとき、$a_n$=$\displaystyle\frac{e}{n!}$-$a_{n-1}$ であることを示せ。
(4)$\displaystyle\lim_{n \to \infty}\sum_{k=2}^n\frac{(-1)^k}{k!}$ を求めよ。
この動画を見る
$\Large\boxed{5}$ $a_n$=$\displaystyle\frac{1}{n!}\int_1^e(\log x)^ndx$ ($n$=1,2,3,...)とおく。
(1)$a_1$を求めよ。
(2)不等式0≦$a_n$≦$\frac{e-1}{n!}$ が成り立つことを示せ。
(3)$n$≧2のとき、$a_n$=$\displaystyle\frac{e}{n!}$-$a_{n-1}$ であることを示せ。
(4)$\displaystyle\lim_{n \to \infty}\sum_{k=2}^n\frac{(-1)^k}{k!}$ を求めよ。
福田の数学〜青山学院大学2023年理工学部第4問〜関数の増減と実数解をもつ条件

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ (1)関数
$y$=$\displaystyle-\frac{\cos3x}{\sin^3x}$ (0<$x$<$\pi$)
の増減と極値を調べ、そのグラフの概形を描け。ただし、グラフの凹凸は調べなくてよい。
(2)$a$を実数の定数とする。$x$についての方程式
$-\cos3x$=$a\sin^3x$
が$\displaystyle\frac{\pi}{6}$<$x$<$\displaystyle\frac{2\pi}{3}$の範囲に実数解をもつような$a$の値の範囲を求めよ。
この動画を見る
$\Large\boxed{4}$ (1)関数
$y$=$\displaystyle-\frac{\cos3x}{\sin^3x}$ (0<$x$<$\pi$)
の増減と極値を調べ、そのグラフの概形を描け。ただし、グラフの凹凸は調べなくてよい。
(2)$a$を実数の定数とする。$x$についての方程式
$-\cos3x$=$a\sin^3x$
が$\displaystyle\frac{\pi}{6}$<$x$<$\displaystyle\frac{2\pi}{3}$の範囲に実数解をもつような$a$の値の範囲を求めよ。
福田の数学〜青山学院大学2023年理工学部第3問〜放物線上の4点で作る四角形の面積の最大
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
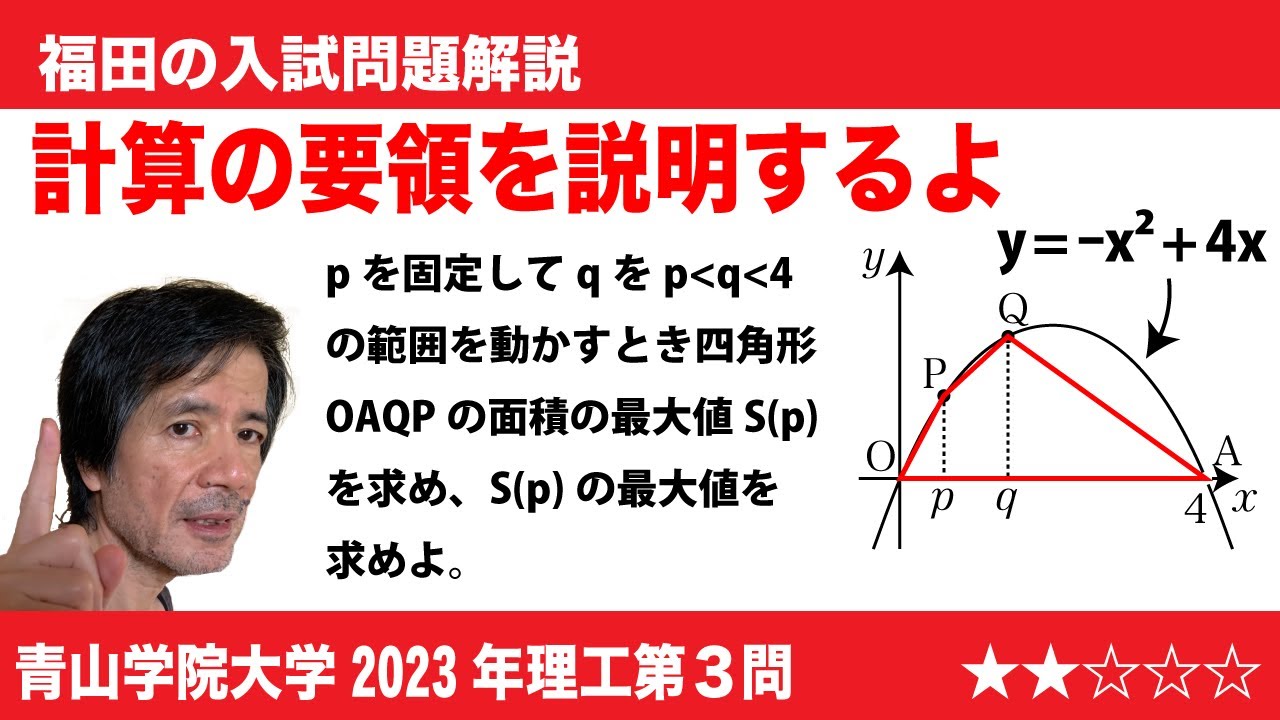
$\Large\boxed{3}$ 点Oを原点とするxy平面上の放物線
$y$=$-x^2$+$4x$
を$C$とする。また、放物線$C$上に点A(4,0), P($p$, $-p^2+4p$), Q($q$, $-q^2+4q$)をとる。ただし、0<$p$<$q$<4 とする。
(1)放物線$C$の接線のうち、直線APと傾きが等しいものを$l$とする。接線$l$の方程式を求めよ。
(2)点Pを固定する。点Qが$p$<$q$<4 を満たしながら動くとき、四角形OAQPの面積の最大値を$p$を用いて表せ。
(3)(2)で求めた四角形OAQPの面積の最大値を$S(p)$とおく。0<$p$<4 のとき、
関数$S(p)$の最大値を求めよ。
この動画を見る
$\Large\boxed{3}$ 点Oを原点とするxy平面上の放物線
$y$=$-x^2$+$4x$
を$C$とする。また、放物線$C$上に点A(4,0), P($p$, $-p^2+4p$), Q($q$, $-q^2+4q$)をとる。ただし、0<$p$<$q$<4 とする。
(1)放物線$C$の接線のうち、直線APと傾きが等しいものを$l$とする。接線$l$の方程式を求めよ。
(2)点Pを固定する。点Qが$p$<$q$<4 を満たしながら動くとき、四角形OAQPの面積の最大値を$p$を用いて表せ。
(3)(2)で求めた四角形OAQPの面積の最大値を$S(p)$とおく。0<$p$<4 のとき、
関数$S(p)$の最大値を求めよ。
福田の数学〜青山学院大学2023年理工学部第2問〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 白石と黒石を手元にたくさん用意する。表が白色、裏が黒色の硬貨1枚を用いて、机の上で以下の操作を繰り返し行う。ただし、最初の操作は机の上に石が1個もない状態から始めるものとする。
操作:効果を投げ、出た色と異なる色の石が机の上にあればその中の1個を取り除き、なければ出た色と同じ色の石を手元から机の上に1個置く。
とくに、机の上に石が1個もなければ、次の回の操作では出た色と同じ色の石を手元から机の上に1個置く。
(1)3回目の操作後に机の上に石がちょうど3個ある確率は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(2)6回目の操作後に机の上に石がちょうど2個ある確率は$\frac{\boxed{\ \ ウエ\ \ }}{\boxed{\ \ オカ\ \ }}$であり、石が1個もない確率は$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ クケ\ \ }}$である。
(3)6回目の操作後に机の上にある石が2個以下であったときに、8回目の操作後に机の上にある石も2個以下である条件付き確率は$\frac{\boxed{\ \ コサ\ \ }}{\boxed{\ \ シス\ \ }}$である。
この動画を見る
$\Large\boxed{2}$ 白石と黒石を手元にたくさん用意する。表が白色、裏が黒色の硬貨1枚を用いて、机の上で以下の操作を繰り返し行う。ただし、最初の操作は机の上に石が1個もない状態から始めるものとする。
操作:効果を投げ、出た色と異なる色の石が机の上にあればその中の1個を取り除き、なければ出た色と同じ色の石を手元から机の上に1個置く。
とくに、机の上に石が1個もなければ、次の回の操作では出た色と同じ色の石を手元から机の上に1個置く。
(1)3回目の操作後に机の上に石がちょうど3個ある確率は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$である。
(2)6回目の操作後に机の上に石がちょうど2個ある確率は$\frac{\boxed{\ \ ウエ\ \ }}{\boxed{\ \ オカ\ \ }}$であり、石が1個もない確率は$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ クケ\ \ }}$である。
(3)6回目の操作後に机の上にある石が2個以下であったときに、8回目の操作後に机の上にある石も2個以下である条件付き確率は$\frac{\boxed{\ \ コサ\ \ }}{\boxed{\ \ シス\ \ }}$である。
福田の数学〜青山学院大学2023年理工学部第1問〜空間ベクトルとと四面体の体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#数C#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 座標空間の3点A(0,1,2), B(3,-2,2), C(-1,4,1)が定める平面を$\alpha$とする。
原点Oから平面$\alpha$に垂線を下ろし、$\alpha$との交点をHとする。
(1)$\overrightarrow{AB}$・$\overrightarrow{AC}$=$\boxed{\ \ アイウ\ \ }$
(2)$\triangle$ABCの面積は$\frac{\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$である。
(3)$\overrightarrow{AH}$=$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ クケ\ \ }}$$\overrightarrow{AB}$+$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$$\overrightarrow{AC}$, $\overrightarrow{OH}$=$\frac{\boxed{\ \ シ\ \ }\sqrt{\boxed{\ \ ス\ \ }}}{\boxed{\ \ セ\ \ }}$
(4)四面体OHBCの体積は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$である。
この動画を見る
$\Large\boxed{1}$ 座標空間の3点A(0,1,2), B(3,-2,2), C(-1,4,1)が定める平面を$\alpha$とする。
原点Oから平面$\alpha$に垂線を下ろし、$\alpha$との交点をHとする。
(1)$\overrightarrow{AB}$・$\overrightarrow{AC}$=$\boxed{\ \ アイウ\ \ }$
(2)$\triangle$ABCの面積は$\frac{\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$である。
(3)$\overrightarrow{AH}$=$\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ クケ\ \ }}$$\overrightarrow{AB}$+$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$$\overrightarrow{AC}$, $\overrightarrow{OH}$=$\frac{\boxed{\ \ シ\ \ }\sqrt{\boxed{\ \ ス\ \ }}}{\boxed{\ \ セ\ \ }}$
(4)四面体OHBCの体積は$\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}$である。
青山学院大学(2007年) #Shorts

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{4} \displaystyle \frac{x^2+1}{x+1} dx$
出典:2007年青山学院大学
この動画を見る
$\displaystyle \int_{0}^{4} \displaystyle \frac{x^2+1}{x+1} dx$
出典:2007年青山学院大学
青山学院大

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
【青山学院大 過去問】
AとB対戦
Aが勝つ確率$\displaystyle \frac{2}{3}$
Bが勝つ確率$\displaystyle \frac{1}{3}$
最大7試合でどちらかが4勝した時点で終了
第6試合で決着する確率
この動画を見る
【青山学院大 過去問】
AとB対戦
Aが勝つ確率$\displaystyle \frac{2}{3}$
Bが勝つ確率$\displaystyle \frac{1}{3}$
最大7試合でどちらかが4勝した時点で終了
第6試合で決着する確率
青山学院大 放物線の中の四角形

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#青山学院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
青山学院大学過去問題
$f(x)=-x^2+4x$
原点O,A(4,0),P(p,f(p)),Q(q,f(q)) (0<p<q<4)
四角形OAQPの面積の最大値
この動画を見る
青山学院大学過去問題
$f(x)=-x^2+4x$
原点O,A(4,0),P(p,f(p)),Q(q,f(q)) (0<p<q<4)
四角形OAQPの面積の最大値
青山学院大 放物線の中の四角形

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#図形の性質#図形と計量#一次不等式(不等式・絶対値のある方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=-x^2+4x$
原点$O,A(4,0),P(p,f_{(p)}),Q(q,f_{(q)})$ $(0\lt p\lt q\lt 4)$
四角形$OAQP$の面積の最大値を求めよ.
青山学院大過去問
この動画を見る
$f(x)=-x^2+4x$
原点$O,A(4,0),P(p,f_{(p)}),Q(q,f_{(q)})$ $(0\lt p\lt q\lt 4)$
四角形$OAQP$の面積の最大値を求めよ.
青山学院大過去問
青山学院大 微分の基礎

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#青山学院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
青山学院大学過去問題
$C:y=x^2$
A(-1,1),B(4,16)
放物線C上にx座標が
$t(-1<t<4)$である点P
直線AB上にx座標がtである点Qととる。
△APQの面積の最大値とそのときのtの値
この動画を見る
青山学院大学過去問題
$C:y=x^2$
A(-1,1),B(4,16)
放物線C上にx座標が
$t(-1<t<4)$である点P
直線AB上にx座標がtである点Qととる。
△APQの面積の最大値とそのときのtの値
