 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
【数学】2022年度神奈川県立高校入試数学大問2

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
(ア)$0.2x+0.8y=1,\dfrac{1}{2}x+\dfrac{7}{8}y=-2$
(イ)$4x^2-x-2=0$
(ウ)$y=\dfrac{-1}{4}x^2,$xの変域が$-2\leqq x\leqq 4$のとき,yの変域は?
(エ)A班の生徒と,A班よりも5人少ないB班の生徒で,体育館にイスを並べた。A班の生徒はそれぞれ3脚ずつ並べ、B班の生徒はそれぞれ4脚ずつ並べたところ,A班の生徒が並べたイスの総数はB班の生徒が並べたイスの総数より3脚多かった。A班の生徒の人数を求めなさい。
(オ)$x=\sqrt6+\sqrt3,y=\sqrt6-\sqrt3$ のとき、$x^2y+xy^2$の値は?
この動画を見る
(ア)$0.2x+0.8y=1,\dfrac{1}{2}x+\dfrac{7}{8}y=-2$
(イ)$4x^2-x-2=0$
(ウ)$y=\dfrac{-1}{4}x^2,$xの変域が$-2\leqq x\leqq 4$のとき,yの変域は?
(エ)A班の生徒と,A班よりも5人少ないB班の生徒で,体育館にイスを並べた。A班の生徒はそれぞれ3脚ずつ並べ、B班の生徒はそれぞれ4脚ずつ並べたところ,A班の生徒が並べたイスの総数はB班の生徒が並べたイスの総数より3脚多かった。A班の生徒の人数を求めなさい。
(オ)$x=\sqrt6+\sqrt3,y=\sqrt6-\sqrt3$ のとき、$x^2y+xy^2$の値は?
高等学校入学試験予想問題:関西学院高等部~全部入試問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
・$(\sqrt{ 5 }-2)(\sqrt{ 5 }+3)-\displaystyle \frac{(\sqrt{ 7 }-2)(\sqrt{ 7 }+\sqrt{ 7 })}{\sqrt{ 20 }}
を計算せよ。
【連立方程式】
$(x+3y):(4x-2y)=3:5$
$3x-5y=12$
$x$と$y$を求めよ。
1から9の数字が書かれたカードが 1枚ずつある。この9枚のカードから3枚を
選んで左から並べて3桁の整数を作る。
(1)整数は全部でいくつか。
(2)偶数はいくつか。
(3) 4の倍数はいくつか。
(4)3の倍数はいくつか
を求めよ。
この動画を見る
・$(\sqrt{ 5 }-2)(\sqrt{ 5 }+3)-\displaystyle \frac{(\sqrt{ 7 }-2)(\sqrt{ 7 }+\sqrt{ 7 })}{\sqrt{ 20 }}
を計算せよ。
【連立方程式】
$(x+3y):(4x-2y)=3:5$
$3x-5y=12$
$x$と$y$を求めよ。
1から9の数字が書かれたカードが 1枚ずつある。この9枚のカードから3枚を
選んで左から並べて3桁の整数を作る。
(1)整数は全部でいくつか。
(2)偶数はいくつか。
(3) 4の倍数はいくつか。
(4)3の倍数はいくつか
を求めよ。
福田の1.5倍速演習〜合格する重要問題096〜早稲田大学2020年度理工学部第3問〜水の問題

単元:
#大学入試過去問(数学)#積分とその応用#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 曲線 x=g(y)のy≧0の部分とx軸上の線分0≦x≦g(0)のなす曲線をCとし、Cをy軸のまわりに1回転してできる容器をVとする。ただし、g(y)はy≧0で定義された正の関数とする。Vに毎秒一定量vの水を注ぐとする。t秒後のV内の水位をy=h(t)とするとき、以下の問に答えよ。
(1)水位が一定の速さで上昇するとき、g(y)は定数関数であることを示せ。
(2)g(y)=$e^y$のとき、h(t)を求めよ。
2020早稲田大学理工学部過去問
この動画を見る
$\Large\boxed{3}$ 曲線 x=g(y)のy≧0の部分とx軸上の線分0≦x≦g(0)のなす曲線をCとし、Cをy軸のまわりに1回転してできる容器をVとする。ただし、g(y)はy≧0で定義された正の関数とする。Vに毎秒一定量vの水を注ぐとする。t秒後のV内の水位をy=h(t)とするとき、以下の問に答えよ。
(1)水位が一定の速さで上昇するとき、g(y)は定数関数であることを示せ。
(2)g(y)=$e^y$のとき、h(t)を求めよ。
2020早稲田大学理工学部過去問
大学入試問題#441「見た目と違って解いてみたら、良問と実感するはず!」 信州大学(2022) #不等式

単元:
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$:自然数
$0 \leqq x$:実数
$log(1+x) \geqq \displaystyle \sum_{k=1}^{2n} \displaystyle \frac{(-1)^{k-1}}{k}x^k$を示せ
出典:2022年信州大学 入試問題
この動画を見る
$n$:自然数
$0 \leqq x$:実数
$log(1+x) \geqq \displaystyle \sum_{k=1}^{2n} \displaystyle \frac{(-1)^{k-1}}{k}x^k$を示せ
出典:2022年信州大学 入試問題
福田の1.5倍速演習〜合格する重要問題095〜明治大学2020年度理工学部第1問(3)〜円順列と確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)A, B, C, D, Eの5人が、無作為に並び、手をつないでひとつの輪を作るという試行を考える。
(a)この試行を1回行うとき、AがBとCの2人と手をつなぐ確率は$\frac{\boxed{コ}}{\boxed{サ}}$である。
(b)この試行を3回行うとき、Aと3回手をつなぐ人が2人いる確率は$\frac{\boxed{シ}}{\boxed{スセ}}$である。
(c)この試行を3回行うとき、Aと3回手をつなぐ人が1人だけいる確率は$\frac{\boxed{ソ}}{\boxed{タ}}$である。
2020明治大学理工学部過去問
この動画を見る
$\Large\boxed{1}$ (3)A, B, C, D, Eの5人が、無作為に並び、手をつないでひとつの輪を作るという試行を考える。
(a)この試行を1回行うとき、AがBとCの2人と手をつなぐ確率は$\frac{\boxed{コ}}{\boxed{サ}}$である。
(b)この試行を3回行うとき、Aと3回手をつなぐ人が2人いる確率は$\frac{\boxed{シ}}{\boxed{スセ}}$である。
(c)この試行を3回行うとき、Aと3回手をつなぐ人が1人だけいる確率は$\frac{\boxed{ソ}}{\boxed{タ}}$である。
2020明治大学理工学部過去問
大学入試問題#440「この積分は初見では、きついが、アイデアは知っておくべき」 東北医科薬科大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{(x^3+1)^2}$
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{x^3+1}=\displaystyle \frac{\sqrt{ 3 }}{9}\pi+\displaystyle \frac{1}{3}log\ 2$
出典:2023年東北医科薬科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{(x^3+1)^2}$
$\displaystyle \int_{0}^{1} \displaystyle \frac{dx}{x^3+1}=\displaystyle \frac{\sqrt{ 3 }}{9}\pi+\displaystyle \frac{1}{3}log\ 2$
出典:2023年東北医科薬科大学 入試問題
近畿大(医)やっぱり出た2023年問題

単元:
#数A#大学入試過去問(数学)#整数の性質#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a,n$は整数$(n \geqq2)a$から始まる連続n個の整数の和が2023となる$(a,n)$の組は,
(1)全部で何通りか?
(2)a,nともに奇数は何通りか?
近畿大(医)過去問
この動画を見る
$ a,n$は整数$(n \geqq2)a$から始まる連続n個の整数の和が2023となる$(a,n)$の組は,
(1)全部で何通りか?
(2)a,nともに奇数は何通りか?
近畿大(医)過去問
福田の1.5倍速演習〜合格する重要問題094〜青山学院大学2020年度理工学部第5問〜グラフと面積と回転体の体積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#体積・表面積・回転体・水量・変化のグラフ#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 関数$f(x)=\displaystyle\frac{1}{x^2+1}$について、以下の問いに答えよ。
(1)y=f(x)のグラフの概形を描け。凹凸も調べること。
(2)原点をOとし、y=f(x)のグラフの変曲点のうちx座標が正のものをPとする。
直線OPとy軸、y=f(x)のグラフとで囲まれた図形をDとする。Dの面積Sを求めよ。
(3)(2)の図形Dをy軸の周りに1回転してできる回転体の体積Vを求めよ。
2020青山学院大学理工学部過去問
この動画を見る
$\Large\boxed{5}$ 関数$f(x)=\displaystyle\frac{1}{x^2+1}$について、以下の問いに答えよ。
(1)y=f(x)のグラフの概形を描け。凹凸も調べること。
(2)原点をOとし、y=f(x)のグラフの変曲点のうちx座標が正のものをPとする。
直線OPとy軸、y=f(x)のグラフとで囲まれた図形をDとする。Dの面積Sを求めよ。
(3)(2)の図形Dをy軸の周りに1回転してできる回転体の体積Vを求めよ。
2020青山学院大学理工学部過去問
大学入試問題#439「国立大学らしい綺麗な問題」 群馬大学(2015) #微分方程式
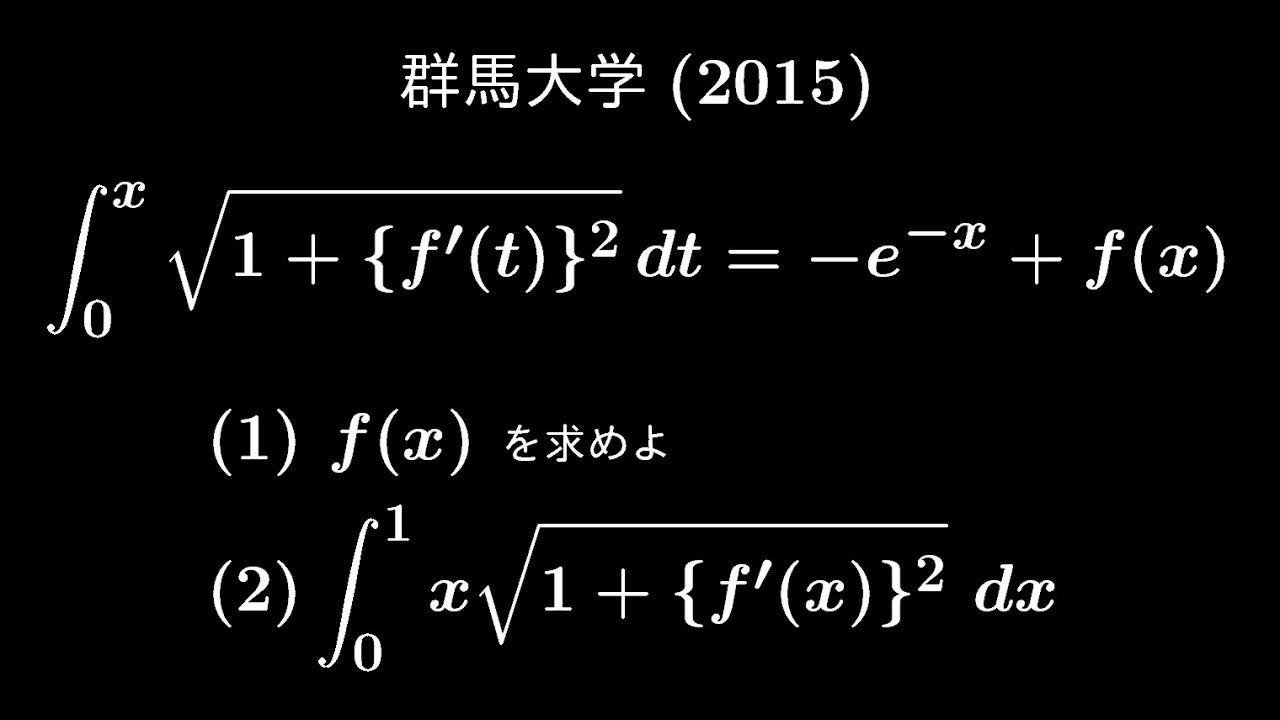
単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{x} \sqrt{ 1+\{f'(t)\}^2 }dt=-e^{-x}+f(x)$
(1)
$f(x)$を求めよ。
(2)
$\displaystyle \int_{0}^{1} x\sqrt{ 1+\{f'(x)\}^2 }\ dx$
出典:2015年群馬大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{x} \sqrt{ 1+\{f'(t)\}^2 }dt=-e^{-x}+f(x)$
(1)
$f(x)$を求めよ。
(2)
$\displaystyle \int_{0}^{1} x\sqrt{ 1+\{f'(x)\}^2 }\ dx$
出典:2015年群馬大学 入試問題
藤田医科大 ドモアブルの定理

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#数学(高校生)#藤田医科大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(1+i)^n=(1-i)n$をみたす2023以下の自然数nの個数を答えよ.
2023藤田医科大過去問
この動画を見る
$(1+i)^n=(1-i)n$をみたす2023以下の自然数nの個数を答えよ.
2023藤田医科大過去問
【工夫あり】二次方程式の解を四捨五入!?【一橋大学】【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$m,n$を正の整数とする。$x$についての二次方程式$12x^2-mx+n=0$の二つの実数解を小数第2位で四捨五入して0.3および0.7を得た。$m,n$を求めよ。
一橋大過去問
この動画を見る
$m,n$を正の整数とする。$x$についての二次方程式$12x^2-mx+n=0$の二つの実数解を小数第2位で四捨五入して0.3および0.7を得た。$m,n$を求めよ。
一橋大過去問
福田の1.5倍速演習〜合格する重要問題093〜中央大学2020年度理工学部第5問〜円周上の点と三角形五角形の面積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#微分法と積分法#三角関数とグラフ#加法定理とその応用#学校別大学入試過去問解説(数学)#面積、体積#中央大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 原点Oを中心とする半径1の円周上に2点
Q($\cos a$, $\sin a$), R($\cos(a+b), \sin(a+b)$)
をとる。ただし、a, bはa >0,b >0, a +b<$\frac{\pi}{2}$を満たす。また、点Qからx軸へ下ろした垂線の足を点Pとし、点Rからy軸へ下した垂線の足を点Sとする。
$\triangle$OPQの面積と$\triangle$ORSの面積の和をA, 五角形OPQRSの面積をBとおく。
(1)Aをaとbで表せ。
(2)bを固定して、aを0<a<$\frac{\pi}{2}$-bの範囲で動かすとき、Aがとりうる値の範囲をbで表し、Aが最大値をとるときのaの値をbで表せ。
(3)Bはa=$\frac{\pi}{8}$, b=$\frac{\pi}{4}$のときに最大値をとることを示せ。
2020中央大学理工学部過去問
この動画を見る
$\Large\boxed{5}$ 原点Oを中心とする半径1の円周上に2点
Q($\cos a$, $\sin a$), R($\cos(a+b), \sin(a+b)$)
をとる。ただし、a, bはa >0,b >0, a +b<$\frac{\pi}{2}$を満たす。また、点Qからx軸へ下ろした垂線の足を点Pとし、点Rからy軸へ下した垂線の足を点Sとする。
$\triangle$OPQの面積と$\triangle$ORSの面積の和をA, 五角形OPQRSの面積をBとおく。
(1)Aをaとbで表せ。
(2)bを固定して、aを0<a<$\frac{\pi}{2}$-bの範囲で動かすとき、Aがとりうる値の範囲をbで表し、Aが最大値をとるときのaの値をbで表せ。
(3)Bはa=$\frac{\pi}{8}$, b=$\frac{\pi}{4}$のときに最大値をとることを示せ。
2020中央大学理工学部過去問
大学入試問題#438「積分区間が[0,π/6]なんですけど・・」 藤田医科大学(2023) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{\sin^33x}{\sin^33x+\cos^33x} dx$
出典:2023年藤田医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{\sin^33x}{\sin^33x+\cos^33x} dx$
出典:2023年藤田医科大学 入試問題
中学生も挑戦して!関西医科 因数分解

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$(a+1)(a-1)(b+1)(b-1)=4ab$をみたす整数を求めよ.$(a,b)(a<b)$
関西医科大過去問
この動画を見る
$(a+1)(a-1)(b+1)(b-1)=4ab$をみたす整数を求めよ.$(a,b)(a<b)$
関西医科大過去問
福田の1.5倍速演習〜合格する重要問題075〜浜松医科大学2017年度医学部第1問〜複素数の実部と虚部

単元:
#大学入試過去問(数学)#複素数平面#関数と極限#複素数平面#図形への応用#数列の極限#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 以下の問いに答えよ。
(1)|z| ≦ |z-($\sqrt 3 + i$)|, |z-$\bar{z}$| ≦ 1および|z-$2i$| ≦ 2を同時にみたす複素数zに対応する点の領域を複素数平面上に図示せよ。
(2)(1)で得られた領域内の点に対応する複素数のうち、実部が最大となるものを$\alpha$、実部と虚部の和が最大となるものを$\beta$とするとき、$\alpha$と$\beta$を求めよ。
(3)次の式で定義される$w_n$の実部を$R_n$とするとき、無限級数$\displaystyle\sum_{n=1}^{\infty}R_n$の和を求めよ。
$w_n=\displaystyle\frac{\{1+(2-\sqrt 3)i\}(\sqrt 3+i)^{3(n-1)}}{2^{4(n-1)}}$ $(n=1,2,3,\dots)$
2017浜松医科大学医学部過去問
この動画を見る
$\Large\boxed{1}$ 以下の問いに答えよ。
(1)|z| ≦ |z-($\sqrt 3 + i$)|, |z-$\bar{z}$| ≦ 1および|z-$2i$| ≦ 2を同時にみたす複素数zに対応する点の領域を複素数平面上に図示せよ。
(2)(1)で得られた領域内の点に対応する複素数のうち、実部が最大となるものを$\alpha$、実部と虚部の和が最大となるものを$\beta$とするとき、$\alpha$と$\beta$を求めよ。
(3)次の式で定義される$w_n$の実部を$R_n$とするとき、無限級数$\displaystyle\sum_{n=1}^{\infty}R_n$の和を求めよ。
$w_n=\displaystyle\frac{\{1+(2-\sqrt 3)i\}(\sqrt 3+i)^{3(n-1)}}{2^{4(n-1)}}$ $(n=1,2,3,\dots)$
2017浜松医科大学医学部過去問
大学入試問題#437「y-xが邪魔なんだけど・・・・」 信州大学(2014) #不等式

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
すべての実数$x,y$に対して
$\displaystyle \frac{1}{1+x^2+(y-x)^2} \leqq \displaystyle \frac{a}{1+x^2+y^2}$が成り立つような$a$の値の範囲を求めよ。
出典:2014年信州大学医学部 入試問題
この動画を見る
すべての実数$x,y$に対して
$\displaystyle \frac{1}{1+x^2+(y-x)^2} \leqq \displaystyle \frac{a}{1+x^2+y^2}$が成り立つような$a$の値の範囲を求めよ。
出典:2014年信州大学医学部 入試問題
立命館大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 55x^2+2xy+y^2=2007$をみたす整数(x,y)をすべて求めよ.
立命館大過去問
この動画を見る
$ 55x^2+2xy+y^2=2007$をみたす整数(x,y)をすべて求めよ.
立命館大過去問
【数学】東大理科2022大問6ガチ解説!(2)一般化して考えるとどのようになっているかを考察しながら初見で解きます!

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
東大理系数学2022大問6
Oを原点とする座標平面上で考える。0以上の整数kに対して、$\vec{v_k}$を
$\vec{v_k}=\left(\cos\dfrac{2k\pi}{3}\right),\sin\left(\dfrac{2k\pi}{3}\right)$
と定める。投げたとき表と裏がどちらも1/2の確率で出るコインをN回投げて座標平面上に点$X_0,X_1,X_2,…,X_N$を以下の規則(i)(ii)に従って定める。
(i)$X_0$はOにある。
(ii)nを1以上N以下の整数とする。$X_{n_1}$が定まったとし、$X_n$を次のように定める。
・n回目のコイン投げで表が出た場合、
$\vec{OX_n}=\vec{OX_{n-1}}+\vec{v_k}$
により$X_n$を定める。ただし、kは1回目からn回目までのコイン投げで裏が出た回数とする。
・n回目のコイン投げで裏が出た場合、$X_n$を$X_{n-1}$と定める。
(1)$N=8$とする。$X_8$がOにある確率を求めよ。
(2)$N=200$とする。$X_{200}$がOにあり、かつ、合計200回のコイン投げで表がちょうどr回出る確率を$p_r$とおく。ただし$0\leqq r\leqq 200$とする。$p_r$を求めよ。また$p_r$が最大となるrの値を求めよ。
この動画を見る
東大理系数学2022大問6
Oを原点とする座標平面上で考える。0以上の整数kに対して、$\vec{v_k}$を
$\vec{v_k}=\left(\cos\dfrac{2k\pi}{3}\right),\sin\left(\dfrac{2k\pi}{3}\right)$
と定める。投げたとき表と裏がどちらも1/2の確率で出るコインをN回投げて座標平面上に点$X_0,X_1,X_2,…,X_N$を以下の規則(i)(ii)に従って定める。
(i)$X_0$はOにある。
(ii)nを1以上N以下の整数とする。$X_{n_1}$が定まったとし、$X_n$を次のように定める。
・n回目のコイン投げで表が出た場合、
$\vec{OX_n}=\vec{OX_{n-1}}+\vec{v_k}$
により$X_n$を定める。ただし、kは1回目からn回目までのコイン投げで裏が出た回数とする。
・n回目のコイン投げで裏が出た場合、$X_n$を$X_{n-1}$と定める。
(1)$N=8$とする。$X_8$がOにある確率を求めよ。
(2)$N=200$とする。$X_{200}$がOにあり、かつ、合計200回のコイン投げで表がちょうどr回出る確率を$p_r$とおく。ただし$0\leqq r\leqq 200$とする。$p_r$を求めよ。また$p_r$が最大となるrの値を求めよ。
福田の1.5倍速演習〜合格する重要問題074〜立教大学2019年度経済学部第1問(6)〜最大公約数を求める

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (6)14351と14803の最大公約数は$\boxed{\ \ キ \ \ }$である。
2019立教大学経済学部過去問
この動画を見る
$\Large\boxed{1}$ (6)14351と14803の最大公約数は$\boxed{\ \ キ \ \ }$である。
2019立教大学経済学部過去問
大学入試問題#436「2次試験までに一度は解くべき問題!!」 東京大学(1995) #不等式

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
すべての正の実数$x,y$に対し、
$\sqrt{ x }+\sqrt{ y } \leqq k\sqrt{ 2x+y }$ が成り立つような実数$k$の最小値を求めよ
出典:1995年東京大学 入試問題
この動画を見る
すべての正の実数$x,y$に対し、
$\sqrt{ x }+\sqrt{ y } \leqq k\sqrt{ 2x+y }$ が成り立つような実数$k$の最小値を求めよ
出典:1995年東京大学 入試問題
東京医科大 3乗根の不等式

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ \sqrt[3]{n+1}-\sqrt[3]{n}<\dfrac{1}{48}$を満たす最小の自然数nを求めよ.
東京医科大過去問
この動画を見る
$ \sqrt[3]{n+1}-\sqrt[3]{n}<\dfrac{1}{48}$を満たす最小の自然数nを求めよ.
東京医科大過去問
福田の1.5倍速演習〜合格する重要問題073〜東京理科大学2019年度理工学部第3問〜定積分と不等式そして極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 関数f(x)を$f(x)=\displaystyle\int_0^x\frac{dt}{1+t^2}$と定める。
(1)t=$\tan\theta$とおく置換積分により$f(1)=\displaystyle\int_0^1\frac{dt}{1+t^2}$の値を求めよ。
(2)0 $\lt$ $\alpha$ $\lt$ 1とし、mを自然数とするとき、以下の不等式が成り立つことを示せ。
$f(a)\displaystyle\int_a^1x^mdx$ $\lt$ $\displaystyle\int_a^1f(x)x^mdx$ $\lt$ $\displaystyle\int_0^1f(x)x^mdx$ $\lt$ $f(1)\displaystyle\int_0^1x^mdx$
(3)$\displaystyle\lim_{m \to \infty}\left(1-\frac{1}{\sqrt m}\right)^m$を求めよ。必要ならばs >1のとき$\displaystyle\left(1-\frac{1}{s}\right)^s \lt \frac{1}{2}$となることを用いてよい。
(4)$\displaystyle\lim_{m \to \infty}m\int_{1-\frac{1}{\sqrt m}}^1f(x)x^mdx$を求めよ。
2019東京理科大学理工学部過去問
この動画を見る
$\Large\boxed{3}$ 関数f(x)を$f(x)=\displaystyle\int_0^x\frac{dt}{1+t^2}$と定める。
(1)t=$\tan\theta$とおく置換積分により$f(1)=\displaystyle\int_0^1\frac{dt}{1+t^2}$の値を求めよ。
(2)0 $\lt$ $\alpha$ $\lt$ 1とし、mを自然数とするとき、以下の不等式が成り立つことを示せ。
$f(a)\displaystyle\int_a^1x^mdx$ $\lt$ $\displaystyle\int_a^1f(x)x^mdx$ $\lt$ $\displaystyle\int_0^1f(x)x^mdx$ $\lt$ $f(1)\displaystyle\int_0^1x^mdx$
(3)$\displaystyle\lim_{m \to \infty}\left(1-\frac{1}{\sqrt m}\right)^m$を求めよ。必要ならばs >1のとき$\displaystyle\left(1-\frac{1}{s}\right)^s \lt \frac{1}{2}$となることを用いてよい。
(4)$\displaystyle\lim_{m \to \infty}m\int_{1-\frac{1}{\sqrt m}}^1f(x)x^mdx$を求めよ。
2019東京理科大学理工学部過去問
大学入試問題#435「基本的な性質が盛り沢山の良問!!」 信州大学(2014) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{3\sin\theta-\sin3\theta}{1+\cos\theta}d\theta$
出典:2014年信州大学理学部後期 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{3\sin\theta-\sin3\theta}{1+\cos\theta}d\theta$
出典:2014年信州大学理学部後期 入試問題
算数できない投資情報誌の記者の記事が医大の入試問題に 小学生もチャレンジしてね!
単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
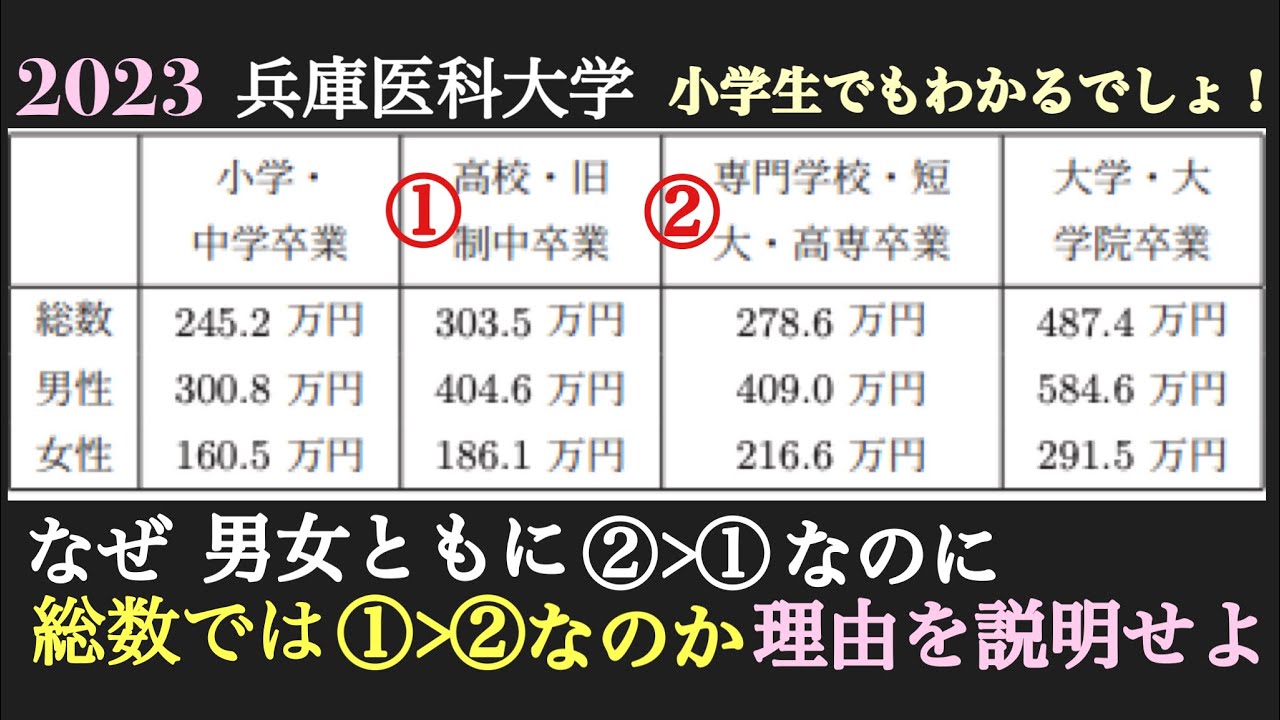
次の文章は,「貯蓄額や所得の多い少ないは「学歴」と関係あるのか?」という記事^1からの抜粋である。表は厚生労働省の令和元年国民生活基礎調査から,学歴ごとの平均所得金額(15歳以上の雇用者1人あたり)をまとめたものです。(中略)
男性・女性ともに専門学校・短大・高専卒の方が所得金額が多いのに,総数となると高校・旧制中卒の方が多いのは統計上の謎です。
男性の所得金額も女性の所得金額もともに,専門学校・短大・高専卒業の方が,高校・旧制中卒業より多いのに,総数(男性+女性)では,逆転した結果になっている。これはどうしてか?説明しなさい。
医大入試問題過去問
この動画を見る
次の文章は,「貯蓄額や所得の多い少ないは「学歴」と関係あるのか?」という記事^1からの抜粋である。表は厚生労働省の令和元年国民生活基礎調査から,学歴ごとの平均所得金額(15歳以上の雇用者1人あたり)をまとめたものです。(中略)
男性・女性ともに専門学校・短大・高専卒の方が所得金額が多いのに,総数となると高校・旧制中卒の方が多いのは統計上の謎です。
男性の所得金額も女性の所得金額もともに,専門学校・短大・高専卒業の方が,高校・旧制中卒業より多いのに,総数(男性+女性)では,逆転した結果になっている。これはどうしてか?説明しなさい。
医大入試問題過去問
図形×整数問題!差がつく問題です【一橋大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
直角三角形の3辺の長さがすべて整数のとき、面積は2の整数倍であることを示せ。
一橋大過去問
この動画を見る
直角三角形の3辺の長さがすべて整数のとき、面積は2の整数倍であることを示せ。
一橋大過去問
福田の1.5倍速演習〜合格する重要問題072〜上智大学2019年度理工学部第3問〜ガウス記号で定義された数列

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $\alpha=\log_23$とし、自然数nに対して
$a_n=[n\alpha]$, $b_n=\left[\displaystyle\frac{n\alpha}{\alpha-1}\right]$
とする。ただし、実数xに対して[x]はxを超えない最大の整数を表す。
(1)$a_5=\boxed{\ \ ス\ \ }$である。
(2)$b_3=k$とおくと、不等式$\displaystyle\frac{3^{k+c}}{2^k} \leqq 1 \lt \frac{3^{k+1+c}}{2^{k+1}}$が整数$c=\boxed{\ \ セ\ \ }$で成り立ち、
$b_3=\boxed{\ \ ソ\ \ }$であることがわかる。
(3)$a_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ タ\ \ }$である。
(4)$b_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ チ\ \ }$である。
(5)$a_n \leqq$ 50を満たす自然数nの個数をsとし、$b_n \leqq$ 50を満たす自然数nの個数をtとする。このとき、s+t=$\boxed{\ \ ツ\ \ }$である。
2019上智大学理工学部過去問
この動画を見る
$\Large{\boxed{3}}$ $\alpha=\log_23$とし、自然数nに対して
$a_n=[n\alpha]$, $b_n=\left[\displaystyle\frac{n\alpha}{\alpha-1}\right]$
とする。ただし、実数xに対して[x]はxを超えない最大の整数を表す。
(1)$a_5=\boxed{\ \ ス\ \ }$である。
(2)$b_3=k$とおくと、不等式$\displaystyle\frac{3^{k+c}}{2^k} \leqq 1 \lt \frac{3^{k+1+c}}{2^{k+1}}$が整数$c=\boxed{\ \ セ\ \ }$で成り立ち、
$b_3=\boxed{\ \ ソ\ \ }$であることがわかる。
(3)$a_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ タ\ \ }$である。
(4)$b_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ チ\ \ }$である。
(5)$a_n \leqq$ 50を満たす自然数nの個数をsとし、$b_n \leqq$ 50を満たす自然数nの個数をtとする。このとき、s+t=$\boxed{\ \ ツ\ \ }$である。
2019上智大学理工学部過去問
大学入試問題#434「基本的な式変形」 藤田医科大学(2023) #式変形

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師:
ますただ
問題文全文(内容文):
$\alpha=\sqrt{ 6+2\sqrt{ 5 } }$のとき
$\alpha^5-\alpha^4-12\alpha^3+12\alpha^2+16\alpha$の値を求めよ。
出典:2023年藤田医科大学 入試問題
この動画を見る
$\alpha=\sqrt{ 6+2\sqrt{ 5 } }$のとき
$\alpha^5-\alpha^4-12\alpha^3+12\alpha^2+16\alpha$の値を求めよ。
出典:2023年藤田医科大学 入試問題
大学入試問題#433「初手が大事」 #一橋大学(2020) #極限
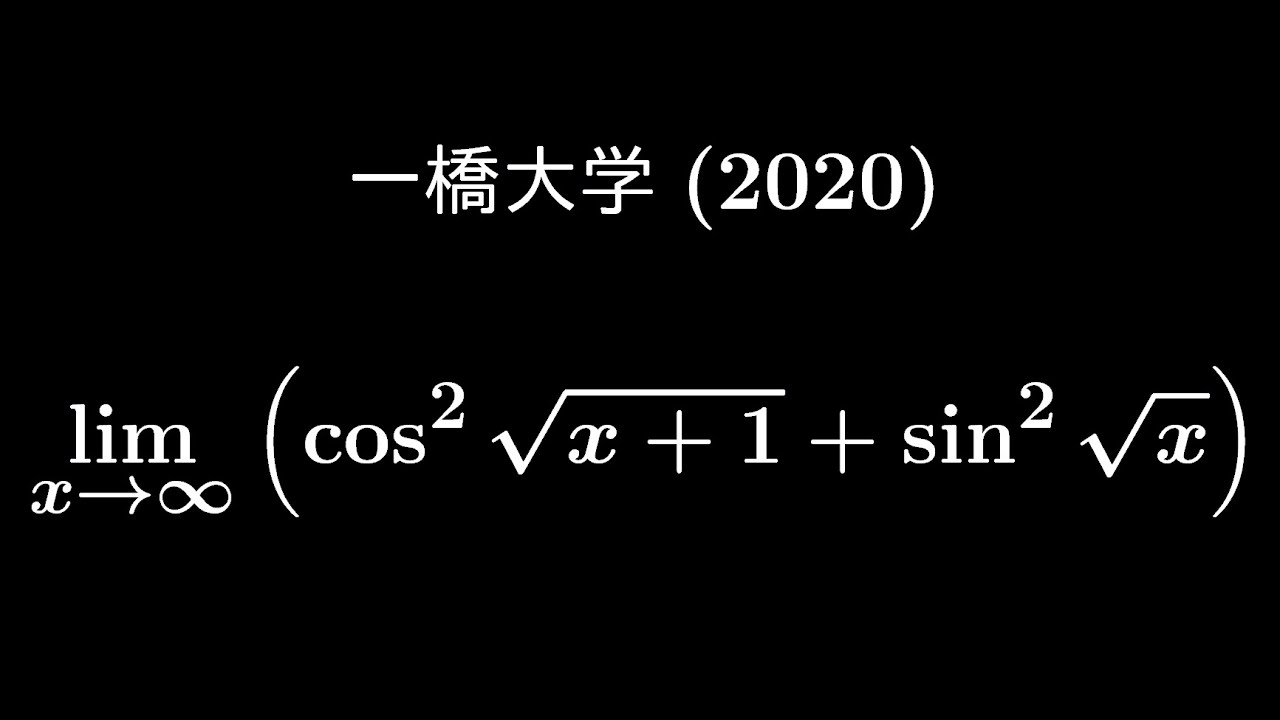
単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to \infty } (\cos^2\sqrt{ x+1 }+\sin^2\sqrt{ x })$
出典:2020年一橋大学(後期) 入試問題
この動画を見る
$\displaystyle \lim_{ x \to \infty } (\cos^2\sqrt{ x+1 }+\sin^2\sqrt{ x })$
出典:2020年一橋大学(後期) 入試問題
福田の1.5倍速演習〜合格する重要問題071〜東京医科歯科大学2017年度医学部第2問〜空間における球面と軌跡の問題

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と方程式#円と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ xyz空間において、点O(0, 0, 0)と点A(0, 0, 1)を結ぶ線分OAを直径にもつ球面を$\sigma$とする。このとき以下の各問に答えよ。
(1) 球面$\sigma$の方程式を求めよ。
(2) xy平面上にあってOと異なる点Pに対して、線分APと球面$\sigma$との交点をQとするとき、$\overrightarrow{ OQ } \bot \overrightarrow{ AP }$を示せ。
(3) 点S(p, q, r)を$\overrightarrow{OS}・\overrightarrow{ AS }=-|\overrightarrow{ OS }|^2$を満たす、xy平面上にない定点とする。$\sigma$上の点Qが$\overrightarrow{ OS } \bot \overrightarrow{ SQ }$を満たしながら動くとき、直線AQとxy平面上の交点Pはどのような図形を描くか。p, q, rを用いて答えよ。
2017東京医科歯科大学医学部過去問
この動画を見る
$\Large{\boxed{2}}$ xyz空間において、点O(0, 0, 0)と点A(0, 0, 1)を結ぶ線分OAを直径にもつ球面を$\sigma$とする。このとき以下の各問に答えよ。
(1) 球面$\sigma$の方程式を求めよ。
(2) xy平面上にあってOと異なる点Pに対して、線分APと球面$\sigma$との交点をQとするとき、$\overrightarrow{ OQ } \bot \overrightarrow{ AP }$を示せ。
(3) 点S(p, q, r)を$\overrightarrow{OS}・\overrightarrow{ AS }=-|\overrightarrow{ OS }|^2$を満たす、xy平面上にない定点とする。$\sigma$上の点Qが$\overrightarrow{ OS } \bot \overrightarrow{ SQ }$を満たしながら動くとき、直線AQとxy平面上の交点Pはどのような図形を描くか。p, q, rを用いて答えよ。
2017東京医科歯科大学医学部過去問
中学生でも解ける大学入試問題!【早稲田大学】【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$x$の二次関数$y=ax^2+bx+c$のグラフが相違なる3点$(a,b),(b,c),(c,a)$を通るものとする。
ただし,$abc≠0$とする。このとき,次の問いに答えよ。
(1)$a$の値を求めよ。
(2)$b,c$の値を求めよ。
早稲田大過去問
この動画を見る
$x$の二次関数$y=ax^2+bx+c$のグラフが相違なる3点$(a,b),(b,c),(c,a)$を通るものとする。
ただし,$abc≠0$とする。このとき,次の問いに答えよ。
(1)$a$の値を求めよ。
(2)$b,c$の値を求めよ。
早稲田大過去問
