 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
こういう問題に苦手意識ある人は必見です【甲南大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
次の2つの等式を満たす多項式$(x),g(x)$及び定数$a$を求めよ。
$\displaystyle \int_{1}^{x} f(t) dt=2xg(x)-3x+a $
$g(x)=x^2+x \displaystyle \int_{0}^{1} f(t)dx+1$
甲南大過去問
この動画を見る
次の2つの等式を満たす多項式$(x),g(x)$及び定数$a$を求めよ。
$\displaystyle \int_{1}^{x} f(t) dt=2xg(x)-3x+a $
$g(x)=x^2+x \displaystyle \int_{0}^{1} f(t)dx+1$
甲南大過去問
福田の数学〜北里大学2022年医学部第1問(4)〜放物線と2法線で囲まれた面積の最小

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
大問1の(4)
放物線 $C:y=x^2$上に、2つの動点P(p,p²), Q (q, q²)がある。点PにおけるCの接線l₁と点 Q における C の接線l₂は垂直であり、 $p>0$であるとする。
このとき、qはpを用いてq=[ス]と表され、$l₁$と$l₂$およびCで囲まれた部分の面積Sはpを用いて S=[セ]と表される。
点PにおけるCの法線と点QにおけるCの法線の交点をRとし、 2つの線分PRとQRおよびCで囲まれた部分の面積をTとおく。 pが正の実数全体を動くとき、Tの最小値は[ソ]である。
この動画を見る
大問1の(4)
放物線 $C:y=x^2$上に、2つの動点P(p,p²), Q (q, q²)がある。点PにおけるCの接線l₁と点 Q における C の接線l₂は垂直であり、 $p>0$であるとする。
このとき、qはpを用いてq=[ス]と表され、$l₁$と$l₂$およびCで囲まれた部分の面積Sはpを用いて S=[セ]と表される。
点PにおけるCの法線と点QにおけるCの法線の交点をRとし、 2つの線分PRとQRおよびCで囲まれた部分の面積をTとおく。 pが正の実数全体を動くとき、Tの最小値は[ソ]である。
大学入試問題#350「見た目とのギャップ」 岩手医科大学2019 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\sqrt{ 3 }}{2}} \displaystyle \frac{dx}{(1-x^2)^2}$
出典:2019年岩手医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\sqrt{ 3 }}{2}} \displaystyle \frac{dx}{(1-x^2)^2}$
出典:2019年岩手医科大学 入試問題
福田の数学〜北里大学2022年医学部第1問(3)〜不定方程式の解

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(3) 等式 $30x-23y=1$を満たす正の整数の組(x, y) のうち、$x+y$ が最小となる
ものは[キ]である。
$A={n|n$ は 600 以下の正の整数であり、30の倍数である}
$B={n|n$ は 600 以下の正の整数であり、 n を 23 で割ると4余る}
とおく。このとき、 AUBに属する正の整数の総和は[ク]である。
また、m を正の整数とし、 $∨m^2 +120$ は整数であるとすると、mのとり得る値は[ヶ],[コ],[サ],[シ]である。
2022北里大学医学部過去問
この動画を見る
(3) 等式 $30x-23y=1$を満たす正の整数の組(x, y) のうち、$x+y$ が最小となる
ものは[キ]である。
$A={n|n$ は 600 以下の正の整数であり、30の倍数である}
$B={n|n$ は 600 以下の正の整数であり、 n を 23 で割ると4余る}
とおく。このとき、 AUBに属する正の整数の総和は[ク]である。
また、m を正の整数とし、 $∨m^2 +120$ は整数であるとすると、mのとり得る値は[ヶ],[コ],[サ],[シ]である。
2022北里大学医学部過去問
大学入試問題#349「定跡どおりの超良問」 獨協医科大学2019 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\sqrt{ 5 }}^{2\sqrt{ 3 }} \sqrt{ 1+(\displaystyle \frac{2}{x})^2 }\ dx$
出典:2019年獨協医科大学 入試問題
この動画を見る
$\displaystyle \int_{\sqrt{ 5 }}^{2\sqrt{ 3 }} \sqrt{ 1+(\displaystyle \frac{2}{x})^2 }\ dx$
出典:2019年獨協医科大学 入試問題
福田の数学〜北里大学2022年医学部第1問(2)〜逆関数と方程式の解

単元:
#大学入試過去問(数学)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
1 (2) $f(x) = log (x/1-x)$ とする。
関数f(x) の逆関数は $f^-1 (x) = [エ]$である。
方程式$f^-1 (x) - a=0$が実数解をもつとき、 定数aのとり得る値の範囲は[オ]である。
方程式 ${f^-1(x)}²-bf^-1 (x)-3b=0$が実数解をもつとき、 定数 bのとり得る値の範囲は[カ]である。
2022北里大学医学部過去問
この動画を見る
1 (2) $f(x) = log (x/1-x)$ とする。
関数f(x) の逆関数は $f^-1 (x) = [エ]$である。
方程式$f^-1 (x) - a=0$が実数解をもつとき、 定数aのとり得る値の範囲は[オ]である。
方程式 ${f^-1(x)}²-bf^-1 (x)-3b=0$が実数解をもつとき、 定数 bのとり得る値の範囲は[カ]である。
2022北里大学医学部過去問
大学入試問題#348「もはや、あれで置換」 横浜国立大学 #定積分

単元:
#大学入試過去問(数学)#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{1}{2}} x^2\sqrt{ 1-x^2 }\ dx$
出典:横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{1}{2}} x^2\sqrt{ 1-x^2 }\ dx$
出典:横浜国立大学 入試問題
数Ⅱ微分の良問です【大阪大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問
この動画を見る
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問
数Ⅱ微分の良問です【大阪大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問
この動画を見る
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問
福田の数学〜北里大学2022年医学部第1問(1)〜複素数平面上の点の軌跡

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
1 (1)iを虚数単位とし、$α= -2+2i,β=3+i$とする。
このとき、$α^5$の値は[ア]である。
zは等式 $2|z-α| = |z-β|$を満たす複素数全体を動くとする。
このとき、複素数平面上の点P(z) が描く図形は円であり、その中心を表す複素数は[イ]である。
また、 |z| の最大値は[ウ]である。
2022北里大学医学部過去問
この動画を見る
1 (1)iを虚数単位とし、$α= -2+2i,β=3+i$とする。
このとき、$α^5$の値は[ア]である。
zは等式 $2|z-α| = |z-β|$を満たす複素数全体を動くとする。
このとき、複素数平面上の点P(z) が描く図形は円であり、その中心を表す複素数は[イ]である。
また、 |z| の最大値は[ウ]である。
2022北里大学医学部過去問
大学入試問題#347 東京電機大学 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京電機大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{3}} (x\ \tan\ x-log(\cos\ x)) dx$
出典:東京電機大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{3}} (x\ \tan\ x-log(\cos\ x)) dx$
出典:東京電機大学 入試問題
福田の数学〜中央大学2022年理工学部第4問〜複素数平面上の共線条件と正三角形になる条件

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$t$を実数とし、xの3次式f(x) を
$f(x) = x^3 + (1-2t)x^2+(4-2t)x+4$
により定める。以下の問いに答えよ。
(1) 3次式f(x) を実数係数の2次式と1次式の積に因数分解し、$f(x) = 0$ が虚数の
解をもつようなtの範囲を求めよ。
実数tが (1) で求めた範囲にあるとき、方程式 $f(x) = 0$ の異なる2つの虚数解を
α, βとし、実数解をγとする。ただし、$α$の虚部は正、$β$の虚部は負とする。
以下、$α, β, γ$を複素数平面上の点とみなす。
(2) $α, β, γ$をtを用いて表せ。また、実数tが (1) で求めた範囲を動くとき、点$α$
が描く図形を複素数平面上に図示せよ。
(3) 3点$α, β, γ$が一直線上にあるようなtの値を求めよ。
(4)3点$α, β, γ$が正三角形の頂点となるようなtの値を求めよ。
2022中央大学理工学部過去問
この動画を見る
$t$を実数とし、xの3次式f(x) を
$f(x) = x^3 + (1-2t)x^2+(4-2t)x+4$
により定める。以下の問いに答えよ。
(1) 3次式f(x) を実数係数の2次式と1次式の積に因数分解し、$f(x) = 0$ が虚数の
解をもつようなtの範囲を求めよ。
実数tが (1) で求めた範囲にあるとき、方程式 $f(x) = 0$ の異なる2つの虚数解を
α, βとし、実数解をγとする。ただし、$α$の虚部は正、$β$の虚部は負とする。
以下、$α, β, γ$を複素数平面上の点とみなす。
(2) $α, β, γ$をtを用いて表せ。また、実数tが (1) で求めた範囲を動くとき、点$α$
が描く図形を複素数平面上に図示せよ。
(3) 3点$α, β, γ$が一直線上にあるようなtの値を求めよ。
(4)3点$α, β, γ$が正三角形の頂点となるようなtの値を求めよ。
2022中央大学理工学部過去問
福田の数学〜中央大学2022年理工学部第4問〜複素数平面上の共線条件と正三角形になる条件

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#剰余の定理・因数定理・組み立て除法と高次方程式#図形への応用#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
中央大学2022年理工学部第4問解説です
tを実数とし、 xの3次式f(x) を
ƒ(x) = x³ + (1 − 2t)x² + (4 − 2t)x +4
により定める。以下の問いに答えよ。
(1) 3 次式f(x) を実数係数の2次式と1次式の積に因数分解し、f(x)=0 が虚数の
解をもつようなtの範囲を求めよ。
実数t が (1) で求めた範囲にあるとき、 方程式 f(x) = 0 の異なる2つの虚数解を
a,βとし、実数解をγとする。ただし、αの虚部は正、βの虚部は負とする。
以下、α, β,γを複素数平面上の点とみなす。
(2) α, β,γをtを用いて表せ。また、実数t が (1) で求めた範囲を動くとき、点α
が描く図形を複素数平面上に図示せよ。
(3) 3点 α, β, γが一直線上にあるようなtの値を求めよ。
(4) 3点 α, β, γが正三角形の頂点となるようなtの値を求めよ。
この動画を見る
中央大学2022年理工学部第4問解説です
tを実数とし、 xの3次式f(x) を
ƒ(x) = x³ + (1 − 2t)x² + (4 − 2t)x +4
により定める。以下の問いに答えよ。
(1) 3 次式f(x) を実数係数の2次式と1次式の積に因数分解し、f(x)=0 が虚数の
解をもつようなtの範囲を求めよ。
実数t が (1) で求めた範囲にあるとき、 方程式 f(x) = 0 の異なる2つの虚数解を
a,βとし、実数解をγとする。ただし、αの虚部は正、βの虚部は負とする。
以下、α, β,γを複素数平面上の点とみなす。
(2) α, β,γをtを用いて表せ。また、実数t が (1) で求めた範囲を動くとき、点α
が描く図形を複素数平面上に図示せよ。
(3) 3点 α, β, γが一直線上にあるようなtの値を求めよ。
(4) 3点 α, β, γが正三角形の頂点となるようなtの値を求めよ。
大学入試問題#346「2種類の解法の紹介」 電気通信大学(2013) #定積分 #キングプロパティ

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:2013年電気通信大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:2013年電気通信大学 入試問題
福田の数学〜中央大学2022年理工学部第3問〜指数関数の接線と囲まれる部分の面積

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数 $f(x) = -xe^x$ を考える。曲線$C: y = f(x)$の点(a, f(a)) における接線を$l_a$と
し、接線$l_a$とy軸の交点を $(0, g(a))$ とおく。以下の問いに答えよ。
(1) 接線$l_a$の方程式と$g (a)$を求めよ。
以下、aの関数$g (a)$ が極大値をとるときのaの値をbとおく。
(2) bを求め、点$(b, f(b))$ は曲線Cの変曲点であることを示せ。
(3) 曲線Cの点 $(b, f(b))$ における接線$l_b$と x軸の交点のx座標cを求めよ。さらに、
$c\leqq x\leqq 0$の範囲で曲線Cの概形と接線l_bをxy 平面上に図示せよ。
(4)曲線C、接線$l_b$およびy軸で囲まれた部分の面積Sを求めよ。
2022中央大学理工学部過去問
この動画を見る
関数 $f(x) = -xe^x$ を考える。曲線$C: y = f(x)$の点(a, f(a)) における接線を$l_a$と
し、接線$l_a$とy軸の交点を $(0, g(a))$ とおく。以下の問いに答えよ。
(1) 接線$l_a$の方程式と$g (a)$を求めよ。
以下、aの関数$g (a)$ が極大値をとるときのaの値をbとおく。
(2) bを求め、点$(b, f(b))$ は曲線Cの変曲点であることを示せ。
(3) 曲線Cの点 $(b, f(b))$ における接線$l_b$と x軸の交点のx座標cを求めよ。さらに、
$c\leqq x\leqq 0$の範囲で曲線Cの概形と接線l_bをxy 平面上に図示せよ。
(4)曲線C、接線$l_b$およびy軸で囲まれた部分の面積Sを求めよ。
2022中央大学理工学部過去問
大学入試問題#345「とりあえず第一感は置換積分っぽい」 大阪大学 改 2010 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} (\displaystyle \frac{e^x}{1+e^x})^2 dx$
出典:2010年大阪大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} (\displaystyle \frac{e^x}{1+e^x})^2 dx$
出典:2010年大阪大学 入試問題
3つの整数の最大公約数!解けますか?【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
この動画を見る
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
3つの整数の最大公約数!解けますか?【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
この動画を見る
$n$を自然数とする。3つの整数$n^2+2,n^4+2,n^6+2$の最大公約数$A_n$を求めよ。
京都大過去問
大学入試問題#344「みるからにあの性質・・・」 富山大学 #定積分 #キングプロパティ

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{x\ sin\ x}{1+e^{-x}}dx$
出典:富山大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{x\ sin\ x}{1+e^{-x}}dx$
出典:富山大学 入試問題
福田の数学〜中央大学2022年理工学部第1問〜定積分で表された関数

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数f(x)が
$f(x)=\int_0^{\pi}tf(t)\cos(x+t)dt+\frac{1}{4}$
を満たしている。このとき,
$A= \int_0^{\pi}tf(t)\cos tdt$,
$B=\int_0^{\pi}tf(t)\sin tdt... ①$
とおいて$f(x)$をAとBで表すと、
$f(x)=A×(\ \ \ \boxed{ア}\ \ \ )+B×(\ \ \ \boxed{イ}\ \ \ )+\frac{1}{4}... ②$
となる。ここで、
$\int_0^{\pi}t\cos tdt=-2,\ \ \ \int_0^{\pi}t\cos^2 tdt=\boxed{ウ},\ \ \ \int_0^{\pi}t\sin tdt=\pi$
$\int_0^{\pi}t\sin^2 tdt=\boxed{エ},\ \ \ \int_0^{\pi}t\cos t\sin tdt=\boxed{オ}$
を用い、①に②を代入して整理すると、AとBの満たす連立方程式
$\left\{
\begin{array}{1}
(\ \ \ \boxed{\ \ カ\ \ }\ \ \ )A-\pi B+2=0\\
\pi A +(\ \ \ \boxed{\ \ キ\ \ }\ \ \ )B-\pi = 0\\
\end{array}
\right.$
が得られる。この連立方程式を解くと
$A=\frac{\boxed{ク}}{\pi^4-\pi^2-16},\ \ \ B=\frac{\pi (\ \ \ \boxed{ケ}\ \ \ )}{\pi^4-\pi^2-16}$
が得られ、したがって
$f(x)= \frac{\boxed{ク}}{\pi^4-\pi^2-16}×(\ \ \ \boxed{ア}\ \ \ )+$
$\frac{\pi (\ \ \ \boxed{ケ}\ \ \ )}{\pi^4-\pi^2-16}×(\ \ \ \boxed{イ}\ \ \ )+\frac{1}{4}$
となる。
$\boxed{ア},\boxed{イ}$の解答群
$ⓐ\sin x\ \ \ ⓑ-\sin x\ \ \ ⓒ\cos x\ \ \ ⓓ-\cos x$
$ⓔ\tan x\ \ \ ⓕ-\tan x$
$\boxed{ウ},\boxed{エ},\boxed{オ}$の解答群
$ⓐ\pi \ \ \ ⓑ\frac{\pi}{2}\ \ \ ⓒ\frac{\pi}{4}\ \ \ ⓓ\frac{\pi}{8}\ \ \ ⓔ-\pi $
$ⓕ-\frac{\pi}{2}\ \ \ ⓖ-\frac{\pi}{4}\ \ \ ⓗ-\frac{\pi}{8}\ \ \ ⓘ\pi^2 \ \ \ ⓙ\frac{\pi^2}{2}$
$ⓚ\frac{\pi^2}{4}\ \ \ ⓛ\frac{\pi^2}{8}\ \ \ ⓜ-\pi^2 \ \ \ ⓝ-\frac{\pi^2}{2}\ \ \ ⓞ-\frac{\pi^2}{4}$
$ⓟ-\frac{\pi^2}{8}\ \ \ ⓠ\frac{\pi^2+4}{16}\ \ \ ⓡ\frac{\pi^2-4}{16}\ \ \ ⓢ\frac{-\pi^2+4}{16}\ \ \ ⓣ-\frac{\pi^2+4}{16}$
$\boxed{カ},\boxed{キ},\boxed{ク},\boxed{ケ}$の解答群
$ⓐ\pi^2+2\ \ \ ⓑ\pi^2-2\ \ \ ⓒ-\pi^2+2\ \ \ ⓓ-\pi^2-2$
$ⓔ\pi^2+4\ \ \ ⓕ\pi^2-4\ \ \ ⓖ-\pi^2+4\ \ \ ⓗ-\pi^2-4$
$ⓘ\pi^2+6\ \ \ ⓙ\pi^2-6\ \ \ ⓚ-\pi^2+6\ \ \ ⓛ-\pi^2-6$
$ⓜ\pi^2+8\ \ \ ⓝ\pi^2-8\ \ \ ⓞ-\pi^2+8\ \ \ ⓟ-\pi^2-8$
2022中央大学理工学部過去問
この動画を見る
関数f(x)が
$f(x)=\int_0^{\pi}tf(t)\cos(x+t)dt+\frac{1}{4}$
を満たしている。このとき,
$A= \int_0^{\pi}tf(t)\cos tdt$,
$B=\int_0^{\pi}tf(t)\sin tdt... ①$
とおいて$f(x)$をAとBで表すと、
$f(x)=A×(\ \ \ \boxed{ア}\ \ \ )+B×(\ \ \ \boxed{イ}\ \ \ )+\frac{1}{4}... ②$
となる。ここで、
$\int_0^{\pi}t\cos tdt=-2,\ \ \ \int_0^{\pi}t\cos^2 tdt=\boxed{ウ},\ \ \ \int_0^{\pi}t\sin tdt=\pi$
$\int_0^{\pi}t\sin^2 tdt=\boxed{エ},\ \ \ \int_0^{\pi}t\cos t\sin tdt=\boxed{オ}$
を用い、①に②を代入して整理すると、AとBの満たす連立方程式
$\left\{
\begin{array}{1}
(\ \ \ \boxed{\ \ カ\ \ }\ \ \ )A-\pi B+2=0\\
\pi A +(\ \ \ \boxed{\ \ キ\ \ }\ \ \ )B-\pi = 0\\
\end{array}
\right.$
が得られる。この連立方程式を解くと
$A=\frac{\boxed{ク}}{\pi^4-\pi^2-16},\ \ \ B=\frac{\pi (\ \ \ \boxed{ケ}\ \ \ )}{\pi^4-\pi^2-16}$
が得られ、したがって
$f(x)= \frac{\boxed{ク}}{\pi^4-\pi^2-16}×(\ \ \ \boxed{ア}\ \ \ )+$
$\frac{\pi (\ \ \ \boxed{ケ}\ \ \ )}{\pi^4-\pi^2-16}×(\ \ \ \boxed{イ}\ \ \ )+\frac{1}{4}$
となる。
$\boxed{ア},\boxed{イ}$の解答群
$ⓐ\sin x\ \ \ ⓑ-\sin x\ \ \ ⓒ\cos x\ \ \ ⓓ-\cos x$
$ⓔ\tan x\ \ \ ⓕ-\tan x$
$\boxed{ウ},\boxed{エ},\boxed{オ}$の解答群
$ⓐ\pi \ \ \ ⓑ\frac{\pi}{2}\ \ \ ⓒ\frac{\pi}{4}\ \ \ ⓓ\frac{\pi}{8}\ \ \ ⓔ-\pi $
$ⓕ-\frac{\pi}{2}\ \ \ ⓖ-\frac{\pi}{4}\ \ \ ⓗ-\frac{\pi}{8}\ \ \ ⓘ\pi^2 \ \ \ ⓙ\frac{\pi^2}{2}$
$ⓚ\frac{\pi^2}{4}\ \ \ ⓛ\frac{\pi^2}{8}\ \ \ ⓜ-\pi^2 \ \ \ ⓝ-\frac{\pi^2}{2}\ \ \ ⓞ-\frac{\pi^2}{4}$
$ⓟ-\frac{\pi^2}{8}\ \ \ ⓠ\frac{\pi^2+4}{16}\ \ \ ⓡ\frac{\pi^2-4}{16}\ \ \ ⓢ\frac{-\pi^2+4}{16}\ \ \ ⓣ-\frac{\pi^2+4}{16}$
$\boxed{カ},\boxed{キ},\boxed{ク},\boxed{ケ}$の解答群
$ⓐ\pi^2+2\ \ \ ⓑ\pi^2-2\ \ \ ⓒ-\pi^2+2\ \ \ ⓓ-\pi^2-2$
$ⓔ\pi^2+4\ \ \ ⓕ\pi^2-4\ \ \ ⓖ-\pi^2+4\ \ \ ⓗ-\pi^2-4$
$ⓘ\pi^2+6\ \ \ ⓙ\pi^2-6\ \ \ ⓚ-\pi^2+6\ \ \ ⓛ-\pi^2-6$
$ⓜ\pi^2+8\ \ \ ⓝ\pi^2-8\ \ \ ⓞ-\pi^2+8\ \ \ ⓟ-\pi^2-8$
2022中央大学理工学部過去問
大学入試問題#343「計算のクセが強すぎる」 防衛大学校2013 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#防衛大学校#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
${}^{ \forall } t \in \Bbb R,$
$\sin\ 3t=f(\sin\ t)$
$\displaystyle \int_{0}^{1} \{f(x)\}^2\sqrt{ 1-x^2 }\ dx$
出典:2013年防衛大学校 入試問題
この動画を見る
${}^{ \forall } t \in \Bbb R,$
$\sin\ 3t=f(\sin\ t)$
$\displaystyle \int_{0}^{1} \{f(x)\}^2\sqrt{ 1-x^2 }\ dx$
出典:2013年防衛大学校 入試問題
福田の数学〜上智大学2022年理工学部第4問〜線分の中点の軌跡と直線の通過範囲

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#図形と方程式#軌跡と領域#2次曲線#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
座標平面上に円C$:x^2+y^2=4$と点$P(6,\ 0)$がある。円C上を点$A(2a,\ 2b)$が
動くとき、線分APの中点をMとし、線分APの垂直二等分線をlとする。
(1)点Mの軌跡の方程式を求め、その軌跡を図示せよ。
(2)直線lの方程式をa,\ bを用いて表せ。
(3)直線lが通過する領域を表す不等式を求め、その領域を図示せよ。
2022上智大理工学部過去問
この動画を見る
座標平面上に円C$:x^2+y^2=4$と点$P(6,\ 0)$がある。円C上を点$A(2a,\ 2b)$が
動くとき、線分APの中点をMとし、線分APの垂直二等分線をlとする。
(1)点Mの軌跡の方程式を求め、その軌跡を図示せよ。
(2)直線lの方程式をa,\ bを用いて表せ。
(3)直線lが通過する領域を表す不等式を求め、その領域を図示せよ。
2022上智大理工学部過去問
大学入試問題#342「深夜24時ストック0の選択」 岡山県立大学(2013) #定積分
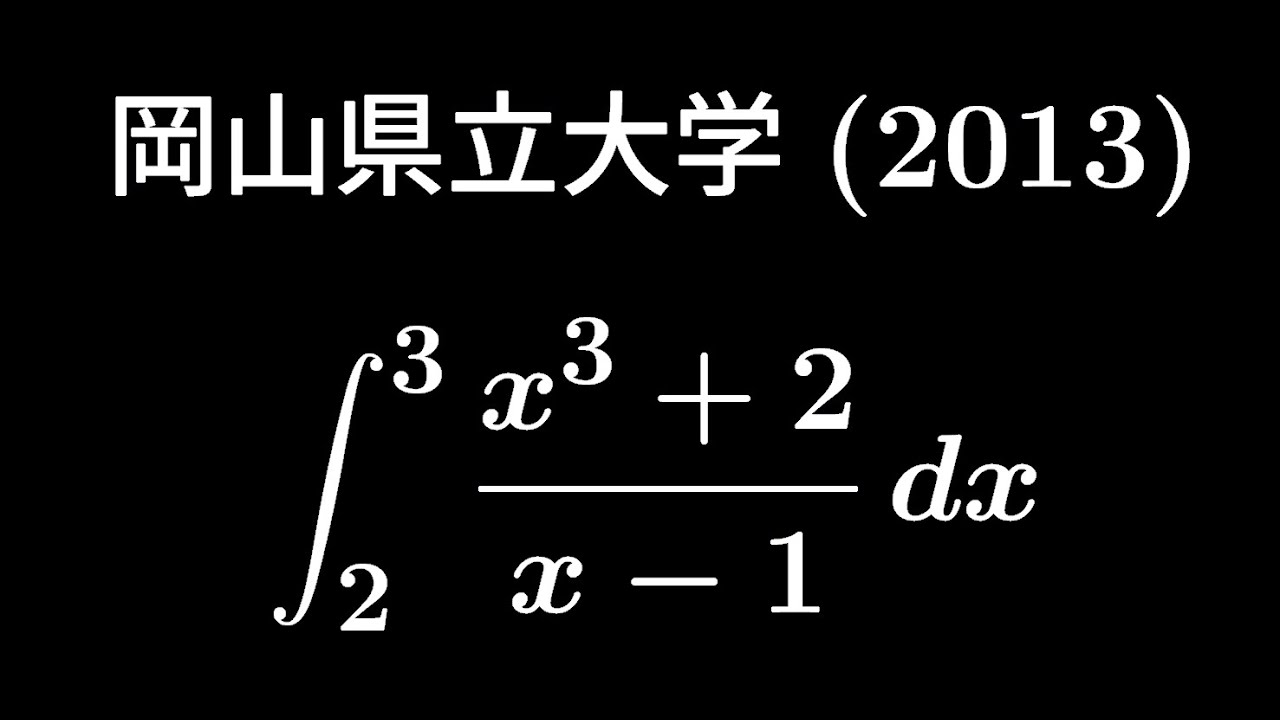
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{3} \displaystyle \frac{x^3+2}{x-1} dx$
出典2013年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{2}^{3} \displaystyle \frac{x^3+2}{x-1} dx$
出典2013年岡山県立大学 入試問題
難問です!三角関数と整数の融合問題!解けますか?【一橋大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形$ABC$において,$ tanA,tanB,tanC$の値がすべて整数であるとき,それらの値を求めよ。
一橋大過去問
この動画を見る
三角形$ABC$において,$ tanA,tanB,tanC$の値がすべて整数であるとき,それらの値を求めよ。
一橋大過去問
福田の数学〜上智大学2022年理工学部第3問〜複素数平面上の点列と三角形の相似

単元:
#大学入試過去問(数学)#複素数平面#相似な図形#数列#漸化式#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数からなる数列${z_n}$を、次の条件で定める。
$z_1=0,\ \ \ z_{n+1}=(1+i)z_n-i \ \ \ (i=1,2,3, \ \ ...)$
正の整数nに対し、z_nに対応する負素数平面上の点をA_nとおく。
(1)$z_2=\boxed{ツ }+\boxed{ツ }\ i, \ \ \ z_3=\boxed{ト}+$
$\boxed{ナ}\ i,\ \ \ z_4=\boxed{二}+\boxed{ヌ}\ i $である。
(2)$r \gt 0,\ 0 \leqq θ \lt 2\pi$ を用いて、$1+i=r(\cos θ+i\sin θ)$のように$1+i$を極形式で
表すとき、$r=\sqrt{\boxed{ネ}},\ θ=\frac{\boxed{ノ }}{\boxed{ハ}}\pi$である。
(3)すべての正の整数nに対する$\triangle PA_nA_{n+1}$が互いに相似になる点Pに対応する
複素数は、$\boxed{ヒ}+\boxed{フ }\ i$である。
(4)$|z_n| \gt 1000$となる最小のnは$n=\boxed{へ}$である。
(5)$A_{2022+k}$が実軸上にある最小の正の整数kは$k=\boxed{ホ}$である。
2022上智大学理工学部過去問
この動画を見る
複素数からなる数列${z_n}$を、次の条件で定める。
$z_1=0,\ \ \ z_{n+1}=(1+i)z_n-i \ \ \ (i=1,2,3, \ \ ...)$
正の整数nに対し、z_nに対応する負素数平面上の点をA_nとおく。
(1)$z_2=\boxed{ツ }+\boxed{ツ }\ i, \ \ \ z_3=\boxed{ト}+$
$\boxed{ナ}\ i,\ \ \ z_4=\boxed{二}+\boxed{ヌ}\ i $である。
(2)$r \gt 0,\ 0 \leqq θ \lt 2\pi$ を用いて、$1+i=r(\cos θ+i\sin θ)$のように$1+i$を極形式で
表すとき、$r=\sqrt{\boxed{ネ}},\ θ=\frac{\boxed{ノ }}{\boxed{ハ}}\pi$である。
(3)すべての正の整数nに対する$\triangle PA_nA_{n+1}$が互いに相似になる点Pに対応する
複素数は、$\boxed{ヒ}+\boxed{フ }\ i$である。
(4)$|z_n| \gt 1000$となる最小のnは$n=\boxed{へ}$である。
(5)$A_{2022+k}$が実軸上にある最小の正の整数kは$k=\boxed{ホ}$である。
2022上智大学理工学部過去問
大学入試問題#341「部分積分の心を・・・」 立教大学 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\sin\ x+x\ \cos\ x)log\ x\ dx$
出典:立教大学 入試問題
この動画を見る
$\displaystyle \int (\sin\ x+x\ \cos\ x)log\ x\ dx$
出典:立教大学 入試問題
2022富山大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\left[\sqrt{3\sqrt3+\dfrac{2}{3\sqrt3-1}}\right]$
これを解け.
富山大過去問
この動画を見る
$\left[\sqrt{3\sqrt3+\dfrac{2}{3\sqrt3-1}}\right]$
これを解け.
富山大過去問
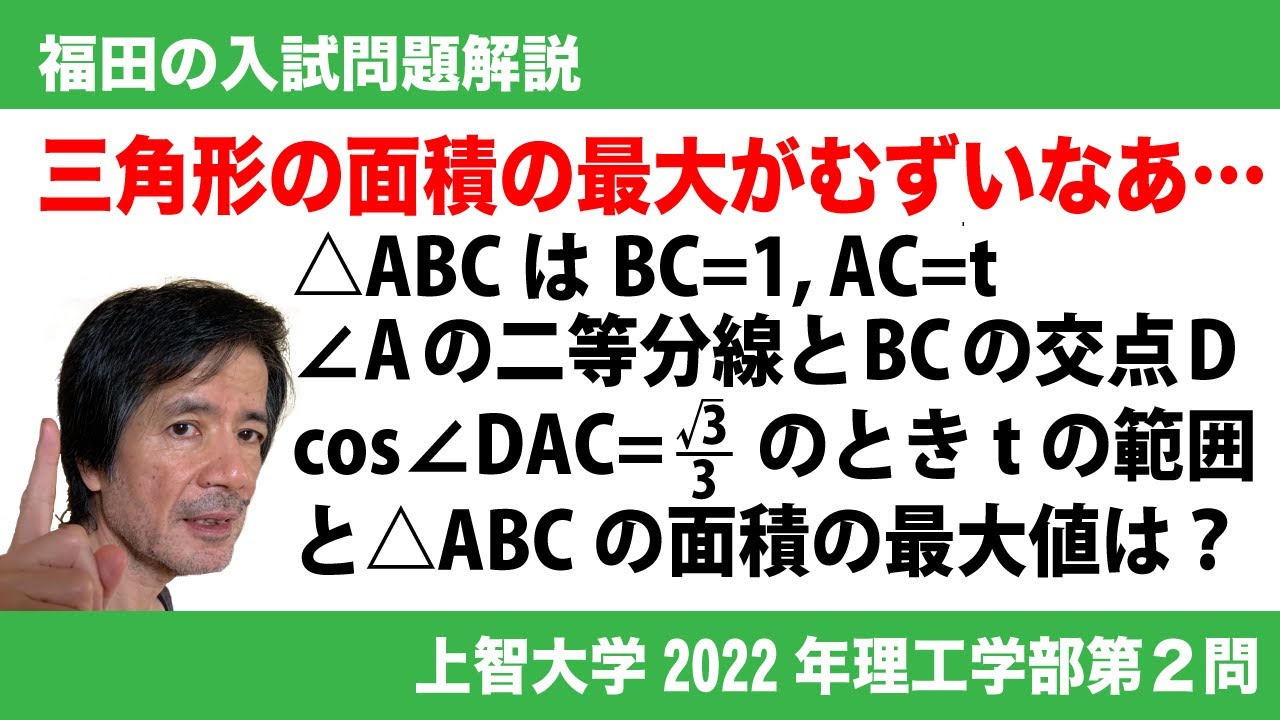
福田の数学〜上智大学2022年理工学部第2問〜三角比と通過領域の体積
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
tを実数とする。次の条件(★)を満たす$\triangle ABC$を考える。
(★)$AC=t,\ BC=1$を満たし、$\angle BAC$の2等分線と辺BCの交点をDとおくと、
$\cos\angle DAC=\frac{\sqrt3}{3}$である。
(1)$\cos\angle DAC=\frac{\boxed{カ}}{\boxed{キ}}$である。
(2)tの取りうる範囲を$t_1\lt t \lt t_2$とするとき、$t_1=\boxed{あ},t_2=\boxed{い}$である。
$\boxed{あ},\ \boxed{い}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{3}\ \ \ (\textrm{c})\frac{1}{2}\ \ \ (\textrm{d})\frac{\sqrt3}{3}\ \ \ (\textrm{e})\frac{2}{3}$
$ (\textrm{f})1\ \ \ (\textrm{g})\frac{2\sqrt3}{2}\ \ \ (\textrm{h})\sqrt3\ \ \ (\textrm{i})2\ \ \ (\textrm{j})3$
(3)辺ABの長さをtの式で表すと$AB=\frac{\boxed{ク}}{\boxed{ケ}}t+$
$\sqrt{1+\frac{\boxed{コ}}{\boxed{サ}}t^2}$である。
(4)$\triangle ABC$の面積は$t=\frac{\sqrt{\boxed{シ}}}{\boxed{ス}}$
で最大値$\frac{\sqrt{\boxed{セ}}}{\boxed{ソ}}$をとる。
(5)$t_1,t_2$を(2)で定めた値とする。
$t_1 \lt t \lt t_2$の範囲で、xyz-座標空間内の平面z=t上に、条件(★)を満たす
$\triangle ABC$が、$B(0,0,t),C(0,1,t)$を満たし、Aのx座標が正であるように
おかれている。まgた、$B_1(0,0,t_1),C_1(0,1,t_1),B_2(0,0,t_2),C_2(0,1,t_2)$と
おく。
$\triangle ABC$を$t_1 \lt t \lt t_2$の範囲で動かしたときに通過してできる図形に線分$B_1C_1$、
線分$B_2C_2$を付け加えた立体の体積は$\frac{\sqrt{\boxed{タ}}}{\boxed{チ}}$である。
この動画を見る
tを実数とする。次の条件(★)を満たす$\triangle ABC$を考える。
(★)$AC=t,\ BC=1$を満たし、$\angle BAC$の2等分線と辺BCの交点をDとおくと、
$\cos\angle DAC=\frac{\sqrt3}{3}$である。
(1)$\cos\angle DAC=\frac{\boxed{カ}}{\boxed{キ}}$である。
(2)tの取りうる範囲を$t_1\lt t \lt t_2$とするとき、$t_1=\boxed{あ},t_2=\boxed{い}$である。
$\boxed{あ},\ \boxed{い}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{3}\ \ \ (\textrm{c})\frac{1}{2}\ \ \ (\textrm{d})\frac{\sqrt3}{3}\ \ \ (\textrm{e})\frac{2}{3}$
$ (\textrm{f})1\ \ \ (\textrm{g})\frac{2\sqrt3}{2}\ \ \ (\textrm{h})\sqrt3\ \ \ (\textrm{i})2\ \ \ (\textrm{j})3$
(3)辺ABの長さをtの式で表すと$AB=\frac{\boxed{ク}}{\boxed{ケ}}t+$
$\sqrt{1+\frac{\boxed{コ}}{\boxed{サ}}t^2}$である。
(4)$\triangle ABC$の面積は$t=\frac{\sqrt{\boxed{シ}}}{\boxed{ス}}$
で最大値$\frac{\sqrt{\boxed{セ}}}{\boxed{ソ}}$をとる。
(5)$t_1,t_2$を(2)で定めた値とする。
$t_1 \lt t \lt t_2$の範囲で、xyz-座標空間内の平面z=t上に、条件(★)を満たす
$\triangle ABC$が、$B(0,0,t),C(0,1,t)$を満たし、Aのx座標が正であるように
おかれている。まgた、$B_1(0,0,t_1),C_1(0,1,t_1),B_2(0,0,t_2),C_2(0,1,t_2)$と
おく。
$\triangle ABC$を$t_1 \lt t \lt t_2$の範囲で動かしたときに通過してできる図形に線分$B_1C_1$、
線分$B_2C_2$を付け加えた立体の体積は$\frac{\sqrt{\boxed{タ}}}{\boxed{チ}}$である。
大学入試問題#340「とりあえず絶対値はずそ」 日本大学医学部(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{4}{3}\pi} |\sqrt{ 3 }\cos\ x-\sin\ x| dx$
出典:2010年日本大学医学部 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{4}{3}\pi} |\sqrt{ 3 }\cos\ x-\sin\ x| dx$
出典:2010年日本大学医学部 入試問題
奈良教育大 超基本問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#奈良教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
7で割ると3余り,17で割ると8余る.自然数,3桁最大は?
奈良教育大過去問
この動画を見る
7で割ると3余り,17で割ると8余る.自然数,3桁最大は?
奈良教育大過去問
