 千葉大学
千葉大学
 千葉大学
千葉大学
大学入試問題#611「ストレートに解けそう」 千葉大学(2014) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} e^{\sin\ x}(\sin2x-2\cos\ x) dx$
出典:2014年千葉大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} e^{\sin\ x}(\sin2x-2\cos\ x) dx$
出典:2014年千葉大学 入試問題
福田の数学〜千葉大学2023年第9問〜関数の増減と最大Part2

単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{9}$ 関数$f(x)$と実数$t$に対し、$x$の関数$tx$-$f(x)$の最大値があればそれを$g(t)$と書く。
(1)$f(x)$=$x^4$のとき、任意の実数$t$について$g(t)$が存在する。この$g(t)$を求めよ。
以下、関数$f(x)$は連続な導関数$f''(x)$を持ち、次の2つの条件(i),(ii)が成り立つものとする。
(i)$f'(x)$は増加関数、すなわち$a$<$b$ならば$f'(a)$<$f'(b)$
(ii)$\displaystyle\lim_{x \to -\infty}f'(x)$=$-\infty$ かつ $\displaystyle\lim_{x \to \infty}f'(x)$=$\infty$
(2)任意の実数$t$に対して、$x$の関数$tx$-$f(x)$は最大値$g(t)$を持つことを示せ。
(3)$s$を実数とする。$t$が実数全体を動くとき、$t$の関数$st$-$g(x)$は最大値$f(s)$となることを示せ。
この動画を見る
$\Large\boxed{9}$ 関数$f(x)$と実数$t$に対し、$x$の関数$tx$-$f(x)$の最大値があればそれを$g(t)$と書く。
(1)$f(x)$=$x^4$のとき、任意の実数$t$について$g(t)$が存在する。この$g(t)$を求めよ。
以下、関数$f(x)$は連続な導関数$f''(x)$を持ち、次の2つの条件(i),(ii)が成り立つものとする。
(i)$f'(x)$は増加関数、すなわち$a$<$b$ならば$f'(a)$<$f'(b)$
(ii)$\displaystyle\lim_{x \to -\infty}f'(x)$=$-\infty$ かつ $\displaystyle\lim_{x \to \infty}f'(x)$=$\infty$
(2)任意の実数$t$に対して、$x$の関数$tx$-$f(x)$は最大値$g(t)$を持つことを示せ。
(3)$s$を実数とする。$t$が実数全体を動くとき、$t$の関数$st$-$g(x)$は最大値$f(s)$となることを示せ。
福田の数学〜千葉大学2023年第9問〜関数の増減と最大Part1

単元:
#大学入試過去問(数学)#微分とその応用#微分法#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{9}$ 関数$f(x)$と実数$t$に対し、$x$の関数$tx$-$f(x)$の最大値があればそれを$g(t)$と書く。
(1)$f(x)$=$x^4$のとき、任意の実数$t$について$g(t)$が存在する。この$g(t)$を求めよ。
以下、関数$f(x)$は連続な導関数$f''(x)$を持ち、次の2つの条件(i),(ii)が成り立つものとする。
(i)$f'(x)$は増加関数、すなわち$a$<$b$ならば$f'(a)$<$f'(b)$
(ii)$\displaystyle\lim_{x \to -\infty}f'(x)$=$-\infty$ かつ $\displaystyle\lim_{x \to \infty}f'(x)$=$\infty$
(2)任意の実数$t$に対して、$x$の関数$tx$-$f(x)$は最大値$g(t)$を持つことを示せ。
(3)$s$を実数とする。$t$が実数全体を動くとき、$t$の関数$st$-$g(x)$は最大値$f(s)$となることを示せ。
この動画を見る
$\Large\boxed{9}$ 関数$f(x)$と実数$t$に対し、$x$の関数$tx$-$f(x)$の最大値があればそれを$g(t)$と書く。
(1)$f(x)$=$x^4$のとき、任意の実数$t$について$g(t)$が存在する。この$g(t)$を求めよ。
以下、関数$f(x)$は連続な導関数$f''(x)$を持ち、次の2つの条件(i),(ii)が成り立つものとする。
(i)$f'(x)$は増加関数、すなわち$a$<$b$ならば$f'(a)$<$f'(b)$
(ii)$\displaystyle\lim_{x \to -\infty}f'(x)$=$-\infty$ かつ $\displaystyle\lim_{x \to \infty}f'(x)$=$\infty$
(2)任意の実数$t$に対して、$x$の関数$tx$-$f(x)$は最大値$g(t)$を持つことを示せ。
(3)$s$を実数とする。$t$が実数全体を動くとき、$t$の関数$st$-$g(x)$は最大値$f(s)$となることを示せ。
福田の数学〜千葉大学2023年第8問〜iのn乗根Part2

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{8}$ 実数$a$,$b$と虚数単位$i$を用いて複素数$z$が$z$=$a$+$bi$の形で表されるとき、$a$を$z$の実部、$b$を$z$の虚部と呼び、それぞれ$a$=$Re(z)$,$b$=$Im(z)$と表す。
(1)$z^3$=$i$を満たす複素数$z$をすべて求めよ。
(2)$z^{100}$=$i$を満たす複素数$z$のうち、$Re(z)$≦$\frac{1}{2}$かつ$Im(z)$≧0を満たすものの個数を求めよ。
(3)$n$を正の整数とする。$z^n$=$i$を満たす複素数$z$のうち、$Re(z)$≧$\frac{1}{2}$を満たすものの個数を$N$とする。$N$>$\frac{n}{3}$となるための$n$に関する必要十分条件を求めよ。
この動画を見る
$\Large\boxed{8}$ 実数$a$,$b$と虚数単位$i$を用いて複素数$z$が$z$=$a$+$bi$の形で表されるとき、$a$を$z$の実部、$b$を$z$の虚部と呼び、それぞれ$a$=$Re(z)$,$b$=$Im(z)$と表す。
(1)$z^3$=$i$を満たす複素数$z$をすべて求めよ。
(2)$z^{100}$=$i$を満たす複素数$z$のうち、$Re(z)$≦$\frac{1}{2}$かつ$Im(z)$≧0を満たすものの個数を求めよ。
(3)$n$を正の整数とする。$z^n$=$i$を満たす複素数$z$のうち、$Re(z)$≧$\frac{1}{2}$を満たすものの個数を$N$とする。$N$>$\frac{n}{3}$となるための$n$に関する必要十分条件を求めよ。
福田の数学〜千葉大学2023年第8問〜iのn乗根Part1

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{8}$ 実数$a$,$b$と虚数単位$i$を用いて複素数$z$が$z$=$a$+$bi$の形で表されるとき、$a$を$z$の実部、$b$を$z$の虚部と呼び、それぞれ$a$=$Re(z)$,$b$=$Im(z)$と表す。
(1)$z^3$=$i$を満たす複素数$z$をすべて求めよ。
(2)$z^{100}$=$i$を満たす複素数$z$のうち、$Re(z)$≦$\frac{1}{2}$かつ$Im(z)$≧0を満たすものの個数を求めよ。
(3)$n$を正の整数とする。$z^n$=$i$を満たす複素数$z$のうち、$Re(z)$≧$\frac{1}{2}$を満たすものの個数を$N$とする。$N$>$\frac{n}{3}$となるための$n$に関する必要十分条件を求めよ。
この動画を見る
$\Large\boxed{8}$ 実数$a$,$b$と虚数単位$i$を用いて複素数$z$が$z$=$a$+$bi$の形で表されるとき、$a$を$z$の実部、$b$を$z$の虚部と呼び、それぞれ$a$=$Re(z)$,$b$=$Im(z)$と表す。
(1)$z^3$=$i$を満たす複素数$z$をすべて求めよ。
(2)$z^{100}$=$i$を満たす複素数$z$のうち、$Re(z)$≦$\frac{1}{2}$かつ$Im(z)$≧0を満たすものの個数を求めよ。
(3)$n$を正の整数とする。$z^n$=$i$を満たす複素数$z$のうち、$Re(z)$≧$\frac{1}{2}$を満たすものの個数を$N$とする。$N$>$\frac{n}{3}$となるための$n$に関する必要十分条件を求めよ。
福田の数学〜千葉大学2023年第7問〜三角関数と定積分の最大Part2

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{7}$ 関数
$f(x)$=$\displaystyle\left|\cos x-\sqrt5\sin x-\frac{3\sqrt2}{2}\right|$
について、以下の問いに答えよ。
(1)$f(x)$の最大値を求めよ。
(2)$\displaystyle\int_0^{2\pi}f(x)dx$ を求めよ。
(3)$S(t)$=$\displaystyle\int_t^{t+\frac{\pi}{3}}f(x)dx$ とおく。このとき$S(t)$の最大値を求めよ。
この動画を見る
$\Large\boxed{7}$ 関数
$f(x)$=$\displaystyle\left|\cos x-\sqrt5\sin x-\frac{3\sqrt2}{2}\right|$
について、以下の問いに答えよ。
(1)$f(x)$の最大値を求めよ。
(2)$\displaystyle\int_0^{2\pi}f(x)dx$ を求めよ。
(3)$S(t)$=$\displaystyle\int_t^{t+\frac{\pi}{3}}f(x)dx$ とおく。このとき$S(t)$の最大値を求めよ。
福田の数学〜千葉大学2023年第7問〜三角関数と定積分の最大Part1

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{7}$ 関数
$f(x)$=$\displaystyle\left|\cos x-\sqrt5\sin x-\frac{3\sqrt2}{2}\right|$
について、以下の問いに答えよ。
(1)$f(x)$の最大値を求めよ。
(2)$\displaystyle\int_0^{2\pi}f(x)dx$ を求めよ。
(3)$S(t)$=$\displaystyle\int_t^{t+\frac{\pi}{3}}f(x)dx$ とおく。このとき$S(t)$の最大値を求めよ。
この動画を見る
$\Large\boxed{7}$ 関数
$f(x)$=$\displaystyle\left|\cos x-\sqrt5\sin x-\frac{3\sqrt2}{2}\right|$
について、以下の問いに答えよ。
(1)$f(x)$の最大値を求めよ。
(2)$\displaystyle\int_0^{2\pi}f(x)dx$ を求めよ。
(3)$S(t)$=$\displaystyle\int_t^{t+\frac{\pi}{3}}f(x)dx$ とおく。このとき$S(t)$の最大値を求めよ。
福田の数学〜千葉大学2023年第6問〜連立漸化式となる確率Part2

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ 1個のさいころを投げて出た目によって数直線上の点Pを動かすことを繰り返すゲームを考える。最初のPの位置を$a_0$=0とし、さいころを$n$回投げたあとのPの位置$a_n$を次のルールで定める。
・$a_{n-1}$=7 のとき、$a_n$=7
・$a_{n-1}$≠7 のとき、$n$回目に出た目$m$に応じて
$a_n$=$
\left\{\begin{array}{1}
a_{n-1}+m (a_{n-1}+m=1,3,4,5,6,7のとき)\\
1 (a_{n-1}+m=2,12のとき)\\
14-(a_{n-1}+m) (a_{n-1}+m=8,9,10,11のとき)\\
\end{array}\right.
$
(1)$a_2$=1 となる確率を求めよ。
(2)$n$≧1について、$a_n$=7 となる確率を求めよ。
(3)$n$≧3について、$a_n$=1 となる確率を求めよ。
この動画を見る
$\Large\boxed{6}$ 1個のさいころを投げて出た目によって数直線上の点Pを動かすことを繰り返すゲームを考える。最初のPの位置を$a_0$=0とし、さいころを$n$回投げたあとのPの位置$a_n$を次のルールで定める。
・$a_{n-1}$=7 のとき、$a_n$=7
・$a_{n-1}$≠7 のとき、$n$回目に出た目$m$に応じて
$a_n$=$
\left\{\begin{array}{1}
a_{n-1}+m (a_{n-1}+m=1,3,4,5,6,7のとき)\\
1 (a_{n-1}+m=2,12のとき)\\
14-(a_{n-1}+m) (a_{n-1}+m=8,9,10,11のとき)\\
\end{array}\right.
$
(1)$a_2$=1 となる確率を求めよ。
(2)$n$≧1について、$a_n$=7 となる確率を求めよ。
(3)$n$≧3について、$a_n$=1 となる確率を求めよ。
福田の数学〜千葉大学2023年第6問〜連立漸化式となる確率Part1

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ 1個のさいころを投げて出た目によって数直線上の点Pを動かすことを繰り返すゲームを考える。最初のPの位置を$a_0$=0とし、さいころを$n$回投げたあとのPの位置$a_n$を次のルールで定める。
・$a_{n-1}$=7 のとき、$a_n$=7
・$a_{n-1}$≠7 のとき、$n$回目に出た目$m$に応じて
$a_n$=$
\left\{\begin{array}{1}
a_{n-1}+m (a_{n-1}+m=1,3,4,5,6,7のとき)\\
1 (a_{n-1}+m=2,12のとき)\\
14-(a_{n-1}+m) (a_{n-1}+m=8,9,10,11のとき)\\
\end{array}\right.
$
(1)$a_2$=1 となる確率を求めよ。
(2)$n$≧1について、$a_n$=7 となる確率を求めよ。
(3)$n$≧3について、$a_n$=1 となる確率を求めよ。
この動画を見る
$\Large\boxed{6}$ 1個のさいころを投げて出た目によって数直線上の点Pを動かすことを繰り返すゲームを考える。最初のPの位置を$a_0$=0とし、さいころを$n$回投げたあとのPの位置$a_n$を次のルールで定める。
・$a_{n-1}$=7 のとき、$a_n$=7
・$a_{n-1}$≠7 のとき、$n$回目に出た目$m$に応じて
$a_n$=$
\left\{\begin{array}{1}
a_{n-1}+m (a_{n-1}+m=1,3,4,5,6,7のとき)\\
1 (a_{n-1}+m=2,12のとき)\\
14-(a_{n-1}+m) (a_{n-1}+m=8,9,10,11のとき)\\
\end{array}\right.
$
(1)$a_2$=1 となる確率を求めよ。
(2)$n$≧1について、$a_n$=7 となる確率を求めよ。
(3)$n$≧3について、$a_n$=1 となる確率を求めよ。
大学入試問題#603「もう飽きた?」 千葉大学(1989) #極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$P_n=\sqrt[ n ]{ \displaystyle \frac{(3n)!}{(2n)!} }$とおく
(1)$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{P_n}{n}$を求めよ
(2)$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{n+2}{n})^{P_n}$を求めよ
出典:1989年千葉大学 入試問題
この動画を見る
$P_n=\sqrt[ n ]{ \displaystyle \frac{(3n)!}{(2n)!} }$とおく
(1)$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{P_n}{n}$を求めよ
(2)$\displaystyle \lim_{ n \to \infty } (\displaystyle \frac{n+2}{n})^{P_n}$を求めよ
出典:1989年千葉大学 入試問題
福田の数学〜千葉大学2023年第5問〜垂線の足の位置ベクトル

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 点Oを原点とする座標平面において、点Aと点Bが$\overrightarrow{OA}$・$\overrightarrow{OA}$=5, $\overrightarrow{OB}$・$\overrightarrow{OB}$=2, $\overrightarrow{OA}$・$\overrightarrow{OB}$=3を満たすとする。
(1)$\overrightarrow{OB}$=$k\overrightarrow{OA}$ となるような実数$k$は存在しないことを示せ。
(2)点Bから直線OAに下ろした垂線とOAとの交点をHとする。$\overrightarrow{HB}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)実数$t$に対し、直線OA上の点Pを$\overrightarrow{OP}$=$t\overrightarrow{OA}$となるようにとる。同様に直線OB上の点Qを$\overrightarrow{OQ}$=(1-$t$)$\overrightarrow{OB}$となるようにとる。点Pを通り直線OAと直交する直線を$l_1$とし、点Qを通り直線OBと直交する直線を$l_2$とする。
$l_1$と$l_2$の交点をRとするとき、$\overrightarrow{OR}$を$\overrightarrow{OA}$,$\overrightarrow{OB}$,$t$を用いて表せ。
(4)3点O,A,Bを通る円の中心をCとするとき、$\overrightarrow{OC}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
この動画を見る
$\Large\boxed{5}$ 点Oを原点とする座標平面において、点Aと点Bが$\overrightarrow{OA}$・$\overrightarrow{OA}$=5, $\overrightarrow{OB}$・$\overrightarrow{OB}$=2, $\overrightarrow{OA}$・$\overrightarrow{OB}$=3を満たすとする。
(1)$\overrightarrow{OB}$=$k\overrightarrow{OA}$ となるような実数$k$は存在しないことを示せ。
(2)点Bから直線OAに下ろした垂線とOAとの交点をHとする。$\overrightarrow{HB}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)実数$t$に対し、直線OA上の点Pを$\overrightarrow{OP}$=$t\overrightarrow{OA}$となるようにとる。同様に直線OB上の点Qを$\overrightarrow{OQ}$=(1-$t$)$\overrightarrow{OB}$となるようにとる。点Pを通り直線OAと直交する直線を$l_1$とし、点Qを通り直線OBと直交する直線を$l_2$とする。
$l_1$と$l_2$の交点をRとするとき、$\overrightarrow{OR}$を$\overrightarrow{OA}$,$\overrightarrow{OB}$,$t$を用いて表せ。
(4)3点O,A,Bを通る円の中心をCとするとき、$\overrightarrow{OC}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
福田の数学〜千葉大学2023年第4問〜関数の増減と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 2つの実数$a$,$b$は0<$b$<$a$を満たすとする。関数
$f(x)$=$\displaystyle\frac{1}{b}\left(e^{-(a-b)x}-e^{-ax}\right)$
の最大値を$M(a,b)$、最大値をとるときの$x$の値を$X(a,b)$と表す。ここで、$e$は自然対数の底である。
(1)$X(a,b)$を求めよ。
(2)極限$\displaystyle\lim_{b \to +0}X(a,b)$ を求めよ。
(3)極限$\displaystyle\lim_{b \to +0}M(a,b)$ を求めよ。
この動画を見る
$\Large\boxed{4}$ 2つの実数$a$,$b$は0<$b$<$a$を満たすとする。関数
$f(x)$=$\displaystyle\frac{1}{b}\left(e^{-(a-b)x}-e^{-ax}\right)$
の最大値を$M(a,b)$、最大値をとるときの$x$の値を$X(a,b)$と表す。ここで、$e$は自然対数の底である。
(1)$X(a,b)$を求めよ。
(2)極限$\displaystyle\lim_{b \to +0}X(a,b)$ を求めよ。
(3)極限$\displaystyle\lim_{b \to +0}M(a,b)$ を求めよ。
福田の数学〜千葉大学2023年第3問〜2次関数と定積分で表された関数

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 以下の問いに答えよ。
(1)$p$を実数とする。曲線$y$=|$x^2$+$x$-2|と直線$y$=$x$+$p$ の共有点の個数を求めよ。
(2)等式$f(x)$=$x^2$+$\displaystyle\int_{-1}^2(xf(t)-t)dt$ を満たす関数$f(x)$を求めよ。
この動画を見る
$\Large\boxed{3}$ 以下の問いに答えよ。
(1)$p$を実数とする。曲線$y$=|$x^2$+$x$-2|と直線$y$=$x$+$p$ の共有点の個数を求めよ。
(2)等式$f(x)$=$x^2$+$\displaystyle\int_{-1}^2(xf(t)-t)dt$ を満たす関数$f(x)$を求めよ。
福田の数学〜千葉大学2023年第2問〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 1個のさいころを投げて出た目によって得点を得るゲームを考える。出た目が1,2であれば得点は2、出た目が3であれば得点は1、出た目が4,5,6であれば得点は0とする。このゲームを$k$回繰り返すとき、得点の合計を$S_k$とする。
(1)$S_2$=3 となる確率を求めよ。
(2)$S_3$が奇数となる確率を求めよ。
(3)$S_4$≧$n$となる確率が$\frac{1}{9}$以下となる最小の整数$n$を求めよ。
この動画を見る
$\Large\boxed{2}$ 1個のさいころを投げて出た目によって得点を得るゲームを考える。出た目が1,2であれば得点は2、出た目が3であれば得点は1、出た目が4,5,6であれば得点は0とする。このゲームを$k$回繰り返すとき、得点の合計を$S_k$とする。
(1)$S_2$=3 となる確率を求めよ。
(2)$S_3$が奇数となる確率を求めよ。
(3)$S_4$≧$n$となる確率が$\frac{1}{9}$以下となる最小の整数$n$を求めよ。
福田の数学〜千葉大学2023年第1問〜三角形の面積と軌跡
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
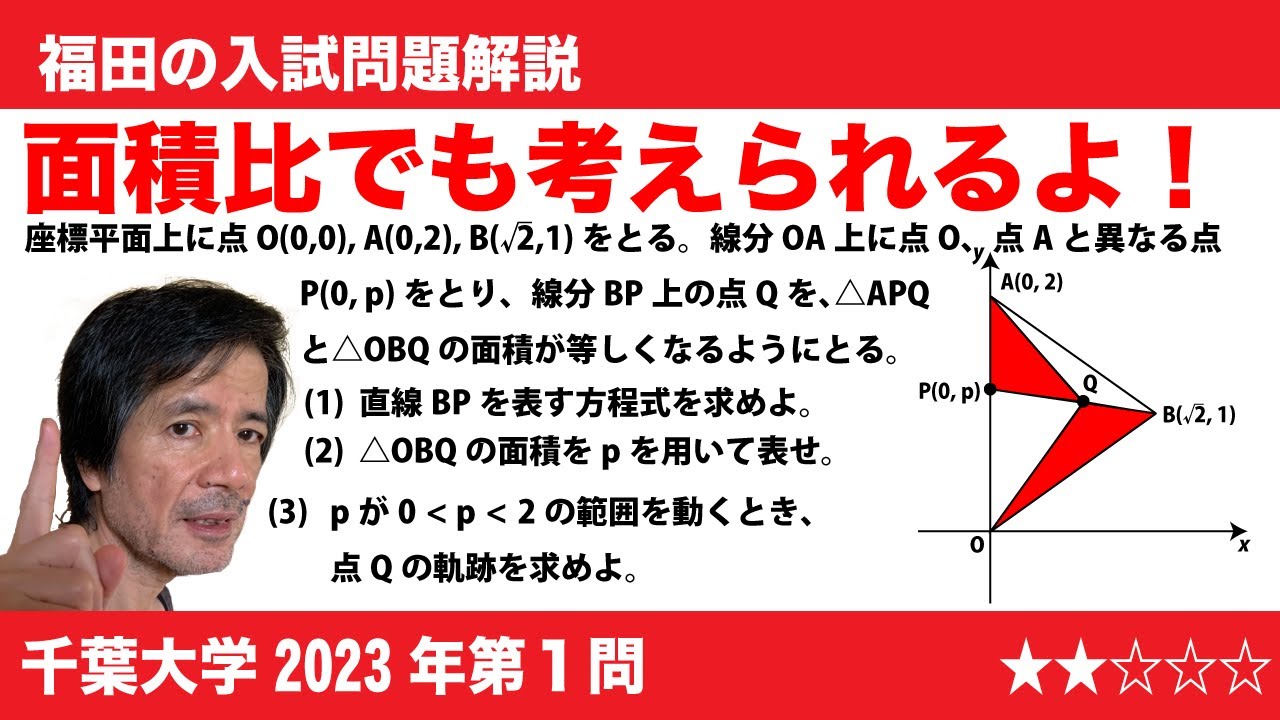
$\Large\boxed{1}$ 座標平面上に点O(0,0), A(0,2), B($\sqrt 2$, 1)をとる。線分OA上に点O、点Aと異なる点P(0,$p$)をとり、線分BP上の点Qを、$\triangle$APQと$\triangle$OBQの面積が等しくなるようにとる。
(1)直線BPを表す方程式を求めよ。
(2)$\triangle$OBQの面積を$p$を用いて表せ。
(3)$p$が0<$p$<2の範囲を動くとき、点Qの軌跡を求めよ。
この動画を見る
$\Large\boxed{1}$ 座標平面上に点O(0,0), A(0,2), B($\sqrt 2$, 1)をとる。線分OA上に点O、点Aと異なる点P(0,$p$)をとり、線分BP上の点Qを、$\triangle$APQと$\triangle$OBQの面積が等しくなるようにとる。
(1)直線BPを表す方程式を求めよ。
(2)$\triangle$OBQの面積を$p$を用いて表せ。
(3)$p$が0<$p$<2の範囲を動くとき、点Qの軌跡を求めよ。
千葉大 整数解を持つ条件

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
Pは素数であり,
$P^2+(5-P^2)x-3P=0$が整数解をもつのは$P=2$に限ることを示せ.
千葉大過去問
この動画を見る
Pは素数であり,
$P^2+(5-P^2)x-3P=0$が整数解をもつのは$P=2$に限ることを示せ.
千葉大過去問
千葉大 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
Pは奇数の素数である.
$N=(P+1)(P+3)(P+5)$
(1)Nは48の倍数であることを示せ.
(2)Nが144の倍数となるPを小さい順に5つ答えよ.
千葉大過去問
この動画を見る
Pは奇数の素数である.
$N=(P+1)(P+3)(P+5)$
(1)Nは48の倍数であることを示せ.
(2)Nが144の倍数となるPを小さい順に5つ答えよ.
千葉大過去問
大学入試問題#469「なんかワクワクする積分」 千葉大学2011 #定積分
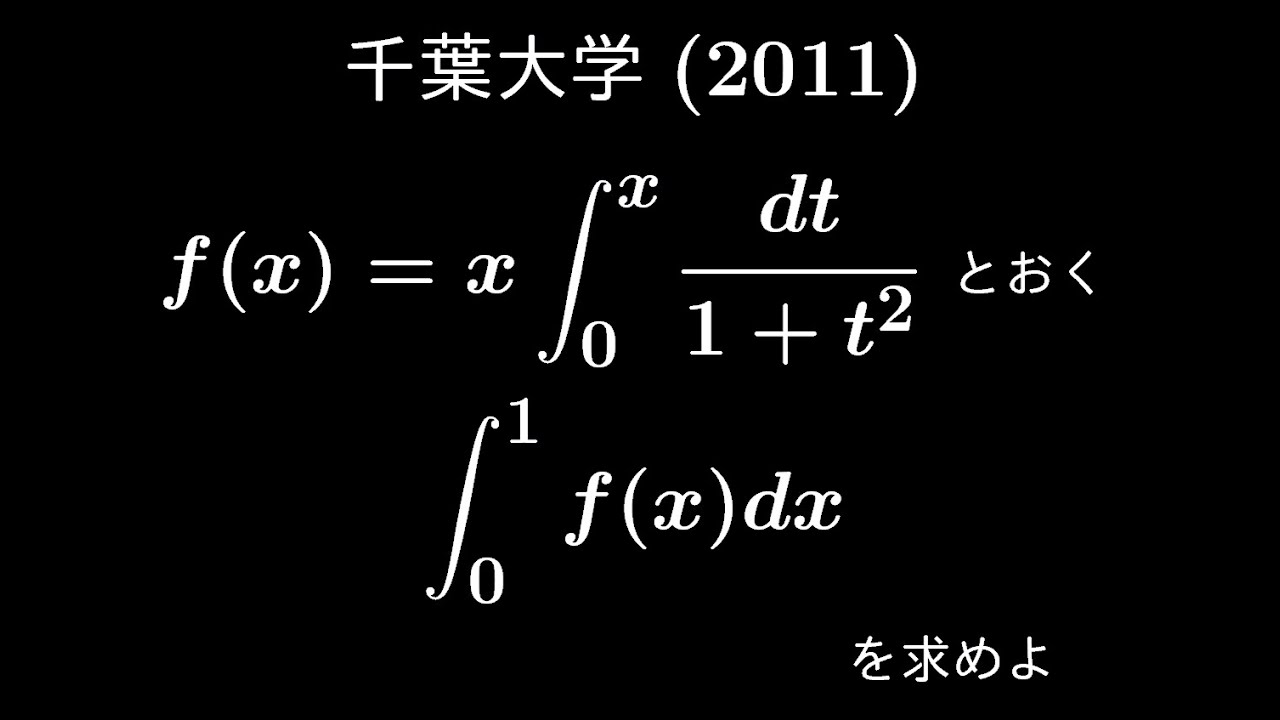
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=x\displaystyle \int_{0}^{x} \displaystyle \frac{dt}{1+t^2}$とおく
$\displaystyle \int_{0}^{1} f(x) dx$を求めよ
出典:2011年千葉大学 入試問題
この動画を見る
$f(x)=x\displaystyle \int_{0}^{x} \displaystyle \frac{dt}{1+t^2}$とおく
$\displaystyle \int_{0}^{1} f(x) dx$を求めよ
出典:2011年千葉大学 入試問題
福田の1.5倍速演習〜合格する重要問題069〜千葉大学2017年度理系第8問〜放物線上の3点を頂点とする三角形の面積

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{8}}$ tを0以上の実数とし、Oを原点とする座標平面上の2点P($p, p^2$), Q($q, q^2$)で3つの条件
PQ=2, p<q, p+q=$\sqrt t$
を満たすものを考える。$\triangle OPQ$の面積をSとする。ただし、点Pまたは点Qが原点Oと一致する場合はS=0とする。
(1) pとqをそれぞれtを用いて表せ。
(2) Sをtを用いて表せ。
(3) S=1となるようなtの個数を求めよ。
2017千葉大学理系過去問
この動画を見る
$\Large{\boxed{8}}$ tを0以上の実数とし、Oを原点とする座標平面上の2点P($p, p^2$), Q($q, q^2$)で3つの条件
PQ=2, p<q, p+q=$\sqrt t$
を満たすものを考える。$\triangle OPQ$の面積をSとする。ただし、点Pまたは点Qが原点Oと一致する場合はS=0とする。
(1) pとqをそれぞれtを用いて表せ。
(2) Sをtを用いて表せ。
(3) S=1となるようなtの個数を求めよ。
2017千葉大学理系過去問
福田の1.5倍速演習〜合格する重要問題068〜千葉大学2017年度理系第11問〜部分和で定義された数列の極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#千葉大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{11}}$ 数列$\left\{a_n\right\}$を次の条件によって定める。
$a_1=2$, $a_{n+1}=1+\frac{1}{\displaystyle1-\sum_{k=1}^n\frac{1}{a_k}}$ (n=1,2,3,$\cdots$)
(1) $a_5$を求めよ。
(2) $a_{n+1}$を$a_n$の式で表せ。
(3) 無限級数$\displaystyle\sum_{k=1}^{\infty}\frac{1}{a_k}$が収束することを示し、その和を求めよ。
2017千葉大学理系過去問
この動画を見る
$\Large{\boxed{11}}$ 数列$\left\{a_n\right\}$を次の条件によって定める。
$a_1=2$, $a_{n+1}=1+\frac{1}{\displaystyle1-\sum_{k=1}^n\frac{1}{a_k}}$ (n=1,2,3,$\cdots$)
(1) $a_5$を求めよ。
(2) $a_{n+1}$を$a_n$の式で表せ。
(3) 無限級数$\displaystyle\sum_{k=1}^{\infty}\frac{1}{a_k}$が収束することを示し、その和を求めよ。
2017千葉大学理系過去問
福田の1.5倍速演習〜合格する重要問題032〜千葉大学2016年度理系第8問〜不等式の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1)$x \gt 0$において、不等式$\log x \lt x $を示せ。
(2)$1 \lt a \lt b$のとき、不等式
$\frac{1}{\log a}-\frac{1}{\log b} \lt \frac{b-a}{a(\log a)^2}$
を示せ。
(3)$x \geqq e$において、不等式
$\int_e^x\frac{dt}{t\log(t+1)} \geqq \log(\log x)+\frac{1}{2(\log x)^2}-\frac{1}{2}$
を示せ。ただし、eは自然対数の底である。
2016千葉大学理系過去問
この動画を見る
以下の問いに答えよ。
(1)$x \gt 0$において、不等式$\log x \lt x $を示せ。
(2)$1 \lt a \lt b$のとき、不等式
$\frac{1}{\log a}-\frac{1}{\log b} \lt \frac{b-a}{a(\log a)^2}$
を示せ。
(3)$x \geqq e$において、不等式
$\int_e^x\frac{dt}{t\log(t+1)} \geqq \log(\log x)+\frac{1}{2(\log x)^2}-\frac{1}{2}$
を示せ。ただし、eは自然対数の底である。
2016千葉大学理系過去問
福田の1.5倍速演習〜合格する重要問題031〜千葉大学2016年度理系第2問〜格子点の個数

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標平面上に5点O$(0,0), A(5,0), B(0,11), P(m,0), Q(0,n)$をとる。
ただし、mとnは$1 \leqq m \leqq 5,1 \leqq n \leqq 11$を満たす整数とする。
(1)三角形OABの内部に含まれる格子点の個数を求めよ。ただし、格子点とは
x座標とy座標が共に整数である点のことであり、内部には辺上の点は含まれない。
(2)三角形OPQの内部に含まれる格子点の個数が三角形OABの内部に含まれる
格子点の個数の半分になるような組(m,n)をすべて求めよ。
2016千葉大学理系過去問
この動画を見る
座標平面上に5点O$(0,0), A(5,0), B(0,11), P(m,0), Q(0,n)$をとる。
ただし、mとnは$1 \leqq m \leqq 5,1 \leqq n \leqq 11$を満たす整数とする。
(1)三角形OABの内部に含まれる格子点の個数を求めよ。ただし、格子点とは
x座標とy座標が共に整数である点のことであり、内部には辺上の点は含まれない。
(2)三角形OPQの内部に含まれる格子点の個数が三角形OABの内部に含まれる
格子点の個数の半分になるような組(m,n)をすべて求めよ。
2016千葉大学理系過去問
大学入試問題#382「初手が重要かと」 千葉大学 改 2009 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{3\sqrt{ 3 }} \displaystyle \frac{1}{1+\sqrt[ 3 ]{ x^2 }} dx$
出典:2009年千葉大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{3\sqrt{ 3 }} \displaystyle \frac{1}{1+\sqrt[ 3 ]{ x^2 }} dx$
出典:2009年千葉大学 入試問題
福田の1.5倍速演習〜合格する重要問題010〜千葉大学2015年度理系数学第6問〜論証と剰余類

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#推理と論証#推理と論証#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
k,m,nを自然数とする。以下の問いに答えよ。
(1)$2^k$を7で割った余りが4であるとする。このとき、kを3で割った余りは
2であることを示せ。
(2)$4m+5n$が3で割り切れるとする。このとき、$2^{mn}$を7で割った余りは
4ではないことを示せ。
2015千葉大学理系過去問
この動画を見る
k,m,nを自然数とする。以下の問いに答えよ。
(1)$2^k$を7で割った余りが4であるとする。このとき、kを3で割った余りは
2であることを示せ。
(2)$4m+5n$が3で割り切れるとする。このとき、$2^{mn}$を7で割った余りは
4ではないことを示せ。
2015千葉大学理系過去問
大学入試問題#323 千葉大学(2010) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$3^n=k^3+1$を満たす正の整数の組$(k,n)$をすべて求めよ。
出典:2010年千葉大学 入試問題
この動画を見る
$3^n=k^3+1$を満たす正の整数の組$(k,n)$をすべて求めよ。
出典:2010年千葉大学 入試問題
大学入試問題#282 千葉大学医学部(2018) #定積分 #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$のとき
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学医学部 入試問題
この動画を見る
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$のとき
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学医学部 入試問題
整数問題!無限降下法を用いた証明!【数学 入試問題】【千葉大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$が3以上の整数のとき,$x^n+2y^n=4z^n$を満たす自然数$x,y,z$は存在しないことを証明せよ。
千葉大過去問
この動画を見る
$n$が3以上の整数のとき,$x^n+2y^n=4z^n$を満たす自然数$x,y,z$は存在しないことを証明せよ。
千葉大過去問
福田の数学〜千葉大学2022年理系第9問〜関数が常に増加する条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
rを正の実数とし、関数
$f(x)=x+\frac{r}{\sqrt{1+\sin^2x}}$
を考える。
(1)$r=1$のとき、f$(x)$は常に増加することを示せ。
(2)次の条件を満たす最大の正の実数cを求めよ。
条件:$0 \lt r \lt c$のときは$f(x)$が常に増加する。
2022千葉大学理系過去問
この動画を見る
rを正の実数とし、関数
$f(x)=x+\frac{r}{\sqrt{1+\sin^2x}}$
を考える。
(1)$r=1$のとき、f$(x)$は常に増加することを示せ。
(2)次の条件を満たす最大の正の実数cを求めよ。
条件:$0 \lt r \lt c$のときは$f(x)$が常に増加する。
2022千葉大学理系過去問
福田の数学〜千葉大学2022年理系第8問〜定積分で著された式の極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
正の整数$m,n$に対して、
$A(m,n)=(m+1)n^{m+1}\int_o^{\frac{1}{n}}x^me^{-x}dx$
とおく。
(1)$e^{-\frac{1}{n}} \leqq A(m,n) \leqq 1$ を証明せよ。
(2)各$m$に対して、$b_m=\lim_{n \to \infty}A(m,n)$ を求めよ。
(3)各$n$に対して、$c_n=\lim_{m \to \infty}A(m,n)$ を求めよ。
2022千葉大学理系過去問
この動画を見る
正の整数$m,n$に対して、
$A(m,n)=(m+1)n^{m+1}\int_o^{\frac{1}{n}}x^me^{-x}dx$
とおく。
(1)$e^{-\frac{1}{n}} \leqq A(m,n) \leqq 1$ を証明せよ。
(2)各$m$に対して、$b_m=\lim_{n \to \infty}A(m,n)$ を求めよ。
(3)各$n$に対して、$c_n=\lim_{m \to \infty}A(m,n)$ を求めよ。
2022千葉大学理系過去問
福田の数学〜千葉大学2022年理系第7問〜不定方程式の自然数解と漸化式で与えられた数列

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$x,y$についての方程式
$x^2-6xy+y^2=9 \ldots\ldots(*)$
に関する次の問いに答えよ。
(1)$x,y$がともに正の整数であるような(*)の解のうち、yが最小であるものを
求めよ。
(2)数列$a_1,a_2,a_3,\ldots$が漸化式
$a_{n+2}-6a_{n+1}+a_n=0 (n=1,2,3,\ldots)$
を満たすとする。このとき、$(x,y)=(a_{n+1},a_n)$が(*)を満たすならば、
$(x,y)=(a_{n+2},a_{n+1})$も(*)を満たすことを示せ。
(3)(*)の整数解(x,y)は無数に存在することを示せ。
2022千葉大学理系過去問
この動画を見る
$x,y$についての方程式
$x^2-6xy+y^2=9 \ldots\ldots(*)$
に関する次の問いに答えよ。
(1)$x,y$がともに正の整数であるような(*)の解のうち、yが最小であるものを
求めよ。
(2)数列$a_1,a_2,a_3,\ldots$が漸化式
$a_{n+2}-6a_{n+1}+a_n=0 (n=1,2,3,\ldots)$
を満たすとする。このとき、$(x,y)=(a_{n+1},a_n)$が(*)を満たすならば、
$(x,y)=(a_{n+2},a_{n+1})$も(*)を満たすことを示せ。
(3)(*)の整数解(x,y)は無数に存在することを示せ。
2022千葉大学理系過去問
