 大学入試過去問(数学)
大学入試過去問(数学)
 大学入試過去問(数学)
大学入試過去問(数学)
福田の数学〜九州大学2022年理系第3問〜約数と倍数と不定方程式の自然数解

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
自然数m,nが
$n^4=1+210m^2 \ldots①$
を満たすとき、以下の問いに答えよ。
(1)$\frac{n^2+1}{2},\ \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
(2)$n^2-1$は168の倍数であることを示せ。
(3)①を満たす自然数の組(m,n)を1つ求めよ。
2022九州大学理系過去問
この動画を見る
自然数m,nが
$n^4=1+210m^2 \ldots①$
を満たすとき、以下の問いに答えよ。
(1)$\frac{n^2+1}{2},\ \frac{n^2-1}{2}$は互いに素な整数であることを示せ。
(2)$n^2-1$は168の倍数であることを示せ。
(3)①を満たす自然数の組(m,n)を1つ求めよ。
2022九州大学理系過去問
大学入試問題#190 奈良県立医科大学(1987) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#奈良県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x}{\sqrt{ 4-3x^2 }}\ dx$を計算せよ。
出典:1987年奈良県立医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x}{\sqrt{ 4-3x^2 }}\ dx$を計算せよ。
出典:1987年奈良県立医科大学 入試問題
福田の数学〜九州大学2022年理系第2問〜商と余りの関係と極限

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n$を3以上の自然数、$\alpha,\beta$を相異なる実数とするとき、以下の問いに答えよ。
(1)次を満たす実数A,B,Cと整式Q(x)が存在することを示せ。
$x^n=(x-\alpha)(x-\beta)^2Q(x)+A(x-\alpha)(x-\beta)+B(x-\alpha)+C$
(2)(1)のA,B,Cを$n,\alpha,\beta$を用いて表せ。
(3)(2)のAについて、nと$\alpha$を固定して、$\beta$を$\alpha$に近づけたときの極限
$\lim_{\beta \to \alpha}A$を求めよ。
2022九州大学理系過去問
この動画を見る
$n$を3以上の自然数、$\alpha,\beta$を相異なる実数とするとき、以下の問いに答えよ。
(1)次を満たす実数A,B,Cと整式Q(x)が存在することを示せ。
$x^n=(x-\alpha)(x-\beta)^2Q(x)+A(x-\alpha)(x-\beta)+B(x-\alpha)+C$
(2)(1)のA,B,Cを$n,\alpha,\beta$を用いて表せ。
(3)(2)のAについて、nと$\alpha$を固定して、$\beta$を$\alpha$に近づけたときの極限
$\lim_{\beta \to \alpha}A$を求めよ。
2022九州大学理系過去問
大学入試問題#189 早稲田大学(2005) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{2}\displaystyle \frac{3}{1-x+x^2}\ dx$を計算せよ。
出典:2005年早稲田大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{2}\displaystyle \frac{3}{1-x+x^2}\ dx$を計算せよ。
出典:2005年早稲田大学 入試問題
福田の数学〜九州大学2022年理系第1問〜空間における折れ線の最小〜平面の方程式を勉強するよ!

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
座標空間内の5点
$O(0,0,0), A(1,1,0), B(2,1,2), P(4,0,-1), Q(4,0,5)$
を考える。3点O,A,Bを通る平面を$\alpha$とし、$\overrightarrow{ a }=\overrightarrow{ OA }, \overrightarrow{ b }=\overrightarrow{ OB }$とおく。
以下の問いに答えよ。
(1)ベクトル$\overrightarrow{ a }, \overrightarrow{ b }$の両方に垂直であり、x成分が正であるような、
大きさが1のベクトル$\overrightarrow{ n }$を求めよ。
(2)平面$\alpha$に関して点Pと対称な点P'の座標を求めよ。
(3)点Rが平面$\alpha$上を動くとき、$|\overrightarrow{ PR }|+|\overrightarrow{ RQ }|$が最小となるような
点Rの座標を求めよ。
2022九州大学理系過去問
この動画を見る
座標空間内の5点
$O(0,0,0), A(1,1,0), B(2,1,2), P(4,0,-1), Q(4,0,5)$
を考える。3点O,A,Bを通る平面を$\alpha$とし、$\overrightarrow{ a }=\overrightarrow{ OA }, \overrightarrow{ b }=\overrightarrow{ OB }$とおく。
以下の問いに答えよ。
(1)ベクトル$\overrightarrow{ a }, \overrightarrow{ b }$の両方に垂直であり、x成分が正であるような、
大きさが1のベクトル$\overrightarrow{ n }$を求めよ。
(2)平面$\alpha$に関して点Pと対称な点P'の座標を求めよ。
(3)点Rが平面$\alpha$上を動くとき、$|\overrightarrow{ PR }|+|\overrightarrow{ RQ }|$が最小となるような
点Rの座標を求めよ。
2022九州大学理系過去問
愛媛大(医)合同式で楽々

単元:
#数A#大学入試過去問(数学)#約数・倍数・整数の割り算と余り・合同式#愛媛大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$33^{20}$を90で割った余りを求めよ.
愛媛大(医)過去問
この動画を見る
$33^{20}$を90で割った余りを求めよ.
愛媛大(医)過去問
分数式の計算 千葉工業大
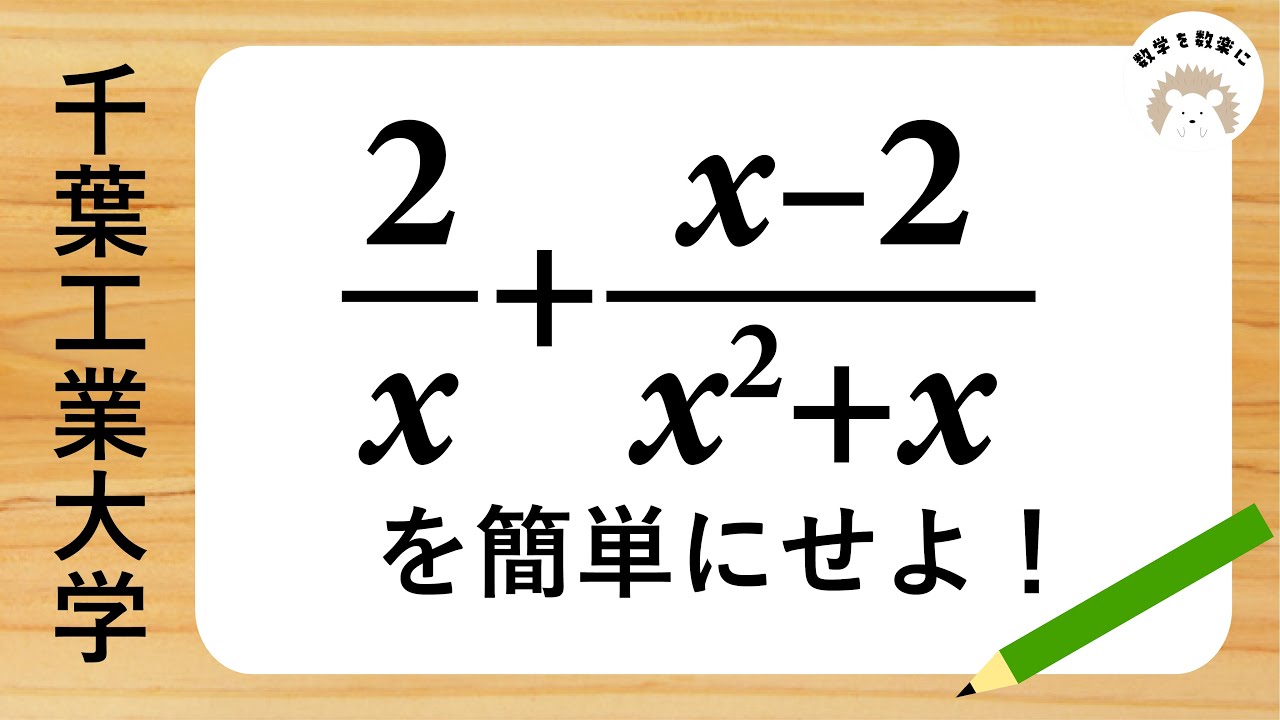
単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{2}{x} + \frac{x-2}{x^2+x}$を簡単にせよ
千葉工業大学
この動画を見る
$\frac{2}{x} + \frac{x-2}{x^2+x}$を簡単にせよ
千葉工業大学
福田の数学〜神戸大学2022年文系第3問〜指数方程式と整数解

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a,b$を実数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)$m,n$を$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{5}$とする。$m,n$の値を求めよ。
(3)$m,n$を自然数とし、$a^m=b^n=(ab)^5$とする。bの値をaを用いて表せ。
2022神戸大学文系過去問
この動画を見る
$a,b$を実数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)$m,n$を$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{5}$とする。$m,n$の値を求めよ。
(3)$m,n$を自然数とし、$a^m=b^n=(ab)^5$とする。bの値をaを用いて表せ。
2022神戸大学文系過去問
大学入試問題#187 慶應義塾大学(2006) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{e}^{e^e}\displaystyle \frac{log(log\ x)}{x\ log\ x}\ dx$を計算せよ。
出典:2006年慶應義塾大学 入試問題
この動画を見る
$\displaystyle \int_{e}^{e^e}\displaystyle \frac{log(log\ x)}{x\ log\ x}\ dx$を計算せよ。
出典:2006年慶應義塾大学 入試問題
大阪府立大 漸化式と数学的帰納法・合同式の基本問題

単元:
#大学入試過去問(数学)#漸化式#大阪府立大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 3(a_n+1)+4^{2n-1}$は13の倍数であることを示せ.
大阪府立大(経済)過去問
この動画を見る
$ 3(a_n+1)+4^{2n-1}$は13の倍数であることを示せ.
大阪府立大(経済)過去問
平方根 津田塾大学

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数nで$\sqrt{n^2-n+20}$の整数部分がnとなるのは全部でいくつ?(n:自然数)
津田塾大学
この動画を見る
自然数nで$\sqrt{n^2-n+20}$の整数部分がnとなるのは全部でいくつ?(n:自然数)
津田塾大学
福田の数学〜神戸大学2022年理系第5問〜指数方程式と整数解

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数、$p$を素数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)m,nを$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{p}$とする。m,nの値をpを用いて表せ。
(3)m,nを自然数とし、$a^m=b^n=(ab)^p$とする。bの値をa,pを用いて表せ。
2022神戸大学理系過去問
この動画を見る
a,bを実数、$p$を素数とし、$1 \lt a \lt b$とする。以下の問いに答えよ。
(1)x,y,zを0でない実数とする。$a^x=b^y=(ab)^z$ならば$\frac{1}{x}+\frac{1}{y}=\frac{1}{z}$であることを示せ。
(2)m,nを$m \gt n$を満たす自然数とし、$\frac{1}{m}+\frac{1}{n}=\frac{1}{p}$とする。m,nの値をpを用いて表せ。
(3)m,nを自然数とし、$a^m=b^n=(ab)^p$とする。bの値をa,pを用いて表せ。
2022神戸大学理系過去問
大学入試問題#186 京都大学医学部(大正15年) 不定積分 たぶん難問

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{(x+1)\sqrt{ x^2-1 }}$を計算せよ。
出典:大正15年京都大学医学部 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{(x+1)\sqrt{ x^2-1 }}$を計算せよ。
出典:大正15年京都大学医学部 入試問題
式の値 日本女子大学 コメントに別解たくさんあり!!視聴者の皆様ありがとうございます。

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
問題文全文(内容文):
$x+ \frac{1}{y} = 1$ $y+ \frac{1}{z} = 1$
xyz=?
日本女子大学
この動画を見る
$x+ \frac{1}{y} = 1$ $y+ \frac{1}{z} = 1$
xyz=?
日本女子大学
福田の数学〜神戸大学2022年文系第2問〜円が切り取る弦の中点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
aを正の実数とし、円$x^2+y^2=1$と直線$y=\sqrt ax-2\sqrt a$が異なる2点P,Q
で交わっているとする。線分PQの中点をR(s,t)とする。以下の問いに答えよ。
(1)aの取りうる値の範囲を求めよ。
(2)$s,t$の値をaを用いて表せ。
(3)aが(1)で求めた範囲を動くときにsのとりうる値の範囲を求めよ。
(4)tの値をsを用いて表せ。
2022神戸大学文系過去問
この動画を見る
aを正の実数とし、円$x^2+y^2=1$と直線$y=\sqrt ax-2\sqrt a$が異なる2点P,Q
で交わっているとする。線分PQの中点をR(s,t)とする。以下の問いに答えよ。
(1)aの取りうる値の範囲を求めよ。
(2)$s,t$の値をaを用いて表せ。
(3)aが(1)で求めた範囲を動くときにsのとりうる値の範囲を求めよ。
(4)tの値をsを用いて表せ。
2022神戸大学文系過去問
大学入試問題#185 大阪府立大学(2010) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#大阪府立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{1}{\sqrt{ (3+x^2)^3 }}dx$を計算せよ。
出典:2010年大阪府立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{1}{\sqrt{ (3+x^2)^3 }}dx$を計算せよ。
出典:2010年大阪府立大学 入試問題
早稲田(教)基本問題

単元:
#約数・倍数を利用する問題#大学入試過去問(数学)#早稲田大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1~15n$の整数のうち3の倍数でも5の倍数でもない数の総和を求めよ.
早稲田(教)過去問
この動画を見る
$1~15n$の整数のうち3の倍数でも5の倍数でもない数の総和を求めよ.
早稲田(教)過去問
福田の数学〜神戸大学2022年理系第4問〜双曲線が直線から切り取る弦の中点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#図形と方程式#点と直線#軌跡と領域#2次曲線#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
aを正の実数とし、双曲線$\frac{x^2}{4}-\frac{y^2}{4}=1$と直線$y=\sqrt ax+\sqrt a$が異なる2点P,Q
で交わっているとする。線分PQの中点をR(s,t)とする。以下の問いに答えよ。
(1)aの取りうる値の範囲を求めよ。
(2)s,tの値をaを用いて表せ。
(3)aが(1)で求めた範囲を動くときにsのとりうる値の範囲を求めよ。
(4)tの値をsを用いて表せ。
2022神戸大学理系過去問
この動画を見る
aを正の実数とし、双曲線$\frac{x^2}{4}-\frac{y^2}{4}=1$と直線$y=\sqrt ax+\sqrt a$が異なる2点P,Q
で交わっているとする。線分PQの中点をR(s,t)とする。以下の問いに答えよ。
(1)aの取りうる値の範囲を求めよ。
(2)s,tの値をaを用いて表せ。
(3)aが(1)で求めた範囲を動くときにsのとりうる値の範囲を求めよ。
(4)tの値をsを用いて表せ。
2022神戸大学理系過去問
大学入試の因数分解 奈良大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
abc+ab+bc+ca+a+b+c+1
奈良大学
この動画を見る
因数分解せよ
abc+ab+bc+ca+a+b+c+1
奈良大学
大学入試問題#184 早稲田大学 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}dx$を計算せよ
出典:早稲田大学 入試問題
この動画を見る
$\displaystyle \int_{4}^{16}\sqrt{ x }\ e^{-\sqrt{ x }}dx$を計算せよ
出典:早稲田大学 入試問題
福田の数学〜神戸大学2022年文系第1問〜場合分けされた放物線と直線の共有点と囲まれた面積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#神戸大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
aを正の実数とする。$x \geqq 0$のとき$f(x)=^2、x \lt 0$のとき$f(x)=-x^2$とし、
曲線$y=f(x)$をC、直線$y=2ax-1$を$l$とする。以下の問いに答えよ。
(1)Cとlの共有点の個数を求めよ。
(2)Cとlがちょうど2個の共有点をもつとする。Cとlで囲まれた図形の面積を求めよ。
2022神戸大学文系過去問
この動画を見る
aを正の実数とする。$x \geqq 0$のとき$f(x)=^2、x \lt 0$のとき$f(x)=-x^2$とし、
曲線$y=f(x)$をC、直線$y=2ax-1$を$l$とする。以下の問いに答えよ。
(1)Cとlの共有点の個数を求めよ。
(2)Cとlがちょうど2個の共有点をもつとする。Cとlで囲まれた図形の面積を求めよ。
2022神戸大学文系過去問
大学入試問題#183 東京理科大学 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{2+3e^x+e^{2x}}$
出典:東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{2+3e^x+e^{2x}}$
出典:東京理科大学 入試問題
分母の有理化 愛知大

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
分母を有理化せよ
$\frac{1}{\sqrt2+\sqrt3+2+\sqrt6}$
愛知大学
この動画を見る
分母を有理化せよ
$\frac{1}{\sqrt2+\sqrt3+2+\sqrt6}$
愛知大学
整式の割り算!頻出です【山梨大学 入試問題】【数学】

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
整式$x^{2014}$を整式$x^4+x^3+x^2+x+1$で割った余りを求めよ。
山梨大過去問
この動画を見る
整式$x^{2014}$を整式$x^4+x^3+x^2+x+1$で割った余りを求めよ。
山梨大過去問
福田の数学〜神戸大学2022年理系第3問〜関数の増減と面積

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
aを実数、$0 \lt a \lt 1$とし、$f(x)=\log(1+x^2)-ax^2$とする。以下の問いに答えよ.
(1)関数f(x)の極値を求めよ。
(2)$f(1)=0$とする。曲線$y=f(x)$とx軸で囲まれた図形の面積を求めよ。
2022神戸大学理系過去問
この動画を見る
aを実数、$0 \lt a \lt 1$とし、$f(x)=\log(1+x^2)-ax^2$とする。以下の問いに答えよ.
(1)関数f(x)の極値を求めよ。
(2)$f(1)=0$とする。曲線$y=f(x)$とx軸で囲まれた図形の面積を求めよ。
2022神戸大学理系過去問
大学入試問題#182 横浜国立大学 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2dx$を計算せよ
出典:横浜国立大学 入試問題
この動画を見る
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2dx$を計算せよ
出典:横浜国立大学 入試問題
ゴリゴリ計算【自治医科大学】【数学】

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
整式$x^5+3x^4+px^3+qx-2$が$x^2+3x+4$で割り切れるとき、$p-q$の値を求めよ。
自治医科大過去問
この動画を見る
整式$x^5+3x^4+px^3+qx-2$が$x^2+3x+4$で割り切れるとき、$p-q$の値を求めよ。
自治医科大過去問
福田の数学〜大阪大学2022年文系第3問〜6分の1公式の証明と面積の最小

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#大阪大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1)実数$\alpha,\beta$に対し、
$\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx=\frac{(\alpha-\beta)^3}{6}$
が成り立つことを示せ。
(2)a,bを$b \gt a^2$を満たす定数とし、座標平面に点$A(a,b)$をとる。さらに、
点Aを通り、傾きがkの直線をlとし、直線lと放物線$y=x^2$で囲まれた部分の面積を
$S(k)$とする。kが実数全体を動くとき、$S(k)$の最小値を求めよ。
2022大阪大学文系過去問
この動画を見る
以下の問いに答えよ。
(1)実数$\alpha,\beta$に対し、
$\int_{\alpha}^{\beta}(x-\alpha)(x-\beta)dx=\frac{(\alpha-\beta)^3}{6}$
が成り立つことを示せ。
(2)a,bを$b \gt a^2$を満たす定数とし、座標平面に点$A(a,b)$をとる。さらに、
点Aを通り、傾きがkの直線をlとし、直線lと放物線$y=x^2$で囲まれた部分の面積を
$S(k)$とする。kが実数全体を動くとき、$S(k)$の最小値を求めよ。
2022大阪大学文系過去問
【誘導形式:概要欄】大学入試問題#181 九州大学改(1987) 定積分 ウォリス積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}x^8\sqrt{ 1-x^2 }\ dx$
出典:1987年九州大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^8\sqrt{ 1-x^2 }\ dx$
出典:1987年九州大学 入試問題
【上手に文字を置ける?】多項式の割り算の入試問題【流通科学大学】【数学】

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
整式$f(x)=x^3+ax^2+bx+c$を$(x+1)^2$で割ると余りが$2x+7$であり、
$x-1$で割ると余りが$17$である。
このときの、$a,b,c$の値は?
流通科学大過去問
この動画を見る
整式$f(x)=x^3+ax^2+bx+c$を$(x+1)^2$で割ると余りが$2x+7$であり、
$x-1$で割ると余りが$17$である。
このときの、$a,b,c$の値は?
流通科学大過去問
