 数と式
数と式
 数と式
数と式
知っていれば一瞬!絶対値の入った2次方程式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2 - 4|x| - 12 = 0$を解け
この動画を見る
$x^2 - 4|x| - 12 = 0$を解け
一発で二重根号を外せ

単元:
#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
二重根号を外せ.
$\sqrt{283-36\sqrt{30}}$
$\sqrt{111+24\sqrt{10}}$
この動画を見る
二重根号を外せ.
$\sqrt{283-36\sqrt{30}}$
$\sqrt{111+24\sqrt{10}}$
ルートと絶対値の入っている連立不等式

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
連立不等式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
(2 - \sqrt 5 )x > -1 \\
|3x-5| < 8
\end{array}
\right.
\end{eqnarray}
この動画を見る
連立不等式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
(2 - \sqrt 5 )x > -1 \\
|3x-5| < 8
\end{array}
\right.
\end{eqnarray}
福田の数学〜慶應義塾大学2023年薬学部第1問(1)〜素因数分解と変数の値

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)整式X=6$a^3bc$+11$a^2b^2c$+3$ab^3c$がある。
(i)Xを因数分解するとX=$\boxed{\ \ ア\ \ }$である。
(ii)X=6270 を満たす(a,b,c)の組を全て求めると、(a,b,c)=$\boxed{\ \ イ\ \ }$である。ただし、a,b,cはそれぞれ2以上の整数とする。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (1)整式X=6$a^3bc$+11$a^2b^2c$+3$ab^3c$がある。
(i)Xを因数分解するとX=$\boxed{\ \ ア\ \ }$である。
(ii)X=6270 を満たす(a,b,c)の組を全て求めると、(a,b,c)=$\boxed{\ \ イ\ \ }$である。ただし、a,b,cはそれぞれ2以上の整数とする。
2023慶應義塾大学薬学部過去問
式の値と平方根
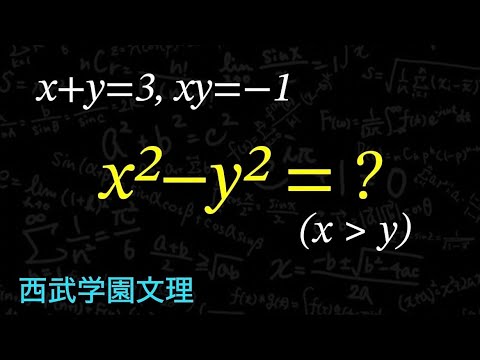
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x + y = 3 , xy = -1$
$x^2 -y^2 = ?$
($x>y$)
西部学園文理高等学校
この動画を見る
$x + y = 3 , xy = -1$
$x^2 -y^2 = ?$
($x>y$)
西部学園文理高等学校
慶應志木 式の値

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=\frac{7}{3+ \sqrt 2}$のとき
$(x-1)(x-2)(x-4)(x-5) = ?$
2023慶應義塾志木高等学校
この動画を見る
$x=\frac{7}{3+ \sqrt 2}$のとき
$(x-1)(x-2)(x-4)(x-5) = ?$
2023慶應義塾志木高等学校
気づくと爽快なルートの計算

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt {33} + \sqrt {21})(\sqrt {77}-7)$
この動画を見る
$(\sqrt {33} + \sqrt {21})(\sqrt {77}-7)$
福田の数学〜北海道大学2023年文系第3問〜絶対値の和の最小値

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#場合の数と確率#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#場合の数#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ nを2以上の自然数とする。1個のさいころをn回投げて出た目の数を順に$a_1$, $a_2$, ...., $a_n$とし、
$K_n$=|1-$a_1$|+|$a_1$-$a_2$|+...+|$a_{n-1}$-$a_n$|+|$a_n$-6|
とおく。また$K_n$のとりうる値の最小値を$q_n$とする。
(1)$K_2$=5 となる確率を求めよ。
(2)$K_3$=5 となる確率を求めよ。
(3)$q_n$を求めよ。また、$K_n$=$q_n$となるための$a_1$, $a_2$, ...., $a_n$に関する必要十分条件を求めよ。
2023北海道大学文系過去問
この動画を見る
$\Large\boxed{3}$ nを2以上の自然数とする。1個のさいころをn回投げて出た目の数を順に$a_1$, $a_2$, ...., $a_n$とし、
$K_n$=|1-$a_1$|+|$a_1$-$a_2$|+...+|$a_{n-1}$-$a_n$|+|$a_n$-6|
とおく。また$K_n$のとりうる値の最小値を$q_n$とする。
(1)$K_2$=5 となる確率を求めよ。
(2)$K_3$=5 となる確率を求めよ。
(3)$q_n$を求めよ。また、$K_n$=$q_n$となるための$a_1$, $a_2$, ...., $a_n$に関する必要十分条件を求めよ。
2023北海道大学文系過去問
因数分解(難)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$x^3y-xy^3-x^2+y^2+2xy-1$
この動画を見る
因数分解せよ.
$x^3y-xy^3-x^2+y^2+2xy-1$
真か偽か

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
真か偽か
(1)$a=2b$ならば$\frac{a}{b}=2$
(2)$ab=2$ならば$a= \frac{2}{b}$
この動画を見る
真か偽か
(1)$a=2b$ならば$\frac{a}{b}=2$
(2)$ab=2$ならば$a= \frac{2}{b}$
関西医科大

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3x^2+xy-2y^2-x+4y=4$をみたす整数(x,y)を求めよ.
関西医科大過去問
この動画を見る
$3x^2+xy-2y^2-x+4y=4$をみたす整数(x,y)を求めよ.
関西医科大過去問
√13に一番近い整数と2番目に近い整数 愛媛県

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {13}$
1番目と2番目に近い整数をそれぞれ求めよ
愛媛県
この動画を見る
$\sqrt {13}$
1番目と2番目に近い整数をそれぞれ求めよ
愛媛県
素因数分解せよ 慶應女子

式の値
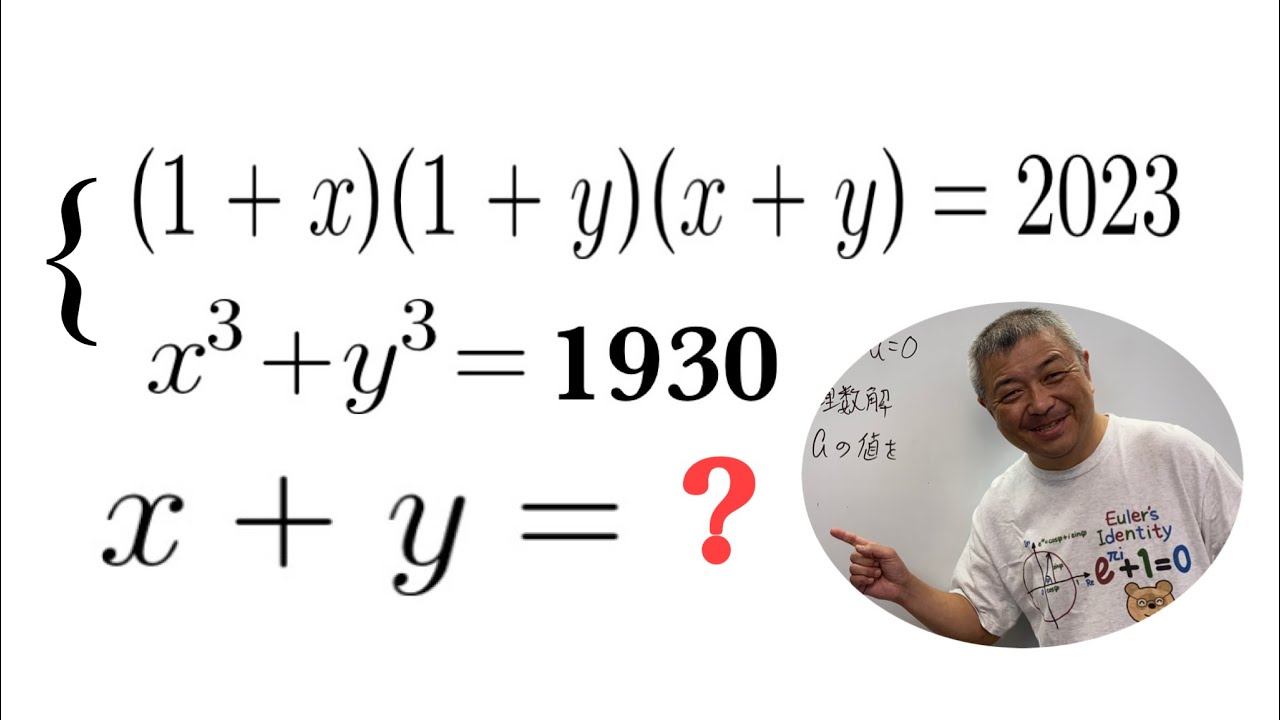
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
(1+x)(1+y)(x+y)=2023 \\
x^3+y^3=1930
\end{array}
\right.
\end{eqnarray}$
$x+y=?$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
(1+x)(1+y)(x+y)=2023 \\
x^3+y^3=1930
\end{array}
\right.
\end{eqnarray}$
$x+y=?$
x二乗をかけろ
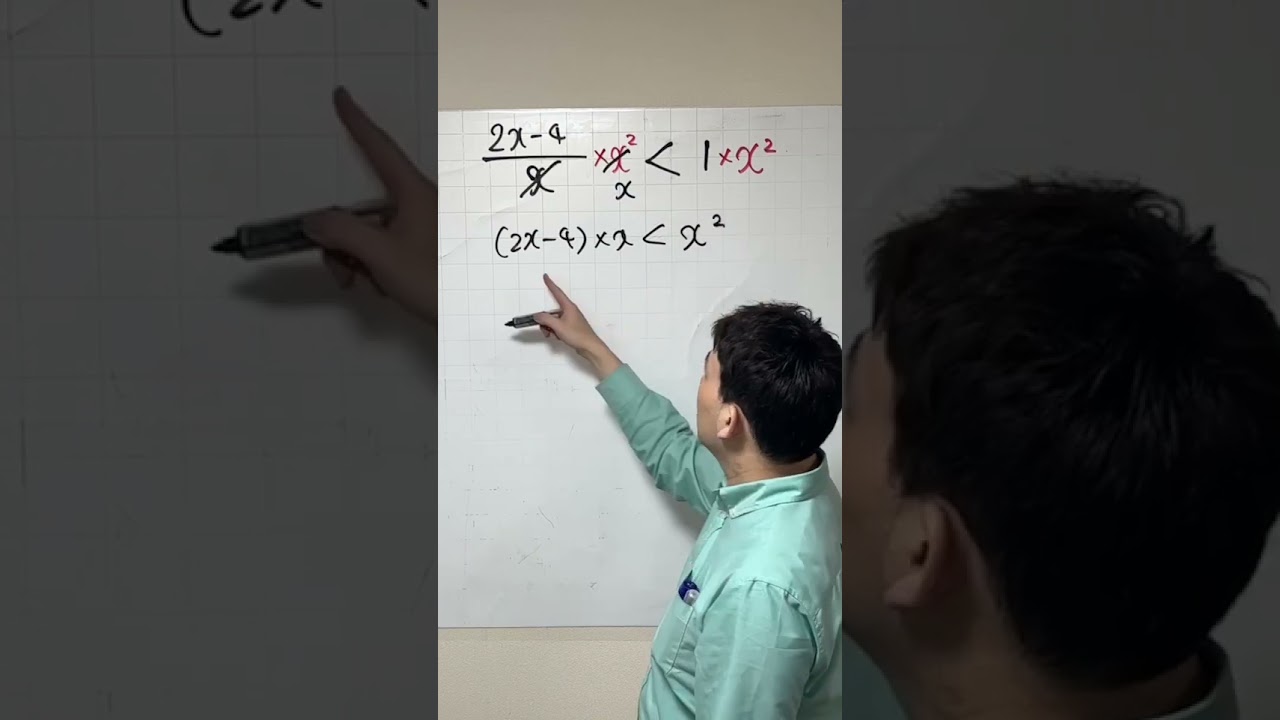
ルートひとりぼっち大作戦 西武文理

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a=\sqrt 3 + 3$のとき
$a^2 -6a+11$
西部学園文理高等学校
この動画を見る
$a=\sqrt 3 + 3$のとき
$a^2 -6a+11$
西部学園文理高等学校
誰もが一度は間違える

単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{2x-4}{x} = 1$
$\frac{2x-4}{x} < 1$
この動画を見る
$\frac{2x-4}{x} = 1$
$\frac{2x-4}{x} < 1$
【高校数学】気持ちいい計算問題!ずばずば消えて残るのはたったのこれだけ!? #Shorts

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\displaystyle \frac{\sqrt{2}-\sqrt{1}}{\sqrt[4]{2}+\sqrt[4]{1}}$+$\displaystyle \frac{\sqrt{3}-\sqrt{2}}{\sqrt[4]{3}+\sqrt[4]{2}}$+・・・・・・+$\displaystyle \frac{\sqrt{20}-\sqrt{19}}{\sqrt[4]{20}+\sqrt[4]{19}}$
気持ちよい計算問題です。
この動画を見る
$\displaystyle \frac{\sqrt{2}-\sqrt{1}}{\sqrt[4]{2}+\sqrt[4]{1}}$+$\displaystyle \frac{\sqrt{3}-\sqrt{2}}{\sqrt[4]{3}+\sqrt[4]{2}}$+・・・・・・+$\displaystyle \frac{\sqrt{20}-\sqrt{19}}{\sqrt[4]{20}+\sqrt[4]{19}}$
気持ちよい計算問題です。
1024143素因数分解せよ

目の前にあるものをいきなり食べてはいけません。
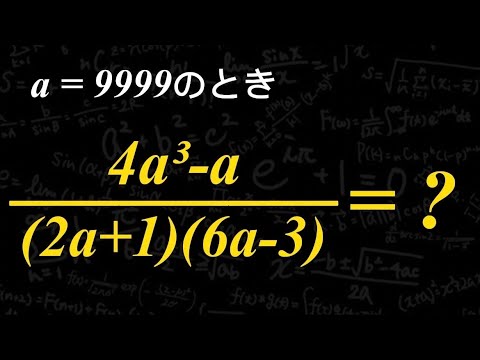
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a= 9999のとき
$\frac{4a^3 - a }{(2a+1)(6a-3)} = ?$
この動画を見る
a= 9999のとき
$\frac{4a^3 - a }{(2a+1)(6a-3)} = ?$
【数検準2級】高校数学:数学検定準2級2次:問2

単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学検定#数学検定準2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問2.次の問いに答えなさい。
(3) 正の数xに対して、xを超えない最大の整数をxの整数部分、xからxの整数部分を引いた値をxの小数部分といいます。
たとえば$\sqrt2(=1.414…)$については、$1\lt\sqrt2\lt2$より、$\sqrt2$の整数部分は1、$\sqrt2$の小数部分は$\sqrt2-1$となります。
$\sqrt5$の小数部分をaとするとき、$a^2+4a$の値を求めなさい。
この動画を見る
問2.次の問いに答えなさい。
(3) 正の数xに対して、xを超えない最大の整数をxの整数部分、xからxの整数部分を引いた値をxの小数部分といいます。
たとえば$\sqrt2(=1.414…)$については、$1\lt\sqrt2\lt2$より、$\sqrt2$の整数部分は1、$\sqrt2$の小数部分は$\sqrt2-1$となります。
$\sqrt5$の小数部分をaとするとき、$a^2+4a$の値を求めなさい。
投稿日は4月1日。2重根号を外せ!!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{ \sqrt {49} - \sqrt {48}} = 1$
この動画を見る
$\sqrt{ \sqrt {49} - \sqrt {48}} = 1$
気付けば一瞬!! 式の値

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a = 49 , b = 51のとき
$\frac{a^2+b^2}{2} + ab$
桃山学院高等学校
この動画を見る
a = 49 , b = 51のとき
$\frac{a^2+b^2}{2} + ab$
桃山学院高等学校
新高校1年生へ!失敗しない(ほぼ一発で)たすきがけ因数分解

生徒にめちゃくちゃ質問されるやつ 絶対値を外せ!

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
場合分けして絶対値を外せ
$|x| ={$
この動画を見る
場合分けして絶対値を外せ
$|x| ={$
福田の数学〜東京慈恵会医科大学2023年医学部第3問〜無理数である証明

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ Oを原点とする座標平面において、第1象限に属する点P($\sqrt 2r$, $\sqrt 3s$)(r,sは有理数)をとるとき、線分OPの長さは無理数となることを示せ。
2023東京慈恵会医科大学医学部過去問
この動画を見る
$\Large\boxed{3}$ Oを原点とする座標平面において、第1象限に属する点P($\sqrt 2r$, $\sqrt 3s$)(r,sは有理数)をとるとき、線分OPの長さは無理数となることを示せ。
2023東京慈恵会医科大学医学部過去問
場合分けは何パターン?多くの絶対値を含んだ問題【京都大学】【数学 入試問題】

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$が整数であるとき$S=\vert n-1 \vert+\vert n-2 \vert+……+\vert n-100 \vert$の最小値を求めよ。
また、そのときの$n$の値を求めよ。
京都大学1961年過去問
この動画を見る
$n$が整数であるとき$S=\vert n-1 \vert+\vert n-2 \vert+……+\vert n-100 \vert$の最小値を求めよ。
また、そのときの$n$の値を求めよ。
京都大学1961年過去問
高1数学の展開

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a+b+c=1$
$a^2+b^2+c^2=13$
$(a-b)^2 + (b-c)^2 + (c-a)^2 = ?$
共通テスト
この動画を見る
$a+b+c=1$
$a^2+b^2+c^2=13$
$(a-b)^2 + (b-c)^2 + (c-a)^2 = ?$
共通テスト
素因数分解しろ! prime factorization

単元:
#数Ⅰ#数A#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$2581を素因数分解せよ。$
この動画を見る
$2581を素因数分解せよ。$
日大(医)中学生もチャレンジして!

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P=a^4-25a^2-50a-25$であり、
$\vert P \vert$が素数となる整数aを求めよ。
日大(医)過去問
この動画を見る
$P=a^4-25a^2-50a-25$であり、
$\vert P \vert$が素数となる整数aを求めよ。
日大(医)過去問
