 数と式
数と式
 数と式
数と式
高校数学 ルートを外せ!
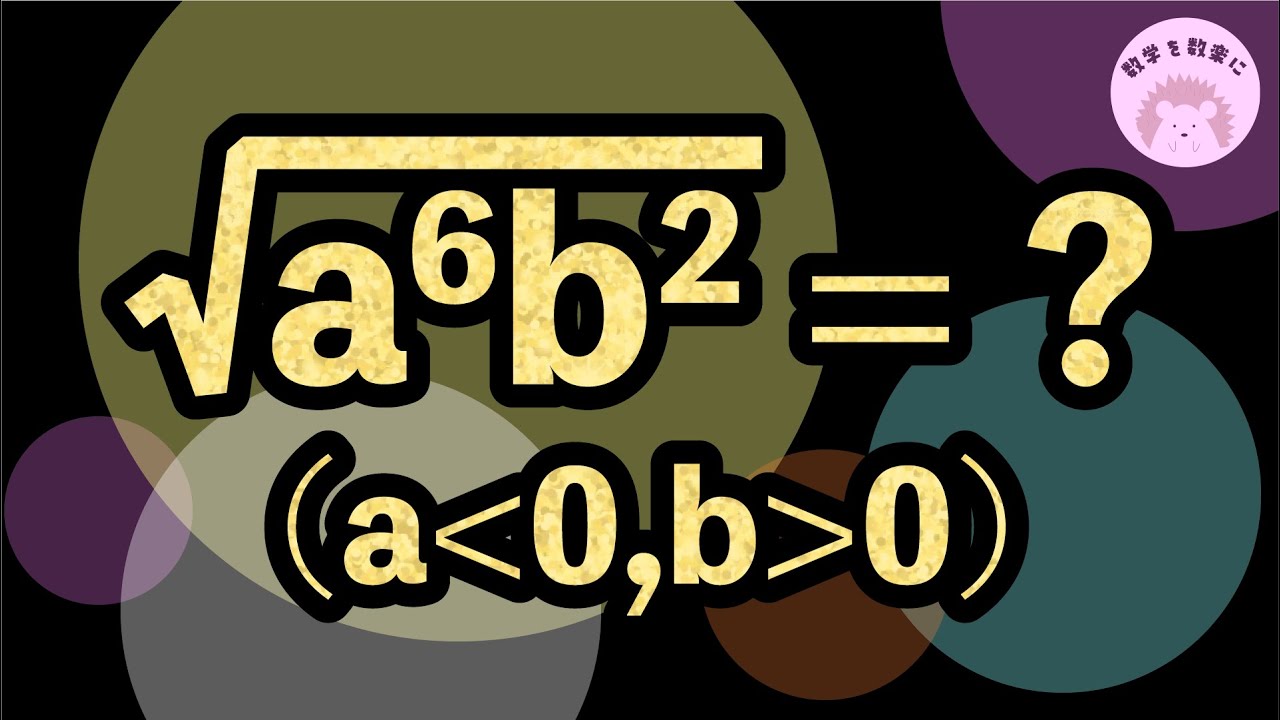
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {a^6b^2} = ?$
($a<0 , b>0$)
この動画を見る
$\sqrt {a^6b^2} = ?$
($a<0 , b>0$)
福田の数学〜京都大学2023年文系第1問〜3乗根の有理化

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#場合の数と確率#式と証明#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 問1 nを自然数とする。1個のさいころをn回投げるとき、出た目の積が5で割り切れる確率を求めよ。
問2 次の式の分母を有理化し、分母に3乗根の記号が含まれない式として表せ。
$\frac{55}{2\sqrt[3]{9}+\sqrt[3]{3}+5}$
2023京都大学文系過去問
この動画を見る
$\Large\boxed{1}$ 問1 nを自然数とする。1個のさいころをn回投げるとき、出た目の積が5で割り切れる確率を求めよ。
問2 次の式の分母を有理化し、分母に3乗根の記号が含まれない式として表せ。
$\frac{55}{2\sqrt[3]{9}+\sqrt[3]{3}+5}$
2023京都大学文系過去問
東京医科大

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\sqrt[3]{30\sqrt{a}-319\sqrt{b}}=\sqrt a-\sqrt b$であるとき、$a,b$の値を求めよ。
東京医科大学過去問
この動画を見る
$\sqrt[3]{30\sqrt{a}-319\sqrt{b}}=\sqrt a-\sqrt b$であるとき、$a,b$の値を求めよ。
東京医科大学過去問
筆算せずに計算する 慶應女子

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{86^2-2 \times 86 \times 77 +77^2}{15^2} +
\frac{15^2+2 \times 15 \times 13 +13^2}{35^2}$
この動画を見る
$\frac{86^2-2 \times 86 \times 77 +77^2}{15^2} +
\frac{15^2+2 \times 15 \times 13 +13^2}{35^2}$
東大寺学園の因数分解はいつも面白い 2023

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$a^2(b+1)^2+2a(b^2 -a)+b(b-2a^2)$
2023東大寺学園高等学校
この動画を見る
因数分解せよ
$a^2(b+1)^2+2a(b^2 -a)+b(b-2a^2)$
2023東大寺学園高等学校
【数Ⅰ】数と式:【難問】開いて閉じて、因数分解②

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$(x-z)^3+(y-z)^3-(x+y-2z)^3$を因数分解しなさい.
この動画を見る
$(x-z)^3+(y-z)^3-(x+y-2z)^3$を因数分解しなさい.
【数Ⅰ】数と式:【難問】開いて閉じて、因数分解①

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$(y-z)^3+(z-x)^3+(x-y)^3$を因数分解しなさい
この動画を見る
$(y-z)^3+(z-x)^3+(x-y)^3$を因数分解しなさい
展開だけど、カラクリわかるかな? 慶應義塾

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(x+2y)(2x-y)(3x+y)(x-3y)を展開せよ
慶應義塾高等学校
この動画を見る
(x+2y)(2x-y)(3x+y)(x-3y)を展開せよ
慶應義塾高等学校
ルートの入っている二次方程式を解け。2023東海

単元:
#数Ⅰ#数と式#2次関数#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#2次方程式と2次不等式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$2\sqrt 2 x^2 - \sqrt{14}x - \sqrt 2 = 0$
2023東海高等学校
この動画を見る
2次方程式を解け
$2\sqrt 2 x^2 - \sqrt{14}x - \sqrt 2 = 0$
2023東海高等学校
ざ・因数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a^4(b-c)+b^4(c-a)+c^4(a-b)$
これを因数分解せよ.
この動画を見る
$a^4(b-c)+b^4(c-a)+c^4(a-b)$
これを因数分解せよ.
ルートの中にマイナス
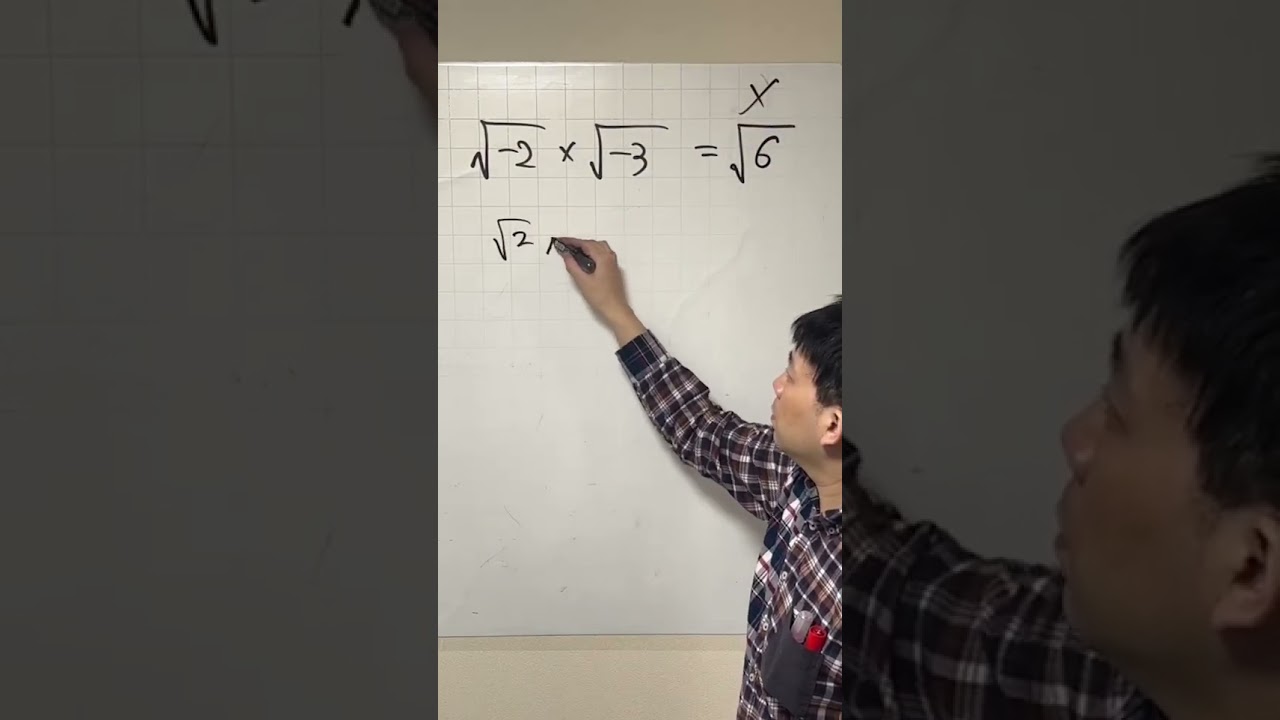
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt {-2} \times \sqrt {-3} = $
この動画を見る
$\sqrt {-2} \times \sqrt {-3} = $
福田の数学〜東京大学2023年理系第4問〜球面と三角形が共有点をもつ条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#空間ベクトル#集合と命題(集合・命題と条件・背理法)#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標空間内の4点O(0,0,0), A(2,0,0), B(1,1,1), C(1,2,3)を考える。
(1)$\overrightarrow{OP}\bot\overrightarrow{OA}$, $\overrightarrow{OP}\bot\overrightarrow{OB}$, $\overrightarrow{OP}\bot\overrightarrow{OC}$=1 を満たす点Pの座標を求めよ。
(2)点Pから直線ABに垂線を下ろし、その垂線と直線ABの交点をHとする。
$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)点Qを$\overrightarrow{OQ}$=$\frac{3}{4}\overrightarrow{OA}$+$\overrightarrow{OP}$により定め、Qを中心とする半径rの球面Sを考える。Sが三角形OHBと共有点を持つようなrの範囲を求めよ。ただし、三角形OHBは3点O, H, Bを含む平面内にあり、周とその内部からなるものとする。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{4}$ 座標空間内の4点O(0,0,0), A(2,0,0), B(1,1,1), C(1,2,3)を考える。
(1)$\overrightarrow{OP}\bot\overrightarrow{OA}$, $\overrightarrow{OP}\bot\overrightarrow{OB}$, $\overrightarrow{OP}\bot\overrightarrow{OC}$=1 を満たす点Pの座標を求めよ。
(2)点Pから直線ABに垂線を下ろし、その垂線と直線ABの交点をHとする。
$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)点Qを$\overrightarrow{OQ}$=$\frac{3}{4}\overrightarrow{OA}$+$\overrightarrow{OP}$により定め、Qを中心とする半径rの球面Sを考える。Sが三角形OHBと共有点を持つようなrの範囲を求めよ。ただし、三角形OHBは3点O, H, Bを含む平面内にあり、周とその内部からなるものとする。
2023東京大学理系過去問
2023早稲田(社)三乗根の計算

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}$とする.
(1)$a^3$をaの一次式で表せ.
(2)aは整数であることを示せ.
(3)$b=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}$とするとき,bを越えない最大の整数を求めよ.
2023早稲田大(社)過去問
この動画を見る
$a=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}$とする.
(1)$a^3$をaの一次式で表せ.
(2)aは整数であることを示せ.
(3)$b=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}$とするとき,bを越えない最大の整数を求めよ.
2023早稲田大(社)過去問
2023高校入試数学解説92問目 逆 反例 静岡県

単元:
#数学(中学生)#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
・逆を書け。
・また逆が正しくないことを示すための反例を1つ書け。
「aもbも正の数ならば、a+bは正の数である」
(2023静岡県)
この動画を見る
・逆を書け。
・また逆が正しくないことを示すための反例を1つ書け。
「aもbも正の数ならば、a+bは正の数である」
(2023静岡県)
【短時間でマスター!!】整数(平方根が自然数になる問題)を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅰ#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学1A
整数
$\sqrt{600n}$が自然数となるような最小の自然数$n$は?
$\sqrt{\frac{72}{n}}$が自然数となるような最小の自然数$n$は?
この動画を見る
数学1A
整数
$\sqrt{600n}$が自然数となるような最小の自然数$n$は?
$\sqrt{\frac{72}{n}}$が自然数となるような最小の自然数$n$は?
2023京都大学 整式の剰余

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2023}-1$を$x^4+x^3+x^2+x+1$で割ったあまりを求めよ.
2023京都大過去問
この動画を見る
$x^{2023}-1$を$x^4+x^3+x^2+x+1$で割ったあまりを求めよ.
2023京都大過去問
2023京都大学 3乗根の分母の有理化

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
分母を有利化せよ.
$\dfrac{55}{2\sqrt[3]{9}+\sqrt[3]{3}+5}$
2023京都大過去問
この動画を見る
分母を有利化せよ.
$\dfrac{55}{2\sqrt[3]{9}+\sqrt[3]{3}+5}$
2023京都大過去問
慈恵医大 座標のフリした整数問題

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
Oを原点とする座標平面において,第一象限に属する点P$(\sqrt2 r,\sqrt3 s)$(r,sは有理数)をとるとき,線分OPの長さは無理数となることを示せ.
慈恵医大過去問
この動画を見る
Oを原点とする座標平面において,第一象限に属する点P$(\sqrt2 r,\sqrt3 s)$(r,sは有理数)をとるとき,線分OPの長さは無理数となることを示せ.
慈恵医大過去問
高等学校入学試験予想問題:鳥取県公立高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#平面図形#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
この動画を見る
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
2023高校入試数学解説45問目 二重根号 灘高校

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt{100+\sqrt{9991}} + \sqrt{100-\sqrt{9991}})^2 =?$
$2\sqrt{100 + \sqrt {9991}} - \sqrt{206}=?$
2023灘高等学校 最初の1問
この動画を見る
$(\sqrt{100+\sqrt{9991}} + \sqrt{100-\sqrt{9991}})^2 =?$
$2\sqrt{100 + \sqrt {9991}} - \sqrt{206}=?$
2023灘高等学校 最初の1問
2023高校入試解説31問目 ルートが外れる問題 桃山学院

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{\frac{2023}{n}}$が自然数となるような自然数nをすべて求めよ。
2023桃山学院高等学校
この動画を見る
$\sqrt{\frac{2023}{n}}$が自然数となるような自然数nをすべて求めよ。
2023桃山学院高等学校
2023高校入試解説27問目 √が入っている因数分解 早稲田本庄

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$3x^2+y^2+2 \sqrt{3}xy+7 \sqrt3x+7y -18$
2023早稲田大学 本庄高等学院
この動画を見る
因数分解せよ
$3x^2+y^2+2 \sqrt{3}xy+7 \sqrt3x+7y -18$
2023早稲田大学 本庄高等学院
2023高校入試解説26問目 √の計算 早稲田本庄最初の一問

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\{ \frac{\sqrt2 + \sqrt3 -\sqrt5}{\sqrt{18}(\sqrt2 -1)} \}^2 \div
\{ \frac{\sqrt2(\sqrt8 + 2 )}{\sqrt{2}+ \sqrt3 + \sqrt5)} \}^2$
2023早稲田大学 本庄高等学院
この動画を見る
$\{ \frac{\sqrt2 + \sqrt3 -\sqrt5}{\sqrt{18}(\sqrt2 -1)} \}^2 \div
\{ \frac{\sqrt2(\sqrt8 + 2 )}{\sqrt{2}+ \sqrt3 + \sqrt5)} \}^2$
2023早稲田大学 本庄高等学院
福田の1.5倍速演習〜合格する重要問題101〜慶應義塾大学2020年度環境情報学部第1問(1)〜不定方程式の解

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#平面上の曲線#一次不等式(不等式・絶対値のある方程式・不等式)#整数の性質#ユークリッド互除法と不定方程式・N進法#三角関数#加法定理とその応用#2次曲線#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)正の実数xとyが9$x^2$+16$y^2$=144 を満たしているとき、xyの最大値は$\boxed{\ \ アイ\ \ }$である。
2020慶應義塾大学環境情報学部過去問
この動画を見る
$\Large\boxed{1}$ (1)正の実数xとyが9$x^2$+16$y^2$=144 を満たしているとき、xyの最大値は$\boxed{\ \ アイ\ \ }$である。
2020慶應義塾大学環境情報学部過去問
素数か?

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$A_{2023}$は素数か?
$A_n=\alpha^n+\beta^n+\delta^n$
$A_1=\alpha+\beta+\delta=1$
$A_2=\alpha^2+\beta^2+\delta^2=3$
$A_3=\alpha^3+\beta^3+\delta^3=10$
この動画を見る
$A_{2023}$は素数か?
$A_n=\alpha^n+\beta^n+\delta^n$
$A_1=\alpha+\beta+\delta=1$
$A_2=\alpha^2+\beta^2+\delta^2=3$
$A_3=\alpha^3+\beta^3+\delta^3=10$
楽しいルートの計算

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{2223^2 - 8888}$
この動画を見る
$\sqrt{2223^2 - 8888}$
ルートと素数 大阪偕星学園

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{p(q+1)}$が1ケタの素数になるようなp,qを求めよ。(p,q:素数)
大阪偕星学園高等学校
この動画を見る
$\sqrt{p(q+1)}$が1ケタの素数になるようなp,qを求めよ。(p,q:素数)
大阪偕星学園高等学校
高校生は知ってるが、中学生は知らない。式の値 同志社国際
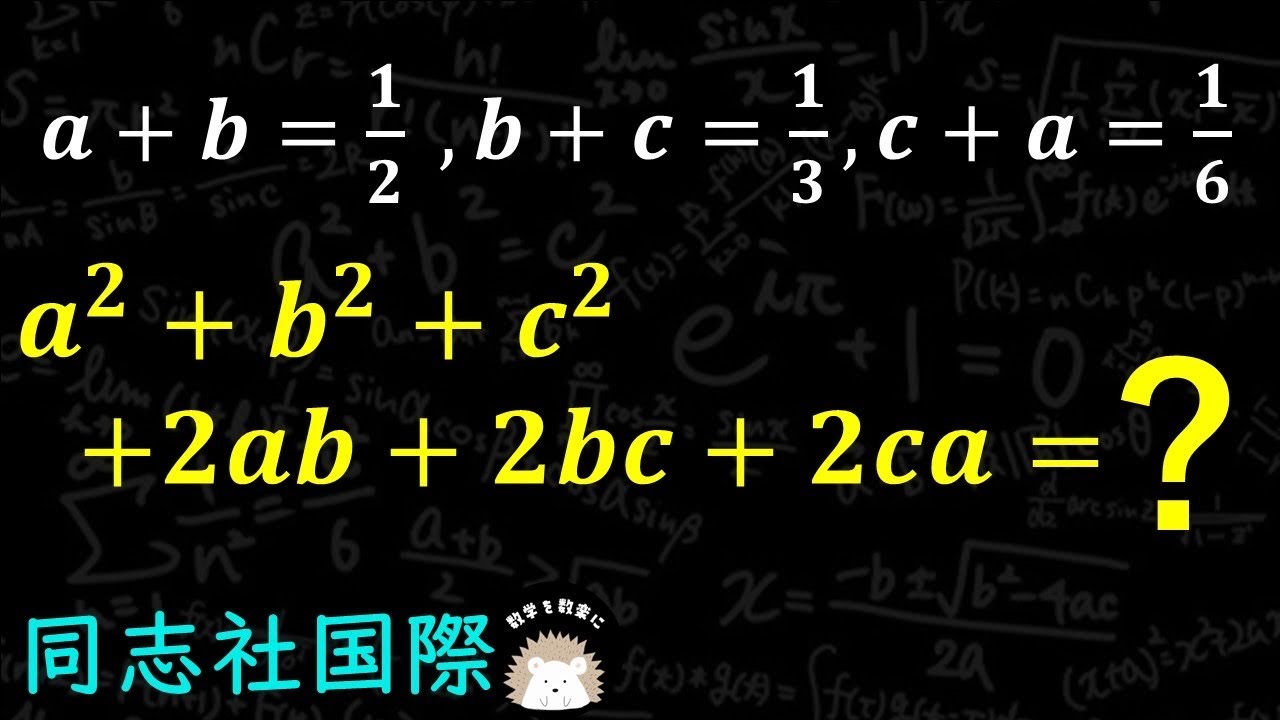
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a + b = \frac{1}{2}$ , $b + c = \frac{1}{3}$ , $c + a = \frac{1}{6}$
$a^2 + b^2 + c^2 +2ab +2bc +2ca = ?$
同志社国際高等学校
この動画を見る
$a + b = \frac{1}{2}$ , $b + c = \frac{1}{3}$ , $c + a = \frac{1}{6}$
$a^2 + b^2 + c^2 +2ab +2bc +2ca = ?$
同志社国際高等学校
福田の数学〜2023年共通テスト速報〜数学IIB第1問三角関数と対数〜三角不等式と対数が有理数とならない条件

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#整数の性質#ユークリッド互除法と不定方程式・N進法#三角関数#指数関数と対数関数#三角関数とグラフ#指数関数#対数関数#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
この動画を見る
第一問
[ 1 ] 三角関数の値の大小関係について考えよう。
(1) $x=\displaystyle\frac{\pi}{6}$のとき$\sin x\boxed{\boxed{\ \ ア\ \ }}\sin 2x$であり、$x=\frac{2}{3}\pi$のとき$\sin x\boxed{\boxed{\ \ イ\ \ }}\sin 2x$である。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ イ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪< ①= ②>
(2) $\sin x$と$\sin 2x$の値の大小関係を詳しく調べよう。
$\sin 2x$-$\sin x$=$\sin 2x\left(\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ }\right)$
であるから、$\sin 2x$-$\sin x$>0が成り立つことは
「$\sin x$>0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \gt 0$」... ①
「$\sin x$<0かつ $\boxed{\ \ ウ\ \ }\cos x-\boxed{\ \ エ\ \ } \lt 0$」... ②
が成り立つことと同値である。$0 \leqq x \leqq 2\pi$のとき、①が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}$
であり、②が成り立つようなxの値の範囲は
$\pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。よって、$0 \leqq x \leqq 2\pi$のとき、$\sin 2x \gt \sin x$が成り立つようなxの値の範囲は
$0 \lt x \lt \displaystyle\frac{\pi}{\boxed{\ \ オ\ \ }}, \pi \lt x \lt \displaystyle\frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}\pi$
である。
(3)$\sin 3x$と$\sin 4x$の値の大小関係を調べよう。
三角関数の加法定理を用いると、等式
$\sin(\alpha+\beta)$-$\sin(\alpha-\beta)$=$2\cos\alpha\sin\beta$...③
が得られる。$\alpha+\beta=4x$, $\alpha-\beta=3x$を満たす$\alpha$, $\beta$に対して③を用いることにより、$\sin 4x-\sin 3x \gt 0$が成り立つことは
「$\cos\boxed{\boxed{\ \ ク\ \ }} \gt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \gt 0$」...④
または
「$\cos\boxed{\boxed{\ \ ク\ \ }} \lt 0$ かつ $\sin\boxed{\boxed{\ \ ケ\ \ }} \lt 0$」...⑤
が成り立つことと同値であることがわかる。
$0 \leqq x \leqq \pi$のとき、④,⑤により、$\sin 4x$>$\sin 3x$が成り立つようなxの値の範囲は
$0 \leqq x \leqq \displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$, $\displaystyle\frac{\boxed{\ \ サ\ \ }}{\boxed{\ \ シ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi$
である。
$\boxed{\boxed{\ \ ク\ \ }}$, $\boxed{\boxed{\ \ ケ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①x ②2x ③3x
④4x ⑤5x ⑥6x ⑦$\frac{x}{2}$
⑧$\frac{3}{2}x$ ⑨$\frac{5}{2}x$ ⓐ$\frac{7}{2}x$ ⓑ$\frac{9}{2}x$
(4)(2), (3)の考察から、$0 \leqq x \leqq \pi$のとき、$\sin 3x \gt \sin 4x \gt \sin 2x$が成り立つようなxの値の範囲は
$\displaystyle\frac{\pi}{\boxed{\ \ コ\ \ }}$ $\lt$ $\displaystyle\frac{\pi}{\boxed{\ \ ソ\ \ }}$, $\displaystyle\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セ\ \ }}\pi \lt x \lt \frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}\pi$
であることがわかる。
[ 2 ]
(1)$a \gt 0$, $a \ne 1$, $b \gt 0$のとき、$\log_ab=x$とおくと、$\boxed{\boxed{\ \ ツ\ \ }}$が成り立つ。
$\boxed{\boxed{\ \ ツ\ \ }}$の解答群
⓪$x^a=b$ ①$x^b=a$ ②$a^x=b$
③$b^x=a$ ④$a^b=x$ ⑤$b^a=x$
(2)様々な対数の値が有理数か無理数かについて考えよう。
(i)$\log_5 25=\boxed{\ \ テ\ \ }$, $\log_9 27=\displaystyle\frac{\boxed{\ \ ト\ \ }}{\boxed{\ \ ナ\ \ }}$であり、どちらも有理数である。
(ii)$\log_2 3$が有理数と無理数のどちらかであるかを考えよう。
$\log_2 3$が有理数であると仮定すると、$\log_2 3$>0であるので、二つの自然数p, qを用いて$\log_2 3=\displaystyle\frac{p}{q}$と表すことができる。このとき、(1)により$\log_2 3=\displaystyle\frac{p}{q}$は$\boxed{\boxed{\ \ ニ\ \ }}$と変形できる。いま、2は偶数であり3は奇数であるので、$\boxed{\boxed{\ \ ニ\ \ }}$を満たす自然数p, qは存在しない。
したがって、$\log_2 3$は無理数であることがわかる。
(iii)a, bを2以上の自然数とするとき、(ii)と同様に考えると、「$\boxed{\boxed{\ \ ヌ\ \ }}$ならば$\log_a b$は常に無理数である」ことがわかる。
$\boxed{\boxed{\ \ ヌ\ \ }}$の解答群
⓪aが偶数 ①bが偶数 ②aが奇数
③bが奇数 ④aとbがともに偶数、またはaとbがともに奇数 ⑤aとbのいずれか一方が偶数で、もう一方が奇数
2023共通テスト過去問
式の値 広島大附属
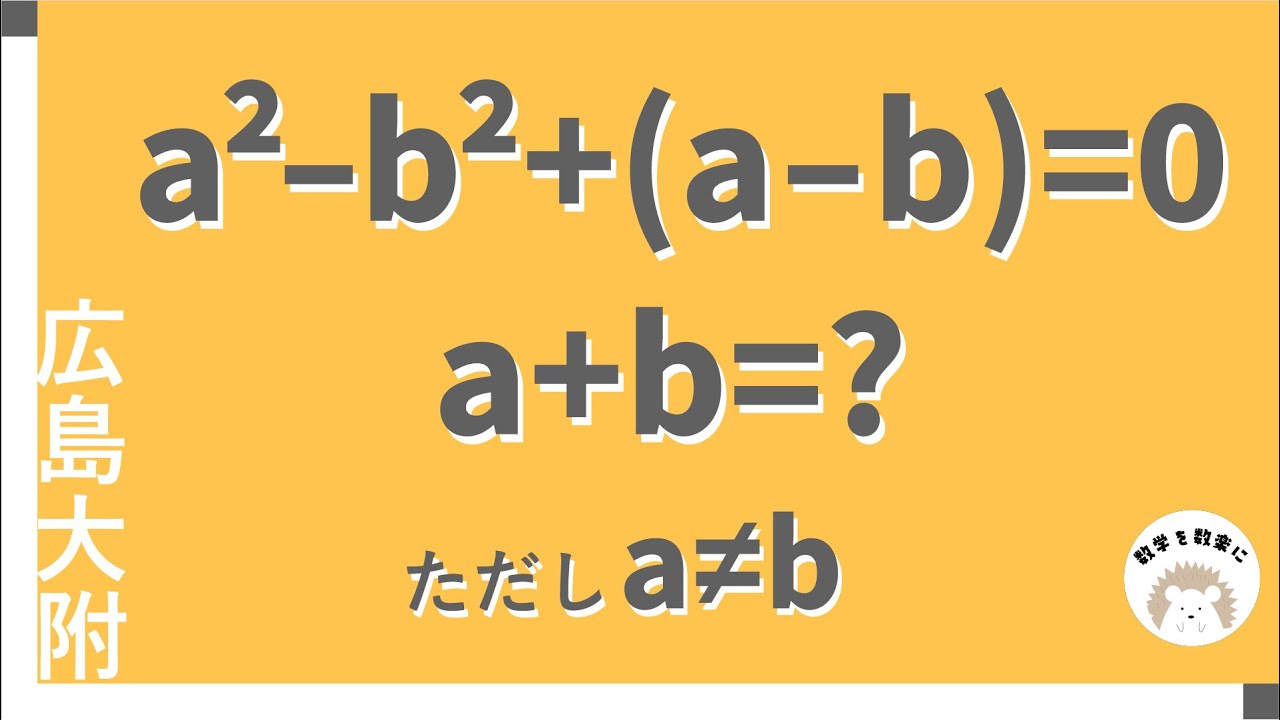
単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2 - b^2 + (a - b) = 0$
$a+b =?$
ただし$a \neq b$
広島大学附属高等学校
この動画を見る
$a^2 - b^2 + (a - b) = 0$
$a+b =?$
ただし$a \neq b$
広島大学附属高等学校
