2次方程式と2次不等式
2次方程式と2次不等式
等式の変形だけど実は2次〇〇○
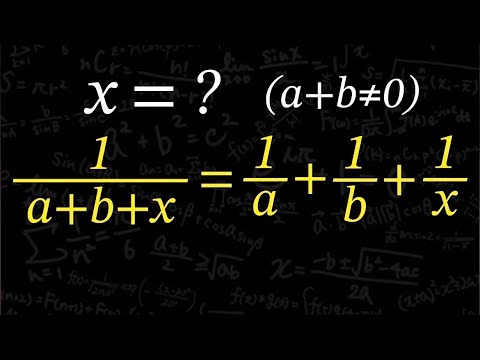
単元：
#数Ⅰ#数と式#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x=?$ $(a+b \neq 0)$
$\frac{1}{a+b+x} = \frac{1}{a} + \frac{1}{b} + \frac{1}{x}$
この動画を見る
$x=?$ $(a+b \neq 0)$
$\frac{1}{a+b+x} = \frac{1}{a} + \frac{1}{b} + \frac{1}{x}$
福田の数学〜慶應義塾大学2023年医学部第１問(2)〜虚数が係数の2次方程式の解
単元：
#大学入試過去問(数学)#２次関数#複素数平面#2次方程式と2次不等式#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (2)式4$z^2$+4$z$-$\sqrt 3 i$=0を満たす複素数zは2つある。それらを$\alpha$,$\beta$とする。ただし、$i$は虚数単位である。$\alpha$,$\beta$に対応する複素数平面上の点をそれぞれP,Qとすると、線分PQの長さは$\boxed{\ \ え\ \ }$であり、PQの中点の座標は($\boxed{\ \ お\ \ }$, $\boxed{\ \ か\ \ }$)である。
また線分PQの垂直二等分線の傾きは$\boxed{\ \ き\ \ }$である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{1}$ (2)式4$z^2$+4$z$-$\sqrt 3 i$=0を満たす複素数zは2つある。それらを$\alpha$,$\beta$とする。ただし、$i$は虚数単位である。$\alpha$,$\beta$に対応する複素数平面上の点をそれぞれP,Qとすると、線分PQの長さは$\boxed{\ \ え\ \ }$であり、PQの中点の座標は($\boxed{\ \ お\ \ }$, $\boxed{\ \ か\ \ }$)である。
また線分PQの垂直二等分線の傾きは$\boxed{\ \ き\ \ }$である。
2023慶應義塾大学医学部過去問
高校入試の頻出問題を手早く解答する動画～全国入試問題解法
単元：
#数学(中学生)#２次関数#2次方程式と2次不等式#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$ x^2-8x+2a+1=0 $の解の1つが$ x=3 $であるとき,
aの値を求めよ.また,もう一つの解を求めなさい.
栃木県高校過去問
この動画を見る
$ x^2-8x+2a+1=0 $の解の1つが$ x=3 $であるとき,
aの値を求めよ.また,もう一つの解を求めなさい.
栃木県高校過去問
慶應義塾高校 2次方程式解け
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$(2021-x)(2022-x) =2023 - x$
慶應義塾高等学校
この動画を見る
$(2021-x)(2022-x) =2023 - x$
慶應義塾高等学校
【数検準2級】高校数学：数学検定準2級2次：問1
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#２次関数#2次方程式と2次不等式#数学検定#数学検定準2級#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
問1.
1辺の長さが6mの正方形の形をした花壇Aがあります。花壇Aより縦が 2a m長く、横が a m長い長方形の形をした
花壇Bをつくるとき、次の問いに答えなさい。ただし、a＞0とします。
(1) 花壇Bの面積は、花壇Aの面積より何m²大きいですか。aを用いて表しなさい。この問題は答えだけを書いてください。
(2) 花壇Bの面積が花壇Aの面積より72m²大きいとき、aを求めるための方程式をつくり、それを解いてaの値を求めなさい。
この動画を見る
問1.
1辺の長さが6mの正方形の形をした花壇Aがあります。花壇Aより縦が 2a m長く、横が a m長い長方形の形をした
花壇Bをつくるとき、次の問いに答えなさい。ただし、a＞0とします。
(1) 花壇Bの面積は、花壇Aの面積より何m²大きいですか。aを用いて表しなさい。この問題は答えだけを書いてください。
(2) 花壇Bの面積が花壇Aの面積より72m²大きいとき、aを求めるための方程式をつくり、それを解いてaの値を求めなさい。
ルートの入っている二次方程式を解け。2023東海
単元：
#数Ⅰ#数と式#２次関数#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式を解け
$2\sqrt 2 x^2 - \sqrt{14}x - \sqrt 2 = 0$
2023東海高等学校
この動画を見る
2次方程式を解け
$2\sqrt 2 x^2 - \sqrt{14}x - \sqrt 2 = 0$
2023東海高等学校
入試問題送って下さった本当にありがとうございました。2023高校入試数学解説100問目 二次方程式 帝京大学高校（改）
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
方程式を解け
$(2x-4)^2 = 8-4(x-2)$
帝京大学高等学校
この動画を見る
方程式を解け
$(2x-4)^2 = 8-4(x-2)$
帝京大学高等学校
2023高校入試数学解説46問目 二次方程式の応用 灘高校 整数問題
単元：
#数学(中学生)#数Ⅰ#数A#２次関数#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
xの方程式$x^2+x-n+1 = 0$が整数解をもつとき
$n-2023$の絶対値が最小となる整数nは？
2023 灘高等学校
この動画を見る
xの方程式$x^2+x-n+1 = 0$が整数解をもつとき
$n-2023$の絶対値が最小となる整数nは？
2023 灘高等学校
2023高校入試解説34問目 知らないと損する2次方程式の偶数バージョン 中大杉並
単元：
#数学(中学生)#数Ⅰ#２次関数#2次方程式と2次不等式#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x^2-6x+4 = 0 $と$y^2 -14y +44 = 0$の解を適当に組み合わせてx-yの値を計算する。その値が有理数になるときx-yの値は?
2023中央大学杉並高等学校
この動画を見る
$x^2-6x+4 = 0 $と$y^2 -14y +44 = 0$の解を適当に組み合わせてx-yの値を計算する。その値が有理数になるときx-yの値は?
2023中央大学杉並高等学校
指数・対数連立不等式 京都府立大
単元：
#２次関数#2次方程式と2次不等式#2次関数とグラフ#指数関数と対数関数#指数関数#対数関数
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a>0,a \neq 1$とする.
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^{2x-4}-1<a^{x+1}-a^{x-5} \\
2\log_a(x-2)\geqq \log_a(x-2)+\log_a5
\end{array}
\right.
\end{eqnarray}$
連立不等式を解け.
この動画を見る
$a>0,a \neq 1$とする.
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^{2x-4}-1<a^{x+1}-a^{x-5} \\
2\log_a(x-2)\geqq \log_a(x-2)+\log_a5
\end{array}
\right.
\end{eqnarray}$
連立不等式を解け.
2023高校入試解説14問目 2次方程式 渋谷教育学園幕張
単元：
#数学(中学生)#数Ⅰ#２次関数#2次方程式と2次不等式#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
方程式を解け
$(x+\sqrt 3 +\sqrt 5)^2 - 3 \sqrt 5(x-2 \sqrt 5 + \sqrt 3 ) -35 = 0$
2023渋谷教育学園幕張高等学校
この動画を見る
方程式を解け
$(x+\sqrt 3 +\sqrt 5)^2 - 3 \sqrt 5(x-2 \sqrt 5 + \sqrt 3 ) -35 = 0$
2023渋谷教育学園幕張高等学校
2023高校入試解説10問目 二次方程式2023 日大習志野
単元：
#数学(中学生)#数Ⅰ#２次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式を解け
$x^2 - 6 \times 17x - 2023 = 0$
2023日本大学習志野高等学校
この動画を見る
2次方程式を解け
$x^2 - 6 \times 17x - 2023 = 0$
2023日本大学習志野高等学校
図で理解する2次方程式の解の公式～ほーみんに数学教えてみた～
単元：
#数学(中学生)#中３数学#２次方程式#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
図で理解する2次方程式の解の公式～ほーみんに数学教えてみた～
この動画を見る
図で理解する2次方程式の解の公式～ほーみんに数学教えてみた～
中学入試だけど、二次方程式使って解いちゃった 灘中2023
単元：
#算数(中学受験)#数Ⅰ#２次関数#2次方程式と2次不等式#過去問解説(学校別)#平面図形#図形の移動#平面図形その他
指導講師：
数学を数楽に
問題文全文(内容文)：
四角形ABCD、CHIEは正方形
正方形BEFGの面積=?
＊図は動画内参照
2023灘中学校
この動画を見る
四角形ABCD、CHIEは正方形
正方形BEFGの面積=?
＊図は動画内参照
2023灘中学校
2023高校入試解説7問目 工夫して解け2次方程式 早稲田佐賀
単元：
#数学(中学生)#数Ⅰ#２次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式を解け
$(2x -1)^2 + 2x -57 = 0$
2023早稲田佐賀高等学校
この動画を見る
2次方程式を解け
$(2x -1)^2 + 2x -57 = 0$
2023早稲田佐賀高等学校
2023高校入試解説5問目 2次方程式の応用 西大和学園
単元：
#数学(中学生)#数Ⅰ#２次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式$x^2 -ax + 1 = 0$の2つの解の差が$\frac{3}{2}$のときa=?
(a＞0)
2023西大和学園高等学校
この動画を見る
2次方程式$x^2 -ax + 1 = 0$の2つの解の差が$\frac{3}{2}$のときa=?
(a＞0)
2023西大和学園高等学校
学習院大 二次不等式
単元：
#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ f(x)=x^2+2(a-5)x+a^2-11a+26$
$f(x)a$を満たす実数xが存在するようなaの範囲を求めよ.
学習院大過去問
この動画を見る
$ f(x)=x^2+2(a-5)x+a^2-11a+26$
$f(x)a$を満たす実数xが存在するようなaの範囲を求めよ.
学習院大過去問
連立二元４次方程式
単元：
#数Ⅰ#数Ⅱ#数と式#２次関数#複素数と方程式#2次方程式と2次不等式#複素数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=2 \\
x^4+y^4=1234
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=2 \\
x^4+y^4=1234
\end{array}
\right.
\end{eqnarray}$
法政大 解の配置
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
周囲の長さが$\ell$,対角線の長さが2の長方形$\ell$の範囲を求めよ.
法政大過去問
この動画を見る
周囲の長さが$\ell$,対角線の長さが2の長方形$\ell$の範囲を求めよ.
法政大過去問
二次方程式
単元：
#数学(中学生)#中３数学#２次方程式#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
これを解け.
$\dfrac{1}{2}x^2-4×10×82×6562=\dfrac{1}{2}$
この動画を見る
これを解け.
$\dfrac{1}{2}x^2-4×10×82×6562=\dfrac{1}{2}$
文字があると中学生は困ってしまうよね。二次方程式の応用。 2通りで解説 芝浦工大柏
単元：
#数学(中学生)#数Ⅰ#２次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
a＞0とする。
xについての二次方程式
$x^2+2ax-a^2=0$の解が$x= - a ± 10 \sqrt 2$のときa=?
芝浦工業大学柏高等学校
この動画を見る
a＞0とする。
xについての二次方程式
$x^2+2ax-a^2=0$の解が$x= - a ± 10 \sqrt 2$のときa=?
芝浦工業大学柏高等学校
二次方程式の応用 慶應志木
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式$2x^2+24x+a= 0$の解が偶数となるような正の整数aを全て求めよ。
慶應義塾志木高等学校
この動画を見る
2次方程式$2x^2+24x+a= 0$の解が偶数となるような正の整数aを全て求めよ。
慶應義塾志木高等学校
2次式 連立方程式 国学院高校
単元：
#数学(中学生)#中２数学#連立方程式#数Ⅰ#２次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
\begin{eqnarray}
\left\{
\begin{array}{l}
x + 2y = 7 \\
(x-y)^2+2(x-y)-15 = 0
\end{array}
\right.
\end{eqnarray}
x=? y=?
(x＜y)
國學院高等学校
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
x + 2y = 7 \\
(x-y)^2+2(x-y)-15 = 0
\end{array}
\right.
\end{eqnarray}
x=? y=?
(x＜y)
國學院高等学校
二次方程式 国学院高校
単元：
#数学(中学生)#数Ⅰ#２次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$a+b=-6$ , $ab = 5$のとき方程式$(x+a)(x+b)=0$を解け
國學院高等学校
この動画を見る
$a+b=-6$ , $ab = 5$のとき方程式$(x+a)(x+b)=0$を解け
國學院高等学校
もう一つの解はどうやってだすか。二次方程式
【数学】2次方程式：二次方程式の活用 みんなが嫌いな動く点Pを得意に！
福田の数学〜明治大学2022年理工学部第１問(2)〜2次方程式の解の存在範囲
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(2)座標平面上の曲線$x^2+2xy+2y^2=5$を$C$とする。
$(\textrm{a})$直線$2x+y=t$が曲線$C$と共有点をもつとき、実数$t$の取り得る値の範囲は
$\boxed{コ}\leqq t \leqq \boxed{サ}$である。
$(\textrm{b})$直線$2x+y=1$が曲線$C$と$x \geqq 0$の範囲で共有点を少なくとも1個もつとき、
実数$t$ の取り得る値の範囲は$-\frac{1}{2}\sqrt{\boxed{シス}} \leqq t \leqq \boxed{セ}$である。
2022明治大学理工学部過去問
この動画を見る
(2)座標平面上の曲線$x^2+2xy+2y^2=5$を$C$とする。
$(\textrm{a})$直線$2x+y=t$が曲線$C$と共有点をもつとき、実数$t$の取り得る値の範囲は
$\boxed{コ}\leqq t \leqq \boxed{サ}$である。
$(\textrm{b})$直線$2x+y=1$が曲線$C$と$x \geqq 0$の範囲で共有点を少なくとも1個もつとき、
実数$t$ の取り得る値の範囲は$-\frac{1}{2}\sqrt{\boxed{シス}} \leqq t \leqq \boxed{セ}$である。
2022明治大学理工学部過去問
中学生にとっては激ムズすぎる 仙台育英（改）
単元：
#数学(中学生)#数Ⅰ#２次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
2次方程式$2x^2-mx-m=0$の解の1つが1よりも大きいとき、mの値の範囲を求めよ。
（仙台育英学園高等学校 誘導省略）
この動画を見る
2次方程式$2x^2-mx-m=0$の解の1つが1よりも大きいとき、mの値の範囲を求めよ。
（仙台育英学園高等学校 誘導省略）
福田の数学〜早稲田大学2022年理工学部第２問〜条件を満たすm個の2次関数の積でできる2m次方程式の異なる解の総和
単元：
#数Ⅰ#数A#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\large\boxed{2}}\ p,q$を相異なる素数とする。次の3条件を満たすxの2次式f(x)を考える。
・係数はすべて整数1で$x^2$の係数は1である。
・$f(1)=pq$である。
・方程式$f(x)=0$は整数解をもつ。
以下の問いに答えよ。
(1)$f(x)$をすべて求めよ。
(2)(1)で求めたものを$f_1(x),f_2(x),\ldots,f_m(x)$とする。2m次方程式
$f_1(x)×f_2(x)×\ldots×f_m(x)=0$
の相異なる解の総和は$p,q$によらないことを示せ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{2}}\ p,q$を相異なる素数とする。次の3条件を満たすxの2次式f(x)を考える。
・係数はすべて整数1で$x^2$の係数は1である。
・$f(1)=pq$である。
・方程式$f(x)=0$は整数解をもつ。
以下の問いに答えよ。
(1)$f(x)$をすべて求めよ。
(2)(1)で求めたものを$f_1(x),f_2(x),\ldots,f_m(x)$とする。2m次方程式
$f_1(x)×f_2(x)×\ldots×f_m(x)=0$
の相異なる解の総和は$p,q$によらないことを示せ。
2022早稲田大学理工学部過去問
x,yの２次式の値の範囲
単元：
#数Ⅰ#２次関数#2次方程式と2次不等式#2次関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
x,yは実数とする.
$x^2+2y^2-4y=2$を満たすとき,
$x+4y^2-8y$の値の範囲を求めよ.
この動画を見る
x,yは実数とする.
$x^2+2y^2-4y=2$を満たすとき,
$x+4y^2-8y$の値の範囲を求めよ.