三角比(三角比・拡張・相互関係・単位円)
三角比(三角比・拡張・相互関係・単位円)
 三角比(三角比・拡張・相互関係・単位円)
三角比(三角比・拡張・相互関係・単位円)
【中学から学ぶ!】正弦定理(1):三角比 特別講義~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \triangle ABC$において$ \sin^2 A=\sin^2 B+\sin^2 C$ならばどんな三角形か.
この動画を見る
$ \triangle ABC$において$ \sin^2 A=\sin^2 B+\sin^2 C$ならばどんな三角形か.
三角形の面積の最大値 九州国際大附属(福岡)
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
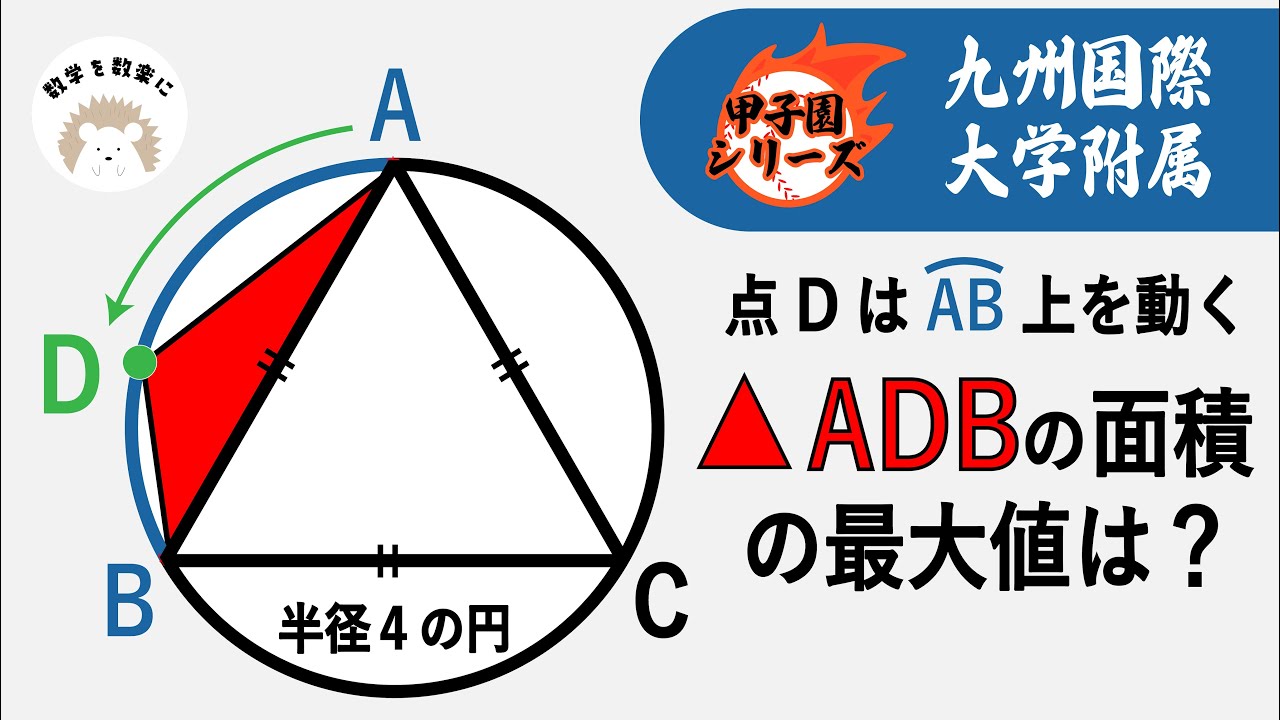
点Dは$\stackrel{\huge\frown}{AB}$上を動く△ADBの面積の最大値は?
*図は動画内参照
九州国際大学付属高等学校
この動画を見る
点Dは$\stackrel{\huge\frown}{AB}$上を動く△ADBの面積の最大値は?
*図は動画内参照
九州国際大学付属高等学校
福田の数学〜早稲田大学2022年教育学部第3問〜円の外接円の半径と円周上の点と原点の距離の最大最小

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形と方程式#点と直線#円と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}\ O(0,0),\ A(0,1),\ B(p,q)$を座標平面上の点とし、pは0でないとする。
AとBを通る直線をlとおく。Oを中心としlに接する円の面積を$D_1$で表す。
また、3点O,A,Bを通る円周で囲まれる円の面積を$D_2$とおく。次の問いに答えよ。
(1)$D_1$を$p,q$を使って表せ。
(2)点$(2,2\sqrt3)$を中心とする半径1の円周をCとする。点BがC上を動くときの
$D_1$と$D_2$の積$D_1D_2$の最小値と最大値を求めよ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{3}}\ O(0,0),\ A(0,1),\ B(p,q)$を座標平面上の点とし、pは0でないとする。
AとBを通る直線をlとおく。Oを中心としlに接する円の面積を$D_1$で表す。
また、3点O,A,Bを通る円周で囲まれる円の面積を$D_2$とおく。次の問いに答えよ。
(1)$D_1$を$p,q$を使って表せ。
(2)点$(2,2\sqrt3)$を中心とする半径1の円周をCとする。点BがC上を動くときの
$D_1$と$D_2$の積$D_1D_2$の最小値と最大値を求めよ。
2022早稲田大学教育学部過去問
福田の数学〜早稲田大学2022年教育学部第1問(3)〜四面体と四面体の共通部分の切り口の面積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
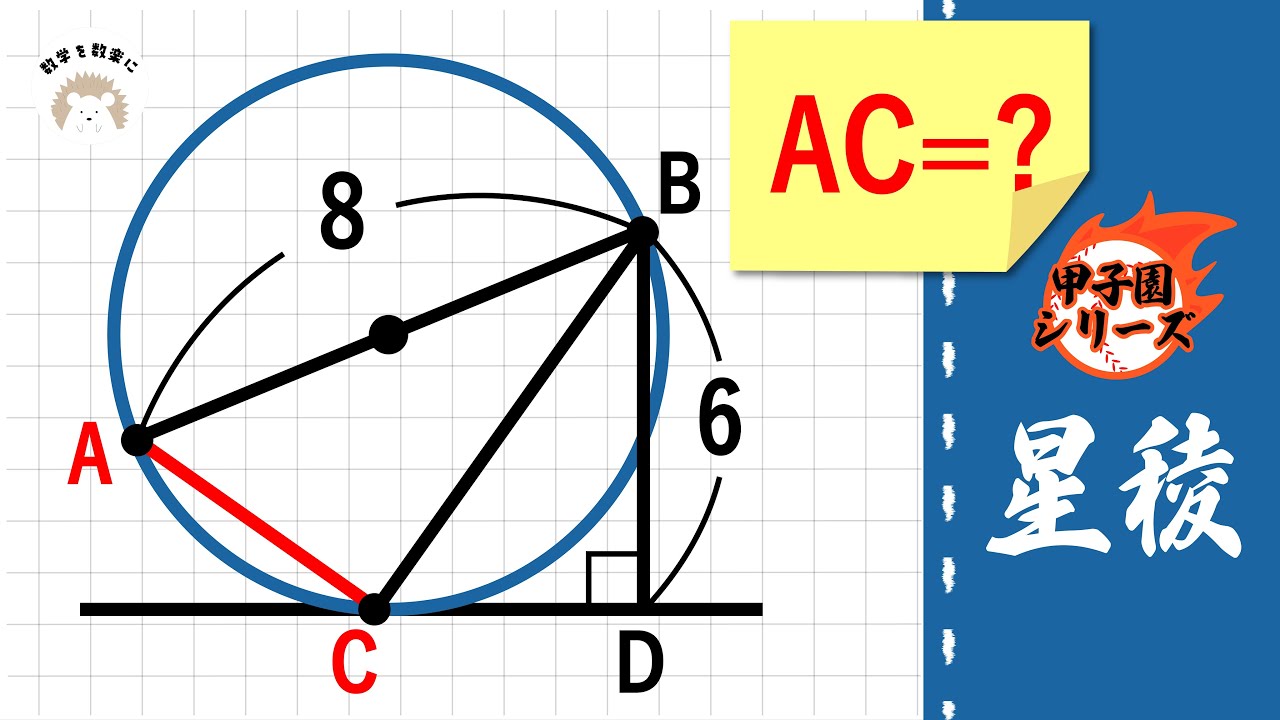
円 星稜
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AC=?
*図は動画内参照
星稜高等学校
この動画を見る
AC=?
*図は動画内参照
星稜高等学校
高校1年生でも解ける!京大の入試問題【京都大学】【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$0≦θ<90°$とする。$x$についての4次方程式
{$x^2-2(\cosθ)x-\cosθ+1$}{$x^2+2(tanθ)x+3$}=0
は虚数解を少なくとも1つ持つことを示せ。
京都大過去問
この動画を見る
$0≦θ<90°$とする。$x$についての4次方程式
{$x^2-2(\cosθ)x-\cosθ+1$}{$x^2+2(tanθ)x+3$}=0
は虚数解を少なくとも1つ持つことを示せ。
京都大過去問
福田の数学〜早稲田大学2022年人間科学部第1問(3)〜三角形の辺の関係から角の関係を求める

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#三角関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)$\triangle ABC$において、3つの角の大きさをA,B,Cとし、
それぞれの対辺の長さをa,b,cとする。
$5a^2-5b^2+6bc-5c^2=0$
のとき、$\sin2A+\cos2A=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{1}}$(3)$\triangle ABC$において、3つの角の大きさをA,B,Cとし、
それぞれの対辺の長さをa,b,cとする。
$5a^2-5b^2+6bc-5c^2=0$
のとき、$\sin2A+\cos2A=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。
2022早稲田大学人間科学部過去問
【ここからでも楽しめる!】三角比の計算(4):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 2\sin \theta +3\cos \theta=1$のとき,$\theta$は第何象限の角か.
この動画を見る
$ 2\sin \theta +3\cos \theta=1$のとき,$\theta$は第何象限の角か.
【中学からの!】三角比の計算(3):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sin\theta +\sqrt3 \cos \theta=1$のとき,$\sin\theta$の値を求めよ.
ただし,$\theta$は第2象限の角である.
この動画を見る
$ \sin\theta +\sqrt3 \cos \theta=1$のとき,$\sin\theta$の値を求めよ.
ただし,$\theta$は第2象限の角である.
【数Ⅰ】相互関係式笑っちゃう覚え方

答えはわかるかもしれないけど、説明できる? 円周角 沖縄県(改)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x,y,zを小さい順に並べよ
*図は動画内参照
沖縄県(改)
この動画を見る
x,y,zを小さい順に並べよ
*図は動画内参照
沖縄県(改)
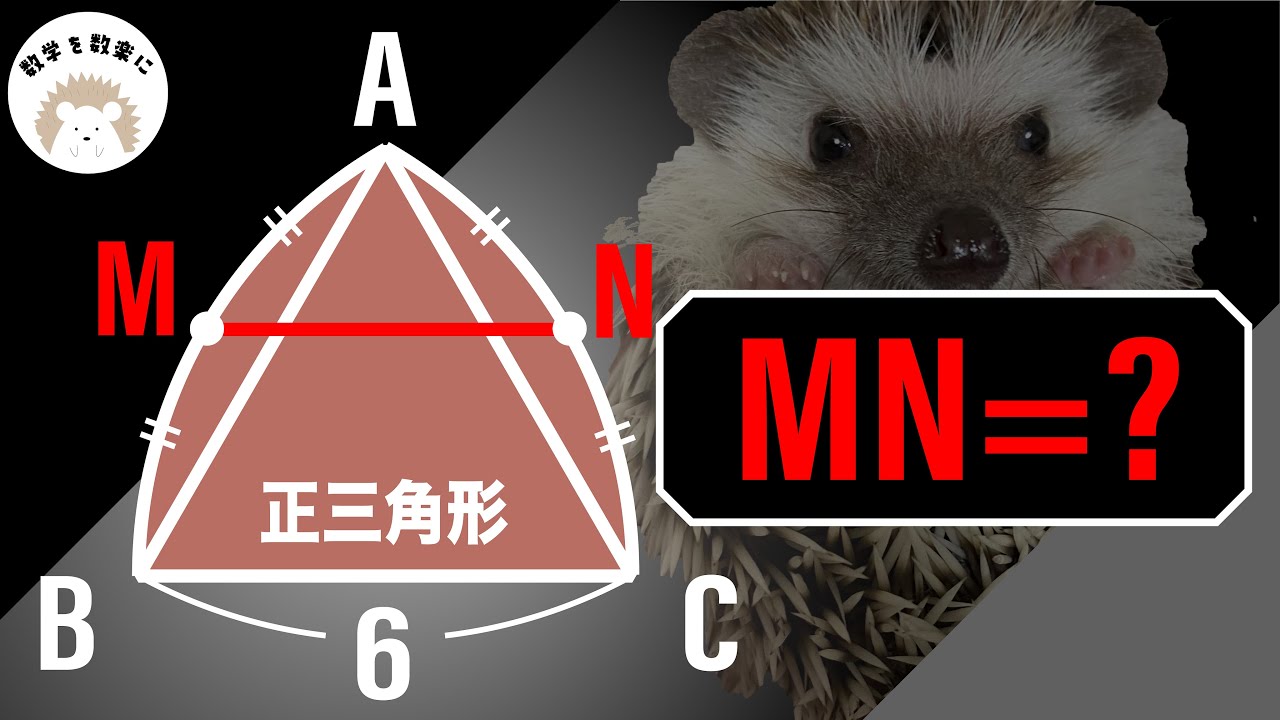
意外と苦戦!?
単元:
#数学(中学生)#中3数学#数Ⅰ#三平方の定理#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
MN=?
*図は動画内参照
この動画を見る
MN=?
*図は動画内参照
【中学からの!】三角比の計算(2):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin^3\theta+\cos^3\theta$の値を求めよ.
この動画を見る
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin^3\theta+\cos^3\theta$の値を求めよ.
【中学からの!】三角比の計算(1):特別講義(トッコー)~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin\theta\cos\theta$の値を求めよ.
この動画を見る
$\sin\theta+\cos\theta=\dfrac{1}{2}$のとき,$\sin\theta\cos\theta$の値を求めよ.
【中学生から理解できる!】三角比(さんかくひ)[ エッセンシャル版 ]:~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
三角比に関して解説していきます.
この動画を見る
三角比に関して解説していきます.
6次式の最大値と最小値!?【数学 入試問題】【自治医科大学】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$sin^6x+cos^6x$の最小値が$A$となるとき、$\dfrac{1}{A}$の値を求めよ。
自治医科大過去問
この動画を見る
$sin^6x+cos^6x$の最小値が$A$となるとき、$\dfrac{1}{A}$の値を求めよ。
自治医科大過去問
tan

円 令和4年度 2022 入試問題100題解説99問目! 愛知県
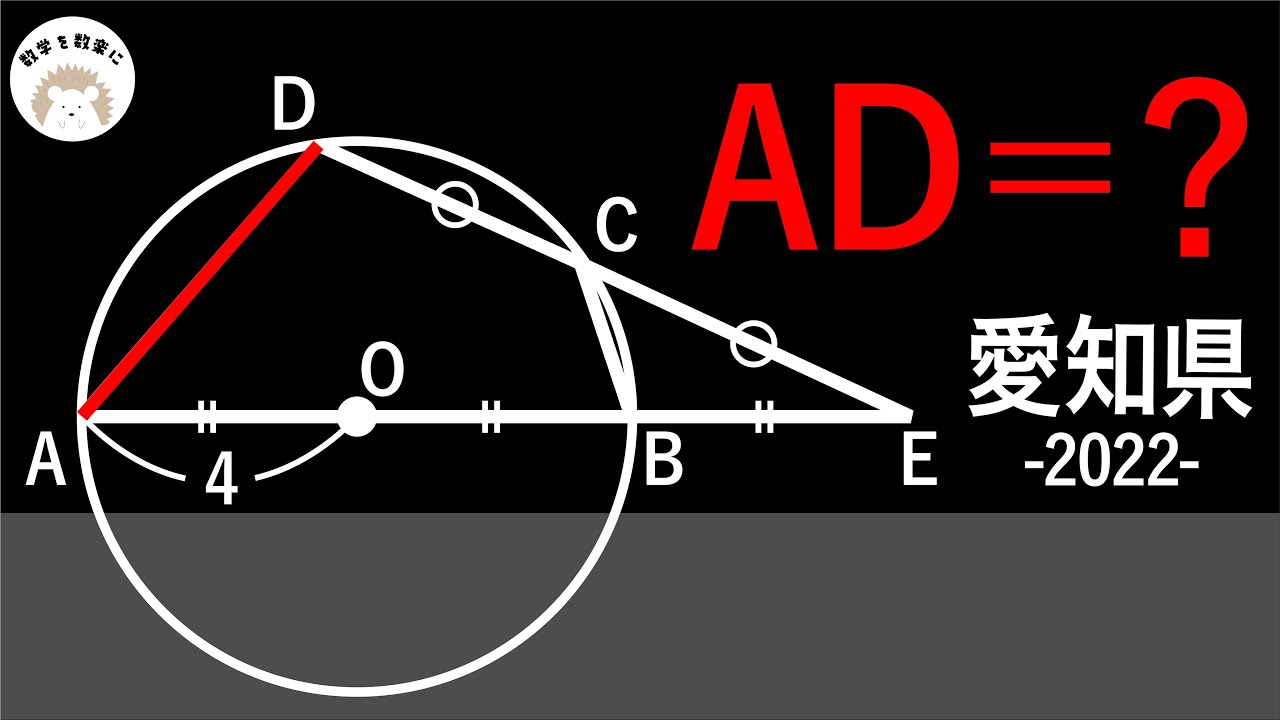
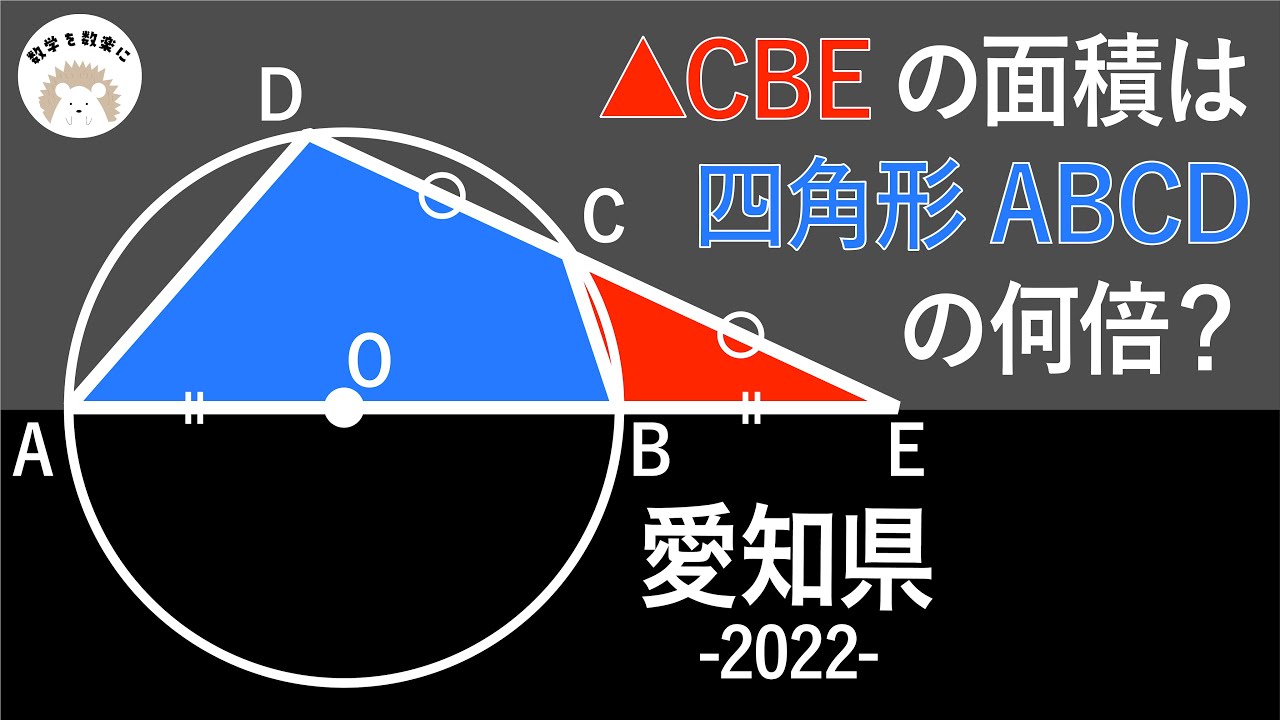
初の試み 面積比 令和4年度 2022 入試問題100題解説98問目! 愛知県
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△CBEの面積は四角形ABCDの何倍?
*図は動画内参照
2022愛知県
この動画を見る
△CBEの面積は四角形ABCDの何倍?
*図は動画内参照
2022愛知県
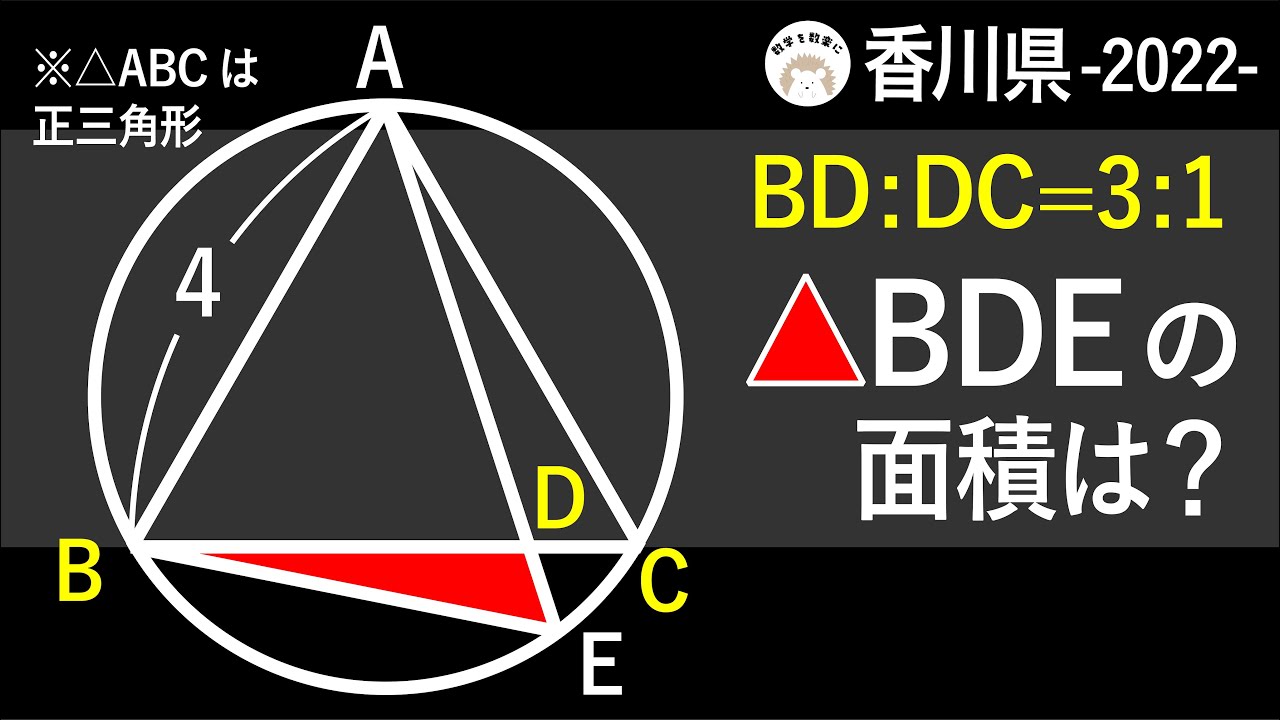
香川県 円 令和4年度 2022 入試問題100題解説94問目!
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BD:DC=3:1
△BDEの面積は?
*図は動画内参照
2022香川県
この動画を見る
BD:DC=3:1
△BDEの面積は?
*図は動画内参照
2022香川県
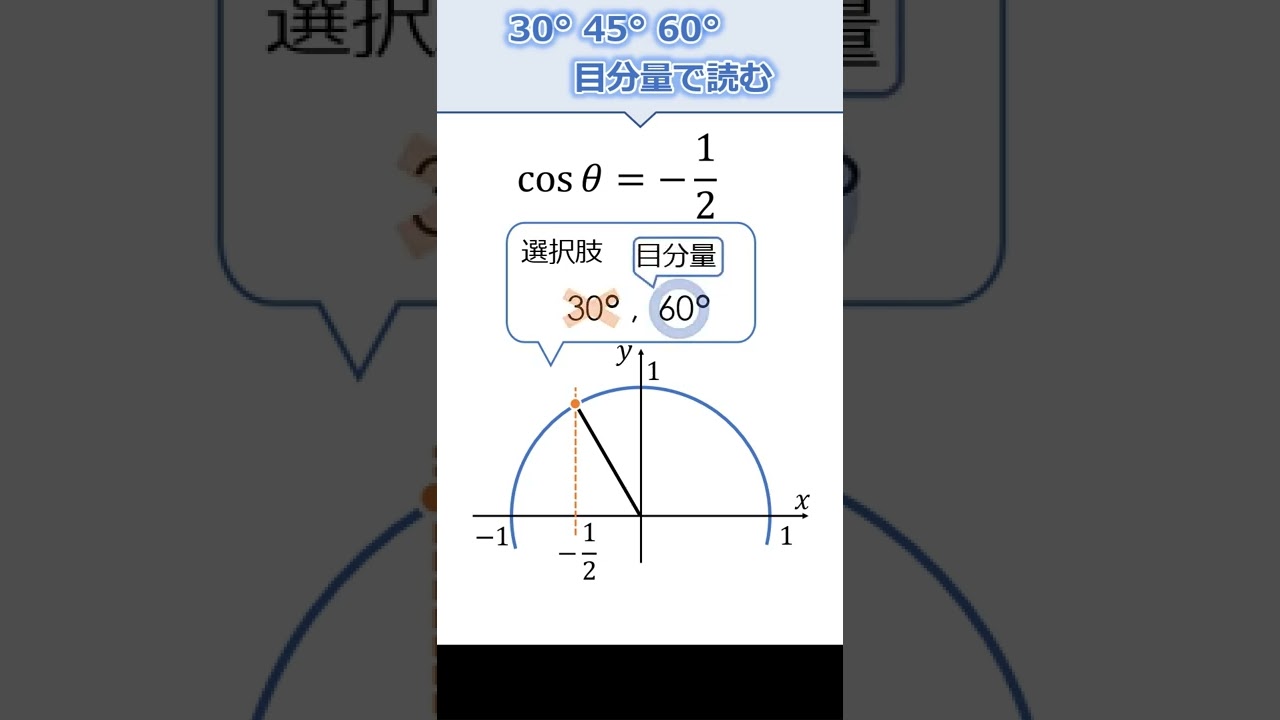
三角比の方程式 #Shorts
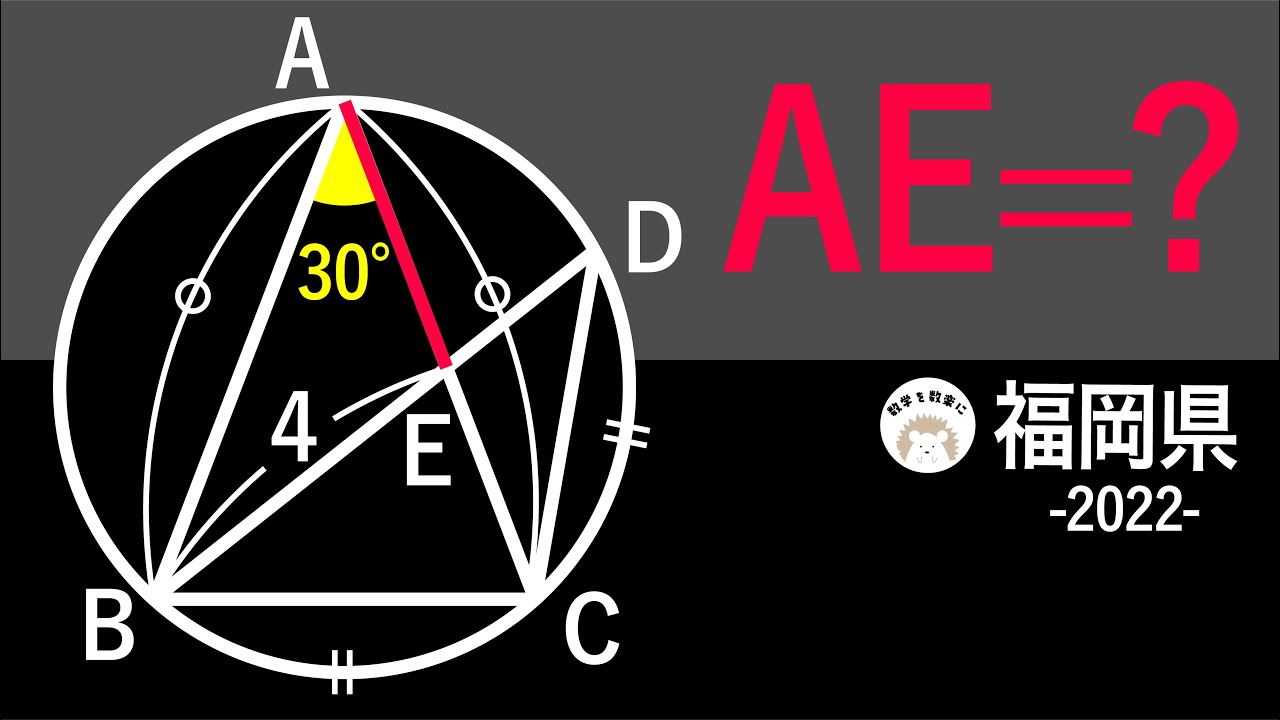
福岡県 円 令和4年度 2022 入試問題100題解説91問目!
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AB=AC
AE=?
*図は動画内参照
2022福岡県
この動画を見る
AB=AC
AE=?
*図は動画内参照
2022福岡県
三角比の90°以上の有名角 #Shorts
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
三角比の90°以上の有名角に関して解説していきます.
この動画を見る
三角比の90°以上の有名角に関して解説していきます.
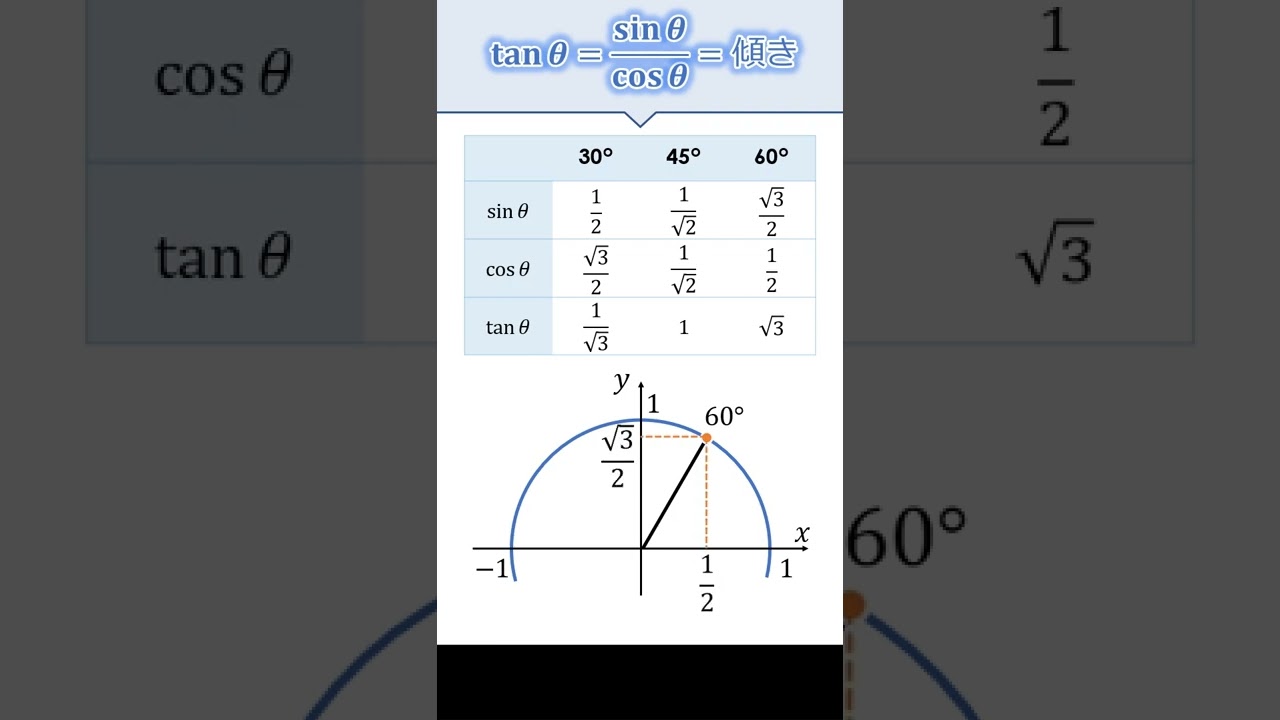
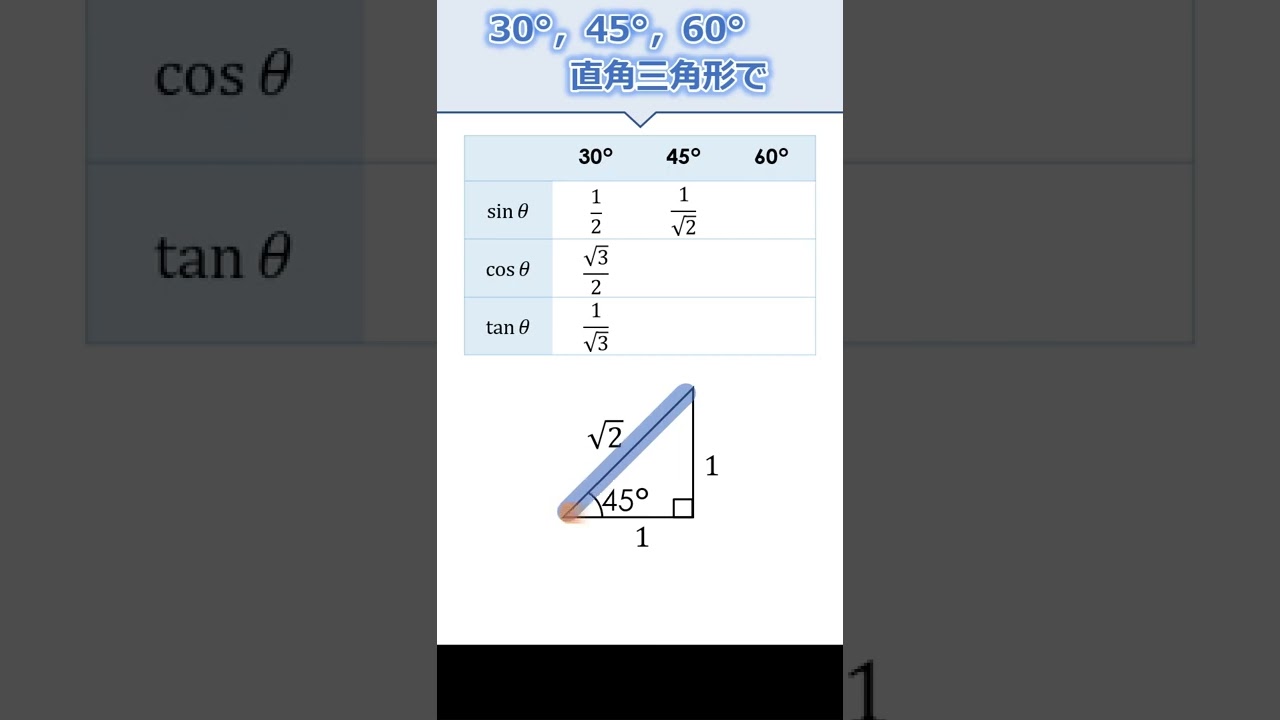
三角比の有名角30°45°60° #Shorts
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
三角比の有名角30°45°60°に関して解説していきます.
この動画を見る
三角比の有名角30°45°60°に関して解説していきます.
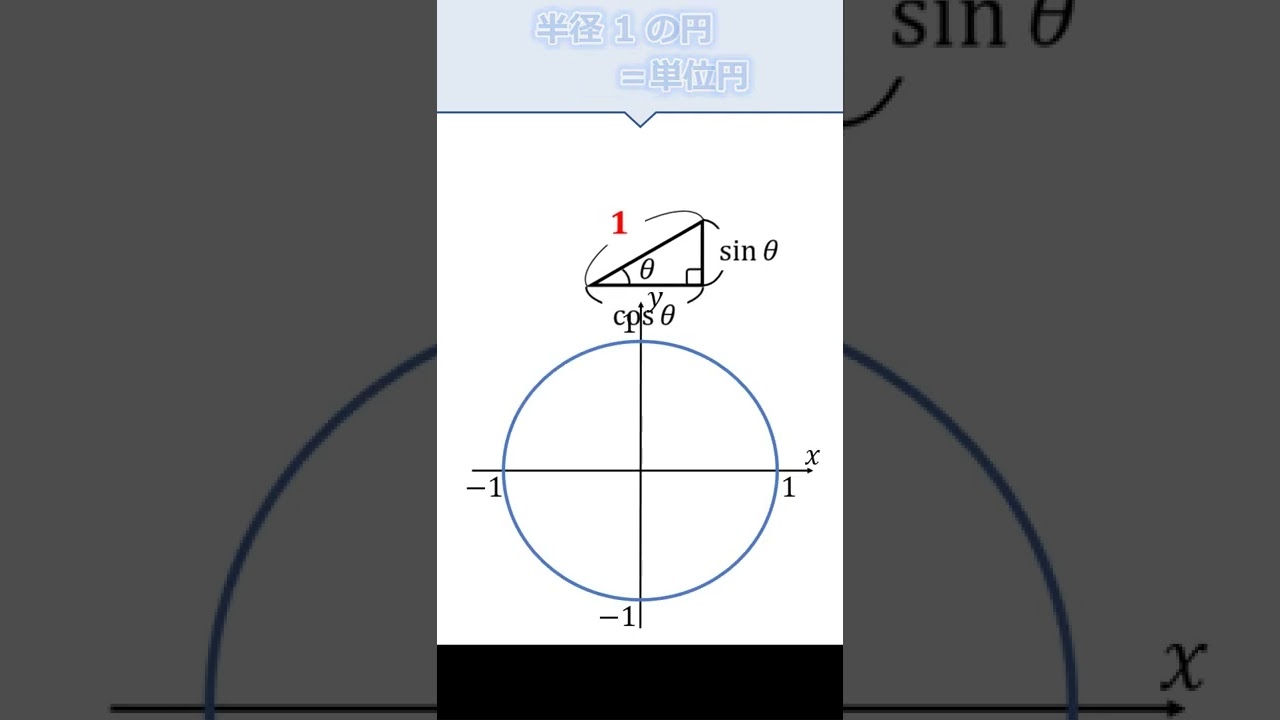
三角比の拡張 #Shorts
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
三角比の拡張に関して解説していきます.
この動画を見る
三角比の拡張に関して解説していきます.
2022年東京大 (理系)最初の一問!!

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$f(x)=(cosx)log(cosx) -cosx + \int_0^x(cost)log(cost)dt$
f(x)は区間$0<x< \frac{π}{2}$において最小値を持つことを示し、その最小値を求めよ。
2022東京大学理系問題文改め
この動画を見る
$f(x)=(cosx)log(cosx) -cosx + \int_0^x(cost)log(cost)dt$
f(x)は区間$0<x< \frac{π}{2}$において最小値を持つことを示し、その最小値を求めよ。
2022東京大学理系問題文改め
三角比の相互関係 #Shorts
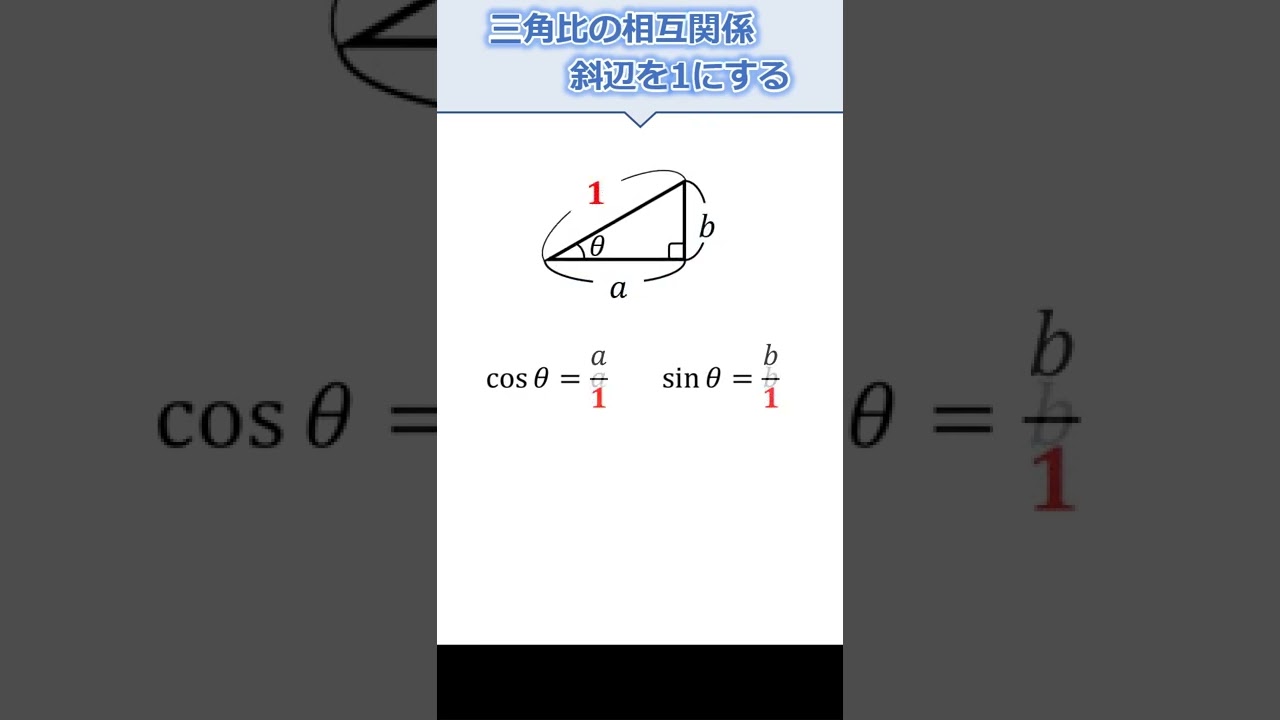
大阪大の問題の背景 特に文系の人見てください

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#図形と計量#三角比(三角比・拡張・相互関係・単位円)#複素数平面#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$ \cos\dfrac{2}{7}\pi, \cos\dfrac{4}{7}\pi, \cos\dfrac{6}{7}\pi$を解にもつ
$3$次方程式$ x^3+ax^2+bx+c=0$を求めよ.*$ z^7=1$
(2)$ f(x)=8x^3+4x^2-4x-1$,$f\left(\cos\dfrac{2}{7}\pi \right)=0$を示せ.
この動画を見る
(1)$ \cos\dfrac{2}{7}\pi, \cos\dfrac{4}{7}\pi, \cos\dfrac{6}{7}\pi$を解にもつ
$3$次方程式$ x^3+ax^2+bx+c=0$を求めよ.*$ z^7=1$
(2)$ f(x)=8x^3+4x^2-4x-1$,$f\left(\cos\dfrac{2}{7}\pi \right)=0$を示せ.
2つの円 埼玉県 令和4年度 数学 2022 入試問題100題解説77問目!
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
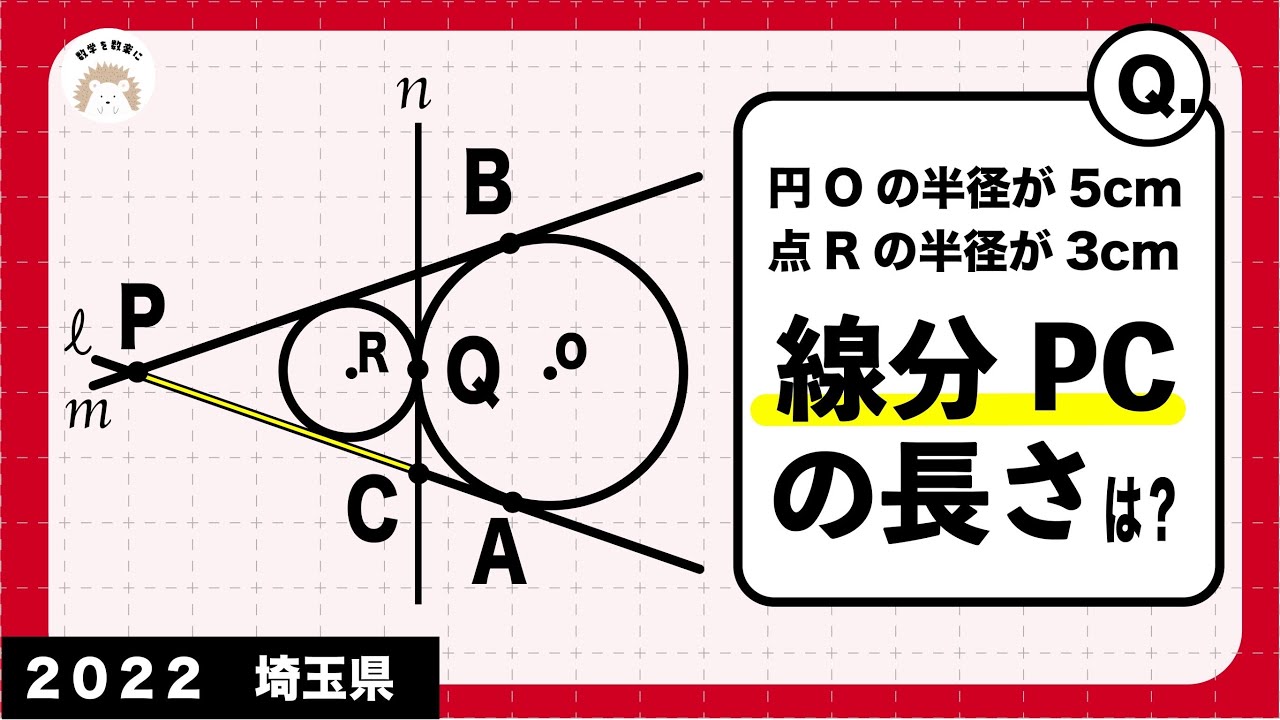
円Oの半径が5㎝
点Rの半径が3㎝
線分PCの長さは?
*図は動画内参照
2022埼玉県
この動画を見る
円Oの半径が5㎝
点Rの半径が3㎝
線分PCの長さは?
*図は動画内参照
2022埼玉県
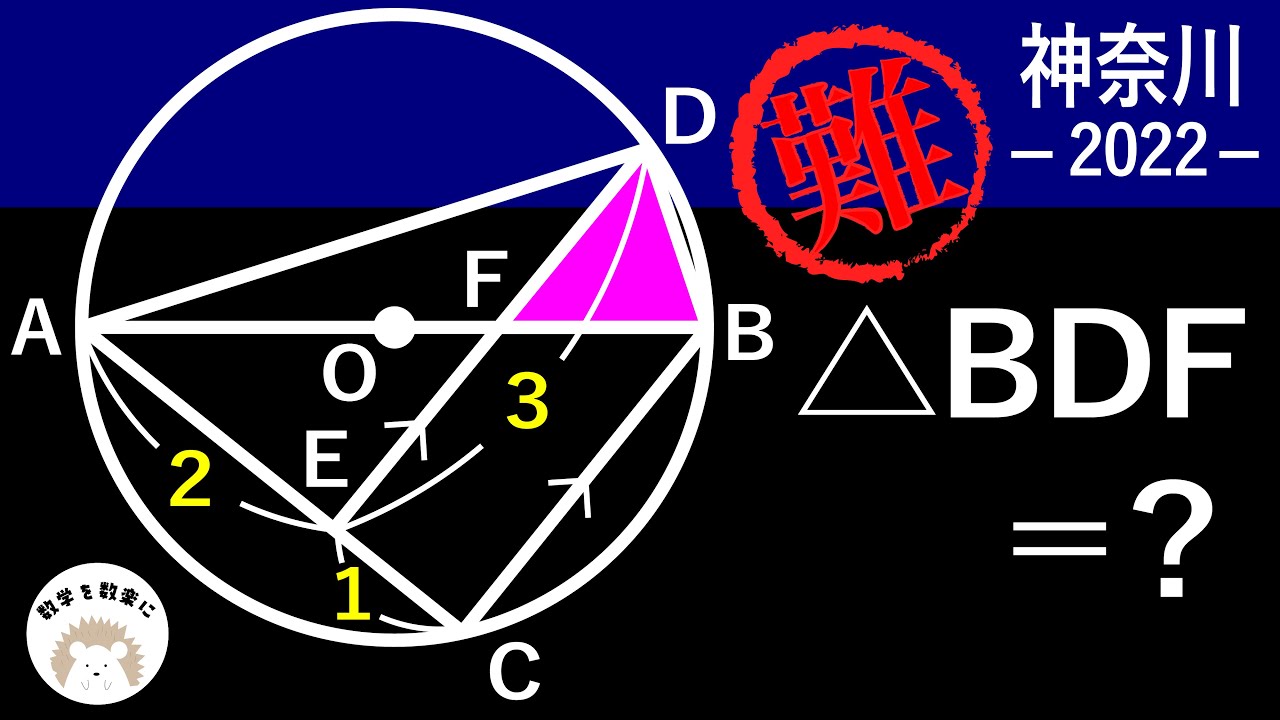
円の問題 良問です。 神奈川県 2022入試問題解説100問解説!!57問目