 図形と計量
図形と計量
 図形と計量
図形と計量
2023高校入試解説16問目 3つの内接円 渋谷教育学園幕張

単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle QPR=?$
*図は動画内参照
2023渋谷教育学園幕張高等学校
この動画を見る
$\angle QPR=?$
*図は動画内参照
2023渋谷教育学園幕張高等学校
【短時間でマスター!!】正弦定理・余弦定理を解説!〔現役塾講師解説、数学〕

2023高校入試解説11問目 円の方程式??2日大習志野(改)
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
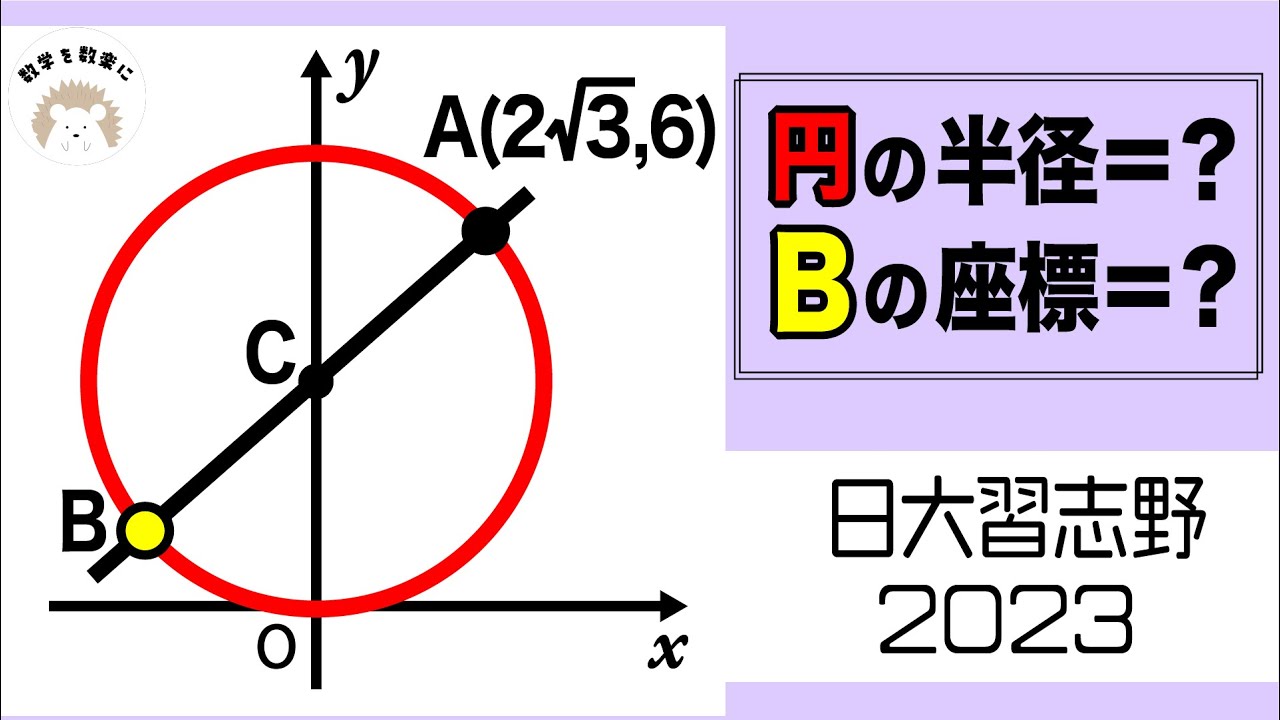
円の半径=?
Bの座標=?
*図は動画内参照
2023日本大学習志野高等学校(改)
この動画を見る
円の半径=?
Bの座標=?
*図は動画内参照
2023日本大学習志野高等学校(改)
大学入試問題#426「基本的な計算問題」 Instagram #三角関数
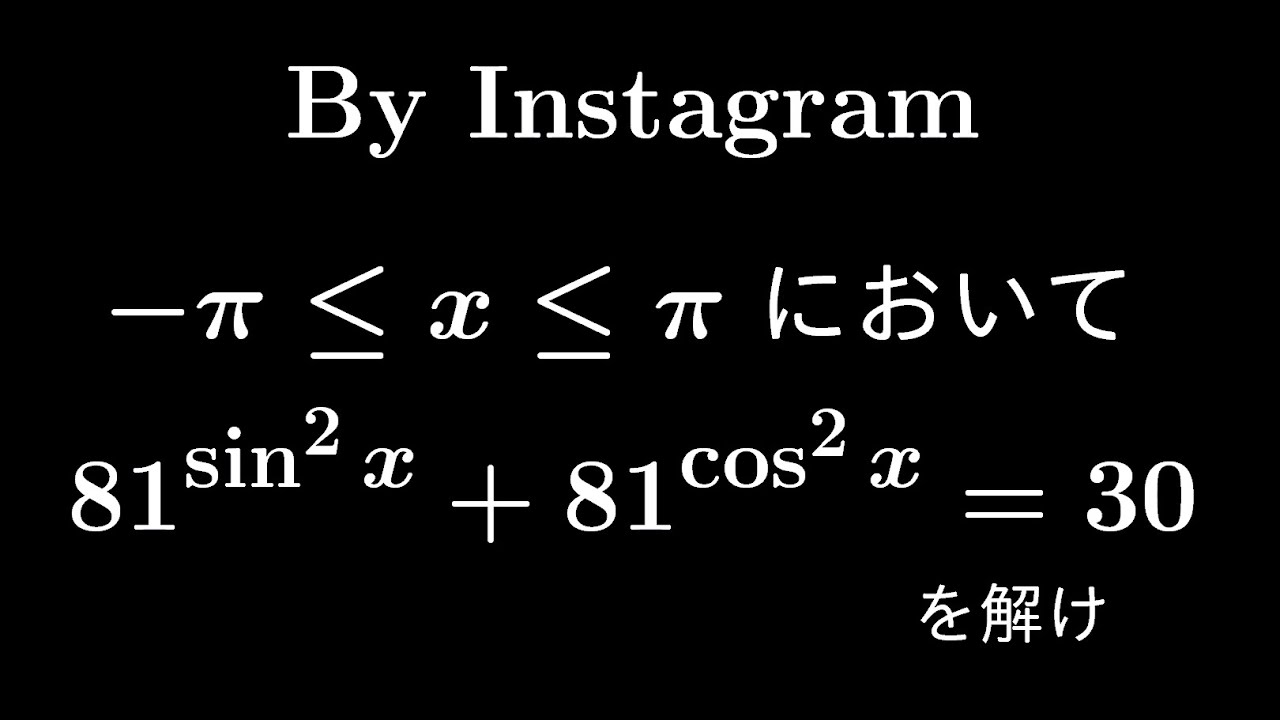
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$-\pi \leqq x \lt \pi$とする。
$81^{\sin^2x}+81^{\cos^2x}=30$
この動画を見る
$-\pi \leqq x \lt \pi$とする。
$81^{\sin^2x}+81^{\cos^2x}=30$
共通テストだけど中学生も解ける!!
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
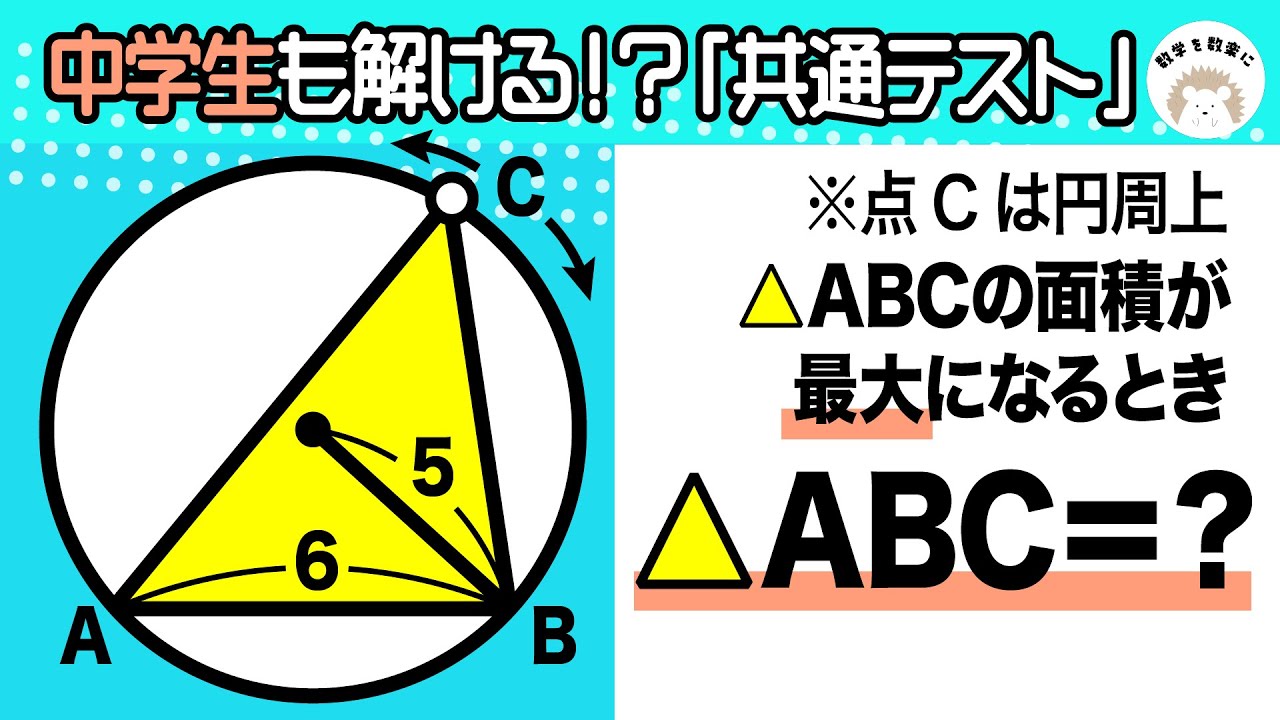
△ABCの面積が最大になるとき△ABC=?
*点Cは円周上
*図は動画内参照
2023共通テスト数ⅠA
この動画を見る
△ABCの面積が最大になるとき△ABC=?
*点Cは円周上
*図は動画内参照
2023共通テスト数ⅠA
福田の数学〜2023年共通テスト速報〜数学IA第1問不等式の解と図形の計量

単元:
#数Ⅰ#数と式#図形と計量#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
第1問
[1]実数xについての不等式
|$x$+6| $\leqq$ 2
の解は
$\boxed{\ \ アイ\ \ } \leqq x \leqq \boxed{\ \ ウエ\ \ }$
である。
よって、実数$a,b,c,d$が
|(1-$\sqrt3$)($a-b$)($c-d$)+6| $\leqq$2
を満たしているとき、1-$\sqrt3$は負であることに注意すると、($a-b$)($c-d$)
の取り得る値の範囲は
$\boxed{\ \ オ\ \ }+\boxed{\ \ カ\ \ }\sqrt3 \leqq (a-b)(c-d) \leqq \boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3$
であることがわかる。
特に
$(a-b)(c-d)=\boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3 \cdots①$
であるとき、さらに
$(a-c)(b-d)=-3+\sqrt3 \cdots②$
が成り立つならば
$(a-d)(c-b)=\boxed{\ \ ケ\ \ }+\boxed{\ \ コ\ \ }\sqrt3 \cdots③$
であることが、等式①,②,③の左辺を展開して比較することによりわかる。
[2]
(1)点Oを中心とし、半径が5である円Oがある。この円周上に2点A,B
をAB=6となるようにとる。また、円Oの円周上に、2点A,Bとは異なる点Cをとる。
(i)$\sin\angle ACB=\boxed{\boxed{\ \ サ\ \ }}$である。また、点Cを\angle ACBが鈍角となるようにとるとき、$\cos\angle ACB=\boxed{\boxed{\ \ シ\ \ }}$である。
(ii)点Cを$\triangle ABC$の面積が最大となるようにとる。点Cから直線ABに垂直な直線を引き、直線ABとの交点をDとするとき、
$\tan\angle OAD=\boxed{\boxed{\ \ ス\ \ }}$である。また、$\triangle ABC$の面積は$\boxed{\ \ セソ\ \ }$である。
$\boxed{\boxed{\ \ サ\ \ }}$ ~ $\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返し選んでもよい)
⓪$\displaystyle\frac{3}{5}$ ①$\displaystyle\frac{3}{4}$ ②$\displaystyle\frac{4}{5}$ ③ 1④$\displaystyle\frac{4}{3}$
⑤$-\displaystyle\frac{3}{5}$ ⑥$-\displaystyle\frac{3}{4}$ ⑦$-\displaystyle\frac{4}{5}$ ⑧ -1⑨$-\displaystyle\frac{4}{3}$
(2)半径が5である球Sがある。この球面上に3点P,Q,Rをとったとき、
これらの3点を通る平面α上でPQ=8, QR=5, RP=9であったとする。
球Sの球面上に点Tを三角錐TPQRの体積が最大となるようにとるとき、その体積を
求めよう。
まず、$\cos\angle QPR=\frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}$である
ことから、$\triangle PQR$の面積は$\boxed{\ \ ツ\ \ }\sqrt{\boxed{\ \ テト\ \ }}$である。
次に、点Tから平面αに垂直な直線を引き、平面αとの交点をHとする。このとき、PH,QH,RHの長さについて、$\boxed{\boxed{\ \ ナ\ \ }}$が成り立つ。
以上より、三角錐TPQRの体積は$\boxed{\ \ ニヌ\ \ }\left(\sqrt{\boxed{\ \ ネノ\ \ }}+\sqrt{\boxed{\ \ ハ\ \ }}\right)$である。
$\boxed{\boxed{\ \ ナ\ \ }}$の解答群
⓪PH<QH<RH ①PH<RH<QH
②QH<PH<RH ③QH<RH<PH
④RH<PH<QH ⑤RH<QH<PH
⑥PH=QH=RH
2023共通テスト過去問
この動画を見る
第1問
[1]実数xについての不等式
|$x$+6| $\leqq$ 2
の解は
$\boxed{\ \ アイ\ \ } \leqq x \leqq \boxed{\ \ ウエ\ \ }$
である。
よって、実数$a,b,c,d$が
|(1-$\sqrt3$)($a-b$)($c-d$)+6| $\leqq$2
を満たしているとき、1-$\sqrt3$は負であることに注意すると、($a-b$)($c-d$)
の取り得る値の範囲は
$\boxed{\ \ オ\ \ }+\boxed{\ \ カ\ \ }\sqrt3 \leqq (a-b)(c-d) \leqq \boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3$
であることがわかる。
特に
$(a-b)(c-d)=\boxed{\ \ キ\ \ }+\boxed{\ \ ク\ \ }\sqrt3 \cdots①$
であるとき、さらに
$(a-c)(b-d)=-3+\sqrt3 \cdots②$
が成り立つならば
$(a-d)(c-b)=\boxed{\ \ ケ\ \ }+\boxed{\ \ コ\ \ }\sqrt3 \cdots③$
であることが、等式①,②,③の左辺を展開して比較することによりわかる。
[2]
(1)点Oを中心とし、半径が5である円Oがある。この円周上に2点A,B
をAB=6となるようにとる。また、円Oの円周上に、2点A,Bとは異なる点Cをとる。
(i)$\sin\angle ACB=\boxed{\boxed{\ \ サ\ \ }}$である。また、点Cを\angle ACBが鈍角となるようにとるとき、$\cos\angle ACB=\boxed{\boxed{\ \ シ\ \ }}$である。
(ii)点Cを$\triangle ABC$の面積が最大となるようにとる。点Cから直線ABに垂直な直線を引き、直線ABとの交点をDとするとき、
$\tan\angle OAD=\boxed{\boxed{\ \ ス\ \ }}$である。また、$\triangle ABC$の面積は$\boxed{\ \ セソ\ \ }$である。
$\boxed{\boxed{\ \ サ\ \ }}$ ~ $\boxed{\boxed{\ \ ス\ \ }}$の解答群(同じものを繰り返し選んでもよい)
⓪$\displaystyle\frac{3}{5}$ ①$\displaystyle\frac{3}{4}$ ②$\displaystyle\frac{4}{5}$ ③ 1④$\displaystyle\frac{4}{3}$
⑤$-\displaystyle\frac{3}{5}$ ⑥$-\displaystyle\frac{3}{4}$ ⑦$-\displaystyle\frac{4}{5}$ ⑧ -1⑨$-\displaystyle\frac{4}{3}$
(2)半径が5である球Sがある。この球面上に3点P,Q,Rをとったとき、
これらの3点を通る平面α上でPQ=8, QR=5, RP=9であったとする。
球Sの球面上に点Tを三角錐TPQRの体積が最大となるようにとるとき、その体積を
求めよう。
まず、$\cos\angle QPR=\frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }}$である
ことから、$\triangle PQR$の面積は$\boxed{\ \ ツ\ \ }\sqrt{\boxed{\ \ テト\ \ }}$である。
次に、点Tから平面αに垂直な直線を引き、平面αとの交点をHとする。このとき、PH,QH,RHの長さについて、$\boxed{\boxed{\ \ ナ\ \ }}$が成り立つ。
以上より、三角錐TPQRの体積は$\boxed{\ \ ニヌ\ \ }\left(\sqrt{\boxed{\ \ ネノ\ \ }}+\sqrt{\boxed{\ \ ハ\ \ }}\right)$である。
$\boxed{\boxed{\ \ ナ\ \ }}$の解答群
⓪PH<QH<RH ①PH<RH<QH
②QH<PH<RH ③QH<RH<PH
④RH<PH<QH ⑤RH<QH<PH
⑥PH=QH=RH
2023共通テスト過去問
ハルハルさんの作成問題「たぶん名作だと思います。難易度は高め」 図形 三角比

単元:
#数Ⅰ#数Ⅱ#式と証明#図形と計量#三角比への応用(正弦・余弦・面積)#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\theta$:実数
3辺の長さが$2\sin\theta,\ 2\cos\theta,\ \displaystyle \frac{\tan\theta}{\sqrt{ 3 }}$の三角形が単位円に内接している。
この条件を満たしている三角形の面積をすべて求めよ。
この動画を見る
$\theta$:実数
3辺の長さが$2\sin\theta,\ 2\cos\theta,\ \displaystyle \frac{\tan\theta}{\sqrt{ 3 }}$の三角形が単位円に内接している。
この条件を満たしている三角形の面積をすべて求めよ。
補助線のセンスを磨け!2通りで解説

高さが等しい面積比

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
高さが等しい図形の面積比
A:B:C=
*図は動画内参照
この動画を見る
高さが等しい図形の面積比
A:B:C=
*図は動画内参照
知っていれば一瞬。傍接円と三角形の周の長さ 清風南海高校
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
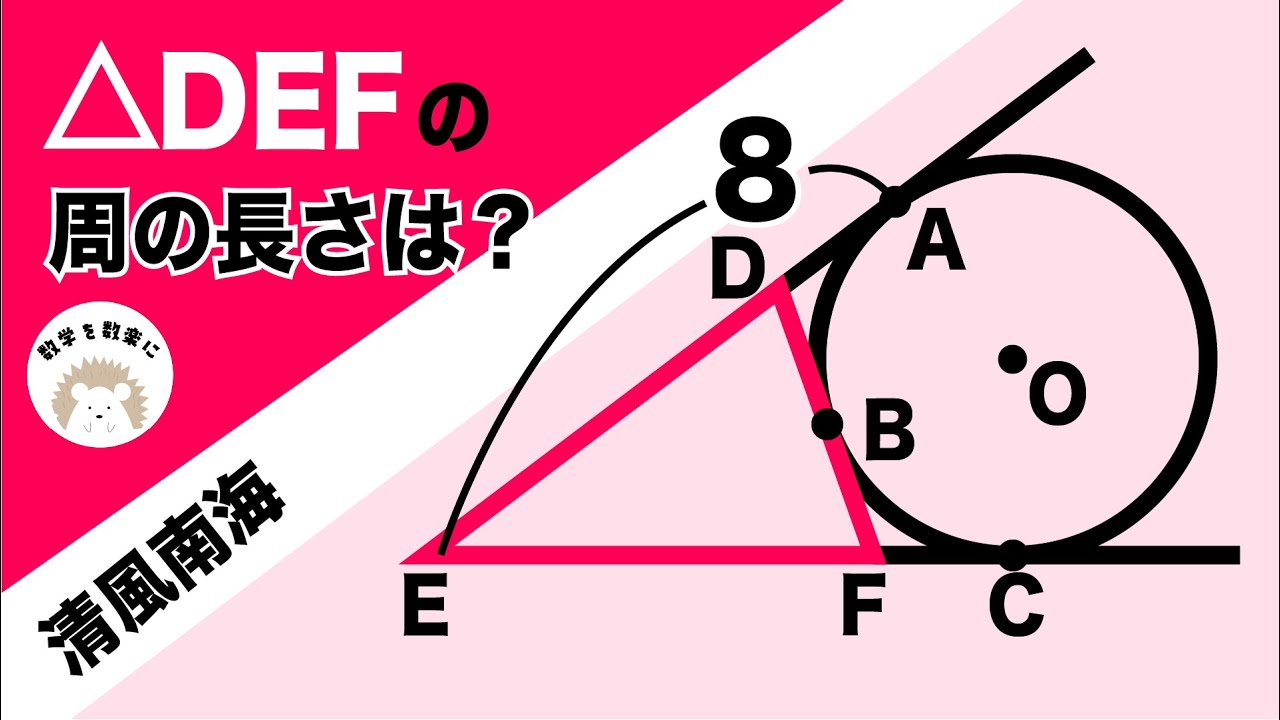
△DEFの周の長さは?
*図は動画内参照
清風南海高等学校
この動画を見る
△DEFの周の長さは?
*図は動画内参照
清風南海高等学校
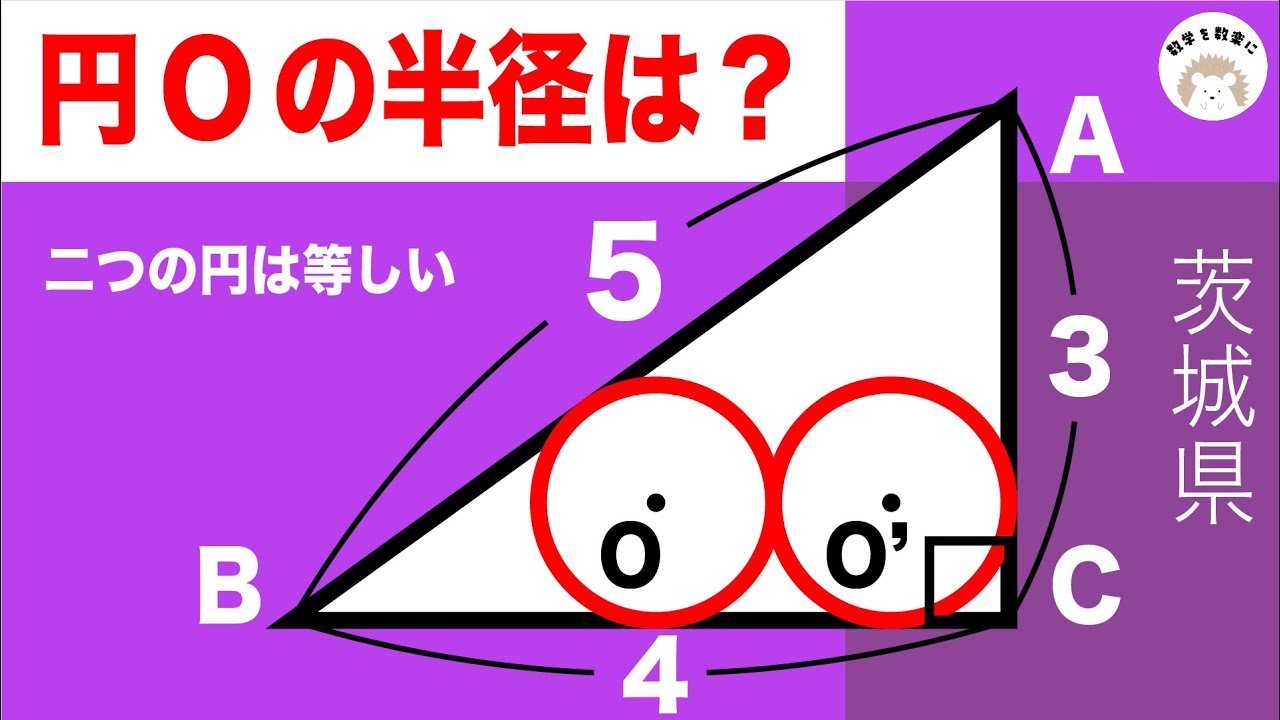
直角三角形と2つの円 茨城県
単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円Oの半径=?
(円Oの半径=円O'の半径)
*図は動画内参照
茨城県
この動画を見る
円Oの半径=?
(円Oの半径=円O'の半径)
*図は動画内参照
茨城県
【わかりやすく解説】三角方程式(高校数学Ⅰ/三角比)

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$の時、次の等式を満たす$\theta$の値を求めよ
(1)$2\sin\theta=1$
(2)$2\cos\theta=-1$
(3)$\sqrt{ 3 }\tan\theta-1=0$
(4)$\cos\theta=0$
この動画を見る
$0^{ \circ } \leqq \theta \leqq 180^{ \circ }$の時、次の等式を満たす$\theta$の値を求めよ
(1)$2\sin\theta=1$
(2)$2\cos\theta=-1$
(3)$\sqrt{ 3 }\tan\theta-1=0$
(4)$\cos\theta=0$
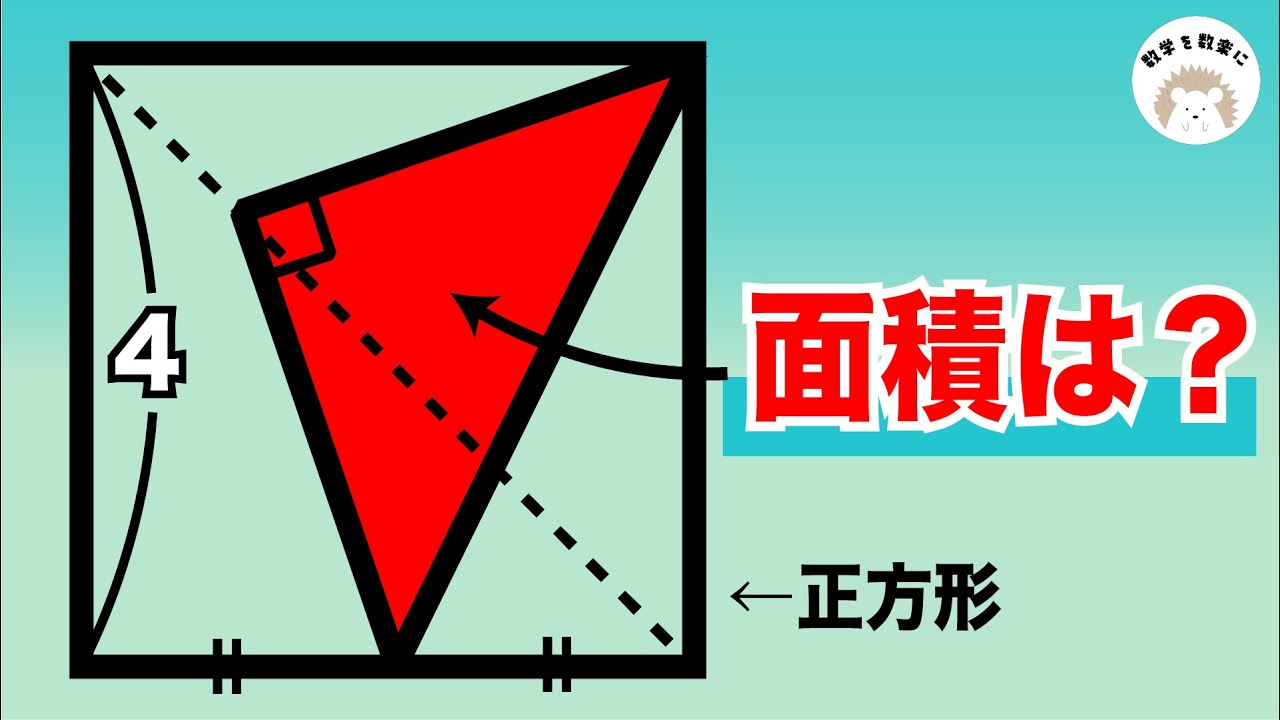
正方形の中にある直角三角形の面積
福田の数学〜北里大学2021年医学部第1問(1)〜空間ベクトルの内積と平面に下ろした垂線の長さ

単元:
#数Ⅰ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と計量#三角比(三角比・拡張・相互関係・単位円)#平面上のベクトルと内積#空間ベクトル#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
(1)一辺の長さが4の正四面体ABCDにおいて、辺BCの中点をEとおく。
動点Pは$PE=\frac{1}{2}AE$を満たしながら$\triangle AED$の内部および周上を動くものとし、
$\angle PED=\theta$とおく。このとき、$\overrightarrow{ PB }・\overrightarrow{ PC }=\boxed{ア}$である。また、$\overrightarrow{ PB }・\overrightarrow{ PC }$を
$\theta$を用いて表すと$\overrightarrow{ PC }・\overrightarrow{ PD }=\boxed{イ}$、その最大値は$\boxed{ウ}$である。
$\overrightarrow{ PC }・\overrightarrow{ PD }$が最大となるときの点Pと平面ACDの距離は$\boxed{エ}$である。
2021北里大学医学部過去問
この動画を見る
(1)一辺の長さが4の正四面体ABCDにおいて、辺BCの中点をEとおく。
動点Pは$PE=\frac{1}{2}AE$を満たしながら$\triangle AED$の内部および周上を動くものとし、
$\angle PED=\theta$とおく。このとき、$\overrightarrow{ PB }・\overrightarrow{ PC }=\boxed{ア}$である。また、$\overrightarrow{ PB }・\overrightarrow{ PC }$を
$\theta$を用いて表すと$\overrightarrow{ PC }・\overrightarrow{ PD }=\boxed{イ}$、その最大値は$\boxed{ウ}$である。
$\overrightarrow{ PC }・\overrightarrow{ PD }$が最大となるときの点Pと平面ACDの距離は$\boxed{エ}$である。
2021北里大学医学部過去問
【裏側】ビビるくらい一瞬で解く
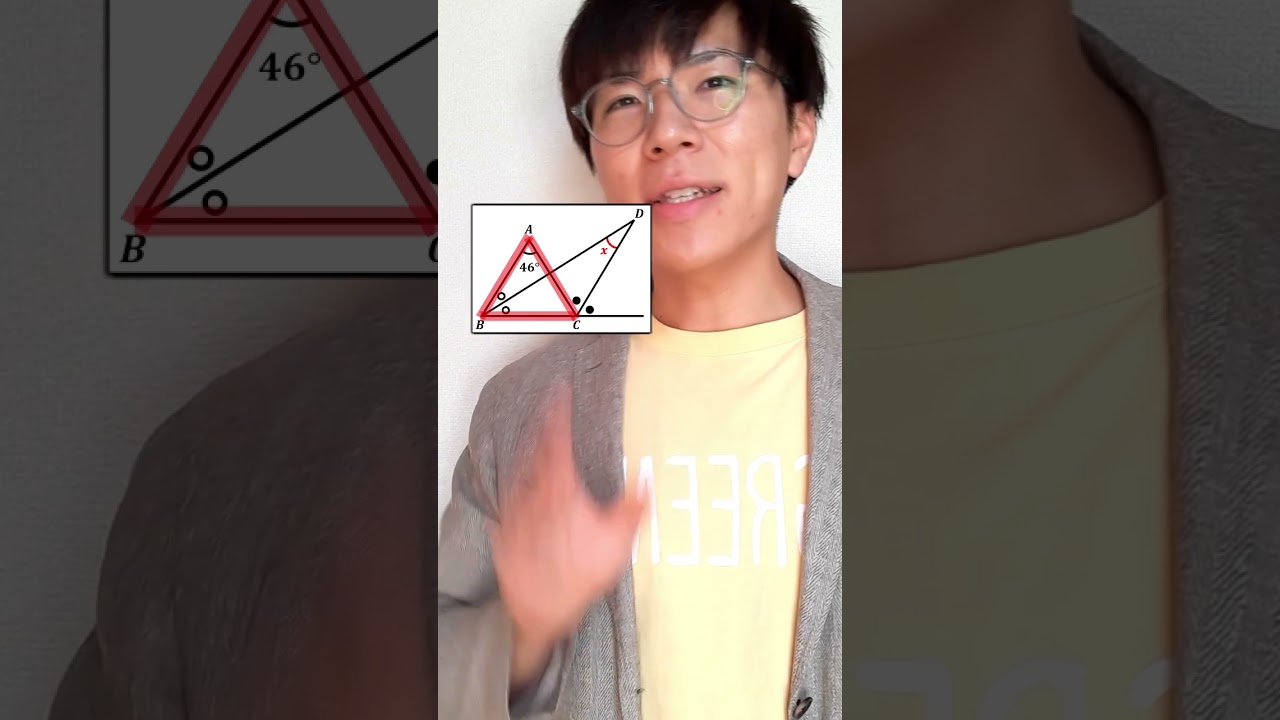
【高校数学】余弦定理の応用~問題演習~ 3-7.5【数学Ⅰ】

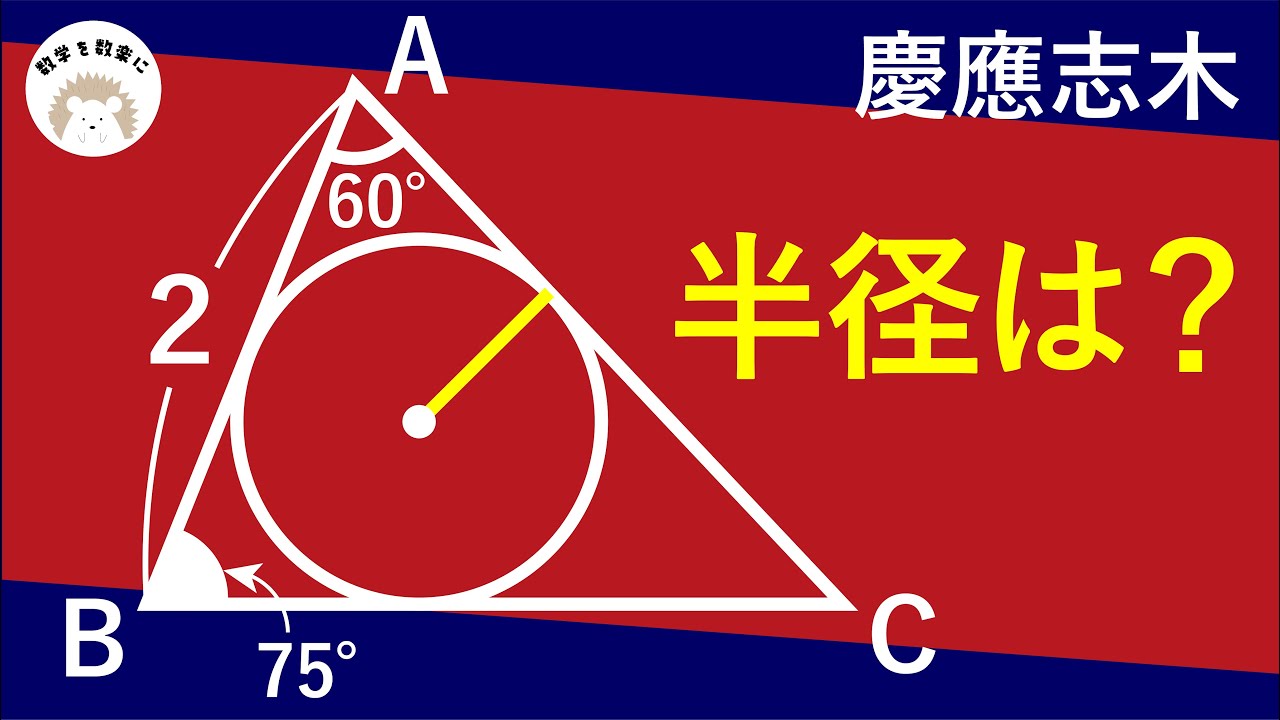
内接円の半径を求める公式で解けるのか? 慶應志木
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の半径=?
*図は動画内参照
慶應義塾志木高等学校
この動画を見る
円の半径=?
*図は動画内参照
慶應義塾志木高等学校
【数検2級】数学検定2級2次:問題6
単元:
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#数学検定#数学検定2級#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
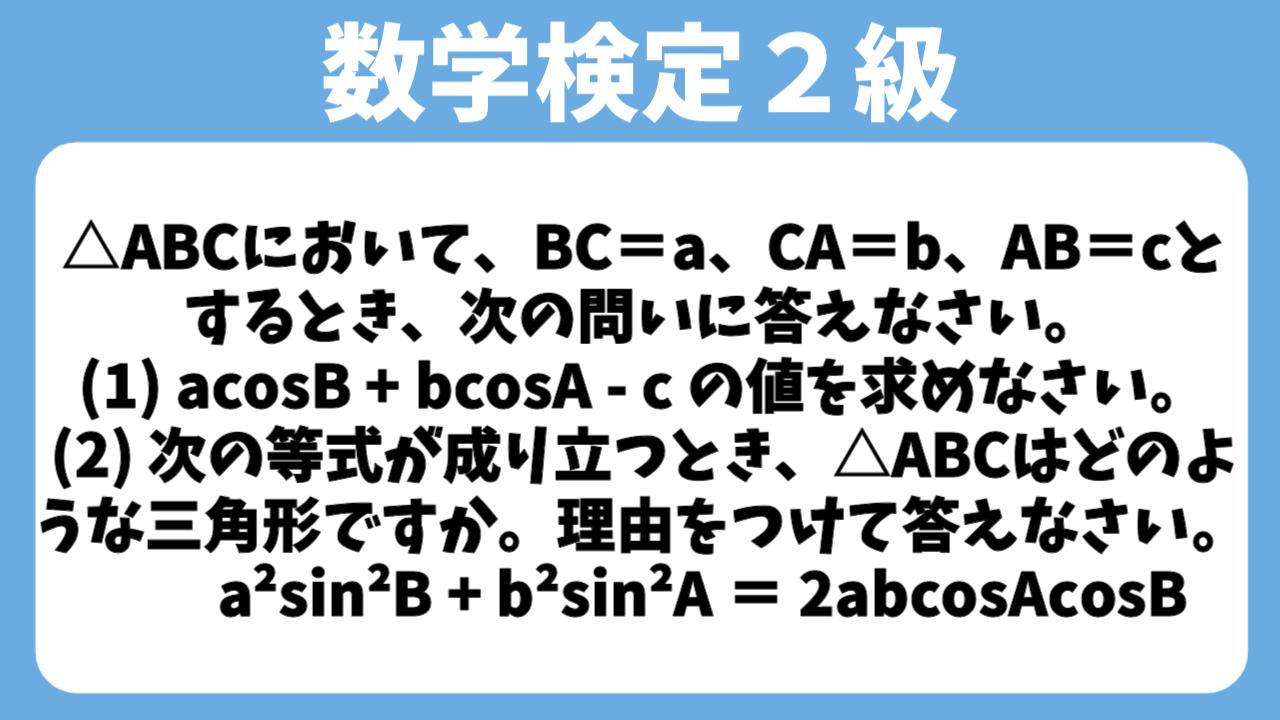
問題6.(必須)
△ABCにおいて、$BC=a、CA=b、AB=c$とするとき、次の問いに答えなさい。
(1)$a\cos B+b\cos A-c$ の値を求めなさい。この問題は解法の過程を記述せずに、答えだけを書いてください。
(2) 次の等式が成り立つとき、△ABCはどのような三角形ですか。理由をつけて答えなさい。
$a^2\sin^2B+b^2\sin^2 A=2ab\cos A\cos B$
この動画を見る
問題6.(必須)
△ABCにおいて、$BC=a、CA=b、AB=c$とするとき、次の問いに答えなさい。
(1)$a\cos B+b\cos A-c$ の値を求めなさい。この問題は解法の過程を記述せずに、答えだけを書いてください。
(2) 次の等式が成り立つとき、△ABCはどのような三角形ですか。理由をつけて答えなさい。
$a^2\sin^2B+b^2\sin^2 A=2ab\cos A\cos B$
正六角形

角の和 茨城県 動画内に誘導あり 茨城県
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
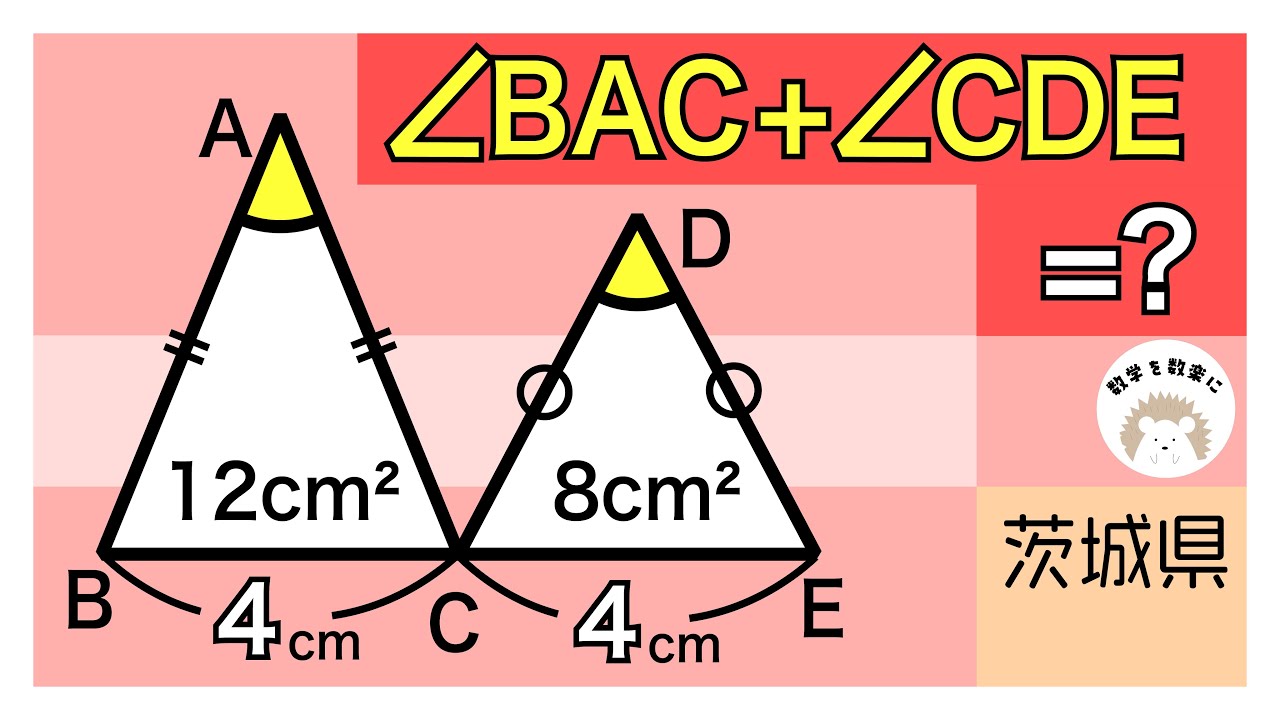
$\angle BAC + \angle CDE$=?
*図は動画内参照
茨城県
この動画を見る
$\angle BAC + \angle CDE$=?
*図は動画内参照
茨城県
円と三角形の面積
引っかけ問題!? 円 斜線部の面積を求めよ 慶應義塾
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
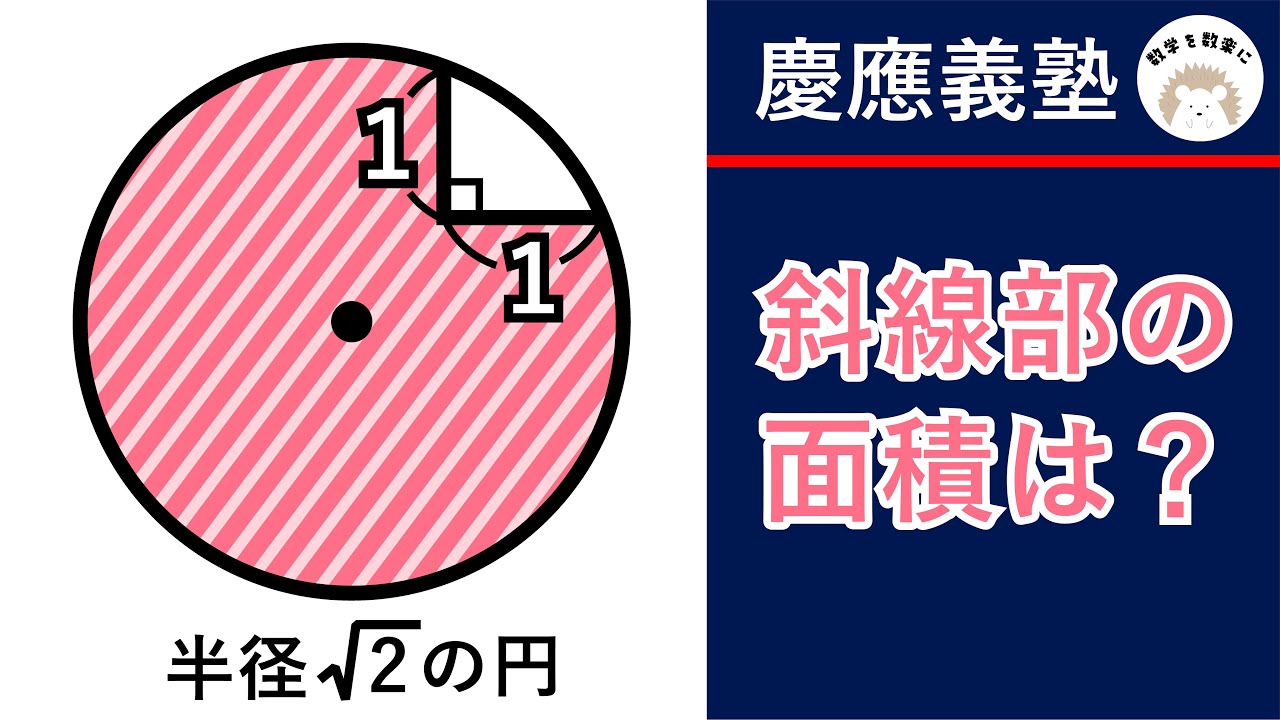
半径$\sqrt 2$の円
斜線部の面積は?
*図は動画内参照
慶應義塾高等学校
この動画を見る
半径$\sqrt 2$の円
斜線部の面積は?
*図は動画内参照
慶應義塾高等学校
正方形と150度

おうぎ形と長方形
福田の数学〜上智大学2022年理工学部第2問〜三角比と通過領域の体積
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
tを実数とする。次の条件(★)を満たす$\triangle ABC$を考える。
(★)$AC=t,\ BC=1$を満たし、$\angle BAC$の2等分線と辺BCの交点をDとおくと、
$\cos\angle DAC=\frac{\sqrt3}{3}$である。
(1)$\cos\angle DAC=\frac{\boxed{カ}}{\boxed{キ}}$である。
(2)tの取りうる範囲を$t_1\lt t \lt t_2$とするとき、$t_1=\boxed{あ},t_2=\boxed{い}$である。
$\boxed{あ},\ \boxed{い}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{3}\ \ \ (\textrm{c})\frac{1}{2}\ \ \ (\textrm{d})\frac{\sqrt3}{3}\ \ \ (\textrm{e})\frac{2}{3}$
$ (\textrm{f})1\ \ \ (\textrm{g})\frac{2\sqrt3}{2}\ \ \ (\textrm{h})\sqrt3\ \ \ (\textrm{i})2\ \ \ (\textrm{j})3$
(3)辺ABの長さをtの式で表すと$AB=\frac{\boxed{ク}}{\boxed{ケ}}t+$
$\sqrt{1+\frac{\boxed{コ}}{\boxed{サ}}t^2}$である。
(4)$\triangle ABC$の面積は$t=\frac{\sqrt{\boxed{シ}}}{\boxed{ス}}$
で最大値$\frac{\sqrt{\boxed{セ}}}{\boxed{ソ}}$をとる。
(5)$t_1,t_2$を(2)で定めた値とする。
$t_1 \lt t \lt t_2$の範囲で、xyz-座標空間内の平面z=t上に、条件(★)を満たす
$\triangle ABC$が、$B(0,0,t),C(0,1,t)$を満たし、Aのx座標が正であるように
おかれている。まgた、$B_1(0,0,t_1),C_1(0,1,t_1),B_2(0,0,t_2),C_2(0,1,t_2)$と
おく。
$\triangle ABC$を$t_1 \lt t \lt t_2$の範囲で動かしたときに通過してできる図形に線分$B_1C_1$、
線分$B_2C_2$を付け加えた立体の体積は$\frac{\sqrt{\boxed{タ}}}{\boxed{チ}}$である。
この動画を見る
tを実数とする。次の条件(★)を満たす$\triangle ABC$を考える。
(★)$AC=t,\ BC=1$を満たし、$\angle BAC$の2等分線と辺BCの交点をDとおくと、
$\cos\angle DAC=\frac{\sqrt3}{3}$である。
(1)$\cos\angle DAC=\frac{\boxed{カ}}{\boxed{キ}}$である。
(2)tの取りうる範囲を$t_1\lt t \lt t_2$とするとき、$t_1=\boxed{あ},t_2=\boxed{い}$である。
$\boxed{あ},\ \boxed{い}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{3}\ \ \ (\textrm{c})\frac{1}{2}\ \ \ (\textrm{d})\frac{\sqrt3}{3}\ \ \ (\textrm{e})\frac{2}{3}$
$ (\textrm{f})1\ \ \ (\textrm{g})\frac{2\sqrt3}{2}\ \ \ (\textrm{h})\sqrt3\ \ \ (\textrm{i})2\ \ \ (\textrm{j})3$
(3)辺ABの長さをtの式で表すと$AB=\frac{\boxed{ク}}{\boxed{ケ}}t+$
$\sqrt{1+\frac{\boxed{コ}}{\boxed{サ}}t^2}$である。
(4)$\triangle ABC$の面積は$t=\frac{\sqrt{\boxed{シ}}}{\boxed{ス}}$
で最大値$\frac{\sqrt{\boxed{セ}}}{\boxed{ソ}}$をとる。
(5)$t_1,t_2$を(2)で定めた値とする。
$t_1 \lt t \lt t_2$の範囲で、xyz-座標空間内の平面z=t上に、条件(★)を満たす
$\triangle ABC$が、$B(0,0,t),C(0,1,t)$を満たし、Aのx座標が正であるように
おかれている。まgた、$B_1(0,0,t_1),C_1(0,1,t_1),B_2(0,0,t_2),C_2(0,1,t_2)$と
おく。
$\triangle ABC$を$t_1 \lt t \lt t_2$の範囲で動かしたときに通過してできる図形に線分$B_1C_1$、
線分$B_2C_2$を付け加えた立体の体積は$\frac{\sqrt{\boxed{タ}}}{\boxed{チ}}$である。
【中学からの!】タンジェントを含む計算:三角比~全国入試問題解法
単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABC$において
$a \tan A=b \tan B$ならばどんな三角形か.
この動画を見る
$\triangle ABC$において
$a \tan A=b \tan B$ならばどんな三角形か.
2つの長方形と面積
気付けば一瞬!! 関数は図形の問題として捉えよ
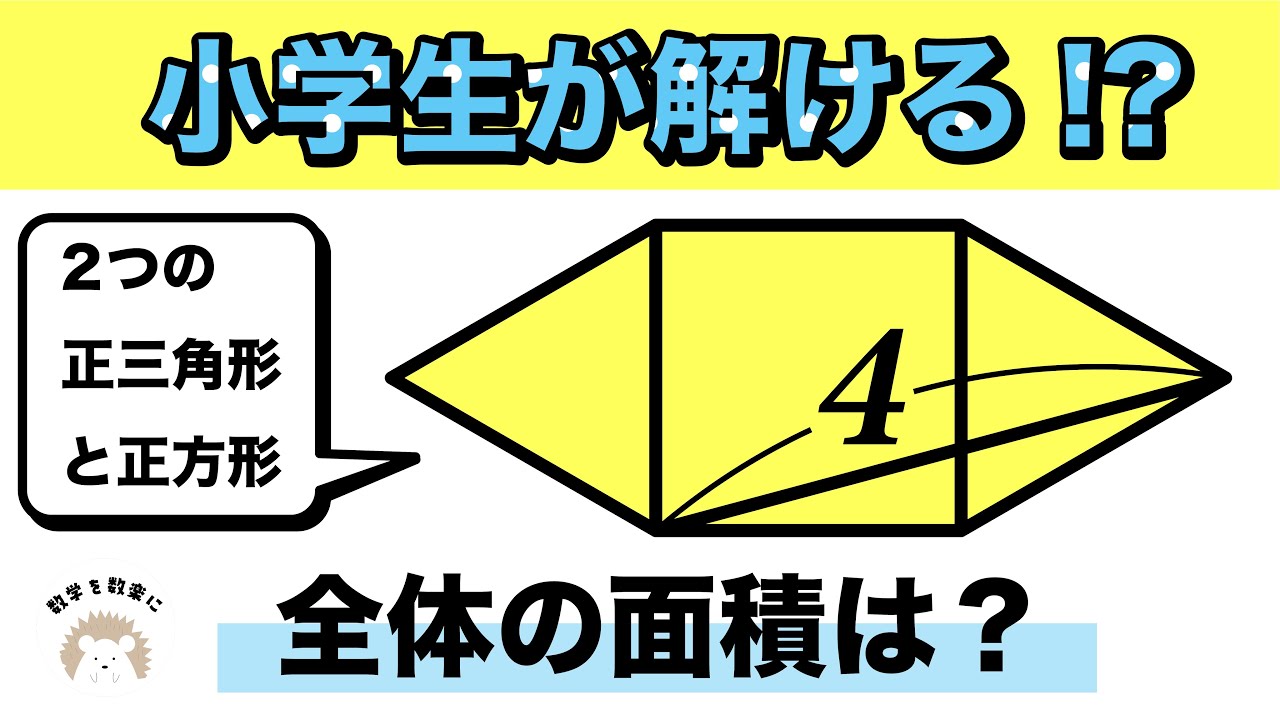
正方形と2つの正三角形の面積の和 2通りで解説
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
2つの正三角形と正方形
全体の面積=?
*図は動画内参照
この動画を見る
2つの正三角形と正方形
全体の面積=?
*図は動画内参照
【中学からの!】余弦定理(2):三角比~全国入試問題解法

単元:
#数学(中学生)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\triangle ABC$において
$ a \cos A=b \cos B$ならばどんな三角形か.
この動画を見る
$\triangle ABC$において
$ a \cos A=b \cos B$ならばどんな三角形か.
