 周角と円に内接する四角形・円と接線・接弦定理
周角と円に内接する四角形・円と接線・接弦定理
 周角と円に内接する四角形・円と接線・接弦定理
周角と円に内接する四角形・円と接線・接弦定理
ロニー先生再生リストあります
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
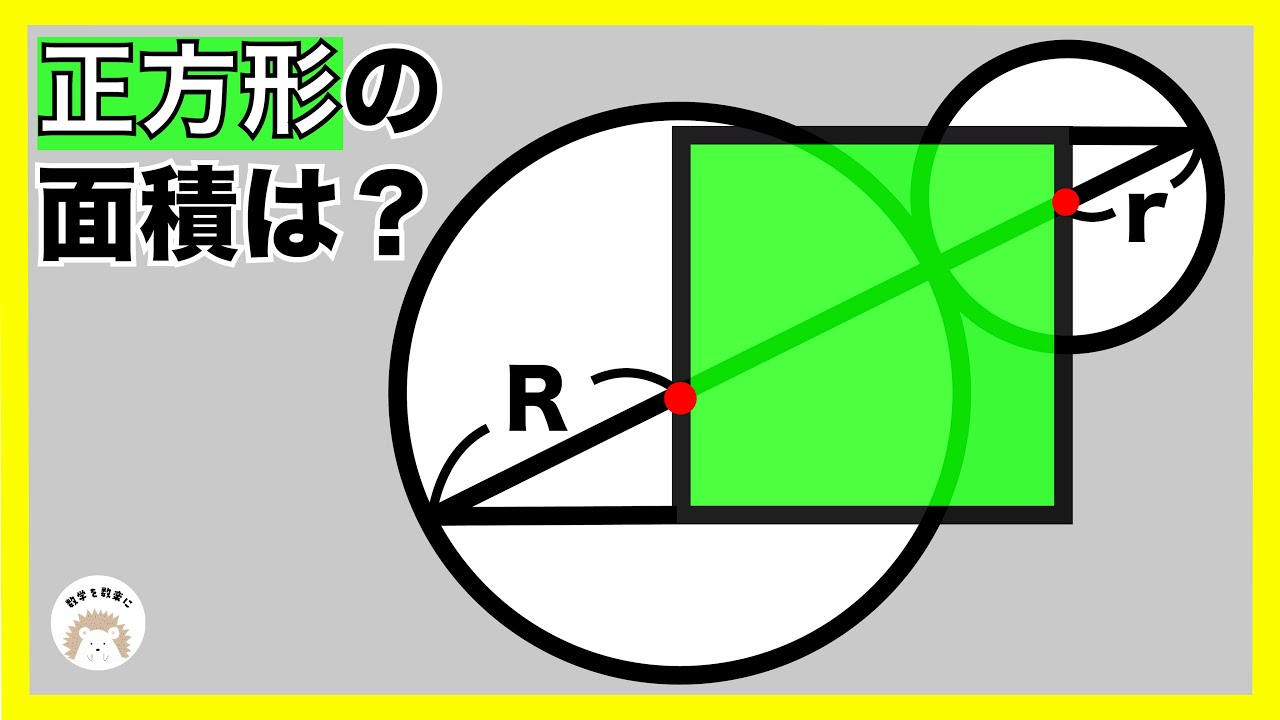
正方形ABCDの面積をR、rで表せ。
*図は動画内参照
この動画を見る
正方形ABCDの面積をR、rで表せ。
*図は動画内参照
福田の数学〜慶應義塾大学2022年総合政策学部第5問〜等脚台形の外接円の中心の位置ベクトル

単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{5}}$いま、ADを下底、BCを上底とする台形ABCDにおいて、$\angle BAD=\angle CDA=60°,$
$|\overrightarrow{ AB }|=2,|\overrightarrow{ BC }|=1$となっている。
(1)$|\overrightarrow{ BD }|=\sqrt{\boxed{\ \ アイ\ \ }}$であり、台形ABCDの外接円の半径は$\frac{\sqrt{\boxed{\ \ ウエ\ \ }}}{\boxed{\ \ オカ\ \ }}$である。
(2)外接円の中心をOとするとき、内積$\overrightarrow{ AB }・\overrightarrow{ AO }=\boxed{\ \ キク\ \ },\overrightarrow{ AD }・\overrightarrow{ AO }=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
(3)$\overrightarrow{ AO }=\frac{\boxed{\ \ スセ\ \ }}{\boxed{\ \ ソタ\ \ }}\ \overrightarrow{ AB }+\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \overrightarrow{ AD }$である。
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\large\boxed{5}}$いま、ADを下底、BCを上底とする台形ABCDにおいて、$\angle BAD=\angle CDA=60°,$
$|\overrightarrow{ AB }|=2,|\overrightarrow{ BC }|=1$となっている。
(1)$|\overrightarrow{ BD }|=\sqrt{\boxed{\ \ アイ\ \ }}$であり、台形ABCDの外接円の半径は$\frac{\sqrt{\boxed{\ \ ウエ\ \ }}}{\boxed{\ \ オカ\ \ }}$である。
(2)外接円の中心をOとするとき、内積$\overrightarrow{ AB }・\overrightarrow{ AO }=\boxed{\ \ キク\ \ },\overrightarrow{ AD }・\overrightarrow{ AO }=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}$である。
(3)$\overrightarrow{ AO }=\frac{\boxed{\ \ スセ\ \ }}{\boxed{\ \ ソタ\ \ }}\ \overrightarrow{ AB }+\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \overrightarrow{ AD }$である。
2022慶應義塾大学総合政策学部過去問
良問!!円の半径を求める 2022和歌山県ラスト問題
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
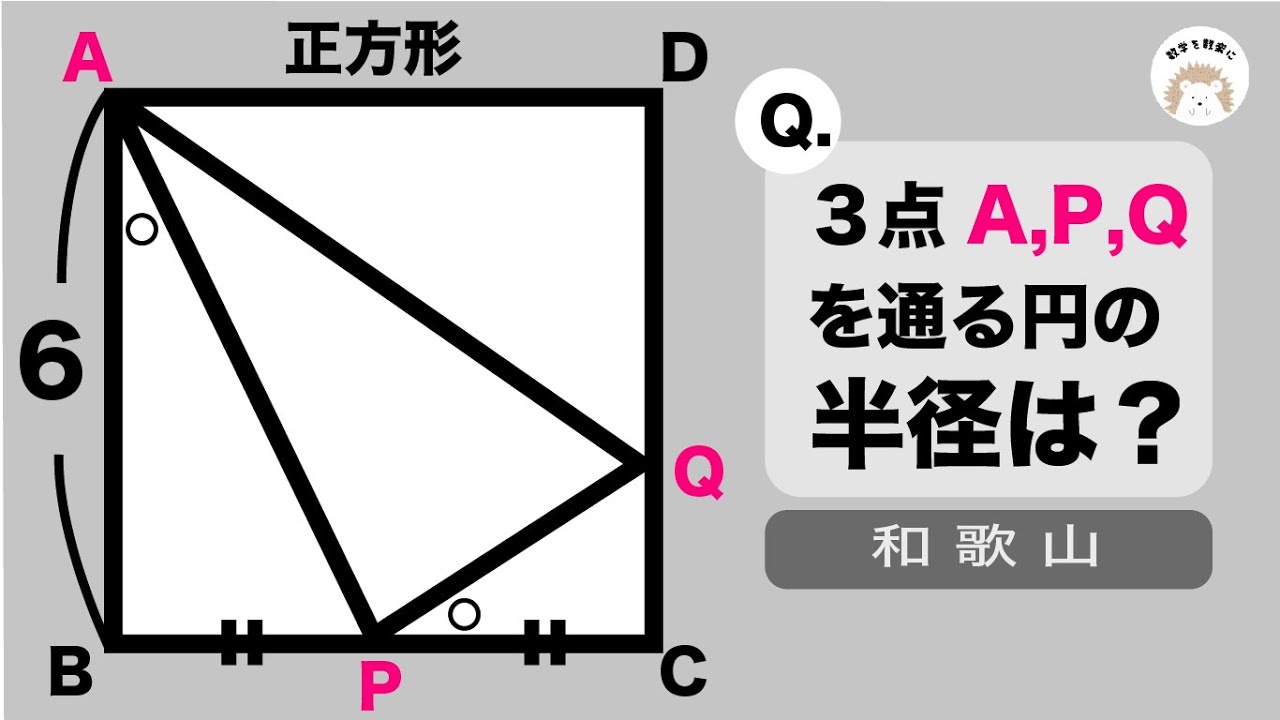
3点A,P,Qを通る円の半径は?
*図は動画内参照
2022和歌山県
この動画を見る
3点A,P,Qを通る円の半径は?
*図は動画内参照
2022和歌山県
気付けば一瞬!!普連土学園
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
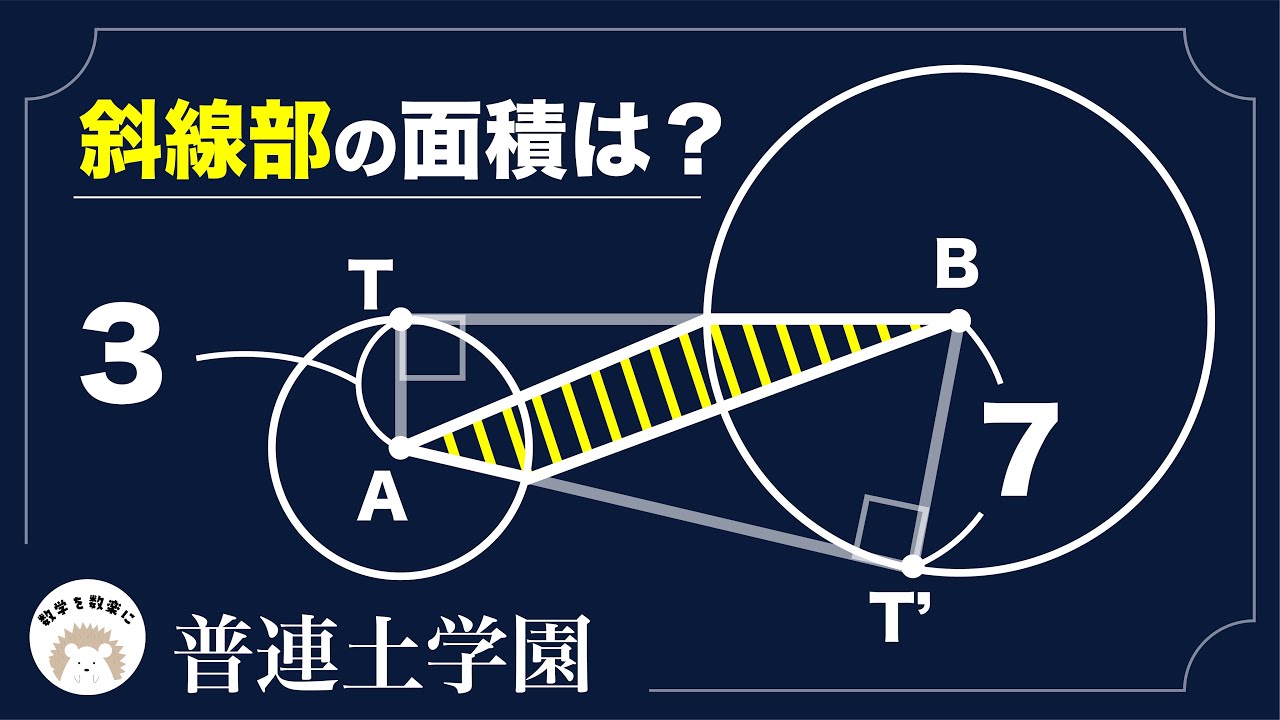
斜線部の面積は?
*図は動画内参照
普連土学園高等学校
この動画を見る
斜線部の面積は?
*図は動画内参照
普連土学園高等学校
半円と2つの合同な長方形
単元:
#数Ⅰ#数A#図形の性質#図形と計量#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
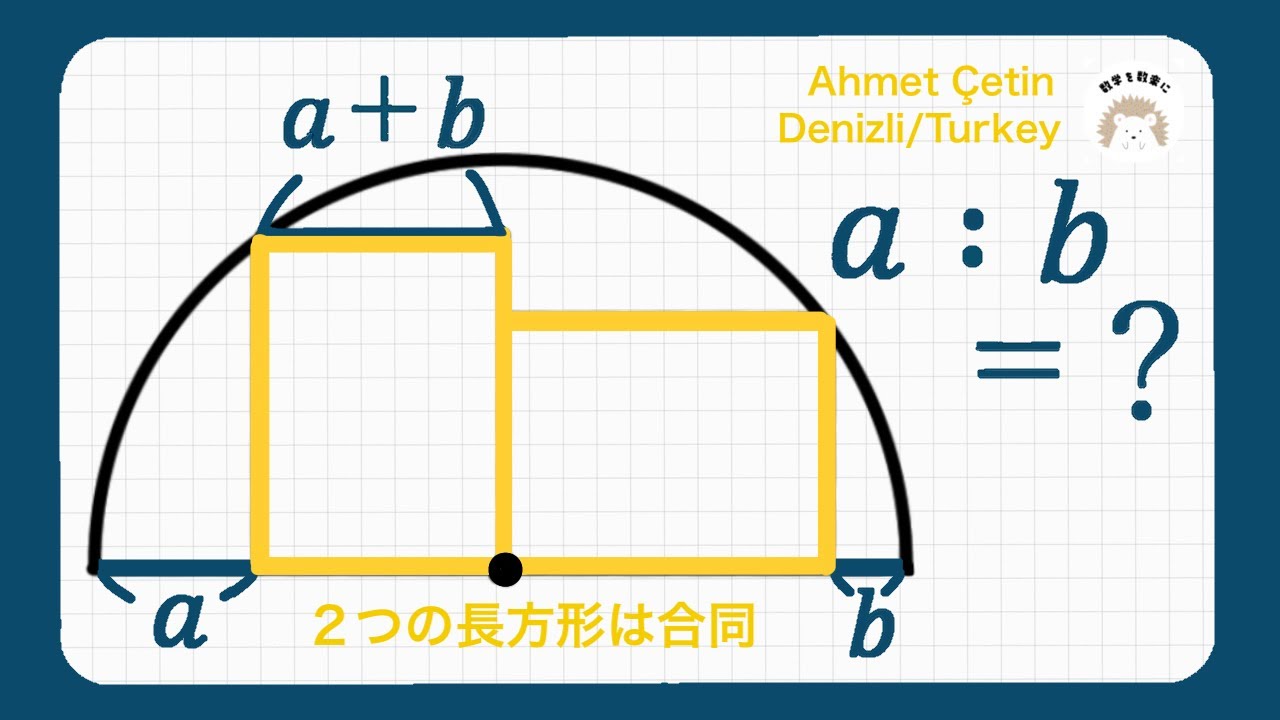
2つの長方形は合同
a:b=?
*図は動画内参照
この動画を見る
2つの長方形は合同
a:b=?
*図は動画内参照
正方形と円と正方形 算数です

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
*四角形は正方形
斜線部の面積は?
*図は動画内参照
この動画を見る
*四角形は正方形
斜線部の面積は?
*図は動画内参照
半円と正方形
2つの円
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
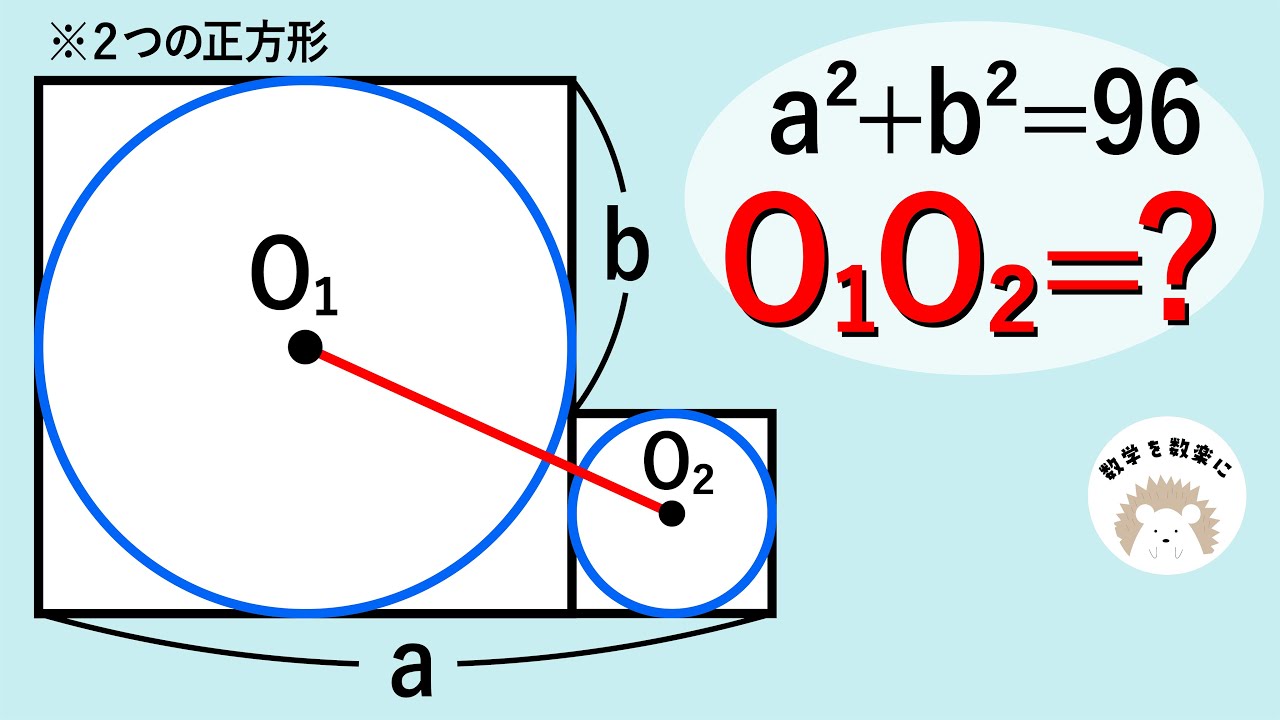
*2つの正方形
$a^2+b^2=96$
$O_1O_2=?$
*図は動画内参照
この動画を見る
*2つの正方形
$a^2+b^2=96$
$O_1O_2=?$
*図は動画内参照
福田の入試問題解説〜北海道大学2022年文系第3問〜直角三角形と内接円

単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
この動画を見る
$\angle A=90°,\angle B=60°$である直角三角形ABCにおいて、
その内接円の中心をO、半径をrとおく。また$a=BC$とする。
(1)rをaで表せ。
(2)次の条件を満たす負でない整数k,l,m,nの組を一つ求めよ。
$OA:OB=1:k+\sqrt{l}, OA:OC=1:m+\sqrt{n}$
2022北海道大学文系過去問
福田の数学・入試問題解説〜東北大学2022年理系第4問〜2つの直線に接し互いに外接する2つの円の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
xy平面の第1象限内において、直線$l:y=mx (m \gt 0)$とx軸の両方に
接している半径aの円をCとし、円Cの中心を通る直線$y=tx (t \gt 0)$を考える。
また、直線lとx軸、および、円Cの全てにそれぞれ1点で接する円の半径をbとする。
ただし、$b \gt a$とする。
(1)mを用いてtを表せ。
(2)tを用いて$\frac{b}{a}$を表せ。
(3)極限値$\lim_{m \to +0}\frac{1}{m}(\frac{b}{a}-1)$を求めよ。
2022東北大学理系過去問
この動画を見る
xy平面の第1象限内において、直線$l:y=mx (m \gt 0)$とx軸の両方に
接している半径aの円をCとし、円Cの中心を通る直線$y=tx (t \gt 0)$を考える。
また、直線lとx軸、および、円Cの全てにそれぞれ1点で接する円の半径をbとする。
ただし、$b \gt a$とする。
(1)mを用いてtを表せ。
(2)tを用いて$\frac{b}{a}$を表せ。
(3)極限値$\lim_{m \to +0}\frac{1}{m}(\frac{b}{a}-1)$を求めよ。
2022東北大学理系過去問
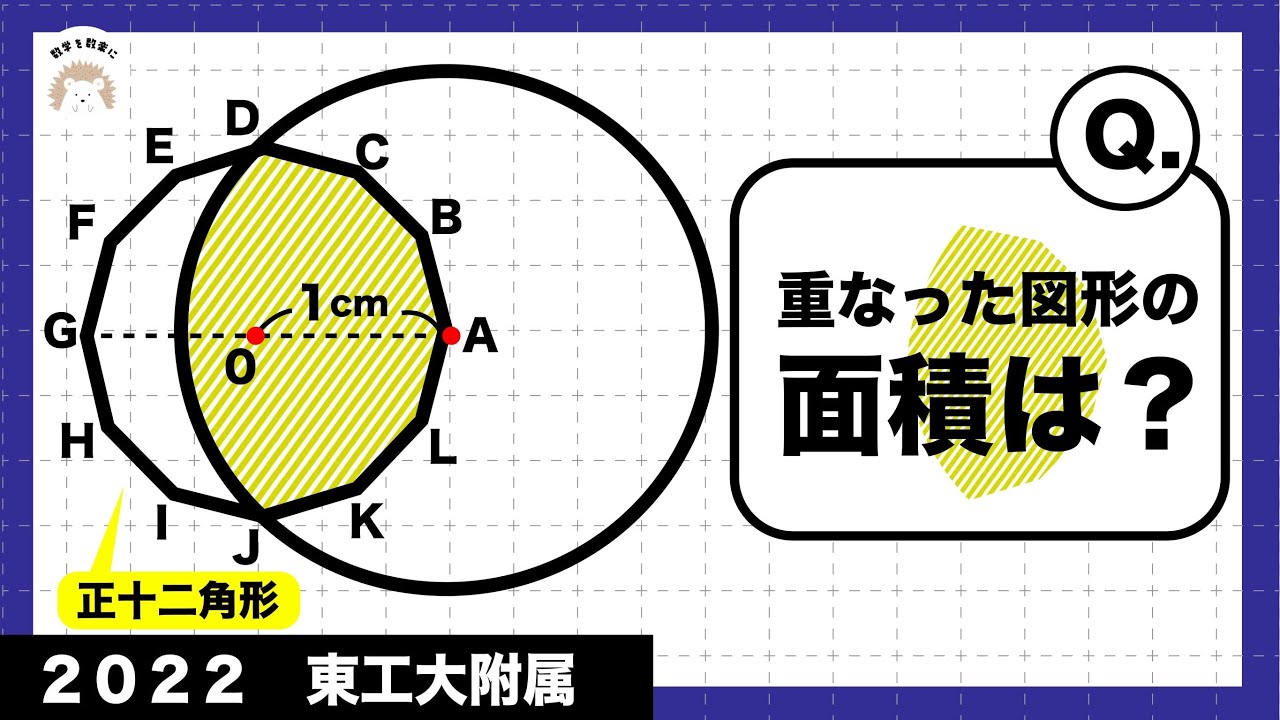
正十二角形と円 東工大附属
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
重なった図形の面積は?
*図は動画内参照
2022東京工業大学附属科学技術高等学校
この動画を見る
重なった図形の面積は?
*図は動画内参照
2022東京工業大学附属科学技術高等学校
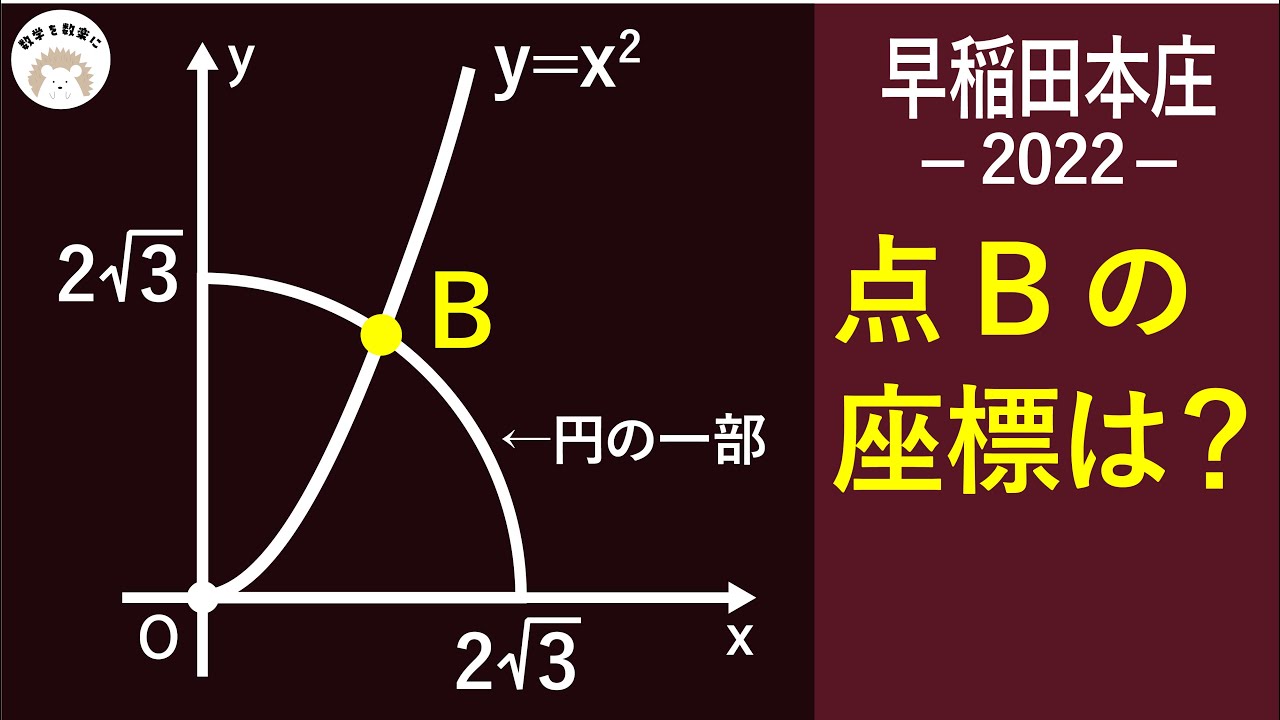
放物線と円 早稲田本庄 令和4年度 2022 入試問題100題解説96問目!
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Bの座標は?
*図は動画内参照
2022早稲田大学 本庄高等学院
この動画を見る
点Bの座標は?
*図は動画内参照
2022早稲田大学 本庄高等学院
2つの円 埼玉県 令和4年度 数学 2022 入試問題100題解説77問目!
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
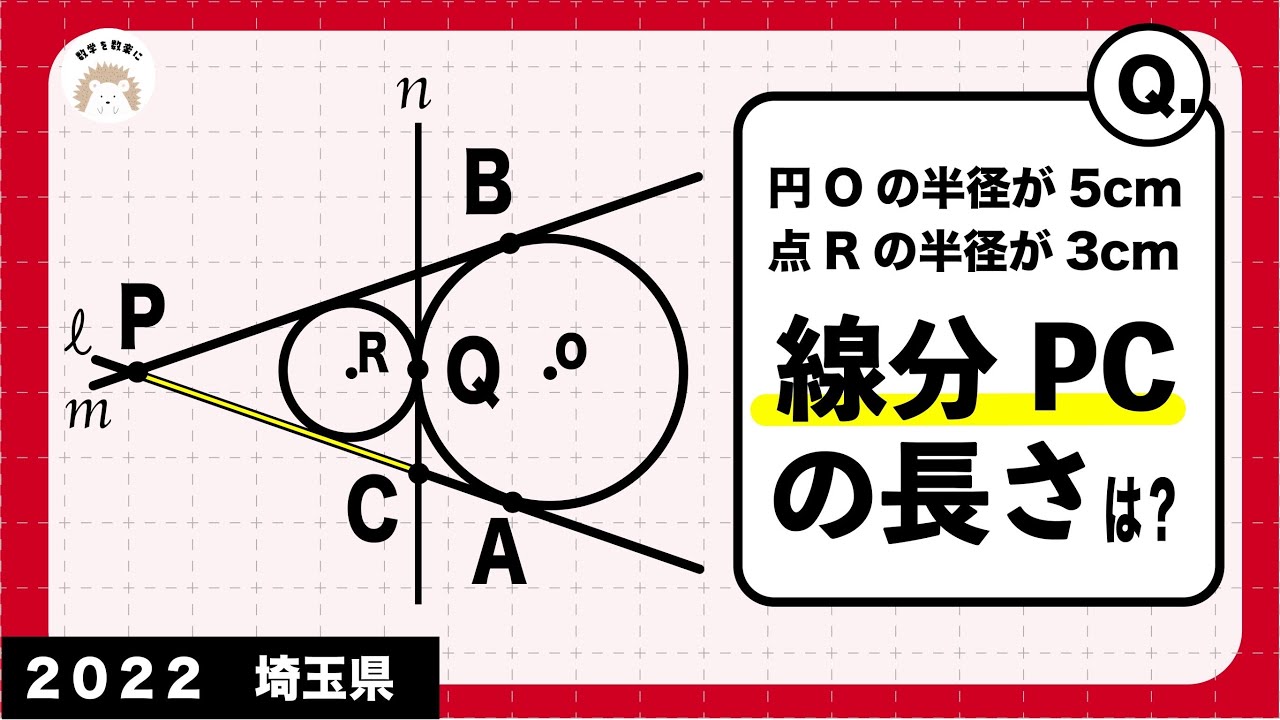
円Oの半径が5㎝
点Rの半径が3㎝
線分PCの長さは?
*図は動画内参照
2022埼玉県
この動画を見る
円Oの半径が5㎝
点Rの半径が3㎝
線分PCの長さは?
*図は動画内参照
2022埼玉県
接線の長さが等しいことの証明 埼玉県 令和4年度 数学 2022 入試問題100題解説76問目!
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
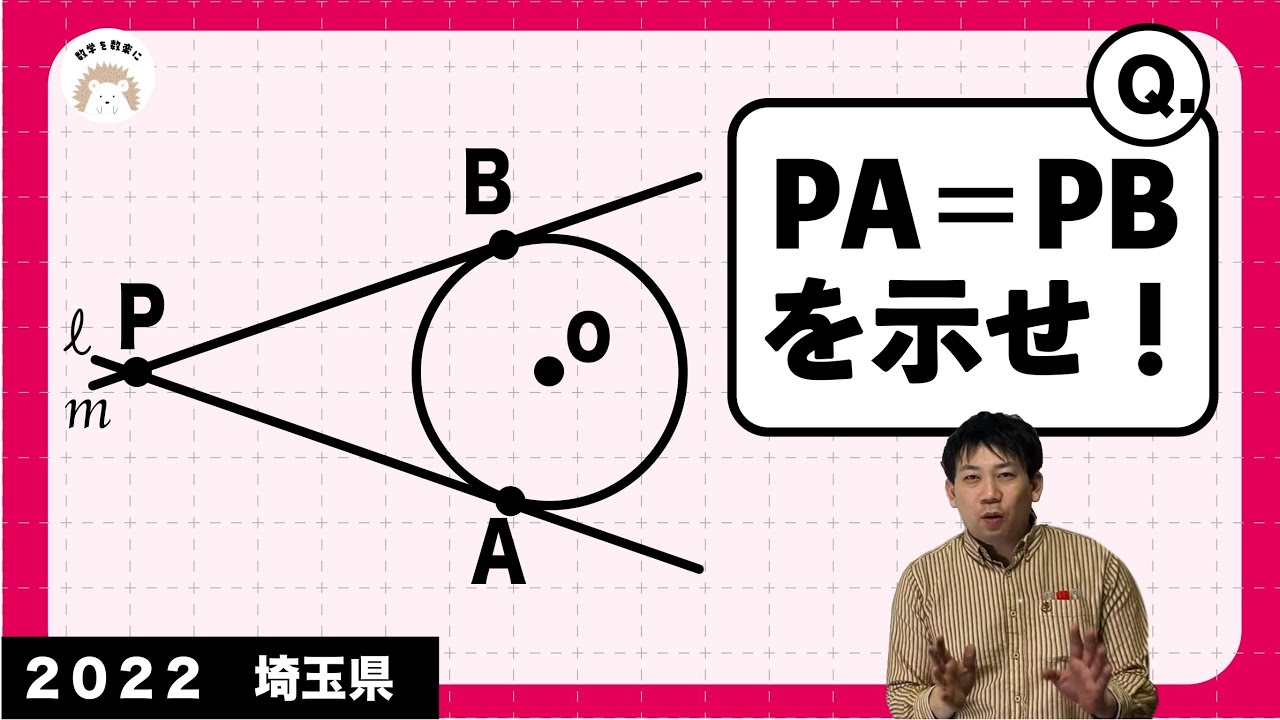
PA=PBを示せ
*図は動画内参照
2022埼玉県
この動画を見る
PA=PBを示せ
*図は動画内参照
2022埼玉県
戸山高校 2022 入試問題100題解説71問目!!
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
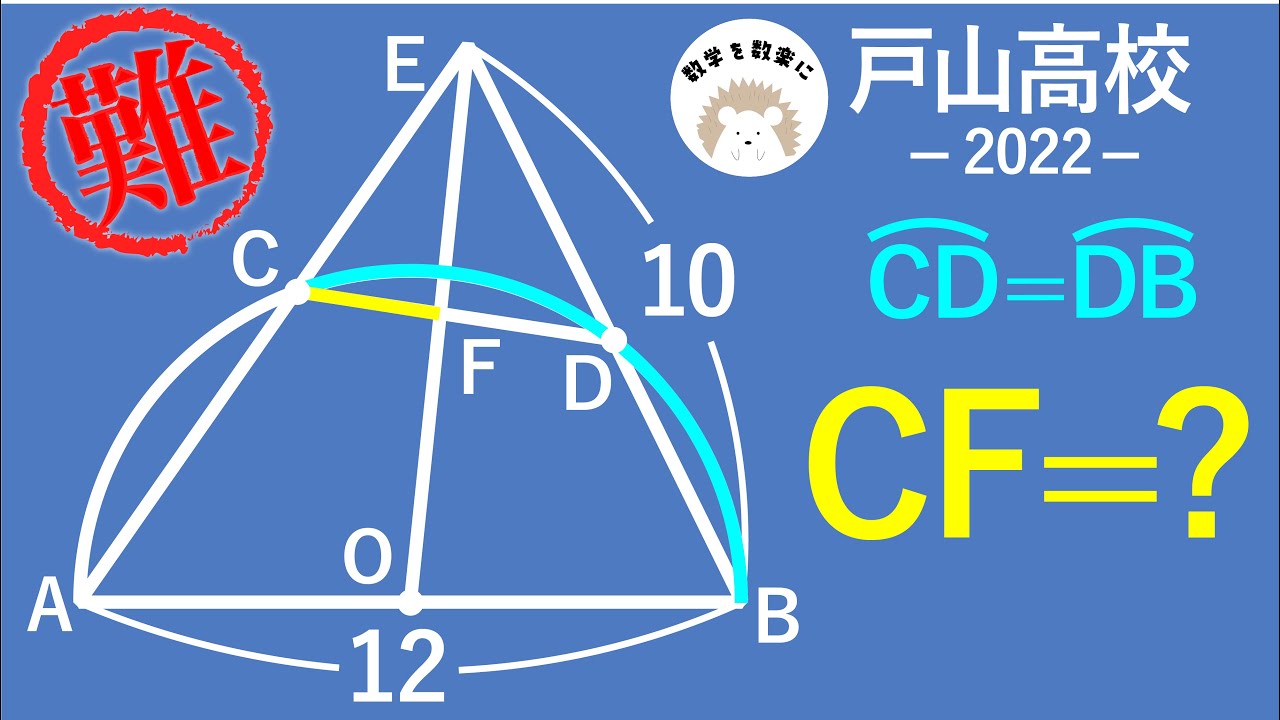
$\stackrel{\huge\frown}{CD}$ = $\stackrel{\huge\frown}{DB}$
CF=?
*図は動画内参照
2022戸山高等学校
この動画を見る
$\stackrel{\huge\frown}{CD}$ = $\stackrel{\huge\frown}{DB}$
CF=?
*図は動画内参照
2022戸山高等学校
斜線部の面積 中京大附属中京 2022入試問題解説100問解説59問目!
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
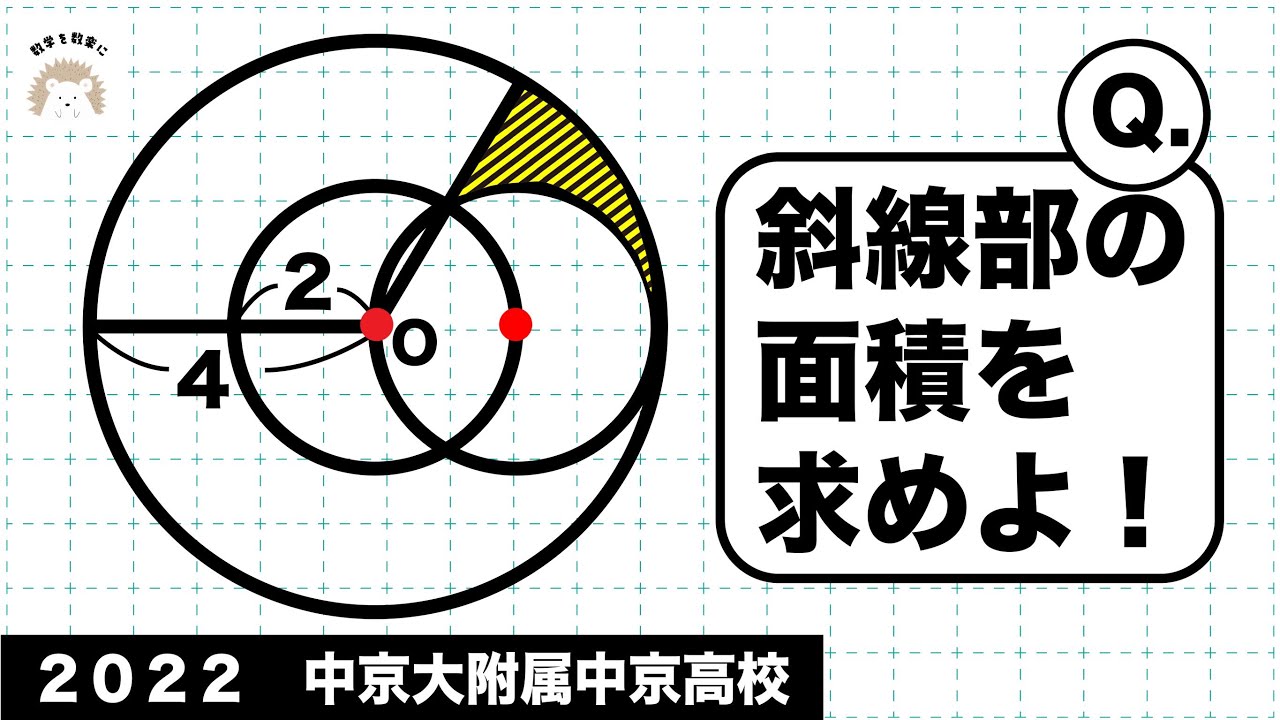
斜線部の面積を求めよ。
*図は動画内参照
2022中京大学附属中京高等学校
この動画を見る
斜線部の面積を求めよ。
*図は動画内参照
2022中京大学附属中京高等学校
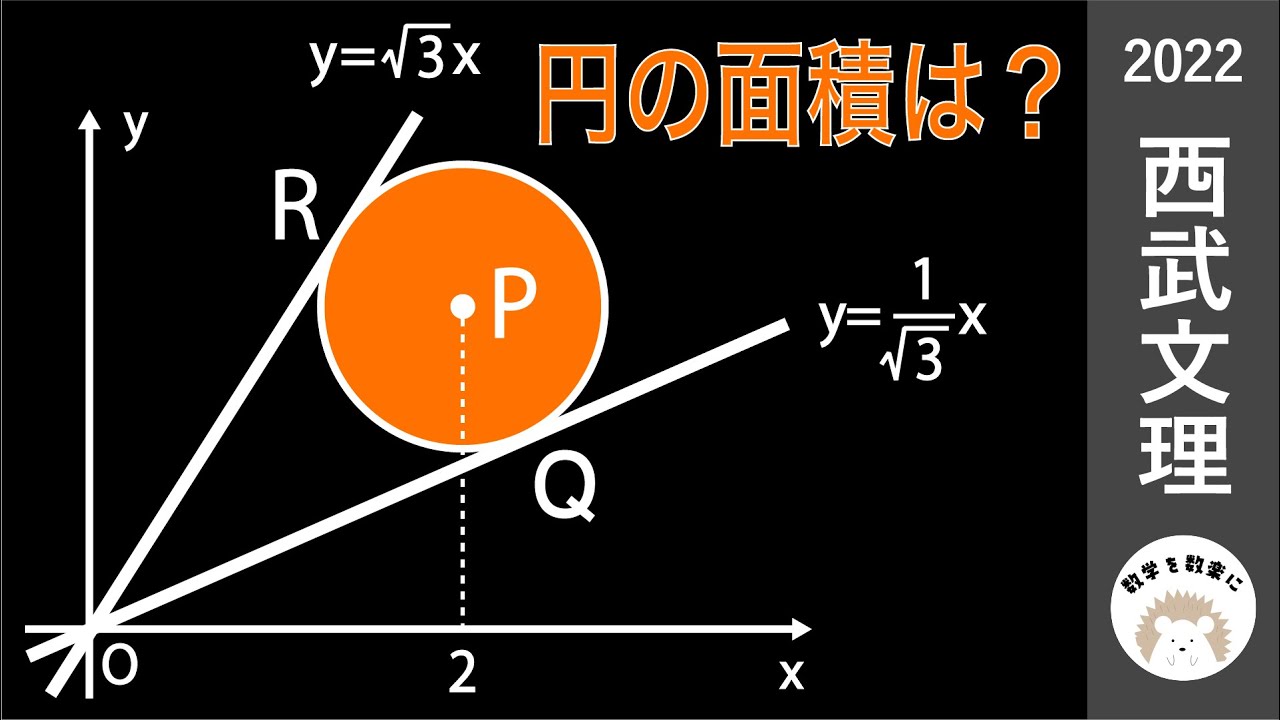
2つの接線に囲まれた円の面積 西武文理 2022入試問題解説 20問目
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の面積は?
*図は動画内参照
2022西武学園文理高等学校
この動画を見る
円の面積は?
*図は動画内参照
2022西武学園文理高等学校
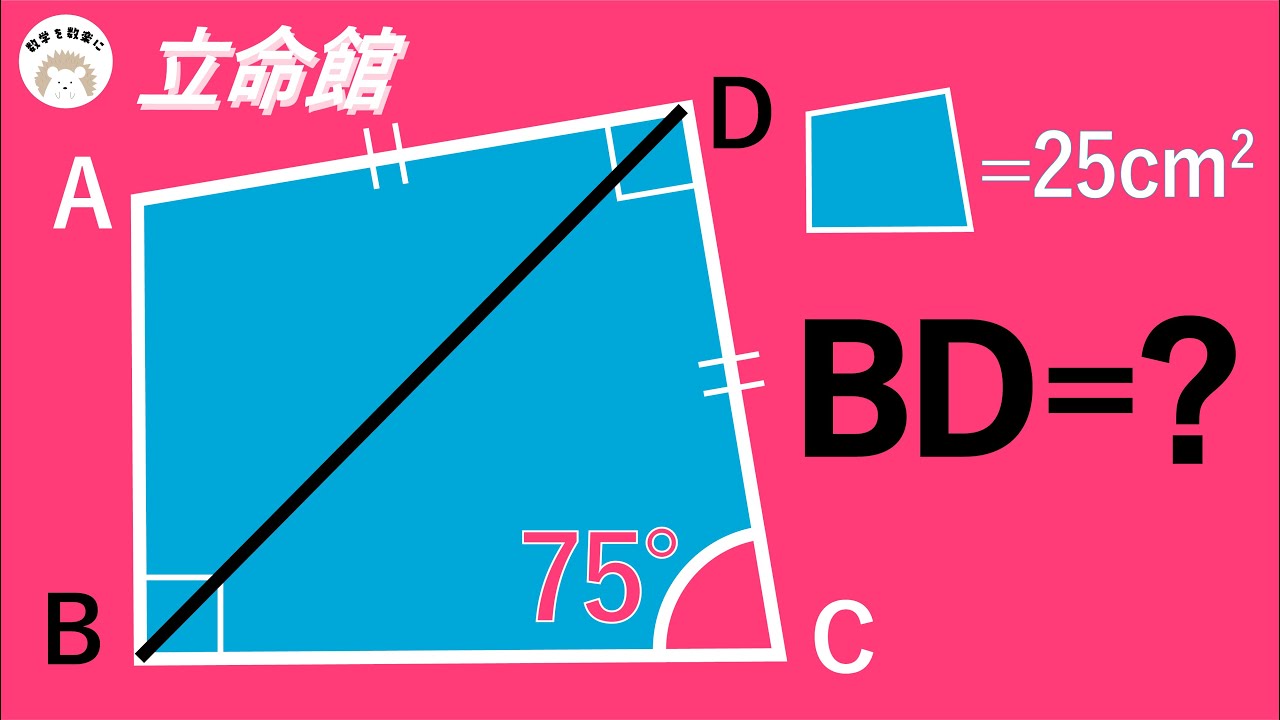
キレイに解けます 立命館高校
単元:
#数学(中学生)#中2数学#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形ABCD=25㎠のとき
BD=?
*図は動画内参照
立命館高等学校
この動画を見る
四角形ABCD=25㎠のとき
BD=?
*図は動画内参照
立命館高等学校
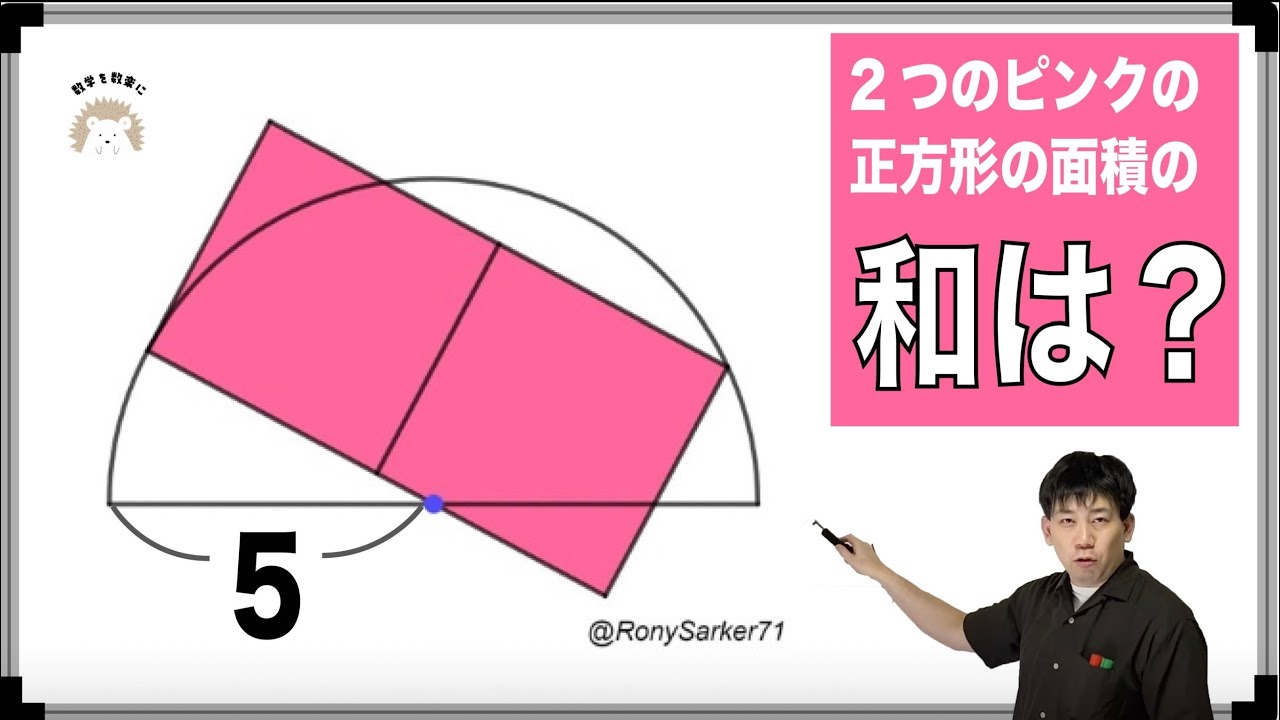
Rony先生の問題はやっぱり面白い!!3通りで解説!!
灘高校に受かるのは難だけど、この問題は難てこともない問題
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
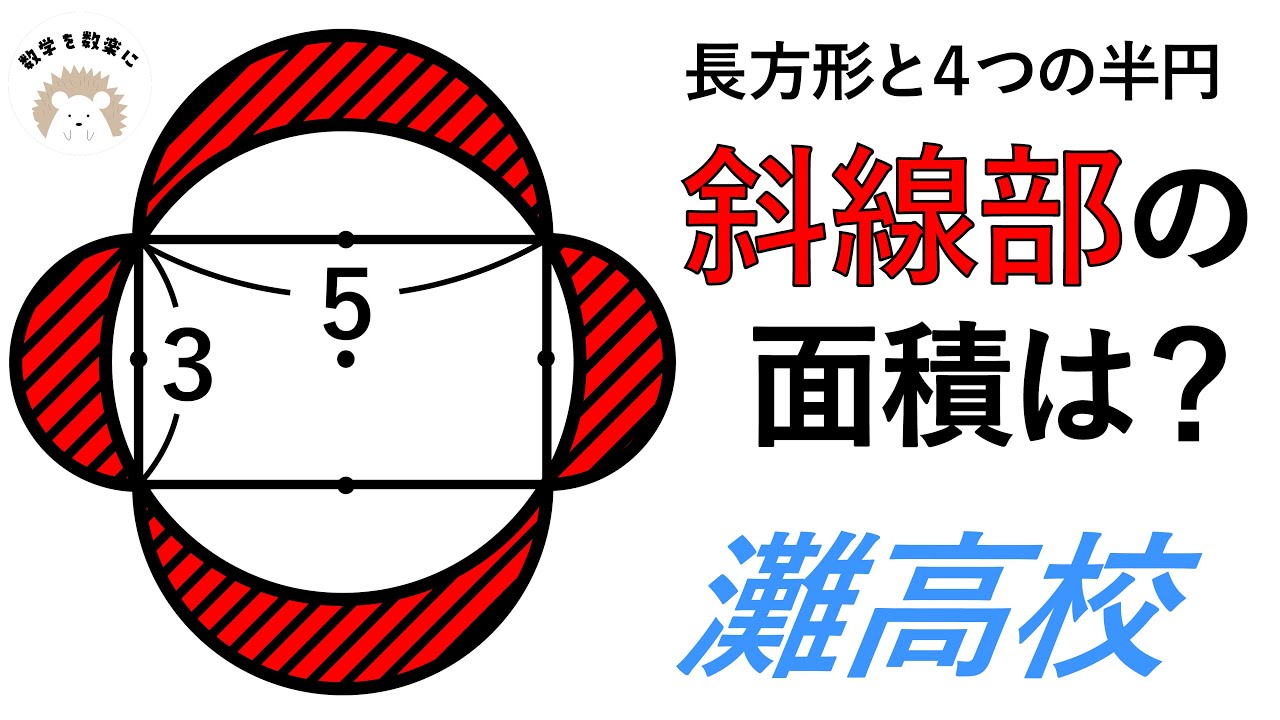
長方形と4つの半円
斜線部の面積は?
*図は動画内参照
灘高等学校
この動画を見る
長方形と4つの半円
斜線部の面積は?
*図は動画内参照
灘高等学校
円と接線と角度 慶應義塾高校
単元:
#数学(中学生)#中3数学#数A#図形の性質#円#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
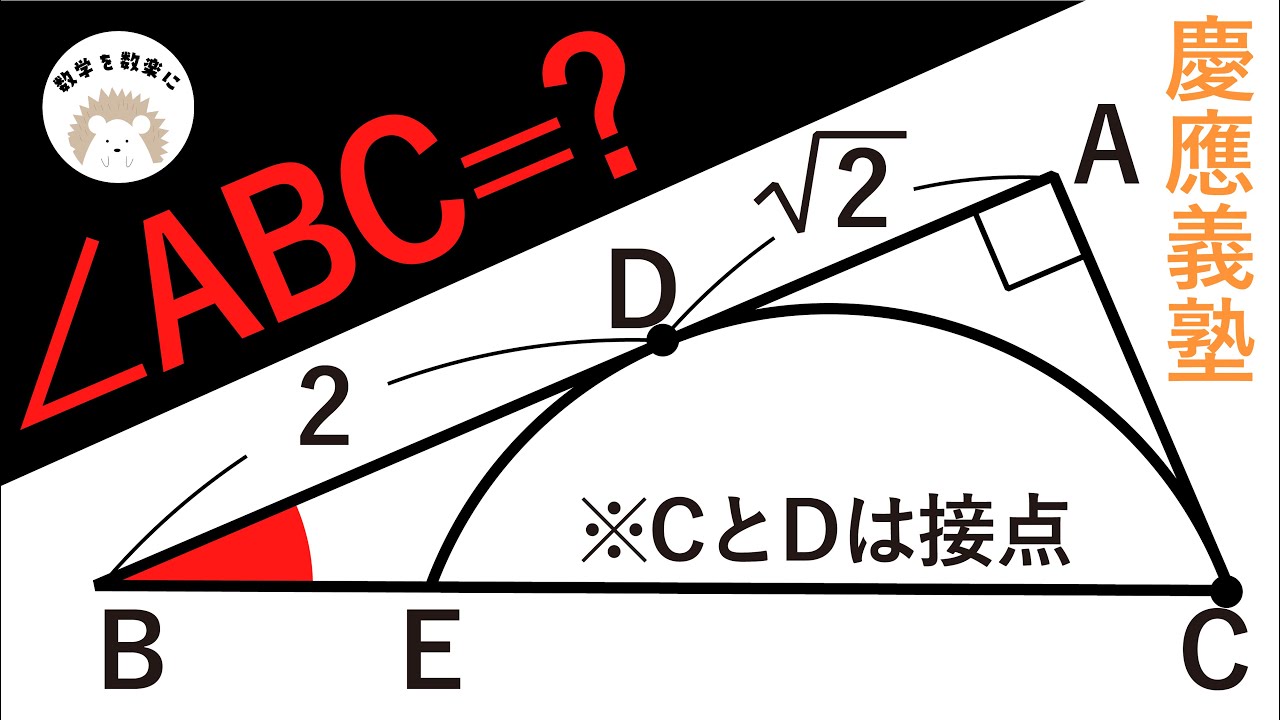
点Cと点Dは接点
$\angle ABC=?$
*図は動画内参照
慶應義塾高等学校
この動画を見る
点Cと点Dは接点
$\angle ABC=?$
*図は動画内参照
慶應義塾高等学校
慶應義塾高校 円
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
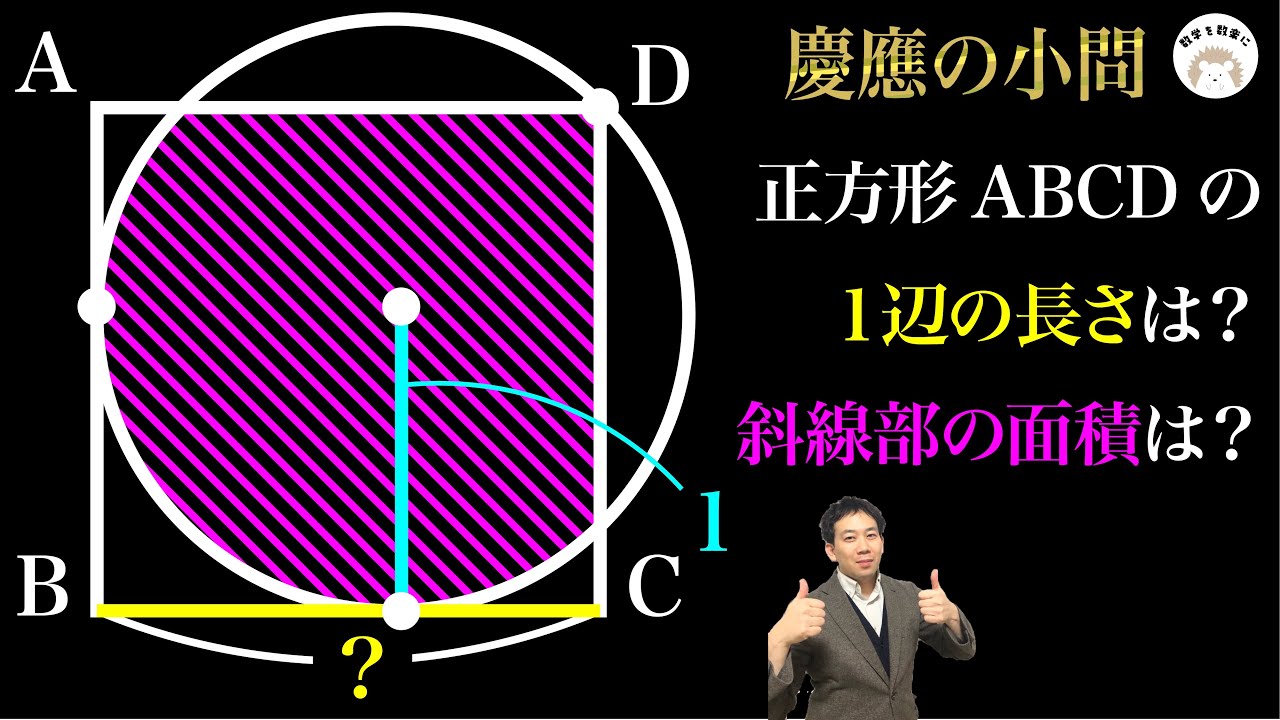
円の半径=1
正方形ABCDの1辺=?
斜線部の面積=?
*図は動画内参照
慶應義塾高等学校
この動画を見る
円の半径=1
正方形ABCDの1辺=?
斜線部の面積=?
*図は動画内参照
慶應義塾高等学校
高校入試の軌跡の問題
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
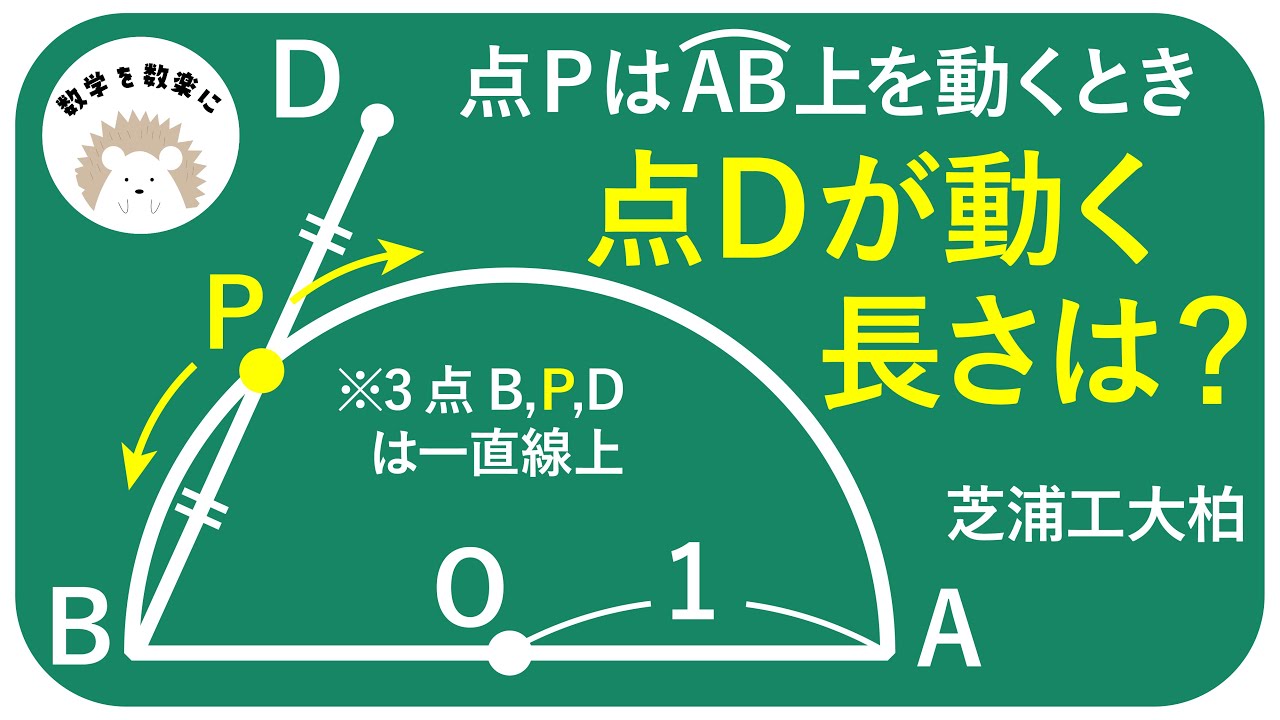
点Pは$\stackrel{\huge\frown}{AB}$上を動く。
BP=DPとなるように点Dを定めるとき点Dが動く長さは?
芝浦工業大学柏高等学校
この動画を見る
点Pは$\stackrel{\huge\frown}{AB}$上を動く。
BP=DPとなるように点Dを定めるとき点Dが動く長さは?
芝浦工業大学柏高等学校
たった4という数字だけで。。。
単元:
#中1数学#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
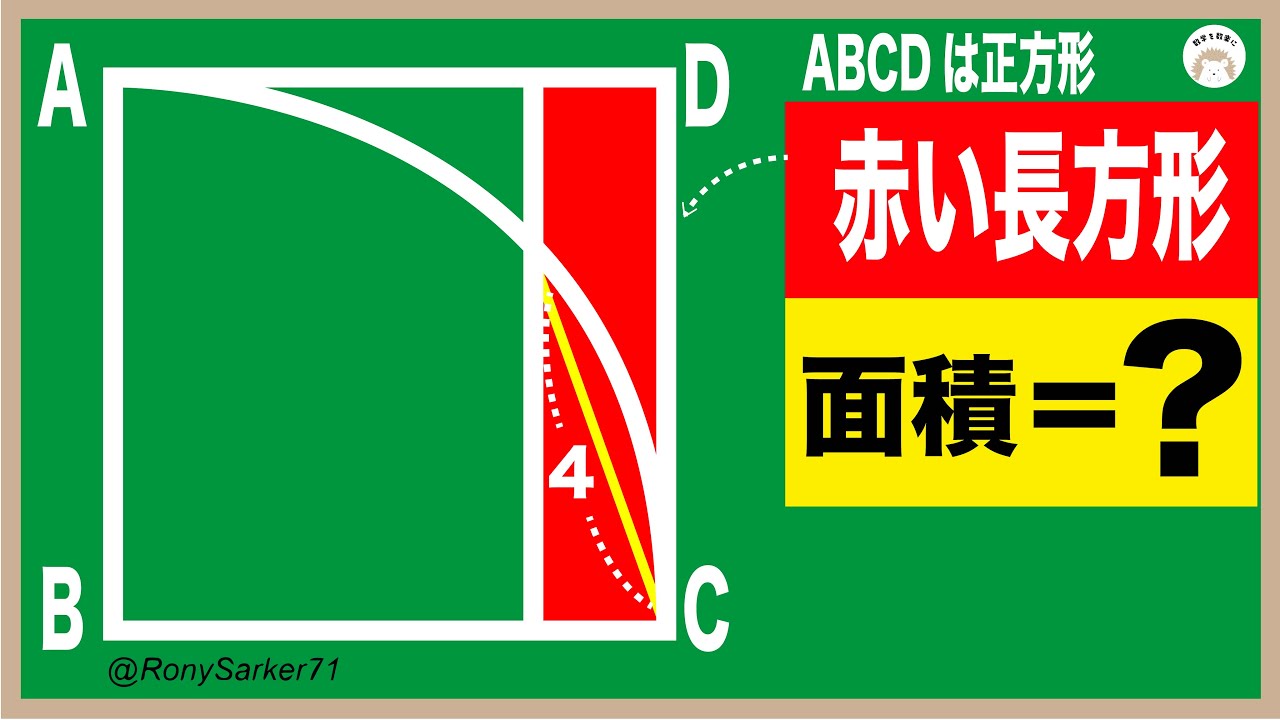
長方形の面積=?
*図は動画内参照
この動画を見る
長方形の面積=?
*図は動画内参照
京都と言ったら八つ橋くらい定番です
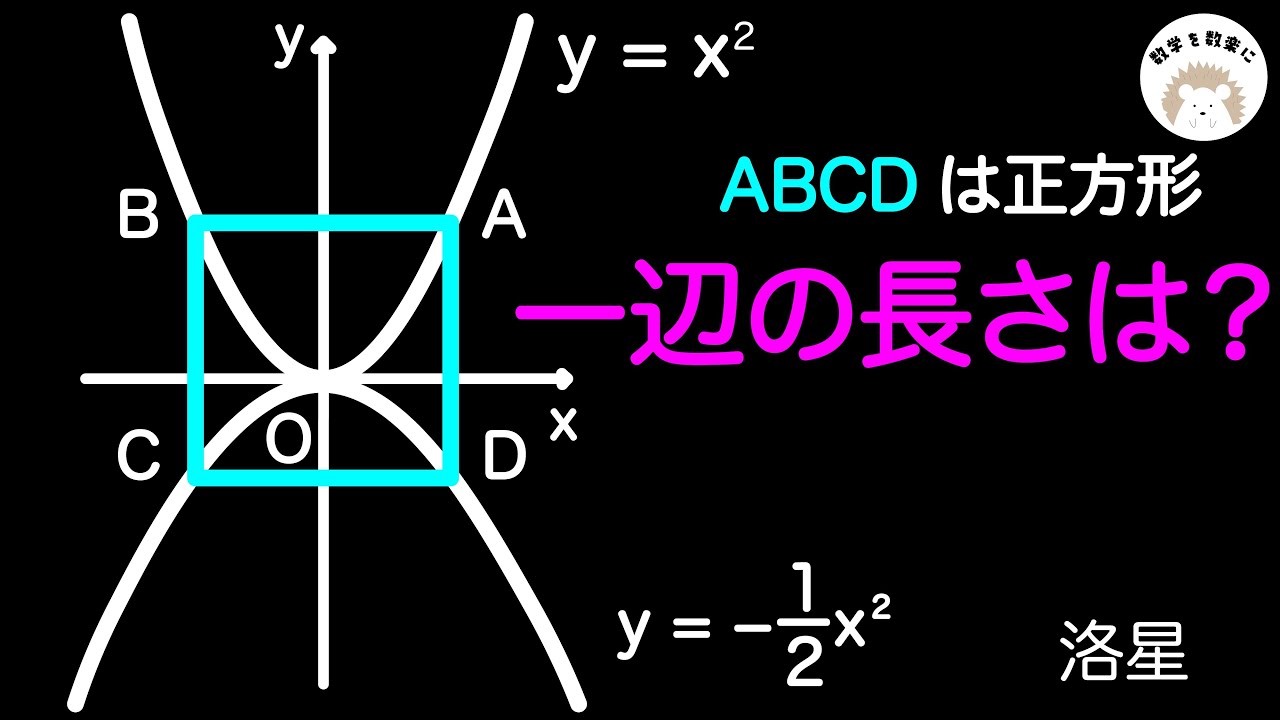
高校入試最上級レベル 球の断面積
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
立方体を次の各面で切断したときの球の断面積=?
(1)四角形BDHF
(2)△ACF
(3)△ACH
*図は動画内参照
城北高等学校
この動画を見る
立方体を次の各面で切断したときの球の断面積=?
(1)四角形BDHF
(2)△ACF
(3)△ACH
*図は動画内参照
城北高等学校
福田の数学〜立教大学2021年経済学部第1問(2)〜円に内接する四角形

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)円Cに内接する四角形PQRSにおいて、対角線PRは円Cの中心Oを通る。
また、各辺の長さは、$PQ=1, QR=8, RS=4, SP=7$であり、
角Pの大きさを$\theta$とする。ただし、$0 \lt \theta \lt \pi$とする。
このとき円Cの直径は$\boxed{イ},\cos\theta=\boxed{ウ}$である。
2021立教大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$(2)円Cに内接する四角形PQRSにおいて、対角線PRは円Cの中心Oを通る。
また、各辺の長さは、$PQ=1, QR=8, RS=4, SP=7$であり、
角Pの大きさを$\theta$とする。ただし、$0 \lt \theta \lt \pi$とする。
このとき円Cの直径は$\boxed{イ},\cos\theta=\boxed{ウ}$である。
2021立教大学経済学部過去問
e^π>22 示せ
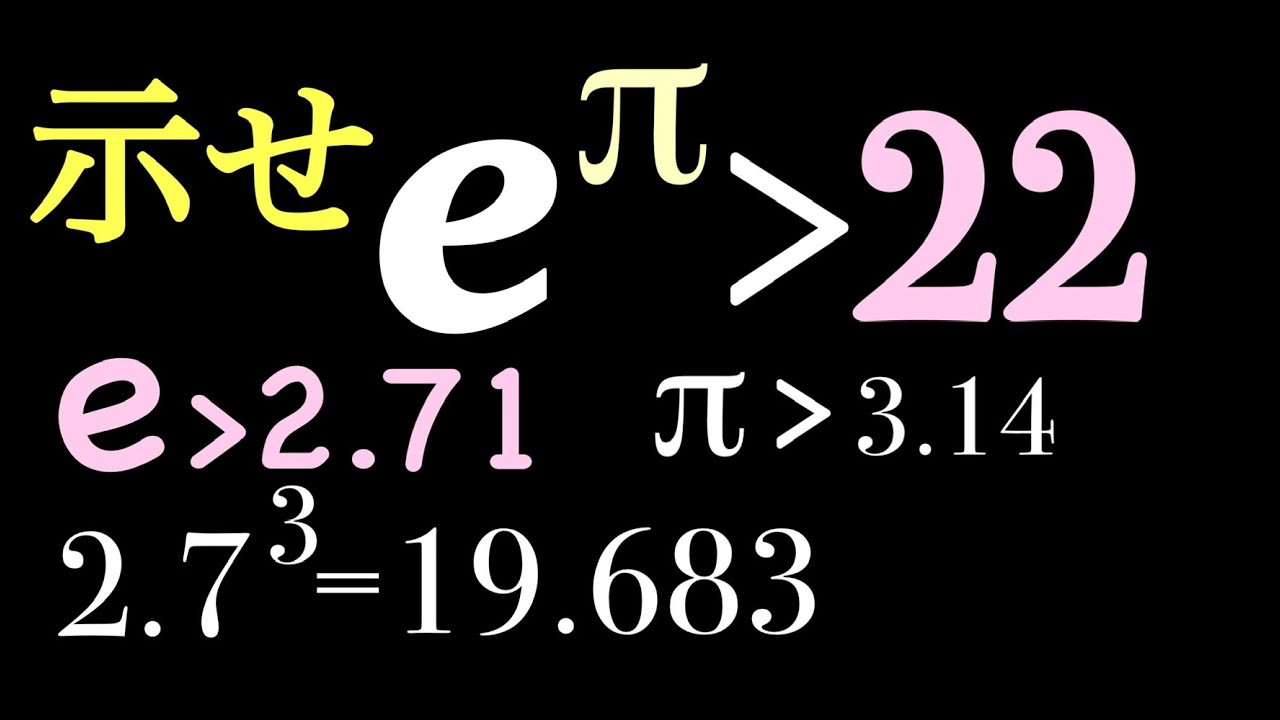
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$e^{\pi}\gt 22$を示せ.
$e \gt 2.71,\pi\gt 3.14$
この動画を見る
$e^{\pi}\gt 22$を示せ.
$e \gt 2.71,\pi\gt 3.14$
おうぎ形と円

単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
赤い円の面積=?
*図は動画内参照
この動画を見る
赤い円の面積=?
*図は動画内参照
もっちゃんと数学 フェルマーの小定理

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
フェルマーの定理に関して解説していきます.
この動画を見る
フェルマーの定理に関して解説していきます.
