約数・倍数・整数の割り算と余り・合同式
約数・倍数・整数の割り算と余り・合同式
福田のおもしろ数学310〜累乗で表された数の大小比較
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
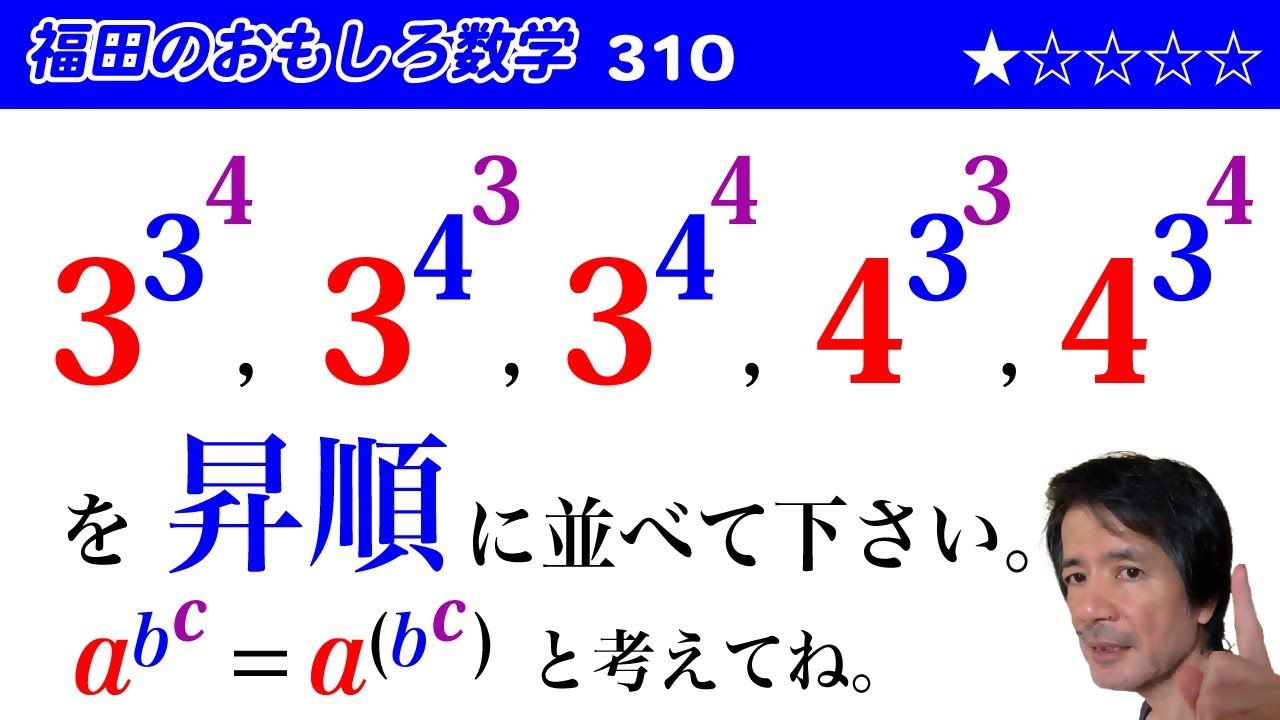
$$\left( \left( 3 \right)^3 \right)^4,\left( \left( 3 \right)^4 \right)^3,\left( \left( 3 \right)^4\right)^4,\left( \left( 4\right)^3 \right)^3,\left( \left( 4 \right)^3 \right)^4を昇順に直してください。ただし、a^{ b^c}=a^{ (b^c)}とする。$$
この動画を見る
$$\left( \left( 3 \right)^3 \right)^4,\left( \left( 3 \right)^4 \right)^3,\left( \left( 3 \right)^4\right)^4,\left( \left( 4\right)^3 \right)^3,\left( \left( 4 \right)^3 \right)^4を昇順に直してください。ただし、a^{ b^c}=a^{ (b^c)}とする。$$
福田のおもしろ数学302〜ベルトランの仮説を利用したn!の約数に関する性質
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$n$を3以上の整数とし、$n!$の正の約数を小さい方から$1=d_1\lt d_2\lt \cdots \lt d_k = n!$とする。$d_2-d_1\leqq d_3-d_2 \leqq \cdots \leqq d_k-d_{k-1}$が成り立つような$n$をすべて求めよ。
この動画を見る
$n$を3以上の整数とし、$n!$の正の約数を小さい方から$1=d_1\lt d_2\lt \cdots \lt d_k = n!$とする。$d_2-d_1\leqq d_3-d_2 \leqq \cdots \leqq d_k-d_{k-1}$が成り立つような$n$をすべて求めよ。
和と積が等しくなるような自然数の組？シンプルだけど難しい！どう解く？
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
相違なるn個の自然数の和と積が等しいとき、nの値とそれらn個の自然数の組をすべて求めよ。ただし、n≧2とする。
この動画を見る
相違なるn個の自然数の和と積が等しいとき、nの値とそれらn個の自然数の組をすべて求めよ。ただし、n≧2とする。
福田のおもしろ数学296〜フェルマーの最終定理とは何か。与えられた不等式を満たす数列の1との大小関係
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
0以上の整数$a, b, c$が$a+b+c=300, a^2b+a^2c+b^2a+b^2c+c^2a+c^2b=6,000,000$を満たしている。そのような$(a, b, c)$の組の個数を求めよ。
この動画を見る
0以上の整数$a, b, c$が$a+b+c=300, a^2b+a^2c+b^2a+b^2c+c^2a+c^2b=6,000,000$を満たしている。そのような$(a, b, c)$の組の個数を求めよ。
【高校数学】京大の整数問題！どう解く？
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
pを3以上の素数とする。４個の整数a,b,c,dが次の３条件
a+b+c+d=0
ad-bc-+p=0
a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
この動画を見る
pを3以上の素数とする。４個の整数a,b,c,dが次の３条件
a+b+c+d=0
ad-bc-+p=0
a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
福田のおもしろ数学293〜三角方程式を満たす正の整数xの最小値
単元：
#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#整数の性質#約数・倍数・整数の割り算と余り・合同式#三角関数とグラフ#加法定理とその応用
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \tan 19x^{\circ}\ =\ \frac{\cos 96^{\circ}+\sin 96^{\circ}}{\cos 96^{\circ}-\sin 96^{\circ}}\ $を満たす最小の正の整数$\ x\ $を求めよ。
この動画を見る
$\displaystyle \tan 19x^{\circ}\ =\ \frac{\cos 96^{\circ}+\sin 96^{\circ}}{\cos 96^{\circ}-\sin 96^{\circ}}\ $を満たす最小の正の整数$\ x\ $を求めよ。
福田の数学〜慶應義塾大学2024環境情報学部第2問〜2べき乗表現の個数
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$b_k$を正の整数、$b_{k-1},\cdots,b_1,b_0$を負でない整数とする($k$は負でない整数であり、$k=0$のときは正の整数$b_0$のみを考える)。正の整数$n$に対して、$b_k,b_{k-1},\cdots,b_1,b_0$が$\ \ \ \ $
$\displaystyle 2^kb_k+2^{k-1}b_{k-1}+\cdots+2^2b_2+2b_1+b_0=\sum_{i=0}^k2^ib_i=n\ \\ $を満たすとき、$\langle b_k,b_{k-1},\cdots,b_1,b_0 \rangle$を$n$の2べき乗表現と呼ぶことにする。これは2進法による数の表現と似ているが、2進法の場合とは異なり、$b_i\ (i=0,1,\cdots,k)$は2以上の値も取りうる。そのため$n\geqq 2$において、$n$の2べき乗表現は1通りではない。$\\$
(1)$\ n=3$の2べき乗表現は$\langle 3 \rangle$と$\langle ア, イ\rangle$の2通りである。$\\ $(2)$\ \langle 3,2,1 \rangle$は$n=(ウエ)$の2べき乗表現である。$\\ $(3) $\ m$を正の整数とするとき、1から$m$までの整数を順に並べた$\langle 1,2,\cdots ,m \rangle$は$\ \ 2^{(m+オカ)}+(キク)m+(ケコ)\ $の2べき乗表現である。$\\ $ (4)$\ n$の2べき乗表現の個数を$a_n$とすると、$\ a_4=(サシ),\ a_5=(スセ),\ a_6=(ソタ),\cdots ,a_{10}=(チツ),\cdots , a_{20}=(テト)$である。
この動画を見る
$b_k$を正の整数、$b_{k-1},\cdots,b_1,b_0$を負でない整数とする($k$は負でない整数であり、$k=0$のときは正の整数$b_0$のみを考える)。正の整数$n$に対して、$b_k,b_{k-1},\cdots,b_1,b_0$が$\ \ \ \ $
$\displaystyle 2^kb_k+2^{k-1}b_{k-1}+\cdots+2^2b_2+2b_1+b_0=\sum_{i=0}^k2^ib_i=n\ \\ $を満たすとき、$\langle b_k,b_{k-1},\cdots,b_1,b_0 \rangle$を$n$の2べき乗表現と呼ぶことにする。これは2進法による数の表現と似ているが、2進法の場合とは異なり、$b_i\ (i=0,1,\cdots,k)$は2以上の値も取りうる。そのため$n\geqq 2$において、$n$の2べき乗表現は1通りではない。$\\$
(1)$\ n=3$の2べき乗表現は$\langle 3 \rangle$と$\langle ア, イ\rangle$の2通りである。$\\ $(2)$\ \langle 3,2,1 \rangle$は$n=(ウエ)$の2べき乗表現である。$\\ $(3) $\ m$を正の整数とするとき、1から$m$までの整数を順に並べた$\langle 1,2,\cdots ,m \rangle$は$\ \ 2^{(m+オカ)}+(キク)m+(ケコ)\ $の2べき乗表現である。$\\ $ (4)$\ n$の2べき乗表現の個数を$a_n$とすると、$\ a_4=(サシ),\ a_5=(スセ),\ a_6=(ソタ),\cdots ,a_{10}=(チツ),\cdots , a_{20}=(テト)$である。
差がつく！素数を扱う整数問題！【京都大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
pを３以上の素数とする。４個の整数a,b,c,dが次の３条件
a+b+c+d=0,ad-bc+p=0,a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
この動画を見る
pを３以上の素数とする。４個の整数a,b,c,dが次の３条件
a+b+c+d=0,ad-bc+p=0,a≧b≧c≧d
を満たすとき、a,b,c,dをpで表せ。
数がでかすぎる！1の位の数字をどう求める？【東京大学】【数学 入試問題】
単元：
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#指数関数#数列#数列とその和（等差・等比・階差・Σ）#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
(10^210)/(10^10+3)の整数部分のけた数と、１の位の数字を求めよ。ただし、3^21=10460353203を用いてよい。
この動画を見る
(10^210)/(10^10+3)の整数部分のけた数と、１の位の数字を求めよ。ただし、3^21=10460353203を用いてよい。
福田のおもしろ数学282〜ガウス記号で表された式の和を求める
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \sum_{n=1}^{1000} [\frac{2^n}{3} ]$を求めて下さい。$[x]$は$x$をこえない最大の整数を表す。
この動画を見る
$\displaystyle \sum_{n=1}^{1000} [\frac{2^n}{3} ]$を求めて下さい。$[x]$は$x$をこえない最大の整数を表す。
福田のおもしろ数学280〜3^x+4^y=5^zを満たす正の整数を求める
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$3^x+4^y=5^z$を満たす正の整数$x,y,z$は$(x,y,z)=(2,2,2)$以外に存在するか。
この動画を見る
$3^x+4^y=5^z$を満たす正の整数$x,y,z$は$(x,y,z)=(2,2,2)$以外に存在するか。
最大公約数ってまずいってこと？
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
スタバ新作のチョコレートムースラテはチョコ好きな人みんな飲んだ方がいい
チョコとナッツの最大公約数
と紹介していたツイートについて
この動画を見る
スタバ新作のチョコレートムースラテはチョコ好きな人みんな飲んだ方がいい
チョコとナッツの最大公約数
と紹介していたツイートについて
福田の数学〜上智大学2024理工学部第2問〜漸化式と約数倍数の証明
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
次の条件によって定められる数列 ${a_n}$ を考える。
$a_1=2, \, a_{n+1}=a_n^2+a_n+1$
$(1)$ $a_n-2$ は $5$ で割り切れることを証明せよ。
$(2)$ $a_n^2+1$ は $5^n$ で割り切れることを証明せよ。
この動画を見る
次の条件によって定められる数列 ${a_n}$ を考える。
$a_1=2, \, a_{n+1}=a_n^2+a_n+1$
$(1)$ $a_n-2$ は $5$ で割り切れることを証明せよ。
$(2)$ $a_n^2+1$ は $5^n$ で割り切れることを証明せよ。
5つの文字を求めよ！？東大の整数問題【東京大学】【数学 入試問題】
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
この動画を見る
n,a,b,c,dは0または正の整数であって、
a^2+b^2+c^2+d^2=n^2-6
a+b+c+d≦n
a≧b≧c≧d
を満たすものとする。このような整数の組(n,a,b,c,d)をすべて求めよ。
福田のおもしろ数学271〜再帰関数の値を計算する
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
整数を定義域とする関数が次のように定義されている。
\begin{eqnarray}
f(n)
=
\begin{cases}
n-3 & ( n \geqq 1000 ) \\
f(f(n+5)) & ( n \lt 1000 )
\end{cases}
\end{eqnarray}
このとき$f(84)$を求めよ
この動画を見る
整数を定義域とする関数が次のように定義されている。
\begin{eqnarray}
f(n)
=
\begin{cases}
n-3 & ( n \geqq 1000 ) \\
f(f(n+5)) & ( n \lt 1000 )
\end{cases}
\end{eqnarray}
このとき$f(84)$を求めよ
福田のおもしろ数学261〜整数解を求めるにはどうすればよいか
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,n$を正の整数とするとき$a^{n+1}-(a+1)^n=2000$を満たす$a,n$を求めて下さい。
この動画を見る
$a,n$を正の整数とするとき$a^{n+1}-(a+1)^n=2000$を満たす$a,n$を求めて下さい。
割って余る問題 国学院高校
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
101と227をｎで割ったときの余りが17になる自然数ｎのうち、最大のものを求めよ
この動画を見る
101と227をｎで割ったときの余りが17になる自然数ｎのうち、最大のものを求めよ
沼に嵌りそうな典型問題 産業医科大学2019 大学入試問題#931
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
実数$x,y$が
$x^2+y^2+2xy+2x-2y+2=0$を満たすとき,
$x-y$の最大値を求めよ.
2019産業医科大学過去問題
この動画を見る
実数$x,y$が
$x^2+y^2+2xy+2x-2y+2=0$を満たすとき,
$x-y$の最大値を求めよ.
2019産業医科大学過去問題
中学生はよく間違えるルートに関する問題 西武文理
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt{4x^2}$が$10$より小さい整数となるような整数$x$は何個あるか
この動画を見る
$\sqrt{4x^2}$が$10$より小さい整数となるような整数$x$は何個あるか
至高かつ王道の整数問題 関西医科大学2019 大学入試問題#928
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師：
ますただ
問題文全文(内容文)：
正の整数の組$(x,y,z)$が
$2x^2+2y^2+z^2+2xy-2xz-2yz=9$を満たすとき
$x+y+z$の最大値を求めよ.
2019関西医科大学過去問題
この動画を見る
正の整数の組$(x,y,z)$が
$2x^2+2y^2+z^2+2xy-2xz-2yz=9$を満たすとき
$x+y+z$の最大値を求めよ.
2019関西医科大学過去問題
#産業医科大学2023#式変形_45
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\dfrac{2-\sqrt 3+\sqrt 7}{2+\sqrt 3-\sqrt7}-\dfrac{2+\sqrt 3-\sqrt7}{2-\sqrt3+\sqrt7}$
を簡単にせよ.
2023産業医科大学過去問題
この動画を見る
$\dfrac{2-\sqrt 3+\sqrt 7}{2+\sqrt 3-\sqrt7}-\dfrac{2+\sqrt 3-\sqrt7}{2-\sqrt3+\sqrt7}$
を簡単にせよ.
2023産業医科大学過去問題
王道の整数問題 産業医科大学2024 大学入試問題#927
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師：
ますただ
問題文全文(内容文)：
$\dfrac{b^2}{a}+\dfrac{a}{b}=6$を満たす
自然数の組$(a,b)$のうち$a+b$の最小値を求めよ.
2024産業医科大学過去問題
この動画を見る
$\dfrac{b^2}{a}+\dfrac{a}{b}=6$を満たす
自然数の組$(a,b)$のうち$a+b$の最小値を求めよ.
2024産業医科大学過去問題
大学入試問題#912「解答を綺麗にする時間がなかった」 #自治医科大学2024
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師：
ますただ
問題文全文(内容文)：
$0 \leq k:$整数
$N=\displaystyle \frac{k^2+k+300}{k^3+k^2+2k+2}$が自然数となるときのすべての$k$の値の和$S$を求めよ。
出典：2024年自治医科大学
この動画を見る
$0 \leq k:$整数
$N=\displaystyle \frac{k^2+k+300}{k^3+k^2+2k+2}$が自然数となるときのすべての$k$の値の和$S$を求めよ。
出典：2024年自治医科大学
大学入試問題#911「私学医学部では出題必須か！？」 #自治医科大学2024
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師：
ますただ
問題文全文(内容文)：
実数$x,y$が$x^2+y^2=1$を満たすとき、$5x^2+4xy+y^2$の最大値を$M,$最小値を$m$とする。
$\displaystyle \frac{(M-m)^2}{4}$の値を求めよ。
出典：2024年自治医科大学
この動画を見る
実数$x,y$が$x^2+y^2=1$を満たすとき、$5x^2+4xy+y^2$の最大値を$M,$最小値を$m$とする。
$\displaystyle \frac{(M-m)^2}{4}$の値を求めよ。
出典：2024年自治医科大学
福田のおもしろ数学232〜1980で割り切れる証明
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$2450^n-1370^n+1150^n-250^n$が$1980$で割り切れることを示せ。
この動画を見る
$2450^n-1370^n+1150^n-250^n$が$1980$で割り切れることを示せ。
大学入試問題#906「色んな要素がモリモリ問題」昭和大学医学部(2012)
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#昭和大学
指導講師：
ますただ
問題文全文(内容文)：
正の数$a,b$が$a^3+b^3=5$を満たすとき、$a+b$のとりうる値の範囲を求めよ。
出典：2012年昭和大学医学部
この動画を見る
正の数$a,b$が$a^3+b^3=5$を満たすとき、$a+b$のとりうる値の範囲を求めよ。
出典：2012年昭和大学医学部
福田の数学〜中央大学2024理工学部第2問〜確率の基本性質と3で割ったときの剰余類
単元：
#数A#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$n$ を $3$ 以上の整数とする。$1, \, 2, \, \ldots, \, n$ の数が1つずつ書かれた $n$ 枚のカードがある。これらをよく混ぜて1枚のカードを引き、そこに書かれた数を $X$ とする。そのカードを元に戻し、よく混ぜてからもう一度1枚のカードを引き、そこに書かれた数を $Y$ とする。このとき $X-Y$ が $3$ の倍数である確率を $p(n)$、$X-Y-1$ が $3$ の倍数である確率を $q(n)$、$X-Y+1$ が $3$ の倍数である確率を $r(n)$ とする。
$(1)$ $q(3)=\fbox{ク}$ である。
$(2)$ $r(n)$ は $q(n)$ を用いて $r(n)=\fbox{ケ}$ と表せる。
$(3)$ $n$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{コ}}{\fbox{サ}}$ が成り立つ。
$(4)$ $n-1$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{シ}}{\fbox{ス}}$ が成り立つ。
$(5)$ $n-2$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{セ}}{\fbox{ソ}}$ が成り立つ。
この動画を見る
$n$ を $3$ 以上の整数とする。$1, \, 2, \, \ldots, \, n$ の数が1つずつ書かれた $n$ 枚のカードがある。これらをよく混ぜて1枚のカードを引き、そこに書かれた数を $X$ とする。そのカードを元に戻し、よく混ぜてからもう一度1枚のカードを引き、そこに書かれた数を $Y$ とする。このとき $X-Y$ が $3$ の倍数である確率を $p(n)$、$X-Y-1$ が $3$ の倍数である確率を $q(n)$、$X-Y+1$ が $3$ の倍数である確率を $r(n)$ とする。
$(1)$ $q(3)=\fbox{ク}$ である。
$(2)$ $r(n)$ は $q(n)$ を用いて $r(n)=\fbox{ケ}$ と表せる。
$(3)$ $n$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{コ}}{\fbox{サ}}$ が成り立つ。
$(4)$ $n-1$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{シ}}{\fbox{ス}}$ が成り立つ。
$(5)$ $n-2$ が $3$ の倍数であるとき、$p(n)=\frac{\fbox{セ}}{\fbox{ソ}}$ が成り立つ。
福田のおもしろ数学224〜3次式が素数となる整数nを求める
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$n^3-7n+9$が素数となるような整数$n$をすべて求めよ。
この動画を見る
$n^3-7n+9$が素数となるような整数$n$をすべて求めよ。
大学入試問題#897「解法の迷走」 #北海道大学(2024)
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \frac{x^2-x+1}{x^2+x+1}$
が整数となるような実数$x$をすべて求めよ。
出典：2024年北海道大学後期
この動画を見る
$\displaystyle \frac{x^2-x+1}{x^2+x+1}$
が整数となるような実数$x$をすべて求めよ。
出典：2024年北海道大学後期
福田の数学〜中央大学2024経済学部第1問(2)〜集合の要素の個数
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。
この動画を見る
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。