 ユークリッド互除法と不定方程式・N進法
ユークリッド互除法と不定方程式・N進法
 ユークリッド互除法と不定方程式・N進法
ユークリッド互除法と不定方程式・N進法
立方根の方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解$x$を求めよ.
$\sqrt[3]{x+28}-\sqrt[3]{x-28}=2$
この動画を見る
実数解$x$を求めよ.
$\sqrt[3]{x+28}-\sqrt[3]{x-28}=2$
対数方程式 華麗に解こう

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$3^{\log_2 x}+3^{\log_2 \frac{8}{x}}=12$
この動画を見る
これを解け.
$3^{\log_2 x}+3^{\log_2 \frac{8}{x}}=12$
ただの累乗根方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\sqrt[x]{4096}-\sqrt[\frac{x}{2}]{2^{3x-6}}+12=0$
この動画を見る
これを解け.
$\sqrt[x]{4096}-\sqrt[\frac{x}{2}]{2^{3x-6}}+12=0$
連立二元二次方程式
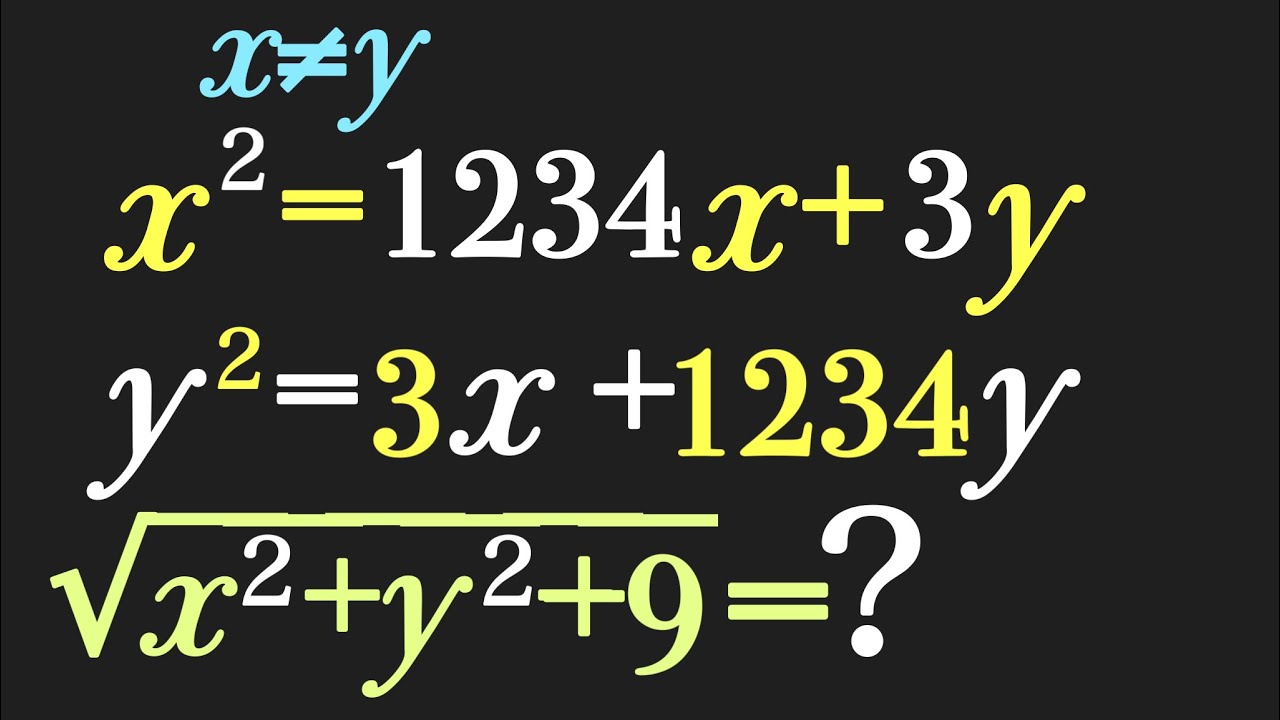
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.$x\neq y$である.
$x^2=1234x+3y$
$y^2=3x+1234y$
$\sqrt{x^2+y^2+9}=?$
この動画を見る
これを解け.$x\neq y$である.
$x^2=1234x+3y$
$y^2=3x+1234y$
$\sqrt{x^2+y^2+9}=?$
福田の数学〜早稲田大学2021年人間科学部第2問(3)〜n進法

単元:
#計算と数の性質#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#規則性(周期算・方陣算・数列・日暦算・N進法)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$
(3)$n$進法で$2021_{(n)}$と表される数が、素数であるような$n$の最小値を十進法で表すと$\boxed{\ \ コ\ \ }$となり、合成数である(素数ではない)ような$n$の最小値を十進法で表すと$\boxed{\ \ サ\ \ }$となる。
この動画を見る
${\Large\boxed{2}}$
(3)$n$進法で$2021_{(n)}$と表される数が、素数であるような$n$の最小値を十進法で表すと$\boxed{\ \ コ\ \ }$となり、合成数である(素数ではない)ような$n$の最小値を十進法で表すと$\boxed{\ \ サ\ \ }$となる。
変わった指数方程式
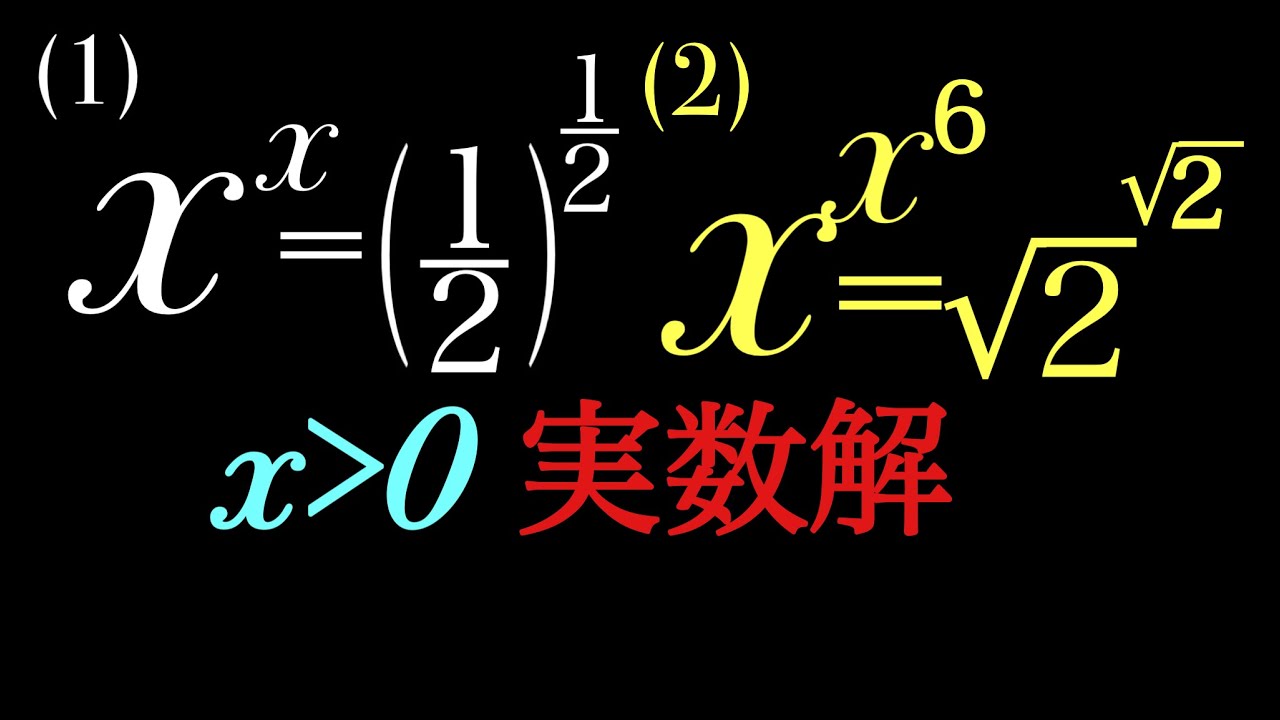
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\gt 0$である.これを解け.
(1)$x^x=\left(\dfrac{1}{2}\right)^{\frac{1}{2}}$
(2)$x^{x^6}=\sqrt2^{\sqrt2}$
この動画を見る
$x\gt 0$である.これを解け.
(1)$x^x=\left(\dfrac{1}{2}\right)^{\frac{1}{2}}$
(2)$x^{x^6}=\sqrt2^{\sqrt2}$
福田のわかった数学〜高校1年生030〜ガウス記号を含んだ方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
数学\textrm{I} ガウス記号を含む方程式\\
次の方程式を解け。\\
(1)[2x]^2=4 (2)[2x]=[x]
\end{eqnarray}
この動画を見る
\begin{eqnarray}
数学\textrm{I} ガウス記号を含む方程式\\
次の方程式を解け。\\
(1)[2x]^2=4 (2)[2x]=[x]
\end{eqnarray}
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^{2x^2-1}+2・3^{(x+1)^2}-5・3^{4(x+1)}=0$
この動画を見る
実数解を求めよ.
$3^{2x^2-1}+2・3^{(x+1)^2}-5・3^{4(x+1)}=0$
良問!ガウス記号の方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{x}{x+4}=\dfrac{5[x]-7}{7[x]-5}$
この動画を見る
これを解け.
$\dfrac{x}{x+4}=\dfrac{5[x]-7}{7[x]-5}$
妙な指数方程式
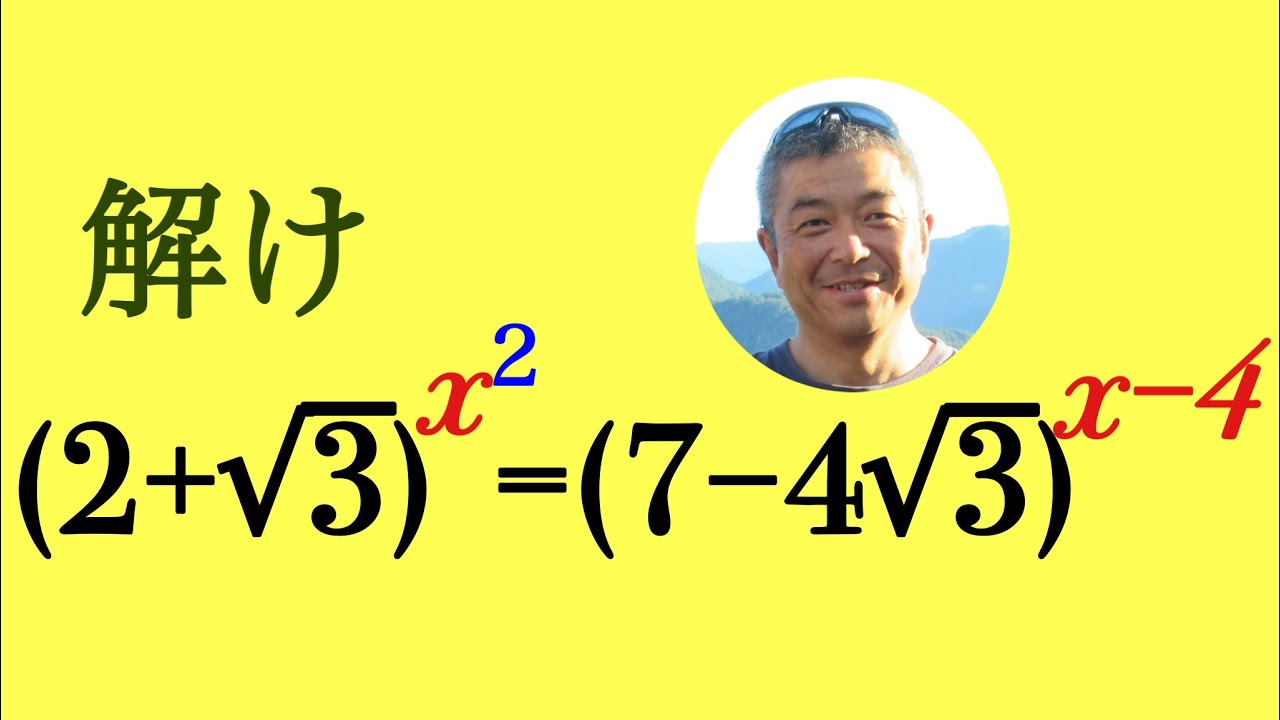
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$(2+\sqrt3)^{x^2}=(7-4\sqrt3)^{x-4}$
この動画を見る
これを解け.
$(2+\sqrt3)^{x^2}=(7-4\sqrt3)^{x-4}$
どってことない指数方程式
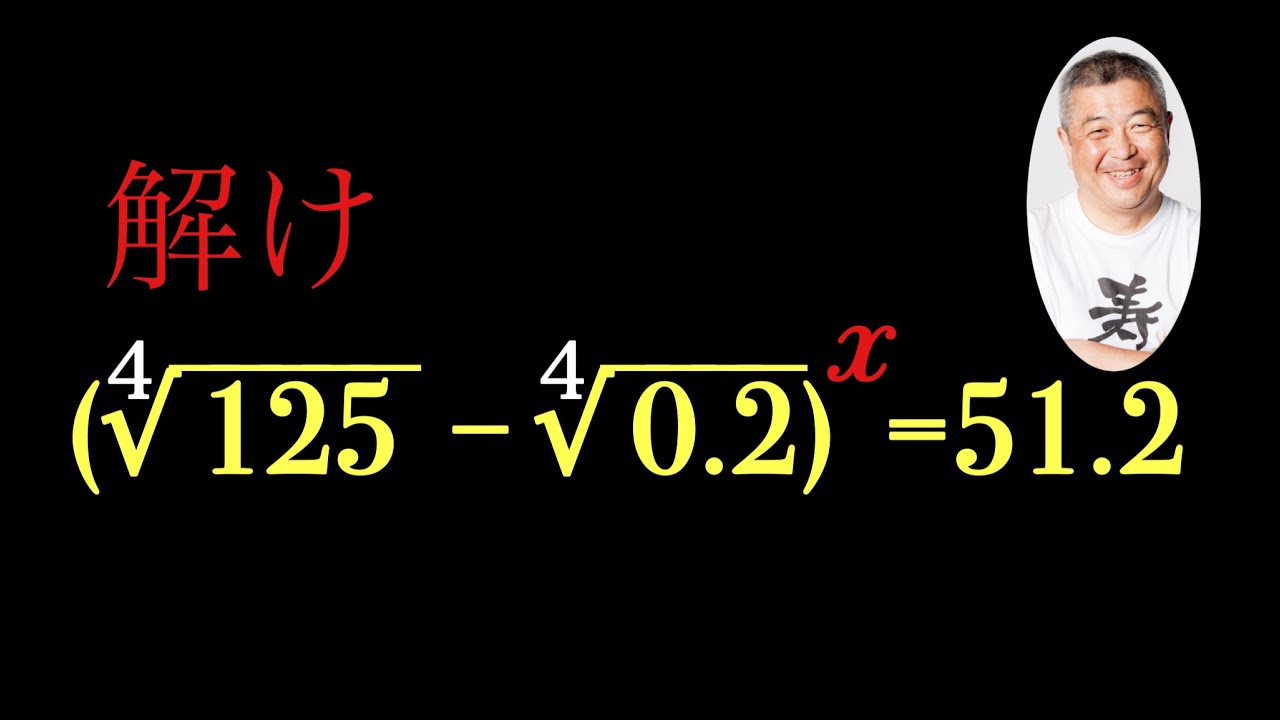
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$(\sqrt[4]{125}-\sqrt[4]{0.2})^x=51.2$
この動画を見る
これを解け.
$(\sqrt[4]{125}-\sqrt[4]{0.2})^x=51.2$
変な指数方程式
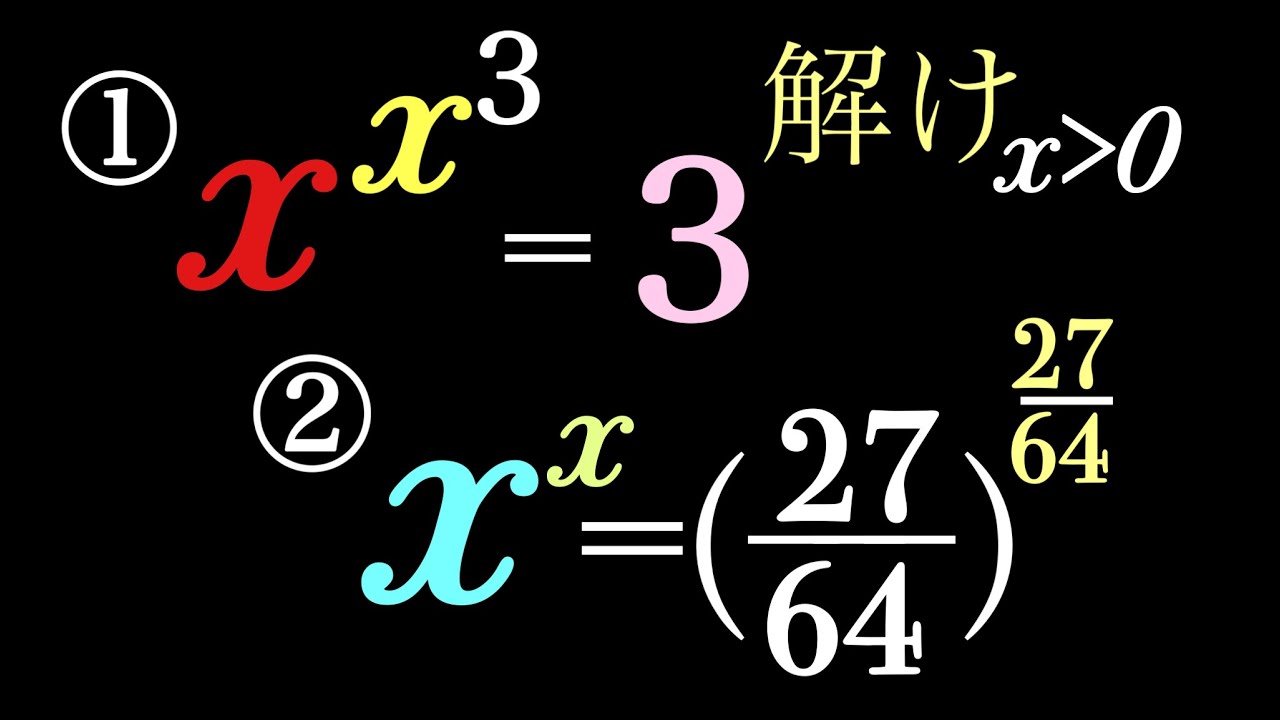
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\gt 0$とする.これを解け.
①$x^{x^3}=3$
②$x^x=\left(\dfrac{27}{64}\right)^{\frac{27}{64}}$
この動画を見る
$x\gt 0$とする.これを解け.
①$x^{x^3}=3$
②$x^x=\left(\dfrac{27}{64}\right)^{\frac{27}{64}}$
【高校数学】1次不定方程式~どこよりも丁寧に教える~ 5-8【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1次不定方程式の分かりやすい解説動画です
この動画を見る
1次不定方程式の分かりやすい解説動画です
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^x-5^x=\sqrt{15^x-25^x}$
この動画を見る
実数解を求めよ.
$3^x-5^x=\sqrt{15^x-25^x}$
ちょっと変わった指数方程式

【高校数学】ユークリッドの互除法の例題2題 5-7.5【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
390と273の最大公約数を求めよ
2⃣
31$x$+22$y$=3を満たす整数$x、y$の組を1つ求めよ
この動画を見る
1⃣
390と273の最大公約数を求めよ
2⃣
31$x$+22$y$=3を満たす整数$x、y$の組を1つ求めよ
【高校数学】中学数学で分かるユークリッドの互除法の原理の証明 5-7.5【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
中学数学で分かるユークリッドの互除法の原理の証明
この動画を見る
中学数学で分かるユークリッドの互除法の原理の証明
【高校数学】ユークリッドの互除法をどこよりも丁寧に教えます 5-7【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
667と299の最大公約数を求めよ
2⃣
31$x$+22$y$=1を満たす整数$x,y$の組を1つ求めよ
この動画を見る
1⃣
667と299の最大公約数を求めよ
2⃣
31$x$+22$y$=1を満たす整数$x,y$の組を1つ求めよ
兵庫医大 普通の基本問題 指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$4^x-2^{x+2}+a^2-3a+4=0$が異なる2つの正の解をもつ$a$の範囲を求めよ.
2019兵庫医大過去問
この動画を見る
$4^x-2^{x+2}+a^2-3a+4=0$が異なる2つの正の解をもつ$a$の範囲を求めよ.
2019兵庫医大過去問
数学「大学入試良問集」【3−6不定方程式②】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$3$以上$9999$以下の奇数$a$で、$a^2-a$が$10000$で割り切れるものをすべて求めよ。
この動画を見る
$3$以上$9999$以下の奇数$a$で、$a^2-a$が$10000$で割り切れるものをすべて求めよ。
数学「大学入試良問集」【3−5 ユークリッド互除法】を宇宙一わかりやすく

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
(1)
自然数$a,b,c,d$に$\displaystyle \frac{b}{a}=\displaystyle \frac{c}{a}+d$の関係があるとき、$a$と$c$が互いに素であれば、$a$と$b$も互いに素であることを証明せよ。
(2)
任意の自然数$n$に対し、$28n+5$と$21n+4$は互いに素であることを証明せよ。
この動画を見る
(1)
自然数$a,b,c,d$に$\displaystyle \frac{b}{a}=\displaystyle \frac{c}{a}+d$の関係があるとき、$a$と$c$が互いに素であれば、$a$と$b$も互いに素であることを証明せよ。
(2)
任意の自然数$n$に対し、$28n+5$と$21n+4$は互いに素であることを証明せよ。
指数方程式を解け
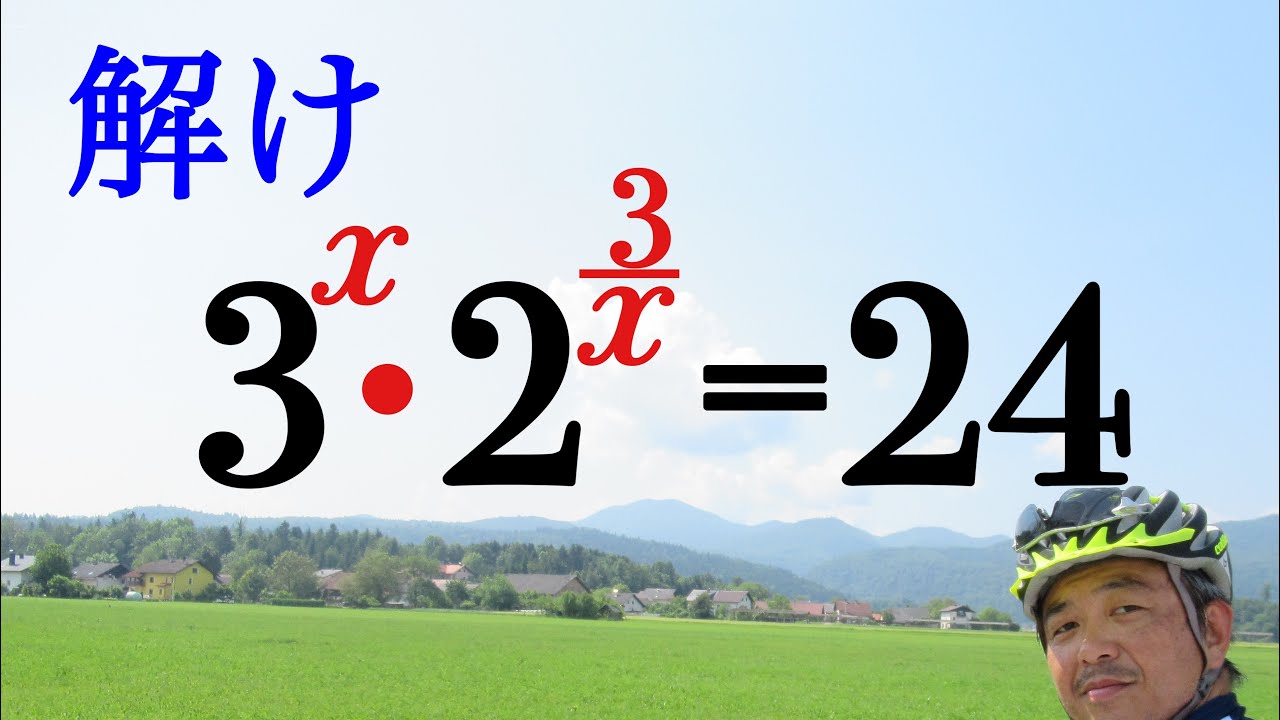
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$3^x・2^{\frac{3}{x}}=24$
この動画を見る
これを解け.
$3^x・2^{\frac{3}{x}}=24$
数学「大学入試良問集」【3−4 整数 n進法】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
7進法で表すと3けたとなる正の整数がある。
これを11進法で表すと、やはり3けたで、数字の順序がもととちょうど反対となる。
このような整数を10進法で表せ。
この動画を見る
7進法で表すと3けたとなる正の整数がある。
これを11進法で表すと、やはり3けたで、数字の順序がもととちょうど反対となる。
このような整数を10進法で表せ。
数学「大学入試良問集」【3−1 整数 不定方程式】を宇宙一わかりやすく

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$p,q,r$は不等式$p \leqq q \leqq r$を満たす正の整数とする。
このとき、次の各問いに答えよ。
(1)
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}=1$を満たす$p,q$をすべて求めよ。
(2)
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r}=1$を満たす$p,q,r$をすべて求めよ。
この動画を見る
$p,q,r$は不等式$p \leqq q \leqq r$を満たす正の整数とする。
このとき、次の各問いに答えよ。
(1)
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}=1$を満たす$p,q$をすべて求めよ。
(2)
$\displaystyle \frac{1}{p}+\displaystyle \frac{1}{q}+\displaystyle \frac{1}{r}=1$を満たす$p,q,r$をすべて求めよ。
横浜市立(医)ド・モアブルと7倍角

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)ド・モアブルの定理を用いて$\sin7\theta$を$\sin\theta,\cos\theta$およびその累乗を用いて表せ.
(2)$7x^3-35x^2+21x-1=0$を解け.
(3)$\dfrac{1}{\tan^2\dfrac{\pi}{7}}+\dfrac{1}{\tan^2\dfrac{2\pi}{7}}+\dfrac{1}{\tan^2\dfrac{3\pi}{7}}$の値を求めよ.
2016横浜市立(医)
この動画を見る
(1)ド・モアブルの定理を用いて$\sin7\theta$を$\sin\theta,\cos\theta$およびその累乗を用いて表せ.
(2)$7x^3-35x^2+21x-1=0$を解け.
(3)$\dfrac{1}{\tan^2\dfrac{\pi}{7}}+\dfrac{1}{\tan^2\dfrac{2\pi}{7}}+\dfrac{1}{\tan^2\dfrac{3\pi}{7}}$の値を求めよ.
2016横浜市立(医)
指数方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$3^{x^2-2\sqrt5 x}=\dfrac{1}{121}$
この動画を見る
実数解を求めよ.
$3^{x^2-2\sqrt5 x}=\dfrac{1}{121}$
方程式 整数解OnlineMathContest

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2-2(m-480)x+4m+97=0$が正整数解のみをもつ整数$m$を求めよ.
この動画を見る
$x^2-2(m-480)x+4m+97=0$が正整数解のみをもつ整数$m$を求めよ.
2021上智大 2つの解法 指数連立方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
4^x+9^y=5 \\
2^x・3^y=S
\end{array}
\right.
\end{eqnarray}$
連立方程式が実数解2組もつための$S$の必要十分条件を求めよ.
2021上智大過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
4^x+9^y=5 \\
2^x・3^y=S
\end{array}
\right.
\end{eqnarray}$
連立方程式が実数解2組もつための$S$の必要十分条件を求めよ.
2021上智大過去問
真面目な方程式 解は2つ
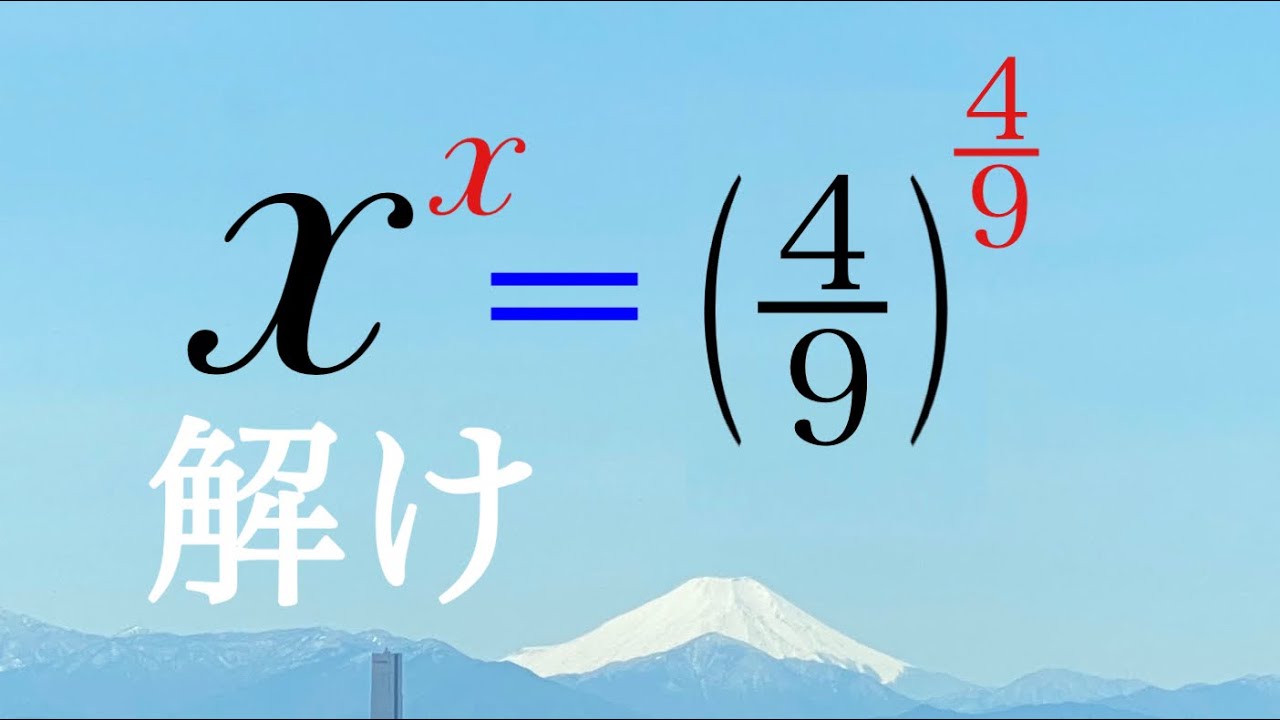
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$x^x=\left(\dfrac{4}{9}\right)^{\frac{4}{9}}$
この動画を見る
これを解け.
$x^x=\left(\dfrac{4}{9}\right)^{\frac{4}{9}}$
共通テスト第2日程2021年数学詳しい解説〜共通テスト第2日程2021年IA第4問〜整数の性質

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第4問}$
正の整数$m$に対して
$a^2+b^2+c^2+d^2=m, $$a \geqq b \geqq c \geqq d \geqq 0$ $\cdots$①
を満たす整数$a,b,c,d$の組がいくつあるかを考える。
(1)$m=14$のとき、①を満たす整数$a,b,c,d$の組$(a,b,c,d)$
は
$(\boxed{\ \ ア\ \ }, \boxed{\ \ イ\ \ }, \boxed{\ \ ウ\ \ }, \boxed{\ \ エ\ \ })$
のただ一つである。
また、$m=28$のとき、①を満たす整数$a,b,c,d$の組の個数は
$\boxed{\ \ オ\ \ }$個である。
(2)$a$が奇数のとき、整数$n$を用いて$a=2n+1$と表すことができる。
このとき、$n(n+1)$は偶数であるから、次の条件が全ての奇数$a$で成り立つ
ような正の整数$h$のうち、最大のものは$h=\boxed{\ \ カ\ \ }$である。
条件:$a^2-1$は$h$の倍数である。
よって、$a$が奇数の時、$a^2$を$\boxed{\ \ カ\ \ }$で割った時の余りは$1$である。
また、$a$が偶数の時、$a^2$を$\boxed{\ \ カ\ \ }$で割った時の余りは、$0$または$4$の
いずれかである。
(3)(2)により、$a^2+b^2+c^2+d^2$が$\boxed{\ \ カ\ \ }$の倍数ならば、整数$a,b,c,d$
のうち、偶数であるものの個数は$\boxed{\ \ キ\ \ }$個である。
(4)(3)を用いることにより、$m$が$\boxed{\ \ カ\ \ }$の倍数であるとき、①を満たす整数
$a,b,c,d$が求めやすくなる。
例えば、$m=224$のとき、①を満たす整数$a,b,c,d$の組$(a,b,c,d)$は
$(\boxed{\ \ クケ\ \ }, \boxed{\ \ コ\ \ }, \boxed{\ \ サ\ \ }, \boxed{\ \ シ\ \ })$
のただ1つであることが分かる。
(5)7の倍数で896の約数である正の整数$m$のうち、①を満たす整数$a,b,c,d$
の組の個数が$\boxed{\ \ オ\ \ }$個であるものの個数は$\boxed{\ \ ス\ \ }$個であり、
そのうち最大のものは$m=\boxed{\ \ セソタ\ \ }$である。
2021共通テスト過去問
この動画を見る
${\large第4問}$
正の整数$m$に対して
$a^2+b^2+c^2+d^2=m, $$a \geqq b \geqq c \geqq d \geqq 0$ $\cdots$①
を満たす整数$a,b,c,d$の組がいくつあるかを考える。
(1)$m=14$のとき、①を満たす整数$a,b,c,d$の組$(a,b,c,d)$
は
$(\boxed{\ \ ア\ \ }, \boxed{\ \ イ\ \ }, \boxed{\ \ ウ\ \ }, \boxed{\ \ エ\ \ })$
のただ一つである。
また、$m=28$のとき、①を満たす整数$a,b,c,d$の組の個数は
$\boxed{\ \ オ\ \ }$個である。
(2)$a$が奇数のとき、整数$n$を用いて$a=2n+1$と表すことができる。
このとき、$n(n+1)$は偶数であるから、次の条件が全ての奇数$a$で成り立つ
ような正の整数$h$のうち、最大のものは$h=\boxed{\ \ カ\ \ }$である。
条件:$a^2-1$は$h$の倍数である。
よって、$a$が奇数の時、$a^2$を$\boxed{\ \ カ\ \ }$で割った時の余りは$1$である。
また、$a$が偶数の時、$a^2$を$\boxed{\ \ カ\ \ }$で割った時の余りは、$0$または$4$の
いずれかである。
(3)(2)により、$a^2+b^2+c^2+d^2$が$\boxed{\ \ カ\ \ }$の倍数ならば、整数$a,b,c,d$
のうち、偶数であるものの個数は$\boxed{\ \ キ\ \ }$個である。
(4)(3)を用いることにより、$m$が$\boxed{\ \ カ\ \ }$の倍数であるとき、①を満たす整数
$a,b,c,d$が求めやすくなる。
例えば、$m=224$のとき、①を満たす整数$a,b,c,d$の組$(a,b,c,d)$は
$(\boxed{\ \ クケ\ \ }, \boxed{\ \ コ\ \ }, \boxed{\ \ サ\ \ }, \boxed{\ \ シ\ \ })$
のただ1つであることが分かる。
(5)7の倍数で896の約数である正の整数$m$のうち、①を満たす整数$a,b,c,d$
の組の個数が$\boxed{\ \ オ\ \ }$個であるものの個数は$\boxed{\ \ ス\ \ }$個であり、
そのうち最大のものは$m=\boxed{\ \ セソタ\ \ }$である。
2021共通テスト過去問
