恒等式・等式・不等式の証明
恒等式・等式・不等式の証明
福田のおもしろ数学580〜100より小さい正の整数を50個選んだとき互いに素な整数が存在する証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$100$より小さい互いに異なる正の整数を
$50$個選んだとき、その中に
互いに素な$2$つの整数が必ず
存在することを証明して下さい。
この動画を見る
$100$より小さい互いに異なる正の整数を
$50$個選んだとき、その中に
互いに素な$2$つの整数が必ず
存在することを証明して下さい。
福田のおもしろ数学578〜3乗根の和が0にはならない証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x,y,z$は相異なる実数とする。
$\sqrt[3]{x-y}+\sqrt[3]{y-z}+\sqrt[3]{z-x}\neq 0$
であることを証明して下さい。
この動画を見る
$x,y,z$は相異なる実数とする。
$\sqrt[3]{x-y}+\sqrt[3]{y-z}+\sqrt[3]{z-x}\neq 0$
であることを証明して下さい。
福田のおもしろ数学572〜対称式に関する等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x+y+z=0$のとき次を証明して下さい。
$\dfrac{x^2+y^2+z^2}{2} \times \dfrac{x^5+y^5+z^5}{5}=\dfrac{x^7+y^7+z^7}{7}$
この動画を見る
$x+y+z=0$のとき次を証明して下さい。
$\dfrac{x^2+y^2+z^2}{2} \times \dfrac{x^5+y^5+z^5}{5}=\dfrac{x^7+y^7+z^7}{7}$
福田のおもしろ数学566〜条件付き不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a\gt 0,b\gt 0,c\gt 0,abc=1$のとき、
$\dfrac{a}{ab+1}+\dfrac{b}{bc+1}+\dfrac{c}{ca+1} \geqq \dfrac{3}{2}$
を証明して下さい。
この動画を見る
$a\gt 0,b\gt 0,c\gt 0,abc=1$のとき、
$\dfrac{a}{ab+1}+\dfrac{b}{bc+1}+\dfrac{c}{ca+1} \geqq \dfrac{3}{2}$
を証明して下さい。
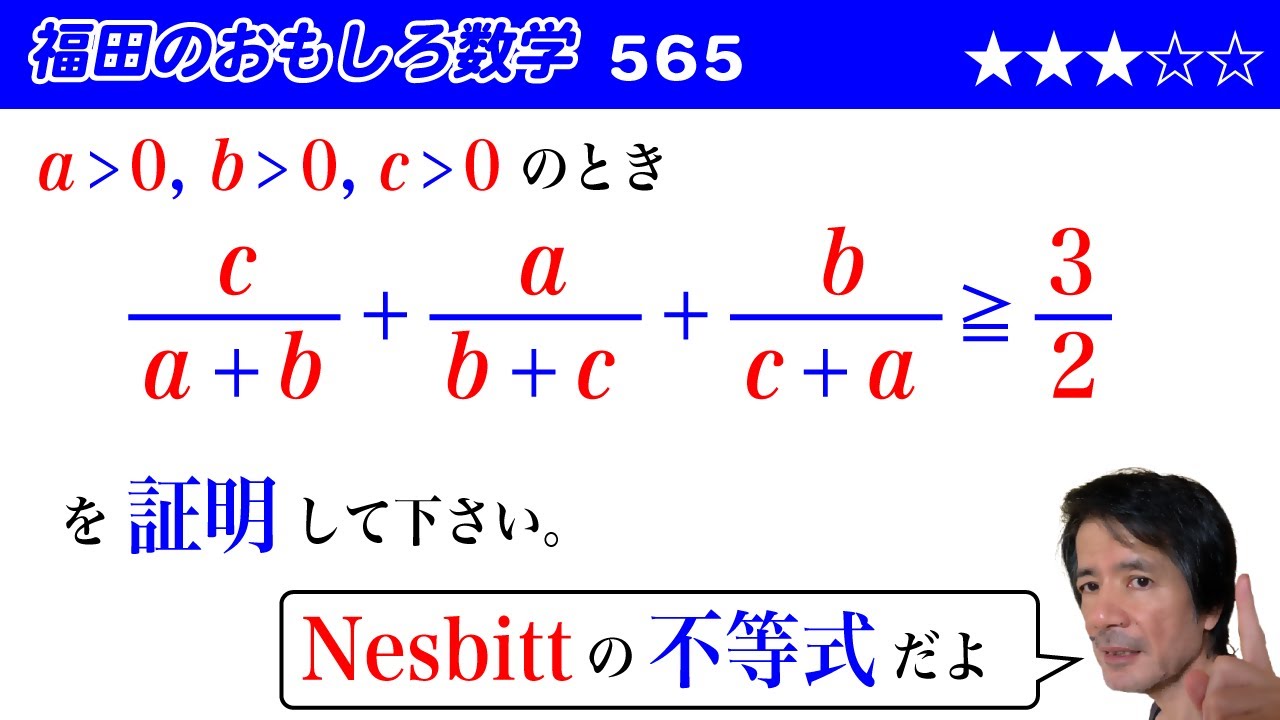
福田のおもしろ数学565〜Nesbittの不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a\gt 0,b\gt 0,c \gt 0$のとき
$\dfrac{c}{a+b}+\dfrac{a}{b+c}+\dfrac{b}{c+a} \geqq \dfrac{3}{2}$
を証明して下さい。
この動画を見る
$a\gt 0,b\gt 0,c \gt 0$のとき
$\dfrac{c}{a+b}+\dfrac{a}{b+c}+\dfrac{b}{c+a} \geqq \dfrac{3}{2}$
を証明して下さい。
福田のおもしろ数学562〜連立漸化式で定まる数列に関する証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数列#数列とその和（等差・等比・階差・Σ）#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
数列$\{a_k\},\{b_k\}$が$a_0=b_0=0$,
$a_{k+1}=b_k,b_{k+1}=\dfrac{a_k b_k+a_k+1}{b_k+1}$
で定義されている。
$a_{2024}+b_{2024}\geqq 88$
であることを証明して下さい。
この動画を見る
数列$\{a_k\},\{b_k\}$が$a_0=b_0=0$,
$a_{k+1}=b_k,b_{k+1}=\dfrac{a_k b_k+a_k+1}{b_k+1}$
で定義されている。
$a_{2024}+b_{2024}\geqq 88$
であることを証明して下さい。
福田のおもしろ数学561〜三角形の3つの内角を度数法で表したときの論証その2
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
三角形の$3$つの内角を度数表で測ったものを
$x,y,z$とする。次を証明して下さい。
$\dfrac{x}{y},\dfrac{y}{z},\dfrac{z}{x}$のうち、
ちょうど$1$つだけ有理数
$\Rightarrow x,y,z$はすべて無理数
この動画を見る
三角形の$3$つの内角を度数表で測ったものを
$x,y,z$とする。次を証明して下さい。
$\dfrac{x}{y},\dfrac{y}{z},\dfrac{z}{x}$のうち、
ちょうど$1$つだけ有理数
$\Rightarrow x,y,z$はすべて無理数
福田のおもしろ数学560〜三角形の3つの内角を度数法で表したときの論証
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
三角形の$3$つの内角を度数法で測ったものを
$x,y,z$とする。次を証明して下さい。
$\dfrac{x}{y},\dfrac{y}{z},\dfrac{z}{x}$がすべて有理数
$\Rightarrow x,y,z$はすべて有理数
この動画を見る
三角形の$3$つの内角を度数法で測ったものを
$x,y,z$とする。次を証明して下さい。
$\dfrac{x}{y},\dfrac{y}{z},\dfrac{z}{x}$がすべて有理数
$\Rightarrow x,y,z$はすべて有理数
福田のおもしろ数学557〜AがBを割り切ることを証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
自然数$a,b,c$が次の性質を満たしている。
$a^b$は$b^a$を割り切る。
$b^c$は$c^b$を割り切る。
このとき、$a^c$は$c^a$を割り切ることを
証明して下さい。
この動画を見る
自然数$a,b,c$が次の性質を満たしている。
$a^b$は$b^a$を割り切る。
$b^c$は$c^b$を割り切る。
このとき、$a^c$は$c^a$を割り切ることを
証明して下さい。
福田のおもしろ数学541〜条件付き不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x,y,z$は
$x+y+z \geqq xyz$
を満たす非負実数とするとき
$x^2+y^2+z^2 \geqq xyz$
を証明して下さい。
この動画を見る
$x,y,z$は
$x+y+z \geqq xyz$
を満たす非負実数とするとき
$x^2+y^2+z^2 \geqq xyz$
を証明して下さい。
福田のおもしろ数学534〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b$が正の実数のとき
$\sqrt[3]{\dfrac{a}{b}}+\sqrt[3]{{b}{a}}\leqq \sqrt[3]{2(a+b)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)}$
を証明して下さい。
この動画を見る
$a,b$が正の実数のとき
$\sqrt[3]{\dfrac{a}{b}}+\sqrt[3]{{b}{a}}\leqq \sqrt[3]{2(a+b)\left(\dfrac{1}{a}+\dfrac{1}{b}\right)}$
を証明して下さい。
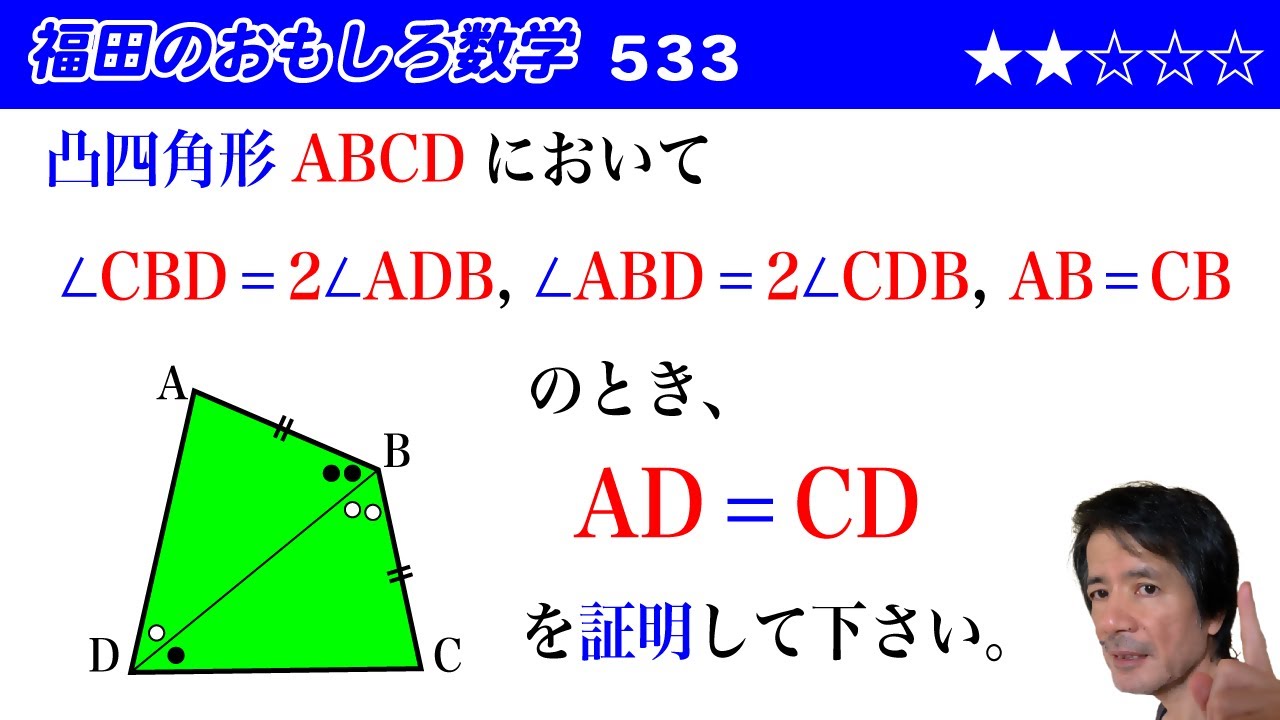
福田のおもしろ数学533〜凸四角形の性質に関する証明
単元：
#数A#数Ⅱ#図形の性質#式と証明#周角と円に内接する四角形・円と接線・接弦定理#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
凸四角形$ABCD$において
$\angle CBD = 2\angle ADB,\angle ABD = 2\angle CDB,AB=CB$
のとき、
$AD=CD$を証明して下さい。
図は動画内参照
この動画を見る
凸四角形$ABCD$において
$\angle CBD = 2\angle ADB,\angle ABD = 2\angle CDB,AB=CB$
のとき、
$AD=CD$を証明して下さい。
図は動画内参照
福田の数学〜大阪大学2025理系第4問〜不等式の証明と関数の極限
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
次の問いに答えよ。
(1)$t\gt 0$のとき
$-\dfrac{1}{t}\lt \displaystyle \int_{t}^{2t} \dfrac{\sin x}{x^2}dx \lt \dfrac{1}{t}$
が成り立つことを示せ。
(2)$\displaystyle \lim_{t\to\infty}\displaystyle \dfrac{\cos x}{x}dx=0$を示せ。
(3)$f(x)=\sin\left(\dfrac{3x}{2}\right)\sin\left(\dfrac{x}{2}\right)$おく。
$\displaystyle \lim_{t\to\infty}\displaystyle \int_{1}^{t} \dfrac{f(x)}{x}dx=\dfrac{1}{2} \displaystyle \int_{1}^{2} \dfrac{\cos x}{x} dx$
を示せ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{4}$
次の問いに答えよ。
(1)$t\gt 0$のとき
$-\dfrac{1}{t}\lt \displaystyle \int_{t}^{2t} \dfrac{\sin x}{x^2}dx \lt \dfrac{1}{t}$
が成り立つことを示せ。
(2)$\displaystyle \lim_{t\to\infty}\displaystyle \dfrac{\cos x}{x}dx=0$を示せ。
(3)$f(x)=\sin\left(\dfrac{3x}{2}\right)\sin\left(\dfrac{x}{2}\right)$おく。
$\displaystyle \lim_{t\to\infty}\displaystyle \int_{1}^{t} \dfrac{f(x)}{x}dx=\dfrac{1}{2} \displaystyle \int_{1}^{2} \dfrac{\cos x}{x} dx$
を示せ。
$2025$年大阪大学理系過去問題
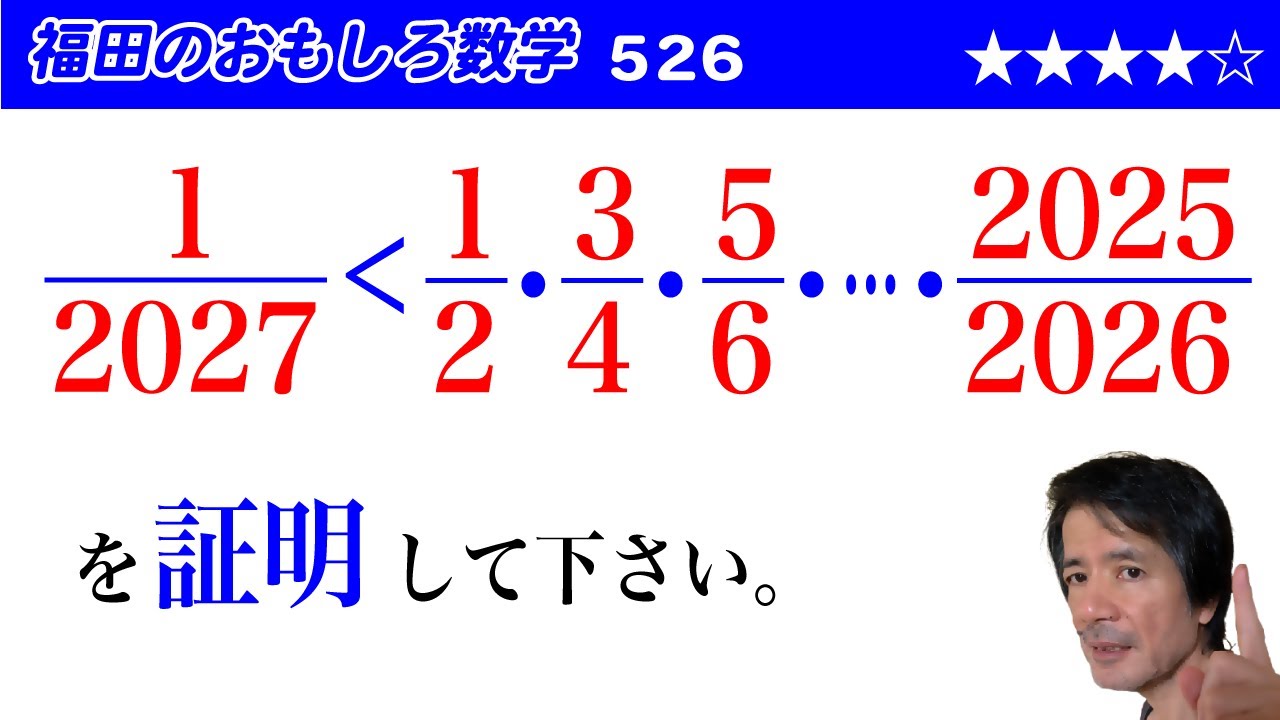
福田のおもしろ数学526〜数値評価
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\dfrac{1}{2027} \lt \dfrac{1}{2}･\dfrac{3}{4}･\dfrac{5}{6}･\cdots ･\dfrac{2025}{2026}$
を証明して下さい。
この動画を見る
$\dfrac{1}{2027} \lt \dfrac{1}{2}･\dfrac{3}{4}･\dfrac{5}{6}･\cdots ･\dfrac{2025}{2026}$
を証明して下さい。
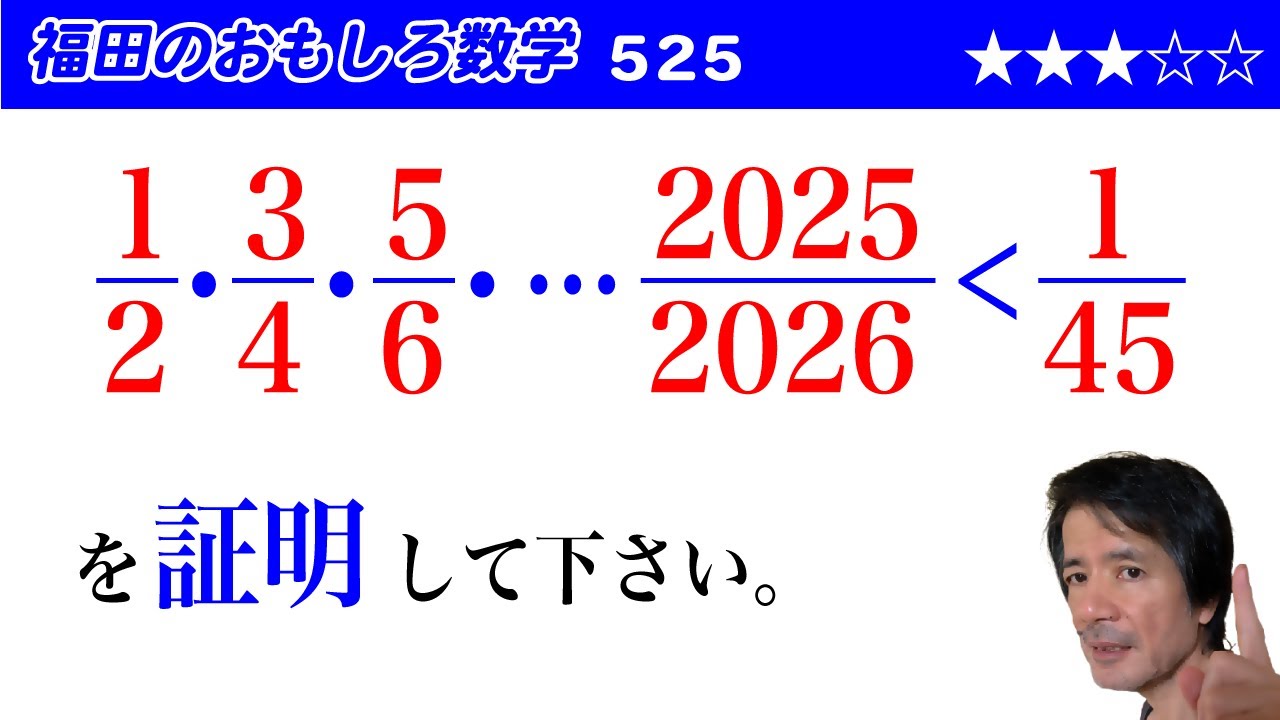
福田のおもしろ数学525〜数値評価
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\dfrac{1}{2}･\dfrac{3}{4}･\dfrac{5}{6}･\cdots \dfrac{2025}{2026}\lt \dfrac{1}{45}$
を証明して下さい。
この動画を見る
$\dfrac{1}{2}･\dfrac{3}{4}･\dfrac{5}{6}･\cdots \dfrac{2025}{2026}\lt \dfrac{1}{45}$
を証明して下さい。
福田のおもしろ数学513〜3つの数のうち少なくとも2つは等しいことの証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x,y,z$は正の実数であり、
任意の自然数$n$について$x^n,y^n,z^n$が
三角形の$3$辺をなすとき、
$x,y,z$の少なくとも$2$つは等しくことを
証明して下さい。
この動画を見る
$x,y,z$は正の実数であり、
任意の自然数$n$について$x^n,y^n,z^n$が
三角形の$3$辺をなすとき、
$x,y,z$の少なくとも$2$つは等しくことを
証明して下さい。
福田のおもしろ数学510〜(n+1/n)のn乗がeより小であることの証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$n$を正の整数とするとき
$\left(1+\dfrac{1}{n}\right)^n \lt e$
を証明して下さい。
$e$は自然対数の底とする。
この動画を見る
$n$を正の整数とするとき
$\left(1+\dfrac{1}{n}\right)^n \lt e$
を証明して下さい。
$e$は自然対数の底とする。
福田のおもしろ数学496〜少なくとも1つは−1より大きくないことの証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
実数$a,b,c,d$が次の式を満たしている。
$a+b+c+d=-2$
$ab+ac+ad+bc+bd+cd=0$
このとき、$a,b,c,d$の少なくとも$1$つは
$-1$より大きくないことを証明して下さい。
この動画を見る
実数$a,b,c,d$が次の式を満たしている。
$a+b+c+d=-2$
$ab+ac+ad+bc+bd+cd=0$
このとき、$a,b,c,d$の少なくとも$1$つは
$-1$より大きくないことを証明して下さい。
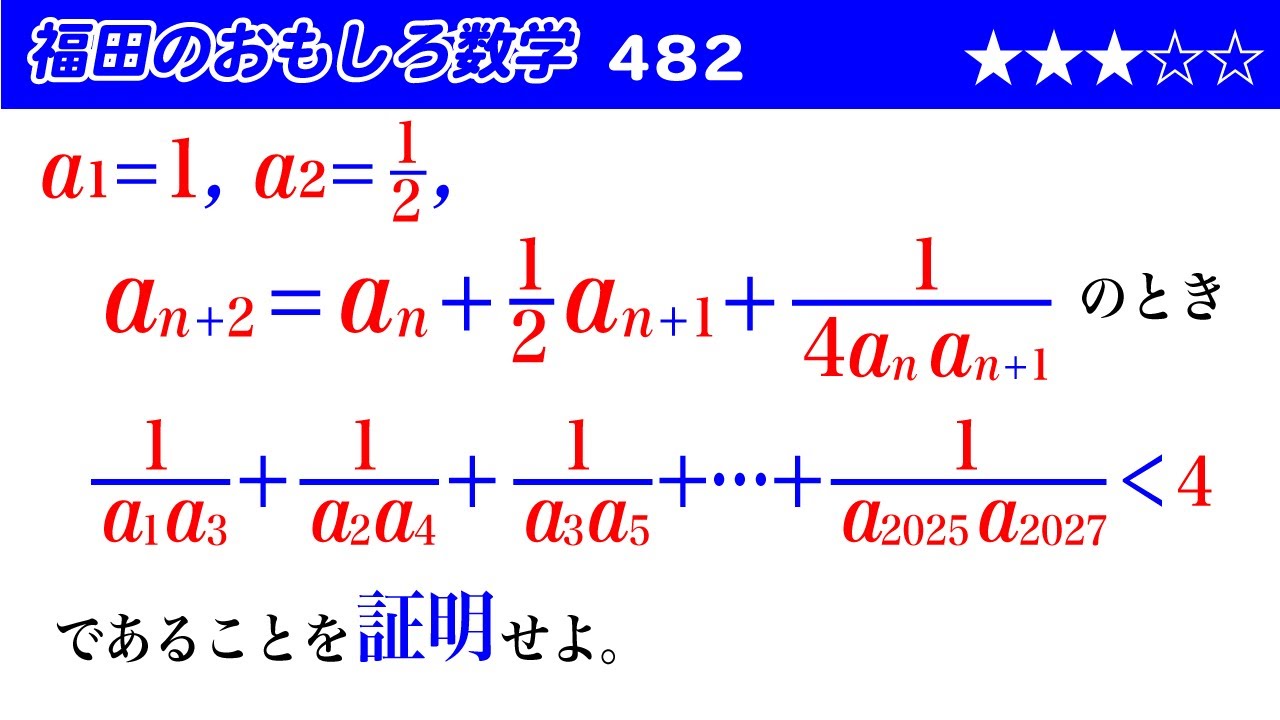
福田のおもしろ数学482〜漸化式で定まる数列に関する不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数列#漸化式#数学(高校生)#数B
指導講師：
福田次郎
問題文全文(内容文)：
$a_1=1,a_2=\dfrac{1}{2},$
$a_{n+2}=a_n+\dfrac{1}{2}a_{n+1}+\dfrac{1}{4a_na_{n+1}}$のとき、
$\dfrac{1}{a_1a_3}+\dfrac{1}{a_2a_4}+\dfrac{1}{a_3a_5}+\cdots +\dfrac{1}{a_{2025}a_{2027}}\lt 4$
であることを証明せよ。
この動画を見る
$a_1=1,a_2=\dfrac{1}{2},$
$a_{n+2}=a_n+\dfrac{1}{2}a_{n+1}+\dfrac{1}{4a_na_{n+1}}$のとき、
$\dfrac{1}{a_1a_3}+\dfrac{1}{a_2a_4}+\dfrac{1}{a_3a_5}+\cdots +\dfrac{1}{a_{2025}a_{2027}}\lt 4$
であることを証明せよ。
福田のおもしろ数学480〜三角関数の不等式の証明とイェンゼンの不等式
単元：
#数Ⅱ#式と証明#三角関数#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$0\leqq \alpha,\beta \gamma \lt 90°$
$\sin \alpha +\sin \beta +\sin \gamma =1$のとき
$\tan^2\alpha+\tan^2\beta+\tan^2\gamma \geqq\dfrac{3}{8}$
を証明して下さい。
この動画を見る
$0\leqq \alpha,\beta \gamma \lt 90°$
$\sin \alpha +\sin \beta +\sin \gamma =1$のとき
$\tan^2\alpha+\tan^2\beta+\tan^2\gamma \geqq\dfrac{3}{8}$
を証明して下さい。
福田のおもしろ数学478〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b,c$を正の数とする。
$a^2+b^2+c^2=3$のとき
$\dfrac{1}{1+2ab}+\dfrac{1}{1+2bc}+\dfrac{1}{1+2ca} \geqq 1$
を証明して下さい。
この動画を見る
$a,b,c$を正の数とする。
$a^2+b^2+c^2=3$のとき
$\dfrac{1}{1+2ab}+\dfrac{1}{1+2bc}+\dfrac{1}{1+2ca} \geqq 1$
を証明して下さい。
福田のおもしろ数学477〜イェンゼンの不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
イェンゼンの不等式
$f(x)$は凸関数、$\lambda i \geqq 0, \sum \lambda i=1$のとき、
$\lambda 1 f(x 1)+\lambda 2 f(x2) \geqq f(\lambda2x2)$
$\lambda 1 f(x 1)+\lambda 2 f(x2)+\lambda3f(x3) \geqq f(\lambda1x1+\lambda2x2+\lambda3x3)$
な成り立つ。証明して下さい。
この動画を見る
イェンゼンの不等式
$f(x)$は凸関数、$\lambda i \geqq 0, \sum \lambda i=1$のとき、
$\lambda 1 f(x 1)+\lambda 2 f(x2) \geqq f(\lambda2x2)$
$\lambda 1 f(x 1)+\lambda 2 f(x2)+\lambda3f(x3) \geqq f(\lambda1x1+\lambda2x2+\lambda3x3)$
な成り立つ。証明して下さい。
福田のおもしろ数学470〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$t\geqq \dfrac{1}{2},n$は自然数のとき
$t^{2n} \geqq (t-1)^{2n} + (2t-1)^{2n}$
を証明して下さい。
この動画を見る
$t\geqq \dfrac{1}{2},n$は自然数のとき
$t^{2n} \geqq (t-1)^{2n} + (2t-1)^{2n}$
を証明して下さい。
福田のおもしろ数学467〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b,c$を正の数とするとき、
不等式
$\sqrt{a^2-ab+b^2}+\sqrt{b^2-bc+c^2} \geqq \sqrt{a^2+ac+c^2}$
を証明して下さい。
この動画を見る
$a,b,c$を正の数とするとき、
不等式
$\sqrt{a^2-ab+b^2}+\sqrt{b^2-bc+c^2} \geqq \sqrt{a^2+ac+c^2}$
を証明して下さい。
福田のおもしろ数学464〜素数でないことを証明する
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
正の整数$a,b,c,d$が
$ab=cd$を満たすとする。
このとき、
$a+b+c+d$が
素数でないことを証明せよ。
この動画を見る
正の整数$a,b,c,d$が
$ab=cd$を満たすとする。
このとき、
$a+b+c+d$が
素数でないことを証明せよ。
福田のおもしろ数学459〜不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
正の数$a,b,c,d$が
$\dfrac{a+c}{a+b}+\dfrac{b+d}{b+c}+\dfrac{c+a}{c+d}+\dfrac{d+b}{d+a}\geqq 4$
を満たすことを証明して下さい。
この動画を見る
正の数$a,b,c,d$が
$\dfrac{a+c}{a+b}+\dfrac{b+d}{b+c}+\dfrac{c+a}{c+d}+\dfrac{d+b}{d+a}\geqq 4$
を満たすことを証明して下さい。
相加相乗平均のイメージ
福田のおもしろ数学455〜二重のシグマがかかった不等式の証明
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
任意の実数$a_1,a_2,\cdots a_n$に対して
$\displaystyle \sum_{j=1}^n \left(\displaystyle \sum_{i=1}^n \dfrac{a_ia_j}{i+j-1}\right)\geqq 0$
を証明して下さい。
この動画を見る
任意の実数$a_1,a_2,\cdots a_n$に対して
$\displaystyle \sum_{j=1}^n \left(\displaystyle \sum_{i=1}^n \dfrac{a_ia_j}{i+j-1}\right)\geqq 0$
を証明して下さい。
福田のおもしろ数学454〜積分に関するシュワルツの不等式の証明と等号成立条件
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$p\leqq x \leqq q$で定義された連続関数$f(x),ｇ(x)$に対して
$\left(\displaystyle \int_{p}^{q} f(x)^2 dx\right)\left(\displaystyle \int_{p}^{q}g(x)^2 dx \right) \geqq \left(\displaystyle \int_{p}^{q} f(x)g(x)dx\right)^2$
を証明して下さい。
また等号成立条件も調べて下さい。
この動画を見る
$p\leqq x \leqq q$で定義された連続関数$f(x),ｇ(x)$に対して
$\left(\displaystyle \int_{p}^{q} f(x)^2 dx\right)\left(\displaystyle \int_{p}^{q}g(x)^2 dx \right) \geqq \left(\displaystyle \int_{p}^{q} f(x)g(x)dx\right)^2$
を証明して下さい。
また等号成立条件も調べて下さい。
福田のおもしろ数学443〜不等式の証明と等号成立条件
単元：
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b,c$は正の実数とする。
$\sqrt[3]{abc}+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c} \geqq 2\sqrt3$
を証明し、等号成立条件を調べてください。
この動画を見る
$a,b,c$は正の実数とする。
$\sqrt[3]{abc}+\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c} \geqq 2\sqrt3$
を証明し、等号成立条件を調べてください。