 図形と方程式
図形と方程式
 図形と方程式
図形と方程式
福田のおもしろ数学115〜円外の点から引いた2本の接線の接点を結んでできる直線の方程式
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
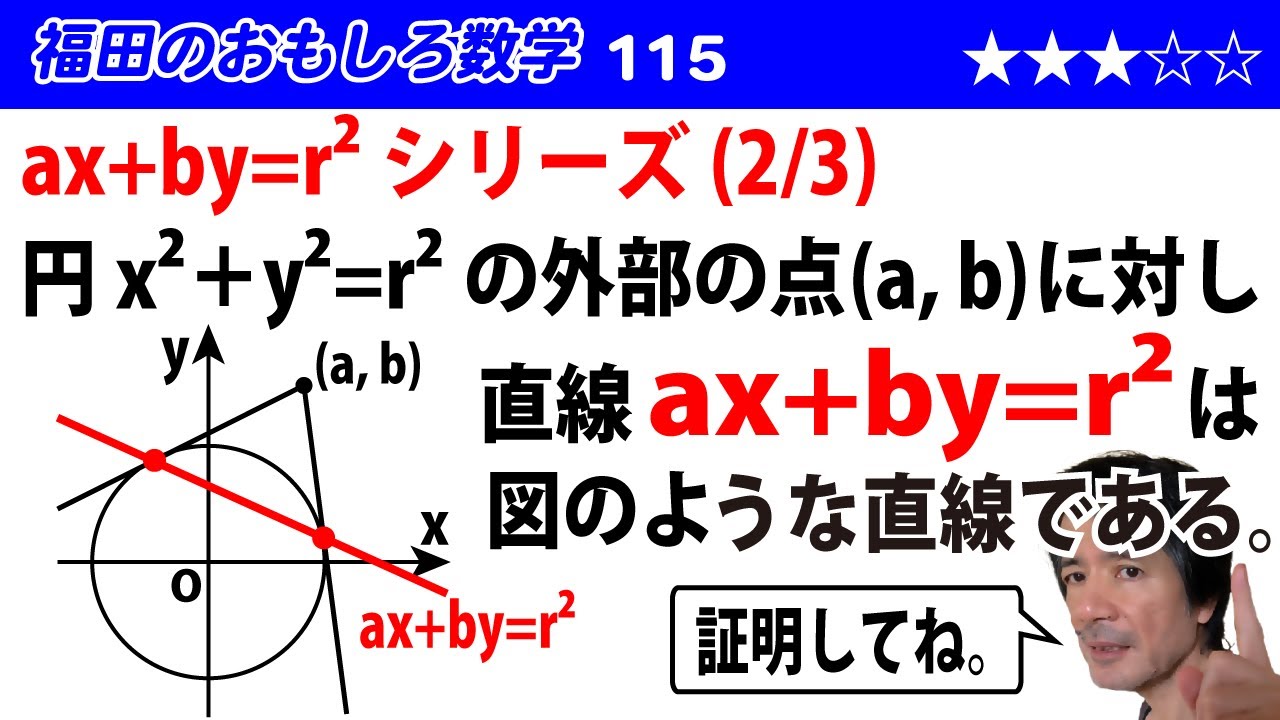
円$x^2$+$y^2$=$r^2$ 上に円外の点($a$,$b$)から2本の接線を引く。このとき2接点P,Qを結ぶ直線の方程式は$ax$+$by$=$r^2$ であることを証明せよ。
この動画を見る
円$x^2$+$y^2$=$r^2$ 上に円外の点($a$,$b$)から2本の接線を引く。このとき2接点P,Qを結ぶ直線の方程式は$ax$+$by$=$r^2$ であることを証明せよ。
福田のおもしろ数学114〜円の接線の公式の証明

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
円$x^2$+$y^2$=$r^2$ 上の点($a$,$b$)における接線の方程式は
$ax$+$by$=$r^2$ であることを証明せよ。
この動画を見る
円$x^2$+$y^2$=$r^2$ 上の点($a$,$b$)における接線の方程式は
$ax$+$by$=$r^2$ であることを証明せよ。
福田のおもしろ数学112〜多変数の式の最大最小

単元:
#数Ⅱ#図形と方程式#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数$x$,$y$,$z$が0≦$x$≦1, 0≦$y$≦1, 2≦$z$≦3 を満たして変わるとき、$\displaystyle\frac{z-y}{z-x}$ の最大値、最小値を求めよ。
この動画を見る
実数$x$,$y$,$z$が0≦$x$≦1, 0≦$y$≦1, 2≦$z$≦3 を満たして変わるとき、$\displaystyle\frac{z-y}{z-x}$ の最大値、最小値を求めよ。
福田の数学〜慶應義塾大学2024年看護医療学部第1問(4)〜円と接線の長さ

単元:
#数Ⅱ#図形と方程式#円と方程式
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (4)円$x^2$+$y^2$-$4x$+$10y$+11=0 を$C$とするとき、円$C$の中心は$\boxed{\ \ オ\ \ }$であり、半径は$\boxed{\ \ カ\ \ }$である。また、この円$C$には点P(3,2)から2本の接線を引くことができるが、その接点の1つをAとする。このとき、線分APの長さはAP=$\boxed{\ \ キ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (4)円$x^2$+$y^2$-$4x$+$10y$+11=0 を$C$とするとき、円$C$の中心は$\boxed{\ \ オ\ \ }$であり、半径は$\boxed{\ \ カ\ \ }$である。また、この円$C$には点P(3,2)から2本の接線を引くことができるが、その接点の1つをAとする。このとき、線分APの長さはAP=$\boxed{\ \ キ\ \ }$である。
福田の数学〜慶應義塾大学2024年薬学部第2問〜放物線と円が接する条件と面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 原点をOとする$xy$平面上に円$x^2$+$y^2$-$12y$=0 があり、円の中心をPとする。
円周上に動点Qがあり、半直線POを始線とする動径PQの回転角を$\theta$とする。
ただし、$\theta$は$-\frac{\pi}{2}$<$\theta$<$\frac{\pi}{2}$を満たす実数とする。
(1)直線PQを表す方程式は、$\theta$=0 のとき$\boxed{\ \ ソ\ \ }$であり、$\theta$≠0 のとき$\boxed{\ \ タ\ \ }$である。
(2)点Qを通る放物線$y$=$ax^2$+$b$ をおく。点Qにおける放物線の接線は、点Qにおける円の接線と一致する。ただし、$a$, $b$は実数であり、$a$は$a$>0 を満たす。
(i)$\theta$≠0 のとき$a$と$b$を$\theta$で表すと、$a$=$\boxed{\ \ チ\ \ }$, $b$=$\boxed{\ \ ツ\ \ }$ である。
(ii)$\theta$=$-\frac{\pi}{3}$ のとき、直線PQと放物線で囲まれる部分の面積は$\boxed{\ \ テ\ \ }$である。
この動画を見る
$\Large\boxed{2}$ 原点をOとする$xy$平面上に円$x^2$+$y^2$-$12y$=0 があり、円の中心をPとする。
円周上に動点Qがあり、半直線POを始線とする動径PQの回転角を$\theta$とする。
ただし、$\theta$は$-\frac{\pi}{2}$<$\theta$<$\frac{\pi}{2}$を満たす実数とする。
(1)直線PQを表す方程式は、$\theta$=0 のとき$\boxed{\ \ ソ\ \ }$であり、$\theta$≠0 のとき$\boxed{\ \ タ\ \ }$である。
(2)点Qを通る放物線$y$=$ax^2$+$b$ をおく。点Qにおける放物線の接線は、点Qにおける円の接線と一致する。ただし、$a$, $b$は実数であり、$a$は$a$>0 を満たす。
(i)$\theta$≠0 のとき$a$と$b$を$\theta$で表すと、$a$=$\boxed{\ \ チ\ \ }$, $b$=$\boxed{\ \ ツ\ \ }$ である。
(ii)$\theta$=$-\frac{\pi}{3}$ のとき、直線PQと放物線で囲まれる部分の面積は$\boxed{\ \ テ\ \ }$である。
福田のおもしろ数学091〜定積分と軌跡

単元:
#数Ⅱ#図形と方程式#軌跡と領域#積分とその応用#不定積分#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle\int_x^y(|t|-1)dt$=0 を満たす点($x$,$y$)の軌跡を図示せよ。
この動画を見る
$\displaystyle\int_x^y(|t|-1)dt$=0 を満たす点($x$,$y$)の軌跡を図示せよ。
福田のおもしろ数学090〜絶対値の付いた方程式が表す点の軌跡

単元:
#数Ⅰ#数Ⅱ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
|$x^2$+$y^2$-1|+|$x^2$-$y^2$|=|$2x^2$-1| を満たす点($x$,$y$)の軌跡を図示せよ。
この動画を見る
|$x^2$+$y^2$-1|+|$x^2$-$y^2$|=|$2x^2$-1| を満たす点($x$,$y$)の軌跡を図示せよ。
福田のおもしろ数学087〜絶対値の付いた2変数の方程式の解

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$|x-1|$+$|x-2|$=$|y-1|$+$|y-2|$ を満たす点($x$,$y$)の集合を図示せよ。
この動画を見る
$|x-1|$+$|x-2|$=$|y-1|$+$|y-2|$ を満たす点($x$,$y$)の集合を図示せよ。
福田のおもしろ数学077〜3通りの解法を考えよう〜4変数の式の最大値

単元:
#数Ⅱ#式と証明#平面上のベクトル#図形と方程式#三角関数#恒等式・等式・不等式の証明#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$a^2$+$b^2$=9, $c^2$+$d^2$=16 のとき$ab$+$cd$ の最大値を求めよ。
この動画を見る
$a^2$+$b^2$=9, $c^2$+$d^2$=16 のとき$ab$+$cd$ の最大値を求めよ。
円と放物線 2024明大中野
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
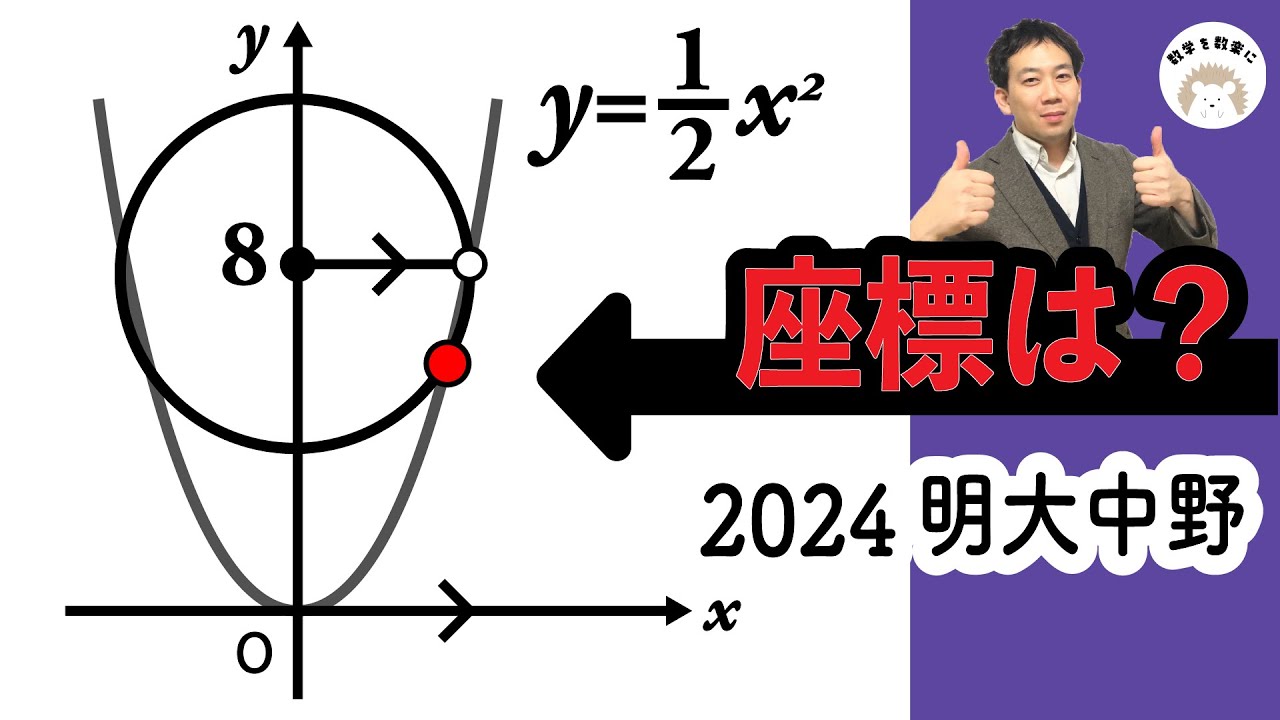
$y=\frac{1}{2}x^2$
座標は?
*図は動画内参照
2024明治大学付属中野高等学校
この動画を見る
$y=\frac{1}{2}x^2$
座標は?
*図は動画内参照
2024明治大学付属中野高等学校
福田のおもしろ数学056〜折り返し問題〜半円を折り返す
単元:
#数A#数Ⅱ#図形の性質#方べきの定理と2つの円の関係#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
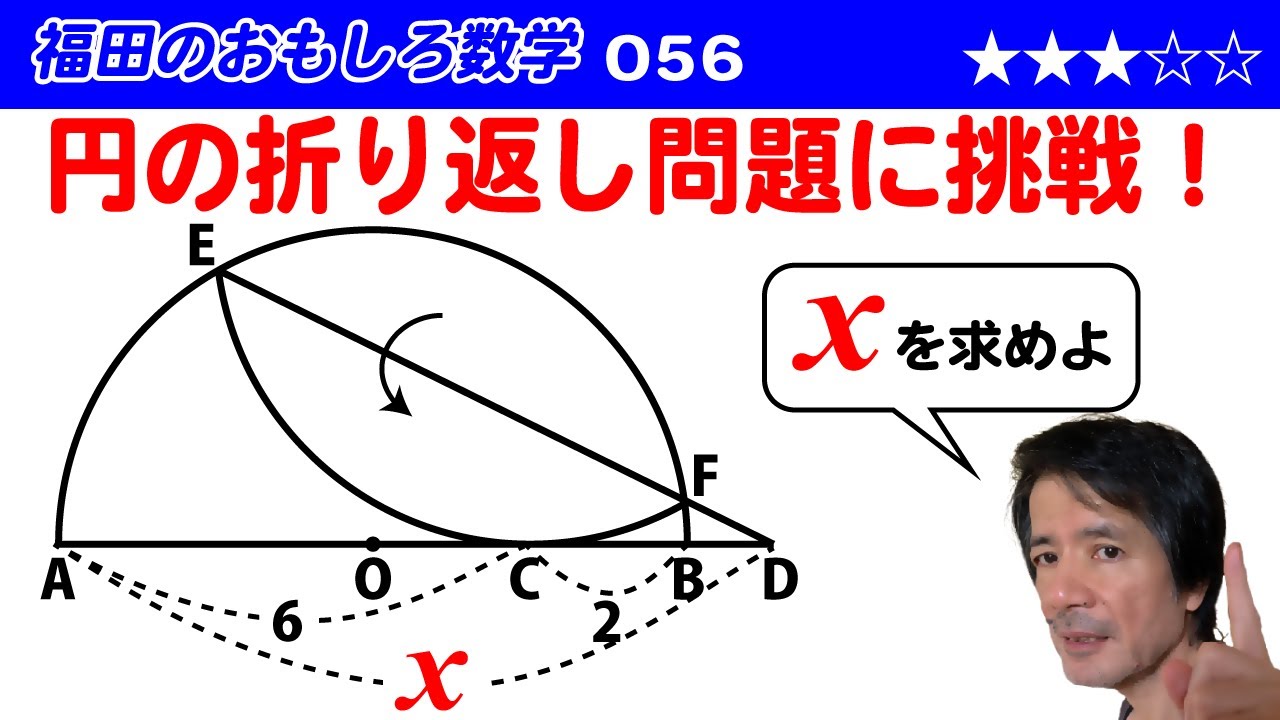
図は半円 O を点 C で接するように折り返したもので EF はその折り目である。EF と AB の交点を D とする。 $AC = 6 , BC = 2$ のとき、 AD の長さを求めよ。
※図は動画内参照
この動画を見る
図は半円 O を点 C で接するように折り返したもので EF はその折り目である。EF と AB の交点を D とする。 $AC = 6 , BC = 2$ のとき、 AD の長さを求めよ。
※図は動画内参照
福田の数学〜東京大学2018年理系第3問〜軌跡と領域そして極限

単元:
#大学入試過去問(数学)#平面上のベクトル#図形と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#関数と極限#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
放物線$y=x^2$のうち$-1 \leqq x \leqq 1$を満たす部分をCとする。座標平面上の原点Oと点A(1,0)を考える。K>0を実数とする。点PがCの上を動き、天Qが線分OA上を動くとき$\overrightarrow{ OR }=\displaystyle \frac{1}{k}\overrightarrow{ OP }+k\overrightarrow{ OQ }$を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle \lim_{ k \to +0 } S(k) ,\displaystyle \lim_{ k \to \infty }S(k)$を求めよ。
2018東京大学理系過去問
この動画を見る
放物線$y=x^2$のうち$-1 \leqq x \leqq 1$を満たす部分をCとする。座標平面上の原点Oと点A(1,0)を考える。K>0を実数とする。点PがCの上を動き、天Qが線分OA上を動くとき$\overrightarrow{ OR }=\displaystyle \frac{1}{k}\overrightarrow{ OP }+k\overrightarrow{ OQ }$を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle \lim_{ k \to +0 } S(k) ,\displaystyle \lim_{ k \to \infty }S(k)$を求めよ。
2018東京大学理系過去問
計算不要! 反比例と面積 2024早稲田佐賀
単元:
#数Ⅱ#図形と方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
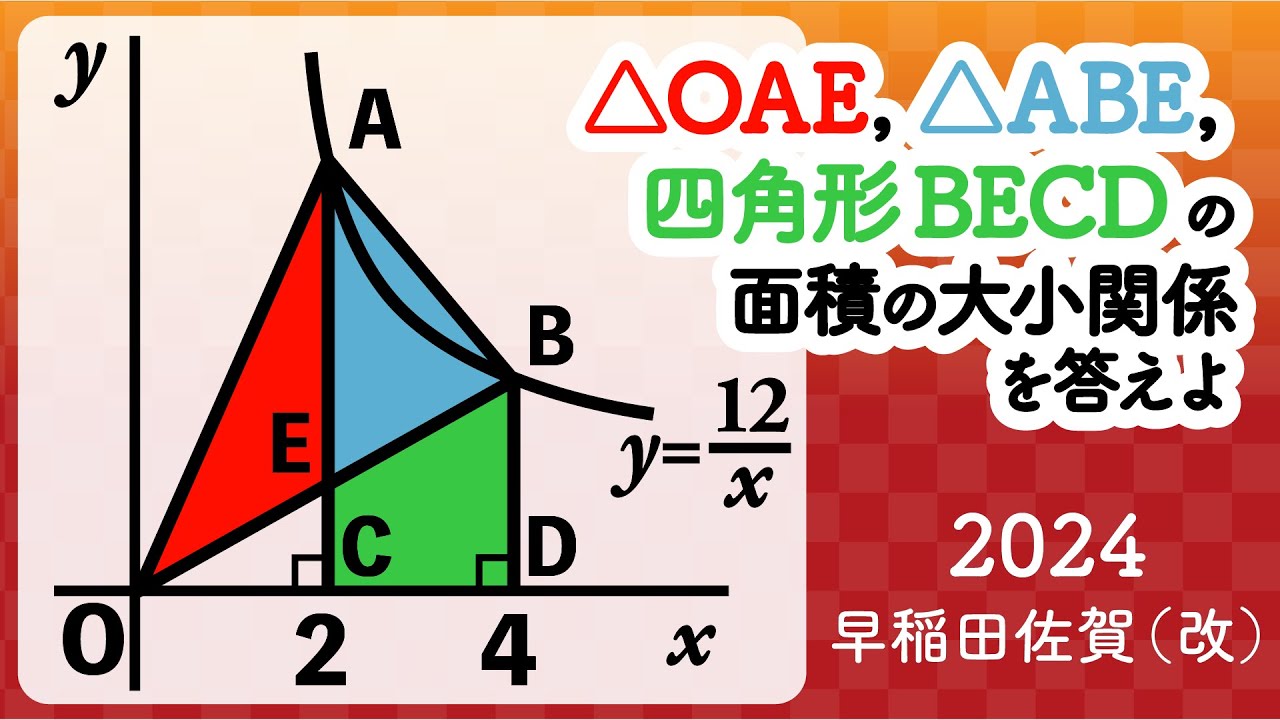
△OAE,△ABE,四角形BECDの面積の大小関係を答えよ
*図は動画内参照
2024早稲田佐賀高等学校(改)
この動画を見る
△OAE,△ABE,四角形BECDの面積の大小関係を答えよ
*図は動画内参照
2024早稲田佐賀高等学校(改)
福田の数学〜不等式の図形的な意味に気づけるか〜東京大学2018年文系第1問(2)〜領域内を動く点が不等式を満たす条件

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標平面上に放物線 C を$y=x^2-3x+4$で定め、領域Dを$y \geqq x^2-3x+4$で定める。原点を通る 2 直線l, m は C に接する。
( 2 )次の条件を満たす点 P(p,q)の動きうる範囲を求め、座標平面上に図示せよ。
条件:領域Dのすべての点は(x,y)に対し、不等式$px+qy\leqq 0$が成り立つ。
2018東京大学文過去問
この動画を見る
座標平面上に放物線 C を$y=x^2-3x+4$で定め、領域Dを$y \geqq x^2-3x+4$で定める。原点を通る 2 直線l, m は C に接する。
( 2 )次の条件を満たす点 P(p,q)の動きうる範囲を求め、座標平面上に図示せよ。
条件:領域Dのすべての点は(x,y)に対し、不等式$px+qy\leqq 0$が成り立つ。
2018東京大学文過去問
福田の数学〜複数の絶対値に対応できるか〜東京大学2018年文系第1問(1)〜絶対値を含む関数の最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面上に放物線 C を$y=x^2-3x+4$ で定め、領域Dを$y \geqq x^2-3x+4$で定める。原点を通る 2 直線l, m は C に接する。
(1) 放物線 C 上を動く点 A と直線l, m の距離をそれぞれL,M とする。$\sqrt{ \mathstrut L } + \sqrt{ \mathstrut M }$が最小値をとるときの点 A の座標を求めよ。
2018東京大学文過去問
この動画を見る
座標平面上に放物線 C を$y=x^2-3x+4$ で定め、領域Dを$y \geqq x^2-3x+4$で定める。原点を通る 2 直線l, m は C に接する。
(1) 放物線 C 上を動く点 A と直線l, m の距離をそれぞれL,M とする。$\sqrt{ \mathstrut L } + \sqrt{ \mathstrut M }$が最小値をとるときの点 A の座標を求めよ。
2018東京大学文過去問
難関高校受験生必見!!放物線と比

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=x^2$ $\quad$ $y=\frac{1}{4}x^2$
a:b=?
*図は動画内参照
この動画を見る
$y=x^2$ $\quad$ $y=\frac{1}{4}x^2$
a:b=?
*図は動画内参照
福田の数学〜最大値を求める問題の3連発!〜北里大学2023年医学部第1問(2)〜領域における最大値

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
点$(x,y)$は$x^2+(y-1)^2 \leqq 1$の表す領域を動くとする。
$\displaystyle \frac{x-y-1}{x+y-3}$の最大値は?
$x(y-1)$の最大値は?
$\displaystyle \frac{x^2-6x+9}{y^2-2y-3}$の最大値は?
2023北里大学医過去問
この動画を見る
点$(x,y)$は$x^2+(y-1)^2 \leqq 1$の表す領域を動くとする。
$\displaystyle \frac{x-y-1}{x+y-3}$の最大値は?
$x(y-1)$の最大値は?
$\displaystyle \frac{x^2-6x+9}{y^2-2y-3}$の最大値は?
2023北里大学医過去問
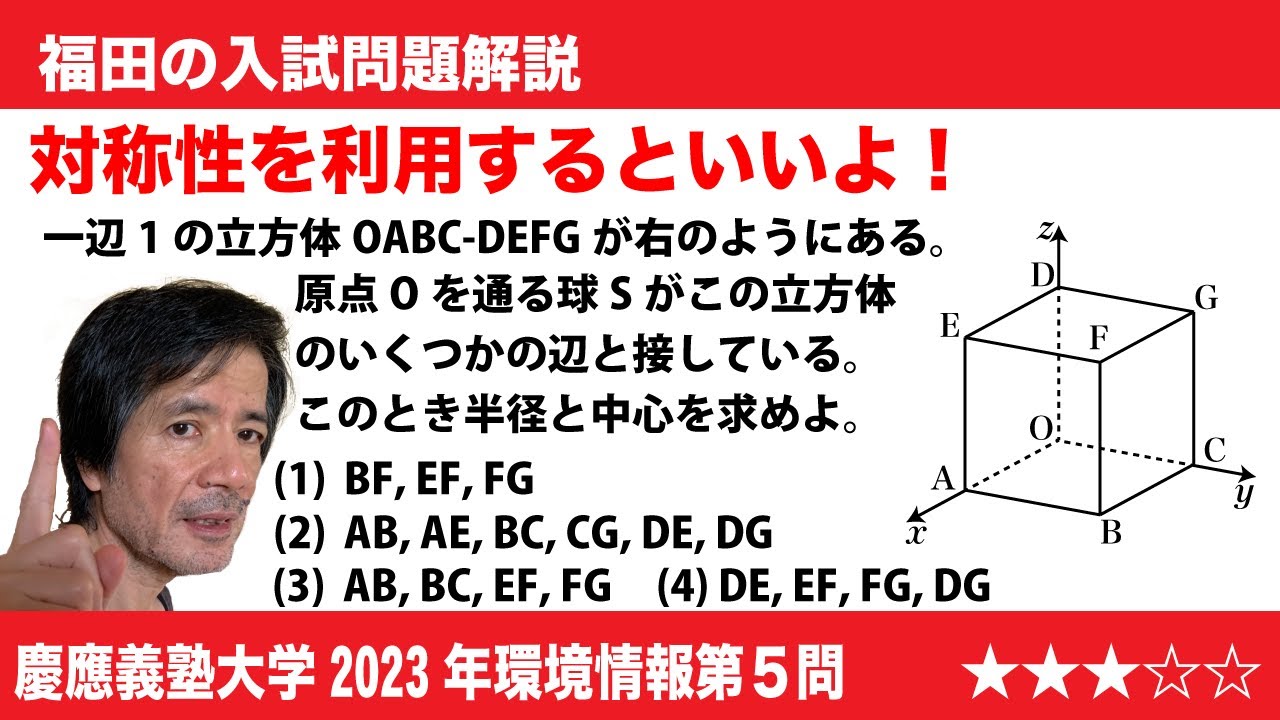
福田の数学〜対称性を意識しよう〜慶應義塾大学2023年環境情報学部第5問〜球が立方体の辺と接する条件
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
xy空間において、O(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,1),E(1,0,1),F(1,1,1),G(0,1,1)を頂点とする立方体 OABC-DEFG が存在する。いま、原点を通る球 S が、立方体 OABC-DEFG のいくつかの辺と接している。以下のそれぞれの場合について、球 S の半径と中心の座標を求めなさい。
※図は動画内
(1)3 つの辺 BF,EF,FG と接する場合
( 2 ) 6 つの辺 AB , AE, BC, CG, DE, DG と接する場合
( 3 ) 4 つの辺 AB, BC, EF, FG と接する場合
(4)4 つの辺 DE, EF, FG, DG と接する場合
慶應義塾大学環境情報学部過去問
この動画を見る
xy空間において、O(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),D(0,0,1),E(1,0,1),F(1,1,1),G(0,1,1)を頂点とする立方体 OABC-DEFG が存在する。いま、原点を通る球 S が、立方体 OABC-DEFG のいくつかの辺と接している。以下のそれぞれの場合について、球 S の半径と中心の座標を求めなさい。
※図は動画内
(1)3 つの辺 BF,EF,FG と接する場合
( 2 ) 6 つの辺 AB , AE, BC, CG, DE, DG と接する場合
( 3 ) 4 つの辺 AB, BC, EF, FG と接する場合
(4)4 つの辺 DE, EF, FG, DG と接する場合
慶應義塾大学環境情報学部過去問
高校数学:数学検定準1級1次:問題1,2 :対数不等式、2直線間の距離

単元:
#数Ⅱ#図形と方程式#指数関数と対数関数#点と直線#対数関数#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題1
次の不等式を解きなさい。
$\log_{ \frac{1}{2}} 2x >\log_{ \frac{1}{2}} x^2-2x+3$
問題2
xy平面上の2直線$3x+4y-20=0$と$3x+4y+50=0$の間の距離を求めなさい。
この動画を見る
問題1
次の不等式を解きなさい。
$\log_{ \frac{1}{2}} 2x >\log_{ \frac{1}{2}} x^2-2x+3$
問題2
xy平面上の2直線$3x+4y-20=0$と$3x+4y+50=0$の間の距離を求めなさい。
福田の数学〜円と直線が共有点をもつ条件は〜慶應義塾大学2023年商学部第1問(2)〜円と直線の位置関係
単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)xy平面上において、点(4,3)を中心とする半径1の円とちょくせん$y=mx$が共有点を持つとき、
定数mの取り得る最大値は$\dfrac{\fbox{ウ}}{\fbox{エ}}+\dfrac{\fbox{オ}\sqrt{\fbox{カ}}}{\fbox{キク}}$である。
2023慶應義塾大学商学部過去問
この動画を見る
(2)xy平面上において、点(4,3)を中心とする半径1の円とちょくせん$y=mx$が共有点を持つとき、
定数mの取り得る最大値は$\dfrac{\fbox{ウ}}{\fbox{エ}}+\dfrac{\fbox{オ}\sqrt{\fbox{カ}}}{\fbox{キク}}$である。
2023慶應義塾大学商学部過去問
福田の数学〜双曲線と直線の位置関係を考えよう〜明治大学2023年全学部統一Ⅲ第3問〜双曲線と直線

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 座標平面上の双曲線$x^2$-$4y^2$=5を$C$とおき、点(1,0)を通り傾き$m$が正となる直線を$l$とおく。$C$の漸近線は$y$=$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$と$y$=$-\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$である。また、$l$と$C$の共有点がただ1つとなるのは、$m$が$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$または$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ のときである。
$m$=$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$ならば$l$は$C$の接線となる。ここで$a$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ とおく。$m$<$a$であるときに、$l$と$C$の共有点の$y$座標のうち最大のものを$y_m$とすれば、
$y_m$=$\displaystyle\frac{m}{\boxed{\ \ キ\ \ }-\boxed{\ \ ク\ \ }m^2}\left(-\boxed{\ \ ケ\ \ }+\sqrt{\boxed{\ \ コ\ \ }-\boxed{\ \ サシ\ \ }m^2}\right)$
となる。このとき、$\displaystyle\lim_{m \to a-0}y_m$=$\boxed{\ \ ス\ \ }$ が成り立つ。
この動画を見る
$\Large{\boxed{3}}$ 座標平面上の双曲線$x^2$-$4y^2$=5を$C$とおき、点(1,0)を通り傾き$m$が正となる直線を$l$とおく。$C$の漸近線は$y$=$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$と$y$=$-\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}x$である。また、$l$と$C$の共有点がただ1つとなるのは、$m$が$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$または$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ のときである。
$m$=$\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$ならば$l$は$C$の接線となる。ここで$a$=$\frac{\boxed{\ \ オ\ \ }}{\boxed{\ \ カ\ \ }}$ とおく。$m$<$a$であるときに、$l$と$C$の共有点の$y$座標のうち最大のものを$y_m$とすれば、
$y_m$=$\displaystyle\frac{m}{\boxed{\ \ キ\ \ }-\boxed{\ \ ク\ \ }m^2}\left(-\boxed{\ \ ケ\ \ }+\sqrt{\boxed{\ \ コ\ \ }-\boxed{\ \ サシ\ \ }m^2}\right)$
となる。このとき、$\displaystyle\lim_{m \to a-0}y_m$=$\boxed{\ \ ス\ \ }$ が成り立つ。
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
【わかりやすく】三角形の頂点Pの軌跡を求める問題(数学Ⅱ 図形と方程式)

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
2点$A(-2,0),B(3,0)$と点$P$を頂点とする$\triangle PAB$が$PA:PB=2:3$を満たしながら変化するとき、点$P$の軌跡を求めよ。
この動画を見る
2点$A(-2,0),B(3,0)$と点$P$を頂点とする$\triangle PAB$が$PA:PB=2:3$を満たしながら変化するとき、点$P$の軌跡を求めよ。
福田の数学〜早稲田大学2023年教育学部第4問〜円との最短距離が一定である点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面上の点(0,1)を中心として半径1の円を$C$とする。点P($x$,$y$)が$y$≧0の範囲にあり、PからCまでの最短距離は$ay$であるとする。ただし$a$は0<$a$<1を満たす定数である。このとき、次の問いに答えよ。
(1)点Pが円$C$の円周上または外部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(2)点Pが円$C$の円周上または内部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(3)$x$=$\displaystyle\frac{1}{2}$かつ0≦$y$≦2を満たす点P($x$,$y$)がちょうど3個存在するような定数$a$の範囲を求めよ。
この動画を見る
$\Large\boxed{4}$ 座標平面上の点(0,1)を中心として半径1の円を$C$とする。点P($x$,$y$)が$y$≧0の範囲にあり、PからCまでの最短距離は$ay$であるとする。ただし$a$は0<$a$<1を満たす定数である。このとき、次の問いに答えよ。
(1)点Pが円$C$の円周上または外部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(2)点Pが円$C$の円周上または内部にあるとき、P($x$,$y$)が満たす方程式を求めよ。
(3)$x$=$\displaystyle\frac{1}{2}$かつ0≦$y$≦2を満たす点P($x$,$y$)がちょうど3個存在するような定数$a$の範囲を求めよ。
【わかりやすく】直線に対して対象の点の座標を求めよう(数学Ⅱ 図形と方程式)

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
直線$y=x+3$に対して、点$A(-2,4)$と対称な点の座標を求めよ。
この動画を見る
直線$y=x+3$に対して、点$A(-2,4)$と対称な点の座標を求めよ。
【わかりやすく】軌跡の求め方をゼロから解説(数学Ⅱ 図形と方程式)

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$y=2x^2$上を動く点$Q$と点$A(4.0)$を結ぶ線分$AQ$の中点$P$の軌跡を求めよ。
この動画を見る
$y=2x^2$上を動く点$Q$と点$A(4.0)$を結ぶ線分$AQ$の中点$P$の軌跡を求めよ。
福田の数学〜上智大学2023年TEAP利用型文系第4問(1)〜命題の真偽と領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ (1)実数$x$, $y$に対する次の2つの条件を$p$, $q$を考える。ただし、$r$は正の定数である。
$p$:|$x+y$|≦3 かつ |$x-y$|≦3
$q$:$(x-1)^2$+$(y-1)^2$≦$r^2$
(i)命題「$p$ならば$q$」が真となるような$r$の最小値は$\sqrt{\boxed{\ \ メ\ \ }}$ である。
(ii)命題「$q$ならば$p$」が真となるような$r$の最大値は$\displaystyle\frac{\boxed{\ \ モ\ \ }}{\boxed{\ \ ヤ\ \ }}\sqrt{\boxed{\ \ ユ\ \ }}$ である。
この動画を見る
$\Large{\boxed{3}}$ (1)実数$x$, $y$に対する次の2つの条件を$p$, $q$を考える。ただし、$r$は正の定数である。
$p$:|$x+y$|≦3 かつ |$x-y$|≦3
$q$:$(x-1)^2$+$(y-1)^2$≦$r^2$
(i)命題「$p$ならば$q$」が真となるような$r$の最小値は$\sqrt{\boxed{\ \ メ\ \ }}$ である。
(ii)命題「$q$ならば$p$」が真となるような$r$の最大値は$\displaystyle\frac{\boxed{\ \ モ\ \ }}{\boxed{\ \ ヤ\ \ }}\sqrt{\boxed{\ \ ユ\ \ }}$ である。
福田の数学〜慶應義塾大学2023年理工学部第5問(1)〜複素数平面上の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ (1)$\alpha$を±1ではない複素数とする。複素数平面上で$\displaystyle\left|\frac{\alpha z+1}{z+\alpha}\right|$=2 を満たす点$z$全体からなる図形を$C$とする。$C$は$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき直線となり、$\boxed{\ \ チ\ \ }$を満たさないとき円となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たさないとき、円$C$の中心を$\alpha$を用いて表すと$\boxed{\ \ ツ\ \ }$となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき、直線$C$上の点$z$のうち、
その絶対値が最小となるものを$\alpha$を用いて表すと$\boxed{\ \ テ\ \ }$となる。
この動画を見る
$\Large\boxed{5}$ (1)$\alpha$を±1ではない複素数とする。複素数平面上で$\displaystyle\left|\frac{\alpha z+1}{z+\alpha}\right|$=2 を満たす点$z$全体からなる図形を$C$とする。$C$は$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき直線となり、$\boxed{\ \ チ\ \ }$を満たさないとき円となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たさないとき、円$C$の中心を$\alpha$を用いて表すと$\boxed{\ \ ツ\ \ }$となる。$\alpha$が$\boxed{\ \ チ\ \ }$を満たすとき、直線$C$上の点$z$のうち、
その絶対値が最小となるものを$\alpha$を用いて表すと$\boxed{\ \ テ\ \ }$となる。
【短時間でマスター!!】不等式の領域の求め方を解説!(直線と円)〔現役講師解説、数学〕

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学2B
次の領域を図示せよ。
①$2x+3y-12<0$
②$x^2+y^2+2x-2y+1\leqq0$
この動画を見る
数学2B
次の領域を図示せよ。
①$2x+3y-12<0$
②$x^2+y^2+2x-2y+1\leqq0$
福田の数学〜慶應義塾大学2023年理工学部第2問〜空間ベクトルと2直線から等距離にある点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#図形と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $k$を正の実数とし、空間内に点O(0,0,0), A(4$k$, $-4k$, $-4\sqrt 2k$), B(7, 5, $-\sqrt 2$)をとる。点CはO, A, Bを含む平面上の点であり、OA=4BCで、四角形OACBはOAを底辺とする台形であるとする。
(1)$\cos\angle$AOB=$\boxed{\ \ ア\ \ }$である。台形OACBの面積を$k$を用いて表すと$\boxed{\ \ イ\ \ }$となる。
また、線分ACの長さを$k$を用いて表すと$\boxed{\ \ ウ\ \ }$となる。
(2)台形OACBが円に内接するとき、$k$=$\boxed{\ \ エ\ \ }$である。
(3)$k$=$\boxed{\ \ エ\ \ }$であるとし、直線OBと直線ACの交点をDとする。△OBPと△ACPの面積が等しい、という条件を満たす空間内の点P全体は、点Dを通る2つの平面上の点全体から点Dを除いたものとなる。これら2つの平面のうち、線分OAと交わらないものを$\alpha$とする。点Oから平面$\alpha$に下ろした垂線の長さは$\boxed{\ \ オ\ \ }$である。
この動画を見る
$\Large\boxed{2}$ $k$を正の実数とし、空間内に点O(0,0,0), A(4$k$, $-4k$, $-4\sqrt 2k$), B(7, 5, $-\sqrt 2$)をとる。点CはO, A, Bを含む平面上の点であり、OA=4BCで、四角形OACBはOAを底辺とする台形であるとする。
(1)$\cos\angle$AOB=$\boxed{\ \ ア\ \ }$である。台形OACBの面積を$k$を用いて表すと$\boxed{\ \ イ\ \ }$となる。
また、線分ACの長さを$k$を用いて表すと$\boxed{\ \ ウ\ \ }$となる。
(2)台形OACBが円に内接するとき、$k$=$\boxed{\ \ エ\ \ }$である。
(3)$k$=$\boxed{\ \ エ\ \ }$であるとし、直線OBと直線ACの交点をDとする。△OBPと△ACPの面積が等しい、という条件を満たす空間内の点P全体は、点Dを通る2つの平面上の点全体から点Dを除いたものとなる。これら2つの平面のうち、線分OAと交わらないものを$\alpha$とする。点Oから平面$\alpha$に下ろした垂線の長さは$\boxed{\ \ オ\ \ }$である。
