 微分法と積分法
微分法と積分法
 微分法と積分法
微分法と積分法
複素関数論⑭ 高専数学*5(1)(2) 複素積分の性質
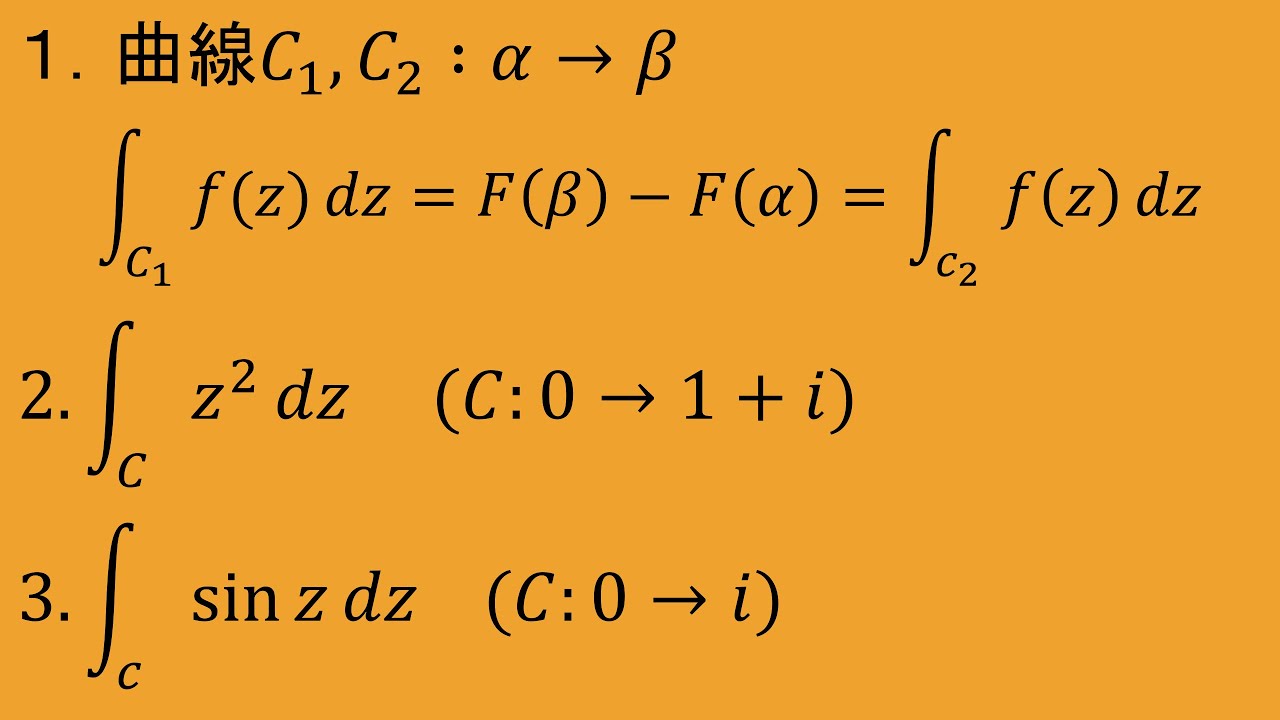
04岡山県教員採用試験(数学:6-(2) 積分)

単元:
#数Ⅱ#微分法と積分法#その他#不定積分・定積分#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6} - (2)$
$\displaystyle \int_{}^{} (\sin^{-1} x)^2 \ dx$を計算せよ.
この動画を見る
$\boxed{6} - (2)$
$\displaystyle \int_{}^{} (\sin^{-1} x)^2 \ dx$を計算せよ.
複素関数論⑬ 高専数学*4(複素積分の極限)
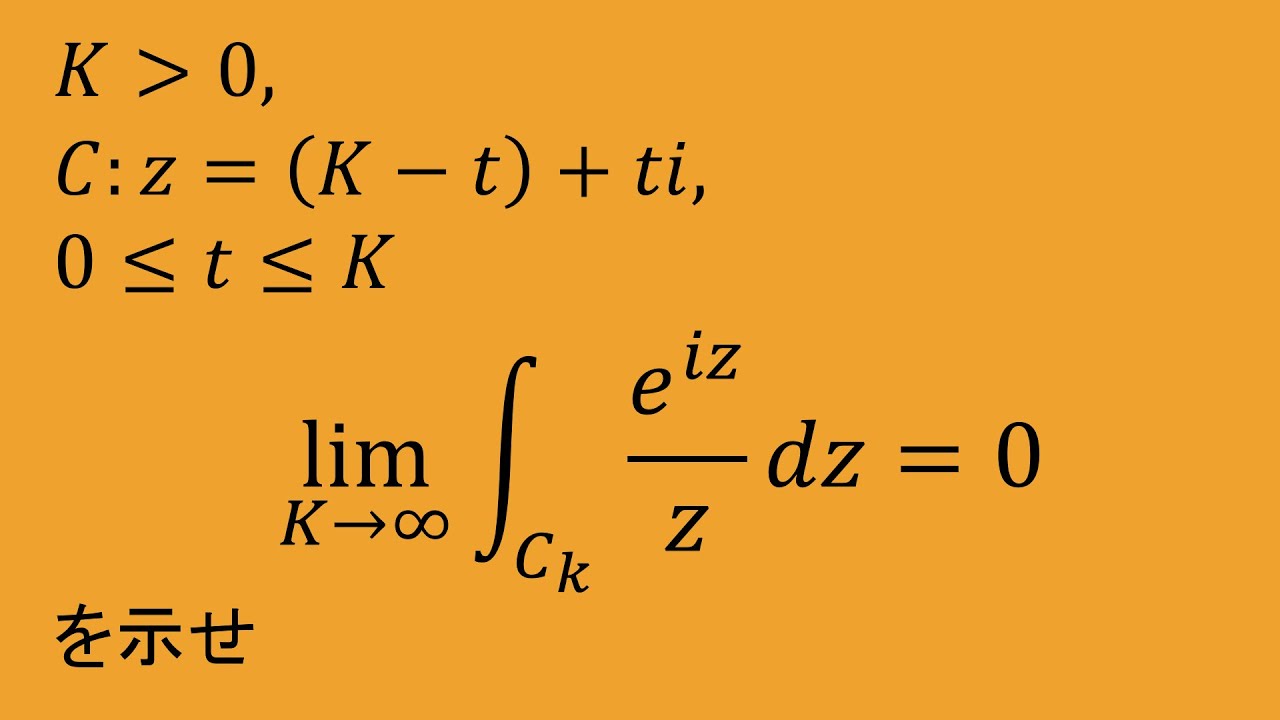
単元:
#数Ⅱ#複素数と方程式#微分法と積分法#複素数#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$k\gt 0$,$C_k:z=(k-t)+it$であり,
$0\leqq t\leqq k$とするとき,以下を解け.
(1)$\vert z\vert \geqq \dfrac{k}{\sqrt2},\left\vert\dfrac{e^{iz}}{z}\right\vert \leqq \dfrac{\sqrt2 e^{-t}}{k}$
(2)$\displaystyle \lim_{k\to\infty} \displaystyle \int_{c_k}^{} \dfrac{e^{iz}}{z} dz=0$
この動画を見る
$k\gt 0$,$C_k:z=(k-t)+it$であり,
$0\leqq t\leqq k$とするとき,以下を解け.
(1)$\vert z\vert \geqq \dfrac{k}{\sqrt2},\left\vert\dfrac{e^{iz}}{z}\right\vert \leqq \dfrac{\sqrt2 e^{-t}}{k}$
(2)$\displaystyle \lim_{k\to\infty} \displaystyle \int_{c_k}^{} \dfrac{e^{iz}}{z} dz=0$
04岡山県教員採用試験(数学:4番 積分)

単元:
#数Ⅱ#微分法と積分法#その他#不定積分・定積分#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$\displaystyle \int_{}^{} \sin^{-1}x \ dx$を計算せよ.
この動画を見る
$\boxed{6}$
$\displaystyle \int_{}^{} \sin^{-1}x \ dx$を計算せよ.
04京都府教員採用試験(数学:6番 ネピアの数の性質)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$n\in IN$,$\displaystyle \lim_{n\to\infty} \left(1+\dfrac{1}{n}\right)^n=e$
を満たすとき,
$x\in IR$,$\displaystyle \lim_{x\to\infty}\left(1+\dfrac{1}{x}\right)^n=e$
を示せ.
この動画を見る
$n\in IN$,$\displaystyle \lim_{n\to\infty} \left(1+\dfrac{1}{n}\right)^n=e$
を満たすとき,
$x\in IR$,$\displaystyle \lim_{x\to\infty}\left(1+\dfrac{1}{x}\right)^n=e$
を示せ.
複素関数論⑫:複素積分の絶対値の評価(高専数学)
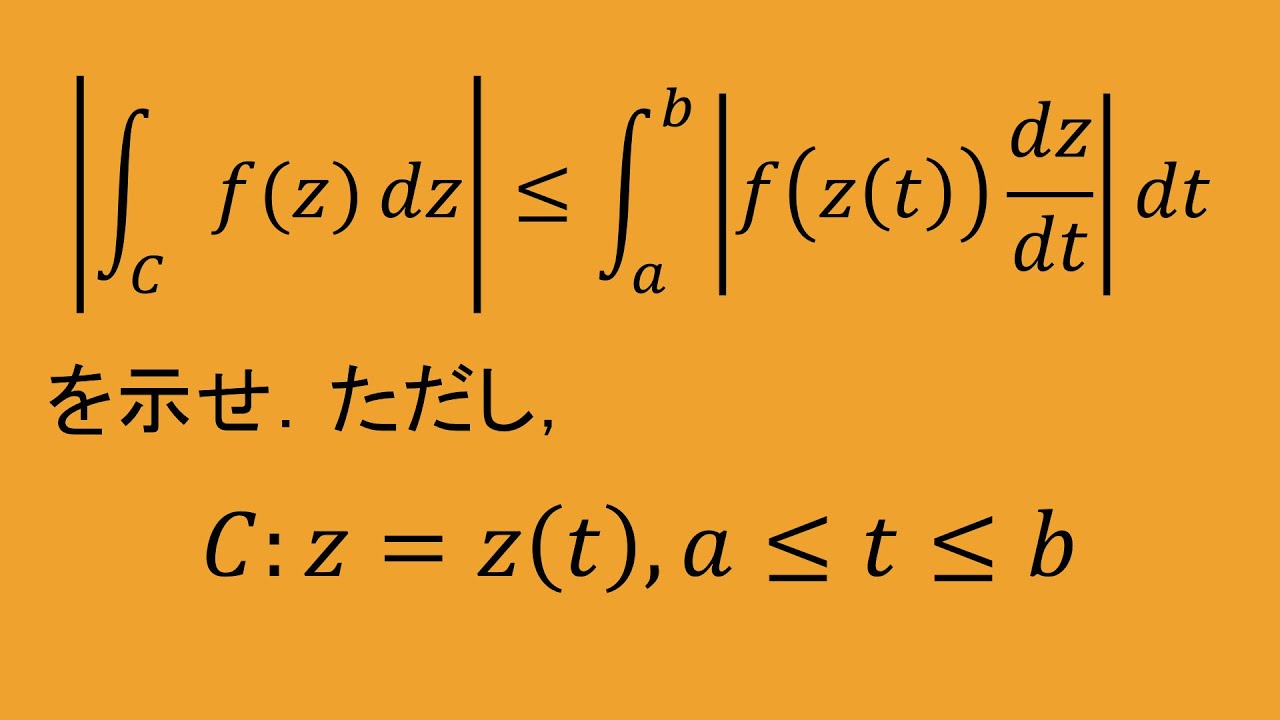
単元:
#数Ⅱ#複素数と方程式#微分法と積分法#複素数#不定積分・定積分#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$C:z=z(t),a\leqq t\leqq b$とする.
$\vert \displaystyle \int_{c}^{} f(z)dz \vert\leqq \displaystyle \int_{a}^{b} \vert f(z(t)\dfrac{dz}{dt}\vert dt $
を示せ.
この動画を見る
$C:z=z(t),a\leqq t\leqq b$とする.
$\vert \displaystyle \int_{c}^{} f(z)dz \vert\leqq \displaystyle \int_{a}^{b} \vert f(z(t)\dfrac{dz}{dt}\vert dt $
を示せ.
とある奈良県教員採用試験の問題(数学:接線の数)

単元:
#数A#数Ⅱ#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分法と積分法#接線と増減表・最大値・最小値#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
点$P(a,0)$を通り,
曲線$y=\dfrac{x}{\log_x}\ (x\gt 1)$に接する直線が
2本引けるように$a$の値の範囲を求めよ.
この動画を見る
点$P(a,0)$を通り,
曲線$y=\dfrac{x}{\log_x}\ (x\gt 1)$に接する直線が
2本引けるように$a$の値の範囲を求めよ.
16京都府教員採用試験(数学:1番 積分)

単元:
#数Ⅱ#微分法と積分法#その他#不定積分・定積分#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$n \in IN$とする.
$2(\sqrt{n+1}-1)\lt 1+\dfrac{1}{\sqrt 2}+\dfrac{1}{\sqrt 3}+・・・+\dfrac{1}{\sqrt n}$
これを解け.
この動画を見る
$\boxed{1}$
$n \in IN$とする.
$2(\sqrt{n+1}-1)\lt 1+\dfrac{1}{\sqrt 2}+\dfrac{1}{\sqrt 3}+・・・+\dfrac{1}{\sqrt n}$
これを解け.
いつかの奈良県教員採用試験(数学:バームクーヘンの定理)

単元:
#数Ⅱ#微分法と積分法#その他#面積、体積#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$y=\sin x\ (0\leqq x \leqq \pi)$と
$x$軸で囲まれた部分を$y$軸を中心として
回転させる体積$V$を求めよ.
この動画を見る
$y=\sin x\ (0\leqq x \leqq \pi)$と
$x$軸で囲まれた部分を$y$軸を中心として
回転させる体積$V$を求めよ.
【数Ⅱ】微分法と積分法:2021年度東大文科第1問を典型解法で攻略!

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
aを正の実数とする。座標平面上の曲線Cを$y=ax^3-2x$で定める。原点を中心とする半径1の円とCの共有点の個数が6個であるようなaの範囲を求めよ。
この動画を見る
aを正の実数とする。座標平面上の曲線Cを$y=ax^3-2x$で定める。原点を中心とする半径1の円とCの共有点の個数が6個であるようなaの範囲を求めよ。
07大阪府教員採用試験(数学:1番 三角関数と極限)

単元:
#数Ⅱ#三角関数#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$x-2\sin\theta-\cos2\theta$
$y=\displaystyle \sum_{n=1}^{\infty} \left(\dfrac{x}{6}\right)^n$のとりうる値の範囲を求めよ.
この動画を見る
$\boxed{1}$
$x-2\sin\theta-\cos2\theta$
$y=\displaystyle \sum_{n=1}^{\infty} \left(\dfrac{x}{6}\right)^n$のとりうる値の範囲を求めよ.
重積分⑥-5 #157【曲面・平面で囲まれた体積】(高専数学 微積II,数検1級1次解析対応)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
直円柱$x^2+y^2=4x$
$xy$平面,曲面$Z=xy^2$で囲まれた体積$V$を求めよ.
この動画を見る
直円柱$x^2+y^2=4x$
$xy$平面,曲面$Z=xy^2$で囲まれた体積$V$を求めよ.
06大阪府教員採用試験(数学:3番 極限値)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$ $\displaystyle \lim_{x\to 2}\ \dfrac{x^2-ax+2b-3}{x^2-x-2}=-\dfrac{1}{3}$
$a,b$の値を求めよ.
この動画を見る
$\boxed{3}$ $\displaystyle \lim_{x\to 2}\ \dfrac{x^2-ax+2b-3}{x^2-x-2}=-\dfrac{1}{3}$
$a,b$の値を求めよ.
重積分⑧-6 #155 【一般の変数変換】(高専数学 微積II,数検1級1次解析対応)
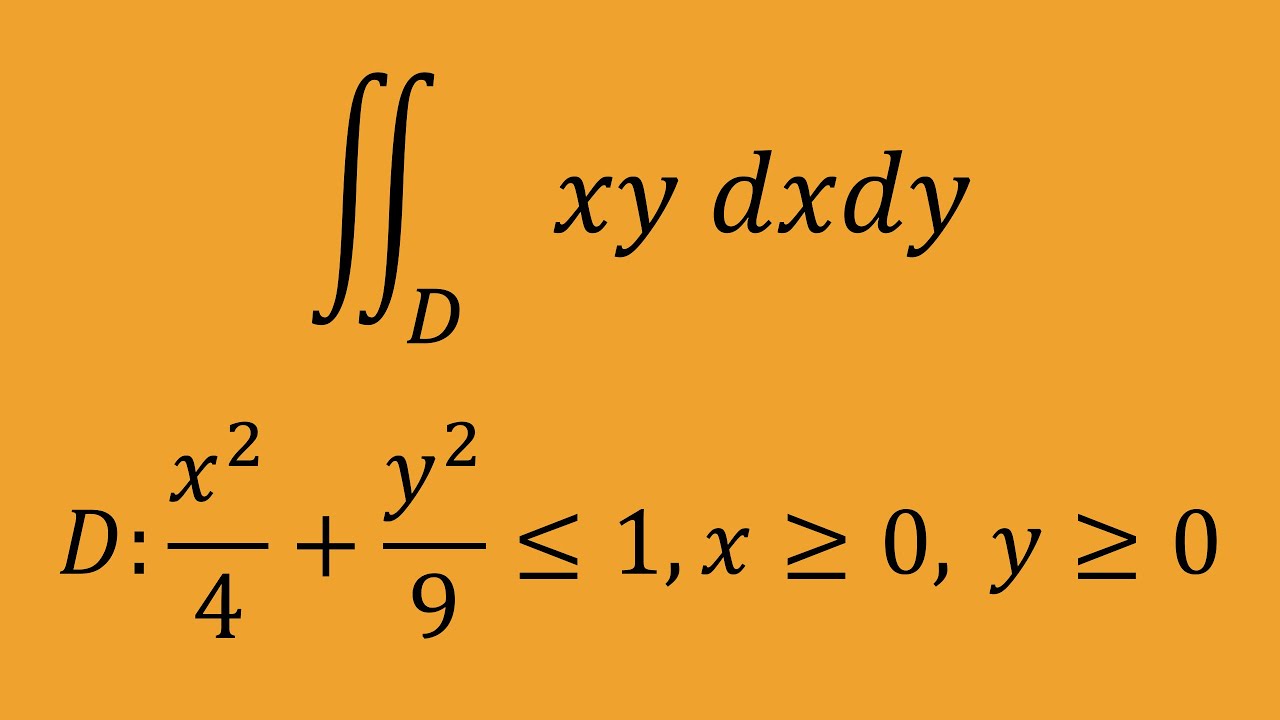
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
これを解け.
$D:\geqq 0,y\geqq 0,\dfrac{x^2}{4}+\dfrac{y^2}{4}\leqq 1$
$\iint_D \ xy \ dx \ dy$
この動画を見る
これを解け.
$D:\geqq 0,y\geqq 0,\dfrac{x^2}{4}+\dfrac{y^2}{4}\leqq 1$
$\iint_D \ xy \ dx \ dy$
共通テスト第2日程2021年数学詳しい解説〜共通テスト第2日程2021年2B第2問〜微分積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#接線と増減表・最大値・最小値#センター試験・共通テスト関連#共通テスト#不定積分・定積分#面積、体積#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第2問}$
[1] $a$を実数とし、$f(x)=(x-a)(x-2)$とおく。また、$F(x)=\int_0^xf(t)dt$とする。
(1)$a=1$のとき、$F(x)はx=\boxed{\ \ ア\ \ }$で極小になる。
(2)$a=\boxed{\ \ イ\ \ }$のとき、$F(x)$は常に増加する。また、$F(0)=\boxed{\ \ ウ\ \ }$
であるから、$a=\boxed{\ \ イ\ \ }$のとき、$F(2)$の値は$\boxed{\boxed{\ \ エ\ \ }}$である。
$\boxed{\boxed{\ \ エ\ \ }}$の解答群
⓪0 ①正 ②負
(3)$a \gt \boxed{\ \ イ\ \ }$とする。
bを実数とし、$G(x)=\int_b^xf(t)dt$とおく。
関数$y=G(x)$のグラフは、$y=F(x)$のグラフを$\boxed{\boxed{\ \ オ\ \ }}$方向に
$\boxed{\boxed{\ \ カ\ \ }}$だけ平行移動したものと一致する。また、$G(x)はx=\boxed{\ \ キ\ \ }$
で極大になり、$x=\boxed{\ \ ク\ \ }$で極小になる。
$G(b)=\boxed{\ \ ケ\ \ }$であるから、$b=\boxed{\ \ キ\ \ }$のとき、曲線$y=G(x)$と
$x$軸との共有点の個数は$\boxed{\ \ コ\ \ }$個である。
$\boxed{\boxed{\ \ オ\ \ }}$の解答群
⓪$x$軸 ①$y$軸
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪$b$ ①$-b$ ②$F(b)$
③$-F(b)$ ④$F(-b)$ ⑤$-F(-b)$
[2] $g(x)=|x|(x+1)$とおく。
点$P(-1,0)$を通り、傾きが$c$の直線を$l$とする。$g'(-1)=\boxed{\ \ サ\ \ }$
であるから、$0 \lt c \lt \boxed{\ \ サ\ \ }$のとき、曲線$y=g(x)$と直線$l$は3点
で交わる。そのうちの1点は$P$であり、残りの2点を点$P$に近い方から順に
$Q,R$とすると、点$Q$の$x$座標は$\boxed{\ \ シス\ \ }$であり、点$R$の$x$座標は
$\boxed{\ \ セ\ \ }$である。
また、$0 \lt c \lt \boxed{\ \ サ\ \ }$のとき、線分$PQ$と曲線$y=g(x)$で囲まれた図形の
面積を$S$とし、線分$QR$と曲線$y=g(x)$で囲まれた図形の面積を$T$とすると
$\scriptsize{S=\displaystyle \frac{\boxed{\ \ ソ\ \ }c^3+\boxed{\ \ タ\ \ }c^2-\boxed{\ \ チ\ \ }c+1}{\boxed{\ \ ツ\ \ }}}$
$T=c^{\boxed{テ}}$
である。
2021共通テスト過去問
この動画を見る
${\large第2問}$
[1] $a$を実数とし、$f(x)=(x-a)(x-2)$とおく。また、$F(x)=\int_0^xf(t)dt$とする。
(1)$a=1$のとき、$F(x)はx=\boxed{\ \ ア\ \ }$で極小になる。
(2)$a=\boxed{\ \ イ\ \ }$のとき、$F(x)$は常に増加する。また、$F(0)=\boxed{\ \ ウ\ \ }$
であるから、$a=\boxed{\ \ イ\ \ }$のとき、$F(2)$の値は$\boxed{\boxed{\ \ エ\ \ }}$である。
$\boxed{\boxed{\ \ エ\ \ }}$の解答群
⓪0 ①正 ②負
(3)$a \gt \boxed{\ \ イ\ \ }$とする。
bを実数とし、$G(x)=\int_b^xf(t)dt$とおく。
関数$y=G(x)$のグラフは、$y=F(x)$のグラフを$\boxed{\boxed{\ \ オ\ \ }}$方向に
$\boxed{\boxed{\ \ カ\ \ }}$だけ平行移動したものと一致する。また、$G(x)はx=\boxed{\ \ キ\ \ }$
で極大になり、$x=\boxed{\ \ ク\ \ }$で極小になる。
$G(b)=\boxed{\ \ ケ\ \ }$であるから、$b=\boxed{\ \ キ\ \ }$のとき、曲線$y=G(x)$と
$x$軸との共有点の個数は$\boxed{\ \ コ\ \ }$個である。
$\boxed{\boxed{\ \ オ\ \ }}$の解答群
⓪$x$軸 ①$y$軸
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪$b$ ①$-b$ ②$F(b)$
③$-F(b)$ ④$F(-b)$ ⑤$-F(-b)$
[2] $g(x)=|x|(x+1)$とおく。
点$P(-1,0)$を通り、傾きが$c$の直線を$l$とする。$g'(-1)=\boxed{\ \ サ\ \ }$
であるから、$0 \lt c \lt \boxed{\ \ サ\ \ }$のとき、曲線$y=g(x)$と直線$l$は3点
で交わる。そのうちの1点は$P$であり、残りの2点を点$P$に近い方から順に
$Q,R$とすると、点$Q$の$x$座標は$\boxed{\ \ シス\ \ }$であり、点$R$の$x$座標は
$\boxed{\ \ セ\ \ }$である。
また、$0 \lt c \lt \boxed{\ \ サ\ \ }$のとき、線分$PQ$と曲線$y=g(x)$で囲まれた図形の
面積を$S$とし、線分$QR$と曲線$y=g(x)$で囲まれた図形の面積を$T$とすると
$\scriptsize{S=\displaystyle \frac{\boxed{\ \ ソ\ \ }c^3+\boxed{\ \ タ\ \ }c^2-\boxed{\ \ チ\ \ }c+1}{\boxed{\ \ ツ\ \ }}}$
$T=c^{\boxed{テ}}$
である。
2021共通テスト過去問
重積分⑧-5 #154 【一般の変数変換(難)】(高専数学 微積II,数検1級1次解析対応)
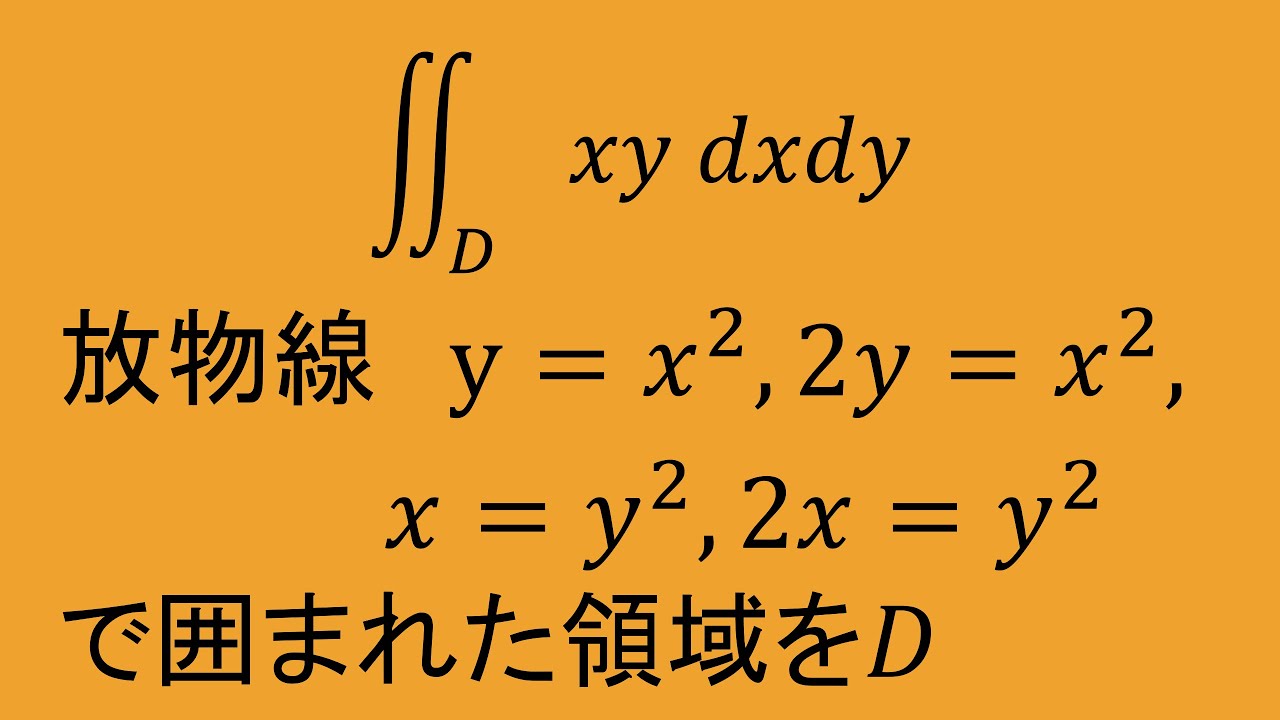
単元:
#数Ⅱ#微分法と積分法#積分とその応用#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\iint_D \ xy\ dx\ dy$
$D:y=x^2,2y=x^2,x=y^2,2x=y^2$で囲まれた領域を求めよ.
この動画を見る
$\iint_D \ xy\ dx\ dy$
$D:y=x^2,2y=x^2,x=y^2,2x=y^2$で囲まれた領域を求めよ.
重積分⑦-6 #153-(3)【極座標による変数変換】(高専数学 微積II,数検1級対応)
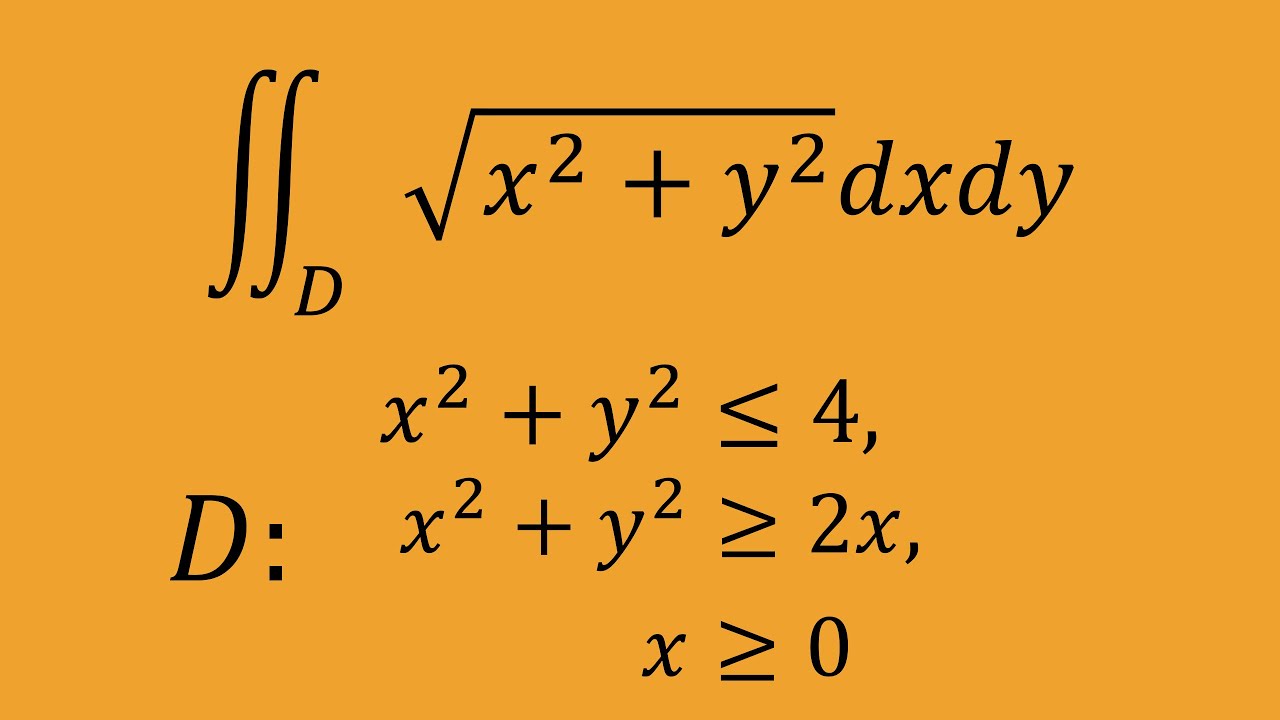
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
これを解け.
$\iint_D \ \sqrt{x^2+y^2}\ dx \ dy$
$D:x^2+y^2\leqq 4,x^2+y^2\geqq 2x,x\geqq 0$
この動画を見る
これを解け.
$\iint_D \ \sqrt{x^2+y^2}\ dx \ dy$
$D:x^2+y^2\leqq 4,x^2+y^2\geqq 2x,x\geqq 0$
重積分⑫-3 #152【図形Dの重心】(高専数学 微積II,数検1級1次解析対応)

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$D:-1\leqq x\leqq 1,0\leqq y\leqq x^2+1$
図形$D$の重心座標$(\overline{x},\overline{y})$を求めよ.
この動画を見る
$D:-1\leqq x\leqq 1,0\leqq y\leqq x^2+1$
図形$D$の重心座標$(\overline{x},\overline{y})$を求めよ.
03愛知県教員採用試験(数学:13 極限値)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{13}$これを解け.
$\displaystyle \lim_{x\to 0}\ \dfrac{\sin^{-1}x-x}{x^3}$
この動画を見る
$\boxed{13}$これを解け.
$\displaystyle \lim_{x\to 0}\ \dfrac{\sin^{-1}x-x}{x^3}$
16愛知県教員採用試験(数学:10番(2) 微分積分)

単元:
#数Ⅱ#微分法と積分法#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{10}$
$f(x)=\displaystyle \int_{0}^{x} \ (1-t^2)e^t \ dt$の極値を求めよ.
この動画を見る
$\boxed{10}$
$f(x)=\displaystyle \int_{0}^{x} \ (1-t^2)e^t \ dt$の極値を求めよ.
重積分⑩-4#150【曲面の面積】(高専数学 微積II,数検1級1次解析対応)
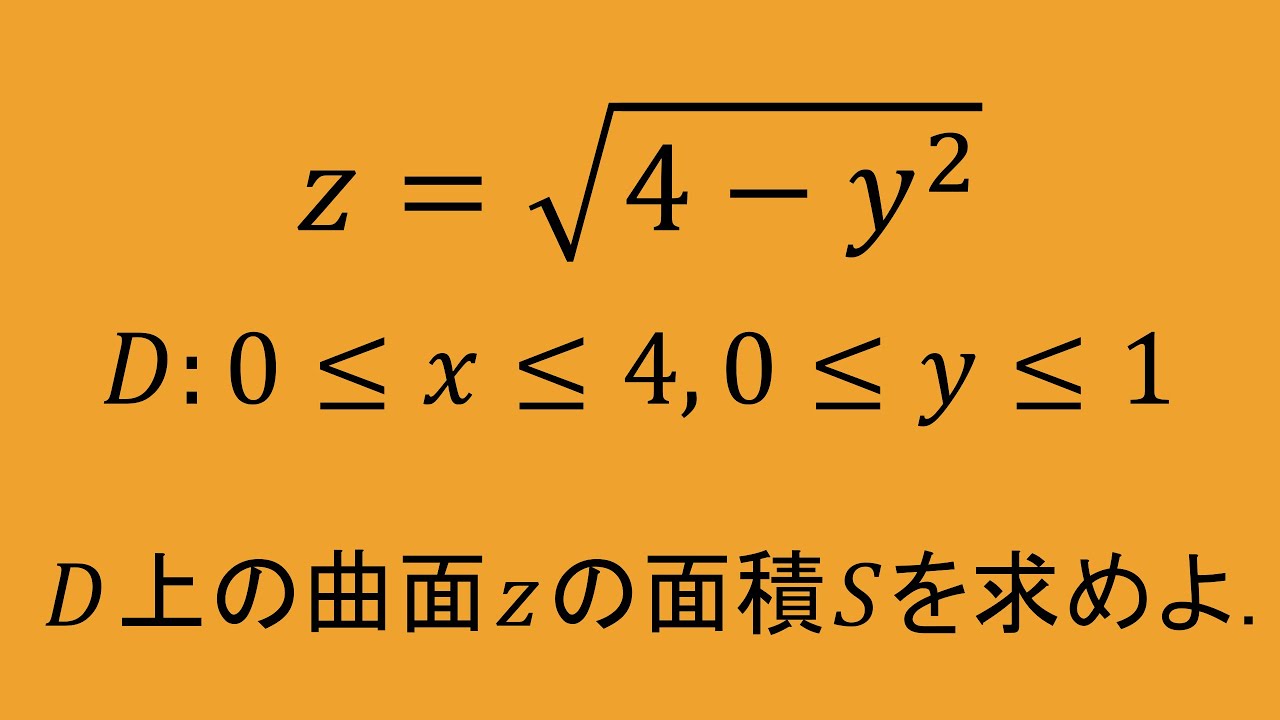
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$D:0\leqq x\leqq 4,0\leqq y\leqq 1$
$D$上における曲面$Z=\sqrt{4-y^2}$の面積$S$を求めよ.
この動画を見る
$D:0\leqq x\leqq 4,0\leqq y\leqq 1$
$D$上における曲面$Z=\sqrt{4-y^2}$の面積$S$を求めよ.
重積分⑨-9#149【広義積分】(高専数学 微積II,数検1級1次解析対応)
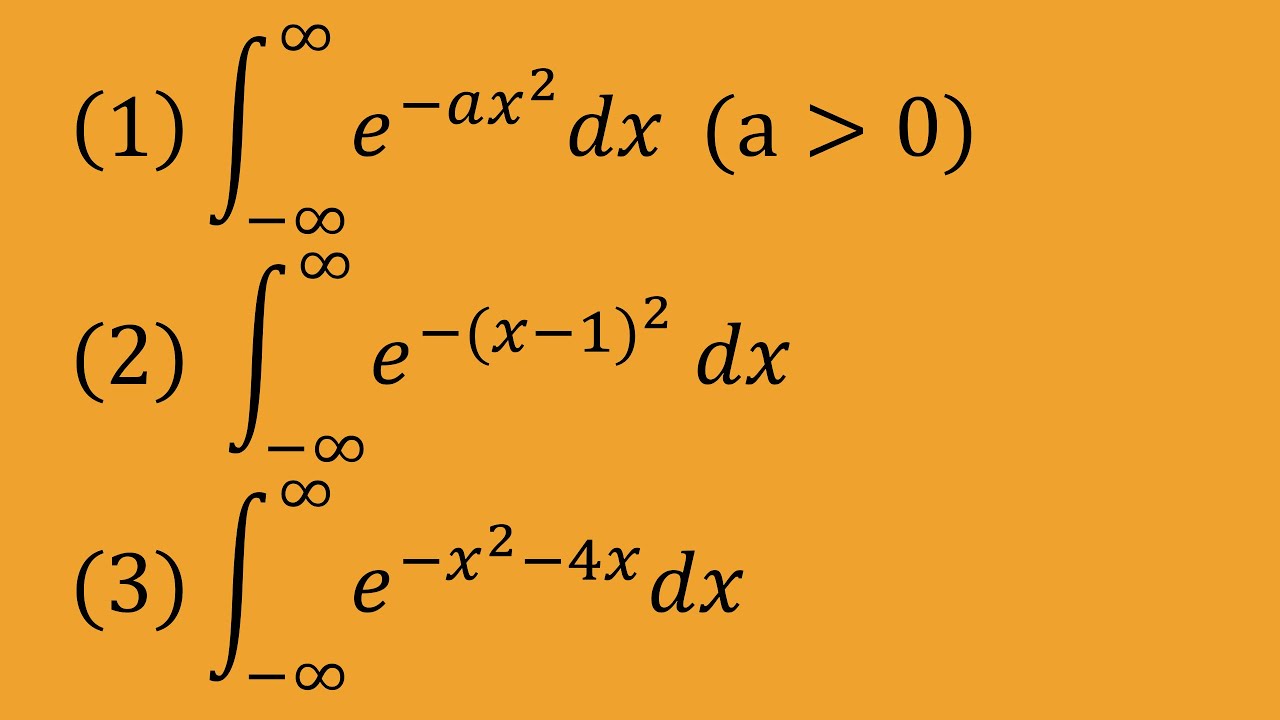
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
これを解け.
(1)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-ax^2} \ dx \ (a\gt 0)$
(2)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-(x-1)^2} \ dx \ $
(3)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-x^2-4x} \ dx \ $
定理$\displaystyle_{0}^{\infty} \ e^{-x^2}\ dx=\dfrac{\sqrt x}{2}$
この動画を見る
これを解け.
(1)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-ax^2} \ dx \ (a\gt 0)$
(2)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-(x-1)^2} \ dx \ $
(3)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-x^2-4x} \ dx \ $
定理$\displaystyle_{0}^{\infty} \ e^{-x^2}\ dx=\dfrac{\sqrt x}{2}$
15愛知県教員採用試験(数学:10番 極限)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{10}\\ \displaystyle \lim_{x\to 2}\\ \dfrac{\sqrt{2x+a}+b}{x-2}=\dfrac{1}{3}$
$a,b$を求めよ.
この動画を見る
$\boxed{10}\\ \displaystyle \lim_{x\to 2}\\ \dfrac{\sqrt{2x+a}+b}{x-2}=\dfrac{1}{3}$
$a,b$を求めよ.
重積分⑦-5【極座標による変数変換】(高専数学 微積II,数検1級対応)
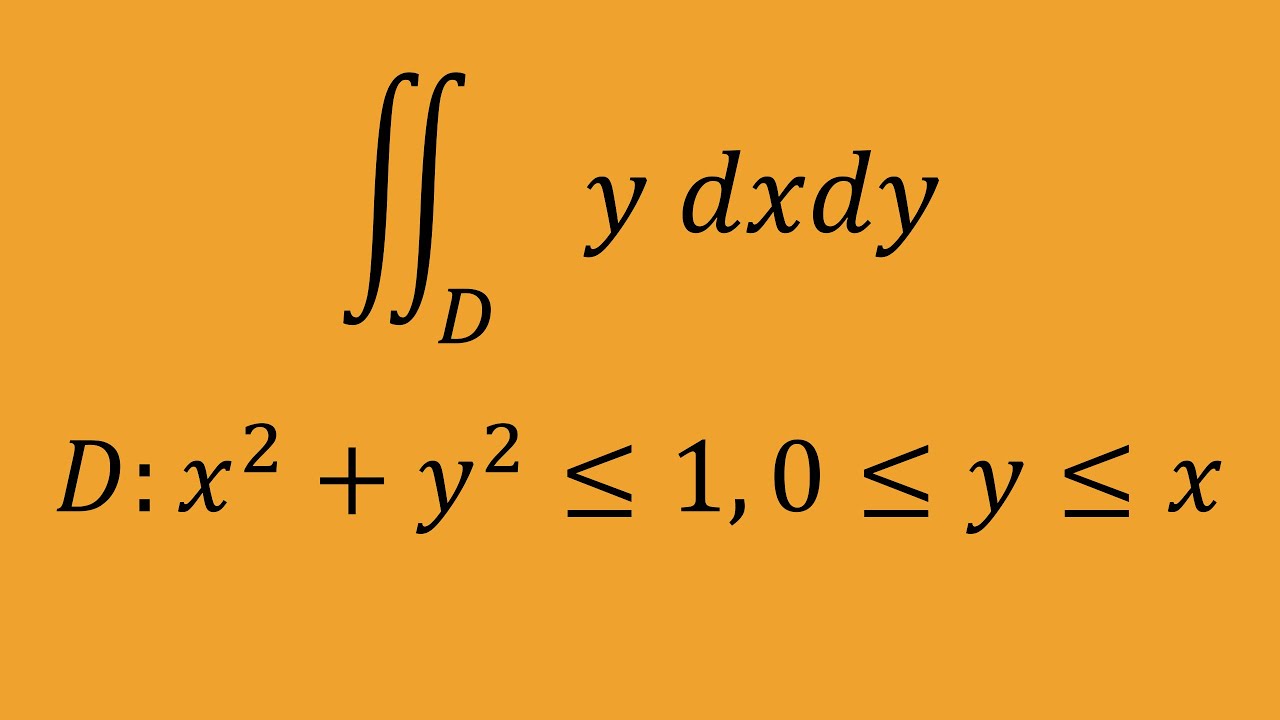
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
これを解け.
$\iint_D\\\ y \ dx \ dy$
$D:x^2+y^2\leqq 1,0\leqq y\leqq x$
この動画を見る
これを解け.
$\iint_D\\\ y \ dx \ dy$
$D:x^2+y^2\leqq 1,0\leqq y\leqq x$
重積分⑧-4【一般の変数変換】(高専数学 微積II,数検1級1次解析対応)
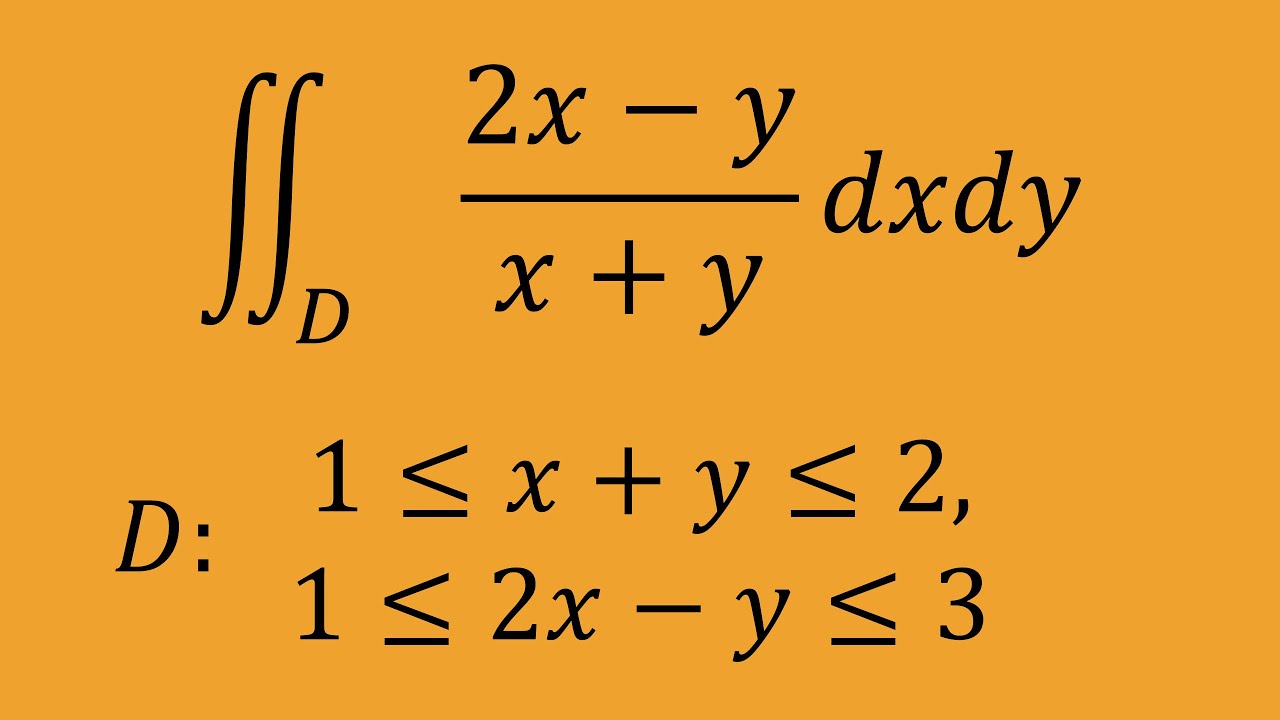
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
これを解け.
$\iint_D \\ \dfrac{2x-y}{x+y}dx\ dy$
$D:1\leqq x+y \leqq 2,1\leqq 2x-y \leqq 3$
この動画を見る
これを解け.
$\iint_D \\ \dfrac{2x-y}{x+y}dx\ dy$
$D:1\leqq x+y \leqq 2,1\leqq 2x-y \leqq 3$
重積分⑨-7【広義積分】(高専数学 微積II,数検1級1次解析対応)
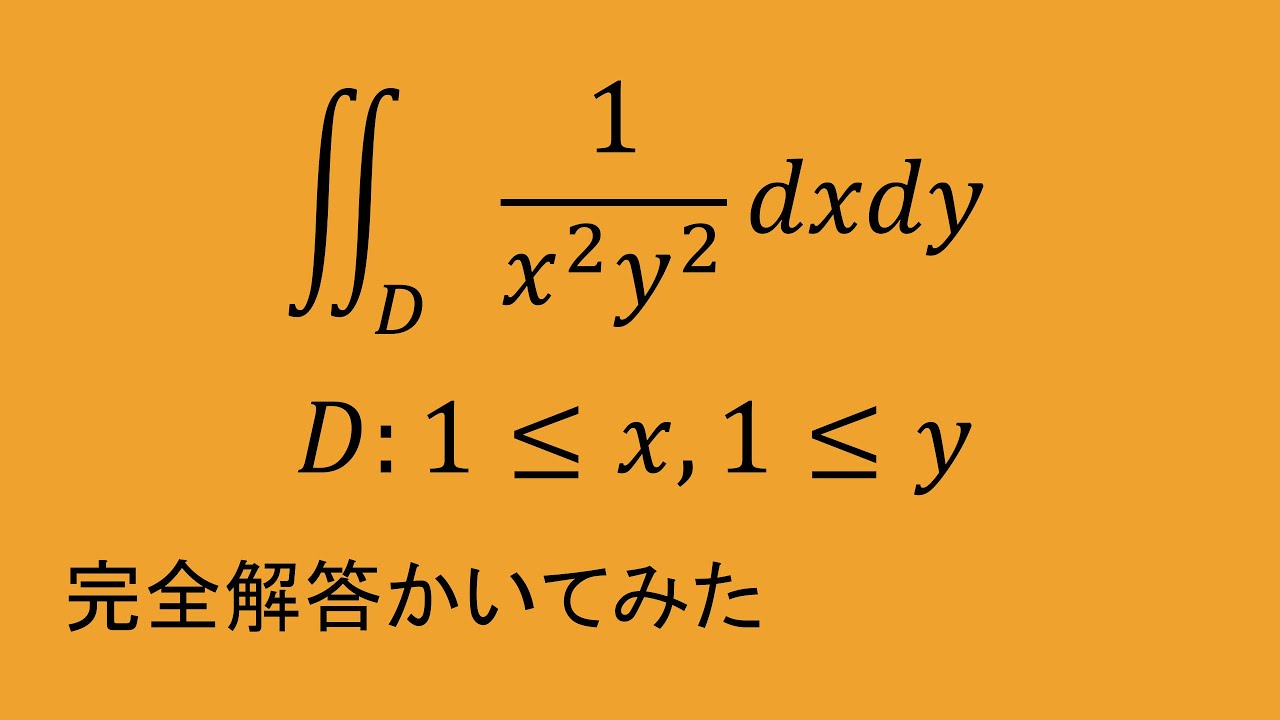
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$D:1\leqq x,1\leqq y$である.
$\iint_D \dfrac{1}{x^2y^2} \ dx \ dy$
これを解け.
この動画を見る
$D:1\leqq x,1\leqq y$である.
$\iint_D \dfrac{1}{x^2y^2} \ dx \ dy$
これを解け.
重積分⑨-5【広義積分】(高専数学 微積II,数検1級1次解析対応)
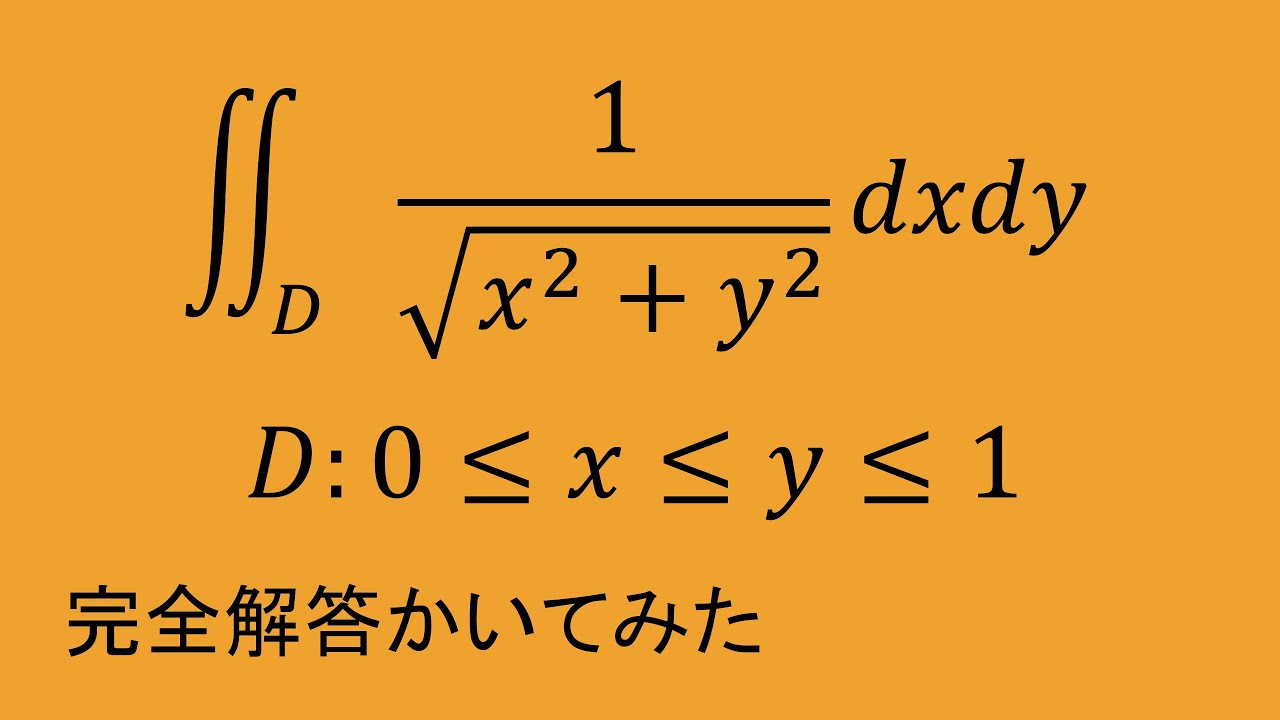
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
これを解け.
$\iint_D \ \dfrac{1}{\sqrt{x^2+y^2}}\ dx \ dy$
$D:0\leqq x\leqq y\leqq 1$
この動画を見る
これを解け.
$\iint_D \ \dfrac{1}{\sqrt{x^2+y^2}}\ dx \ dy$
$D:0\leqq x\leqq y\leqq 1$
重積分⑨-4【広義積分】(高専数学 微積II,数検1級1次解析対応)
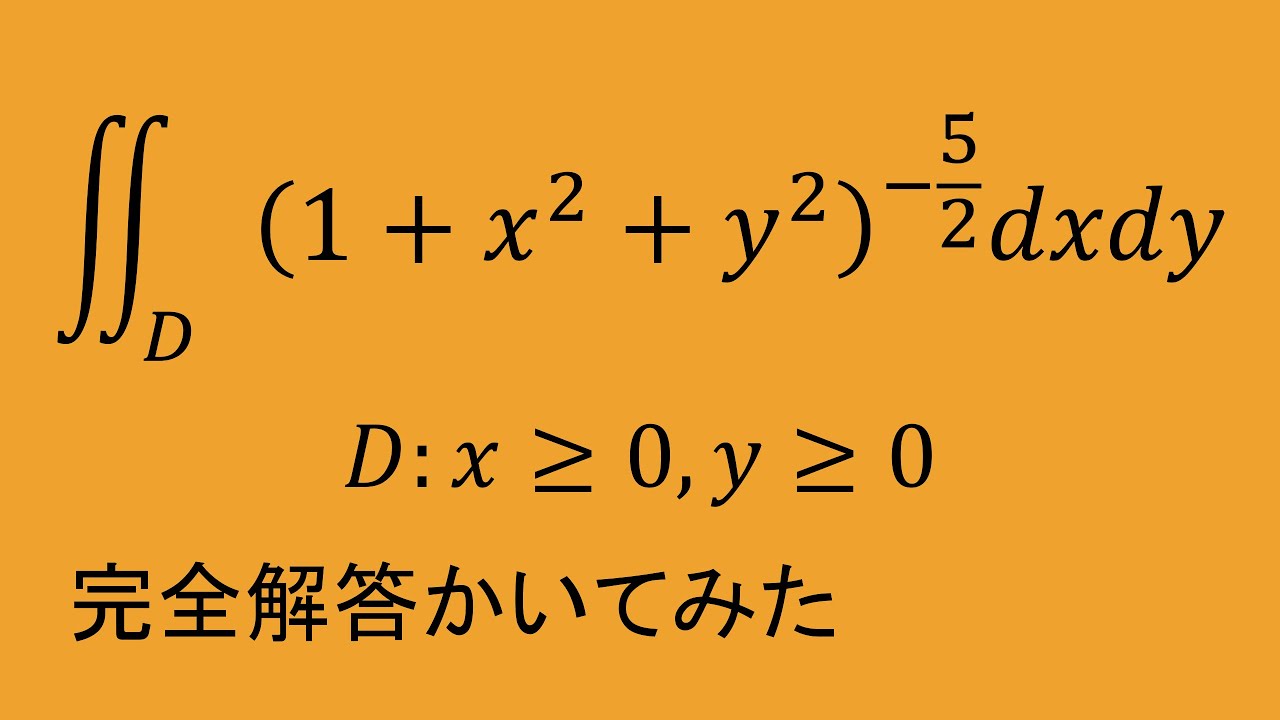
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
これを解け.
$\iint_D\ (1+x^2+y^2)^{-\frac{5}{2}}dx\ dy $
$D:x\geqq 0,y \geqq 0$とする.
この動画を見る
これを解け.
$\iint_D\ (1+x^2+y^2)^{-\frac{5}{2}}dx\ dy $
$D:x\geqq 0,y \geqq 0$とする.
共通テスト2021年数学詳しい解説〜共通テスト2021年2B第2問〜微分積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#接線と増減表・最大値・最小値#センター試験・共通テスト関連#共通テスト#不定積分・定積分#面積、体積#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large第2問}$
(1)座標平面上で、次の二つの2次関数のグラフについて考える。
$y=3x^2+2x+3$ $\cdots$①
$y=2x^2+2x+3$ $\cdots$②
①、②の2次関数のグラフには次の共通点がある。
共通点
・$y$軸との交点の$y$座標は$\boxed{\ \ ア\ \ }$である。
・$y$軸との交点における接線の方程式は$y=\boxed{\ \ イ\ \ }x+\boxed{\ \ ウ\ \ }$である。
次の⓪~⑤の2次関数のグラフのうち、$y$軸との交点における接線の方程式
が$y=\boxed{\ \ イ\ \ }x+\boxed{\ \ ウ\ \ }$となるものは$\boxed{\boxed{\ \ エ\ \ }}$である。
$\boxed{\boxed{\ \ エ\ \ }}$の解答群
⓪$y=3x^2-2x-3$
①$y=-3x^2+2x-3$
②$y=2x^2+2x-3$
③$y=2x^2-2x+3$
④$y=-x^2+2x+3$
⑤$y=-x^2-2x+3$
$a,b,c$を$0$でない実数とする。
曲線$y=ax^2+bx+c$上の点$\left(0, \boxed{\ \ オ\ \ }\right)$における接線をlとすると
その方程式は$y=\boxed{\ \ カ\ \ }x+\boxed{\ \ キ\ \ }$である。
接線$l$と$x$軸との交点の$x$座標は$\displaystyle \frac{\boxed{\ \ クケ\ \ }}{\boxed{\ \ コ\ \ }}$である。
$a,b,c$が正の実数であるとき、曲線$y=ax^2+bx+c$と接線lおよび直線
$x=\displaystyle \frac{\boxed{\ \ クケ\ \ }}{\boxed{\ \ コ\ \ }}$で囲まれた図形の面積をSとすると
$S=\displaystyle \frac{ac^{\boxed{サ}}}{\boxed{\ \ シ\ \ }\ b^{\boxed{ス}}}$ $\cdots$③
である。
③において、$a=1$とし、$S$の値が一定となるように正の実数$b,c$の値を
変化させる。このとき、$b$と$c$の関係を表すグラフの概形は$\boxed{\boxed{\ \ セ\ \ }}$る。
$\boxed{\boxed{\ \ セ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
(※選択肢は動画参照)
(2)座標平面上で、次の三つの3次関数のグラフについて考える。
$y=4x^3+2x^2+3x+5$ $\cdots$④
$y=-2x^3+7x^2+3x+5$ $\cdots$⑤
$y=5x^3-x^2+3x+5$ $\cdots$⑥
④、⑤、⑥の3次関数のグラフには次の共通点がある。
共通点
・$y$軸との交点の$y$座標は$\boxed{\ \ ソ\ \ }$である。
・$y$軸との交点における接線の方程式は$y=\boxed{\ \ タ\ \ }\ x+\boxed{\ \ チ\ \ }$である。
$a,b,c,d$を$0$でない実数とする。
曲線$y=ax^3+bx^2+cx+d$上の点$\left(0, \boxed{\ \ ツ\ \ }\right)$における接線の
方程式は$y=\boxed{\ \ テ\ \ }\ x+\boxed{\ \ ト\ \ }$である。
次に、$f(x)=ax^3+bx^2+cx+d,$ $g(x)=\boxed{\ \ テ\ \ }\ x+\boxed{\ \ ト\ \ }$とし、
$f(x)-g(x)$について考える。
$h(x)=f(x)-g(x)$とおく。$a,b,c,d$が正の実数であるとき、$y=h(x)$
のグラフの概形は$\boxed{\boxed{\ \ ナ\ \ }}$である。
$y=f(x)$のグラフと$y=g(x)$のグラフの共有点の$x$座標は$\displaystyle \frac{\boxed{\ \ ニヌ\ \ }}{\boxed{\ \ ネ\ \ }}$
と$\boxed{\ \ ノ\ \ }$である。また、$x$が$\displaystyle \frac{\boxed{\ \ ニヌ\ \ }}{\boxed{\ \ ネ\ \ }}$と$\boxed{\ \ ノ\ \ }$の間を動くとき、
$|f(x)-g(x)|$の値が最大となるのは、$x=\displaystyle \frac{\boxed{\ \ ハヒフ\ \ }}{\boxed{\ \ ヘホ\ \ }}$のときである。
$\boxed{\boxed{\ \ ナ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
(※選択肢は動画参照)
2021共通テスト過去問
この動画を見る
${\large第2問}$
(1)座標平面上で、次の二つの2次関数のグラフについて考える。
$y=3x^2+2x+3$ $\cdots$①
$y=2x^2+2x+3$ $\cdots$②
①、②の2次関数のグラフには次の共通点がある。
共通点
・$y$軸との交点の$y$座標は$\boxed{\ \ ア\ \ }$である。
・$y$軸との交点における接線の方程式は$y=\boxed{\ \ イ\ \ }x+\boxed{\ \ ウ\ \ }$である。
次の⓪~⑤の2次関数のグラフのうち、$y$軸との交点における接線の方程式
が$y=\boxed{\ \ イ\ \ }x+\boxed{\ \ ウ\ \ }$となるものは$\boxed{\boxed{\ \ エ\ \ }}$である。
$\boxed{\boxed{\ \ エ\ \ }}$の解答群
⓪$y=3x^2-2x-3$
①$y=-3x^2+2x-3$
②$y=2x^2+2x-3$
③$y=2x^2-2x+3$
④$y=-x^2+2x+3$
⑤$y=-x^2-2x+3$
$a,b,c$を$0$でない実数とする。
曲線$y=ax^2+bx+c$上の点$\left(0, \boxed{\ \ オ\ \ }\right)$における接線をlとすると
その方程式は$y=\boxed{\ \ カ\ \ }x+\boxed{\ \ キ\ \ }$である。
接線$l$と$x$軸との交点の$x$座標は$\displaystyle \frac{\boxed{\ \ クケ\ \ }}{\boxed{\ \ コ\ \ }}$である。
$a,b,c$が正の実数であるとき、曲線$y=ax^2+bx+c$と接線lおよび直線
$x=\displaystyle \frac{\boxed{\ \ クケ\ \ }}{\boxed{\ \ コ\ \ }}$で囲まれた図形の面積をSとすると
$S=\displaystyle \frac{ac^{\boxed{サ}}}{\boxed{\ \ シ\ \ }\ b^{\boxed{ス}}}$ $\cdots$③
である。
③において、$a=1$とし、$S$の値が一定となるように正の実数$b,c$の値を
変化させる。このとき、$b$と$c$の関係を表すグラフの概形は$\boxed{\boxed{\ \ セ\ \ }}$る。
$\boxed{\boxed{\ \ セ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
(※選択肢は動画参照)
(2)座標平面上で、次の三つの3次関数のグラフについて考える。
$y=4x^3+2x^2+3x+5$ $\cdots$④
$y=-2x^3+7x^2+3x+5$ $\cdots$⑤
$y=5x^3-x^2+3x+5$ $\cdots$⑥
④、⑤、⑥の3次関数のグラフには次の共通点がある。
共通点
・$y$軸との交点の$y$座標は$\boxed{\ \ ソ\ \ }$である。
・$y$軸との交点における接線の方程式は$y=\boxed{\ \ タ\ \ }\ x+\boxed{\ \ チ\ \ }$である。
$a,b,c,d$を$0$でない実数とする。
曲線$y=ax^3+bx^2+cx+d$上の点$\left(0, \boxed{\ \ ツ\ \ }\right)$における接線の
方程式は$y=\boxed{\ \ テ\ \ }\ x+\boxed{\ \ ト\ \ }$である。
次に、$f(x)=ax^3+bx^2+cx+d,$ $g(x)=\boxed{\ \ テ\ \ }\ x+\boxed{\ \ ト\ \ }$とし、
$f(x)-g(x)$について考える。
$h(x)=f(x)-g(x)$とおく。$a,b,c,d$が正の実数であるとき、$y=h(x)$
のグラフの概形は$\boxed{\boxed{\ \ ナ\ \ }}$である。
$y=f(x)$のグラフと$y=g(x)$のグラフの共有点の$x$座標は$\displaystyle \frac{\boxed{\ \ ニヌ\ \ }}{\boxed{\ \ ネ\ \ }}$
と$\boxed{\ \ ノ\ \ }$である。また、$x$が$\displaystyle \frac{\boxed{\ \ ニヌ\ \ }}{\boxed{\ \ ネ\ \ }}$と$\boxed{\ \ ノ\ \ }$の間を動くとき、
$|f(x)-g(x)|$の値が最大となるのは、$x=\displaystyle \frac{\boxed{\ \ ハヒフ\ \ }}{\boxed{\ \ ヘホ\ \ }}$のときである。
$\boxed{\boxed{\ \ ナ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
(※選択肢は動画参照)
2021共通テスト過去問
鳴門教育大 最大値最小値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^2+y^2=18$を満たすとき$(x+y)^2-6(x+y)+12$の最大値・最小値とその時の$x,y$の値を求めよ
出典:2013年鳴門教育大学 過去問
この動画を見る
$x^2+y^2=18$を満たすとき$(x+y)^2-6(x+y)+12$の最大値・最小値とその時の$x,y$の値を求めよ
出典:2013年鳴門教育大学 過去問
