 数Ⅱ
数Ⅱ
 数Ⅱ
数Ⅱ
【誘導あり:概要欄】大学入試問題#256 神戸大学2012 #極限 #はさみうちの定理

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#対数関数#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
(1)
$2 \leqq k$:自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
(2)
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典:2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$S_n=\displaystyle \sum_{k=1}^{n^3-1}\displaystyle \frac{1}{k\ log\ k}$
(1)
$2 \leqq k$:自然数
$\displaystyle \frac{1}{(k+1)log(k+1)} \lt \displaystyle \int_{k}^{k+1}\displaystyle \frac{dx}{x\ log\ x} \lt \displaystyle \frac{1}{k\ log\ k}$
(2)
$\displaystyle \lim_{ n \to \infty }S_n$を求めよ。
出典:2012年神戸大学 入試問題
5次式の因数分解 R15中学生はご遠慮ください

単元:
#数Ⅰ#数と式#複素数と方程式#式の計算(整式・展開・因数分解)#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^5+16x+32$
これを因数分解(整数係数)せよ.
この動画を見る
$ x^5+16x+32$
これを因数分解(整数係数)せよ.
福田の数学〜慶應義塾大学2022年看護医療学部第1問(3)〜三角関数の最大最小の種類

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)関数$f(\theta)=\cos2\theta+2\cos\theta$が
$0 \leqq \theta \leqq \pi$ の範囲で最小値をとるのは$\theta=\boxed{\ \ ア\ \ }$
のときであり、最大値を取るのは$\theta=\boxed{\ \ イ\ \ }$のときである。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(3)関数$f(\theta)=\cos2\theta+2\cos\theta$が
$0 \leqq \theta \leqq \pi$ の範囲で最小値をとるのは$\theta=\boxed{\ \ ア\ \ }$
のときであり、最大値を取るのは$\theta=\boxed{\ \ イ\ \ }$のときである。
2022慶應義塾大学看護医療学科過去問
ハルハル様の作成問題③ #複素数

単元:
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$z$:複素数
$a$:実数
$2Z^2+3|Z|Z=a$を解け
この動画を見る
$z$:複素数
$a$:実数
$2Z^2+3|Z|Z=a$を解け
福田の数学〜慶應義塾大学2022年看護医療学部第1問(2)〜指数計算

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
問題文全文(内容文):
${\large\boxed{1}}$(2)aを正の実数、pを実数とする。$a^{2p}=3$のとき、
$\frac{a^{2p}-a^{-2p}}{a^p-a^{-p}}$の値は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(2)aを正の実数、pを実数とする。$a^{2p}=3$のとき、
$\frac{a^{2p}-a^{-2p}}{a^p-a^{-p}}$の値は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
福田の数学〜慶應義塾大学2022年看護医療学部第1問(1)〜対数計算

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(1)$\log_3\sqrt6\ -\log_3\frac{2}{3}+\log_3\sqrt2\ $を有理数で表すと$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(1)$\log_3\sqrt6\ -\log_3\frac{2}{3}+\log_3\sqrt2\ $を有理数で表すと$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学看護医療学科過去問
大学入試問題#254 神戸大学2012 #定積分
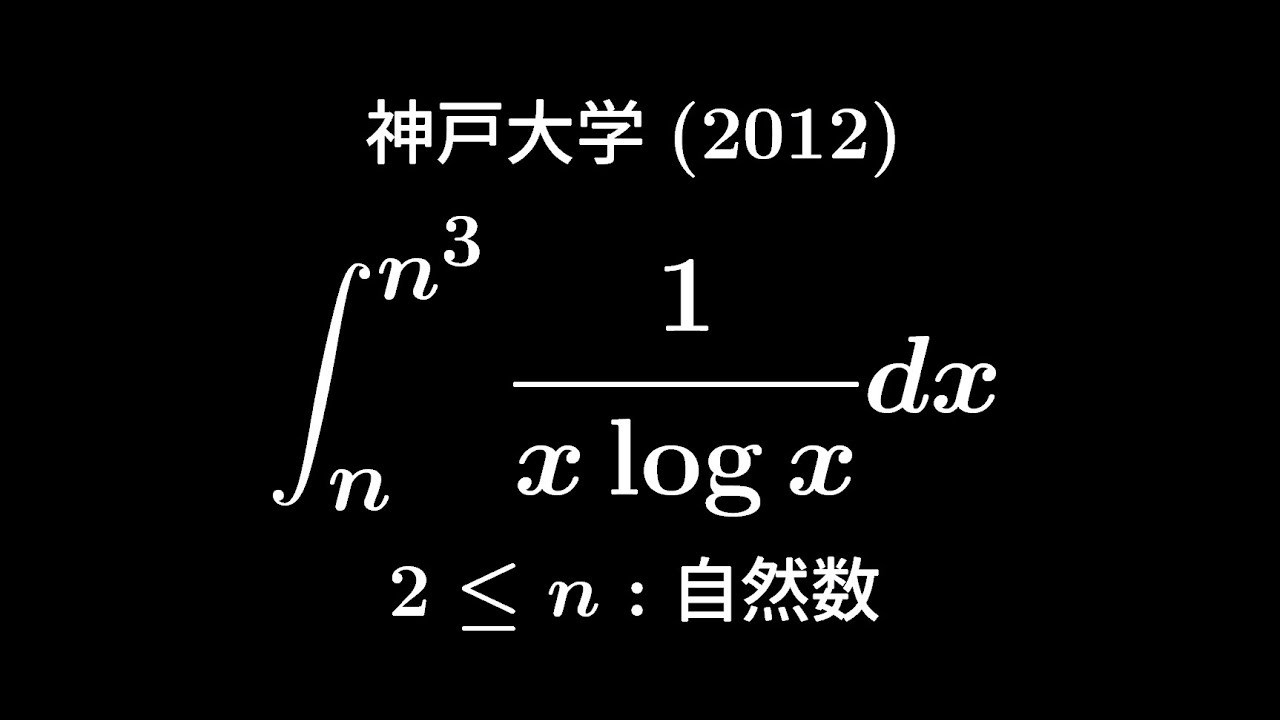
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典:2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典:2012年神戸大学 入試問題
福田の数学〜慶應義塾大学2022年環境情報学部第6問〜新型ウィルス感染拡大による大学の授業形態の決定

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#図形と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{6}}$ある大学で来学期の授業の形式をどうするかを検討している。
授業形式の選択としては、通常の対面形式(授業形式uと呼ぶことにする)、
$\textrm{Web}$上で試料を閲覧できたり課題を行ったりできるオンデマンド形式(授業形式vと呼ぶことにする)
$\textrm{Web}$会議システムを使用するオンライン配信形式(授業形式wと呼ぶことにする)
の3つがあるとする。
また、来学期の新型ウイルスの感染状況については、
急激に拡大している状況(感染状況xと呼ぶことにする)、
ピークは過ぎたが十分な収束にはいたっていない状況(感染状況yとよぶことにする)、
ある程度収束した状況(感染状況zとよぶことにする)の3つが考えられるとする。
いま、この大学は授業形式と新型ウイルスの感染状況の組み合わせについて、
次の表(※動画参照)に示す評論値(値が高いほど評価も高い)を定めているものとする。
来学期の感染状況について、感染状況xである確率を$p_x$、
感染状況yである確率をp_y、感染状況zである確率を$p_z$とすると、
xyz空間において点$p=(p_x,p_y,p_z)は(1,0,0),(0,1,0),(0,0,1)$を頂点とする正三角形上の
点としてあらわすことができる。この正三角形上において、点pから各辺に垂線を下ろしたとき、
(1,0,0)と向かいの辺に下ろした垂線の長さをl_x、(0,1,0)と向かいの辺に下した垂線の長さを$l_y$、
(0,0,1)と向かいの辺に下した垂線の長さを$l_z$とする。
(1)このとき$p_x=\frac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\ l_x,\ \ \ \,$
$p_y=\frac{\sqrt{\boxed{\ \ オカ\ \ }}}{\boxed{\ \ キク\ \ }}\ l_y,\ \ \ \ p_z=\frac{\sqrt{\boxed{\ \ ケコ\ \ }}}{\boxed{\ \ サシ\ \ }}\ l_z$が成り立つ。
いま、正三角形上の点$p=(p_x,p_y,p_z)$に対して、上記の評価の期待値を最大にする
授業形式のラベルをつけることにする。ただし、pによっては評価値を最大にする選択が
複数ある場合もあり、その場合にはpに複数のラベルをつけることにする。
さらに、原点と(0,1,0),(0,0,1)を原点とするyz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にxという感染状況のラベルをつけ、
原点と(1,0,0),(0,0,1)を原点とするxz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にyという感染状況のラベルをつけ、
原点と(1,0,0),(0,1,0)を原点とするxy平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にzという感染状況のラベルをつけることにする。
すると、正三角形と3つの直角二等辺三角形からなる四面体の面上(頂点、辺も含む)
のそれぞれの点には、1つもしくは複数のラベルがつくことになる。例えば、
原点には$\left\{x,y,z\right\}$の3つのラベルがつく。
(2)このとき、正三角形の面上(頂点、辺も含む)の各点pにつけられるラベルの
可能性を列挙すると、以下の通りとなる。ただし、複数のラベルがつけられる場合には、
それぞれの中括弧内では、アルファベット順に書くものとする。空欄に入る
ラベルについて下記の選択肢から選びなさい。
単一のラベルがつく場合:$\left\{\boxed{\ \ ス\ \ }\right\},\left\{w\right\}$
2つのラベルがつく場合:$\left\{\boxed{\ \ セ\ \ },w\right\},\left\{u,\boxed{\ \ ソ\ \ }\right\},$
$\left\{\boxed{\ \ タ\ \ },y\right\},\left\{w,y\right\},\left\{\boxed{\ \ チ\ \ },z\right\}$
3つのラベルがつく場合:$\left\{\boxed{\ \ ツ\ \ },w,\boxed{\ \ テ\ \ }\right\},\left\{\boxed{\ \ ト\ \ },\boxed{\ \ ナ\ \ },\boxed{\ \ ニ\ \ }\right\}$
4つのラベルがつく場合:$\left\{u,\boxed{\ \ ヌ\ \ },\boxed{\ \ ネ\ \ },\boxed{\ \ ノ\ \ }\right\},\left\{\boxed{\ \ ハ\ \ },\boxed{\ \ ヒ\ \ },\boxed{\ \ フ\ \ },\boxed{\ \ ヘ\ \ }\right\}$
選択肢:$(1)\ \ \ u\ \ \ (2)\ \ \ v\ \ \ (3)\ \ \ w\ \ \ (4)\ \ \ x\ \ \ (5)\ \ \ y\ \ \ (6)\ \ \ z$
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{6}}$ある大学で来学期の授業の形式をどうするかを検討している。
授業形式の選択としては、通常の対面形式(授業形式uと呼ぶことにする)、
$\textrm{Web}$上で試料を閲覧できたり課題を行ったりできるオンデマンド形式(授業形式vと呼ぶことにする)
$\textrm{Web}$会議システムを使用するオンライン配信形式(授業形式wと呼ぶことにする)
の3つがあるとする。
また、来学期の新型ウイルスの感染状況については、
急激に拡大している状況(感染状況xと呼ぶことにする)、
ピークは過ぎたが十分な収束にはいたっていない状況(感染状況yとよぶことにする)、
ある程度収束した状況(感染状況zとよぶことにする)の3つが考えられるとする。
いま、この大学は授業形式と新型ウイルスの感染状況の組み合わせについて、
次の表(※動画参照)に示す評論値(値が高いほど評価も高い)を定めているものとする。
来学期の感染状況について、感染状況xである確率を$p_x$、
感染状況yである確率をp_y、感染状況zである確率を$p_z$とすると、
xyz空間において点$p=(p_x,p_y,p_z)は(1,0,0),(0,1,0),(0,0,1)$を頂点とする正三角形上の
点としてあらわすことができる。この正三角形上において、点pから各辺に垂線を下ろしたとき、
(1,0,0)と向かいの辺に下ろした垂線の長さをl_x、(0,1,0)と向かいの辺に下した垂線の長さを$l_y$、
(0,0,1)と向かいの辺に下した垂線の長さを$l_z$とする。
(1)このとき$p_x=\frac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\ l_x,\ \ \ \,$
$p_y=\frac{\sqrt{\boxed{\ \ オカ\ \ }}}{\boxed{\ \ キク\ \ }}\ l_y,\ \ \ \ p_z=\frac{\sqrt{\boxed{\ \ ケコ\ \ }}}{\boxed{\ \ サシ\ \ }}\ l_z$が成り立つ。
いま、正三角形上の点$p=(p_x,p_y,p_z)$に対して、上記の評価の期待値を最大にする
授業形式のラベルをつけることにする。ただし、pによっては評価値を最大にする選択が
複数ある場合もあり、その場合にはpに複数のラベルをつけることにする。
さらに、原点と(0,1,0),(0,0,1)を原点とするyz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にxという感染状況のラベルをつけ、
原点と(1,0,0),(0,0,1)を原点とするxz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にyという感染状況のラベルをつけ、
原点と(1,0,0),(0,1,0)を原点とするxy平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にzという感染状況のラベルをつけることにする。
すると、正三角形と3つの直角二等辺三角形からなる四面体の面上(頂点、辺も含む)
のそれぞれの点には、1つもしくは複数のラベルがつくことになる。例えば、
原点には$\left\{x,y,z\right\}$の3つのラベルがつく。
(2)このとき、正三角形の面上(頂点、辺も含む)の各点pにつけられるラベルの
可能性を列挙すると、以下の通りとなる。ただし、複数のラベルがつけられる場合には、
それぞれの中括弧内では、アルファベット順に書くものとする。空欄に入る
ラベルについて下記の選択肢から選びなさい。
単一のラベルがつく場合:$\left\{\boxed{\ \ ス\ \ }\right\},\left\{w\right\}$
2つのラベルがつく場合:$\left\{\boxed{\ \ セ\ \ },w\right\},\left\{u,\boxed{\ \ ソ\ \ }\right\},$
$\left\{\boxed{\ \ タ\ \ },y\right\},\left\{w,y\right\},\left\{\boxed{\ \ チ\ \ },z\right\}$
3つのラベルがつく場合:$\left\{\boxed{\ \ ツ\ \ },w,\boxed{\ \ テ\ \ }\right\},\left\{\boxed{\ \ ト\ \ },\boxed{\ \ ナ\ \ },\boxed{\ \ ニ\ \ }\right\}$
4つのラベルがつく場合:$\left\{u,\boxed{\ \ ヌ\ \ },\boxed{\ \ ネ\ \ },\boxed{\ \ ノ\ \ }\right\},\left\{\boxed{\ \ ハ\ \ },\boxed{\ \ ヒ\ \ },\boxed{\ \ フ\ \ },\boxed{\ \ ヘ\ \ }\right\}$
選択肢:$(1)\ \ \ u\ \ \ (2)\ \ \ v\ \ \ (3)\ \ \ w\ \ \ (4)\ \ \ x\ \ \ (5)\ \ \ y\ \ \ (6)\ \ \ z$
2022慶應義塾大学環境情報学部過去問
大学入試問題#253 青山学院大学(2011) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典:2011年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典:2011年青山学院大学 入試問題
数学オリンピック予選

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#解と判別式・解と係数の関係#数学オリンピック#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
有理数係数の2次方程式
$ x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+$
$・・・・・・+a_{2n-1}x+a_{2n}=0$
の解はすべて$x^2+5x+7=0$の解にもなっている.
$a_1$の値を求めよ.
この動画を見る
有理数係数の2次方程式
$ x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+$
$・・・・・・+a_{2n-1}x+a_{2n}=0$
の解はすべて$x^2+5x+7=0$の解にもなっている.
$a_1$の値を求めよ.
大学入試問題#252 茨城大学(2012) #定積分

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
注意ポイントあり!定数分離の良問です【数学 入試問題】【北海道大学】

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
関数 $f(\theta)=\dfrac{1}{\sqrt 2}sin2 \theta-sin \theta+cos\theta$ ($0≦\theta≦\pi)$を考える。
(3)$a$を実数の定数とする。
$f(\theta)=a$となる$\theta$がちょうど2個であるような$a$のい範囲を求めよ。
北海道大過去問
この動画を見る
関数 $f(\theta)=\dfrac{1}{\sqrt 2}sin2 \theta-sin \theta+cos\theta$ ($0≦\theta≦\pi)$を考える。
(3)$a$を実数の定数とする。
$f(\theta)=a$となる$\theta$がちょうど2個であるような$a$のい範囲を求めよ。
北海道大過去問
福田の数学〜慶應義塾大学2022年環境情報学部第4問〜ピラミッドを切って体積を求める

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$(1)$xyz$空間において$|x|+|y|+|z| \leqq 1$を満たす立体の体積は$\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}$である。
(2)aを実数としたとき、xyz空間において
$|x-a|+|y-a|+|z| \leqq 1,\ \ \ x \geqq 0,\ \ \ y \geqq 0,\ \ \ z \geqq 0$
を満たす立体の体積V(a)は
$(\textrm{a})a \lt \frac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}$のとき、$V(a)=0$,
$(\textrm{b})\frac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }} \leqq a \lt 0$のとき、
$V(a)=\frac{\boxed{\ \ ケコ\ \ }a^3+\boxed{\ \ サシ\ \ }a^2+\boxed{\ \ スセ\ \ }a+\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }},$
$(\textrm{c})0 \leqq a \lt \frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニ\ \ }}$のとき、
$V(a)=\frac{\boxed{\ \ ヌネ\ \ }a^3+\boxed{\ \ ノハ\ \ }a+\boxed{\ \ ヒフ\ \ }}{\boxed{\ \ ヘホ\ \ }},$
$(\textrm{d})\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニ\ \ }} \leqq a \lt \frac{\boxed{\ \ マミ\ \ }}{\boxe$d{\ \ ムメ\ \ }}$のとき、
$V(a)=\frac{\boxed{\ \ モヤ\ \ }a^3+\boxed{\ \ ユヨ\ \ }a^2+\boxed{\ \ ラリ\ \ }a}{\boxed{\ \ ルレ\ \ }},$
$(\textrm{e})\frac{\boxed{\ \ マミ\ \ }}{\boxed{\ \ ムメ\ \ }} \leqq a$のとき、
$V(a)=\frac{\boxed{\ \ ロワ\ \ }}{\boxed{\ \ ヲン\ \ }}$
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{4}}$(1)$xyz$空間において$|x|+|y|+|z| \leqq 1$を満たす立体の体積は$\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}$である。
(2)aを実数としたとき、xyz空間において
$|x-a|+|y-a|+|z| \leqq 1,\ \ \ x \geqq 0,\ \ \ y \geqq 0,\ \ \ z \geqq 0$
を満たす立体の体積V(a)は
$(\textrm{a})a \lt \frac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }}$のとき、$V(a)=0$,
$(\textrm{b})\frac{\boxed{\ \ オカ\ \ }}{\boxed{\ \ キク\ \ }} \leqq a \lt 0$のとき、
$V(a)=\frac{\boxed{\ \ ケコ\ \ }a^3+\boxed{\ \ サシ\ \ }a^2+\boxed{\ \ スセ\ \ }a+\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }},$
$(\textrm{c})0 \leqq a \lt \frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニ\ \ }}$のとき、
$V(a)=\frac{\boxed{\ \ ヌネ\ \ }a^3+\boxed{\ \ ノハ\ \ }a+\boxed{\ \ ヒフ\ \ }}{\boxed{\ \ ヘホ\ \ }},$
$(\textrm{d})\frac{\boxed{\ \ テト\ \ }}{\boxed{\ \ ナニ\ \ }} \leqq a \lt \frac{\boxed{\ \ マミ\ \ }}{\boxe$d{\ \ ムメ\ \ }}$のとき、
$V(a)=\frac{\boxed{\ \ モヤ\ \ }a^3+\boxed{\ \ ユヨ\ \ }a^2+\boxed{\ \ ラリ\ \ }a}{\boxed{\ \ ルレ\ \ }},$
$(\textrm{e})\frac{\boxed{\ \ マミ\ \ }}{\boxed{\ \ ムメ\ \ }} \leqq a$のとき、
$V(a)=\frac{\boxed{\ \ ロワ\ \ }}{\boxed{\ \ ヲン\ \ }}$
2022慶應義塾大学環境情報学部過去問
大学入試問題#251 新潟大学(2012) #相加相乗平均

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学
指導講師:
ますただ
問題文全文(内容文):
$a,b,c,d$:正の実数
$\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[ 4 ]{ abcd }$を示せ
出典:2012年新潟大学 入試問題
この動画を見る
$a,b,c,d$:正の実数
$\displaystyle \frac{a+b+c+d}{4} \geqq \sqrt[ 4 ]{ abcd }$を示せ
出典:2012年新潟大学 入試問題
福田の数学〜慶應義塾大学2022年環境情報学部第3問〜4次関数のグラフの接線と囲まれた面積

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}$xy平面上の曲線Cを$y=x^2(x-1)(x+2)$とする。
(1)Cに2点で下から接する直線Lの方程式は
$y=\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカ\ \ }}\ x+\frac{\boxed{\ \ キクケ\ \ }}{\boxed{\ \ コサシ\ \ }}$である。
(2)CとLが囲む図の斜線部分の面積(※動画参照)は
$\frac{\boxed{\ \ スセソ\ \ }\sqrt{\boxed{\ \ タチツ\ \ }}}{\boxed{\ \ テトナ\ \ }}$となる。
ただし、次の公式を使ってもかまわない(m,nは正の整数)
$\int_{\alpha}^{\beta}(x-\alpha)^m(x-\beta)^ndx=\frac{(-1)^nm!n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}$
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{3}}$xy平面上の曲線Cを$y=x^2(x-1)(x+2)$とする。
(1)Cに2点で下から接する直線Lの方程式は
$y=\frac{\boxed{\ \ アイウ\ \ }}{\boxed{\ \ エオカ\ \ }}\ x+\frac{\boxed{\ \ キクケ\ \ }}{\boxed{\ \ コサシ\ \ }}$である。
(2)CとLが囲む図の斜線部分の面積(※動画参照)は
$\frac{\boxed{\ \ スセソ\ \ }\sqrt{\boxed{\ \ タチツ\ \ }}}{\boxed{\ \ テトナ\ \ }}$となる。
ただし、次の公式を使ってもかまわない(m,nは正の整数)
$\int_{\alpha}^{\beta}(x-\alpha)^m(x-\beta)^ndx=\frac{(-1)^nm!n!}{(m+n+1)!}(\beta-\alpha)^{m+n+1}$
2022慶應義塾大学環境情報学部過去問
大学入試問題#250 福井大学(2012) #定積分
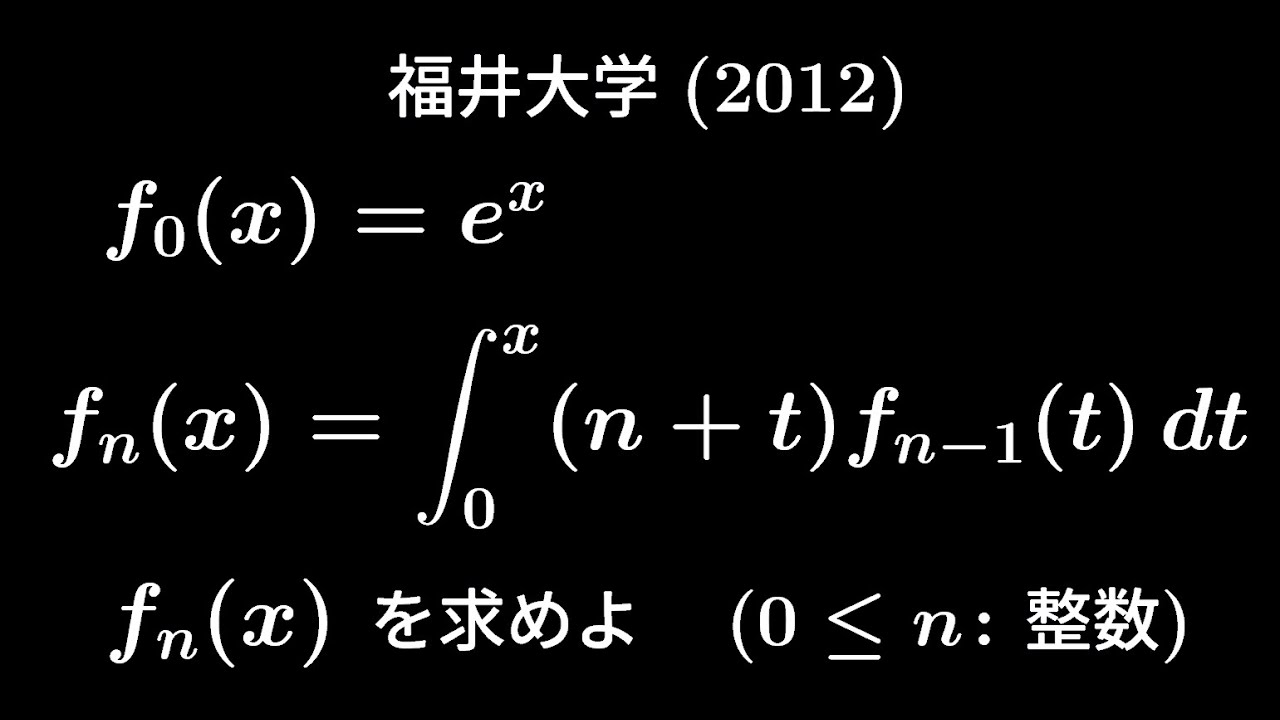
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#数列#漸化式#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
この動画を見る
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
虚数解の6乗が実数
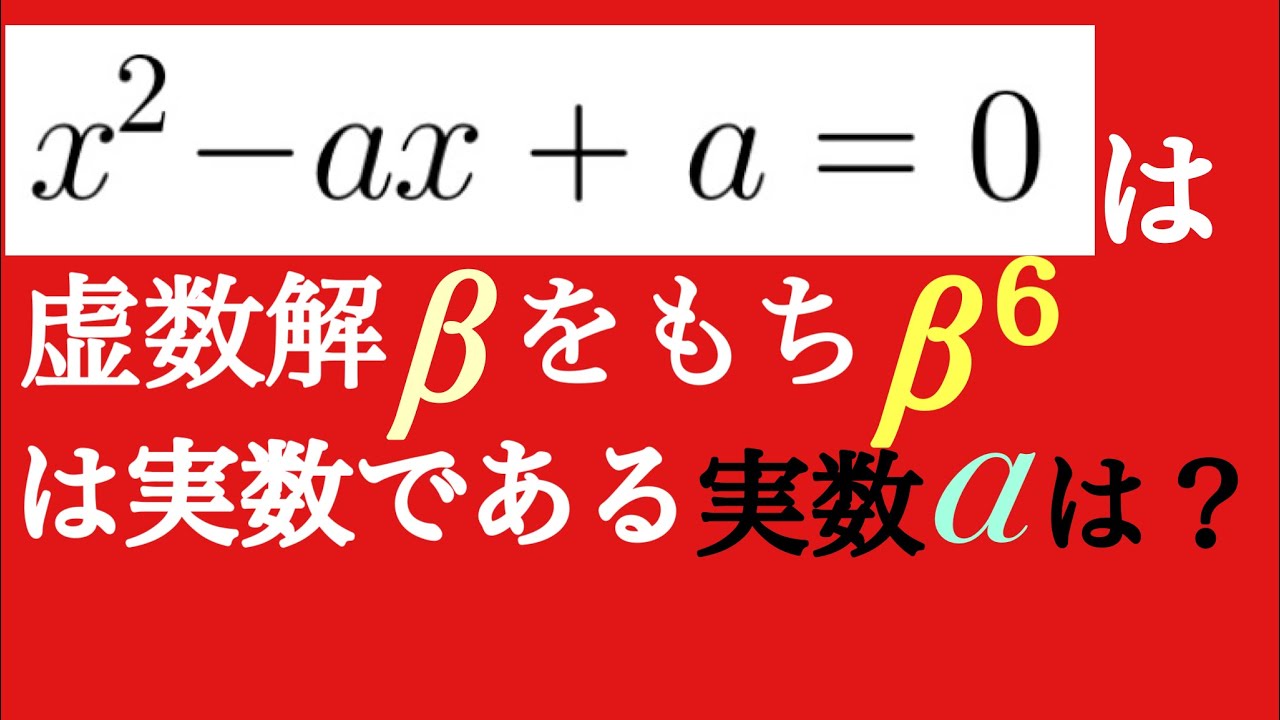
単元:
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^2-ax+a=0$は虚数解$\beta$をもち$\beta^6$は実数である.
aの値を求めよ.
この動画を見る
$ x^2-ax+a=0$は虚数解$\beta$をもち$\beta^6$は実数である.
aの値を求めよ.
福田の数学〜慶應義塾大学2022年環境情報学部第2問〜三角関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}\ 0 \leqq \theta \leqq \pi $のとき、関数$y=\sin3\theta-3\cos(\theta-\frac{\pi}{6})$の最大値と最小値を求めたい。
(1)$x=\cos(\theta-\frac{\pi}{6})$とおくと、もとの関数は
$y=\boxed{\ \ アイ\ \ }\ x^3+\boxed{\ \ ウエ\ \ }\ x^2+\boxed{\ \ オカ\ \ }\ x+\boxed{\ \ キク\ \ }$
と書き直すことができる。
(2)このことから、もとの関数の最大値は$\theta=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}\ \pi$のときに
$\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}$
であり、最小値は$\theta=\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \pi$のときに
$\boxed{\ \ ナニ\ \ }\sqrt{\boxed{\ \ ヌネ\ \ }}$であることがわかる。
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{2}}\ 0 \leqq \theta \leqq \pi $のとき、関数$y=\sin3\theta-3\cos(\theta-\frac{\pi}{6})$の最大値と最小値を求めたい。
(1)$x=\cos(\theta-\frac{\pi}{6})$とおくと、もとの関数は
$y=\boxed{\ \ アイ\ \ }\ x^3+\boxed{\ \ ウエ\ \ }\ x^2+\boxed{\ \ オカ\ \ }\ x+\boxed{\ \ キク\ \ }$
と書き直すことができる。
(2)このことから、もとの関数の最大値は$\theta=\frac{\boxed{\ \ ケコ\ \ }}{\boxed{\ \ サシ\ \ }}\ \pi$のときに
$\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }}$
であり、最小値は$\theta=\frac{\boxed{\ \ チツ\ \ }}{\boxed{\ \ テト\ \ }}\ \pi$のときに
$\boxed{\ \ ナニ\ \ }\sqrt{\boxed{\ \ ヌネ\ \ }}$であることがわかる。
2022慶應義塾大学環境情報学部過去問
大学入試問題#249 早稲田大学(2014) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典:2014年早稲田大学 入試問題
この動画を見る
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典:2014年早稲田大学 入試問題
簡単な指数方程式

単元:
#数Ⅱ#複素数と方程式#指数関数と対数関数#剰余の定理・因数定理・組み立て除法と高次方程式#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 2^x-3^x=\sqrt{6^x-9^x}$
これの実数解を求めよ.
この動画を見る
$ 2^x-3^x=\sqrt{6^x-9^x}$
これの実数解を求めよ.
何乗しても実数にならない数

式の値 虚数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
3次方程式$x^3+1 = 0$の虚数解の1つをαとするとき
$α^{300} + α^{200} + α^{100} + \frac {1}{α^{100}} + \frac {1}{α^{200}} +\frac {1}{α^{300}} = ?$
甲南大学
この動画を見る
3次方程式$x^3+1 = 0$の虚数解の1つをαとするとき
$α^{300} + α^{200} + α^{100} + \frac {1}{α^{100}} + \frac {1}{α^{200}} +\frac {1}{α^{300}} = ?$
甲南大学
【9分でマスター!!】とても重要な加法定理を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅱ#図形と方程式#三角関数#加法定理とその応用#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学2B
加法定理について解説します。
①$\cos15$℃
②$\sin75$℃
$\alpha$は第1象限の角で$\sin\alpha=\frac{5}{13}$、$\beta$は第3象限の角で$\cos\beta=-\frac{3}{5}$とする。
$\sin(\alpha+\beta)$、$\cos(\alpha+\beta)$の値は?
この動画を見る
数学2B
加法定理について解説します。
①$\cos15$℃
②$\sin75$℃
$\alpha$は第1象限の角で$\sin\alpha=\frac{5}{13}$、$\beta$は第3象限の角で$\cos\beta=-\frac{3}{5}$とする。
$\sin(\alpha+\beta)$、$\cos(\alpha+\beta)$の値は?
福田の数学〜慶應義塾大学2022年総合政策学部第3問〜定積分で表された関数の最小値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}$実数$k \gt 0$ に対して、関数$A(k)=\int_0^2|x^2-kx|dx$とすると
$A(k)=
\left\{\begin{array}{1}
\frac{\boxed{\ \ アイ\ \ }\ k^3+\ \boxed{\ \ ウエ\ \ }\ k^2+\ \boxed{\ \ オカ\ \ }\ k+\ \boxed{\ \ キク\ \ }}{\boxed{\ \ ケコ\ \ }}
(0 \lt k \lt \boxed{\ \ サシ\ \ })
\frac{\boxed{\ \ スセ\ \ }\ k+\ \boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}(\boxed{\ \ サシ\ \ } \leqq k)
\end{array}
\right.$
となる。この関数A(k)が最小となるのは$k=\sqrt{\boxed{\ \ テト\ \ }}$のときで、そのときの
A(k)の値は$\frac{\boxed{\ \ ナニ\ \ }+\boxed{\ \ ヌネ\ \ }\sqrt{\boxed{\ \ ノハ\ \ }}}{\boxed{\ \ ヒフ\ \ }}$
2022慶應義塾大学総合政策学部過去問
この動画を見る
${\large\boxed{3}}$実数$k \gt 0$ に対して、関数$A(k)=\int_0^2|x^2-kx|dx$とすると
$A(k)=
\left\{\begin{array}{1}
\frac{\boxed{\ \ アイ\ \ }\ k^3+\ \boxed{\ \ ウエ\ \ }\ k^2+\ \boxed{\ \ オカ\ \ }\ k+\ \boxed{\ \ キク\ \ }}{\boxed{\ \ ケコ\ \ }}
(0 \lt k \lt \boxed{\ \ サシ\ \ })
\frac{\boxed{\ \ スセ\ \ }\ k+\ \boxed{\ \ ソタ\ \ }}{\boxed{\ \ チツ\ \ }}(\boxed{\ \ サシ\ \ } \leqq k)
\end{array}
\right.$
となる。この関数A(k)が最小となるのは$k=\sqrt{\boxed{\ \ テト\ \ }}$のときで、そのときの
A(k)の値は$\frac{\boxed{\ \ ナニ\ \ }+\boxed{\ \ ヌネ\ \ }\sqrt{\boxed{\ \ ノハ\ \ }}}{\boxed{\ \ ヒフ\ \ }}$
2022慶應義塾大学総合政策学部過去問
大学入試問題#245 津田塾大学2014 #三角関数 基本的な問題ですが、数IIの範囲で解ける良問だと思いました。

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#津田塾大学
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq \theta \leqq 2\pi$
$\sin^3\theta+\cos^3\theta$の最大値、最小値を求めよ。
出典:2014年津田塾大学 入試問題
この動画を見る
$0 \leqq \theta \leqq 2\pi$
$\sin^3\theta+\cos^3\theta$の最大値、最小値を求めよ。
出典:2014年津田塾大学 入試問題
基本問題

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x^4-2x^3+3x^2-2x+1=0$のとき,
$\dfrac{x^{2222}}{x^{2224}+1}$の値を求めよ.
この動画を見る
$ x^4-2x^3+3x^2-2x+1=0$のとき,
$\dfrac{x^{2222}}{x^{2224}+1}$の値を求めよ.
大学入試問題#243 慶應義塾大学(2014) #3次方程式の性質

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$k$:実数
$x^3-kx+1=0$は実数の重解とそれと異なる実数解をもつ
このとき$k$の値を求めよ。
出典:2014年慶應義塾大学 入試問題
この動画を見る
$k$:実数
$x^3-kx+1=0$は実数の重解とそれと異なる実数解をもつ
このとき$k$の値を求めよ。
出典:2014年慶應義塾大学 入試問題
整式の剰余

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2022}$を$x^6-x^5+x^4-x^3+x^2-x+1$で割った余りを求めよ.
この動画を見る
$x^{2022}$を$x^6-x^5+x^4-x^3+x^2-x+1$で割った余りを求めよ.
あの公式が力を発揮する良問!微分・積分のよく出る問題です【数学 入試問題】【九州大学】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a≧0$とする。2つの放物線$ C_1:y=x^2,C_2:y=3(x-a)^2+a^3-40$を考える。
(1)$C_1$と$C_2$が異なる2点で交わるような定数$a$の値の範囲を求めよ。
九州大過去問
この動画を見る
$a≧0$とする。2つの放物線$ C_1:y=x^2,C_2:y=3(x-a)^2+a^3-40$を考える。
(1)$C_1$と$C_2$が異なる2点で交わるような定数$a$の値の範囲を求めよ。
九州大過去問
大学入試問題#241 早稲田大学(2014) #指数

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
関数$f(x)=(27^x+\displaystyle \frac{1}{27^x})-5(9^x+\displaystyle \frac{1}{9^x})$
$-5(3^x+\displaystyle \frac{1}{3^x})+1$の最小値と、そのときの$x$の値を求めよ。
出典:2014年早稲田大学 入試問題
この動画を見る
関数$f(x)=(27^x+\displaystyle \frac{1}{27^x})-5(9^x+\displaystyle \frac{1}{9^x})$
$-5(3^x+\displaystyle \frac{1}{3^x})+1$の最小値と、そのときの$x$の値を求めよ。
出典:2014年早稲田大学 入試問題
