 数列
数列
 数列
数列
数学「大学入試良問集」【13−4 漸化式(逆数型)】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a_1=1,a_{n+1}=\displaystyle \frac{a_n}{4a_n+1}(n=1,2,・・・)$で定まる数列$\{a_n\}$に関して、次の各問に答えよ。
(1)
$\displaystyle \frac{1}{a_n}$を$n$の式で表せ。
(2)
$\displaystyle \sum_{k=1}^n\left[ \dfrac{ 12 }{ a_k-a_{k+1} }+9 \right]$を$n$の式で表せ。
この動画を見る
$a_1=1,a_{n+1}=\displaystyle \frac{a_n}{4a_n+1}(n=1,2,・・・)$で定まる数列$\{a_n\}$に関して、次の各問に答えよ。
(1)
$\displaystyle \frac{1}{a_n}$を$n$の式で表せ。
(2)
$\displaystyle \sum_{k=1}^n\left[ \dfrac{ 12 }{ a_k-a_{k+1} }+9 \right]$を$n$の式で表せ。
数学「大学入試良問集」【13−3 等差×等比の和】を宇宙一わかりやすく
単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#名古屋市立大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
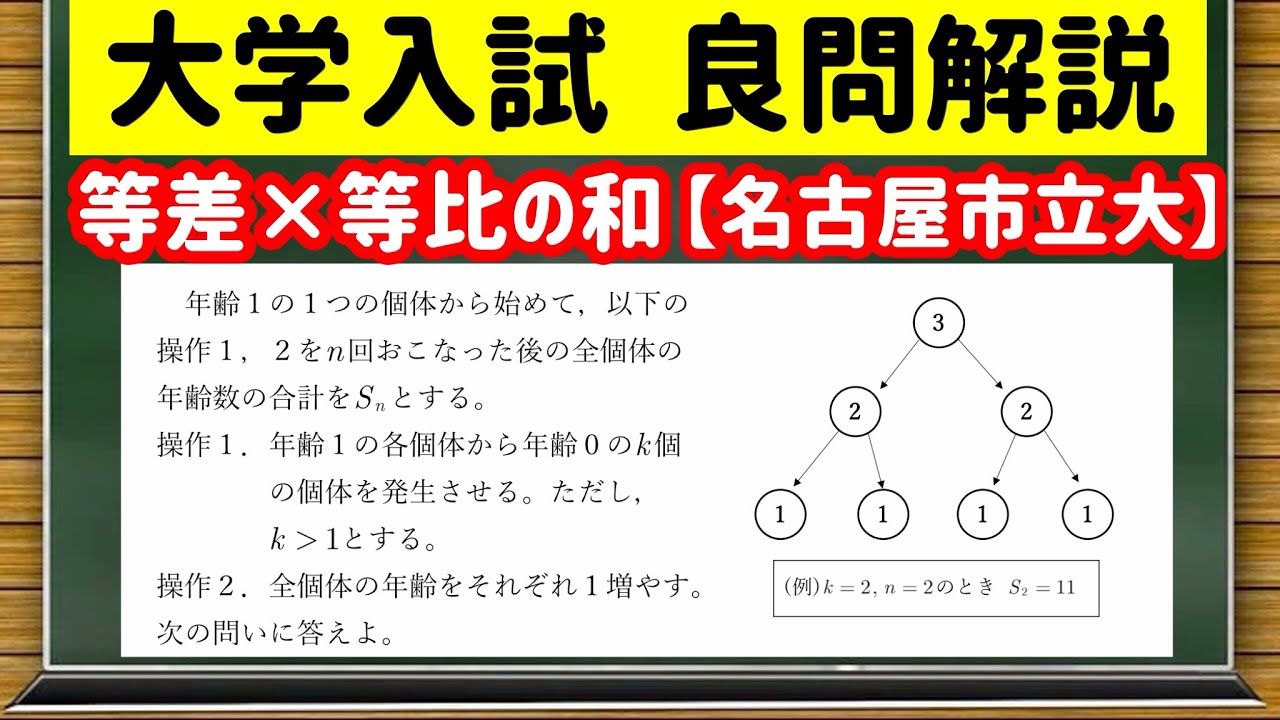
年齢1の1つの個体から始めて、以下の操作1,2を$n$回おこなった後の全個体の年齢数の合計を$S_n$とする。
操作1.
年齢1の各個体から年齢0の$k$個の個体を発生される。
ただし、$k \gt 1$とする。
操作2.
全個体の年齢をそれぞれ1増やす。
次の問いに答えよ。
(1)
$k=2$のとき$S_4$を求めよ。
(2)
操作1,2を$n$回おこなった後の平均年齢を$A_n$とするとき、$A_n \lt \displaystyle \frac{k}{k-1}$となることを示せ。
この動画を見る
年齢1の1つの個体から始めて、以下の操作1,2を$n$回おこなった後の全個体の年齢数の合計を$S_n$とする。
操作1.
年齢1の各個体から年齢0の$k$個の個体を発生される。
ただし、$k \gt 1$とする。
操作2.
全個体の年齢をそれぞれ1増やす。
次の問いに答えよ。
(1)
$k=2$のとき$S_4$を求めよ。
(2)
操作1,2を$n$回おこなった後の平均年齢を$A_n$とするとき、$A_n \lt \displaystyle \frac{k}{k-1}$となることを示せ。
数学「大学入試良問集」【13−2 部分分数分解による和】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#滋賀大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
数列$2,6,12,20,30,42,・・・$について、$n$を自然数として以下の問いに答えよ。
(1)
第$n$項$a_n$と、初項から第$n$項までの和$S_n$を求めよ。
(2)
$\displaystyle \frac{1}{a_1}+\displaystyle \frac{1}{a_2}+\displaystyle \frac{1}{a_3}+・・・+\displaystyle \frac{1}{a_n}$を求めよ。
(3)
$\displaystyle \frac{1}{S_1}+\displaystyle \frac{1}{S_2}+\displaystyle \frac{1}{S_3}+・・・+\displaystyle \frac{1}{S_n}$を求めよ。
この動画を見る
数列$2,6,12,20,30,42,・・・$について、$n$を自然数として以下の問いに答えよ。
(1)
第$n$項$a_n$と、初項から第$n$項までの和$S_n$を求めよ。
(2)
$\displaystyle \frac{1}{a_1}+\displaystyle \frac{1}{a_2}+\displaystyle \frac{1}{a_3}+・・・+\displaystyle \frac{1}{a_n}$を求めよ。
(3)
$\displaystyle \frac{1}{S_1}+\displaystyle \frac{1}{S_2}+\displaystyle \frac{1}{S_3}+・・・+\displaystyle \frac{1}{S_n}$を求めよ。
数学「大学入試良問集」【13−1 Snとanの取り扱い】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#明星大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
数列$\{a_n\}$の初項から第$n$項までの和を$S_n$とする。
$S_n=-2a_n+3n$が成り立つとき、次の問いに答えよ。
(1)$a_1$と$a_2$を求めよ。
(2)$a_{n+1}$を$a_n$を用いて表せ。
(3)$a_n$を$n$を用いて表せ。
この動画を見る
数列$\{a_n\}$の初項から第$n$項までの和を$S_n$とする。
$S_n=-2a_n+3n$が成り立つとき、次の問いに答えよ。
(1)$a_1$と$a_2$を求めよ。
(2)$a_{n+1}$を$a_n$を用いて表せ。
(3)$a_n$を$n$を用いて表せ。
09岡山県教員採用試験(数学:1-(5) 行列式)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(5)$
$A=\begin{pmatrix}
1 & x & 2 \\
1 & x^2 & 4 \\
1 & x^3 & 8
\end{pmatrix}$
$\vert A \vert=0$となるとき$x$の値を求めよ.
この動画を見る
$\boxed{1}-(5)$
$A=\begin{pmatrix}
1 & x & 2 \\
1 & x^2 & 4 \\
1 & x^3 & 8
\end{pmatrix}$
$\vert A \vert=0$となるとき$x$の値を求めよ.
18岡山県教員採用試験(数学:5番 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
等差数列${a_n}$は
$a_9=0,a_{12}=25$を満たしている.
$2^{a_1}\times 2^{a_2}\times ・・・ \times 2^{a_n}=4096^{10}$となる
$n$を求めよ.
この動画を見る
$\boxed{5}$
等差数列${a_n}$は
$a_9=0,a_{12}=25$を満たしている.
$2^{a_1}\times 2^{a_2}\times ・・・ \times 2^{a_n}=4096^{10}$となる
$n$を求めよ.
15和歌山県教員採用試験(数学:5番 行列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$A=\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}$
$A^2-3A+2E=\theta$をみたすとき,
$(a+d,ad-bc)$を全て求めよ.
この動画を見る
$\boxed{5}$
$A=\begin{pmatrix}
a & b \\
c & d
\end{pmatrix}$
$A^2-3A+2E=\theta$をみたすとき,
$(a+d,ad-bc)$を全て求めよ.
【数B】数列:Σを使った等比数列の和の考え方

13滋賀県教員採用試験(数学:2番 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
$a_1=48$
$a_{n+1}=2a_n+2^{n+3}n-21\ 2^{n+1}$とする.
一般項$a_n$を求めよ.
この動画を見る
$\boxed{2}$
$a_1=48$
$a_{n+1}=2a_n+2^{n+3}n-21\ 2^{n+1}$とする.
一般項$a_n$を求めよ.
#14 数検1級1次過去問 数列 数検・教員採用試験

単元:
#数学検定・数学甲子園・数学オリンピック等#数列#数列とその和(等差・等比・階差・Σ)#その他#数学検定#数学検定1級#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$A=\begin{pmatrix}
3 & 0 & 2 \\
-4 & 1 & -3 \\
1 & 5 & -2
\end{pmatrix}$
次の行列を,$\ell A^2+mA+nE$で表せ.
$(\ell,m,n=IR)$
(1)$A^3$
(2)$A^5-5A^4+16A^3-24A^2$
この動画を見る
$\boxed{4}$
$A=\begin{pmatrix}
3 & 0 & 2 \\
-4 & 1 & -3 \\
1 & 5 & -2
\end{pmatrix}$
次の行列を,$\ell A^2+mA+nE$で表せ.
$(\ell,m,n=IR)$
(1)$A^3$
(2)$A^5-5A^4+16A^3-24A^2$
福田のわかった数学〜高校3年生理系010〜極限(10)解けない漸化式の極限

単元:
#数列#漸化式#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(10)
$a_1=2, a_{n+1}=\sqrt{a_n+30}$ のとき、
$\lim_{n \to \infty}a_n$ を調べよ。
この動画を見る
数学$\textrm{III}$ 極限(10)
$a_1=2, a_{n+1}=\sqrt{a_n+30}$ のとき、
$\lim_{n \to \infty}a_n$ を調べよ。
20和歌山県教員採用試験(数学:3番 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$S_1=3$
$S_{n+1}-5S_n=3・2^{n+1}-3$
一般項$a_n$を求めよ.
この動画を見る
$\boxed{3}$
$S_1=3$
$S_{n+1}-5S_n=3・2^{n+1}-3$
一般項$a_n$を求めよ.
背景を見破れ!
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
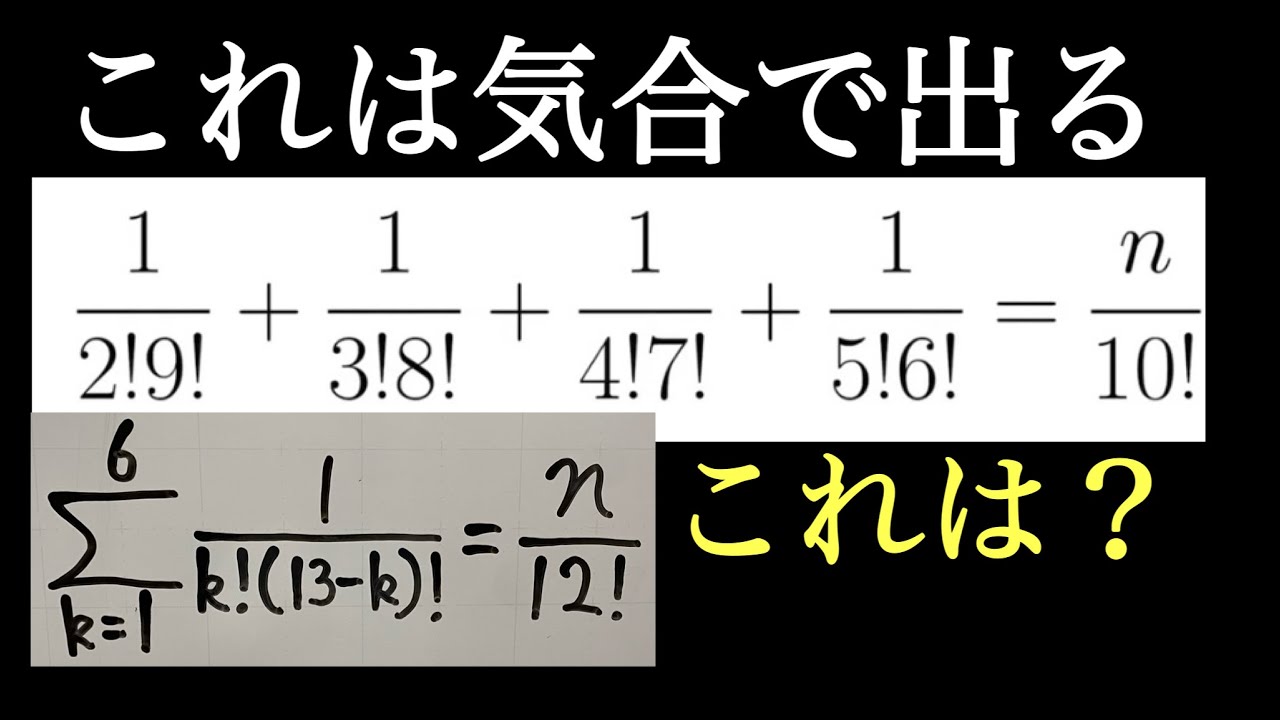
これを解け.
$\dfrac{1}{2!9!}+\dfrac{1}{3!8!}+\dfrac{1}{4!7!}+\dfrac{1}{5!6!}=\dfrac{n}{10!}$
$\displaystyle \sum_{k=1}^{6}\dfrac{1}{k!(13-k)!}=\dfrac{n}{12!}$
この動画を見る
これを解け.
$\dfrac{1}{2!9!}+\dfrac{1}{3!8!}+\dfrac{1}{4!7!}+\dfrac{1}{5!6!}=\dfrac{n}{10!}$
$\displaystyle \sum_{k=1}^{6}\dfrac{1}{k!(13-k)!}=\dfrac{n}{12!}$
大分大 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
一般項$a_n$を求めよ.
$S_n=(n+3)(\dfrac{1}{3}a_n-2)$
2020大分大過去問
この動画を見る
一般項$a_n$を求めよ.
$S_n=(n+3)(\dfrac{1}{3}a_n-2)$
2020大分大過去問
【数B】漸化式:東大1995年 タイルの敷き詰め

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2辺の長さが1と2の長方形と1辺の長さが2の正方形の2種類のタイルがある。縦2,横nの長方形の部屋をこれらのタイルで過不足なく敷き詰めることを考える。その並べ方の総数をA[n]で表す。ただし,nは正の整数である。たとえば$ A_1=1, A_2=3, A_3=5$ である。このとき,以下の問いに答えよう。
(1)$n≧3$のとき,$A_n$を$A_{n-1},A_{n-2}$を用いて表そう。
(2)$A_n$をnで表そう。
この動画を見る
2辺の長さが1と2の長方形と1辺の長さが2の正方形の2種類のタイルがある。縦2,横nの長方形の部屋をこれらのタイルで過不足なく敷き詰めることを考える。その並べ方の総数をA[n]で表す。ただし,nは正の整数である。たとえば$ A_1=1, A_2=3, A_3=5$ である。このとき,以下の問いに答えよう。
(1)$n≧3$のとき,$A_n$を$A_{n-1},A_{n-2}$を用いて表そう。
(2)$A_n$をnで表そう。
数列の和 解説2通り!!
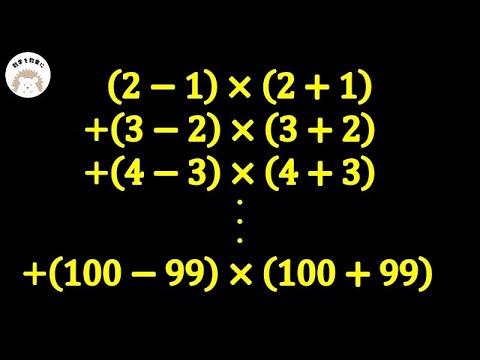
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$(2-1) \times (2+1) + (3-2)(3+2)+(4-3)(4+3)+ \cdots +(99-98)(99+98)+(100-99)(100+99)$
この動画を見る
$(2-1) \times (2+1) + (3-2)(3+2)+(4-3)(4+3)+ \cdots +(99-98)(99+98)+(100-99)(100+99)$
【数B・Ⅲ】漸化式と極限:連立漸化式:数列{x[n]},{y[n]}をx[1]=y[1]=1, x[n+1]=(2/3)x[n]+(1/6)y[n], y[n+1]=(1/3)x[n]+(5/6)y…

単元:
#数列#漸化式#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
数列{$x_n$},{$y_n$}を$x_1=y_1=1, x_{n+1}=\dfrac{2}{3}x_n+\dfrac{1}{6}y_n, y_{n+1}=\dfrac{1}{3}x_n+\dfrac{5}{6}y_n$で定めるとき、
(1)$x_{n+1}+αy_{n+1}=\beta(x_n+αy_n)$を満たす$\alpha,\beta$の組を2組求めよう。
(2)数列{$x_n$},{$y_n$}の一般項を求めよう。
(3)数列{$x_n$},{$y_n$}の極限を求めよう。
この動画を見る
数列{$x_n$},{$y_n$}を$x_1=y_1=1, x_{n+1}=\dfrac{2}{3}x_n+\dfrac{1}{6}y_n, y_{n+1}=\dfrac{1}{3}x_n+\dfrac{5}{6}y_n$で定めるとき、
(1)$x_{n+1}+αy_{n+1}=\beta(x_n+αy_n)$を満たす$\alpha,\beta$の組を2組求めよう。
(2)数列{$x_n$},{$y_n$}の一般項を求めよう。
(3)数列{$x_n$},{$y_n$}の極限を求めよう。
【数B】数列:2以上の自然数に対して、y=x²,y=-x²+2nxで囲まれる部分に含まれる格子点の個数をnの式で表そう。ただし、境界線も含む。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2以上の自然数に対して、$y=x^2,y=-x^2+2nx$で囲まれる部分に含まれる格子点の個数をnの式で表そう。ただし、境界線も含む。
この動画を見る
2以上の自然数に対して、$y=x^2,y=-x^2+2nx$で囲まれる部分に含まれる格子点の個数をnの式で表そう。ただし、境界線も含む。
2つの解法レピュニット数の和

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
和を求めよ.
$1+11+111+・・・・\underbrace{111・・・・1}_{n桁}$
この動画を見る
和を求めよ.
$1+11+111+・・・・\underbrace{111・・・・1}_{n桁}$
0か1か
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
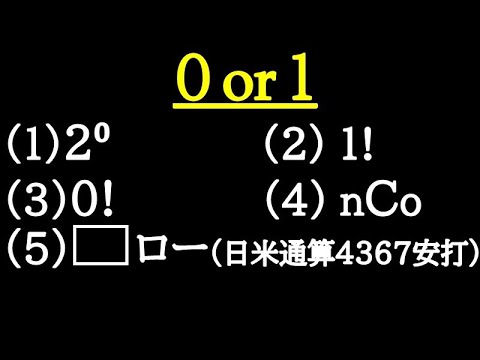
0 or 1
(1) $2^0=$
(2) $1!=$
(3) $0!=$
(4) ${}_nC_0=$
(5) $□ロ- (日米通算4367安打)$
この動画を見る
0 or 1
(1) $2^0=$
(2) $1!=$
(3) $0!=$
(4) ${}_nC_0=$
(5) $□ロ- (日米通算4367安打)$
07京都府教員採用試験(数学:3番 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$a_1=1,a_2=2$
$a_{n+2}=a_{n+1}+a_n$
一般項$a_n$を求めよ.
この動画を見る
$\boxed{3}$
$a_1=1,a_2=2$
$a_{n+2}=a_{n+1}+a_n$
一般項$a_n$を求めよ.
15京都府教員採用試験(数学:5番 帰納法)

単元:
#数列#数学的帰納法#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$4\leqq n:$自然数とする.
$3^{n-2}\gt n^2-3n+4$を示せ.
この動画を見る
$\boxed{5}$
$4\leqq n:$自然数とする.
$3^{n-2}\gt n^2-3n+4$を示せ.
階乗!!
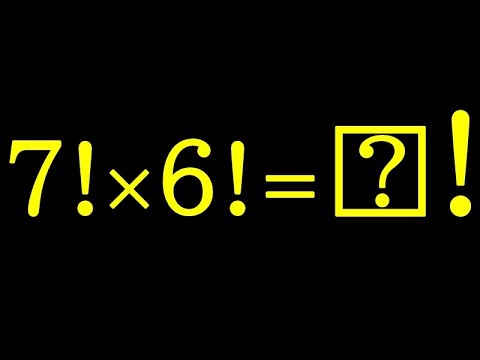
13愛知県教員採用試験(数学:8番 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{8}$
$S_n=n^2-3n$を満たす数列${a_n}$において
$a_2+a_9+a_6+・・・+a_{2n}$を求めよ.
この動画を見る
$\boxed{8}$
$S_n=n^2-3n$を満たす数列${a_n}$において
$a_2+a_9+a_6+・・・+a_{2n}$を求めよ.
12愛知県教員採用試験(数学:2番 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
$n$桁の自然数の総和$S_n$を$n$で表せ.
この動画を見る
$\boxed{2}$
$n$桁の自然数の総和$S_n$を$n$で表せ.
岩手大 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n=1,2,3・・・・$
$a_1=31$
$a_{n+1}=\dfrac{(n+3)a_n-28}{n+2}$
一般項を求めよ.
2020岩手大過去問
この動画を見る
$n=1,2,3・・・・$
$a_1=31$
$a_{n+1}=\dfrac{(n+3)a_n-28}{n+2}$
一般項を求めよ.
2020岩手大過去問
難問!奇問!正しいのは1つだけ!

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
正しいものを1つ選べ
(1)4の倍数かつ6の倍数の数は24の倍数
(2)0.14はπの小数部分
(3)$\sqrt{2n}$が整数となる最小の整数nは2
(4)$230-220 \div 2=5$
この動画を見る
正しいものを1つ選べ
(1)4の倍数かつ6の倍数の数は24の倍数
(2)0.14はπの小数部分
(3)$\sqrt{2n}$が整数となる最小の整数nは2
(4)$230-220 \div 2=5$
04岡山県教員採用試験(数学:1-(4) 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(4)$
$a_1=1,S_n=n^2a_n$とする.
一般項$a_n$を求めよ.
この動画を見る
$\boxed{1}-(4)$
$a_1=1,S_n=n^2a_n$とする.
一般項$a_n$を求めよ.
【数B】数列:Σ計算、公式暗記の「前」に、「意味」を理解しよう!

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\displaystyle \sum_{k=1}^{n}(2k+3)$の値を求めなさい。
$\displaystyle \sum_{k=3}^{10}(k^2)$の値を求めなさい。
この動画を見る
$\displaystyle \sum_{k=1}^{n}(2k+3)$の値を求めなさい。
$\displaystyle \sum_{k=3}^{10}(k^2)$の値を求めなさい。
旭川医科大2021 確率漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
コイン2枚 表表+2,表裏+1,裏裏0であり,0からスタートする.
$n$回の合計が
(1)$a_1,b_1,c_1,a_2,b_2,c_2$のとき,求めよ.
(2)$a_{n+1},b_{n+1},c_{n+1}$を,$a_n,b_n,c_n$で求めよ.
(3)$x_{n+1}=\dfrac{1}{4}x_n;\dfrac{1}{4}$を$x_1$を用いて表せ.
(4)$a_n$を求めよ.
2021旭川医大過去問
この動画を見る
コイン2枚 表表+2,表裏+1,裏裏0であり,0からスタートする.
$n$回の合計が
(1)$a_1,b_1,c_1,a_2,b_2,c_2$のとき,求めよ.
(2)$a_{n+1},b_{n+1},c_{n+1}$を,$a_n,b_n,c_n$で求めよ.
(3)$x_{n+1}=\dfrac{1}{4}x_n;\dfrac{1}{4}$を$x_1$を用いて表せ.
(4)$a_n$を求めよ.
2021旭川医大過去問
