 数列
数列
 数列
数列
福田の数学〜立教大学2023年理学部第4問〜数学的帰納法とはさみうちの原理

単元:
#大学入試過去問(数学)#数列#数学的帰納法#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 正の数列$x_1$,$x_2$,$x_3$,...,$x_n$,... は以下を満たすとする。
$x_1$=8, $x_{n+1}$=$\sqrt{1+x_n}$ ($n$=1,2,3,...)
このとき、次の問いに答えよ。
(1)$x_2$,$x_3$,$x_4$をそれぞれ求めよ。
(2)すべての$n$≧1について($x_{n+1}$-$\alpha$)($x_{n+1}$+$\alpha$)=$x_n$-$\alpha$ となる定数$\alpha$で、
正であるものを求めよ。
(3)$\alpha$を(2)で求めたものとする。すべての$n$≧1について$x_n$>$\alpha$であることを$n$に関する数学的帰納法で示せ。
(4)極限値$\displaystyle\lim_{n \to \infty}x_n$を求めよ。
この動画を見る
$\Large\boxed{4}$ 正の数列$x_1$,$x_2$,$x_3$,...,$x_n$,... は以下を満たすとする。
$x_1$=8, $x_{n+1}$=$\sqrt{1+x_n}$ ($n$=1,2,3,...)
このとき、次の問いに答えよ。
(1)$x_2$,$x_3$,$x_4$をそれぞれ求めよ。
(2)すべての$n$≧1について($x_{n+1}$-$\alpha$)($x_{n+1}$+$\alpha$)=$x_n$-$\alpha$ となる定数$\alpha$で、
正であるものを求めよ。
(3)$\alpha$を(2)で求めたものとする。すべての$n$≧1について$x_n$>$\alpha$であることを$n$に関する数学的帰納法で示せ。
(4)極限値$\displaystyle\lim_{n \to \infty}x_n$を求めよ。
慶應義塾大(経済)数列の最大値

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#慶應義塾大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
2011慶應義塾大学過去問題
n=1,2,・・・100
$a_n=n3^n$・${}_{100} \mathrm{ C }_n$
$a_n$を最大にするnの値
この動画を見る
2011慶應義塾大学過去問題
n=1,2,・・・100
$a_n=n3^n$・${}_{100} \mathrm{ C }_n$
$a_n$を最大にするnの値
【高校数学】等差数列×等比数列の和~どこよりも丁寧に分かりやすく~ 3-12【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
等差×等比
$S=1・1+2・2++3・2²+…n・2^{n-1}$
を求めよ
この動画を見る
等差×等比
$S=1・1+2・2++3・2²+…n・2^{n-1}$
を求めよ
福田の数学〜立教大学2023年理学部第1問(3)〜線分上の格子点の個数

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (3)座標平面上の2点O(0, 0)とP(2023, 1071)について、線分OA上にある点(x, y)でx, yが共に整数であるものの個数は$\boxed{\ \ ウ\ \ }$である。
ただし、線分OPは両端点を含むものとする。
2023立教大学理学部過去問
この動画を見る
$\Large\boxed{1}$ (3)座標平面上の2点O(0, 0)とP(2023, 1071)について、線分OA上にある点(x, y)でx, yが共に整数であるものの個数は$\boxed{\ \ ウ\ \ }$である。
ただし、線分OPは両端点を含むものとする。
2023立教大学理学部過去問
等比数列の和を1から解説
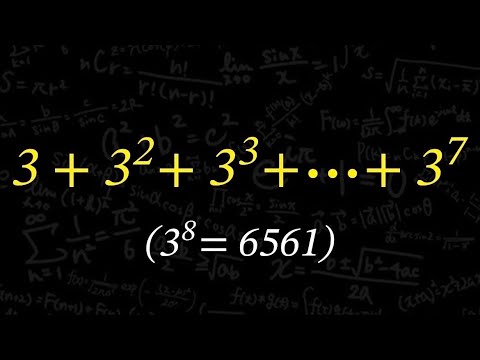
単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$3+3^2+3^3+ \cdots +3^7$ $(3^8=6561)$
この動画を見る
$3+3^2+3^3+ \cdots +3^7$ $(3^8=6561)$
虚数単位の入った漸化式 学習院大

単元:
#大学入試過去問(数学)#複素数平面#数列#漸化式#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数C#学習院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2019学習院大学過去問題
$Z_1=1$
$Z_{n+1}=iZ_n+2$
(1)$Z_{2019}$
(2)$Z_n$が通る円の中心と半径
この動画を見る
2019学習院大学過去問題
$Z_1=1$
$Z_{n+1}=iZ_n+2$
(1)$Z_{2019}$
(2)$Z_n$が通る円の中心と半径
学習院大 漸化式の基本問題

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#学習院大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
学習院大学過去問題
数列$\{ a_n \}$の初項から第n項までの和を$S_n$とする
$S_n=2n^2+n-a_n$
$a_n$の一般項を求めよ
この動画を見る
学習院大学過去問題
数列$\{ a_n \}$の初項から第n項までの和を$S_n$とする
$S_n=2n^2+n-a_n$
$a_n$の一般項を求めよ
【数学A】一橋大学文系2010 確率の問題(解説)

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
$n$を3以上の自然数とする
サイコロを$n$回投げ、出た目の数をそれぞれ順に$X_1,X_2,$・・・$,X_n$とする
$i=2,3,…n$に対して$Xi=Xi-1$となる事象を$Ai$ことする。
(1)$A_2,A_3,…,A_n$のうち少なくとも1つが起こる確率$pn$は?
(2)$A_2,A_3,…,A_n$少なくとも2つが起こる確率$gn$は?
この動画を見る
$n$を3以上の自然数とする
サイコロを$n$回投げ、出た目の数をそれぞれ順に$X_1,X_2,$・・・$,X_n$とする
$i=2,3,…n$に対して$Xi=Xi-1$となる事象を$Ai$ことする。
(1)$A_2,A_3,…,A_n$のうち少なくとも1つが起こる確率$pn$は?
(2)$A_2,A_3,…,A_n$少なくとも2つが起こる確率$gn$は?
中央大 三項間漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023中央大学過去問題
$a_n=(2+\sqrt{3})^n+(2-\sqrt{3})^n$
①$a_{n+2}+a_n=4a_{n+1}$を示せ
②$a_{n+1}+a_n$は3の倍数であることを示せ
③$a_{2023}$を3で割った余り
この動画を見る
2023中央大学過去問題
$a_n=(2+\sqrt{3})^n+(2-\sqrt{3})^n$
①$a_{n+2}+a_n=4a_{n+1}$を示せ
②$a_{n+1}+a_n$は3の倍数であることを示せ
③$a_{2023}$を3で割った余り
福田の数学〜神戸大学2023年理系第3問〜確率の基本性質と数え上げ

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ nを2以上の整数とする。袋の中には1から2nまでの整数が1つずつ書いてある2n枚のカードが入っている。以下の問いに答えよ。
(1)この袋から同時に2枚のカードを取り出したとき、そのカードに書かれている数の和が偶数である確率を求めよ。
(2)この袋から同時に3枚のカードを取り出したとき、そのカードに書かれている数の和が偶数である確率を求めよ。
(3)この袋から同時に2枚のカードを取り出したとき、そのカードに書かれている数の和が2n+1以上である確率を求めよ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{3}$ nを2以上の整数とする。袋の中には1から2nまでの整数が1つずつ書いてある2n枚のカードが入っている。以下の問いに答えよ。
(1)この袋から同時に2枚のカードを取り出したとき、そのカードに書かれている数の和が偶数である確率を求めよ。
(2)この袋から同時に3枚のカードを取り出したとき、そのカードに書かれている数の和が偶数である確率を求めよ。
(3)この袋から同時に2枚のカードを取り出したとき、そのカードに書かれている数の和が2n+1以上である確率を求めよ。
2023神戸大学理系過去問
福田の数学〜神戸大学2023年理系第1問〜漸化式の解法

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 関数$f(x)$を
$f(x)$=$\left\{\begin{array} \\
\frac{1}{2}x+\frac{1}{2} (x≦ 1)\\
2x-1 (x \gt 1)\\
\end{array}\right.$
で定める。aを実数とし、数列$\left\{a_n\right\}$を
$a_1$=a, $a_{n+1}$=$f(a_n)$ (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)すべての実数xについて$f(x)$≧x が成り立つことを示せ。
(2)a≦1のとき、すべての正の整数nについて$a_n$≦1が成り立つことを示せ。
(3)数列$\left\{a_n\right\}$の一般項をnとaを用いて表せ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{1}$ 関数$f(x)$を
$f(x)$=$\left\{\begin{array} \\
\frac{1}{2}x+\frac{1}{2} (x≦ 1)\\
2x-1 (x \gt 1)\\
\end{array}\right.$
で定める。aを実数とし、数列$\left\{a_n\right\}$を
$a_1$=a, $a_{n+1}$=$f(a_n)$ (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)すべての実数xについて$f(x)$≧x が成り立つことを示せ。
(2)a≦1のとき、すべての正の整数nについて$a_n$≦1が成り立つことを示せ。
(3)数列$\left\{a_n\right\}$の一般項をnとaを用いて表せ。
2023神戸大学理系過去問
上智大 連立漸化式

単元:
#大学入試過去問(数学)#漸化式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
上智大学過去問題
$a_1 =0,b_1=6$
$a_{n+1}=\frac{a_n+b_n}{2}$,$b_{n+1}=a_n$
点Pの$(a_n,b_n)$はある直線上にある。その式は?
$n \to \infty$のときの$P_n$
この動画を見る
上智大学過去問題
$a_1 =0,b_1=6$
$a_{n+1}=\frac{a_n+b_n}{2}$,$b_{n+1}=a_n$
点Pの$(a_n,b_n)$はある直線上にある。その式は?
$n \to \infty$のときの$P_n$
福田の数学〜九州大学2023年文系第4問PART2〜確率漸化式

単元:
#数A#大学入試過去問(数学)#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $w$を$x^3$=1 の虚数解のうち虚部が正であるものとする。さいころを繰り返し投げて、次の規則で4つの複素数0, 1, $w$, $w^2$を並べていくことにより、複素数の列$z_1$, $z_2$, $z_3$, ... を定める。
・$z_1$=0 とする。
・$z_k$まで定まった時、さいころを投げて、出た目を$t$とする。このとき$z_{k+1}$を以下のように定める。
・$z_k$=0 のとき、$z_{k+1}$=$w^t$ とする。
・$z_k$≠0, $t$=1, 2のとき、$z_{k+1}$=0 とする。
・$z_k$≠0, $t$=3のとき、$z_{k+1}$=$wz_k$ とする。
・$z_k$≠0, $t$=4のとき、$z_{k+1}$=$\bar{wz_k}$ とする。
・$z_k$≠0, $t$=5のとき、$z_{k+1}$=$z_k$ とする。
・$z_k$≠0, $t$=6のとき、$z_{k+1}$=$\bar{z_k}$ とする。
ここで複素数$z$に対し、$\bar{z}$は$z$と共役な複素数を表す。以下の問いに答えよ。
(1)$ω^2$=$\bar{ω}$であることを示せ。
(2)$z_n$=0となる確率を$n$の式で表せ。
(3)$z_3$=1, $z_3$=$ω$, $z_3$=$ω^2$となる確率をそれぞれ求めよ。
(4)$z_n$=1となる確率を$n$の式で表せ。
2023九州大学文系過去問
この動画を見る
$\Large\boxed{4}$ $w$を$x^3$=1 の虚数解のうち虚部が正であるものとする。さいころを繰り返し投げて、次の規則で4つの複素数0, 1, $w$, $w^2$を並べていくことにより、複素数の列$z_1$, $z_2$, $z_3$, ... を定める。
・$z_1$=0 とする。
・$z_k$まで定まった時、さいころを投げて、出た目を$t$とする。このとき$z_{k+1}$を以下のように定める。
・$z_k$=0 のとき、$z_{k+1}$=$w^t$ とする。
・$z_k$≠0, $t$=1, 2のとき、$z_{k+1}$=0 とする。
・$z_k$≠0, $t$=3のとき、$z_{k+1}$=$wz_k$ とする。
・$z_k$≠0, $t$=4のとき、$z_{k+1}$=$\bar{wz_k}$ とする。
・$z_k$≠0, $t$=5のとき、$z_{k+1}$=$z_k$ とする。
・$z_k$≠0, $t$=6のとき、$z_{k+1}$=$\bar{z_k}$ とする。
ここで複素数$z$に対し、$\bar{z}$は$z$と共役な複素数を表す。以下の問いに答えよ。
(1)$ω^2$=$\bar{ω}$であることを示せ。
(2)$z_n$=0となる確率を$n$の式で表せ。
(3)$z_3$=1, $z_3$=$ω$, $z_3$=$ω^2$となる確率をそれぞれ求めよ。
(4)$z_n$=1となる確率を$n$の式で表せ。
2023九州大学文系過去問
福田の数学〜九州大学2023年文系第4問PART1〜確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $w$を$x^3$=1 の虚数解のうち虚部が正であるものとする。さいころを繰り返し投げて、次の規則で4つの複素数0, 1, $w$, $w^2$を並べていくことにより、複素数の列$z_1$, $z_2$, $z_3$, ... を定める。
・$z_1$=0 とする。
・$z_k$まで定まった時、さいころを投げて、出た目を$t$とする。このとき$z_{k+1}$を以下のように定める。
・$z_k$=0 のとき、$z_{k+1}$=$w^t$ とする。
・$z_k$≠0, $t$=1, 2のとき、$z_{k+1}$=0 とする。
・$z_k$≠0, $t$=3のとき、$z_{k+1}$=$wz_k$ とする。
・$z_k$≠0, $t$=4のとき、$z_{k+1}$=$\bar{wz_k}$ とする。
・$z_k$≠0, $t$=5のとき、$z_{k+1}$=$z_k$ とする。
・$z_k$≠0, $t$=6のとき、$z_{k+1}$=$\bar{z_k}$ とする。
ここで複素数$z$に対し、$\bar{z}$は$z$と共役な複素数を表す。以下の問いに答えよ。
(1)$ω^2$=$\bar{ω}$であることを示せ。
(2)$z_n$=0となる確率を$n$の式で表せ。
(3)$z_3$=1, $z_3$=$ω$, $z_3$=$ω^2$となる確率をそれぞれ求めよ。
(4)$z_n$=1となる確率を$n$の式で表せ。
2023九州大学文系過去問
この動画を見る
$\Large\boxed{4}$ $w$を$x^3$=1 の虚数解のうち虚部が正であるものとする。さいころを繰り返し投げて、次の規則で4つの複素数0, 1, $w$, $w^2$を並べていくことにより、複素数の列$z_1$, $z_2$, $z_3$, ... を定める。
・$z_1$=0 とする。
・$z_k$まで定まった時、さいころを投げて、出た目を$t$とする。このとき$z_{k+1}$を以下のように定める。
・$z_k$=0 のとき、$z_{k+1}$=$w^t$ とする。
・$z_k$≠0, $t$=1, 2のとき、$z_{k+1}$=0 とする。
・$z_k$≠0, $t$=3のとき、$z_{k+1}$=$wz_k$ とする。
・$z_k$≠0, $t$=4のとき、$z_{k+1}$=$\bar{wz_k}$ とする。
・$z_k$≠0, $t$=5のとき、$z_{k+1}$=$z_k$ とする。
・$z_k$≠0, $t$=6のとき、$z_{k+1}$=$\bar{z_k}$ とする。
ここで複素数$z$に対し、$\bar{z}$は$z$と共役な複素数を表す。以下の問いに答えよ。
(1)$ω^2$=$\bar{ω}$であることを示せ。
(2)$z_n$=0となる確率を$n$の式で表せ。
(3)$z_3$=1, $z_3$=$ω$, $z_3$=$ω^2$となる確率をそれぞれ求めよ。
(4)$z_n$=1となる確率を$n$の式で表せ。
2023九州大学文系過去問
漸化式 関西医科大

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#関西医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
2021関西医科大学過去問題
$a_1=\frac{1}{13}$ n=1,2,・・・自然数
$5a_{n+1}=10a_n-a_{n+1}・a_n$
一般項$a_n$を求めよ
この動画を見る
2021関西医科大学過去問題
$a_1=\frac{1}{13}$ n=1,2,・・・自然数
$5a_{n+1}=10a_n-a_{n+1}・a_n$
一般項$a_n$を求めよ
大学入試問題#562「証明問題じゃなきゃ解けるのか?」 東京帝国大学1937 #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#加法定理とその応用#数列#数学的帰納法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$:正の整数
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{\sin(2n-1)x}{\sin\ x}\ dx=\pi$を示せ
出典:1937年東京帝国大学 入試問題
この動画を見る
$n$:正の整数
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{\sin(2n-1)x}{\sin\ x}\ dx=\pi$を示せ
出典:1937年東京帝国大学 入試問題
福田の数学〜九州大学2023年理系第2問〜数列の収束発散の判定

単元:
#大学入試過去問(数学)#数列#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $\alpha$を実数とする。数列$\left\{a_n\right\}$が
$a_1$=$\alpha$, $a_{n+1}$=|$a_n$-1|+$a_n$-1 (n=1,2,3,...)
で定められるとき、以下の問いに答えよ。
(1)$\alpha$≦1のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(2)$\alpha$>2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(3)1<$\alpha$<$\frac{3}{2}$のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(4)$\frac{3}{2}≦\alpha$<2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
2023九州大学理系過去問
この動画を見る
$\Large\boxed{2}$ $\alpha$を実数とする。数列$\left\{a_n\right\}$が
$a_1$=$\alpha$, $a_{n+1}$=|$a_n$-1|+$a_n$-1 (n=1,2,3,...)
で定められるとき、以下の問いに答えよ。
(1)$\alpha$≦1のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(2)$\alpha$>2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(3)1<$\alpha$<$\frac{3}{2}$のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
(4)$\frac{3}{2}≦\alpha$<2のとき、数列$\left\{a_n\right\}$の収束、発散を調べよ。
2023九州大学理系過去問
特性方程式を解いてる場合じゃないよ

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
A,B,C,Dの5人がパス回しをする。
Aから始めて、ボールを持った人は等しい確率で自分以外の人にパスを出す。
n回目にBがボールを持っている確率は?
この動画を見る
A,B,C,Dの5人がパス回しをする。
Aから始めて、ボールを持った人は等しい確率で自分以外の人にパスを出す。
n回目にBがボールを持っている確率は?
東京医科大 見掛け倒しな問題

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B#東京医科大学#東京医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$1008$の正の約数$n$個を大きい順に並べた数列を
$a_1,a_2・・・・・・,a_n$とし、$S(x)$を$S(x)=\displaystyle \sum_{k=1}^n a_k^x $とする。
①$S(0)$ ②$S(1)$ ③$S(-1)$ ④$\dfrac{S(2)}{S(1)}$
この動画を見る
$1008$の正の約数$n$個を大きい順に並べた数列を
$a_1,a_2・・・・・・,a_n$とし、$S(x)$を$S(x)=\displaystyle \sum_{k=1}^n a_k^x $とする。
①$S(0)$ ②$S(1)$ ③$S(-1)$ ④$\dfrac{S(2)}{S(1)}$
整数問題

単元:
#大学入試過去問(数学)#数列#数学的帰納法#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とするとき、
$2^{3n-2}+3^n$は5の倍数であることを
数学的帰納法によって証明せよ。
会津大過去問
この動画を見る
$n$を自然数とするとき、
$2^{3n-2}+3^n$は5の倍数であることを
数学的帰納法によって証明せよ。
会津大過去問
【短時間でマスター!!】等差×等比数列の型の和の求め方を解説!〔現役講師解説、数学〕

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
等差×等比数列の型の和の求め方を解説します。
$S=1+2×2+3×2^3+\cdots+n\cdot2^{n-1}$を求めよ。
この動画を見る
等差×等比数列の型の和の求め方を解説します。
$S=1+2×2+3×2^3+\cdots+n\cdot2^{n-1}$を求めよ。
福田の数学〜一橋大学2023年文系第5問〜反復試行の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ A, B, Cの3人が、A, B, C, A, B, C, A, ... という順番にさいころを投げ、最初に1を出した人を勝ちとする。だれかが1を出すか、全員が$n$回ずつ投げたら、ゲームを終了する。A, B, Cが勝つ確率$P_A$, $P_B$, $P_C$をそれぞれ求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{5}$ A, B, Cの3人が、A, B, C, A, B, C, A, ... という順番にさいころを投げ、最初に1を出した人を勝ちとする。だれかが1を出すか、全員が$n$回ずつ投げたら、ゲームを終了する。A, B, Cが勝つ確率$P_A$, $P_B$, $P_C$をそれぞれ求めよ。
2023一橋大学文系過去問
産業医科大 区分求積法を使わなくても出せるよ

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#積分とその応用#数列の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#産業医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\dfrac{1^4+2^4+3^4+・・・・+n^4}{n^5}$
これを求めよ。
産業医科大過去問
この動画を見る
$\displaystyle \lim_{ n \to \infty }\dfrac{1^4+2^4+3^4+・・・・+n^4}{n^5}$
これを求めよ。
産業医科大過去問
福田の数学〜一橋大学2023年文系第4問〜群数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ xy平面上で、x座標とy座標がともに正の整数であるような各点に、下の図のような番号をつける。(※動画参照)点(m, n)につけた番号をf(m, n)とする。
たとえば、$f(1, 1)=1, f(3, 4)=19$ である。
(1)$f(m, n)+f(m+1, n+1)=2f(m, n+1)$
が成り立つことを示せ。
(2)$f(m, n)+f(m+1, n)+f(m, n+1)+f(m+1, n+1)=2023$
となるような整数の組(m, n)を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{4}$ xy平面上で、x座標とy座標がともに正の整数であるような各点に、下の図のような番号をつける。(※動画参照)点(m, n)につけた番号をf(m, n)とする。
たとえば、$f(1, 1)=1, f(3, 4)=19$ である。
(1)$f(m, n)+f(m+1, n+1)=2f(m, n+1)$
が成り立つことを示せ。
(2)$f(m, n)+f(m+1, n)+f(m, n+1)+f(m+1, n+1)=2023$
となるような整数の組(m, n)を求めよ。
2023一橋大学文系過去問
誘導がなければ素晴らしい解法も出てくるんじゃね?

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#大阪教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
点Pは原点を出発して,「確率pで+1,確率1-pで+2」の移動を繰り返す.
ただし$0\leqq p \leqq 1$とする.このような移動を繰り返して自然数nの点に到達する確率を$p_n$と表す.次の問に答えよ.
(1)$p_1,p_2,p_3$を$p$を用いて表せ.
(2)$p_n,p_{n+1},p_{n+2}$の間の関係式を求めよ.
(3)$a_n=p_{n+1}-p_n(n \geqq 1)$とおくとき,数列${a_n}$が満たす漸化式を求めよ.
(4)pとnを用いて,一般項$p_n$を表せ.
(5)数列${p_n}$の極限を調べよ.
この動画を見る
点Pは原点を出発して,「確率pで+1,確率1-pで+2」の移動を繰り返す.
ただし$0\leqq p \leqq 1$とする.このような移動を繰り返して自然数nの点に到達する確率を$p_n$と表す.次の問に答えよ.
(1)$p_1,p_2,p_3$を$p$を用いて表せ.
(2)$p_n,p_{n+1},p_{n+2}$の間の関係式を求めよ.
(3)$a_n=p_{n+1}-p_n(n \geqq 1)$とおくとき,数列${a_n}$が満たす漸化式を求めよ.
(4)pとnを用いて,一般項$p_n$を表せ.
(5)数列${p_n}$の極限を調べよ.
この答えあっているのか?指数関数と等差数列 自治医科大
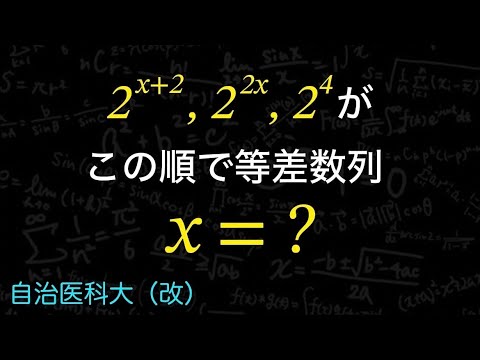
単元:
#数Ⅱ#指数関数と対数関数#指数関数#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{x+2} , 2^x , 2^4$がこの順で等差数列をなすとき、x=?
(自治医科大学(改))
この動画を見る
$2^{x+2} , 2^x , 2^4$がこの順で等差数列をなすとき、x=?
(自治医科大学(改))
超不人気!確率漸化式だよ

単元:
#数Ⅰ#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
点Pは原点を出発して確率$p(0\leqq P\leqq 1)$で$+1$, $1-p$で$+2$進む.
自然数nの地点に到達する確率$P_n$を求めよ.
大阪教育大過去問
この動画を見る
点Pは原点を出発して確率$p(0\leqq P\leqq 1)$で$+1$, $1-p$で$+2$進む.
自然数nの地点に到達する確率$P_n$を求めよ.
大阪教育大過去問
福田の数学〜東北大学2023年理系第3問〜漸化式と数列の和

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ sを実数とし、数列$\left\{a_n\right\}$を
$a_1$=s, (n+2)$a_{n+1}$=n$a_n$+2 (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)$a_n$をnとsを用いて表せ。
(2)ある正の整数$m$に対して、$\displaystyle\sum_{n=1}^ma_n$=0が成り立つとする。sをmを用いて表せ。
2023東北大学理系過去問
この動画を見る
$\Large\boxed{3}$ sを実数とし、数列$\left\{a_n\right\}$を
$a_1$=s, (n+2)$a_{n+1}$=n$a_n$+2 (n=1,2,3,...)
で定める。以下の問いに答えよ。
(1)$a_n$をnとsを用いて表せ。
(2)ある正の整数$m$に対して、$\displaystyle\sum_{n=1}^ma_n$=0が成り立つとする。sをmを用いて表せ。
2023東北大学理系過去問
大学入試問題#538「数列のバリューセット」 室蘭工業大学(2018) #数列

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#室蘭工業大学
指導講師:
ますただ
問題文全文(内容文):
$a_1=\displaystyle \frac{1}{2}$
$a_{n+1}=\displaystyle \frac{(n+1)a_n}{n+3^na_n}$のとき
一般項$a_n$を求めよ
出典:2018年室蘭工業大学 入試問題
この動画を見る
$a_1=\displaystyle \frac{1}{2}$
$a_{n+1}=\displaystyle \frac{(n+1)a_n}{n+3^na_n}$のとき
一般項$a_n$を求めよ
出典:2018年室蘭工業大学 入試問題
【短時間でマスター!!】和と一般項の問題の求め方を解説!(数列)〔現役講師解説、数学〕

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
3rd School
問題文全文(内容文):
数学2B
和と一般項
数列$\{a_n\}$の初項から第$n$項までの和$S_n$が$S_n=3n(n+5)$で表されるとき、一般項$a_n$を求めよ。
この動画を見る
数学2B
和と一般項
数列$\{a_n\}$の初項から第$n$項までの和$S_n$が$S_n=3n(n+5)$で表されるとき、一般項$a_n$を求めよ。
