 関数と極限
関数と極限
 関数と極限
関数と極限
【数Ⅲ】極限:関数の極限 x=-tの置換

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限を求めよう。
$\displaystyle \lim_{x\to-\infty}(\sqrt{x^2+2x+3}+x)$
この動画を見る
次の極限を求めよう。
$\displaystyle \lim_{x\to-\infty}(\sqrt{x^2+2x+3}+x)$
【数Ⅲ】極限:3乗根を含む極限、3乗根の有理化:次の極限を求めよう。lim[x→0]{∛(1+x)-∛(1-x)}/x

単元:
#関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限を求めよう。
$\displaystyle \lim_{x\to 0}\dfrac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x}$
この動画を見る
次の極限を求めよう。
$\displaystyle \lim_{x\to 0}\dfrac{\sqrt[3]{1+x}-\sqrt[3]{1-x}}{x}$
【数Ⅲ】極限:3乗根を含む極限、3乗根の有理化

福田のわかった数学〜高校3年生理系076〜平均値の定理(4)数列の極限の問題

単元:
#数列#漸化式#関数と極限#微分とその応用#数列の極限#接線と法線・平均値の定理#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$平均値の定理(4)
微分可能な関数$f(x)$が$f(1)=1, 0 \lt f'(x) \leqq \frac{1}{2}$を満たしている。
$a_{n+1}=f(a_n)$で定義される数列$\left\{a_n\right\}$について、
$\lim_{n \to \infty}a_n=1$であることを示せ。
この動画を見る
数学$\textrm{III}$平均値の定理(4)
微分可能な関数$f(x)$が$f(1)=1, 0 \lt f'(x) \leqq \frac{1}{2}$を満たしている。
$a_{n+1}=f(a_n)$で定義される数列$\left\{a_n\right\}$について、
$\lim_{n \to \infty}a_n=1$であることを示せ。
福田のわかった数学〜高校3年生理系074〜平均値の定理(2)極限の問題

単元:
#関数と極限#微分とその応用#関数の極限#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 平均値の定理(2)
極限値
$\lim_{x \to 0}\frac{e^x-e^{\sin x}}{x-\sin x}$
を求めよ。
この動画を見る
数学$\textrm{III}$ 平均値の定理(2)
極限値
$\lim_{x \to 0}\frac{e^x-e^{\sin x}}{x-\sin x}$
を求めよ。
【数Ⅲ】 極限:r^nの極限を含むグラフの概形

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数の極限:$r^n$の極限:次の関数のグラフの概形をかき、関数の連続性を調べよう
$f(x)=\displaystyle \lim_{x\to\infty}\dfrac{x^{2n-1}+x+2}{x^{2n}+1}$
この動画を見る
関数の極限:$r^n$の極限:次の関数のグラフの概形をかき、関数の連続性を調べよう
$f(x)=\displaystyle \lim_{x\to\infty}\dfrac{x^{2n-1}+x+2}{x^{2n}+1}$
数学「大学入試良問集」【19−8 極限で定義された関数】を宇宙一わかりやすく

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
正の数$x$に対して定義された次の関数$f(x)$を考える。
$f(x)=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{4x^{n+1}+ax^n+log\ x+1}{x^{n+2}+x^n+1}$
ここで、$a$は定数である。
このとき、次の各問いに答えよ。
(1)
極限計算により関数$f(x)$を求めると
$0 \lt x \lt 1$のとき$f(x)=\fcolorbox{black}{ #fffff }{ ア },f(1)=\fcolorbox{black}{ #fffff }{ イ },x \gt 1$のとき$f(x)=\fcolorbox{black}{ #fffff }{ ウ }$。
(2)
関数$f(x)$が$x=1$で連続になるときの$a$の値を求めよ。
以下、$a$はこの値とする。
(3)
関数$f(x)$の増減、極値および$f(x)=0$をみたす$x$の値を調べて、関数$f(x)$のグラフ$C$の概形を描け。
(4)
関数$f(x)$のグラフ$C$と直線$x=\sqrt{ 3 }$および$x$軸で囲まれる部分の面積を求めよ。
この動画を見る
正の数$x$に対して定義された次の関数$f(x)$を考える。
$f(x)=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{4x^{n+1}+ax^n+log\ x+1}{x^{n+2}+x^n+1}$
ここで、$a$は定数である。
このとき、次の各問いに答えよ。
(1)
極限計算により関数$f(x)$を求めると
$0 \lt x \lt 1$のとき$f(x)=\fcolorbox{black}{ #fffff }{ ア },f(1)=\fcolorbox{black}{ #fffff }{ イ },x \gt 1$のとき$f(x)=\fcolorbox{black}{ #fffff }{ ウ }$。
(2)
関数$f(x)$が$x=1$で連続になるときの$a$の値を求めよ。
以下、$a$はこの値とする。
(3)
関数$f(x)$の増減、極値および$f(x)=0$をみたす$x$の値を調べて、関数$f(x)$のグラフ$C$の概形を描け。
(4)
関数$f(x)$のグラフ$C$と直線$x=\sqrt{ 3 }$および$x$軸で囲まれる部分の面積を求めよ。
【数Ⅲ】極限:三角関数の合成の利用

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限値を求めよう。
$\displaystyle \lim_{x\to\dfrac{\pi}{4}}\dfrac{\sin x-\cos x}{x-\dfrac{\pi}{4}}$
この動画を見る
次の極限値を求めよう。
$\displaystyle \lim_{x\to\dfrac{\pi}{4}}\dfrac{\sin x-\cos x}{x-\dfrac{\pi}{4}}$
【数Ⅲ】極限:三角関数と極限(sinx/x=1の利用3)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限値を求めよう。
$\displaystyle \lim_{x\to\infty}\dfrac{\sin\left(\dfrac{\sin x}{\pi}\right)}{x}$
この動画を見る
次の極限値を求めよう。
$\displaystyle \lim_{x\to\infty}\dfrac{\sin\left(\dfrac{\sin x}{\pi}\right)}{x}$
【数Ⅲ】極限:三角関数と極限(sinx/x=1の利用2)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限値を求めよう。
$\displaystyle \lim_{x\to\infty}\dfrac{\sin x}{x^0}$
この動画を見る
次の極限値を求めよう。
$\displaystyle \lim_{x\to\infty}\dfrac{\sin x}{x^0}$
【数Ⅲ】極限:三角関数と極限(sinx/x=1の利用1)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の極限値を求めよう。
$\displaystyle \lim_{x\to\infty}x\sin・\dfrac{1}{x}$
この動画を見る
次の極限値を求めよう。
$\displaystyle \lim_{x\to\infty}x\sin・\dfrac{1}{x}$
練習問題48 岡山大学2011 面積、極限
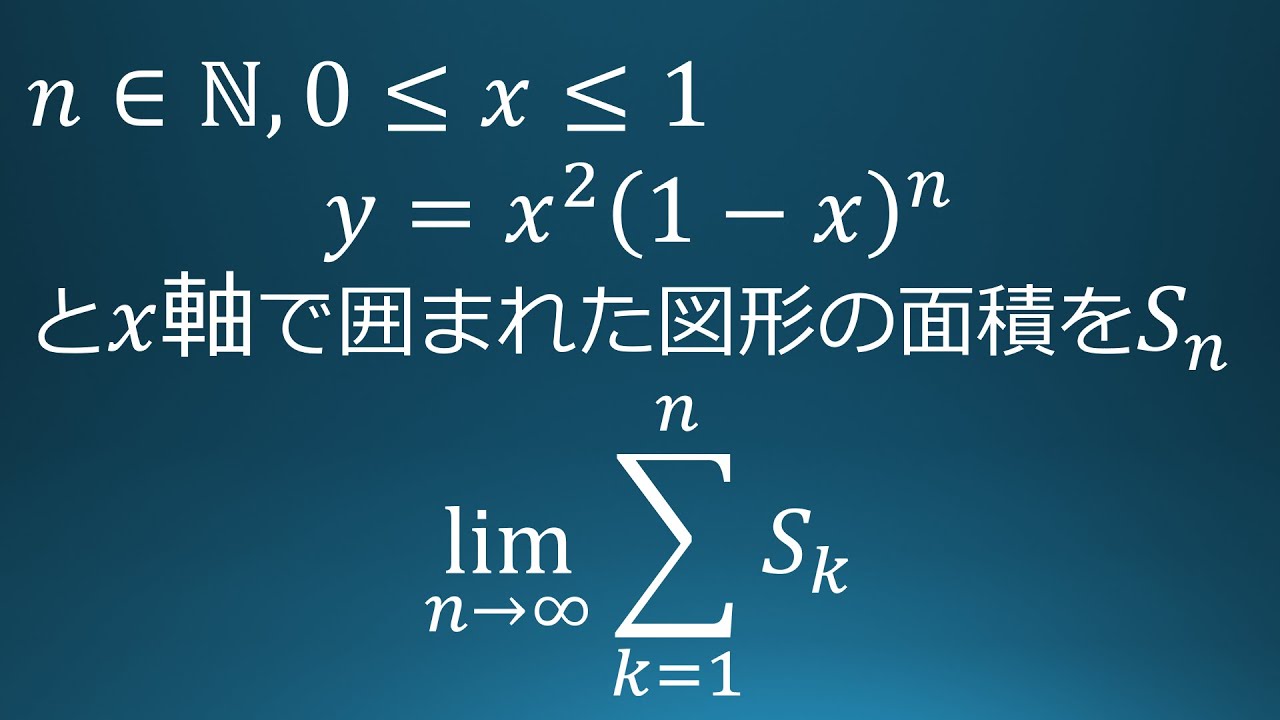
単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#岡山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n \in IN,\ 0 \leqq x \leqq 1$
曲線$y=x^2(1-x)^n$と$x$軸で囲まれた図形の面積を$S_n$とする。
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\ S_k$を求めよ。
出典:2011年岡山大学 練習問題
この動画を見る
$n \in IN,\ 0 \leqq x \leqq 1$
曲線$y=x^2(1-x)^n$と$x$軸で囲まれた図形の面積を$S_n$とする。
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\ S_k$を求めよ。
出典:2011年岡山大学 練習問題
福田の数学〜中央大学2021年理工学部第4問〜定積分と不等式、極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$自然数$n$に対し,$f_n(x)=x^{-1+\frac{1}{n}}(x\gt 0)$とおく.
また,正の実数$a_n$は$\displaystyle \int_{1}^{a_n}f_n(x)dx=1$満たすものとする.次の問い
答えよ.
(1)関数$f_n(x)$の不定積分を求めよ.
(2)$a_n$の値と極限$\displaystyle \lim_{n\to\infty}a_n$を求めよ.また,正の実数$b_n$が$\displaystyle \int_{1}^{b_n}f_{n+1}(x)dx=-1$を満たすとき,$b_n$の値と極限$\displaystyle \lim_{n\to\infty}b_n$を求めよ.
(3)2以上の自然数$k$に対して$\displaystyle \int_{k-1}^{k}f_n(x)dx \gt \dfrac{1}{k}$を示し,これを利用して$a_n\lt 4$を証明せよ.
(4)$\displaystyle \int_{1}^{a_n}f_{n+1}(x)dx\lt 1$を示し,これを利用して$a_n\lt a_{n+1}$を証明せよ.
2021中央大理工学部過去問
この動画を見る
$\boxed{4}$自然数$n$に対し,$f_n(x)=x^{-1+\frac{1}{n}}(x\gt 0)$とおく.
また,正の実数$a_n$は$\displaystyle \int_{1}^{a_n}f_n(x)dx=1$満たすものとする.次の問い
答えよ.
(1)関数$f_n(x)$の不定積分を求めよ.
(2)$a_n$の値と極限$\displaystyle \lim_{n\to\infty}a_n$を求めよ.また,正の実数$b_n$が$\displaystyle \int_{1}^{b_n}f_{n+1}(x)dx=-1$を満たすとき,$b_n$の値と極限$\displaystyle \lim_{n\to\infty}b_n$を求めよ.
(3)2以上の自然数$k$に対して$\displaystyle \int_{k-1}^{k}f_n(x)dx \gt \dfrac{1}{k}$を示し,これを利用して$a_n\lt 4$を証明せよ.
(4)$\displaystyle \int_{1}^{a_n}f_{n+1}(x)dx\lt 1$を示し,これを利用して$a_n\lt a_{n+1}$を証明せよ.
2021中央大理工学部過去問
練習問題44 東京工業大学 極限値 数検1級 教員採用試験(数学)

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数列の極限#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }(\displaystyle \frac{{}_{ 3n } C_n}{{}_{ 2n } C_n})^\frac{1}{n}$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
出典:東京工業大学 練習問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }(\displaystyle \frac{{}_{ 3n } C_n}{{}_{ 2n } C_n})^\frac{1}{n}$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
出典:東京工業大学 練習問題
高専数学 微積II #67 2変数関数の極限
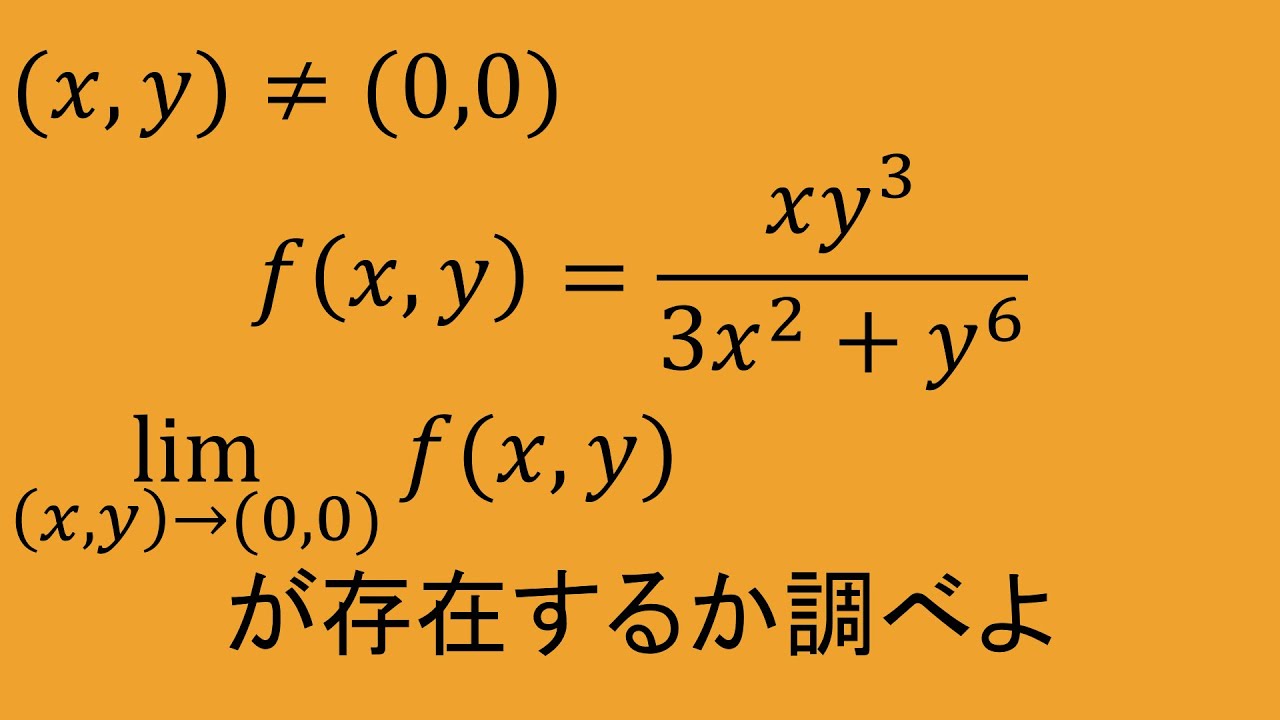
単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x,y)=\displaystyle \frac{xy^3}{3x^2+y^6}$
$(x,y) \neq (0,0)$において
$\displaystyle \lim_{ (x,y) \to (0,0) }f(x,y)$が存在するか調べよ。
この動画を見る
$f(x,y)=\displaystyle \frac{xy^3}{3x^2+y^6}$
$(x,y) \neq (0,0)$において
$\displaystyle \lim_{ (x,y) \to (0,0) }f(x,y)$が存在するか調べよ。
【数学Ⅲ/微分】逆関数の微分

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
逆関数の微分法の公式を用いて、次の関数を微分せよ。
$y=x^{\frac{1}{5}}$
この動画を見る
逆関数の微分法の公式を用いて、次の関数を微分せよ。
$y=x^{\frac{1}{5}}$
高専数学 微積II #61(1)(2) 合成関数の微分法
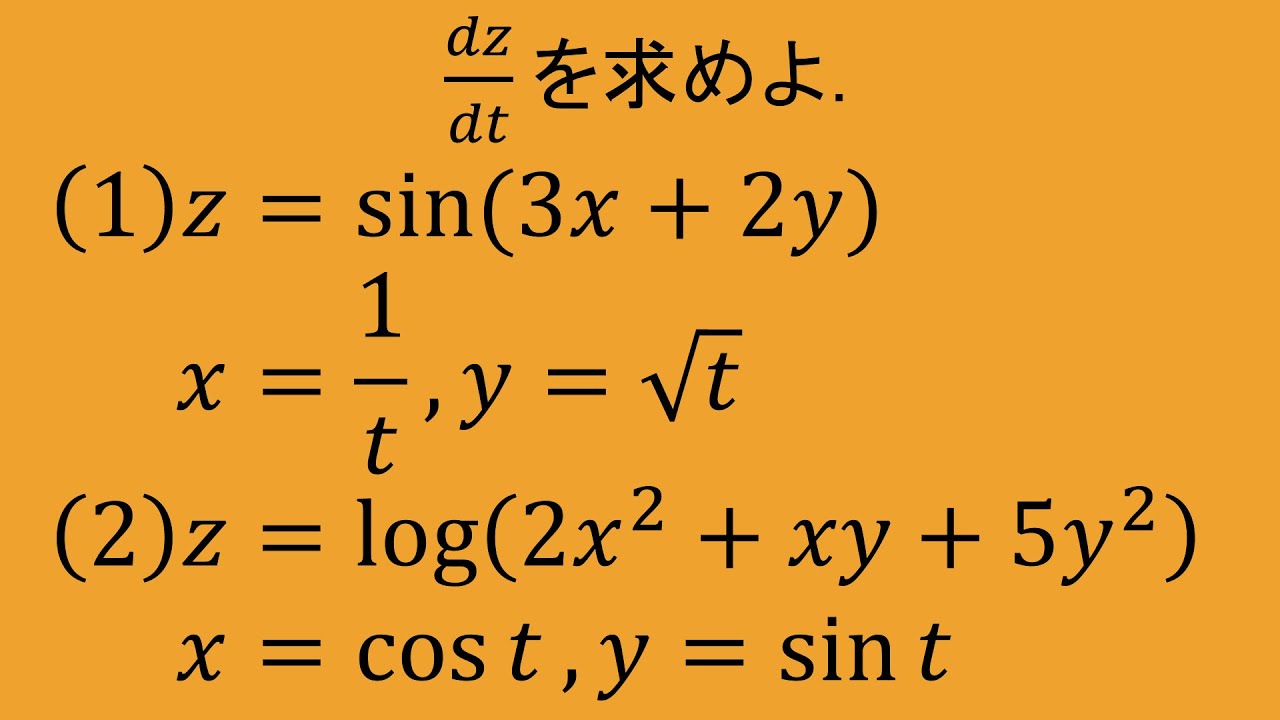
単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\dfrac{dz}{dt}$を求めよ.
(1)$z=\sin (3x+2y)$
$x=\dfrac{1}{t},y=\sqrt t$
(2)$z=\log(2x^2+xy+5y^2)$
$x=\cos t,y=\sin t$
この動画を見る
$\dfrac{dz}{dt}$を求めよ.
(1)$z=\sin (3x+2y)$
$x=\dfrac{1}{t},y=\sqrt t$
(2)$z=\log(2x^2+xy+5y^2)$
$x=\cos t,y=\sin t$
お茶の水女子大 3次関数と放物線

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=x^3+(k+1)x^2+kx$と$y=x^2q$とが全ての実数$q$において
共有点がただ1つである$k$の範囲を求めよ.
2021お茶の水女子大過去問
この動画を見る
$y=x^3+(k+1)x^2+kx$と$y=x^2q$とが全ての実数$q$において
共有点がただ1つである$k$の範囲を求めよ.
2021お茶の水女子大過去問
高専数学 微積II #53(3)(4) 合成関数の微分法

単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を,$u,\nu,z_x,z_y$で表せ.
(3)$x=\tan\dfrac{\nu}{u},y-\cos(u+\nu)$
(4)$x=u\log\nu,y=e^u \nu$
この動画を見る
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を,$u,\nu,z_x,z_y$で表せ.
(3)$x=\tan\dfrac{\nu}{u},y-\cos(u+\nu)$
(4)$x=u\log\nu,y=e^u \nu$
高専数学 微積II #53(1)(2) 合成関数の微分法
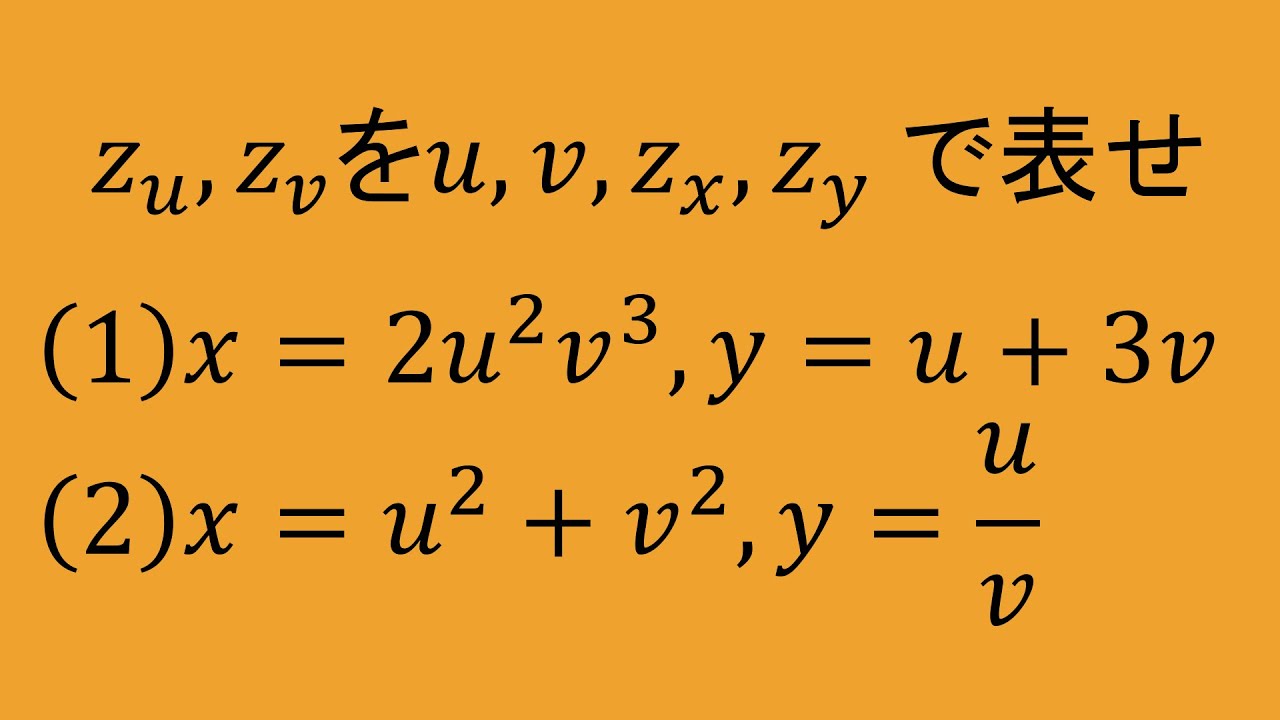
単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を$u,\nu,z_x,z_y$で表せ.
(1)$x=2u^2 \nu^3,y=u+3\nu$
(2)$x=u^2+\nu^2,y=\dfrac{u}{\nu}$
この動画を見る
$z=f(x,y)$:全微分可能
$z_u,z_{\nu}$を$u,\nu,z_x,z_y$で表せ.
(1)$x=2u^2 \nu^3,y=u+3\nu$
(2)$x=u^2+\nu^2,y=\dfrac{u}{\nu}$
高専数学 微積II #51(3)(4) 合成関数の微分法
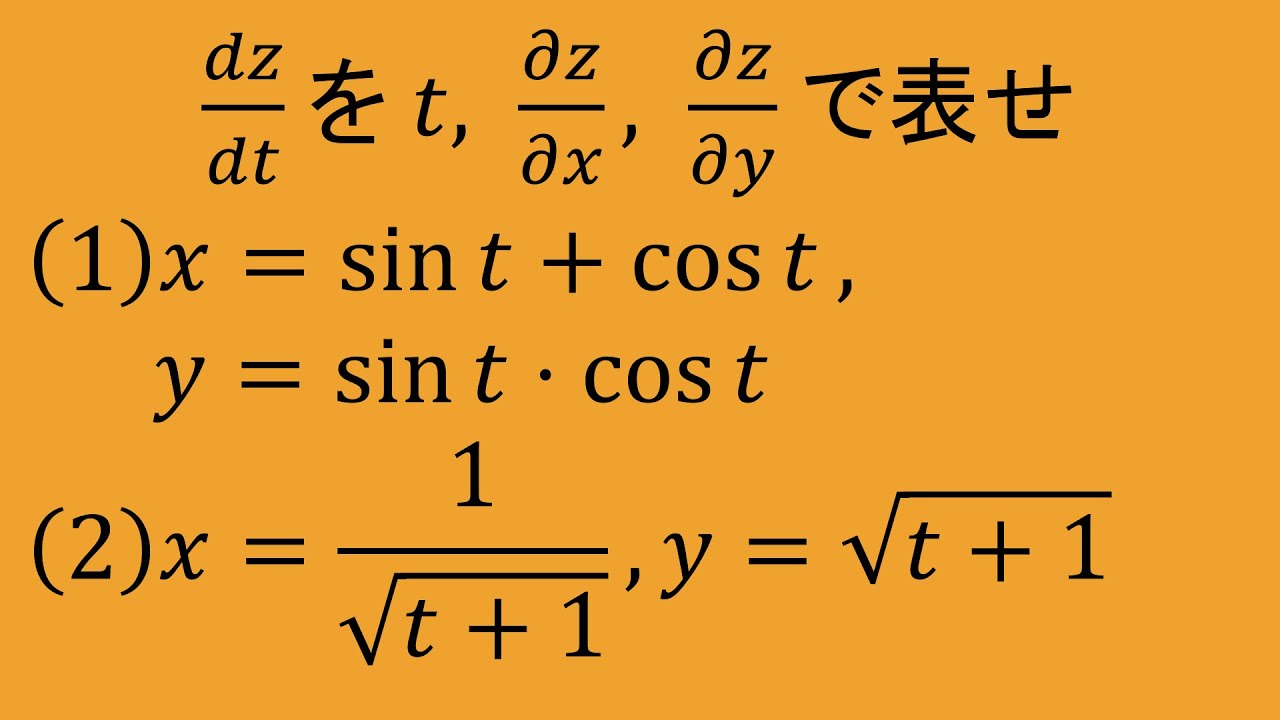
単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能
$\dfrac{dz}{dt}$を$t,\dfrac{\alpha z}{\alpha x},\dfrac{\alpha z}{\alpha y}$で表せ.
(3)$x=\sin t+\cos t$
$y=\sin t \cos t$
(4)$x=\dfrac{1}{\sqrt{x+1}}$
$y=\sqrt{t+1}$
この動画を見る
$z=f(x,y)$:全微分可能
$\dfrac{dz}{dt}$を$t,\dfrac{\alpha z}{\alpha x},\dfrac{\alpha z}{\alpha y}$で表せ.
(3)$x=\sin t+\cos t$
$y=\sin t \cos t$
(4)$x=\dfrac{1}{\sqrt{x+1}}$
$y=\sqrt{t+1}$
高専数学 微積II #51(1)(2) 合成関数の微分法

単元:
#数Ⅱ#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$z=f(x,y)$:全微分可能である.
$\dfrac{dz}{dt}$を$t,\dfrac{\delta z}{\delta x},\dfrac{\delta z}{\delta y}$で表せ.
(1)$x-te^t,y=\log t$
(2)$x=\dfrac{t}{2t+1},y=\dfrac{t+1}{2t+1}$
この動画を見る
$z=f(x,y)$:全微分可能である.
$\dfrac{dz}{dt}$を$t,\dfrac{\delta z}{\delta x},\dfrac{\delta z}{\delta y}$で表せ.
(1)$x-te^t,y=\log t$
(2)$x=\dfrac{t}{2t+1},y=\dfrac{t+1}{2t+1}$
福田のわかった数学〜高校3年生理系055〜格子点の個数と極限
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
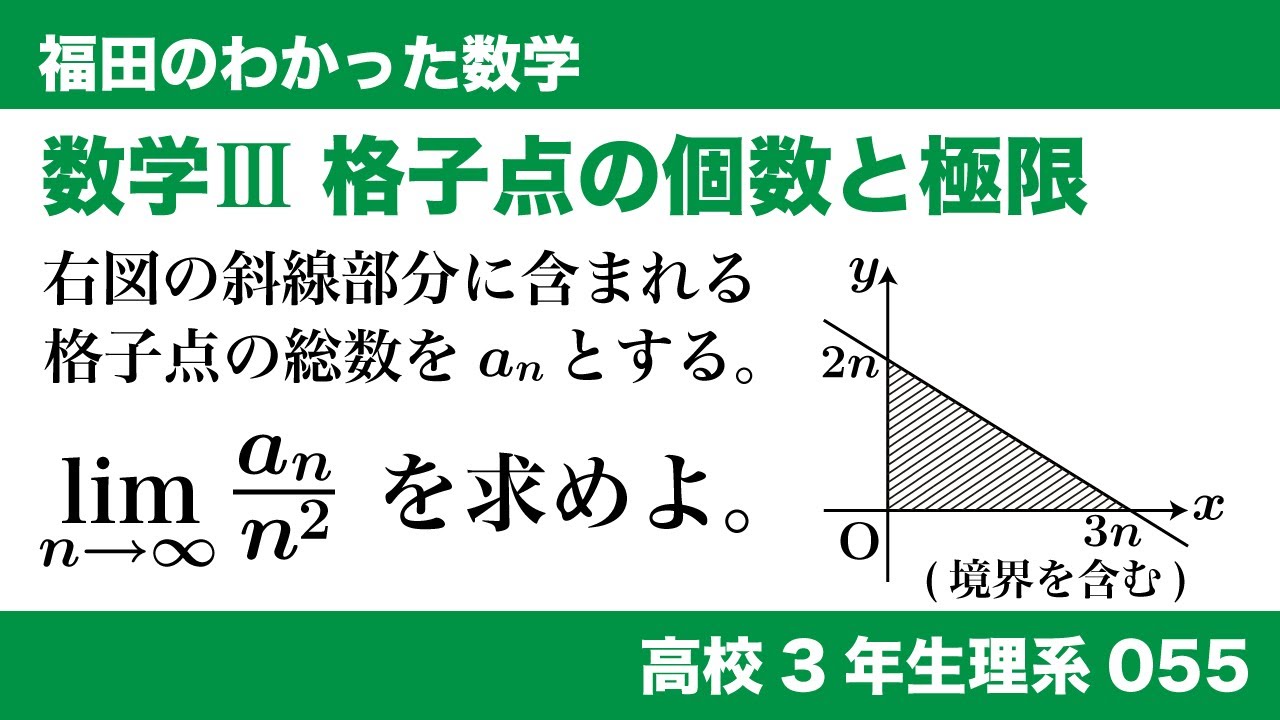
数学$\textrm{III}$ 格子点の個数と極限
右図の斜線部分(※動画参照)に含まれる
格子点の総数を$a_n$とする。
$\lim_{n \to \infty}\frac{a_n}{n^2}$を求めよ。
この動画を見る
数学$\textrm{III}$ 格子点の個数と極限
右図の斜線部分(※動画参照)に含まれる
格子点の総数を$a_n$とする。
$\lim_{n \to \infty}\frac{a_n}{n^2}$を求めよ。
福田のわかった数学〜高校3年生理系050〜極限(50)連続と微分可能(1)

単元:
#関数と極限#微分とその応用#関数の極限#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$
連続と微分可能(1)
$f(x)$が$x=a$で微分可能 $\Rightarrow f(x)$は$x=a$で連続
を示せ。また、逆が成り立たないことを示せ。
この動画を見る
数学$\textrm{III}$
連続と微分可能(1)
$f(x)$が$x=a$で微分可能 $\Rightarrow f(x)$は$x=a$で連続
を示せ。また、逆が成り立たないことを示せ。
東京海洋大 3次関数の基本

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=x^3-x$と$y=ax+b$が相異なる3点で交わる$a,b$の条件を求めよ.
2021東京海洋大過去問
この動画を見る
$y=x^3-x$と$y=ax+b$が相異なる3点で交わる$a,b$の条件を求めよ.
2021東京海洋大過去問
福田のわかった数学〜高校3年生理系049〜極限(49)中間値の定理(3)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 中間値の定理(3)
Aさんは300km離れた地点まで車でちょうど5時間かけて移動した。
このときこの300kmの中のどこか60kmの区間を
ちょうど1時間で通過したことを示せ。
この動画を見る
数学$\textrm{III}$ 中間値の定理(3)
Aさんは300km離れた地点まで車でちょうど5時間かけて移動した。
このときこの300kmの中のどこか60kmの区間を
ちょうど1時間で通過したことを示せ。
06滋賀県教員採用試験(数学:1-(3) 関数のグラフ)
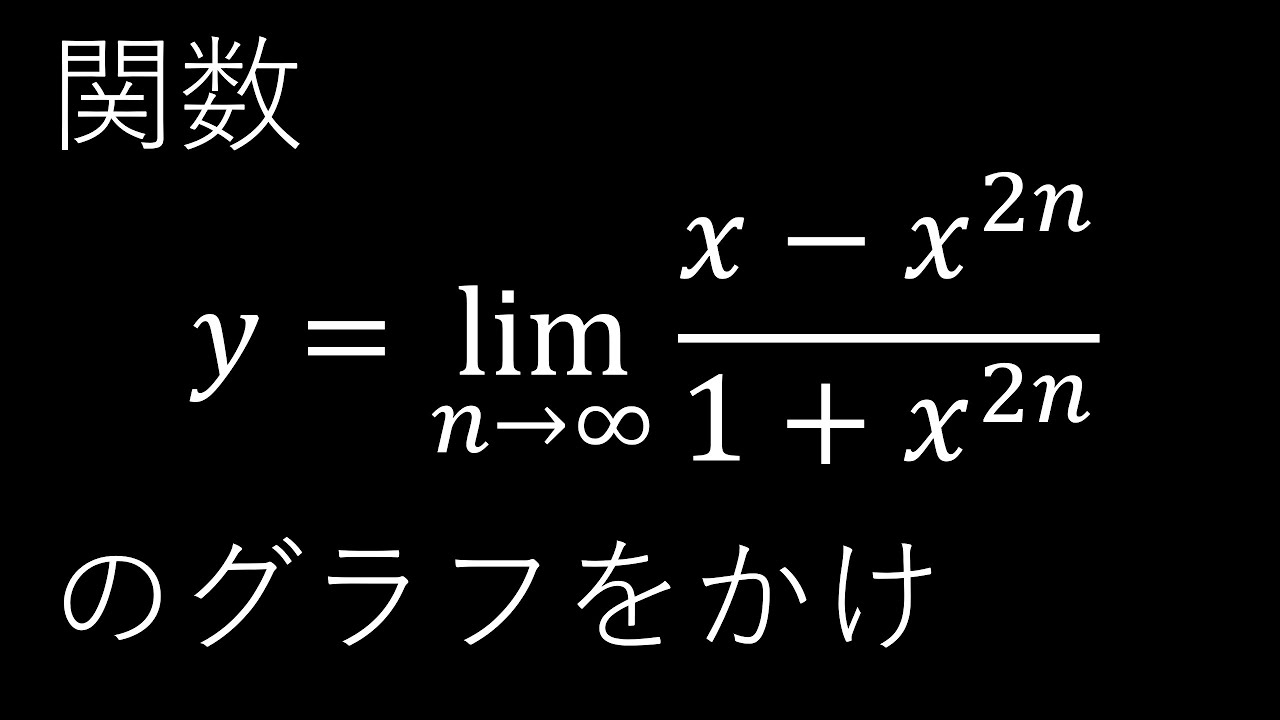
単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#関数と極限#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}-(3)$
$y=\displaystyle \lim_{n\to\infty} \dfrac{x-x^{2n}}{1+x^{2n}}$
のグラフをかけ.
この動画を見る
$\boxed{1}-(3)$
$y=\displaystyle \lim_{n\to\infty} \dfrac{x-x^{2n}}{1+x^{2n}}$
のグラフをかけ.
福田のわかった数学〜高校3年生理系048〜極限(48)中間値の定理(2)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 中間値の定理(2)
関数$f(x),g(x)$は区間[a,b]で連続でf(x)の最大値はg(x)の最大値よりも大きく、
f(x)の最小値はg(x)の最小値よりも小さい。このとき、方程式$f(x)=g(x)$は$a \leqq x \leqq b$
に実数解をもつことを示せ。
この動画を見る
数学$\textrm{III}$ 中間値の定理(2)
関数$f(x),g(x)$は区間[a,b]で連続でf(x)の最大値はg(x)の最大値よりも大きく、
f(x)の最小値はg(x)の最小値よりも小さい。このとき、方程式$f(x)=g(x)$は$a \leqq x \leqq b$
に実数解をもつことを示せ。
福田のわかった数学〜高校3年生理系047〜極限(47)中間値の定理(1)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 中間値の定理(1)
方程式$\sqrt x-2\log_3x=0$は、
$1 \lt x \lt 3$に実数解をもつことを示せ。
この動画を見る
数学$\textrm{III}$ 中間値の定理(1)
方程式$\sqrt x-2\log_3x=0$は、
$1 \lt x \lt 3$に実数解をもつことを示せ。
福田のわかった数学〜高校3年生理系046〜極限(46)関数の連続性(3)

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 関数の連続性(3)
$f(x)=\left\{\begin{array}{1}
\displaystyle\frac{x^2}{|x|} (x≠0)\\
0 (x=0)\\
\end{array}\right.$
は、$x=0$で連続か、調べよ。
この動画を見る
数学$\textrm{III}$ 関数の連続性(3)
$f(x)=\left\{\begin{array}{1}
\displaystyle\frac{x^2}{|x|} (x≠0)\\
0 (x=0)\\
\end{array}\right.$
は、$x=0$で連続か、調べよ。
