 色々な関数の導関数
色々な関数の導関数
 色々な関数の導関数
色々な関数の導関数
福田のおもしろ数学449〜3次式が常に0以上となるxの範囲

単元:
#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数$a$に対して関数$f(x)$を考える。
$f(x)=x^3-2x^2+(2a-1)x-2a$
$0\leqq a \leqq 1$のとき、
常に$f(x)\geqq 0$となる$x$の範囲を求めよ。
この動画を見る
実数$a$に対して関数$f(x)$を考える。
$f(x)=x^3-2x^2+(2a-1)x-2a$
$0\leqq a \leqq 1$のとき、
常に$f(x)\geqq 0$となる$x$の範囲を求めよ。
福田の数学〜京都大学2025理系第3問〜関数の増減と値域

単元:
#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$
$e$は自然対数の底とする。
$x\gt \dfrac{1}{\sqrt e}$において定義された次の関数
$f(x),g(x)$を考える。
$f(x)=x^2 \log x$
$g(x)=x^2\log x - \dfrac{1}{1+2\log x}$
実数$t$は$t\gt \dfrac{1}{\sqrt e}$を満たすとする。
曲線$y=f(x)$上の店$(t,f(t))$における接線に垂直で、
点$(t,g(t))$を通る直線を$l_t$とする。
直線$l_t$が$x$軸と交わる点の$x$座標を$p(t)$とする。
$t$が$\dfrac{1}{\sqrt e} \lt t \leqq e$の範囲を動くとき、
$p(t)$の取りうる値の範囲を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{3}$
$e$は自然対数の底とする。
$x\gt \dfrac{1}{\sqrt e}$において定義された次の関数
$f(x),g(x)$を考える。
$f(x)=x^2 \log x$
$g(x)=x^2\log x - \dfrac{1}{1+2\log x}$
実数$t$は$t\gt \dfrac{1}{\sqrt e}$を満たすとする。
曲線$y=f(x)$上の店$(t,f(t))$における接線に垂直で、
点$(t,g(t))$を通る直線を$l_t$とする。
直線$l_t$が$x$軸と交わる点の$x$座標を$p(t)$とする。
$t$が$\dfrac{1}{\sqrt e} \lt t \leqq e$の範囲を動くとき、
$p(t)$の取りうる値の範囲を求めよ。
$2025$年京都大学理系過去問題
【数Ⅲ】【微分とその応用】n次導関数と微分の表し方 ※問題文は概要欄

単元:
#微分とその応用#微分法#色々な関数の導関数#数学(高校生)#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数について, $\frac{ dy }{ dx }$ を求めよ。ただし (1)(2)では $y$ を用いて表してもよい。また(3)(4)では、t$$ の関数として表せ。$a,b$は正の定数とする。
$x²+3xy-y²=1$
$x$の関数 $y$ が、$t$ を媒介変数として $x=cost +tsint, y= sint - tcost$ と表せるとき、$\frac{ d^2 y }{ dx^2 }$ を$ t $の関数として表せ。
この動画を見る
次の関数について, $\frac{ dy }{ dx }$ を求めよ。ただし (1)(2)では $y$ を用いて表してもよい。また(3)(4)では、t$$ の関数として表せ。$a,b$は正の定数とする。
$x²+3xy-y²=1$
$x$の関数 $y$ が、$t$ を媒介変数として $x=cost +tsint, y= sint - tcost$ と表せるとき、$\frac{ d^2 y }{ dx^2 }$ を$ t $の関数として表せ。
【数Ⅲ】【微分とその応用】色々な関数の微分2 ※問題文は概要欄

単元:
#微分とその応用#色々な関数の導関数#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
対数微分法により次の関数を微分せよ。ただし、aは定数とする。
y= (x+1)²/((x+2)³(x+3)⁴)
以下、略
次の関数を微分せよ。ただし x>0 とする。
y= x^sinx
以下、略
lim_(k→0) (1+k)^(1/k)=e を用いて、次の極限を求めよ。
lim_(x→0) ((log(1+x)/x)
以下、略
この動画を見る
対数微分法により次の関数を微分せよ。ただし、aは定数とする。
y= (x+1)²/((x+2)³(x+3)⁴)
以下、略
次の関数を微分せよ。ただし x>0 とする。
y= x^sinx
以下、略
lim_(k→0) (1+k)^(1/k)=e を用いて、次の極限を求めよ。
lim_(x→0) ((log(1+x)/x)
以下、略
【数Ⅲ】【微分とその応用】色々な関数の微分1 ※問題文は概要欄

単元:
#微分とその応用#色々な関数の導関数#数Ⅲ
教材:
#4S数学#4S数学ⅢのB問題解説#中高教材#微分法の応用
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の関数を微分せよ
y= sin²3x
y= sin⁵x+cos5x
y= sin⁴xcos⁴x
y= √(1+sin²x)
y= sin√(x²+x+1)
y= (tanx + 1/tanx)²
y= cosx/(1-sinx)
y= (1-sinx) / (1+cosx)
次の極限値を求めよ
lim_(x→a) (sinx - sina) / sin(x-a)
lim_(x→a) (x²sina - a²sinx) / (x-a)
次の関数を微分せよ。ただしa,bは定数で、a>0,a≠0 とする。
y= e^(-2x) sin2x
y= 10^sinx
y= log_x(a)
y= log(logx)
y= log_a(sinx)
y= log(1-cosx)
y= log_a(x+√(x²-a²)
y= log ((x²-b) / (x²+b))
この動画を見る
次の関数を微分せよ
y= sin²3x
y= sin⁵x+cos5x
y= sin⁴xcos⁴x
y= √(1+sin²x)
y= sin√(x²+x+1)
y= (tanx + 1/tanx)²
y= cosx/(1-sinx)
y= (1-sinx) / (1+cosx)
次の極限値を求めよ
lim_(x→a) (sinx - sina) / sin(x-a)
lim_(x→a) (x²sina - a²sinx) / (x-a)
次の関数を微分せよ。ただしa,bは定数で、a>0,a≠0 とする。
y= e^(-2x) sin2x
y= 10^sinx
y= log_x(a)
y= log(logx)
y= log_a(sinx)
y= log(1-cosx)
y= log_a(x+√(x²-a²)
y= log ((x²-b) / (x²+b))
福田の数学〜上智大学2024TEAP利用型理系第1問(3)〜対数不等式を満たす最小の整数

単元:
#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(i) $\log_{10} 2=0.301$とする。このとき、$\log_{10} 1.28=0.\boxed{ウ}$である。
(ii)$n$は$2$以上の整数とする。$n^{100}<1.28^n$となる最小の$n$について、$2^a \leqq n < 2^{a+1}$となる整数$a$は$\boxed{エ}$
この動画を見る
(i) $\log_{10} 2=0.301$とする。このとき、$\log_{10} 1.28=0.\boxed{ウ}$である。
(ii)$n$は$2$以上の整数とする。$n^{100}<1.28^n$となる最小の$n$について、$2^a \leqq n < 2^{a+1}$となる整数$a$は$\boxed{エ}$
福田の数学〜明治大学2024理工学部第2問〜三角関数の増減と面積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\sin{3x}-\sqrt3\cos{2x}$とし、座標平面上の曲線$y=f(x)$を$C$とする。
(1) 点$(0,f(0))$における曲線$C$の接線の方程式は$y=\boxed{あ}$である。
(2) $t$についての整式$g(t)$で、$f'(x)=g(\sin x)\cos x$が成り立つものを求めると、$g(t)=\boxed{い}$である。
(3) $x>0$の範囲で、$f'(x)=0$となる$x$の値を小さい順に$x_1,x_2,x_3,\cdots$とすると、$x_1=\boxed{う},x_2=\boxed{え},x_3=\boxed{お}$である。
(4) $0\leqq x\leqq \pi$の範囲での$f(x)$の最大値は$\boxed{か}$、最小値は$\boxed{き}$である。
(5) (4)で定めた$x_1$と$x_3$に対して、2点$(x_1,f(x_1)),(x_3,f(x_3))$を通る直線を$l$とする。このとき、$x_1\leqq x\leqq x_3$の範囲において直線$l$と曲線$C$で囲まれた部分の面積は$\boxed{く}$である。
この動画を見る
$f(x)=\sin{3x}-\sqrt3\cos{2x}$とし、座標平面上の曲線$y=f(x)$を$C$とする。
(1) 点$(0,f(0))$における曲線$C$の接線の方程式は$y=\boxed{あ}$である。
(2) $t$についての整式$g(t)$で、$f'(x)=g(\sin x)\cos x$が成り立つものを求めると、$g(t)=\boxed{い}$である。
(3) $x>0$の範囲で、$f'(x)=0$となる$x$の値を小さい順に$x_1,x_2,x_3,\cdots$とすると、$x_1=\boxed{う},x_2=\boxed{え},x_3=\boxed{お}$である。
(4) $0\leqq x\leqq \pi$の範囲での$f(x)$の最大値は$\boxed{か}$、最小値は$\boxed{き}$である。
(5) (4)で定めた$x_1$と$x_3$に対して、2点$(x_1,f(x_1)),(x_3,f(x_3))$を通る直線を$l$とする。このとき、$x_1\leqq x\leqq x_3$の範囲において直線$l$と曲線$C$で囲まれた部分の面積は$\boxed{く}$である。
福田のおもしろ数学241〜e^πとπ^eの大小

福田の数学〜中央大学202理工学部第3問〜関数の列と漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#微分とその応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数$f(x),g(x)$に対し、$s_n(x)=f(x)^n+g(x)^n$とおき、さらに$s_1(x)=x, s_2(x)=x^2+2$が成り立つとする。
(1) $f(x)+g(x)$と$s_3(x)$を求めよ。
(2) $s_{n+2}(x)$を$s_n(x)$と$s_{n+1}(x)$を用いて表せ。
(3) $s_n(x)$の$x=0$における値$s_n(0)$と微分係数$s_n'(0)$を求めよ。
この動画を見る
関数$f(x),g(x)$に対し、$s_n(x)=f(x)^n+g(x)^n$とおき、さらに$s_1(x)=x, s_2(x)=x^2+2$が成り立つとする。
(1) $f(x)+g(x)$と$s_3(x)$を求めよ。
(2) $s_{n+2}(x)$を$s_n(x)$と$s_{n+1}(x)$を用いて表せ。
(3) $s_n(x)$の$x=0$における値$s_n(0)$と微分係数$s_n'(0)$を求めよ。
福田の数学〜東京大学2018年理系第1問〜関数の増減と極限の計算

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\dfrac{x}{\sin x}+\cos x (0 \lt x \lt \pi)$のぞうげんひょうを作り、$x→+0,x→\pi-0$のときの極限を調べよ。
2018東京大学理過去問
この動画を見る
$f(x)=\dfrac{x}{\sin x}+\cos x (0 \lt x \lt \pi)$のぞうげんひょうを作り、$x→+0,x→\pi-0$のときの極限を調べよ。
2018東京大学理過去問
福田の数学〜陰関数を考える貴重な問題〜明治大学2023年全学部統一Ⅲ第4問〜陰関数のグラフの増減とグラフ

単元:
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ 座標空間において、2点(-2,0),(2,0)からの距離の積が4であるような点Pの軌跡を考える。点Pの座標を($x$,$y$)とすると、$x$,$y$は次の方程式を満たす。
$y^4$+$\boxed{\ \ ア\ \ }y^2$+$(\boxed{\ \ イ\ \ })^2$=16 ...(1)
方程式(1)が表す曲線を$C$とする。$C$の概形を描くことにしよう。まず、曲線$C$と$x$軸との共有点の$x$座標は$\boxed{\ \ ウ\ \ }$と$±\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$である。次に、(1)を$y^2$に関する2次方程式とみて解けば、$y^2$≧0 であるので、
$y^2$=$\boxed{\ \ カ\ \ }$+$4\sqrt{\boxed{\ \ キ\ \ }}$ ...(2)
となり、また$x$のとりうる値の範囲は
$-\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$
となる。$x$≧0, $y$≧0とすれば、方程式(2)は0≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$を定義域とする$x$の関数$y$を定める。このとき、0<$x$$\boxed{\ \ サ\ \ }$のとき共有点はなく、0≦$a$≦$\boxed{\ \ サ\ \ }$のとき共有点がある。
共有点の個数は、$a$=0のとき$\boxed{\ \ シ\ \ }$個、0<$a$<$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ ス\ \ }$個、$a$=$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ セ\ \ }$個となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ カ\ \ }$、$\boxed{\ \ キ\ \ }$の解答群
⓪$x^2+1$ ①$-(x^2+1)$ ②$x^2-1$ ③$-(x^2-1)$ ④$x^2+4$
⑤$2(x^2+4)$ ⑥$x^2-4$ ⑦$2(x^2-4)$ ⑧$-(x^2+4)$ ⑨$-2(x^2-4)$
この動画を見る
$\Large{\boxed{4}}$ 座標空間において、2点(-2,0),(2,0)からの距離の積が4であるような点Pの軌跡を考える。点Pの座標を($x$,$y$)とすると、$x$,$y$は次の方程式を満たす。
$y^4$+$\boxed{\ \ ア\ \ }y^2$+$(\boxed{\ \ イ\ \ })^2$=16 ...(1)
方程式(1)が表す曲線を$C$とする。$C$の概形を描くことにしよう。まず、曲線$C$と$x$軸との共有点の$x$座標は$\boxed{\ \ ウ\ \ }$と$±\boxed{\ \ エ\ \ }\sqrt{\boxed{\ \ オ\ \ }}$である。次に、(1)を$y^2$に関する2次方程式とみて解けば、$y^2$≧0 であるので、
$y^2$=$\boxed{\ \ カ\ \ }$+$4\sqrt{\boxed{\ \ キ\ \ }}$ ...(2)
となり、また$x$のとりうる値の範囲は
$-\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$
となる。$x$≧0, $y$≧0とすれば、方程式(2)は0≦$x$≦$\boxed{\ \ ク\ \ }\sqrt{\boxed{\ \ ケ\ \ }}$を定義域とする$x$の関数$y$を定める。このとき、0<$x$$\boxed{\ \ サ\ \ }$のとき共有点はなく、0≦$a$≦$\boxed{\ \ サ\ \ }$のとき共有点がある。
共有点の個数は、$a$=0のとき$\boxed{\ \ シ\ \ }$個、0<$a$<$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ ス\ \ }$個、$a$=$\boxed{\ \ サ\ \ }$のとき$\boxed{\ \ セ\ \ }$個となる。
$\boxed{\ \ ア\ \ }$、$\boxed{\ \ イ\ \ }$、$\boxed{\ \ カ\ \ }$、$\boxed{\ \ キ\ \ }$の解答群
⓪$x^2+1$ ①$-(x^2+1)$ ②$x^2-1$ ③$-(x^2-1)$ ④$x^2+4$
⑤$2(x^2+4)$ ⑥$x^2-4$ ⑦$2(x^2-4)$ ⑧$-(x^2+4)$ ⑨$-2(x^2-4)$
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
関数はパターンだ!!宮崎学園 (宮崎)
単元:
#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
数学を数楽に
問題文全文(内容文):
点Dの座標は?
*図は動画内参照
宮崎学園高等学校
この動画を見る
点Dの座標は?
*図は動画内参照
宮崎学園高等学校
関数はパターンだ!!北陸高校(福井県)
単元:
#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
数学を数楽に
問題文全文(内容文):
△OAB=△PAB
S=?(S>2)
*図は動画内参照
北陸(改)
この動画を見る
△OAB=△PAB
S=?(S>2)
*図は動画内参照
北陸(改)
福田の数学〜筑波大学2023年理系第5問〜関数の増減と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ $f(x)$=$x^{-2}e^x$ ($x$>0)とし、曲線$y$=$f(x)$をCとする。また$h$を正の実数とする。さらに、正の実数$t$に対して、曲線C、2直線$x$=$t$, $x$=$t$+$h$、および$x$軸で囲まれた図形の面積を$g(t)$とする。
(1)$g'(t)$を求めよ。
(2)$g(t)$を最小にする$t$がただ1つ存在することを示し、その$t$を$h$を用いて表せ。
(3)(2)で得られた$t$を$t(h)$とする。このとき極限値$\displaystyle\lim_{h \to +0}t(h)$を求めよ。
この動画を見る
$\Large\boxed{5}$ $f(x)$=$x^{-2}e^x$ ($x$>0)とし、曲線$y$=$f(x)$をCとする。また$h$を正の実数とする。さらに、正の実数$t$に対して、曲線C、2直線$x$=$t$, $x$=$t$+$h$、および$x$軸で囲まれた図形の面積を$g(t)$とする。
(1)$g'(t)$を求めよ。
(2)$g(t)$を最小にする$t$がただ1つ存在することを示し、その$t$を$h$を用いて表せ。
(3)(2)で得られた$t$を$t(h)$とする。このとき極限値$\displaystyle\lim_{h \to +0}t(h)$を求めよ。
福田の数学〜神戸大学2023年理系第5問〜媒介変数表示で表された曲線と面積

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#神戸大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 媒介変数表示
$x$=$\sin t$, $y$=$\cos(t-\frac{\pi}{6})\sin t$ (0≦$t$≦$\pi$)
で表される曲線をCとする。以下の問いに答えよ。
(1)$\frac{dx}{dt}$=0 または $\frac{dy}{dt}$=0 となる$t$の値を求めよ。
(2)Cの概形を$xy$平面上に描け。
(3)Cの$y$≦0 の部分と$x$軸で囲まれた図形の面積を求めよ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{5}$ 媒介変数表示
$x$=$\sin t$, $y$=$\cos(t-\frac{\pi}{6})\sin t$ (0≦$t$≦$\pi$)
で表される曲線をCとする。以下の問いに答えよ。
(1)$\frac{dx}{dt}$=0 または $\frac{dy}{dt}$=0 となる$t$の値を求めよ。
(2)Cの概形を$xy$平面上に描け。
(3)Cの$y$≦0 の部分と$x$軸で囲まれた図形の面積を求めよ。
2023神戸大学理系過去問
福田の数学〜名古屋大学2023年理系第2問〜回転体の体積と関数の増減と最大

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#積分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#面積、体積#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 0<b<a とする。xy平面において、原点を中心とする半径rの円Cと点(a, 0)を中心とする半径bの円Dが2点で交わっている。
(1)半径rの満たすべき条件を求めよ。
(2)CとDの交点のうちy座標が正のものをPとする。Pのx座標h(r)を求めよ。
(3)点Q(r, 0)と点R(a-b, 0)をとる。Dの内部にあるCの弧PQ、線分QR、および線分RPで囲まれる図形をAとする。xyz空間においてAをx軸の周りに1回転して得られる立体の体積V(r)を求めよ。ただし答えにh(r)を用いてもよい。
(4)(3)の最大値を与えるrを求めよ。また、そのrをr(a)とおいたとき、
$\displaystyle\lim_{a \to \infty}(r(a)-a)$を求めよ。
2023名古屋大学理系過去問
この動画を見る
$\Large\boxed{2}$ 0<b<a とする。xy平面において、原点を中心とする半径rの円Cと点(a, 0)を中心とする半径bの円Dが2点で交わっている。
(1)半径rの満たすべき条件を求めよ。
(2)CとDの交点のうちy座標が正のものをPとする。Pのx座標h(r)を求めよ。
(3)点Q(r, 0)と点R(a-b, 0)をとる。Dの内部にあるCの弧PQ、線分QR、および線分RPで囲まれる図形をAとする。xyz空間においてAをx軸の周りに1回転して得られる立体の体積V(r)を求めよ。ただし答えにh(r)を用いてもよい。
(4)(3)の最大値を与えるrを求めよ。また、そのrをr(a)とおいたとき、
$\displaystyle\lim_{a \to \infty}(r(a)-a)$を求めよ。
2023名古屋大学理系過去問
福田の数学〜早稲田大学2023年理工学部第4問〜複素数平面上の点の軌跡

単元:
#大学入試過去問(数学)#複素数平面#微分とその応用#複素数平面#図形への応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 複素数平面上に2点A(1), B($\sqrt 3 i$)がある。ただし、$i$は虚数単位である。
複素数zに対し$w$=$\frac{3}{z}$で表される点$w$を考える。以下の問いに答えよ。
(1)z=1, $\frac{1+\sqrt 3i}{2}$, $\sqrt 3 i$のときのwをそれぞれ計算せよ。
(2)実数tに対し、z=(1-t)+t$\sqrt 3 i$とする。$\alpha$=$\frac{3-\sqrt 3 i}{2}$について、$\alpha z$の実部を求め、さらに($w-\alpha$)($\bar{w-\alpha}$)を求めよ。
(3)wと原点を結んでできる線分Lを考える。zが線分AB上を動くとき、線分Lが通過する範囲を図示し、その面積を求めよ。
この動画を見る
$\Large\boxed{4}$ 複素数平面上に2点A(1), B($\sqrt 3 i$)がある。ただし、$i$は虚数単位である。
複素数zに対し$w$=$\frac{3}{z}$で表される点$w$を考える。以下の問いに答えよ。
(1)z=1, $\frac{1+\sqrt 3i}{2}$, $\sqrt 3 i$のときのwをそれぞれ計算せよ。
(2)実数tに対し、z=(1-t)+t$\sqrt 3 i$とする。$\alpha$=$\frac{3-\sqrt 3 i}{2}$について、$\alpha z$の実部を求め、さらに($w-\alpha$)($\bar{w-\alpha}$)を求めよ。
(3)wと原点を結んでできる線分Lを考える。zが線分AB上を動くとき、線分Lが通過する範囲を図示し、その面積を求めよ。
大学入試問題#470「誘導なくてもどうにかできそう」 信州大学 理・医学部(2021) #微積の応用

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#色々な関数の導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\forall\ a,b$
$f(a+b)=f(a)+f(b)+4ab$
$f'(0)=2$
(1)
$f(0)$を求めよ
(2)
$f(x)$は微分可能を示せ
$f(x)$を求めよ
(3)
$\displaystyle \lim_{ x \to \infty } \displaystyle \int_{1}^{x} \displaystyle \frac{1}{f(t)}dt(x \gt 1)$
出典:2021年信州大学 入試問題
この動画を見る
$\forall\ a,b$
$f(a+b)=f(a)+f(b)+4ab$
$f'(0)=2$
(1)
$f(0)$を求めよ
(2)
$f(x)$は微分可能を示せ
$f(x)$を求めよ
(3)
$\displaystyle \lim_{ x \to \infty } \displaystyle \int_{1}^{x} \displaystyle \frac{1}{f(t)}dt(x \gt 1)$
出典:2021年信州大学 入試問題
福田の1.5倍速演習〜合格する重要問題080〜京都大学2018年度理系第5問〜曲線の長さと極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 曲線y=$\log x$上の点A(t, $\log t$)における法線上に、点BをAB=1となるようにとる。ただしBのx座標はtより大きい。
(1)点Bの座標(u(t), v(t))を求めよ。また$\left(\frac{du}{dt}, \frac{dv}{dt}\right)$を求めよ。
(2)実数rは0<r<1を満たすとし、tがrから1まで動くときに点Aと点Bが描く曲線の長さをそれぞれ$L_1(r)$, $L_2(r)$とする。このとき、極限$\displaystyle\lim_{r \to +0}(L_1(r)-L_2(r))$を求めよ。
2018京都大学理系過去問
この動画を見る
$\Large\boxed{5}$ 曲線y=$\log x$上の点A(t, $\log t$)における法線上に、点BをAB=1となるようにとる。ただしBのx座標はtより大きい。
(1)点Bの座標(u(t), v(t))を求めよ。また$\left(\frac{du}{dt}, \frac{dv}{dt}\right)$を求めよ。
(2)実数rは0<r<1を満たすとし、tがrから1まで動くときに点Aと点Bが描く曲線の長さをそれぞれ$L_1(r)$, $L_2(r)$とする。このとき、極限$\displaystyle\lim_{r \to +0}(L_1(r)-L_2(r))$を求めよ。
2018京都大学理系過去問
大学入試問題#441「見た目と違って解いてみたら、良問と実感するはず!」 信州大学(2022) #不等式

単元:
#大学入試過去問(数学)#微分とその応用#色々な関数の導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$:自然数
$0 \leqq x$:実数
$log(1+x) \geqq \displaystyle \sum_{k=1}^{2n} \displaystyle \frac{(-1)^{k-1}}{k}x^k$を示せ
出典:2022年信州大学 入試問題
この動画を見る
$n$:自然数
$0 \leqq x$:実数
$log(1+x) \geqq \displaystyle \sum_{k=1}^{2n} \displaystyle \frac{(-1)^{k-1}}{k}x^k$を示せ
出典:2022年信州大学 入試問題
#大学への数学「大学受験で、たまに使う技」 学力コンテスト (1)(2) #定積分
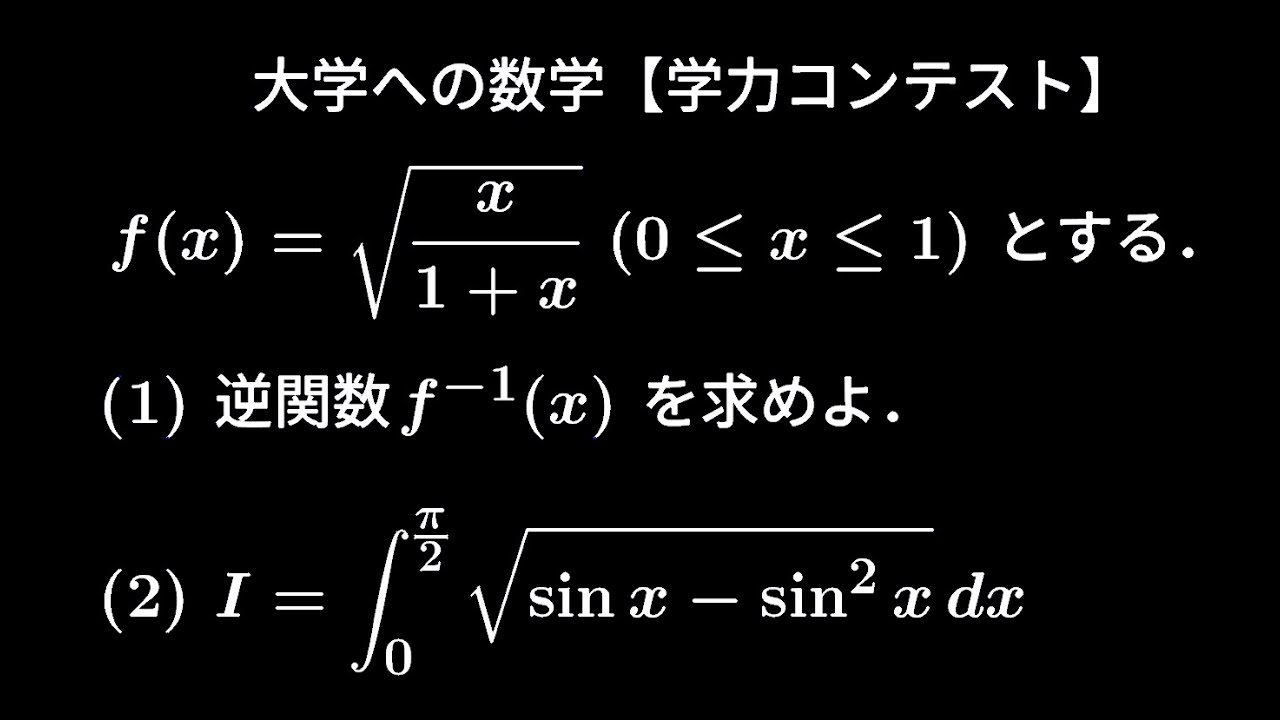
単元:
#微分とその応用#積分とその応用#微分法#色々な関数の導関数#定積分#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\sqrt{ \displaystyle \frac{x}{1+x} }(0 \leqq x \leqq 1)$
(1)
逆関数$f^{-1}(x)$を求めよ。
(2)
$I=\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin\ x-\sin^2x }\ dx$
(3)
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin^3x-\sin^4x }\ dx$
この動画を見る
$f(x)=\sqrt{ \displaystyle \frac{x}{1+x} }(0 \leqq x \leqq 1)$
(1)
逆関数$f^{-1}(x)$を求めよ。
(2)
$I=\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin\ x-\sin^2x }\ dx$
(3)
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin^3x-\sin^4x }\ dx$
【数Ⅲ】三角関数・指数・対数の微分公式【合成関数との合せ技】

【数Ⅲ】微分法・積分法:<公式忘れても大丈夫!>三角関数の微積分 ~ぐるぐる回そう~

単元:
#微分とその応用#積分とその応用#色々な関数の導関数#不定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
この動画を見る
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
福田のわかった数学〜高校3年生理系077〜極値(1)極大値をもつ条件

単元:
#数Ⅱ#三角関数#三角関数とグラフ#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極値(1)
$f(x)=\frac{a-\cos x}{a+\sin x}\ が0 \lt x \lt \frac{\pi}{2}$の範囲で
極大値をもつように定数aの値の範囲を定めよ。
この動画を見る
数学$\textrm{III}$ 極値(1)
$f(x)=\frac{a-\cos x}{a+\sin x}\ が0 \lt x \lt \frac{\pi}{2}$の範囲で
極大値をもつように定数aの値の範囲を定めよ。
福田の数学〜明治大学2021年全学部統一入試Ⅲ第1問〜関数の増減と面積

単元:
#微分とその応用#積分とその応用#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#数学(高校生)#大学入試解答速報#数学#明治大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$関数$f(x)=\frac{1}{2}(x+\sqrt{2-3x^2})$の定義域は$-\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }} \leqq x \leqq \frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$であり、
$f(x)$は$x=\frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$のとき、
最大値$\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$をとる。曲線$y=f(x)$、
直線$y=2x$およびy軸で囲まれた図形の面積は$\boxed{\ \ ケ\ \ }$となる。
$\boxed{\ \ ケ\ \ }$の解答群
$⓪\frac{\sqrt3}{18}\pi ①\frac{\sqrt3}{36}\pi ②\frac{\sqrt3}{72}\pi ③\frac{1}{6}+\frac{\sqrt3}{36}\pi ④\frac{1}{24}+\frac{\sqrt3}{36}\pi$
$⑤\frac{5}{24}+\frac{\sqrt3}{36}\pi ⑥\frac{1}{3}+\frac{\sqrt3}{18}\pi ⑦\frac{1}{6}+\frac{\sqrt3}{18}\pi ⑧\frac{1}{8}+\frac{\sqrt3}{18}\pi ⑨\frac{7}{24}+\frac{\sqrt3}{18}\pi$
この動画を見る
${\Large\boxed{1}}$関数$f(x)=\frac{1}{2}(x+\sqrt{2-3x^2})$の定義域は$-\frac{\sqrt{\boxed{\ \ ア\ \ }}}{\boxed{\ \ イ\ \ }} \leqq x \leqq \frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$であり、
$f(x)$は$x=\frac{\sqrt{\boxed{\ \ オ\ \ }}}{\boxed{\ \ カ\ \ }}$のとき、
最大値$\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$をとる。曲線$y=f(x)$、
直線$y=2x$およびy軸で囲まれた図形の面積は$\boxed{\ \ ケ\ \ }$となる。
$\boxed{\ \ ケ\ \ }$の解答群
$⓪\frac{\sqrt3}{18}\pi ①\frac{\sqrt3}{36}\pi ②\frac{\sqrt3}{72}\pi ③\frac{1}{6}+\frac{\sqrt3}{36}\pi ④\frac{1}{24}+\frac{\sqrt3}{36}\pi$
$⑤\frac{5}{24}+\frac{\sqrt3}{36}\pi ⑥\frac{1}{3}+\frac{\sqrt3}{18}\pi ⑦\frac{1}{6}+\frac{\sqrt3}{18}\pi ⑧\frac{1}{8}+\frac{\sqrt3}{18}\pi ⑨\frac{7}{24}+\frac{\sqrt3}{18}\pi$
福田の数学〜上智大学2021年TEAP利用理系第4問〜楕円と弦の中点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#図形と方程式#軌跡と領域#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$Oを原点とする座標平面において、楕円$D:\frac{x^2}{6}+\frac{y^2}{2}=1$ 上に異なる2点$P_1,P_2$
がある。$P_1$における接線$l_1$と$P_2$における接線$l_2$の交点を$Q(a,\ b)$とし、線分$P_1P_2$の
中点をRとする。
(1)$P_1$の座標を$(x_1,\ y_1)$とするとき、$l_1$の方程式は$x_1x+\boxed{\ \ チ\ \ }\ y_1y+\boxed{\ \ ツ\ \ }=0$
と表される。
(2)直線$P_1P_2$の方程式は、a,bを用いて$ax+\boxed{\ \ テ\ \ }\ by+\boxed{\ \ ト\ \ }=0$と表される。
(3)3点O,R,Qは一直線上にあって$\overrightarrow{ OR }=\frac{\boxed{\ \ ナ\ \ }}{a^2+\boxed{\ \ ニ\ \ }\ b^2}\overrightarrow{ OQ }$が成り立つ。
(4)$l_1$と$l_2$のどちらもy軸と平行ではないとする。このとき、$l_1$と$l_2$の傾きは
tの方程式$(a^2+\boxed{\ \ ヌ\ \ })t^2+\boxed{\ \ ネ\ \ }abt+(b^2+\boxed{\ \ ノ\ \ })=0$ の解である。
(5)$l_1$と$l_2$が直交しながら$P_1,P_2$が動くとする。
$(\textrm{i})Q$の軌跡の方程式を求めよ。 $(\textrm{ii})R$のy座標の最大値を求めよ。
$(\textrm{iii})R$の軌跡の概形を描け。
2021上智大学理系過去問
この動画を見る
${\Large\boxed{4}}$Oを原点とする座標平面において、楕円$D:\frac{x^2}{6}+\frac{y^2}{2}=1$ 上に異なる2点$P_1,P_2$
がある。$P_1$における接線$l_1$と$P_2$における接線$l_2$の交点を$Q(a,\ b)$とし、線分$P_1P_2$の
中点をRとする。
(1)$P_1$の座標を$(x_1,\ y_1)$とするとき、$l_1$の方程式は$x_1x+\boxed{\ \ チ\ \ }\ y_1y+\boxed{\ \ ツ\ \ }=0$
と表される。
(2)直線$P_1P_2$の方程式は、a,bを用いて$ax+\boxed{\ \ テ\ \ }\ by+\boxed{\ \ ト\ \ }=0$と表される。
(3)3点O,R,Qは一直線上にあって$\overrightarrow{ OR }=\frac{\boxed{\ \ ナ\ \ }}{a^2+\boxed{\ \ ニ\ \ }\ b^2}\overrightarrow{ OQ }$が成り立つ。
(4)$l_1$と$l_2$のどちらもy軸と平行ではないとする。このとき、$l_1$と$l_2$の傾きは
tの方程式$(a^2+\boxed{\ \ ヌ\ \ })t^2+\boxed{\ \ ネ\ \ }abt+(b^2+\boxed{\ \ ノ\ \ })=0$ の解である。
(5)$l_1$と$l_2$が直交しながら$P_1,P_2$が動くとする。
$(\textrm{i})Q$の軌跡の方程式を求めよ。 $(\textrm{ii})R$のy座標の最大値を求めよ。
$(\textrm{iii})R$の軌跡の概形を描け。
2021上智大学理系過去問
福田のわかった数学〜高校3年生理系072〜接線(4)共通接線(2)

単元:
#数Ⅱ#微分とその応用#微分法#色々な関数の導関数#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 接線(4) 共通接線(2)
2曲線$y=x^2$と$y=\frac{1}{x}$の両方に接する直線の方程式を求めよ。
この動画を見る
数学$\textrm{III}$ 接線(4) 共通接線(2)
2曲線$y=x^2$と$y=\frac{1}{x}$の両方に接する直線の方程式を求めよ。
福田のわかった数学〜高校3年生理系071〜接線(3)共通接線(1)

単元:
#微分とその応用#微分法#色々な関数の導関数#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 接線(3) 共通接線(1)
2曲線$\ y=e^xとy=\sqrt{x+a}$がともに点Pを通り、点Pにおいて共通の
接線をもつとき、aの値と接線の方程式を求めよ。
この動画を見る
数学$\textrm{III}$ 接線(3) 共通接線(1)
2曲線$\ y=e^xとy=\sqrt{x+a}$がともに点Pを通り、点Pにおいて共通の
接線をもつとき、aの値と接線の方程式を求めよ。
福田のわかった数学〜高校3年生理系070〜接線(2)媒介変数表示の接線

単元:
#平面上の曲線#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#媒介変数表示と極座標#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$接線(2) 媒介変数表示の接線
$\left\{
\begin{array}{1}
x=\theta-\sin\theta\\
y=1-\cos\theta
\end{array}
\right.$
で表される曲線の$\theta=\frac{3\pi}{2}$のときの点Pにおける接線を求めよ。
この動画を見る
数学$\textrm{III}$接線(2) 媒介変数表示の接線
$\left\{
\begin{array}{1}
x=\theta-\sin\theta\\
y=1-\cos\theta
\end{array}
\right.$
で表される曲線の$\theta=\frac{3\pi}{2}$のときの点Pにおける接線を求めよ。
