 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
16愛知県教員採用試験(数学:10番(2) 微分積分)

単元:
#数Ⅱ#微分法と積分法#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{10}$
$f(x)=\displaystyle \int_{0}^{x} \ (1-t^2)e^t \ dt$の極値を求めよ.
この動画を見る
$\boxed{10}$
$f(x)=\displaystyle \int_{0}^{x} \ (1-t^2)e^t \ dt$の極値を求めよ.
2021藤田医科大 微分の公式

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=\sqrt{x+\sqrt{x^2-9}}$
$f`_{(5)}=\Box$
$\Box$を求めよ.
2021藤田医科大過去問
この動画を見る
$f(x)=\sqrt{x+\sqrt{x^2-9}}$
$f`_{(5)}=\Box$
$\Box$を求めよ.
2021藤田医科大過去問
ε-δ論法 #1 f(x)=√xが連続
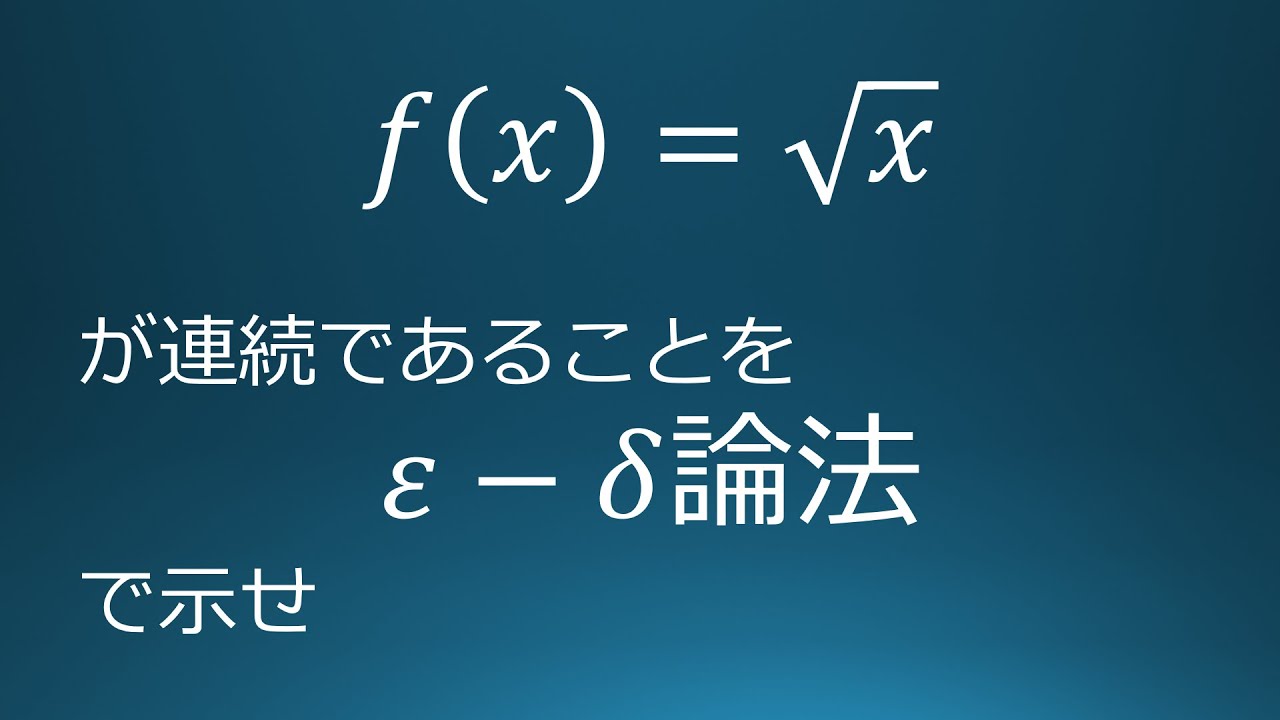
単元:
#数Ⅱ#式と証明#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
Question
$f(x)=\sqrt x\ (x\geqq 0)$が連続であることを$\xi -\vartheta$論法で示せ.
この動画を見る
Question
$f(x)=\sqrt x\ (x\geqq 0)$が連続であることを$\xi -\vartheta$論法で示せ.
重積分⑩-4#150【曲面の面積】(高専数学 微積II,数検1級1次解析対応)
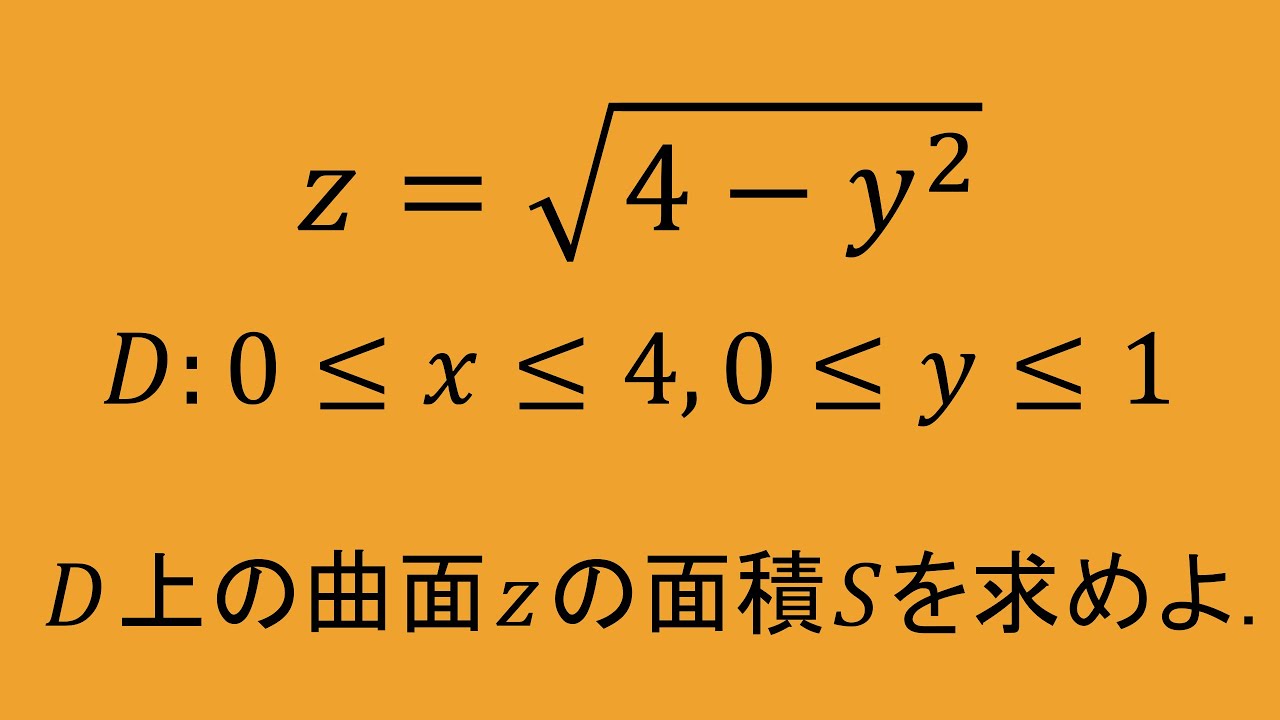
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$D:0\leqq x\leqq 4,0\leqq y\leqq 1$
$D$上における曲面$Z=\sqrt{4-y^2}$の面積$S$を求めよ.
この動画を見る
$D:0\leqq x\leqq 4,0\leqq y\leqq 1$
$D$上における曲面$Z=\sqrt{4-y^2}$の面積$S$を求めよ.
重積分⑨-9#149【広義積分】(高専数学 微積II,数検1級1次解析対応)
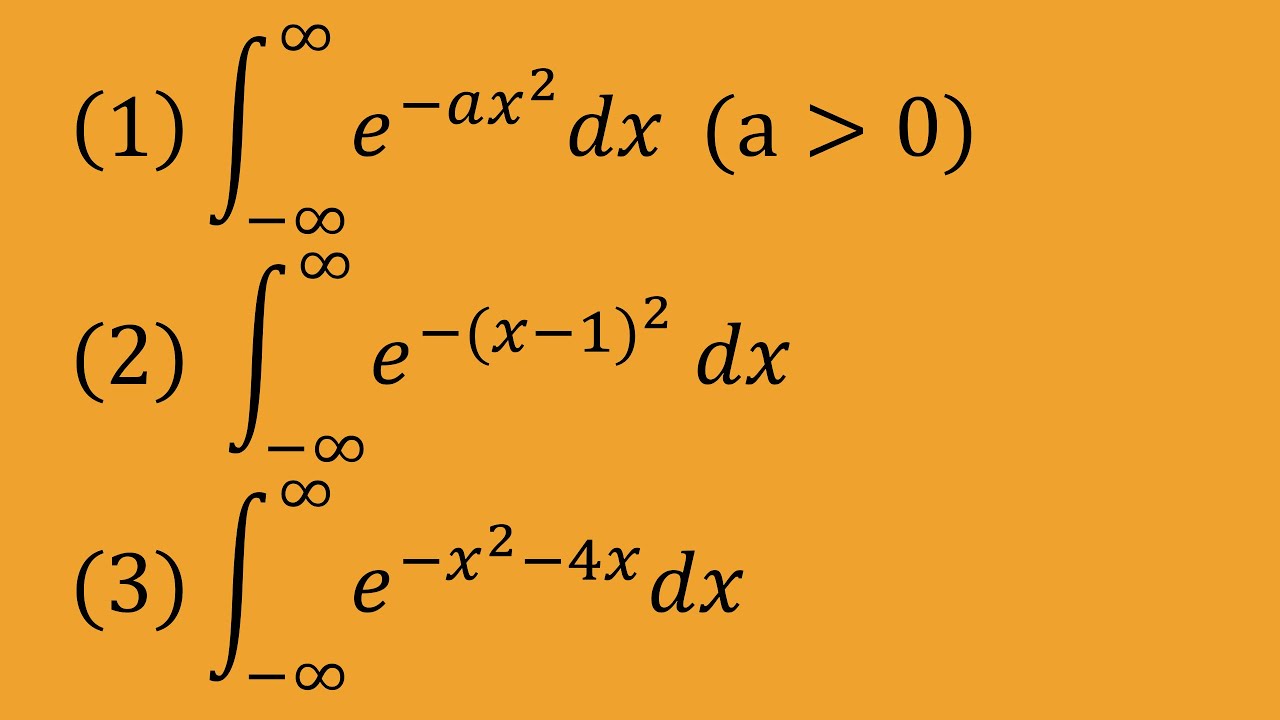
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
これを解け.
(1)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-ax^2} \ dx \ (a\gt 0)$
(2)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-(x-1)^2} \ dx \ $
(3)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-x^2-4x} \ dx \ $
定理$\displaystyle_{0}^{\infty} \ e^{-x^2}\ dx=\dfrac{\sqrt x}{2}$
この動画を見る
これを解け.
(1)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-ax^2} \ dx \ (a\gt 0)$
(2)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-(x-1)^2} \ dx \ $
(3)$\displaystyle \int_{-\infty}^{\infty}\\ e^{-x^2-4x} \ dx \ $
定理$\displaystyle_{0}^{\infty} \ e^{-x^2}\ dx=\dfrac{\sqrt x}{2}$
直角三角形の中の正方形 A 解き方2通り 岡山白陵
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
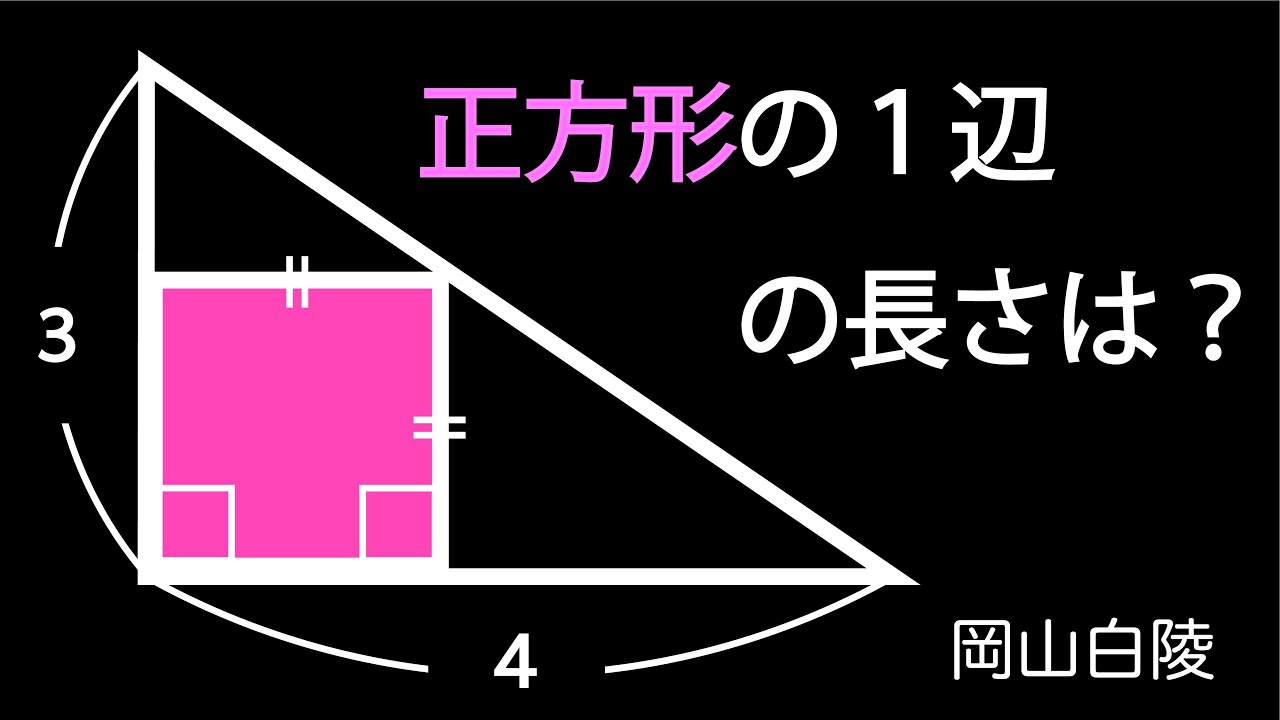
正方形の1辺の長さは?
*図は動画内参照
岡山白陵高等学校
この動画を見る
正方形の1辺の長さは?
*図は動画内参照
岡山白陵高等学校
15愛知県教員採用試験(数学:10番 極限)

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{10}\\ \displaystyle \lim_{x\to 2}\\ \dfrac{\sqrt{2x+a}+b}{x-2}=\dfrac{1}{3}$
$a,b$を求めよ.
この動画を見る
$\boxed{10}\\ \displaystyle \lim_{x\to 2}\\ \dfrac{\sqrt{2x+a}+b}{x-2}=\dfrac{1}{3}$
$a,b$を求めよ.
2021年藤田医科大

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x,y$は実数である.
$\left(\dfrac{2+\sqrt{-77}}{9}\right)^{2021}=\dfrac{x+y\sqrt{-77}}{9}$
$x^2+77y^2$の値を求めよ.
2021藤田医科大過去問
この動画を見る
$x,y$は実数である.
$\left(\dfrac{2+\sqrt{-77}}{9}\right)^{2021}=\dfrac{x+y\sqrt{-77}}{9}$
$x^2+77y^2$の値を求めよ.
2021藤田医科大過去問
【簡単すぎ】4分で不定方程式が得意になります。

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$ax+by=d$を満たす整数$x,y$をすべて求めよ
$(a,b,d$は整数$)$
この動画を見る
$ax+by=d$を満たす整数$x,y$をすべて求めよ
$(a,b,d$は整数$)$
重積分⑥-4 #146【曲面・平面で囲まれた体積】(高専数学 微積II,数検1級1次解析対応)

単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
直円柱$x^2+y^2\leqq 4$
平面$Z=0$,曲面$Z=4-x^2$で囲まれた体積$V$を求めよ.
この動画を見る
直円柱$x^2+y^2\leqq 4$
平面$Z=0$,曲面$Z=4-x^2$で囲まれた体積$V$を求めよ.
重積分⑦-5【極座標による変数変換】(高専数学 微積II,数検1級対応)
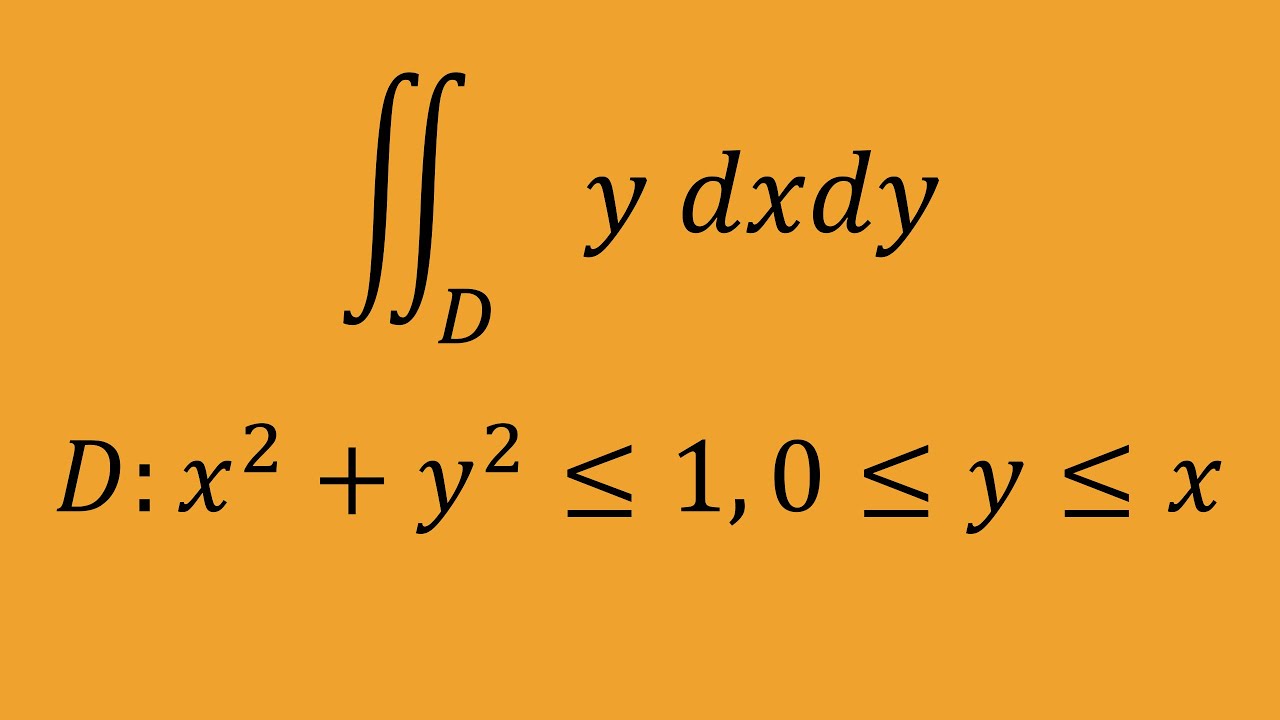
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
これを解け.
$\iint_D\\\ y \ dx \ dy$
$D:x^2+y^2\leqq 1,0\leqq y\leqq x$
この動画を見る
これを解け.
$\iint_D\\\ y \ dx \ dy$
$D:x^2+y^2\leqq 1,0\leqq y\leqq x$
13東京都教員採用試験(数学1-(6) 複素数)

単元:
#数Ⅱ#複素数と方程式#複素数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1} - (6)$
$arg Z=\dfrac{4}{3}\pi,arg(1-Z)=\dfrac{\pi}{4}$のとき,
$arg \dfrac{Z}{(1-Z)^2},\vert Z \vert$を求めよ.
この動画を見る
$\boxed{1} - (6)$
$arg Z=\dfrac{4}{3}\pi,arg(1-Z)=\dfrac{\pi}{4}$のとき,
$arg \dfrac{Z}{(1-Z)^2},\vert Z \vert$を求めよ.
秘技!瞬間平方完成
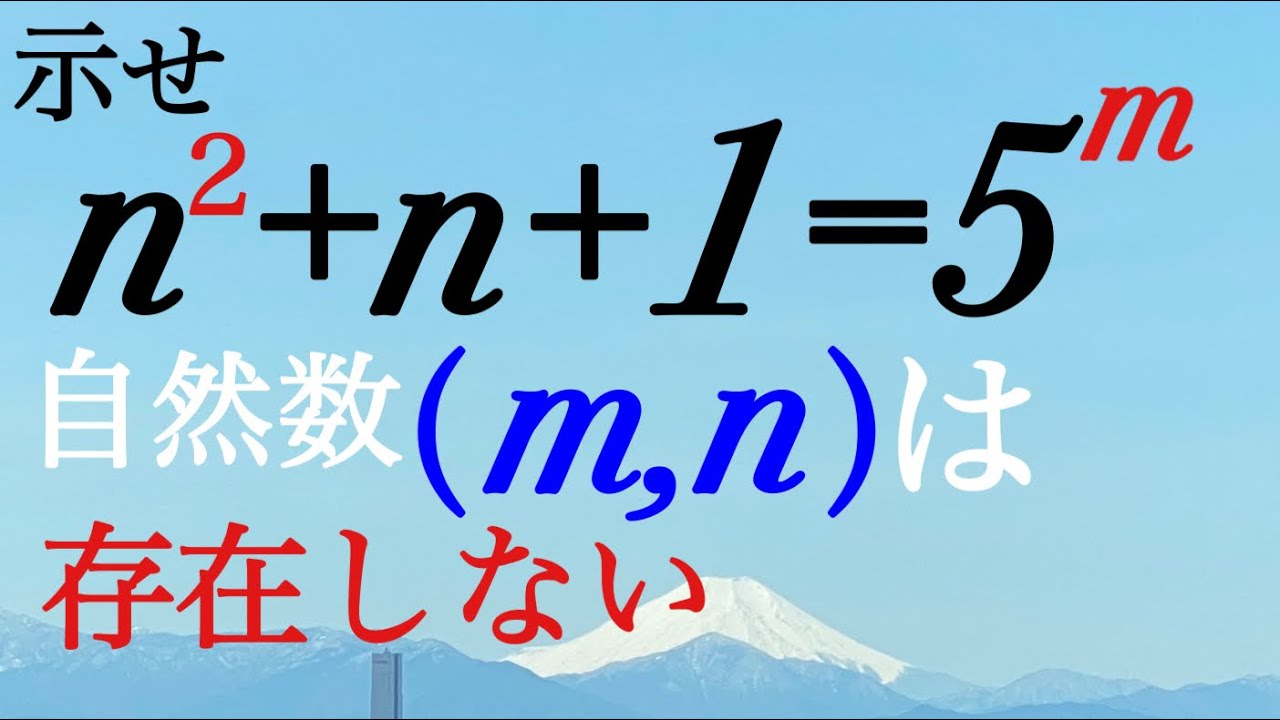
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n^2+n+1=5^m$を満たす自然数$(m,n)$は存在しないことを示せ.
この動画を見る
$n^2+n+1=5^m$を満たす自然数$(m,n)$は存在しないことを示せ.
重積分⑧-4【一般の変数変換】(高専数学 微積II,数検1級1次解析対応)
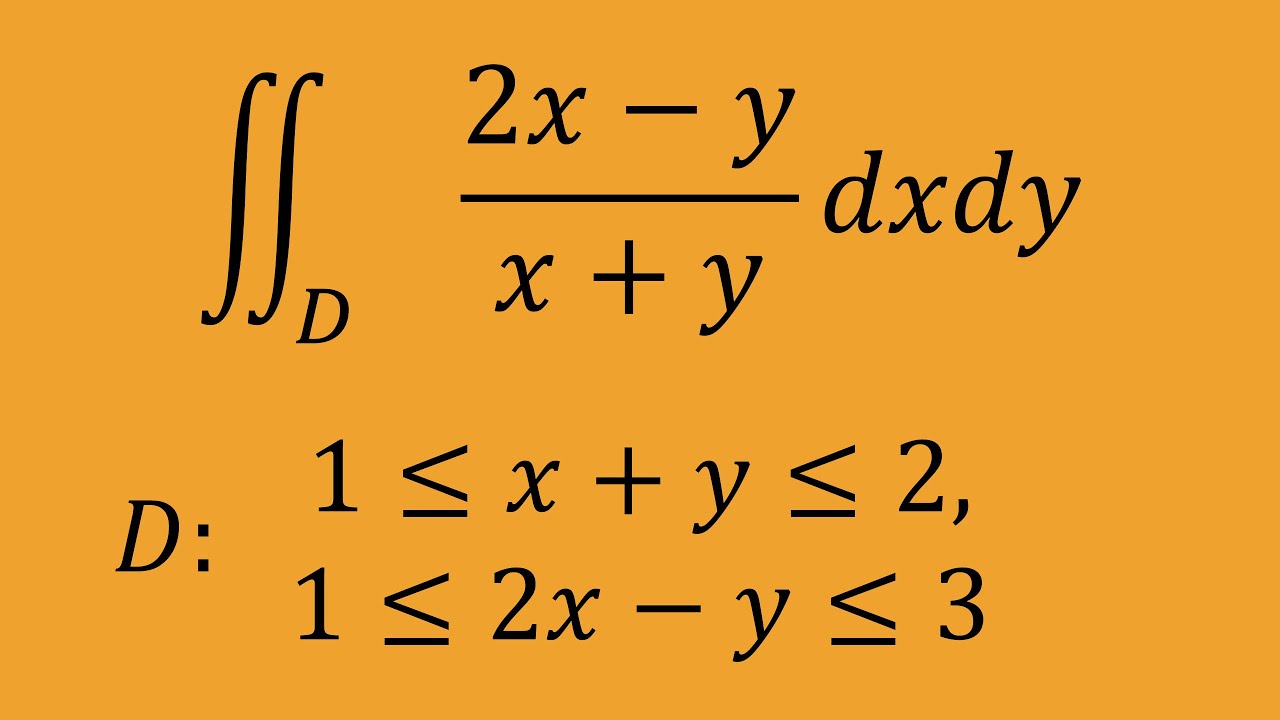
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
これを解け.
$\iint_D \\ \dfrac{2x-y}{x+y}dx\ dy$
$D:1\leqq x+y \leqq 2,1\leqq 2x-y \leqq 3$
この動画を見る
これを解け.
$\iint_D \\ \dfrac{2x-y}{x+y}dx\ dy$
$D:1\leqq x+y \leqq 2,1\leqq 2x-y \leqq 3$
【数学II】対数の本質・必殺技、教えます(対数のまとめ)【固定コメ必読】

単元:
#数Ⅱ#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
①$2^{30}$は何桁?
②$(\displaystyle \frac{1}{3})^{10}$を小数に小数第何位に初めて0出ない数字が現れるか
この動画を見る
①$2^{30}$は何桁?
②$(\displaystyle \frac{1}{3})^{10}$を小数に小数第何位に初めて0出ない数字が現れるか
気がつけば爽快!! B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BD:DC=?
*図は動画内参照
2021西大和学園高等学校
この動画を見る
BD:DC=?
*図は動画内参照
2021西大和学園高等学校
重積分⑨-8【広義積分】(高専数学 微積II,数検1級1次解析対応)
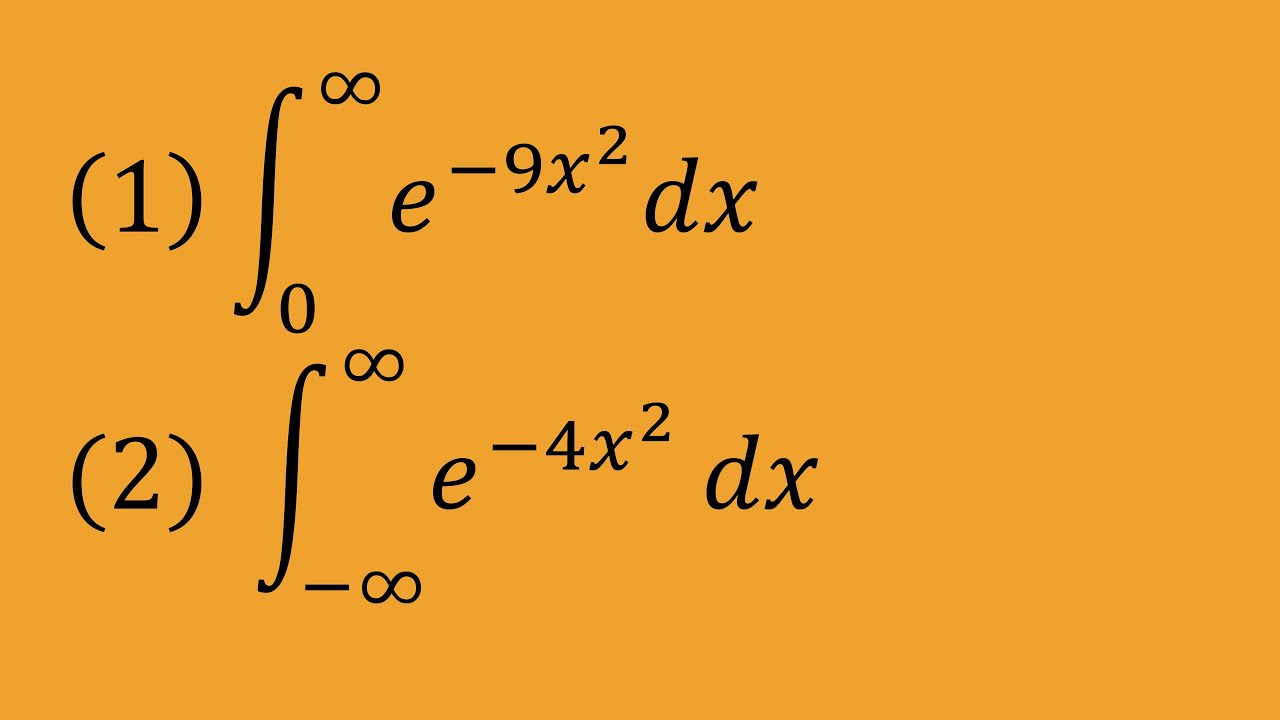
単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
これを解け.
(1)$\displaystyle \int_{0}^{\infty} \\ e^{-9x^2}\ dx$
(2)$\displaystyle \int_{-\infty}^{\infty} \\ e^{-4x^2}\ dx$
(3)$\displaystyle \int_{0}^{\infty} \\ e^{-x^2} dx=\dfrac{\sqrt x}{2}$
この動画を見る
これを解け.
(1)$\displaystyle \int_{0}^{\infty} \\ e^{-9x^2}\ dx$
(2)$\displaystyle \int_{-\infty}^{\infty} \\ e^{-4x^2}\ dx$
(3)$\displaystyle \int_{0}^{\infty} \\ e^{-x^2} dx=\dfrac{\sqrt x}{2}$
15東京都教員採用試験(数学1-(5) 数列の和の最小値)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#その他#数学(高校生)#数B#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1} - (5)$
$a_n=n^3-20n$
$S_n$の最小値とそのときの$n$の値を求めよ.
この動画を見る
$\boxed{1} - (5)$
$a_n=n^3-20n$
$S_n$の最小値とそのときの$n$の値を求めよ.
重積分⑨-7【広義積分】(高専数学 微積II,数検1級1次解析対応)
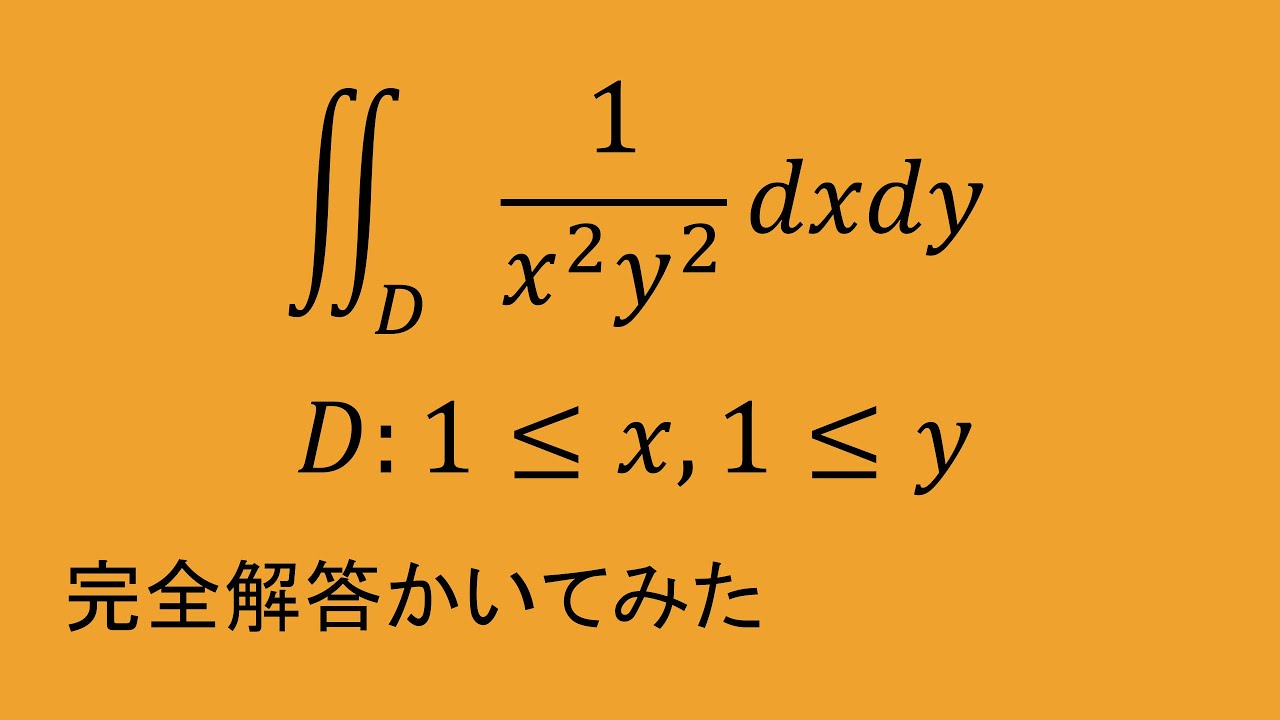
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$D:1\leqq x,1\leqq y$である.
$\iint_D \dfrac{1}{x^2y^2} \ dx \ dy$
これを解け.
この動画を見る
$D:1\leqq x,1\leqq y$である.
$\iint_D \dfrac{1}{x^2y^2} \ dx \ dy$
これを解け.
重積分⑨-6【広義積分】(高専数学 微積II,数検1級1次解析対応)
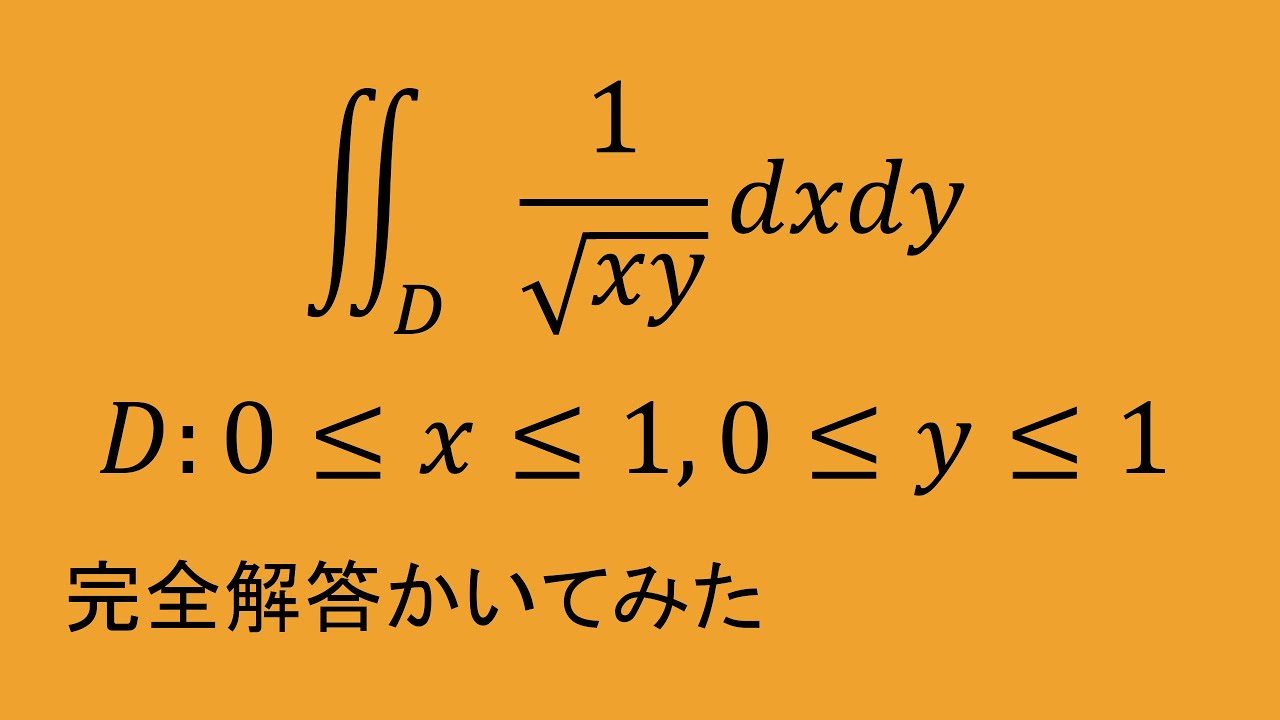
単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$D:0\leqq x\leqq 1,0\leqq y\leqq 1$とする.
$\iint_D \ \dfrac{1}{\sqrt{xy}}\ dx \ dy$
これを解け.
この動画を見る
$D:0\leqq x\leqq 1,0\leqq y\leqq 1$とする.
$\iint_D \ \dfrac{1}{\sqrt{xy}}\ dx \ dy$
これを解け.
割ると余りと商が等しい 2021西大和学園B

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
自然数Nを49で割ったとき商と余りが等しくなった。
このようなNのうち2021より大きいNの個数は?
2021西大和学園高等学校
この動画を見る
自然数Nを49で割ったとき商と余りが等しくなった。
このようなNのうち2021より大きいNの個数は?
2021西大和学園高等学校
03兵庫県教員採用試験(数学:3番 三角関数)

単元:
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$0\leqq x\leqq 2\pi$である.
$y=3\sin^2x-2\sin x+\cos^2 x+3$の最大値,最小値と
そのときの$x$の値を求めよ.
この動画を見る
$\boxed{3}$
$0\leqq x\leqq 2\pi$である.
$y=3\sin^2x-2\sin x+\cos^2 x+3$の最大値,最小値と
そのときの$x$の値を求めよ.
式の値
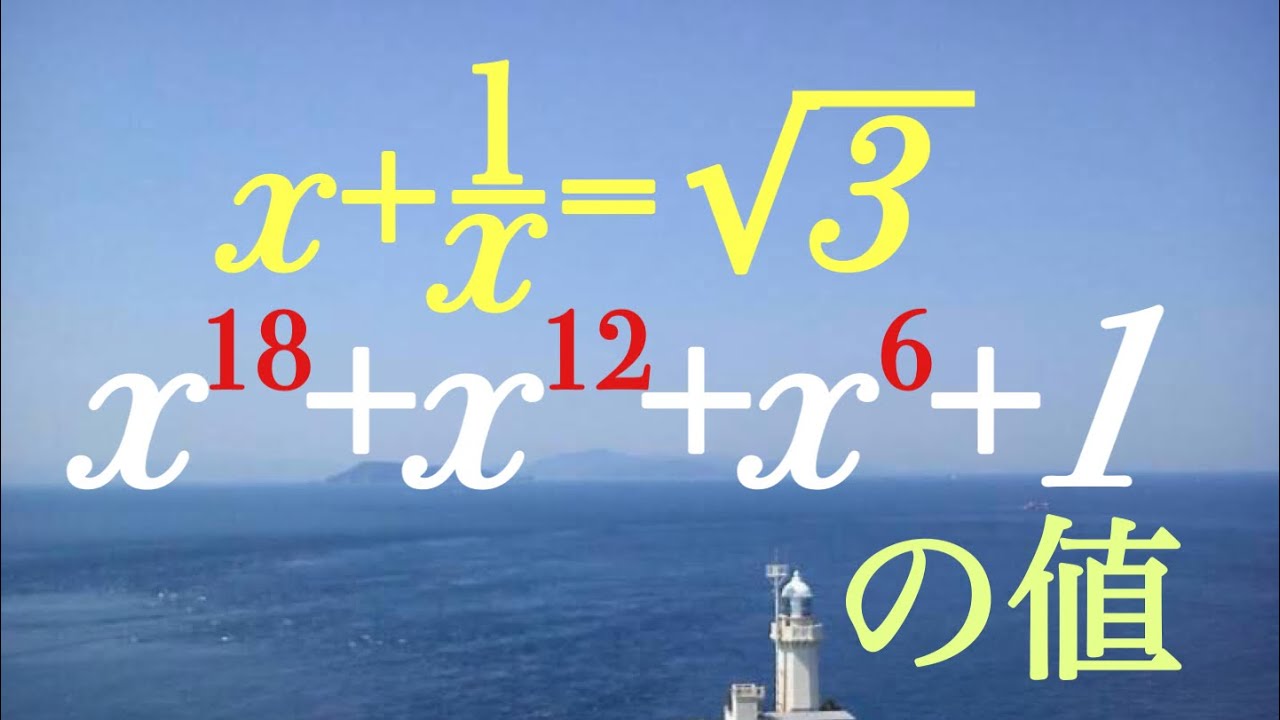
単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x+\dfrac{1}{x}=\sqrt3$のとき,$x^{18}+x^{12}+x^6+1$の値を求めよ.
この動画を見る
$x+\dfrac{1}{x}=\sqrt3$のとき,$x^{18}+x^{12}+x^6+1$の値を求めよ.
#3 数検準1級2次過去問 三角関数

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$\tan \alpha=k,-\dfrac{\pi}{2}\lt \alpha \lt \dfrac{\pi}{2}$をみたす
$\alpha$を$T(k)$で表す
(1)$xy\neq 1$のとき,
$ \\\ \tan (T(x)+T(y))$
(2)$4T\left(\dfrac{1}{5}\right)-T\left(\dfrac{1}{239}\right)=\dfrac{\pi}{4}$を示せ.
*$-\dfrac{\pi}{2} \lt \beta\lt \dfrac{\pi}{2}$は利用してよい.
この動画を見る
$\boxed{1}$
$\tan \alpha=k,-\dfrac{\pi}{2}\lt \alpha \lt \dfrac{\pi}{2}$をみたす
$\alpha$を$T(k)$で表す
(1)$xy\neq 1$のとき,
$ \\\ \tan (T(x)+T(y))$
(2)$4T\left(\dfrac{1}{5}\right)-T\left(\dfrac{1}{239}\right)=\dfrac{\pi}{4}$を示せ.
*$-\dfrac{\pi}{2} \lt \beta\lt \dfrac{\pi}{2}$は利用してよい.
8進数の7の倍数・3の倍数判定法

単元:
#数Ⅰ#数A#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$8$進法で表記された
$\boxed{a}\boxed{b}\boxed{c}\boxed{d}\boxed{e}\boxed{f}$
が①$7$で割り切れる必要十分条件を求めよ.
②$3$で割り切れる必要十分条件を求めよ.
この動画を見る
$8$進法で表記された
$\boxed{a}\boxed{b}\boxed{c}\boxed{d}\boxed{e}\boxed{f}$
が①$7$で割り切れる必要十分条件を求めよ.
②$3$で割り切れる必要十分条件を求めよ.
重積分⑥-3【曲面・平面で囲まれた体積】(高専数学 微積II,数検1級1次解析対応)

単元:
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#数学検定#数学検定準1級#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a\gt 0$とする.
曲面$Z=4a^2-x^2-y^2$と
$xy$平面で囲まれた体積$V$を求めよ.
この動画を見る
$a\gt 0$とする.
曲面$Z=4a^2-x^2-y^2$と
$xy$平面で囲まれた体積$V$を求めよ.
共通テスト2021年詳しい解説〜共通テスト2021年2B第3問〜統計

単元:
#数学(中学生)#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#統計的な推測#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large第3問}$
Q高校の校長先生は、ある日、新聞で高校生の読書に関する記事を読んだ。そこで、
Q高校の生徒全員を対象に、直前の1週間の読書時間に関して、100人の
生徒を無作為に抽出して調査を行った。その結果、100人の生徒のうち、この
1週間に全く読書をしなかった生徒が36人であり、100人の生徒のこの1週間の
読書時間(分)の平均値は204であった。Q高校の生徒全員のこの1週間の読書時間
の母平均を$m$, 母標準偏差を150とする。
(1)全く読書をしなかった生徒の母比率を0.5とする。このとき、100人の無作為標本の
うちで全く読書をしなかった生徒の数を表す確率変数をXとすると、$X$は$\boxed{\boxed{\ \ ア\ \ }}$
に従う。また、Xの平均(期待値)は$\boxed{\ \ イウ\ \ }$、標準偏差は$\boxed{\ \ エ\ \ }$である。
$\boxed{\boxed{\ \ ア\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪正規分布$N(0,1)$
①二項分布$B(0,1)$
②正規分布$N(100,0.5)$
③二項分布$B(100,0.5)$
④正規分布$N(100,36)$
⑤二項分布$B(100,36)$
(2)標本の大きさ100は十分に大きいので、100人のうち全く読書をしなかった生徒
の数は近似的に正規分布に従う。
全く読書をしなかった生徒の母比率を0.5とするとき、全く読書をしなかった生徒
が36人以下となる確率を$p_5$とおく。$p_5$の近似値を求めると、$p_5=\boxed{\boxed{\ \ オ\ \ }}$である。
また、全く読書をしなかった生徒の母比率を0.4とするとき、全く読書をしなかった
生徒が36人以下となる確率を$p_4$とおくと、$\boxed{\boxed{\ \ カ\ \ }}$である。
$\boxed{\boxed{\ \ オ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪$0.001$
①$0.003$
②$0.026$
③$0.050$
④$0.133$
⑤$0.497$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪$p_4 \lt p_5$
①$p_4 = p_5$
②$p_4 \gt p_5$
(3)1週間の読書時間の母平均$m$に対する信頼度95%の信頼区間を
$C_1 \leqq m \leqq C_2$とする。標本の大きさ100は十分大きいことと、1週間
の読書時間の標本平均が204、母標準偏差が150であることを用いると、
$C_1+C_2=\boxed{\ \ キクケ\ \ }$、$C_2-C_1=\boxed{\ \ コサ\ \ }.\boxed{\ \ シ\ \ }$であることがわかる。
また、母平均$m$と$C_1,C_2$については$\boxed{\boxed{\ \ ス\ \ }}$。
$\boxed{\boxed{\ \ ス\ \ }}$の解答群
⓪$C_1 \leqq m \leqq C_2$が必ず成り立つ
①$m \leqq C_2$は必ず成り立つが、$C_1 \leqq m$が成り立つとは限らない
②$C_1 \leqq m$は必ず成り立つが、$m \leqq C_2$が成り立つとは限らない
③$C_1 \leqq m$も$m \leqq C_2$も成り立つとは限らない
(4)Q高校の図書委員長も、校長先生と同じ新聞記事を読んだため、校長先生が
調査をしていることを知らずに、図書委員会として校長先生と同様の調査を
独自に行った。ただし、調査期間は校長先生による調査と同じ直前の1週間であり、
対象をQ高校の生徒全員として100人の生徒を無作為に抽出した。その調査における
全く読書をしなかった生徒の数を$n$とする。
校長先生の調査結果によると全く読書をしなかった生徒は36人であり、
$\boxed{\boxed{\ \ セ\ \ }}$。
$\boxed{\boxed{\ \ セ\ \ }}$の解答群
⓪$n$は必ず36に等しい
①$n$は必ず36未満である
②$n$は必ず36より大きい
③$n$と36との大小はわからない
(5)(4)の図書委員会が行った調査結果による母平均$m$に対する信頼度95%の
信頼区間を$D_1 \leqq m \leqq D_2$、校長先生が行った調査結果による母平均$m$に対す
る信頼度95%の信頼区間を(3)の$C_1 \leqq m \leqq C_2$とする。ただし、母集団は同一
であり、1週間の読書時間の母標準偏差は150とする。
このとき、次の⓪~⑤のうち、正しいものは$\boxed{\boxed{\ \ ソ\ \ }}と\boxed{\boxed{\ \ タ\ \ }}$である。
$\boxed{\boxed{\ \ ソ\ \ }}$, $\boxed{\boxed{\ \ タ\ \ }}$の解答群(解答の順序は問わない。)
⓪$C_1=D_1とC_2=D_2$が必ず成り立つ。
①$C_1 \lt D_2$または$D_1 \lt C_2$のどちらか一方のみが成り立つ。
②$D_2 \lt C_1$または$C_2 \lt D_1$となる場合もある。
③$C_2-C_1 \gt D_2-D_1$が必ず成り立つ。
④$C_2-C_1 = D_2-D_1$が必ず成り立つ。
⑤$C_2-C_1 \lt D_2-D_1$が必ず成り立つ。
2021共通テスト過去問
この動画を見る
${\large第3問}$
Q高校の校長先生は、ある日、新聞で高校生の読書に関する記事を読んだ。そこで、
Q高校の生徒全員を対象に、直前の1週間の読書時間に関して、100人の
生徒を無作為に抽出して調査を行った。その結果、100人の生徒のうち、この
1週間に全く読書をしなかった生徒が36人であり、100人の生徒のこの1週間の
読書時間(分)の平均値は204であった。Q高校の生徒全員のこの1週間の読書時間
の母平均を$m$, 母標準偏差を150とする。
(1)全く読書をしなかった生徒の母比率を0.5とする。このとき、100人の無作為標本の
うちで全く読書をしなかった生徒の数を表す確率変数をXとすると、$X$は$\boxed{\boxed{\ \ ア\ \ }}$
に従う。また、Xの平均(期待値)は$\boxed{\ \ イウ\ \ }$、標準偏差は$\boxed{\ \ エ\ \ }$である。
$\boxed{\boxed{\ \ ア\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪正規分布$N(0,1)$
①二項分布$B(0,1)$
②正規分布$N(100,0.5)$
③二項分布$B(100,0.5)$
④正規分布$N(100,36)$
⑤二項分布$B(100,36)$
(2)標本の大きさ100は十分に大きいので、100人のうち全く読書をしなかった生徒
の数は近似的に正規分布に従う。
全く読書をしなかった生徒の母比率を0.5とするとき、全く読書をしなかった生徒
が36人以下となる確率を$p_5$とおく。$p_5$の近似値を求めると、$p_5=\boxed{\boxed{\ \ オ\ \ }}$である。
また、全く読書をしなかった生徒の母比率を0.4とするとき、全く読書をしなかった
生徒が36人以下となる確率を$p_4$とおくと、$\boxed{\boxed{\ \ カ\ \ }}$である。
$\boxed{\boxed{\ \ オ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪$0.001$
①$0.003$
②$0.026$
③$0.050$
④$0.133$
⑤$0.497$
$\boxed{\boxed{\ \ カ\ \ }}$の解答群
⓪$p_4 \lt p_5$
①$p_4 = p_5$
②$p_4 \gt p_5$
(3)1週間の読書時間の母平均$m$に対する信頼度95%の信頼区間を
$C_1 \leqq m \leqq C_2$とする。標本の大きさ100は十分大きいことと、1週間
の読書時間の標本平均が204、母標準偏差が150であることを用いると、
$C_1+C_2=\boxed{\ \ キクケ\ \ }$、$C_2-C_1=\boxed{\ \ コサ\ \ }.\boxed{\ \ シ\ \ }$であることがわかる。
また、母平均$m$と$C_1,C_2$については$\boxed{\boxed{\ \ ス\ \ }}$。
$\boxed{\boxed{\ \ ス\ \ }}$の解答群
⓪$C_1 \leqq m \leqq C_2$が必ず成り立つ
①$m \leqq C_2$は必ず成り立つが、$C_1 \leqq m$が成り立つとは限らない
②$C_1 \leqq m$は必ず成り立つが、$m \leqq C_2$が成り立つとは限らない
③$C_1 \leqq m$も$m \leqq C_2$も成り立つとは限らない
(4)Q高校の図書委員長も、校長先生と同じ新聞記事を読んだため、校長先生が
調査をしていることを知らずに、図書委員会として校長先生と同様の調査を
独自に行った。ただし、調査期間は校長先生による調査と同じ直前の1週間であり、
対象をQ高校の生徒全員として100人の生徒を無作為に抽出した。その調査における
全く読書をしなかった生徒の数を$n$とする。
校長先生の調査結果によると全く読書をしなかった生徒は36人であり、
$\boxed{\boxed{\ \ セ\ \ }}$。
$\boxed{\boxed{\ \ セ\ \ }}$の解答群
⓪$n$は必ず36に等しい
①$n$は必ず36未満である
②$n$は必ず36より大きい
③$n$と36との大小はわからない
(5)(4)の図書委員会が行った調査結果による母平均$m$に対する信頼度95%の
信頼区間を$D_1 \leqq m \leqq D_2$、校長先生が行った調査結果による母平均$m$に対す
る信頼度95%の信頼区間を(3)の$C_1 \leqq m \leqq C_2$とする。ただし、母集団は同一
であり、1週間の読書時間の母標準偏差は150とする。
このとき、次の⓪~⑤のうち、正しいものは$\boxed{\boxed{\ \ ソ\ \ }}と\boxed{\boxed{\ \ タ\ \ }}$である。
$\boxed{\boxed{\ \ ソ\ \ }}$, $\boxed{\boxed{\ \ タ\ \ }}$の解答群(解答の順序は問わない。)
⓪$C_1=D_1とC_2=D_2$が必ず成り立つ。
①$C_1 \lt D_2$または$D_1 \lt C_2$のどちらか一方のみが成り立つ。
②$D_2 \lt C_1$または$C_2 \lt D_1$となる場合もある。
③$C_2-C_1 \gt D_2-D_1$が必ず成り立つ。
④$C_2-C_1 = D_2-D_1$が必ず成り立つ。
⑤$C_2-C_1 \lt D_2-D_1$が必ず成り立つ。
2021共通テスト過去問
#2 数検準1級1次過去問 数列

単元:
#数学検定・数学甲子園・数学オリンピック等#数列#数列とその和(等差・等比・階差・Σ)#数学検定#数学検定準1級#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$\boxed{3}$
$2a_n-S_n=2^n$
一般鋼$a_n$を求めよ.
この動画を見る
$\boxed{3}$
$2a_n-S_n=2^n$
一般鋼$a_n$を求めよ.
整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$p,q$は素数であり,$n$は自然数とする.これを解け.
$p^2+pq+q^2=n^2$
この動画を見る
$p,q$は素数であり,$n$は自然数とする.これを解け.
$p^2+pq+q^2=n^2$
受験生必見!!円と相似

単元:
#数学(中学生)#中3数学#数A#図形の性質#相似な図形#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円と相似まとめ
*図は動画内参照
この動画を見る
円と相似まとめ
*図は動画内参照
