 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
ベン図 野球もサッカーも好き 法政二高

単元:
#数学(中学生)#数Ⅰ#データの分析#データの分析#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
100人の生徒に調査を行った。
野球が好きな生徒が60人
サッカーが好きな生徒が50人だった。
「どちらも好き」と答えた人は何人以上何人以下?
2021法政大学第二高等学校
この動画を見る
100人の生徒に調査を行った。
野球が好きな生徒が60人
サッカーが好きな生徒が50人だった。
「どちらも好き」と答えた人は何人以上何人以下?
2021法政大学第二高等学校
1から6のサイコロです。 慶應志木(改)B

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
nの目が1の目のn倍の確率で出るサイコロがある。
サイコロを1回投げて1の目が出る確率は?
2021慶應義塾志木高等学校
この動画を見る
nの目が1の目のn倍の確率で出るサイコロがある。
サイコロを1回投げて1の目が出る確率は?
2021慶應義塾志木高等学校
困ったら解の公式!? C 2021 明大明治

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt 2 + \sqrt 3 + \sqrt 6)(2\sqrt 2 - \sqrt 3 - \sqrt 6)=?$
$x^2+(\sqrt 2 - 2\sqrt 3 - 2\sqrt 6)x + (5+6\sqrt 2 -2\sqrt 3 -\sqrt 6 ) = 0$を解け
2021明治大学付属明治高等学校
この動画を見る
$(\sqrt 2 + \sqrt 3 + \sqrt 6)(2\sqrt 2 - \sqrt 3 - \sqrt 6)=?$
$x^2+(\sqrt 2 - 2\sqrt 3 - 2\sqrt 6)x + (5+6\sqrt 2 -2\sqrt 3 -\sqrt 6 ) = 0$を解け
2021明治大学付属明治高等学校
【みんな大好き】因数分解:長崎総合科学~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#長崎総合科学大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 長崎総合科学
$x^3+4x^2+x-6$
因数分解せよ。
この動画を見る
入試問題 長崎総合科学
$x^3+4x^2+x-6$
因数分解せよ。
食塩水2回くみ出し

単元:
#数学(中学生)#文章題#売買損益と食塩水#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
濃度10%の食塩水10kg入れた容器に次のA,Bの操作をする。
A:x kgをくんで同量の水を戻す。
B:2x kgをくんで同量の水を戻す。
操作Aののち、操作Bを行ったら食塩水の濃度は2.8%。
x=?
2021中央大学杉並高等学校
この動画を見る
濃度10%の食塩水10kg入れた容器に次のA,Bの操作をする。
A:x kgをくんで同量の水を戻す。
B:2x kgをくんで同量の水を戻す。
操作Aののち、操作Bを行ったら食塩水の濃度は2.8%。
x=?
2021中央大学杉並高等学校
ルートを外せ11 B 2021 中央大附属

単元:
#数学(中学生)#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{60(n+1)(n^2-1)}$が整数となるような2ケタの整数nをすべて求めよ。
2021中央大学附属高等学校
この動画を見る
$\sqrt{60(n+1)(n^2-1)}$が整数となるような2ケタの整数nをすべて求めよ。
2021中央大学附属高等学校
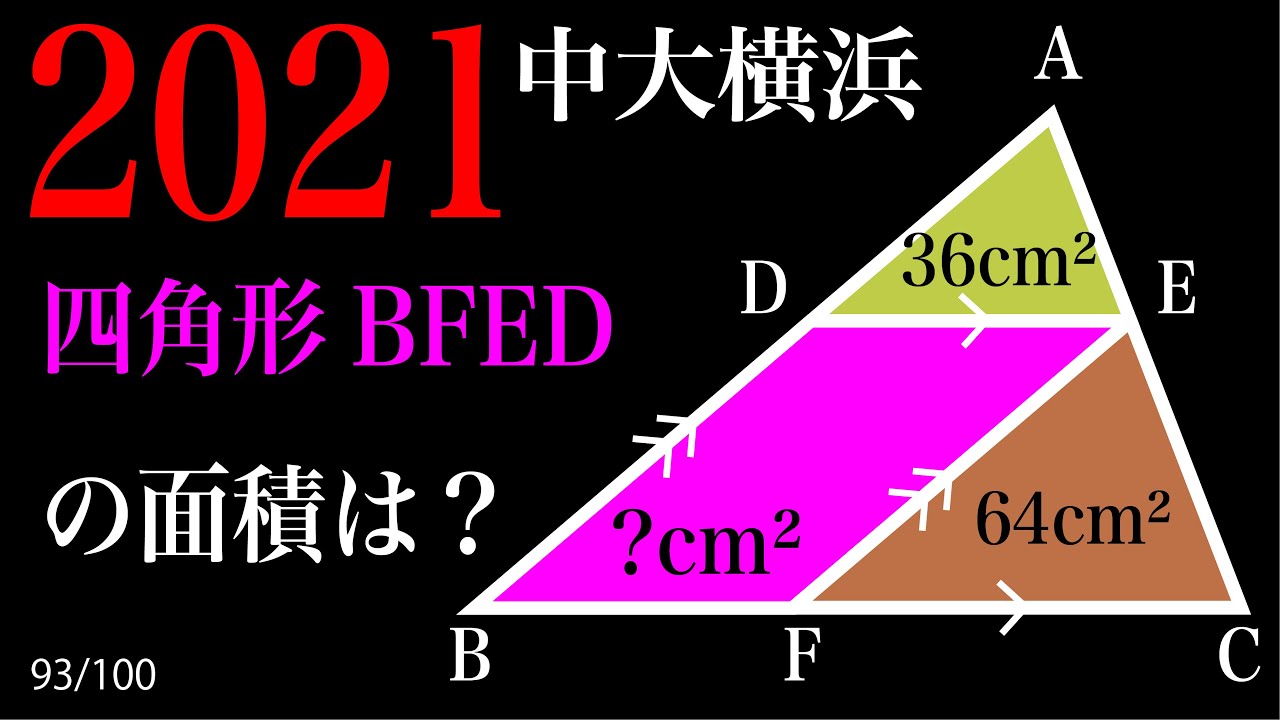
面積比!! A
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形BFEDの面積は?
*図は動画内参照
2021中央大学附属横浜高等学校
この動画を見る
四角形BFEDの面積は?
*図は動画内参照
2021中央大学附属横浜高等学校
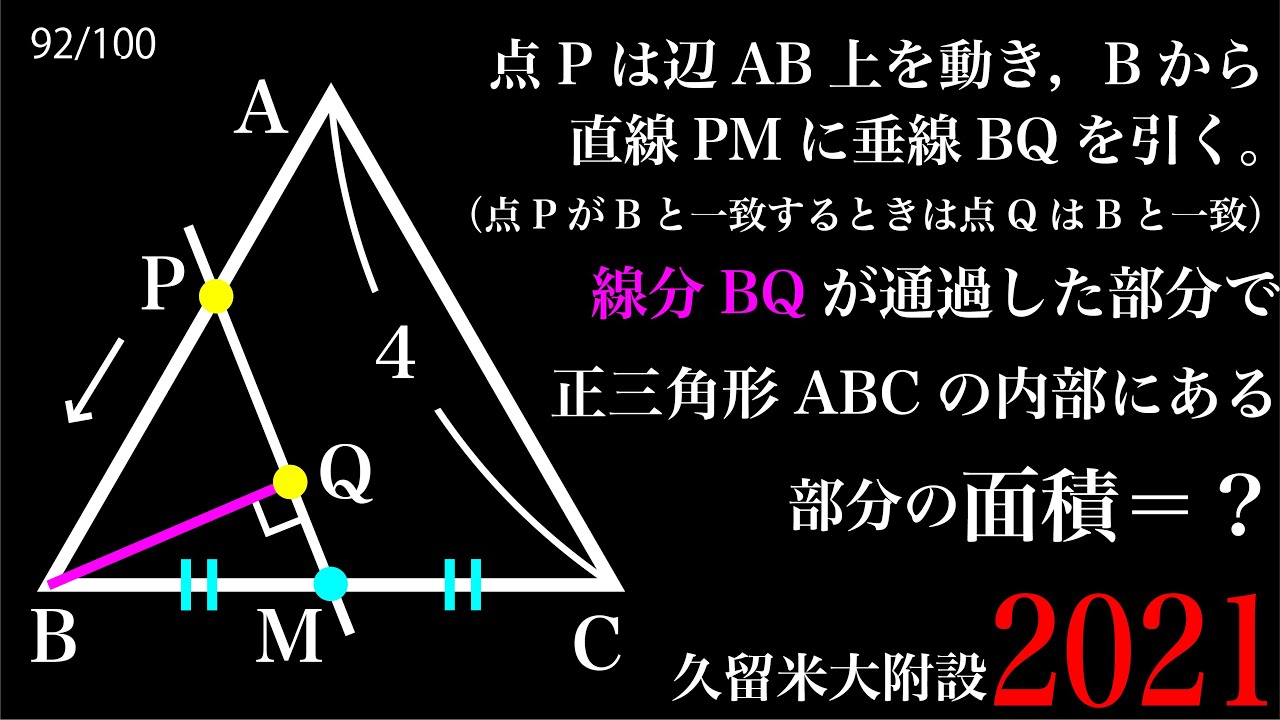
軌跡 C 2021久留米大附設
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Pは辺AB上を動き、Bから直線PMに垂線BQを引く。
(点PがBと一致するときは点QはBと一致するとする)
線分BQが通過した部分で正三角形ABCの内部にある部分の面積=?
(2021久留米大学附設高等学校)
この動画を見る
点Pは辺AB上を動き、Bから直線PMに垂線BQを引く。
(点PがBと一致するときは点QはBと一致するとする)
線分BQが通過した部分で正三角形ABCの内部にある部分の面積=?
(2021久留米大学附設高等学校)
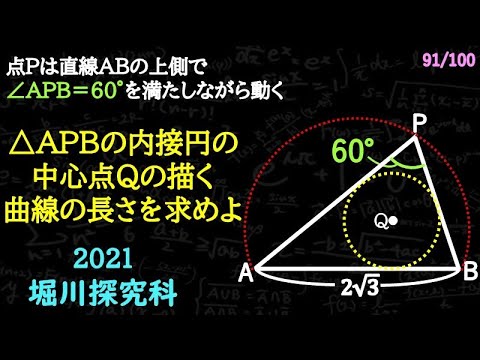
軌跡その2 C
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Pが$\angle APB = 60°$をみたしながら動く
(ただし点Pは直線ABの上側)
△APBの内接円の中心点Qの描く曲線の長さを求めよ
*図は動画内参照
(2021京都市立堀川高校探究科)
この動画を見る
点Pが$\angle APB = 60°$をみたしながら動く
(ただし点Pは直線ABの上側)
△APBの内接円の中心点Qの描く曲線の長さを求めよ
*図は動画内参照
(2021京都市立堀川高校探究科)
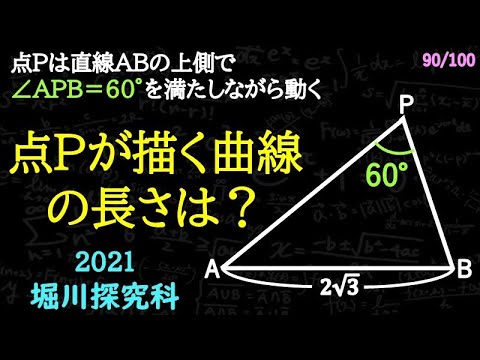
軌跡その1 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
点Pが$\angle APB = 60°$を満たしながら動く。
(ただし、点Pは直線ABの上側)
点Pがえがく曲線の長さは??
*図は動画内参照
京都市立堀川高校探究科
この動画を見る
点Pが$\angle APB = 60°$を満たしながら動く。
(ただし、点Pは直線ABの上側)
点Pがえがく曲線の長さは??
*図は動画内参照
京都市立堀川高校探究科
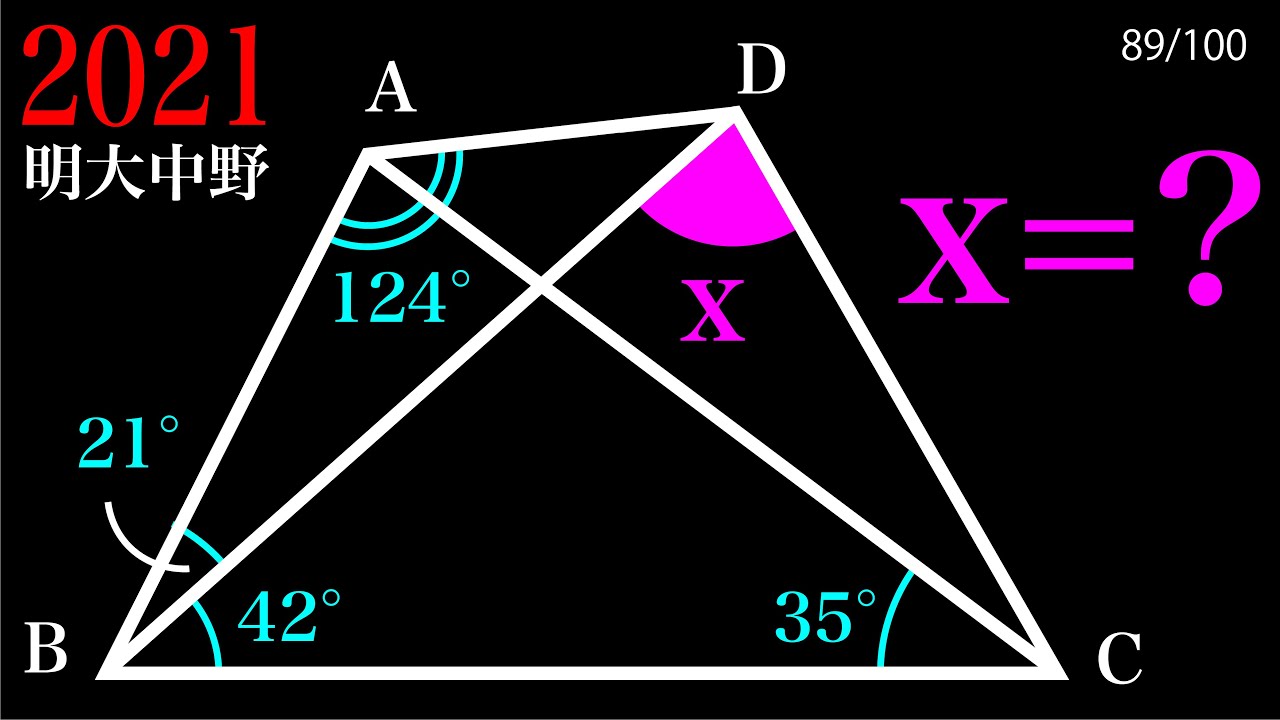
小学生は求められない!角度 2021明大中野A
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x =?$
*図は動画内参照
2021明治大学付属中野高等学校
この動画を見る
$\angle x =?$
*図は動画内参照
2021明治大学付属中野高等学校
難C(むずかしー) 円に外接する正八角形 2021中大横浜

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
円の面積=?
*図は動画内参照
2021中央大学附属横浜高等学校
この動画を見る
円の面積=?
*図は動画内参照
2021中央大学附属横浜高等学校
相似の証明 面積比 B 2021 埼玉県

単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△ADH∽△ACFを示せ
△ABC=18のとき△GFC=?
*図は動画内参照
2021埼玉県
この動画を見る
△ADH∽△ACFを示せ
△ABC=18のとき△GFC=?
*図は動画内参照
2021埼玉県
正六角形と円 A 中大横浜 2021

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正六角形の周の長さは?
*図は動画内参照
2021中央大学附属横浜高等学校
この動画を見る
正六角形の周の長さは?
*図は動画内参照
2021中央大学附属横浜高等学校
ピザを切れ!! B 中大横浜2021

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正八角形の面積=?
*図は動画内参照
2021中央大学附属横浜高等学校
この動画を見る
正八角形の面積=?
*図は動画内参照
2021中央大学附属横浜高等学校
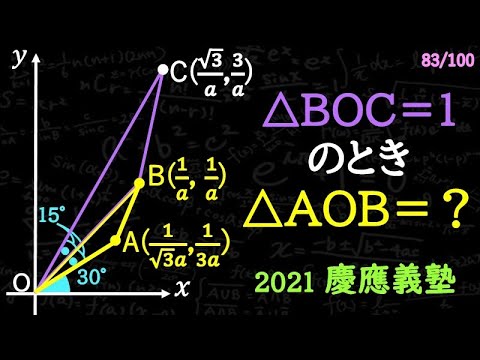
2つの三角形の関係に注目!! B 2021 慶應義塾
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△BOC=1のとき△AOBの面積=?
*図は動画内参照
2021慶應義塾高等学校
この動画を見る
△BOC=1のとき△AOBの面積=?
*図は動画内参照
2021慶應義塾高等学校
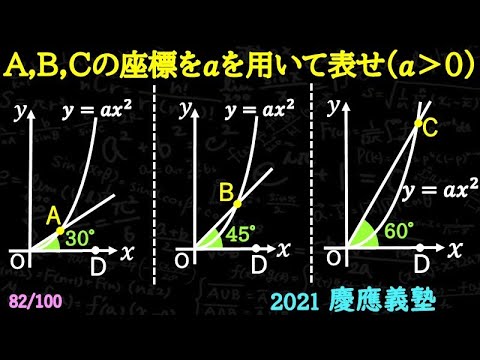
30度 45度 60度の直線の式 A 慶應義塾 2021
単元:
#数学(中学生)#数Ⅱ#三角関数#三角関数とグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
A,B,Cの座標をaを用いて表せ
*図は動画内参照
2021慶應義塾高等学校
この動画を見る
A,B,Cの座標をaを用いて表せ
*図は動画内参照
2021慶應義塾高等学校
証明:長崎県高校入試~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 長崎県の高校
文字$n$を使って証明せよ。
2つの続いた奇数では、大きい奇数の 平方から小さい奇数の平方を引いた差 は、8の倍数となる。
※例えば、3、5について、 $5^2-3^2$ を計算すると、$16$になり、これは$18$の倍数である。
この動画を見る
入試問題 長崎県の高校
文字$n$を使って証明せよ。
2つの続いた奇数では、大きい奇数の 平方から小さい奇数の平方を引いた差 は、8の倍数となる。
※例えば、3、5について、 $5^2-3^2$ を計算すると、$16$になり、これは$18$の倍数である。
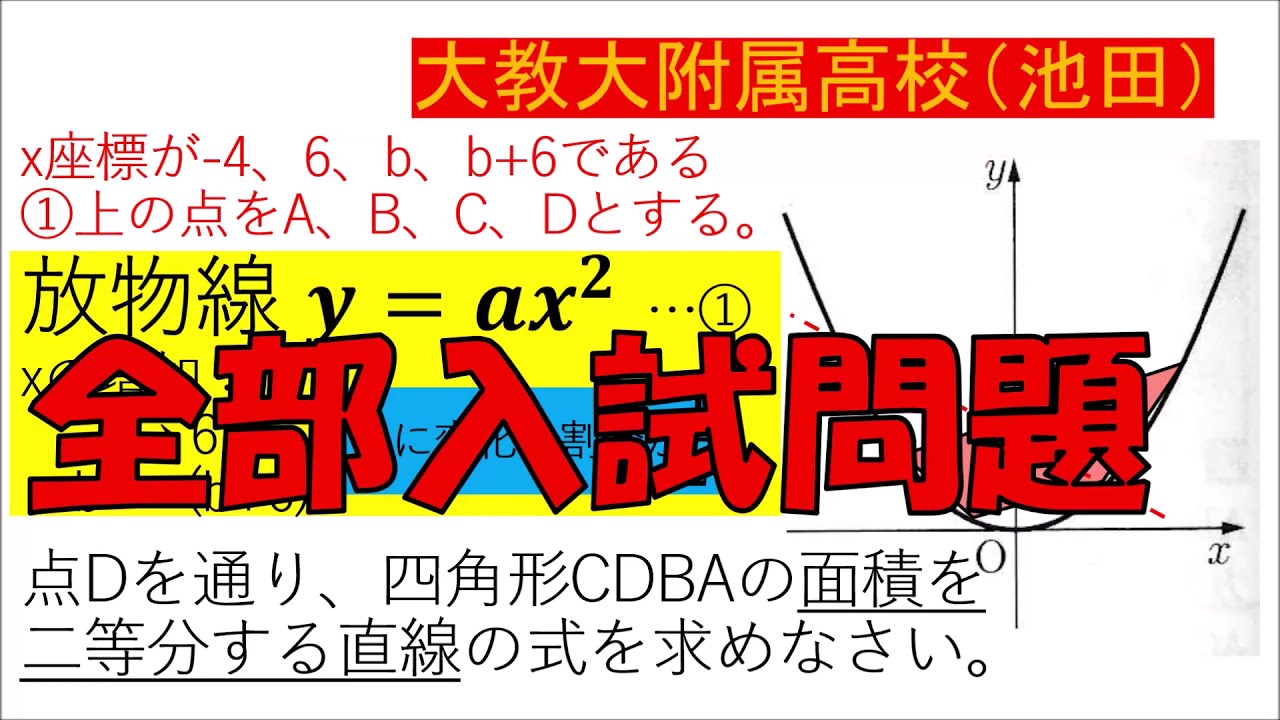
二次関数:大阪教育大学附属高等学校池田校舎~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 大阪教育大学附属高等学校池田校舎
$x$座標が$-4、6、b、b+6$である
①上の点を$A、B、C、D$とする。
放物線$y = ax^2$ ...①
$x$の増加:
$-4-6$
$b→ (b+6)$
共に変化の割合が$\displaystyle \frac{1}{2}$
点$D$を通り、四角形$CDBA$の面積を
二等分する直線の式を求めなさい。
※図は動画内参照
この動画を見る
入試問題 大阪教育大学附属高等学校池田校舎
$x$座標が$-4、6、b、b+6$である
①上の点を$A、B、C、D$とする。
放物線$y = ax^2$ ...①
$x$の増加:
$-4-6$
$b→ (b+6)$
共に変化の割合が$\displaystyle \frac{1}{2}$
点$D$を通り、四角形$CDBA$の面積を
二等分する直線の式を求めなさい。
※図は動画内参照
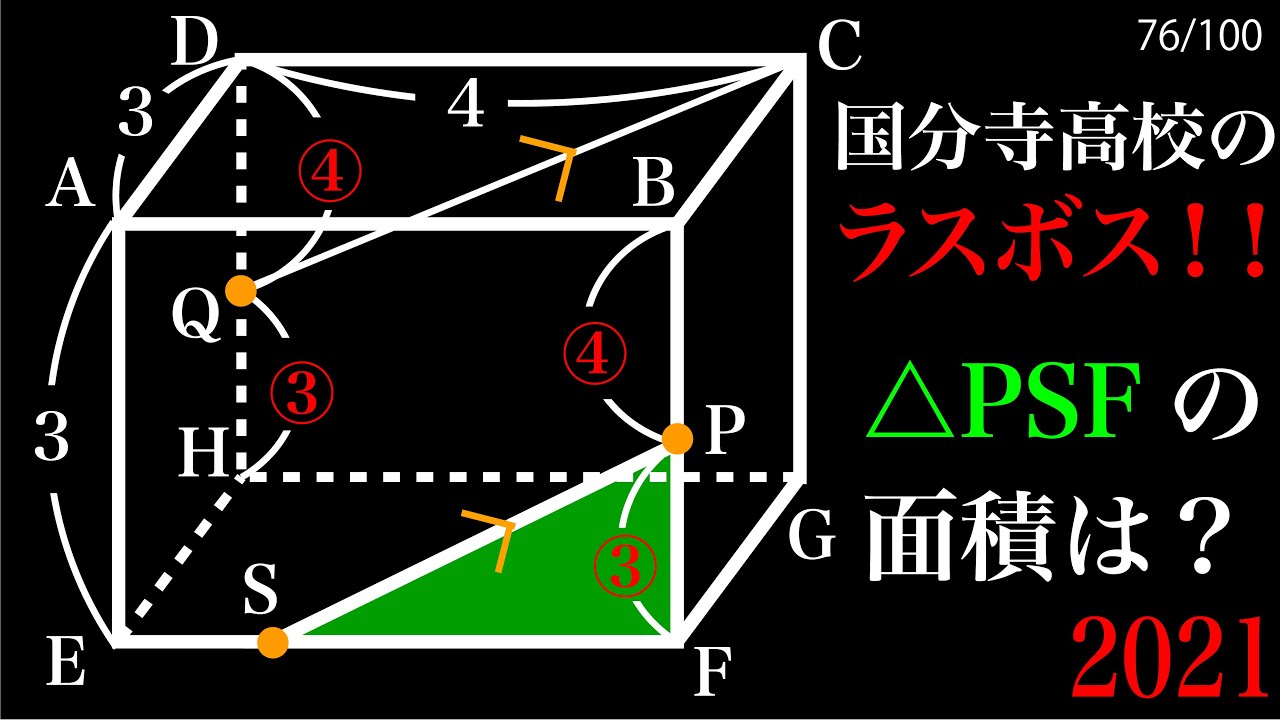
2021 国分寺ラスト問題 B
単元:
#数学(中学生)#中1数学#空間図形#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△PSFの面積=?
*図は動画内参照
2021国分寺高等学校
この動画を見る
△PSFの面積=?
*図は動画内参照
2021国分寺高等学校
2通りで解説!! 都立青山 B

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
DP=?
*図は動画内参照
2021東京都立青山高等学校
この動画を見る
DP=?
*図は動画内参照
2021東京都立青山高等学校
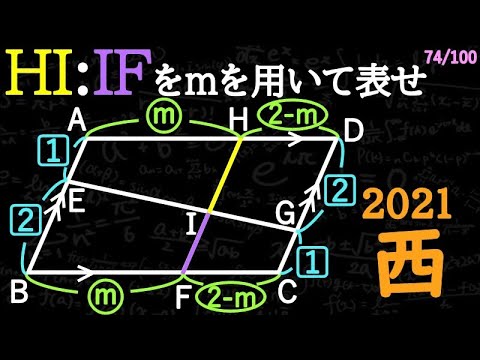
平行四辺形と比 都立西 B 2021
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
HI:IFをmを用いて表せ
*図は動画内参照
2021東京都立西高等学校
この動画を見る
HI:IFをmを用いて表せ
*図は動画内参照
2021東京都立西高等学校
コインを4回投げる 国分寺 2021 A

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
1枚のコインを投げ
表が出たら2点
裏が出たら-1点となる。
4回投げて得点の合計が2点となる確率は?
2021東京都立国分寺高等学校
この動画を見る
1枚のコインを投げ
表が出たら2点
裏が出たら-1点となる。
4回投げて得点の合計が2点となる確率は?
2021東京都立国分寺高等学校
約束記号 C 慶應義塾 2021
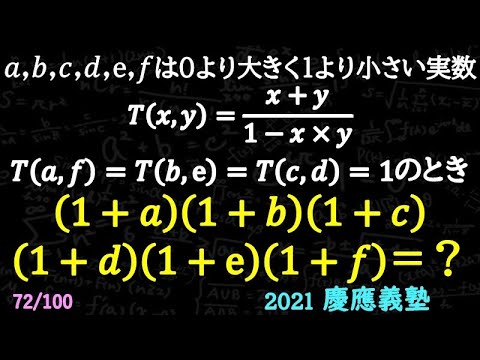
単元:
#数学(中学生)#数Ⅱ#三角関数#加法定理とその応用#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,c,d,e,fは0より大きく1より小さい実数
$T(x,y)=\frac{x+y}{1-x \times y}$
$T(a,f) = T(b,e) = T(c,d) = 1$のとき
$(1+a)(1+b)(1+c)(1+d)(1+e)(1+f) =$
2021慶應義塾高等学校
この動画を見る
a,b,c,d,e,fは0より大きく1より小さい実数
$T(x,y)=\frac{x+y}{1-x \times y}$
$T(a,f) = T(b,e) = T(c,d) = 1$のとき
$(1+a)(1+b)(1+c)(1+d)(1+e)(1+f) =$
2021慶應義塾高等学校
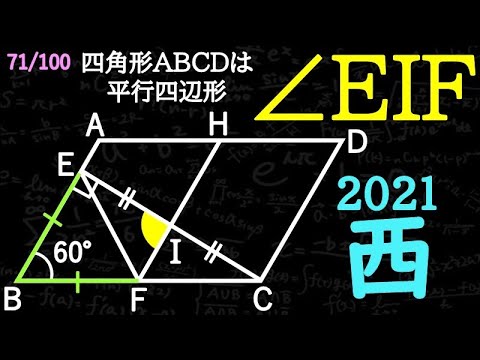
角度を求める A 都立西 2021
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形ABCDは平行四辺形
$\angle EIF = ?$
*図は動画内参照
2021東京都立西高等学校
この動画を見る
四角形ABCDは平行四辺形
$\angle EIF = ?$
*図は動画内参照
2021東京都立西高等学校
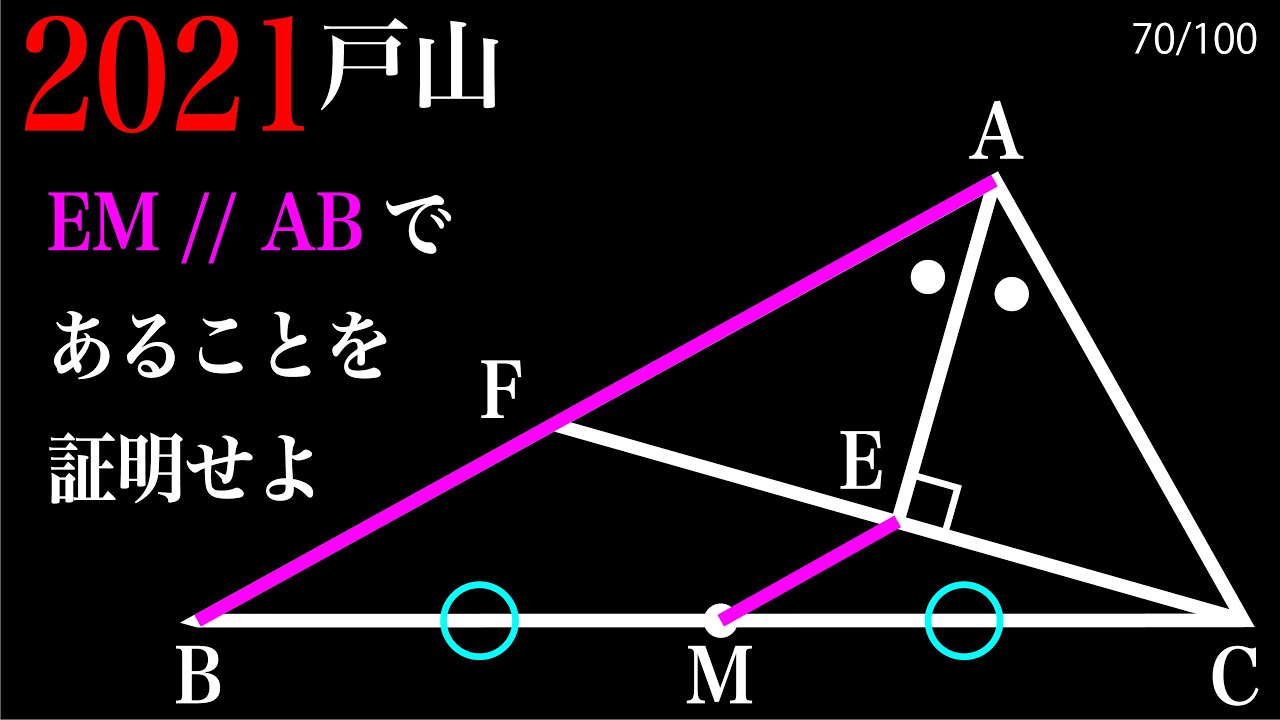
平行であることの証明 2021 戸山(改) A
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
EM//ABを示せ
*図は動画内参照
2021戸山高等学校
この動画を見る
EM//ABを示せ
*図は動画内参照
2021戸山高等学校
角度が等しい作図 2021 日比谷 B
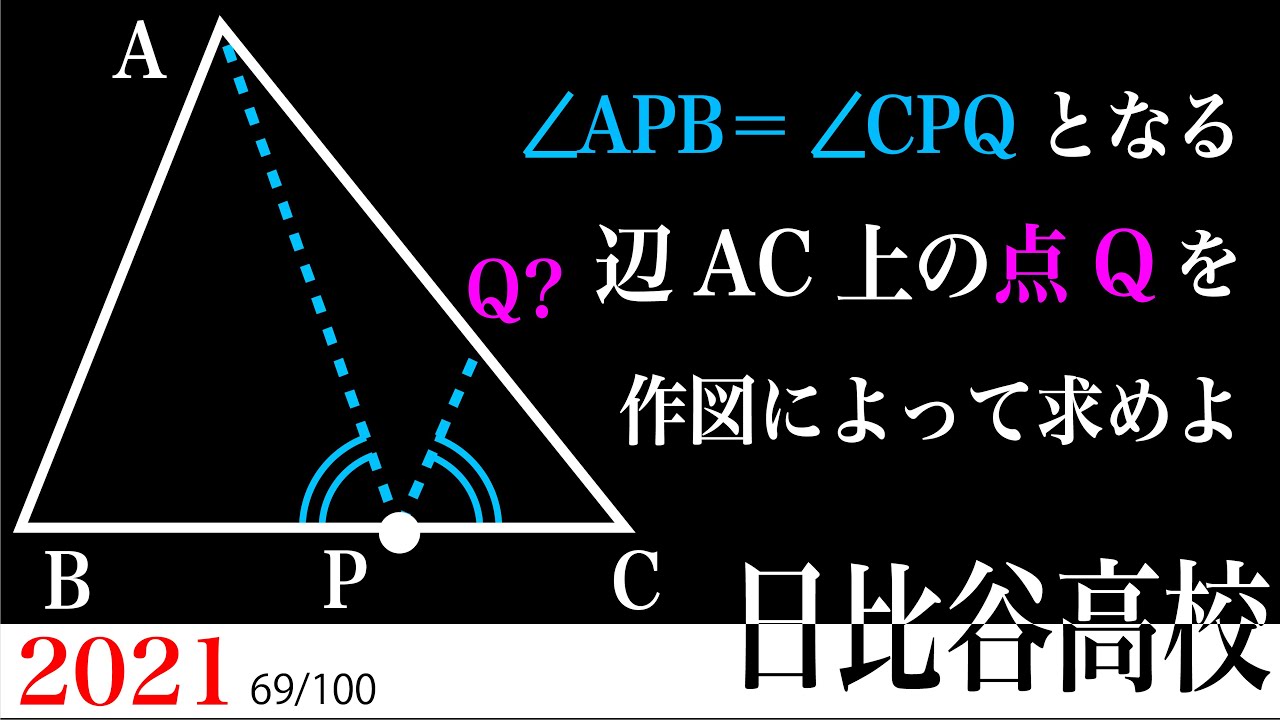
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle APB = \angle CPQ$となる辺AC上の点Qを作図によって求めよ。
*図は動画内参照
2021日比谷高等学校
この動画を見る
$\angle APB = \angle CPQ$となる辺AC上の点Qを作図によって求めよ。
*図は動画内参照
2021日比谷高等学校
2021 八王子東高校最初の一問 A

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{\sqrt 6 + 2}{\sqrt 2})(\frac{\sqrt 2 - \sqrt 3 }{3})$
2021八王子東高等学校
この動画を見る
$(\frac{\sqrt 6 + 2}{\sqrt 2})(\frac{\sqrt 2 - \sqrt 3 }{3})$
2021八王子東高等学校
平行四辺形であることの証明 2021 西 A
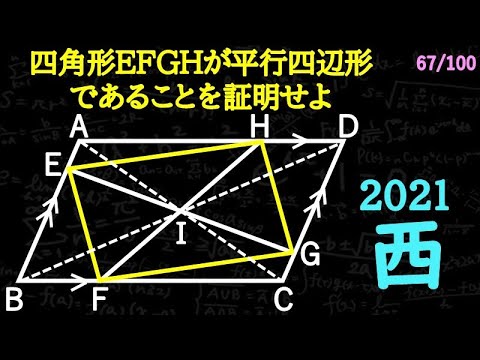
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形EFGHは平行四辺形であることを示せ
*図は動画内参照
2021都立西高等学校
この動画を見る
四角形EFGHは平行四辺形であることを示せ
*図は動画内参照
2021都立西高等学校
○か✖️か 2021 中大横浜 B

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正しいものをすべて選べ
(ア)$\frac{-4+2\sqrt 3}{2} = -2+2\sqrt 3$
(イ)1は素数である
(ウ)$\sqrt{1.69}$は有理数
(エ)$\frac{3}{0}=0$である
(オ)$\sqrt 9 + \sqrt{16} = \sqrt{25}$
2021中央大学附属横浜高等学校
この動画を見る
正しいものをすべて選べ
(ア)$\frac{-4+2\sqrt 3}{2} = -2+2\sqrt 3$
(イ)1は素数である
(ウ)$\sqrt{1.69}$は有理数
(エ)$\frac{3}{0}=0$である
(オ)$\sqrt 9 + \sqrt{16} = \sqrt{25}$
2021中央大学附属横浜高等学校
