 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
平方根:東京都立新宿高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立新宿高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立新宿高等学校
$x=\displaystyle \frac{5-4\sqrt{ 7 }}{2},y=\displaystyle \frac{5+8\sqrt{ 7 }}{2}$
のとき
→$x^2+2xy+y^2+4x-4y$
の値を求めよ。
この動画を見る
入試問題 東京都立新宿高等学校
$x=\displaystyle \frac{5-4\sqrt{ 7 }}{2},y=\displaystyle \frac{5+8\sqrt{ 7 }}{2}$
のとき
→$x^2+2xy+y^2+4x-4y$
の値を求めよ。
ビンゴの確率 ラ・サール B

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
カード1⃣~9⃣から無造作に3枚取り出し、書かれている数字のマスを塗る。
縦、横、斜めのいずれか1列が塗りつぶされる確率は?
ラ・サール高等学校
この動画を見る
カード1⃣~9⃣から無造作に3枚取り出し、書かれている数字のマスを塗る。
縦、横、斜めのいずれか1列が塗りつぶされる確率は?
ラ・サール高等学校
三平方の定理の利用 成城学園
単元:
#数学(中学生)#中3数学#三平方の定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
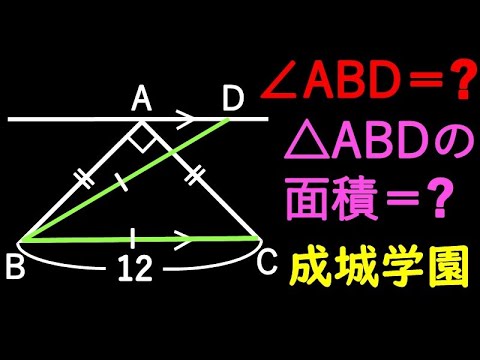
$\angle ABD=?$
$△ABD=?$
*図は動画内参照
成城学園高等学校
この動画を見る
$\angle ABD=?$
$△ABD=?$
*図は動画内参照
成城学園高等学校
二次方程式:東京都立八王子東高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#東京都立八王子東高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立八王子東高等学校
次の問いに答えよ。
2次方程式
$(x + 4)^2−6(x + 4) + 7 = 0 $
を解け。
この動画を見る
入試問題 東京都立八王子東高等学校
次の問いに答えよ。
2次方程式
$(x + 4)^2−6(x + 4) + 7 = 0 $
を解け。
相似 三平方の定理 芝浦工大柏
単元:
#数学(中学生)#中3数学#相似な図形#三平方の定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
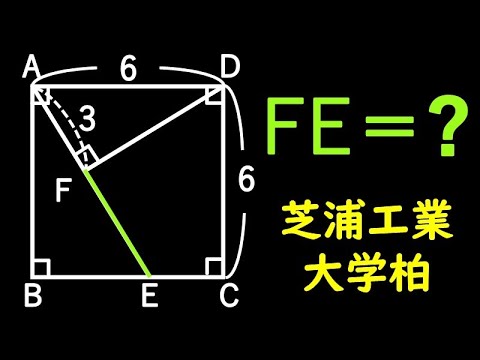
四角形ABCDは正方形
EF=?
*図は動画内参照
芝浦工業大学柏高等学校
この動画を見る
四角形ABCDは正方形
EF=?
*図は動画内参照
芝浦工業大学柏高等学校
【中学数学】連立方程式の演習~愛媛県公立高校入試2019~【高校受験】

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
花子さんが住む市の1ヵ月の水道料金は、使用量が8m³までは基本料金のみであり、
使用量が8㎡を超えると、超えた使用量に対して1m³当たりいくらかの超過料金が
発生する。
今月から水道料金が値上げされ、先月に比べて、基本料金が20%、1㎡当たりの
超過料金が15円、それぞれ高くなった。
花子さんの家の使用量は先月も今月も25m³であった。
先月の水道料金は4260円であり、今月の水道料金は先月の水道料金と比べると
495円高くなった。
先月の基本料金と、先月の1m³当たりの超過料金をそれぞれ求めよ。
この動画を見る
花子さんが住む市の1ヵ月の水道料金は、使用量が8m³までは基本料金のみであり、
使用量が8㎡を超えると、超えた使用量に対して1m³当たりいくらかの超過料金が
発生する。
今月から水道料金が値上げされ、先月に比べて、基本料金が20%、1㎡当たりの
超過料金が15円、それぞれ高くなった。
花子さんの家の使用量は先月も今月も25m³であった。
先月の水道料金は4260円であり、今月の水道料金は先月の水道料金と比べると
495円高くなった。
先月の基本料金と、先月の1m³当たりの超過料金をそれぞれ求めよ。
整数:東京都立立川高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立立川高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立立川高等学校
次の問に答えよ。
$\sqrt{ 2020n }$が整数となるような
$9999$以下の自然数$n$
の個数を求めよ。
この動画を見る
入試問題 東京都立立川高等学校
次の問に答えよ。
$\sqrt{ 2020n }$が整数となるような
$9999$以下の自然数$n$
の個数を求めよ。
確率:東京都立青山高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#東京都立青山高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
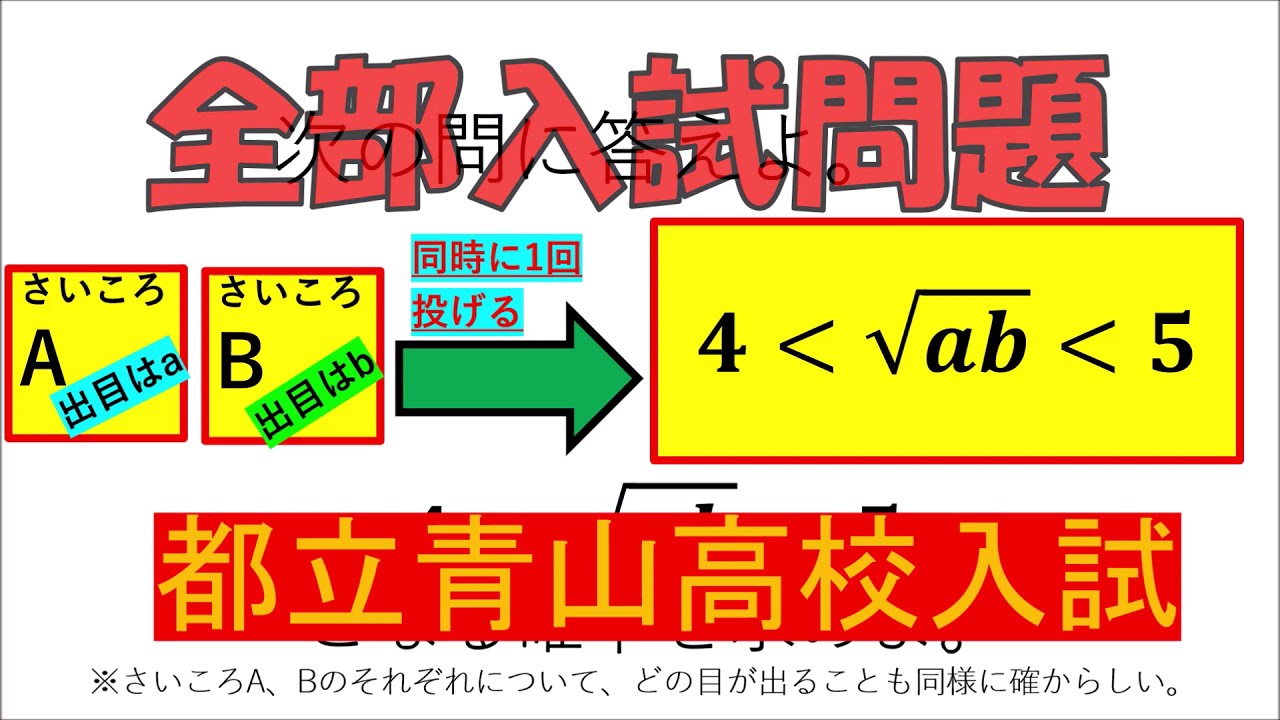
入試問題 東京都立青山高等学校
サイズが異なるさいころを同時に1回投げ、
$4 \lt \sqrt{ ab } \lt 5$
となる確率を求めよ。
※さいころA、Bのそれぞれについて、どの目が出ることも同様に確からしい。
この動画を見る
入試問題 東京都立青山高等学校
サイズが異なるさいころを同時に1回投げ、
$4 \lt \sqrt{ ab } \lt 5$
となる確率を求めよ。
※さいころA、Bのそれぞれについて、どの目が出ることも同様に確からしい。
整数:東京都立西高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#東京都立西高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立西高等学校
次の各問に答えよ。
2つの自然数$x, y$は、
$ x^2 - 4y^2 = 13$ を満たしている。
$x, y$の値をそれぞれ求めよ。
この動画を見る
入試問題 東京都立西高等学校
次の各問に答えよ。
2つの自然数$x, y$は、
$ x^2 - 4y^2 = 13$ を満たしている。
$x, y$の値をそれぞれ求めよ。
計算問題:東京都立青山高等学校~全国入試問題解法【VAMBI】

単元:
#数学(中学生)#高校入試過去問(数学)#東京都立青山高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立青山高等学校
次の問いに答えよ。
$\displaystyle \frac{4^2 \times (-3)^2}{11^2-(-13)^2}$
を計算をせよ。
この動画を見る
入試問題 東京都立青山高等学校
次の問いに答えよ。
$\displaystyle \frac{4^2 \times (-3)^2}{11^2-(-13)^2}$
を計算をせよ。
図形:東京都立高校入試~全国入試問題解法【とんとん♪】

単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#東京都立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立の高校
図で、
円$O$:線分$AB$が直径
$C, D$は周上の点
$4$点:$A, C, B, D$の順 (一致しない)
$\angle AOC=\angle BDC$
$\angle ABD=34^{ \circ }$
$x$で示した$\angle OCD$の大きさは$口$度である。
$口$部分を求めよ。
※図は動画内参照
この動画を見る
入試問題 東京都立の高校
図で、
円$O$:線分$AB$が直径
$C, D$は周上の点
$4$点:$A, C, B, D$の順 (一致しない)
$\angle AOC=\angle BDC$
$\angle ABD=34^{ \circ }$
$x$で示した$\angle OCD$の大きさは$口$度である。
$口$部分を求めよ。
※図は動画内参照
平方根:日比谷高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 日比谷高等学校
次の各問に答えよ。
$(\displaystyle \frac{\sqrt{ 7 }-\sqrt{ 12 }}{2})(\displaystyle \frac{\sqrt{ 7 }}{2}+\sqrt{ 3 })+\sqrt{ 18 }$
を計算せよ。
この動画を見る
入試問題 日比谷高等学校
次の各問に答えよ。
$(\displaystyle \frac{\sqrt{ 7 }-\sqrt{ 12 }}{2})(\displaystyle \frac{\sqrt{ 7 }}{2}+\sqrt{ 3 })+\sqrt{ 18 }$
を計算せよ。
確率:愛光高等学校~全国入試問題解法【そして、深夜にYouTube】
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#愛光高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
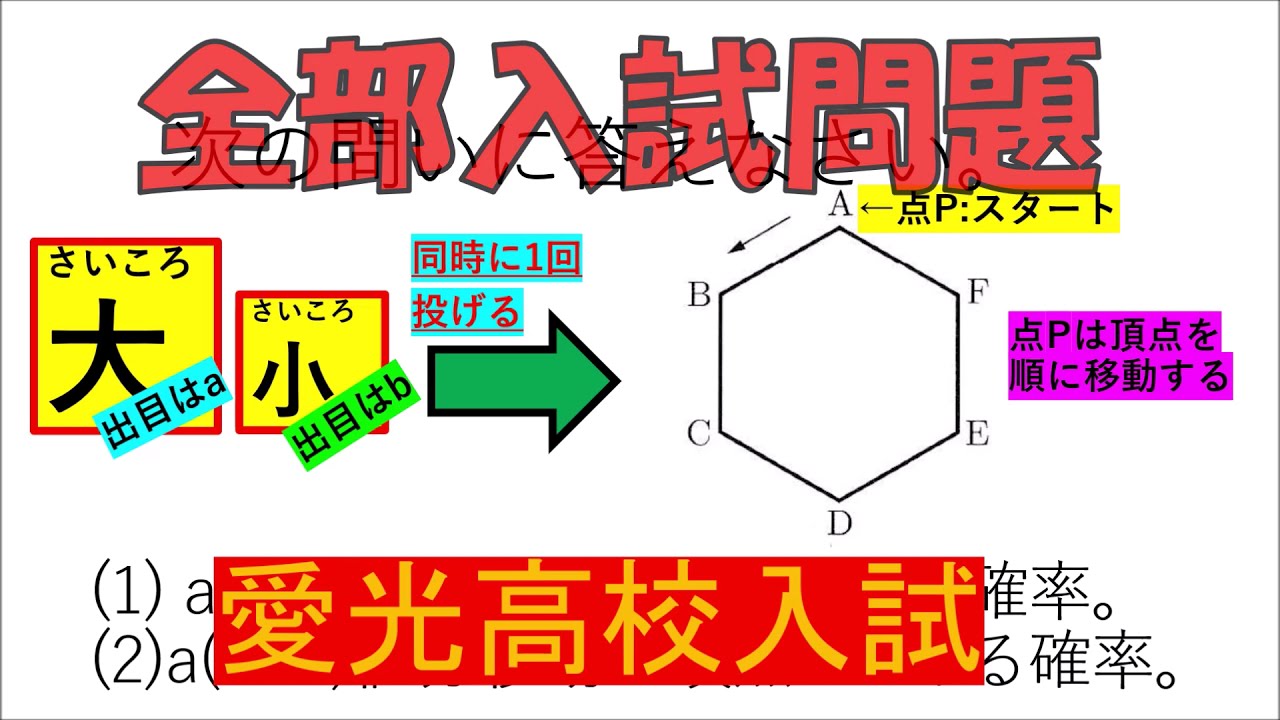
入試問題 愛光高等学校
(1)$a+b$値分移動で頂点Cにある確率。
(2)$a(b+1)$値分移動で頂点Dにある確率
※図は動画内参照
この動画を見る
入試問題 愛光高等学校
(1)$a+b$値分移動で頂点Cにある確率。
(2)$a(b+1)$値分移動で頂点Dにある確率
※図は動画内参照
【エナドリ!】連立方程式:久留米大学附設高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#久留米大学附設高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 久留米大学附設高等学校
次の問いに答えよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{1}{2x-3y}+\displaystyle \frac{2}{x+2y}=3 \\
\displaystyle \frac{3}{2x-3y}+\displaystyle \frac{2}{x+2y}=5
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
この動画を見る
入試問題 久留米大学附設高等学校
次の問いに答えよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{1}{2x-3y}+\displaystyle \frac{2}{x+2y}=3 \\
\displaystyle \frac{3}{2x-3y}+\displaystyle \frac{2}{x+2y}=5
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
確率:千葉県高校入試~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#千葉県立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 千葉県の高校
サイズが異なるさいころを同時に1回投げ、
$a:$さいころ大の出た目
$b:$さいころ小の出た目
$\displaystyle \frac{\sqrt{ ab }}{2}$の値が、有理数となる 確率を求めなさい。
※さいころを投げるとき、1から6までのどの目が出ることも同様に確からしい
この動画を見る
入試問題 千葉県の高校
サイズが異なるさいころを同時に1回投げ、
$a:$さいころ大の出た目
$b:$さいころ小の出た目
$\displaystyle \frac{\sqrt{ ab }}{2}$の値が、有理数となる 確率を求めなさい。
※さいころを投げるとき、1から6までのどの目が出ることも同様に確からしい
平方根:開成高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#開成高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 開成高等学校
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sqrt{ 3 }x +\sqrt{ 5 } y = \sqrt{ 7 } \\
\displaystyle \frac{ 1 }{\sqrt{ 3 }}+\displaystyle \frac{ 1 }{\sqrt{ 5 }} = \displaystyle \frac{ 1 }{\sqrt{ 7 }}
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
この動画を見る
入試問題 開成高等学校
$\begin{eqnarray}
\left\{
\begin{array}{l}
\sqrt{ 3 }x +\sqrt{ 5 } y = \sqrt{ 7 } \\
\displaystyle \frac{ 1 }{\sqrt{ 3 }}+\displaystyle \frac{ 1 }{\sqrt{ 5 }} = \displaystyle \frac{ 1 }{\sqrt{ 7 }}
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
【エナドリ】平方根:埼玉県高校入試~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#埼玉県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 埼玉県の高校
下の問に答えよ。
$x=2+\sqrt{ 3 }$
$y=2-\sqrt{ 3 }$
のとき
→$(1+\displaystyle \frac{ 1 }{x})(1+\displaystyle \frac{ 1 }{y})$
の値を求めよ。
この動画を見る
入試問題 埼玉県の高校
下の問に答えよ。
$x=2+\sqrt{ 3 }$
$y=2-\sqrt{ 3 }$
のとき
→$(1+\displaystyle \frac{ 1 }{x})(1+\displaystyle \frac{ 1 }{y})$
の値を求めよ。
【中学数学】規則性の演習~岐阜県公立高校入試2019~【高校受験】

単元:
#数学(中学生)#中1数学#方程式#高校入試過去問(数学)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
規則性の演習 入試頻発問題を使用しての解説動画です
この動画を見る
規則性の演習 入試頻発問題を使用しての解説動画です
【キミのやり方であっている!】連立方程式:関西学院高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#関西学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 関西学院高等学校
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3(\displaystyle \frac{ 5 }{6}x+\displaystyle \frac{ 14 }{3})-5(\displaystyle \frac{ 1 }{3}y-\displaystyle \frac{ 14 }{5})=33 \\
2(\displaystyle \frac{ 5 }{6}x+\displaystyle \frac{ 14 }{3})-5(\displaystyle \frac{ 1 4}{5}-\displaystyle \frac{ 1 }{3}y)=-3
\end{array}
\right.
\end{eqnarray}$
を解け。
この動画を見る
入試問題 関西学院高等学校
連立方程式
$\begin{eqnarray}
\left\{
\begin{array}{l}
3(\displaystyle \frac{ 5 }{6}x+\displaystyle \frac{ 14 }{3})-5(\displaystyle \frac{ 1 }{3}y-\displaystyle \frac{ 14 }{5})=33 \\
2(\displaystyle \frac{ 5 }{6}x+\displaystyle \frac{ 14 }{3})-5(\displaystyle \frac{ 1 4}{5}-\displaystyle \frac{ 1 }{3}y)=-3
\end{array}
\right.
\end{eqnarray}$
を解け。
【続けて他の動画も見てほしい!】文字式:近畿大学附属高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)#近畿大学付属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 近畿大学附属高等学校
次の問いに答えよ。
$\displaystyle \frac{ 4x-3y }{7}-\displaystyle \frac{ 3x-2y }{5}$
を計算せよ。
この動画を見る
入試問題 近畿大学附属高等学校
次の問いに答えよ。
$\displaystyle \frac{ 4x-3y }{7}-\displaystyle \frac{ 3x-2y }{5}$
を計算せよ。
【大学入試の簡易版!】二次方程式:お茶の水女子大学付属高等学校②~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#お茶の水女子大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 お茶の水女子大学付属高等学校
$x$についての$2$次方程式
$x^2 + (a + 2)x + a^2+2a − 1 = 0$
解の$1$つが$a$である。
$a$の値を求めよ。
(ただし、$a \gt 0$)
この動画を見る
入試問題 お茶の水女子大学付属高等学校
$x$についての$2$次方程式
$x^2 + (a + 2)x + a^2+2a − 1 = 0$
解の$1$つが$a$である。
$a$の値を求めよ。
(ただし、$a \gt 0$)
【一度は解きたい入試の良問】二次方程式:お茶の水女子大学付属高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#お茶の水女子大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 お茶の水女子大学付属高等学校
$x$についての$2$次方程式
$x^2 + (a + 2)x + a^2+2a − 1 = 0$
解の$1$つが$a$である。
$a$の値を求めよ。
この動画を見る
入試問題 お茶の水女子大学付属高等学校
$x$についての$2$次方程式
$x^2 + (a + 2)x + a^2+2a − 1 = 0$
解の$1$つが$a$である。
$a$の値を求めよ。
【入試は高校数学へのパスポート!】文字式:石川県高校入試~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#石川県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 石川県の高校
$x=\sqrt{ 7 }+\sqrt{ 2 } $
$y=\sqrt{ 7 }-\sqrt{ 2 } $
のとき
$x^2-y^2$の値を求めなさい。
この動画を見る
入試問題 石川県の高校
$x=\sqrt{ 7 }+\sqrt{ 2 } $
$y=\sqrt{ 7 }-\sqrt{ 2 } $
のとき
$x^2-y^2$の値を求めなさい。
【頭を使うな!目で考えろ!】一次関数:和歌山県高校入試~全国入試問題解法
単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#和歌山県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
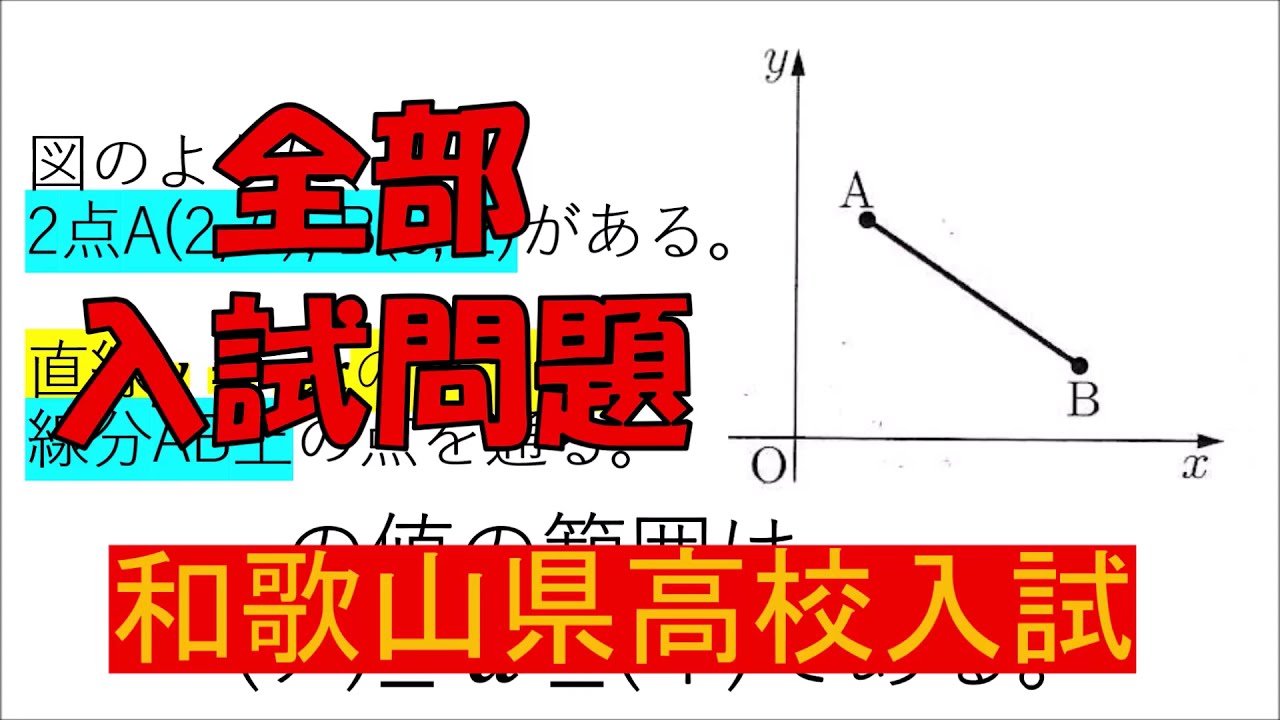
入試問題 和歌山県の高校
図のように、 $2$点$A(2, 6), B(8, 2)$がある。
直線$y = ax$のグラフが
線分$AB$上の点を通る。
$a$の値の範囲は、 (ア)$ \leqq a \leqq $(イ)である。
※図は動画内参照
この動画を見る
入試問題 和歌山県の高校
図のように、 $2$点$A(2, 6), B(8, 2)$がある。
直線$y = ax$のグラフが
線分$AB$上の点を通る。
$a$の値の範囲は、 (ア)$ \leqq a \leqq $(イ)である。
※図は動画内参照
【その本質を調べることも数学】連立方程式:滋賀県高校入試~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#滋賀県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 滋賀県の高校
次の問いに答えよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x - 3y = 1 \\
3x + 2y = 8
\end{array}
\right.
\end{eqnarray}$
連立方程式を解きなさい。
この動画を見る
入試問題 滋賀県の高校
次の問いに答えよ。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x - 3y = 1 \\
3x + 2y = 8
\end{array}
\right.
\end{eqnarray}$
連立方程式を解きなさい。
【大切だから解いて欲しい!】図形:岐阜県高校入試~全国入試問題解法
単元:
#数学(中学生)#中2数学#平行と合同#高校入試過去問(数学)#岐阜県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
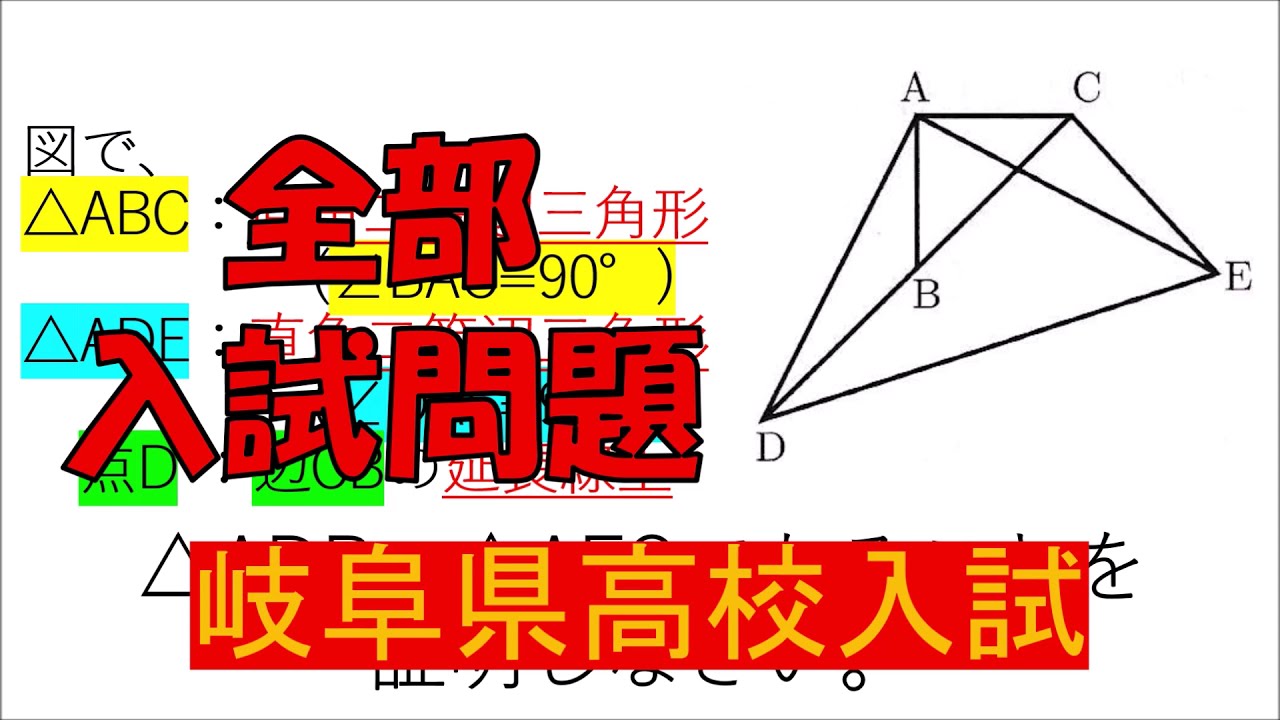
入試問題 岐阜県の高校
図で、
$\triangle ABC$:直角二等辺三角形
$(\angle BAC=90°)$
$\triangle AED$:直角二等辺三角形
$(\angle DAE=90°)$
点$D$:辺$CB$の延長線上
$\triangle ADB = \triangle AEC$であることを
証明しなさい。
※図は動画内参照
この動画を見る
入試問題 岐阜県の高校
図で、
$\triangle ABC$:直角二等辺三角形
$(\angle BAC=90°)$
$\triangle AED$:直角二等辺三角形
$(\angle DAE=90°)$
点$D$:辺$CB$の延長線上
$\triangle ADB = \triangle AEC$であることを
証明しなさい。
※図は動画内参照
【解き方は1つじゃない!】二次方程式:立教新座高校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#立教新座高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 立教新座高等学校
二次方程式
$(x-\sqrt{ 2 })^2+6(x-\sqrt{ 2 })+7=0$
を解きなさい。
この動画を見る
入試問題 立教新座高等学校
二次方程式
$(x-\sqrt{ 2 })^2+6(x-\sqrt{ 2 })+7=0$
を解きなさい。
【高校数学へのパスポート】二次関数:滋賀県高校入試~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#滋賀県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 滋賀県の高校
次の問いに答えなさい。
関数$y = ax^2$ について、
$ -3\leqq x \leqq 1$のとき、
$ 0\leqq y \leqq 1$である。
このとき、$a$の値を求めなさい。
この動画を見る
入試問題 滋賀県の高校
次の問いに答えなさい。
関数$y = ax^2$ について、
$ -3\leqq x \leqq 1$のとき、
$ 0\leqq y \leqq 1$である。
このとき、$a$の値を求めなさい。
【円周角を制すものは…】図形:京都府高校入試~全国入試問題解法

単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#京都府公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 京都府の高校
図で、
$4$点$A, B, C, D$は、
円$O$の周上にあり、 線分$BD$は、
円$O$の直径である。
$ \angle x$の大きさを求めよ。
※図は動画内参照
この動画を見る
入試問題 京都府の高校
図で、
$4$点$A, B, C, D$は、
円$O$の周上にあり、 線分$BD$は、
円$O$の直径である。
$ \angle x$の大きさを求めよ。
※図は動画内参照
【その実態!整数論…】確率:三重県高校入試~全国入試問題解法

単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#三重県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 三重県の高校
あとの問いに答えなさい。
サイズが異なるさいころを同時に1回投げ、
$2$桁の整数$m:$
十の位: さいころ大の出た目
一の位: さいころ小の出た目
$m$が素数となる確率を求めなさい。
※さいころの目は$1,2,3,4,5,6$であり、
どの目が出ることも同様に確からしい
この動画を見る
入試問題 三重県の高校
あとの問いに答えなさい。
サイズが異なるさいころを同時に1回投げ、
$2$桁の整数$m:$
十の位: さいころ大の出た目
一の位: さいころ小の出た目
$m$が素数となる確率を求めなさい。
※さいころの目は$1,2,3,4,5,6$であり、
どの目が出ることも同様に確からしい
