鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
北海道大学 ２種類の数字でできてるｎ桁の数字の個数 Japanese university entrance exam questions
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
(1)2種類の数でできている4桁の数の個数
(2)n桁の場合
北海道大過去問
この動画を見る
(1)2種類の数でできている4桁の数の個数
(2)n桁の場合
北海道大過去問
大阪大学 自然数（２以上）の立方の逆数の和 1/4未満 示せ 高校数学 Japanese university entrance exam questions
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
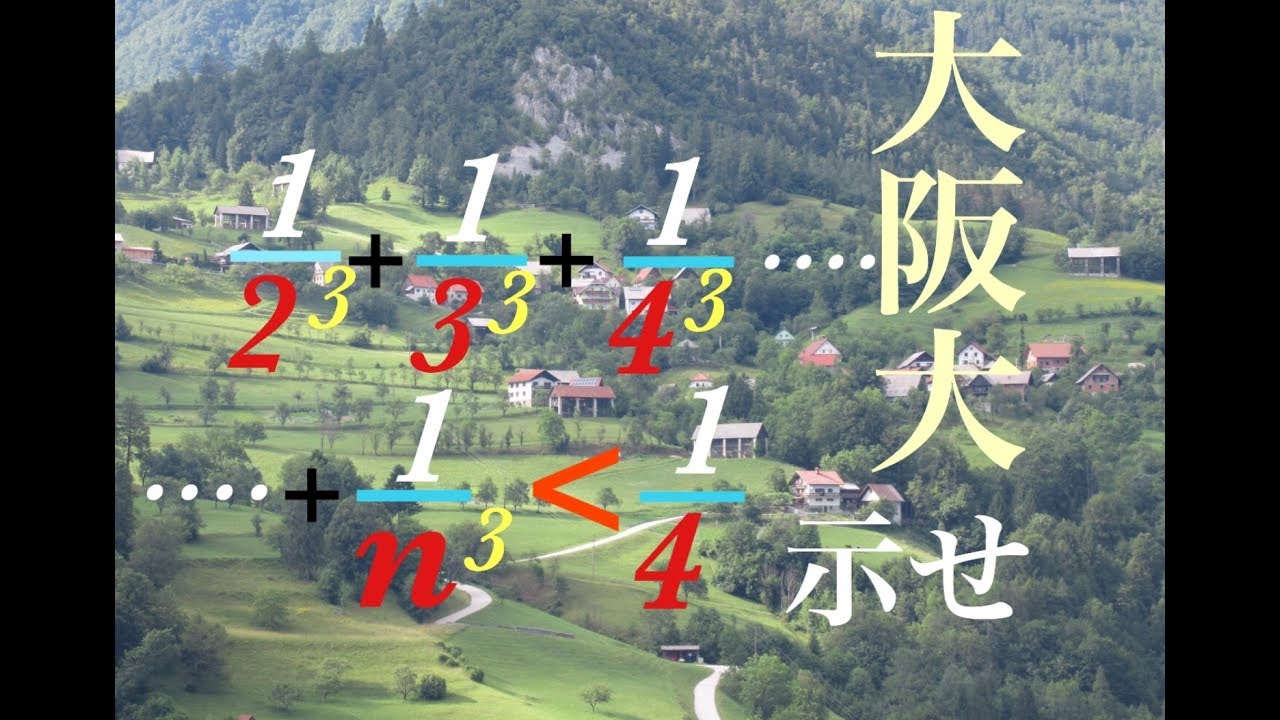
自然数（２以上）の立方の逆数の和 が1/4未満であることを示せ.
大阪大学過去問
この動画を見る
自然数（２以上）の立方の逆数の和 が1/4未満であることを示せ.
大阪大学過去問
整数問題。1,1,2,2,3,3,4,4,を適当に並べてできる数は平方数でないことを証明せよ。
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
1,1,2,2,3,3,4,4
この8個の数を並べてできる8桁の数は平方数でないことを証明せよ。
この動画を見る
1,1,2,2,3,3,4,4
この8個の数を並べてできる8桁の数は平方数でないことを証明せよ。
京都大学入試問題 ３次方程式が整数解を持たない時、解は無理数であることの証明 高校数学
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
方程式$x^3+x-8=0$は
(1)ただ1つの実根を1と2との間にもつことを示せ。
(2)この根は無理数であることを証明せよ。
京大過去問
この動画を見る
方程式$x^3+x-8=0$は
(1)ただ1つの実根を1と2との間にもつことを示せ。
(2)この根は無理数であることを証明せよ。
京大過去問
伝説の東大入試問題 π＞3.05を証明せよ 高校数学 Japanese university entrance exam questions Tokyo University
東大入試問題 無限級数 数列の和 Japanese university entrance exam questions Tokyo University
単元：
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
東京大学過去問題
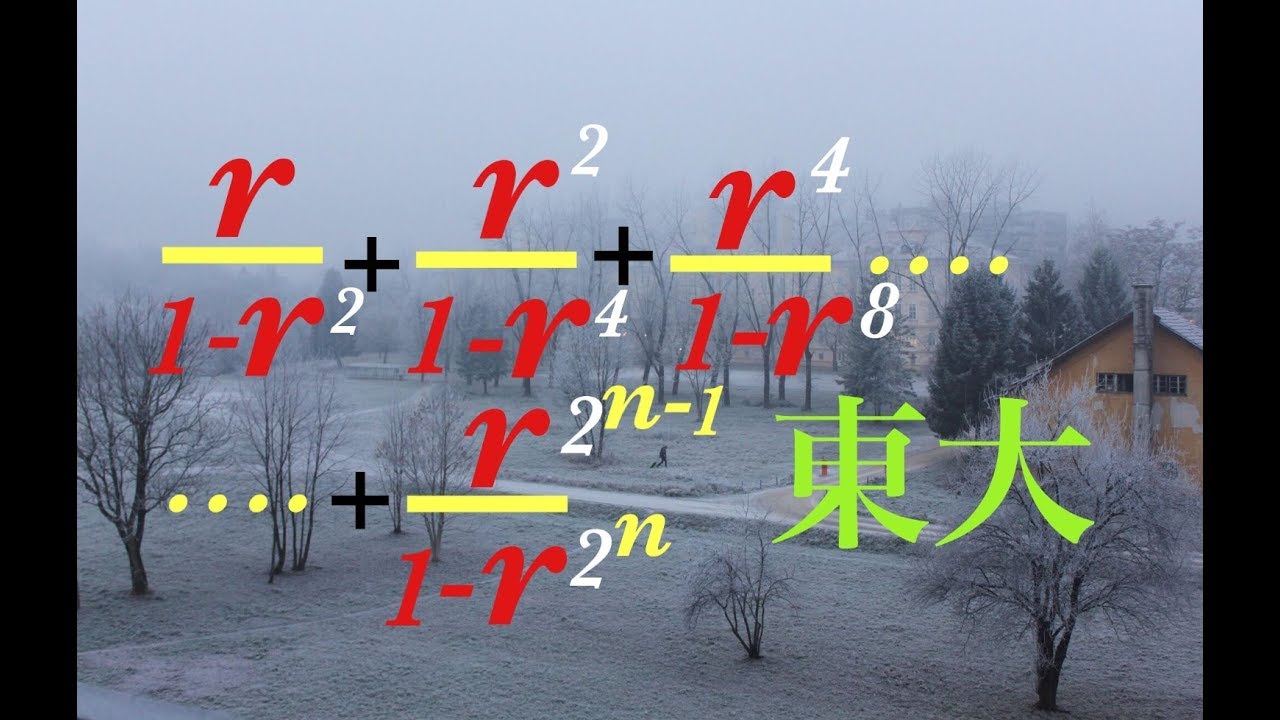
無限級数
$\frac{r}{1-r^2}$+$\frac{r^2}{1-r^4}$+$\frac{r^4}{1-r^8}$+$\cdots$+$\frac{r^{2^{n-1}}}{1-r^{2^{n}}}$
この動画を見る
東京大学過去問題
無限級数
$\frac{r}{1-r^2}$+$\frac{r^2}{1-r^4}$+$\frac{r^4}{1-r^8}$+$\cdots$+$\frac{r^{2^{n-1}}}{1-r^{2^{n}}}$
東京医科歯科大学、数学、中学生でも解いてみたくなる大学入試問題 高校数学 Japanese university entrance exam questions
単元：
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科歯科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
東京医科歯科大学'73 過去問題
m,n自然数$(m \geqq n)$
$x^2-mnx+m+n = 0$
の2つの解がともに整数となるm,nをすべて求めよ。
東京医科歯科大学過去問
この動画を見る
東京医科歯科大学'73 過去問題
m,n自然数$(m \geqq n)$
$x^2-mnx+m+n = 0$
の2つの解がともに整数となるm,nをすべて求めよ。
東京医科歯科大学過去問
組立除法、三角関数の合成、視聴者からの質問への返答
単元：
#複素数と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#加法定理とその応用#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
組立除法、三角関数の合成、視聴者からの質問への返答です.
\begin{array}{r}
x-α\enclose{longdiv}{ax^3+bx^2+cx+d\phantom{0}} \\[-3pt]
\end{array}
この動画を見る
組立除法、三角関数の合成、視聴者からの質問への返答です.
\begin{array}{r}
x-α\enclose{longdiv}{ax^3+bx^2+cx+d\phantom{0}} \\[-3pt]
\end{array}
京大入試問題 数学 頑張れば小中学生にも解けるぞ Japanese university entrance exam questions Kyoto University
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
京都大学過去問題
$n \geqq 3$とする。1,2,・・・,nのうちから重複を許して６個の数字をえらびそれを並べた順列を考える。
このような順列のうちで、どの数字もそれ以外の５つの数字のどれかに等しくなっているようなものの個数を求めよ。
この動画を見る
京都大学過去問題
$n \geqq 3$とする。1,2,・・・,nのうちから重複を許して６個の数字をえらびそれを並べた順列を考える。
このような順列のうちで、どの数字もそれ以外の５つの数字のどれかに等しくなっているようなものの個数を求めよ。
頑張れば小中学生にもできる 東大入試問題 数学 Japanese university entrance exam questions Tokyo University
単元：
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
3人でジャンケン
負けた人は以後参加できない。
k回目に１人の勝者が決まる確率を求めよ.
東大過去問
この動画を見る
3人でジャンケン
負けた人は以後参加できない。
k回目に１人の勝者が決まる確率を求めよ.
東大過去問
漸化式・特性方程式・三項間漸化式・視聴者からの質問への返答
単元：
#数列#漸化式#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
漸化式・特性方程式・三項間漸化式・視聴者からの質問への返答です.
$a_{n+2}-3a_{n+1}-4a_n=0$ $a_1=1$ $a_2=2$
この動画を見る
漸化式・特性方程式・三項間漸化式・視聴者からの質問への返答です.
$a_{n+2}-3a_{n+1}-4a_n=0$ $a_1=1$ $a_2=2$
東大入試問題、場合の数、頑張れば、中学生、中学受験生にも解けるぞ Japanese university entrance exam questions Tokyo University
単元：
#数A#大学入試過去問(数学)#場合の数と確率#場合の数#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
nを正の整数とし、n個のボールを3つの箱に分けて入れる問題を考える。ただし、1個のボールも入らない箱があってもよいものとする。以下に述べる4つの場合について、それぞれ相異なるなる入れ方の総数を求めたい。
(1)１からnまで異なる番号のついたこのボールを、A,B,Cと区別された3つの箱に入れる場合、その入れ方は全部で何通りあるか 。
(2)互いに区別のつかないn個のボールを、A,B,Cと区別された3つの箱に入れる場合、その入れ方は全部で何通りあるか。
(3) 1からnまで異なる番号のついたn個のボールを、区別のつかない3つの箱に入れる場合、その入れ方は全部で何通りあるか。
(4)nが6の倍数6mであるとき、n個の互いに区別のつかないボールを、区別のつかない3つの箱に入れる場合、その入れ方は全部で何通りあるか。
東大過去問
この動画を見る
nを正の整数とし、n個のボールを3つの箱に分けて入れる問題を考える。ただし、1個のボールも入らない箱があってもよいものとする。以下に述べる4つの場合について、それぞれ相異なるなる入れ方の総数を求めたい。
(1)１からnまで異なる番号のついたこのボールを、A,B,Cと区別された3つの箱に入れる場合、その入れ方は全部で何通りあるか 。
(2)互いに区別のつかないn個のボールを、A,B,Cと区別された3つの箱に入れる場合、その入れ方は全部で何通りあるか。
(3) 1からnまで異なる番号のついたn個のボールを、区別のつかない3つの箱に入れる場合、その入れ方は全部で何通りあるか。
(4)nが6の倍数6mであるとき、n個の互いに区別のつかないボールを、区別のつかない3つの箱に入れる場合、その入れ方は全部で何通りあるか。
東大過去問
小学生の知識で解ける東大入試問題,整数問題 Japanese university entrance exam questions Tokyo University
単元：
#数A#大学入試過去問(数学)#整数の性質#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
円周上にm個の赤い点とn個の青い点を任意の順序に並べる。これらの点により、円周はm+n個の弧に分けられる。
このとき、これらの弧のうち両端の点の色が異なるものの数は偶数であることを証明せよ。
ただし、$m \geqq 1$,$n \geqq 1$とする。
東大過去問
この動画を見る
円周上にm個の赤い点とn個の青い点を任意の順序に並べる。これらの点により、円周はm+n個の弧に分けられる。
このとき、これらの弧のうち両端の点の色が異なるものの数は偶数であることを証明せよ。
ただし、$m \geqq 1$,$n \geqq 1$とする。
東大過去問
整数、素数、京都大学入試問題 数学 Japanese university entrance exam questions Kyoto University
単元：
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
p,qともに素数
$p^q+q^p$が素数となるp,qをすべて求めよ
京大過去問
この動画を見る
p,qともに素数
$p^q+q^p$が素数となるp,qをすべて求めよ
京大過去問
原点を中心とする円周上には無数に有理点がある。ピタゴラス数と関係が？
単元：
#数A#数Ⅱ#整数の性質#図形と方程式#微分法と積分法#円と方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
原点を中心とする円周上には無数に有理点がある。ピタゴラス数と関係があるのか解説していきます.
この動画を見る
原点を中心とする円周上には無数に有理点がある。ピタゴラス数と関係があるのか解説していきます.
質問への返答 因数分解 a^3+b^3+c^3-3abc
π／２＝（２✕２✕４✕４✕６……）／（１✕３✕３✕５✕５……）ウォリスの公式
偏差値と標準偏差。ワイルズ教授は偏差値100,0050
約数の個数、総和、完全数
ピタゴラス数、三平方の定理、整数解の求め方、質問への返答
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
ピタゴラス数,三平方の定理,整数解の求め方,質問への回答に関して解説していきます.
この動画を見る
ピタゴラス数,三平方の定理,整数解の求め方,質問への回答に関して解説していきます.
平均の速さ。算数的思考でマラソン３時間半を切る
質問に対する返答。別解。整数問題、場合の数
単元：
#数A#場合の数と確率#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$1 \leqq t < u <v \leqq 6m$
$t+u+v =6m$
この動画を見る
$1 \leqq t < u <v \leqq 6m$
$t+u+v =6m$
２つの自然数が互いに素ある確率。６／πの２乗
単元：
#数A#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
任意の2つの自然数が互いに素である確率は
$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\cdots = \frac{\pi^2}{6}$
この動画を見る
任意の2つの自然数が互いに素である確率は
$\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\frac{1}{5^2}+\cdots = \frac{\pi^2}{6}$
質問に対する返答です。整数問題,数列の和
単元：
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和（等差・等比・階差・Σ）#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$1 \leqq t< u < v \leqq 6m$
$t+u+v=6m$
この動画を見る
$1 \leqq t< u < v \leqq 6m$
$t+u+v=6m$
素数発見法を考えたエラトステネス、２千年以上前に地球の大きさを測っていた。
奇数の４乗の逆数の和 オイラー級数 πが登場
単元：
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\frac{1}{1^4}+\frac{1}{3^4}+\frac{1}{5^4}+\frac{1}{7^4}+\cdots=\dfrac{\pi^4}{96}$
この動画を見る
$\frac{1}{1^4}+\frac{1}{3^4}+\frac{1}{5^4}+\frac{1}{7^4}+\cdots=\dfrac{\pi^4}{96}$
分母が奇数の分数を無限に足したい引いたり、何故か答えにπが登場
単元：
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}+\cdots=\dfrac{\pi}{4}$
この動画を見る
$\frac{1}{1}-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\frac{1}{9}+\cdots=\dfrac{\pi}{4}$
自然数の４乗の逆数の和 オイラー級数（Euler） やっぱりπが登場
単元：
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\frac{1}{1^4}$+$\frac{1}{2^4}$+$\frac{1}{3^4}$+$\frac{1}{4^4}$+$\cdots$$\frac{1}{n^4}$=$\frac{\pi^4}{90}$
この動画を見る
$\frac{1}{1^4}$+$\frac{1}{2^4}$+$\frac{1}{3^4}$+$\frac{1}{4^4}$+$\cdots$$\frac{1}{n^4}$=$\frac{\pi^4}{90}$
天才オイラーが解決した問題。奇数の平方の逆数の和にπが登場
平方数でない自然数の平方根は全て無理数であることの証明
