 立体切断
立体切断
 立体切断
立体切断
【受験算数】下の図のようにすべての辺の長さが等しい三角すいAーBCDがあります。辺AC、ADをそれぞれ3等分点のうち、頂点C、Dに近い方の点をそれぞれ点P、Qとし、点Rは辺AB上の点とします。この…

単元:
#算数(中学受験)#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ
教材:
#予習シ#予習シ・算数・小6上#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図のようにすべての辺の長さが等しい三角すいAーBCDがあります。辺AC、ADをそれぞれ3等分点のうち、頂点C、Dに近い方の点をそれぞれ点P、Qとし、点Rは辺AB上の点とします。
この立体を点P、Q、Rで切ったとき、頂点Aを含む方の立体の体積は三角すいA―BCDの体積の1/3になりました。このとき、AR:RBを求めなさい。
この動画を見る
下の図のようにすべての辺の長さが等しい三角すいAーBCDがあります。辺AC、ADをそれぞれ3等分点のうち、頂点C、Dに近い方の点をそれぞれ点P、Qとし、点Rは辺AB上の点とします。
この立体を点P、Q、Rで切ったとき、頂点Aを含む方の立体の体積は三角すいA―BCDの体積の1/3になりました。このとき、AR:RBを求めなさい。
福田の数学〜慶應義塾大学薬学部2025第1問(2)〜正八面体に内接する立方体の体積

単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#立体図形#立体切断#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2)$a$は$a\gt 0$を満たす実数とする。
$xyz$空間に$6$点$(a,0,0),(0,a,0),(0,0,a),$
$(-a,0,0)(0,-a,0)(0,0,-a)$を頂点とする多面体
$S$がある。
(i)$S$の体積は$\boxed{オ}$である。
(ii)立方体$U$のすべての頂点が$S$の辺上にあるとき、
$U$の体積は$\boxed{カ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(2)$a$は$a\gt 0$を満たす実数とする。
$xyz$空間に$6$点$(a,0,0),(0,a,0),(0,0,a),$
$(-a,0,0)(0,-a,0)(0,0,-a)$を頂点とする多面体
$S$がある。
(i)$S$の体積は$\boxed{オ}$である。
(ii)立方体$U$のすべての頂点が$S$の辺上にあるとき、
$U$の体積は$\boxed{カ}$である。
$2025$年慶應義塾大学薬学部過去問題
【小6算数手元解説】受験算数 全部で8回切って、表面積が3倍になる?【問題文は概要欄】

単元:
#算数(中学受験)#立体図形#立体切断#立体図形その他
教材:
#SPX#中学受験教材#6年算数D-支援
指導講師:
理数個別チャンネル
問題文全文(内容文):
2つの直方体を合わせた形の立体があります。斜線をつけた面「あ」または面「い」に平行な平面で、この立体の形をくずさないで、8回切ります。
その時、切り離された立体の表面積の和が、もとの立体の表面積の3倍になるようにします。
1)切り離された立体の表面積の和を求めなさい。
2)8回のうち辺 AB は何回切ればよいでしょうか。すべての場合を求めなさい。
この動画を見る
2つの直方体を合わせた形の立体があります。斜線をつけた面「あ」または面「い」に平行な平面で、この立体の形をくずさないで、8回切ります。
その時、切り離された立体の表面積の和が、もとの立体の表面積の3倍になるようにします。
1)切り離された立体の表面積の和を求めなさい。
2)8回のうち辺 AB は何回切ればよいでしょうか。すべての場合を求めなさい。
中学受験生必見!!「立体(とうふ)の切断」

単元:
#算数(中学受験)#立体図形#立体切断
指導講師:
重吉
問題文全文(内容文):
4. 底辺が2cmで高さが2cmの二等辺三角形を底面とする、高さ2cmの三角柱を考えます。
この三角柱を以下の図のように1辺の長さが2cmの立方体ABCD-EFGH の中に置きます。
なお、角すいの体積は「(底面積)×(高さ) +3」で求められます。
(1) 図1のように、三角柱の向きを変えて2通りの置き方をしました。これらの共通部分の立体の体積を答えなさい。
※図は動画内参照
この動画を見る
4. 底辺が2cmで高さが2cmの二等辺三角形を底面とする、高さ2cmの三角柱を考えます。
この三角柱を以下の図のように1辺の長さが2cmの立方体ABCD-EFGH の中に置きます。
なお、角すいの体積は「(底面積)×(高さ) +3」で求められます。
(1) 図1のように、三角柱の向きを変えて2通りの置き方をしました。これらの共通部分の立体の体積を答えなさい。
※図は動画内参照
2024年渋谷教育学園渋谷中算数大問②中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#過去問解説(学校別)#立体図形#立体切断#渋谷教育学園渋谷中学
指導講師:
重吉
問題文全文(内容文):
2⃣図は動画内参照
図1は18個の立方体を積み上げて作った直方体です。図1の直方体を平面で切り、その後、 すべてバラバラにしたときの立体の個数を考えます。
例えば図1の直方体を3点ア、イ、ウを通る平面で切り、その後、すべてバラバラにすると、 9個の立方体と18個の切られた立体に分かれ、立体は合計で27個となります。 次の問いに答えなさい。
(1) 図1の直方体を3点イ、ウ、エを通る平面で切り、その後、すべてバラバラにすると、 立体は合計で何個になりますか。
図2は36個の立方体を積み上げて、直方体を作ったものです。
(2) 図2の直方体を3点A, B. Cを通る平面で切り、その後、すべてバラバラにすると、 立体は合計で何個になりますか。
(3) 図2の直方体を3点A、B、Dを通る平面で切り、その後、ずべてバラバラにすると、 立体は合計で何個になりますか。
この動画を見る
2⃣図は動画内参照
図1は18個の立方体を積み上げて作った直方体です。図1の直方体を平面で切り、その後、 すべてバラバラにしたときの立体の個数を考えます。
例えば図1の直方体を3点ア、イ、ウを通る平面で切り、その後、すべてバラバラにすると、 9個の立方体と18個の切られた立体に分かれ、立体は合計で27個となります。 次の問いに答えなさい。
(1) 図1の直方体を3点イ、ウ、エを通る平面で切り、その後、すべてバラバラにすると、 立体は合計で何個になりますか。
図2は36個の立方体を積み上げて、直方体を作ったものです。
(2) 図2の直方体を3点A, B. Cを通る平面で切り、その後、すべてバラバラにすると、 立体は合計で何個になりますか。
(3) 図2の直方体を3点A、B、Dを通る平面で切り、その後、ずべてバラバラにすると、 立体は合計で何個になりますか。
2024年渋谷教育学園渋谷中算数大問②中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#立体図形#立体切断#立体図形その他
指導講師:
重吉
問題文全文(内容文):
図1は18個の立方体を積み上げて作った直方体です。図1の直方体を平面で切り、その後、 すべてバラバラにしたときの立体の個数を考えます。
例えば図1の直方体を3点ア、イ、ウを通る平面で切り、その後、すべてバラバラにすると、 9個の立方体と18個の切られた立体に分かれ、立体は合計で27個となります。
次の問いに答えなさい。
(1) 図1の直方体を3点イ、ウ、エを通る平面で切り、その後、すべてバラバラにすると。 立体は合計で何個になりますか。
図2は36個の立方体を積み上げて、直方体を作ったものです。
(2) 図2の直方体を3点A, B. Cを通る平面で切り、その後、すべてバラバラにすると、 立体は合計で何個になりますか。
(3) 図2の直方体を3点A、B、Dを通る平面で切り、その後、ずべてバラバラにすると、 立体は合計で何個になりますか
※図は動画内参照
この動画を見る
図1は18個の立方体を積み上げて作った直方体です。図1の直方体を平面で切り、その後、 すべてバラバラにしたときの立体の個数を考えます。
例えば図1の直方体を3点ア、イ、ウを通る平面で切り、その後、すべてバラバラにすると、 9個の立方体と18個の切られた立体に分かれ、立体は合計で27個となります。
次の問いに答えなさい。
(1) 図1の直方体を3点イ、ウ、エを通る平面で切り、その後、すべてバラバラにすると。 立体は合計で何個になりますか。
図2は36個の立方体を積み上げて、直方体を作ったものです。
(2) 図2の直方体を3点A, B. Cを通る平面で切り、その後、すべてバラバラにすると、 立体は合計で何個になりますか。
(3) 図2の直方体を3点A、B、Dを通る平面で切り、その後、ずべてバラバラにすると、 立体は合計で何個になりますか
※図は動画内参照
2024年浦和明の星女子中算数大問②、③中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#立体図形#立体切断#立体図形その他#速さ#速さその他
指導講師:
重吉
問題文全文(内容文):
A駅とB駅はまっすぐな線路で結ばれており、2つの駅は3.6km離れています。太郎さんは自転車でA駅を9時ちょうどに出発し、線路に沿った道をB駅に向かって分速150mで進みました。すると、9時4分に、B駅を9時ちょうどに出発した電車の先頭とすれ違いました。その後、太郎さんはすぐに速さを変えて進み、9時10分に、次にB駅から来た電車の先頭とすれ違いました。太郎さんはそのままの速さで進み、9時16分にB駅に到着しました。
2本の電車は同じ速さで進むものとしたとき、次の問いに答えなさい。
(1)電車の速さは分速何mですか。
(2)太郎さんが9時4分に電車の先頭とすれ違った後の、自転車の速さは分速何mですか。
(3)太郎さんが9時10分にすれ違った電車は、9時何分にB駅を出発しましたか。
1辺が1cmの立方体を125個すきまなくぴったりと貼り合わせて、1辺が5cmの立方体を作りました。
この立方体について、次の問いに答えなさい。
(1)1辺が5cmの立方体から、図1にある色の塗られた部分を、それぞれ反対側の面までまっすぐくり抜きます。このとき、くり抜かれた後に残る立体の体積を求めなさい。
(2)1辺が5cmの立方体から、図2にある色の塗られた部分を、それぞれ反対側の面までまっすぐくり抜きます。このとき、くり抜かれた後に残る立体の体積を求めなさい。
※図は動画内参照
この動画を見る
A駅とB駅はまっすぐな線路で結ばれており、2つの駅は3.6km離れています。太郎さんは自転車でA駅を9時ちょうどに出発し、線路に沿った道をB駅に向かって分速150mで進みました。すると、9時4分に、B駅を9時ちょうどに出発した電車の先頭とすれ違いました。その後、太郎さんはすぐに速さを変えて進み、9時10分に、次にB駅から来た電車の先頭とすれ違いました。太郎さんはそのままの速さで進み、9時16分にB駅に到着しました。
2本の電車は同じ速さで進むものとしたとき、次の問いに答えなさい。
(1)電車の速さは分速何mですか。
(2)太郎さんが9時4分に電車の先頭とすれ違った後の、自転車の速さは分速何mですか。
(3)太郎さんが9時10分にすれ違った電車は、9時何分にB駅を出発しましたか。
1辺が1cmの立方体を125個すきまなくぴったりと貼り合わせて、1辺が5cmの立方体を作りました。
この立方体について、次の問いに答えなさい。
(1)1辺が5cmの立方体から、図1にある色の塗られた部分を、それぞれ反対側の面までまっすぐくり抜きます。このとき、くり抜かれた後に残る立体の体積を求めなさい。
(2)1辺が5cmの立方体から、図2にある色の塗られた部分を、それぞれ反対側の面までまっすぐくり抜きます。このとき、くり抜かれた後に残る立体の体積を求めなさい。
※図は動画内参照
2024年広尾学園中算数大問①(1)~(6)中学受験指導歴20年以上のプロ解説

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#規則性(周期算・方陣算・数列・日暦算・N進法)#文章題#単位・比と割合・比例・反比例#平面図形#角度と面積#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ
指導講師:
重吉
問題文全文(内容文):
※図は動画内参照
(1) 次の計算をしなさい。
$253\div8+25.3\times3.25+11\times2.3\times5.5$
(2) $\dfrac{1}{1+\dfrac{1}{\boxed{ ア }+\dfrac{1}{\boxed{ イ }}}}=\dfrac{3}{5}$ となるように、$\boxed{ ア }$、$\boxed{ イ }$に当てはまる整数を求めなさい。
(3) 広尾小学校のある学年で、算数と国語についてそれぞれ「好きか、好きではないか」のどちらかについて調査をしました。調査の結果、算数が好きな児童の数は学年全体の人数の$\dfrac{1}{3}$、国語が好きな児童の数は学年全体の人数の$\dfrac{2}{5}$、算数も国語も好きな児童の数は算数の好きな児童の数の$\dfrac{3}{10}$であり、算数も国語も好きではない児童の数は44人でした。算数も国語も好きな児童の数を求めなさい。
(4) 時計の長針と短針について、4時と5時の間で長針と短針が反対向きに一直線になるときの時刻は4時何分か求めなさい。
(5) 右の図は、正方形の図の中に同じ大きさの四分円を4つ描いた図です。斜線部分の面積を求めなさい。ただし円周率は3.14とします。
(6) 図1のような長方形があり、上、正面、横の面をそれぞれ面ア、面イ、面ウとします。面ア、面イにそれぞれ平行な面でこの直方体を切断すると、できた4つの直方体の表面積の合計は、もとの直方体の表面積よりも1400 ㎠大きくなります(図2)。同様に面イと面ウにそれぞれ平行な面で切断すると、できた4つの直方体の表面積の表面積の合計は、もとの直方体の表面積よりも1000 ㎠大きくなり、面アと面ウにそれぞれ平行な面で切断すると、もとの直方体の表面積よりも1200 ㎠大きくなります。もとの直方体の表面積を求めなさい。
この動画を見る
※図は動画内参照
(1) 次の計算をしなさい。
$253\div8+25.3\times3.25+11\times2.3\times5.5$
(2) $\dfrac{1}{1+\dfrac{1}{\boxed{ ア }+\dfrac{1}{\boxed{ イ }}}}=\dfrac{3}{5}$ となるように、$\boxed{ ア }$、$\boxed{ イ }$に当てはまる整数を求めなさい。
(3) 広尾小学校のある学年で、算数と国語についてそれぞれ「好きか、好きではないか」のどちらかについて調査をしました。調査の結果、算数が好きな児童の数は学年全体の人数の$\dfrac{1}{3}$、国語が好きな児童の数は学年全体の人数の$\dfrac{2}{5}$、算数も国語も好きな児童の数は算数の好きな児童の数の$\dfrac{3}{10}$であり、算数も国語も好きではない児童の数は44人でした。算数も国語も好きな児童の数を求めなさい。
(4) 時計の長針と短針について、4時と5時の間で長針と短針が反対向きに一直線になるときの時刻は4時何分か求めなさい。
(5) 右の図は、正方形の図の中に同じ大きさの四分円を4つ描いた図です。斜線部分の面積を求めなさい。ただし円周率は3.14とします。
(6) 図1のような長方形があり、上、正面、横の面をそれぞれ面ア、面イ、面ウとします。面ア、面イにそれぞれ平行な面でこの直方体を切断すると、できた4つの直方体の表面積の合計は、もとの直方体の表面積よりも1400 ㎠大きくなります(図2)。同様に面イと面ウにそれぞれ平行な面で切断すると、できた4つの直方体の表面積の表面積の合計は、もとの直方体の表面積よりも1000 ㎠大きくなり、面アと面ウにそれぞれ平行な面で切断すると、もとの直方体の表面積よりも1200 ㎠大きくなります。もとの直方体の表面積を求めなさい。
【改良版】立体の展開図のイメージ

福田の中学入試の算数007〜ラサール中学校2006年〜立体の平面による切り口の面積
単元:
#算数(中学受験)#過去問解説(学校別)#立体図形#立体切断#ラ・サール中学
指導講師:
福田次郎
問題文全文(内容文):
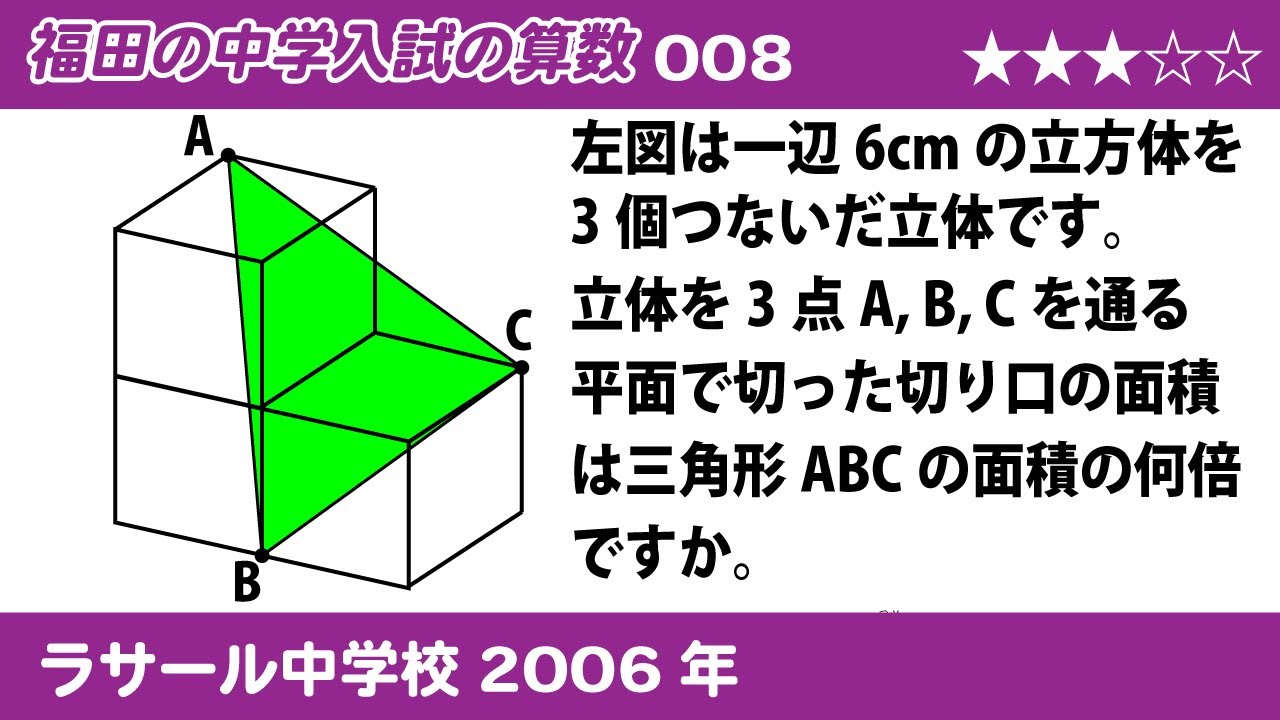
左図(動画参照)は一辺6cmの立方体を3個つないだ立体です。
立体を3点A,B,Cを通る平面で切った切り口の面積は三角形ABCの面積の何倍ですか。
この動画を見る
左図(動画参照)は一辺6cmの立方体を3個つないだ立体です。
立体を3点A,B,Cを通る平面で切った切り口の面積は三角形ABCの面積の何倍ですか。
【SPX小6算数手元解説】多面体を切る③【D-支援解説】

単元:
#算数(中学受験)#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ#立体図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
受験算数の森
問題文全文(内容文):
次の(ア)~(カ)に当てはまる数を求めなさい。
図1の立体は、20個の同じ大きさの正三角形で囲まれていて、どの頂点のまわりにも5個の正三角形が集まってできています。この立体は正二十面体と呼ばれています。正二十面体の頂点の個数は(ア)個、辺の本数は(イ)本あります。
次に正二十面体の各頂点から出ている5本の辺を図2のように、その1/3の長さのところで切り落としていくと、図3のような立体ができます。この立体には正六角形の面は(ウ)面、正五角形の面は(エ)面ありますから、この立体の辺の本数は(オ)本です。また、この立体の頂点の個数は(カ)個です。
この動画を見る
次の(ア)~(カ)に当てはまる数を求めなさい。
図1の立体は、20個の同じ大きさの正三角形で囲まれていて、どの頂点のまわりにも5個の正三角形が集まってできています。この立体は正二十面体と呼ばれています。正二十面体の頂点の個数は(ア)個、辺の本数は(イ)本あります。
次に正二十面体の各頂点から出ている5本の辺を図2のように、その1/3の長さのところで切り落としていくと、図3のような立体ができます。この立体には正六角形の面は(ウ)面、正五角形の面は(エ)面ありますから、この立体の辺の本数は(オ)本です。また、この立体の頂点の個数は(カ)個です。
【SPX小6算数手元解説】多面体を切る②【D-支援解説】

単元:
#算数(中学受験)#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ#立体図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
受験算数の森
問題文全文(内容文):
下図のように正八面体から各頂点に集まる4つの辺の真ん中の点を通る平面で、かどを切り取って1つの立体を作ります。この立体について、次の問いに答えなさい。
(1)この立体の面、辺、頂点の数はそれぞれいくつありますか
(2)この立体の体積もとの正八面体の何分のいくつになりますか。
この動画を見る
下図のように正八面体から各頂点に集まる4つの辺の真ん中の点を通る平面で、かどを切り取って1つの立体を作ります。この立体について、次の問いに答えなさい。
(1)この立体の面、辺、頂点の数はそれぞれいくつありますか
(2)この立体の体積もとの正八面体の何分のいくつになりますか。
【SPX小6算数手元解説】多面体を切る➀【D-支援解説】

単元:
#算数(中学受験)#立体図形#立体切断#体積・表面積・回転体・水量・変化のグラフ#立体図形その他
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
受験算数の森
問題文全文(内容文):
下図のように立方体から各頂点に集まる3つの辺の真ん中を通る平面で、かどを切り取って1つの立方体を作ります。この立体について、次の問いに答えなさい。
この動画を見る
下図のように立方体から各頂点に集まる3つの辺の真ん中を通る平面で、かどを切り取って1つの立方体を作ります。この立体について、次の問いに答えなさい。
福田の中学入試の算数001〜桜蔭中学校2005年〜立体の断面
単元:
#算数(中学受験)#立体図形#立体切断
指導講師:
福田次郎
問題文全文(内容文):
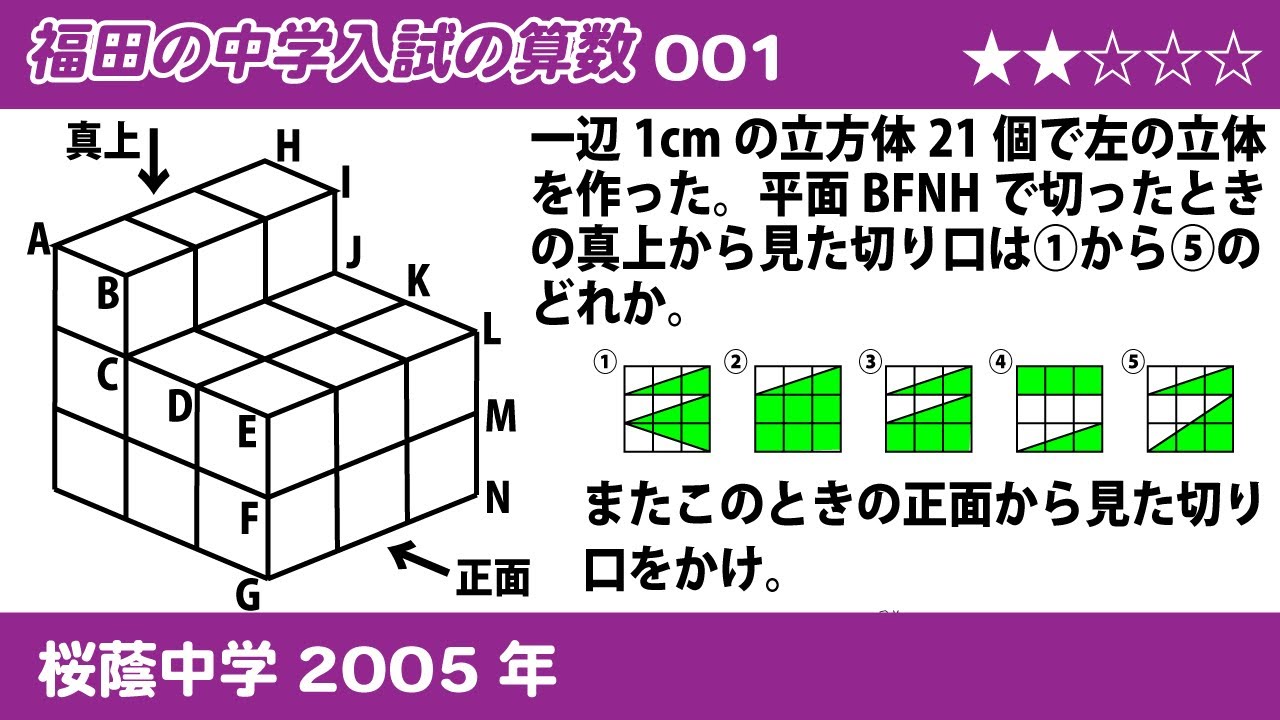
1辺が1 cmの立方体を21個使って下のような立体を作った。平面BFNHで切ったときの真上から見た切り口を①~⑤から選びなさい。またこのときの正面から見た切り口を図示してください。(※動画参照)
この動画を見る
1辺が1 cmの立方体を21個使って下のような立体を作った。平面BFNHで切ったときの真上から見た切り口を①~⑤から選びなさい。またこのときの正面から見た切り口を図示してください。(※動画参照)
福田のおもしろ数学045〜これができたら切断のプロ〜立方体の切断
単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#立体図形#立体切断
指導講師:
福田次郎
問題文全文(内容文):
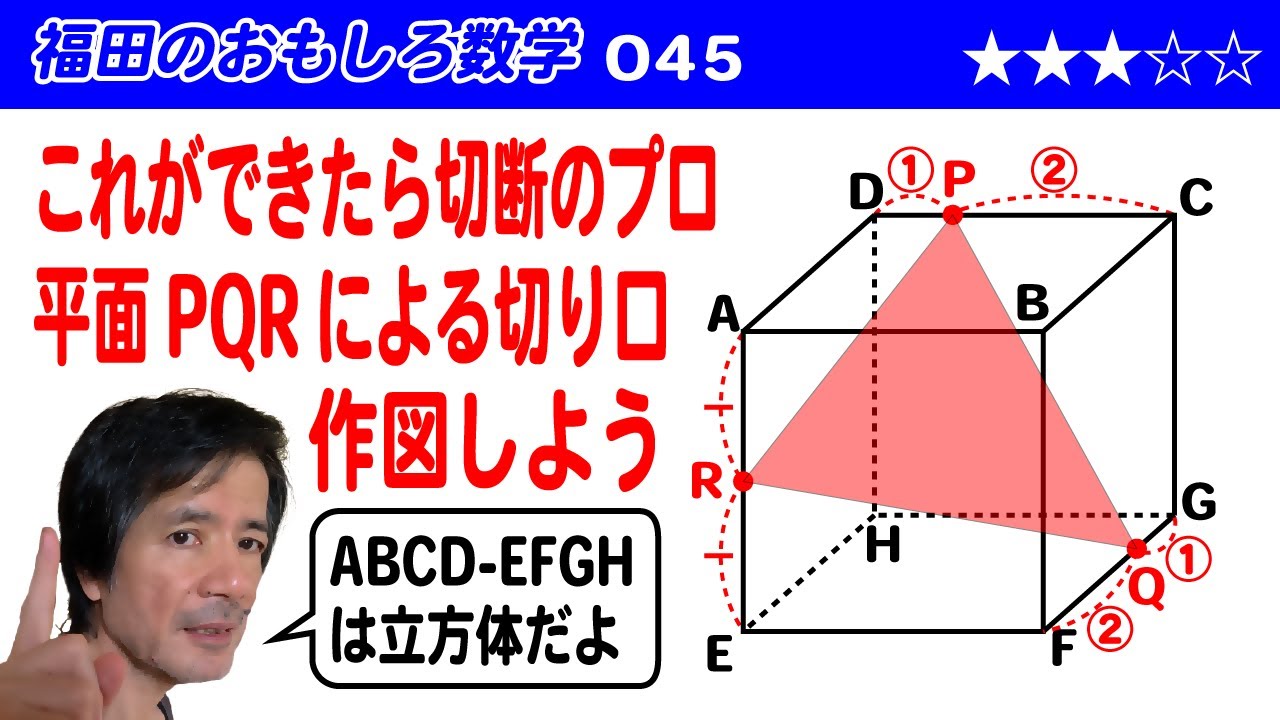
立方体 ABCD ー EFGH を 3 点 P , Q , R を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
この動画を見る
立方体 ABCD ー EFGH を 3 点 P , Q , R を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
福田のおもしろ数学041〜立体の切断〜立方体を切った切り口
単元:
#算数(中学受験)#数学(中学生)#中1数学#空間図形#立体図形#立体切断
指導講師:
福田次郎
問題文全文(内容文):
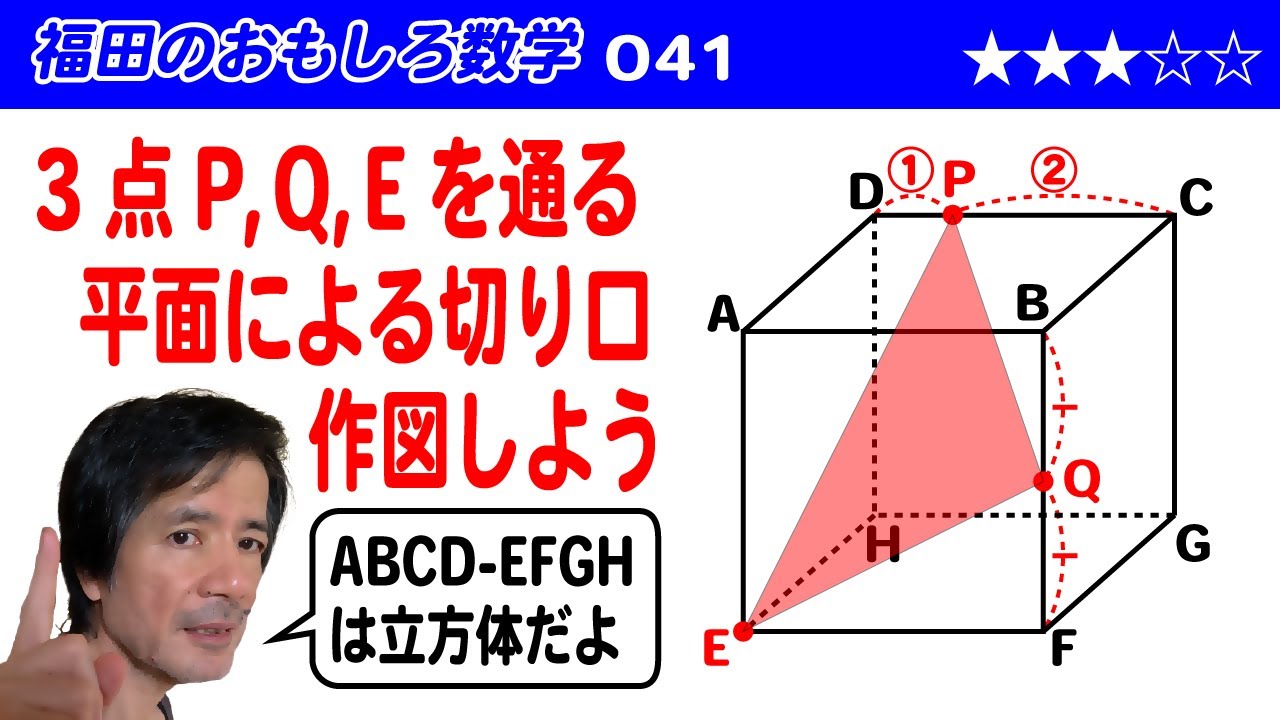
立方体 ABCD-EFGH を 3 点 P,Q,E を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
この動画を見る
立方体 ABCD-EFGH を 3 点 P,Q,E を通る平面で切ったときの切り口を作図せよ。
※図は動画内参照
福田の数学〜上智大学2023年TEAP利用型理系第2問〜立方体の切断と位置ベクトル

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#立体図形#立体切断#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 一辺の長さが2である立方体OADB-CFGEを考える。
$\overrightarrow{OA}$=$\overrightarrow{a}$, $\overrightarrow{OB}$=$\overrightarrow{b}$, $\overrightarrow{OC}$=$\overrightarrow{c}$とおく。辺AFの中点をM、辺BDの中点をNとし、3点O,M,Nを通る平面$\pi$で立方体を切断する。
(1)平面$\pi$は辺AF,BD以外に辺$\boxed{\ \ あ\ \ }$とその両端以外で交わる。
(2)平面$\pi$と辺$\boxed{\ \ あ\ \ }$との交点をPとすると$\overrightarrow{OP}$=$\boxed{\ \ い\ \ } \overrightarrow{a}$+$\boxed{\ \ う\ \ } \overrightarrow{b}$+$\boxed{\ \ え\ \ } \overrightarrow{c}$
(3)断面の面積は$\displaystyle\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\sqrt{\boxed{\ \ ケ\ \ }}$である。
(4)切断されてできる立体のうち、頂点Aを含むものの体積は$\displaystyle\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
(5)平面$\pi$と線分CDとの交点をQとする。
(i)点Qは線分CDを$\boxed{\ \ お\ \ }$に内分する。
(ii)$\overrightarrow{OQ}$=$\boxed{\ \ か\ \ } \overrightarrow{a}$+$\boxed{\ \ き\ \ } \overrightarrow{b}$+$\boxed{\ \ く\ \ } \overrightarrow{c}$である。
$\boxed{\ \ い\ \ }~\boxed{\ \ え\ \ }$, $\boxed{\ \ か\ \ }~\boxed{\ \ く\ \ }$の選択肢
(a)0 (b)1 (c)$\frac{1}{2}$ (d)$\frac{1}{3}$ (e)$\frac{2}{3}$ (f)$\frac{1}{4}$ (g)$\frac{3}{4}$ (h)$\frac{1}{5}$
(i)$\frac{2}{5}$ (j)$\frac{3}{5}$ (k)$\frac{4}{5}$ (l)$\frac{1}{6}$ (m)$\frac{5}{6}$
$\boxed{\ \ お\ \ }$の選択肢
(a)1:1 (b)2:1 (c)1:2 (d)3:1 (e)1:3 (f)4:1 (g)3:2
(h)2:3 (i)1:4 (j)5:1 (k)1:5
この動画を見る
$\Large{\boxed{2}}$ 一辺の長さが2である立方体OADB-CFGEを考える。
$\overrightarrow{OA}$=$\overrightarrow{a}$, $\overrightarrow{OB}$=$\overrightarrow{b}$, $\overrightarrow{OC}$=$\overrightarrow{c}$とおく。辺AFの中点をM、辺BDの中点をNとし、3点O,M,Nを通る平面$\pi$で立方体を切断する。
(1)平面$\pi$は辺AF,BD以外に辺$\boxed{\ \ あ\ \ }$とその両端以外で交わる。
(2)平面$\pi$と辺$\boxed{\ \ あ\ \ }$との交点をPとすると$\overrightarrow{OP}$=$\boxed{\ \ い\ \ } \overrightarrow{a}$+$\boxed{\ \ う\ \ } \overrightarrow{b}$+$\boxed{\ \ え\ \ } \overrightarrow{c}$
(3)断面の面積は$\displaystyle\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}\sqrt{\boxed{\ \ ケ\ \ }}$である。
(4)切断されてできる立体のうち、頂点Aを含むものの体積は$\displaystyle\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。
(5)平面$\pi$と線分CDとの交点をQとする。
(i)点Qは線分CDを$\boxed{\ \ お\ \ }$に内分する。
(ii)$\overrightarrow{OQ}$=$\boxed{\ \ か\ \ } \overrightarrow{a}$+$\boxed{\ \ き\ \ } \overrightarrow{b}$+$\boxed{\ \ く\ \ } \overrightarrow{c}$である。
$\boxed{\ \ い\ \ }~\boxed{\ \ え\ \ }$, $\boxed{\ \ か\ \ }~\boxed{\ \ く\ \ }$の選択肢
(a)0 (b)1 (c)$\frac{1}{2}$ (d)$\frac{1}{3}$ (e)$\frac{2}{3}$ (f)$\frac{1}{4}$ (g)$\frac{3}{4}$ (h)$\frac{1}{5}$
(i)$\frac{2}{5}$ (j)$\frac{3}{5}$ (k)$\frac{4}{5}$ (l)$\frac{1}{6}$ (m)$\frac{5}{6}$
$\boxed{\ \ お\ \ }$の選択肢
(a)1:1 (b)2:1 (c)1:2 (d)3:1 (e)1:3 (f)4:1 (g)3:2
(h)2:3 (i)1:4 (j)5:1 (k)1:5
立方体はいくつ切られるか問題の簡単な解き方!【図形問題基礎講座41】

単元:
#算数(中学受験)#立体図形#立体切断
指導講師:
こばちゃん塾
問題文全文(内容文):
例1 下図の立体に、真正面、真横、真上から、真向いの面までまっすぐ穴をあけたとき、穴のあいた立方体は何個?
例2 下図の立体をA,B,Cを通る平面で切断したとき、切断される立方体はいくつ?
単元卒業テスト
右図のように同じ大きさの立方体を27個積み上げて作った立体を3点A,B,Cを通過する平面で切断しました。
このとき、切断される立方体の個数は全部で何個?
*図は動画内参照
この動画を見る
例1 下図の立体に、真正面、真横、真上から、真向いの面までまっすぐ穴をあけたとき、穴のあいた立方体は何個?
例2 下図の立体をA,B,Cを通る平面で切断したとき、切断される立方体はいくつ?
単元卒業テスト
右図のように同じ大きさの立方体を27個積み上げて作った立体を3点A,B,Cを通過する平面で切断しました。
このとき、切断される立方体の個数は全部で何個?
*図は動画内参照
【立方体の切断】をこれ一本で完全攻略!!解き方・演習・全パターン紹介!正直永久保存版の内容です【中学受験算数】

単元:
#算数(中学受験)#立体図形#立体切断
指導講師:
こばちゃん塾
問題文全文(内容文):
例1 下図の立方体をA,B,Cを通る平面で切断した断面の形は?
例2 下図の立方体をA,P,Gを通る平面で切断した断面の形は?
単元卒業テスト
下図の立方体で3点A,P,Gを通る平面で切断したとき、平面と辺BFの交点をRとすると、BRは何㎝?
*図は動画内参照
この動画を見る
例1 下図の立方体をA,B,Cを通る平面で切断した断面の形は?
例2 下図の立方体をA,P,Gを通る平面で切断した断面の形は?
単元卒業テスト
下図の立方体で3点A,P,Gを通る平面で切断したとき、平面と辺BFの交点をRとすると、BRは何㎝?
*図は動画内参照
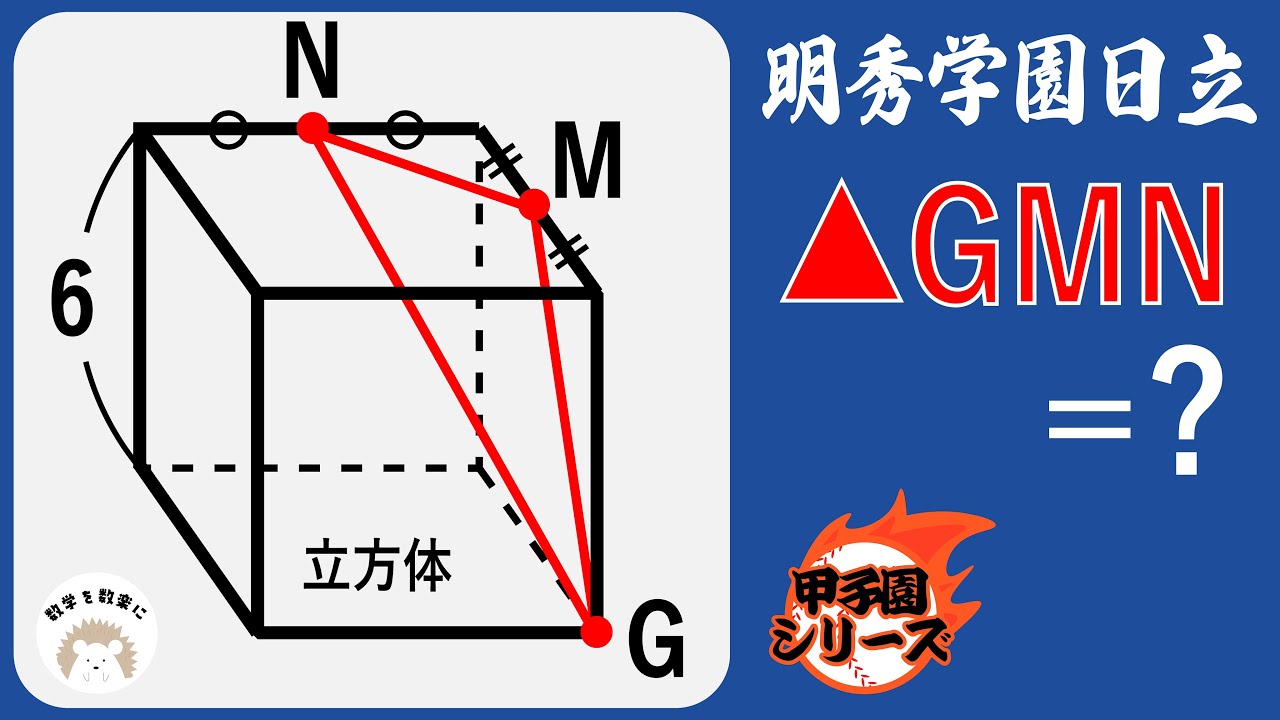
立方体の中の三角形の面積を求める 明秀学園日立高校(茨城)
単元:
#数学(中学生)#中2数学#立体図形#立体切断#立体図形その他#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△GMN=?
*図は動画内参照
明秀学園日立高等学校
この動画を見る
△GMN=?
*図は動画内参照
明秀学園日立高等学校
立方体の3点切断 聖望学園(埼玉)
単元:
#数学(中学生)#立体図形#立体切断#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
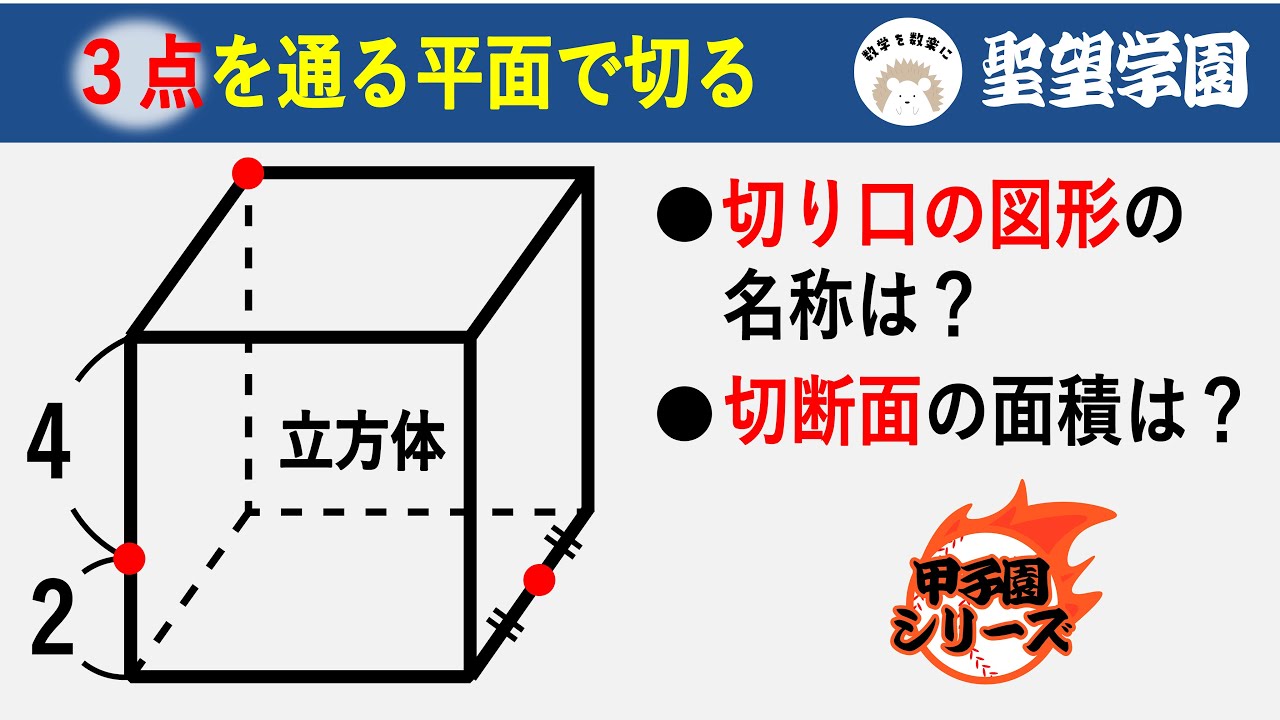
3点を通る平面で切る
・切り口の図形の名称は?
・切断面の面積は?
*図は動画内参照
聖望学園高等学校
この動画を見る
3点を通る平面で切る
・切り口の図形の名称は?
・切断面の面積は?
*図は動画内参照
聖望学園高等学校
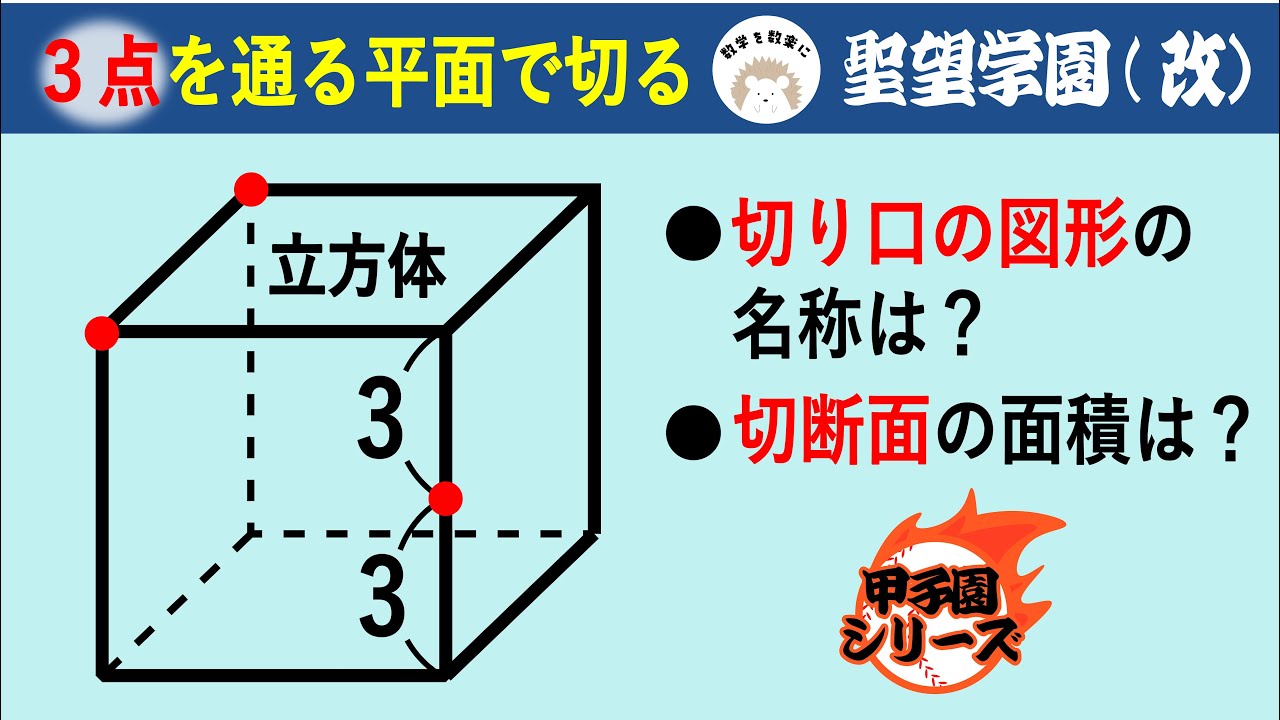
立方体の3点切断 聖望学園(改)
単元:
#数学(中学生)#立体図形#立体切断#立体図形その他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
3点を通る平面で切る
・切り口の図形の名称は?
・切断面の面積は?
*図は動画内参照
聖望学園高等学校
この動画を見る
3点を通る平面で切る
・切り口の図形の名称は?
・切断面の面積は?
*図は動画内参照
聖望学園高等学校
【受験算数】立体切断演習問題その17「断面部の体積を求める問題7」
単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
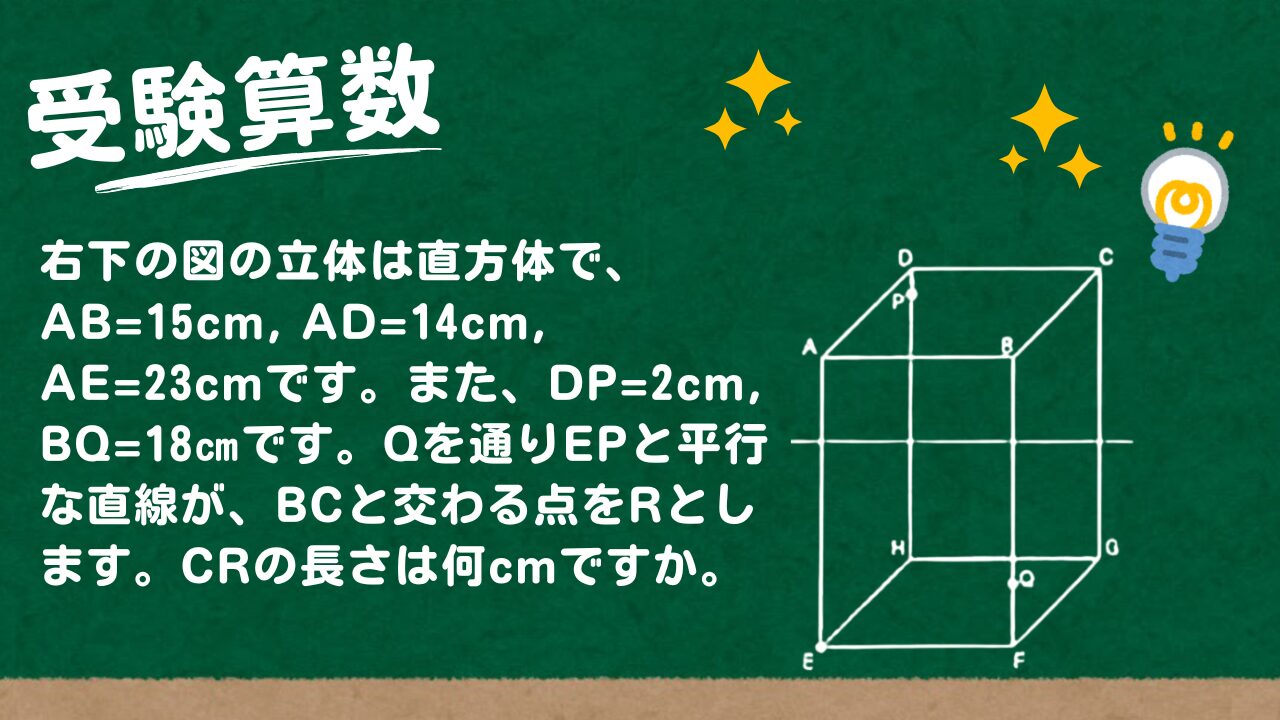
右下の図の立体は直方体で、AB=15cm, AD=14cm, AE=23cmです。また、DP=2cm, BQ=18㎝です。
(1) Qを通りEPと平行な直線が、BCと交わる点をRとします。CRの長さは何cmですか。
(2) Pを通りEQと平行な直線が、CDと交わる点をSとします。CSの長さは何cmですか。
(3) PSをSの方向へ延長した直線が、GCをCの方向へ延長した直線と交わる点をTとします。CTの長さは何cmですか。
この動画を見る
右下の図の立体は直方体で、AB=15cm, AD=14cm, AE=23cmです。また、DP=2cm, BQ=18㎝です。
(1) Qを通りEPと平行な直線が、BCと交わる点をRとします。CRの長さは何cmですか。
(2) Pを通りEQと平行な直線が、CDと交わる点をSとします。CSの長さは何cmですか。
(3) PSをSの方向へ延長した直線が、GCをCの方向へ延長した直線と交わる点をTとします。CTの長さは何cmですか。
【受験算数】立体切断演習問題その16「断面部の体積を求める問題6」
単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
立体切断演習問題その16
61-16(体積を求める④ー1)
この動画を見る
立体切断演習問題その16
61-16(体積を求める④ー1)
【受験算数】立体切断演習問題その15「断面部の体積を求める問題5」
単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
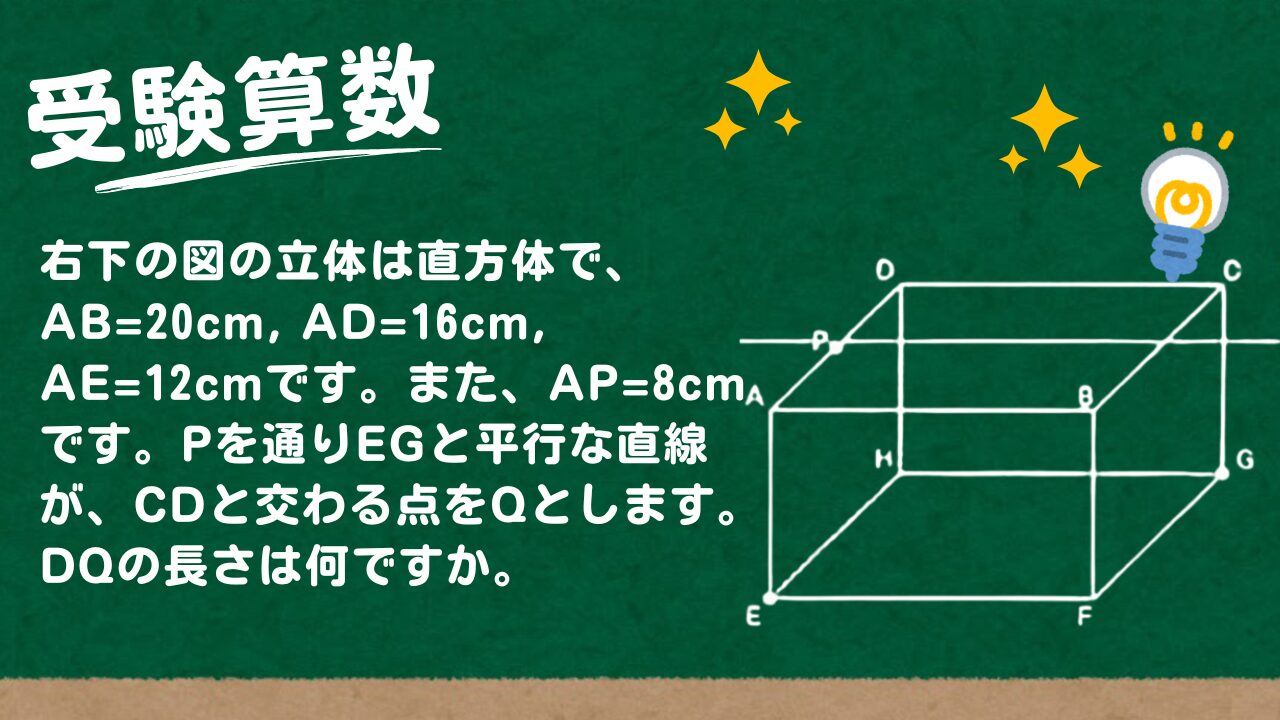
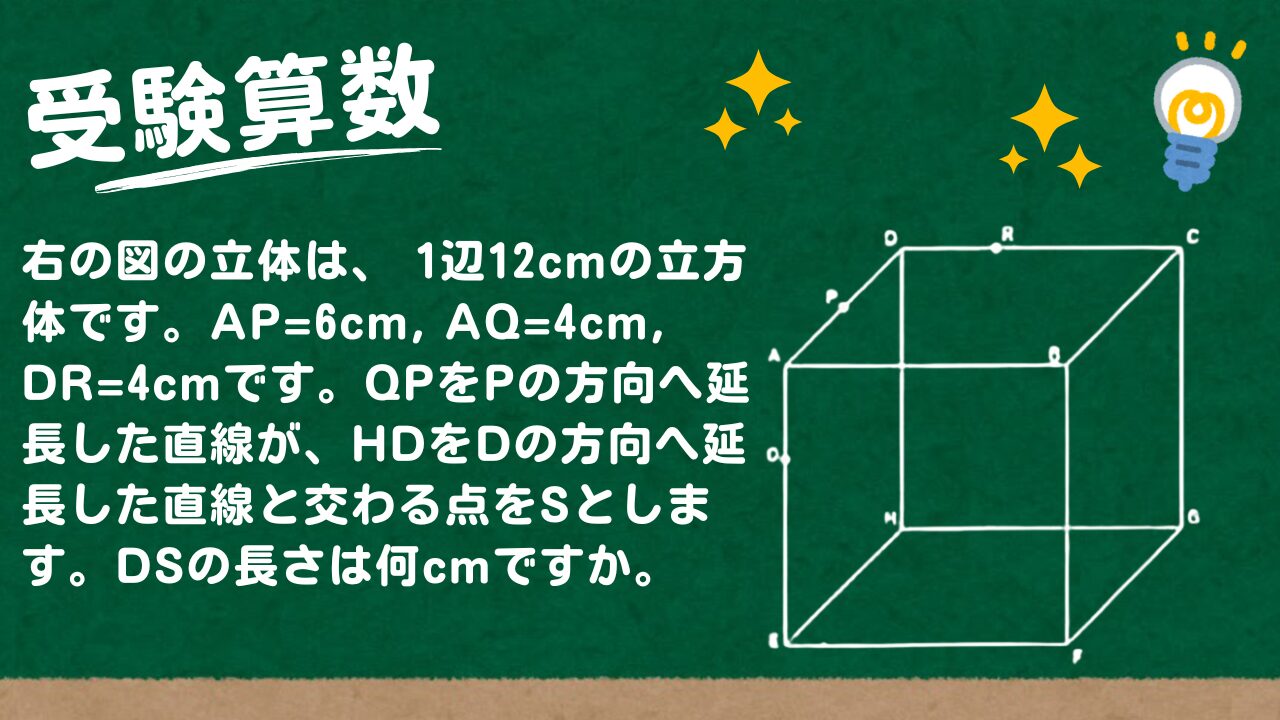
右の図の立体は、 1辺12cmの立方体です。AP=6cm, AQ=4cm, DR=4cmです。
(1) QPをPの方向へ延長した直線が、HDをDの方向へ延長した直線と交わる点をSとします。DSの長さは何cmですか。
(2) SRをRの方向へ延長した直線が、CGと交わる点をTとします。GTの長さは何cmですか。
(3) Tを通りPQと平行な直線が、GFと交わる点をUとします。GUの長さは何cmですか。
(4) Uを通りRPと平行な直線が、EFと交わる点をVとします。EVの長さは何cmですか。
この動画を見る
右の図の立体は、 1辺12cmの立方体です。AP=6cm, AQ=4cm, DR=4cmです。
(1) QPをPの方向へ延長した直線が、HDをDの方向へ延長した直線と交わる点をSとします。DSの長さは何cmですか。
(2) SRをRの方向へ延長した直線が、CGと交わる点をTとします。GTの長さは何cmですか。
(3) Tを通りPQと平行な直線が、GFと交わる点をUとします。GUの長さは何cmですか。
(4) Uを通りRPと平行な直線が、EFと交わる点をVとします。EVの長さは何cmですか。
【受験算数】立体切断演習問題その14「断面部の体積を求める問題4」
単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
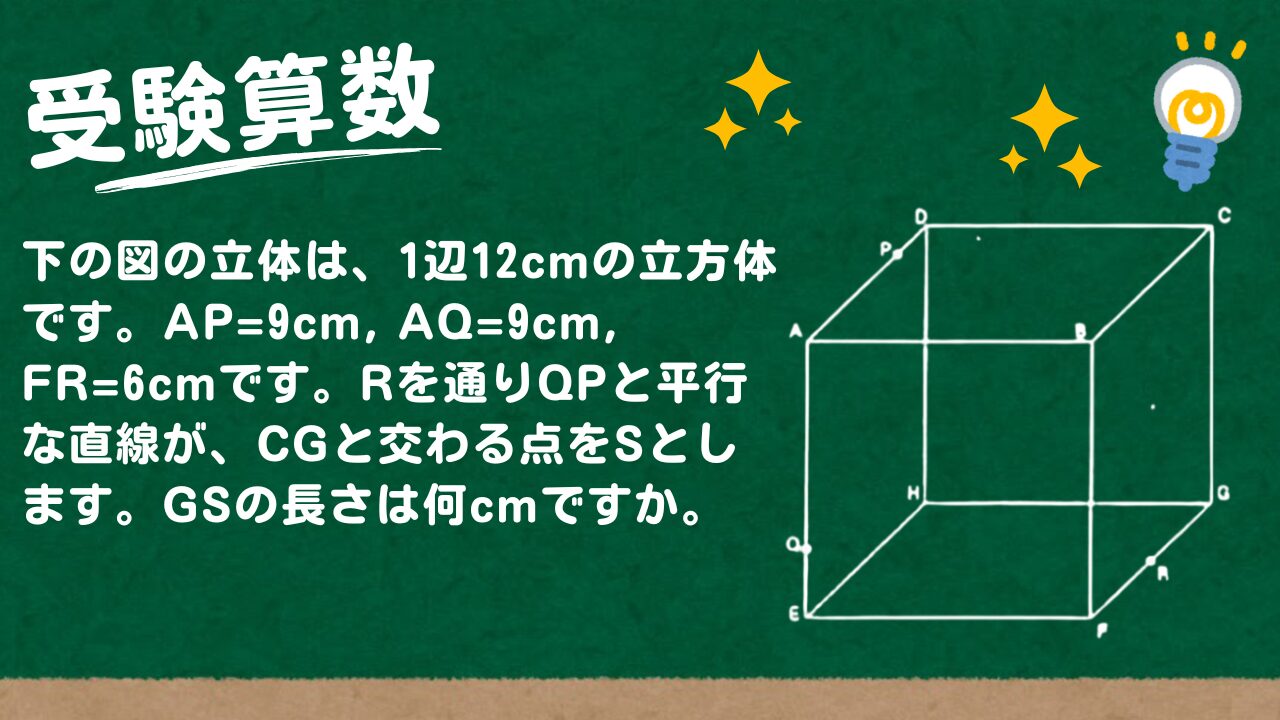
下の図の立体は、1辺12cmの立方体です。AP=9cm, AQ=9cm, FR=6cmです。
(1) Rを通りQPと平行な直線が、CGと交わる点をSとします。GSの長さは何cmですか。
(2) PQをQの方向へ延長した直線が、HEをEの方向へ延長した直線と交わる点をTとします。ETの長さは何cmですか。
(3) TRがEFと交わる点をUとします。EUの長さは何cmですか。
(4) Pを通りTUと平行な直線が、CDと交わる点をVとします。DVの長さは何cmですか。
この動画を見る
下の図の立体は、1辺12cmの立方体です。AP=9cm, AQ=9cm, FR=6cmです。
(1) Rを通りQPと平行な直線が、CGと交わる点をSとします。GSの長さは何cmですか。
(2) PQをQの方向へ延長した直線が、HEをEの方向へ延長した直線と交わる点をTとします。ETの長さは何cmですか。
(3) TRがEFと交わる点をUとします。EUの長さは何cmですか。
(4) Pを通りTUと平行な直線が、CDと交わる点をVとします。DVの長さは何cmですか。
【受験算数】立体切断演習問題その13「断面部の体積を求める問題3」
単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
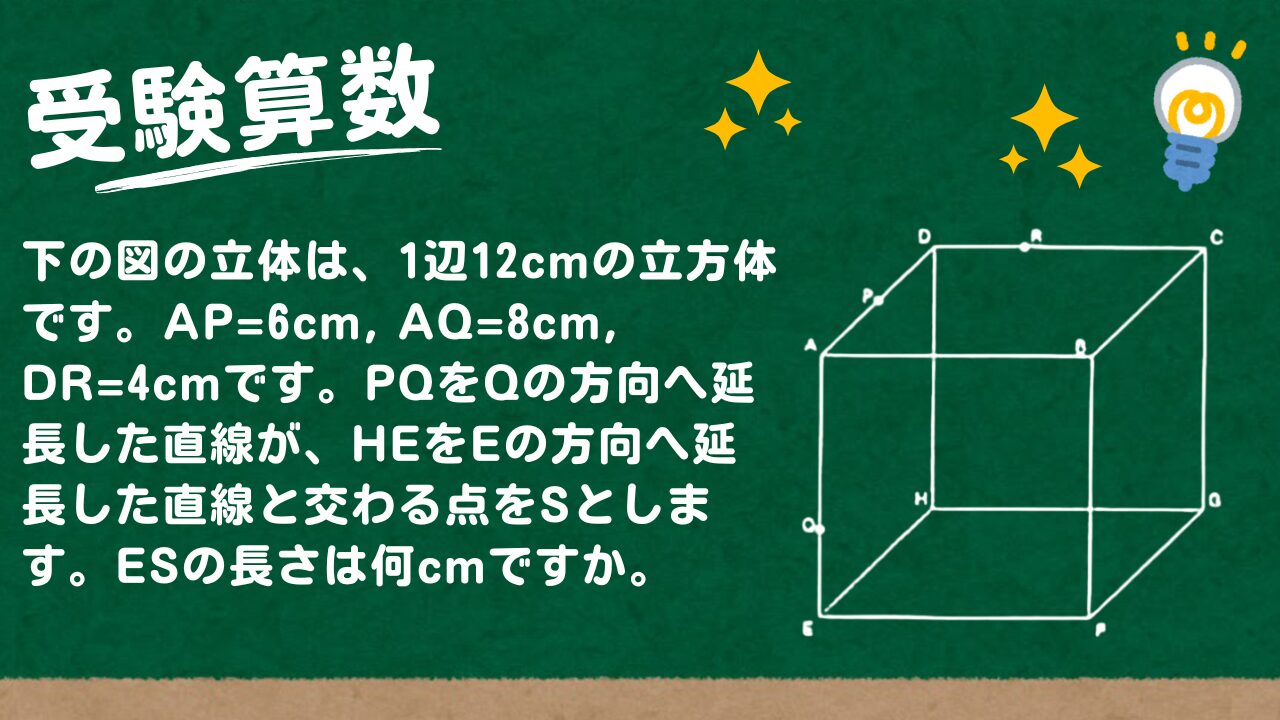
下の図の立体は、1辺12cmの立方体です。AP=6cm, AQ=8cm, DR=4cmです。
(I) PQをQの方向へ延長した直線が、HEをEの方向へ延長した直線と交わる点をSとします。ESの長さは何cmですか。
(2) QPをPの方向へ延長した直線が、HDをDの方向へ延長した直線と交わる点をTとします。DTの長さは何cmですか。
(3) TRをRの方向へ延長した直線が、GHと交わる点をUとします。HUの長さは何cmですか。
(4) この立方体を3つの点P, Q, Rを過る平面で切断してできる立体のうち、 点Hをふくむ立体の体積は何㎤ですか。
この動画を見る
下の図の立体は、1辺12cmの立方体です。AP=6cm, AQ=8cm, DR=4cmです。
(I) PQをQの方向へ延長した直線が、HEをEの方向へ延長した直線と交わる点をSとします。ESの長さは何cmですか。
(2) QPをPの方向へ延長した直線が、HDをDの方向へ延長した直線と交わる点をTとします。DTの長さは何cmですか。
(3) TRをRの方向へ延長した直線が、GHと交わる点をUとします。HUの長さは何cmですか。
(4) この立方体を3つの点P, Q, Rを過る平面で切断してできる立体のうち、 点Hをふくむ立体の体積は何㎤ですか。
【受験算数】立体切断演習問題その12「断面部の体積を求める問題2」
単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
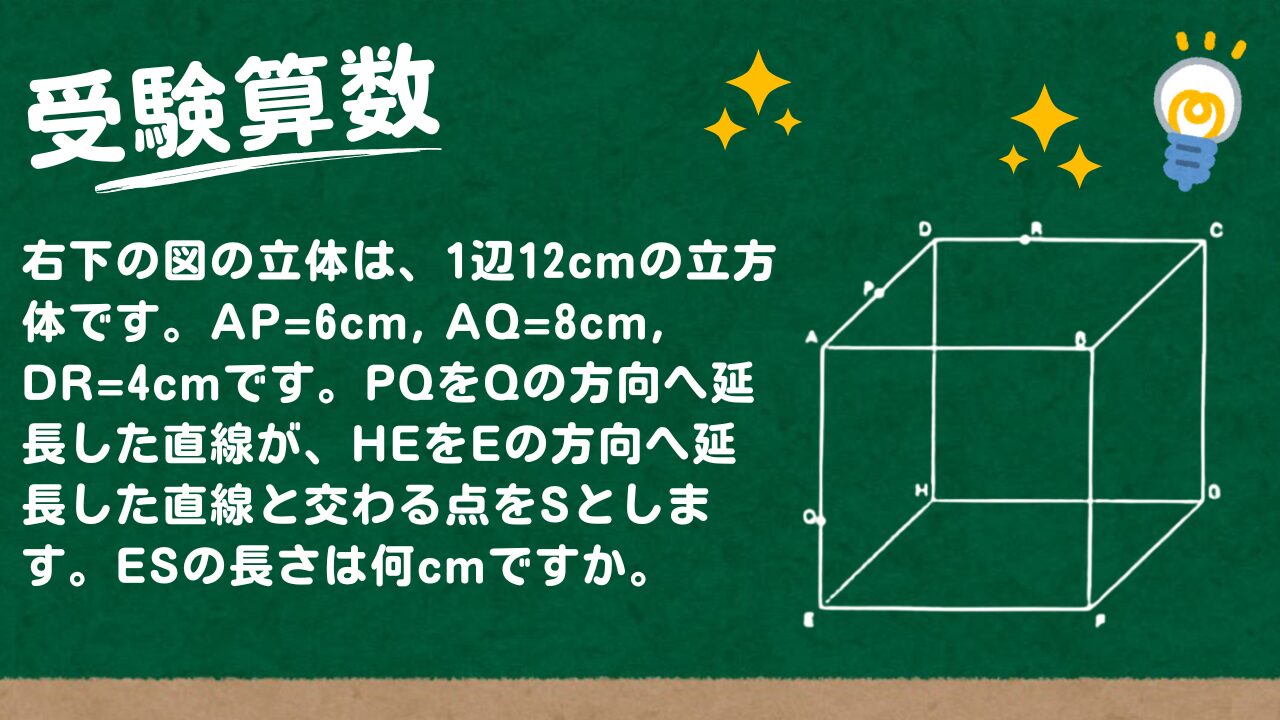
右下の図の立体は、1辺12cmの立方体です。AP=6cm, AQ=8cm, DR=4cmです。
PQをQの方向へ延長した直線が、HEをEの方向へ延長した直線と交わる点をSとします。ESの長さは何cmですか。
この動画を見る
右下の図の立体は、1辺12cmの立方体です。AP=6cm, AQ=8cm, DR=4cmです。
PQをQの方向へ延長した直線が、HEをEの方向へ延長した直線と交わる点をSとします。ESの長さは何cmですか。
【受験算数】立体切断演習問題その11「断面部の体積を求める問題1」
単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
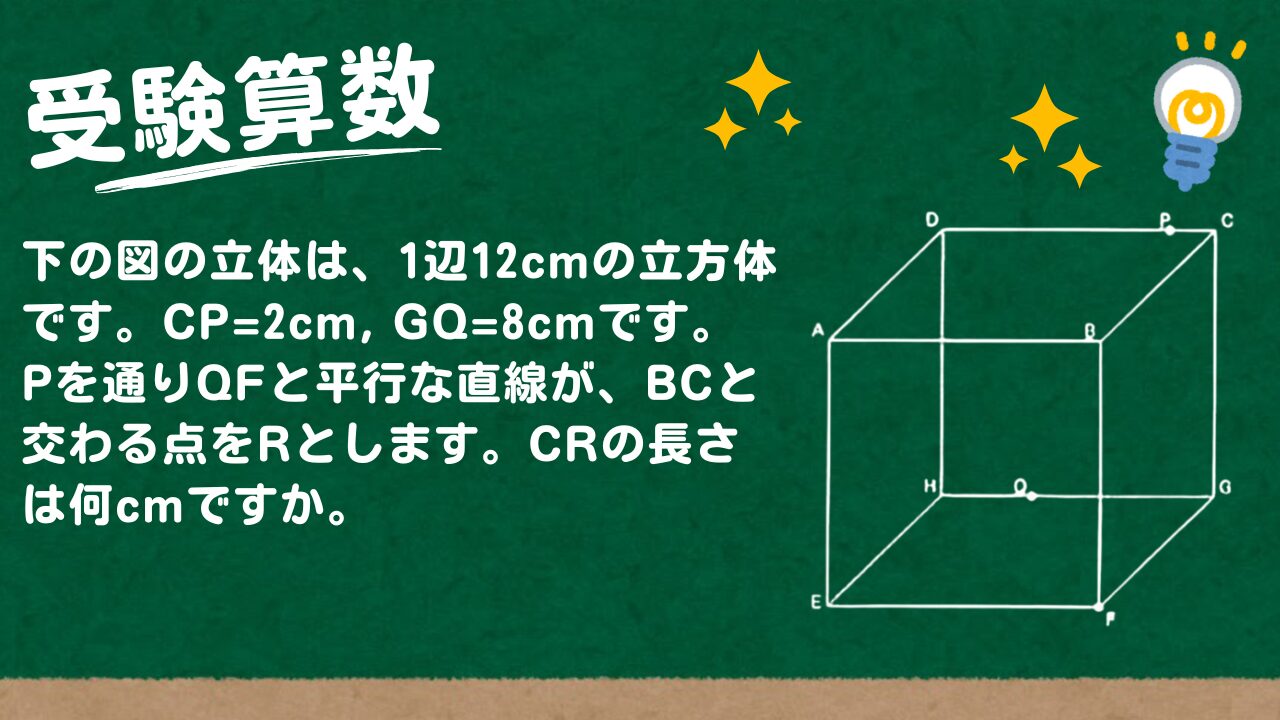
下の図の立体は、1辺12cmの立方体です。CP=2cm, GQ=8cmです。
Pを通りQFと平行な直線が、BCと交わる点をRとします。CRの長さは何cmですか。
この動画を見る
下の図の立体は、1辺12cmの立方体です。CP=2cm, GQ=8cmです。
Pを通りQFと平行な直線が、BCと交わる点をRとします。CRの長さは何cmですか。
【受験算数】立体切断演習問題その10「切断面が複雑になる問題4」

単元:
#算数(中学受験)#立体図形#立体切断
教材:
#SPX#6年算数W-支援#中学受験教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
下の図1から図5の立体は、すべて立方体です。図の辺上にある・は、すべてそれぞれの辺を4等分する点のうちの1つです。図1から図5の斜線部分について、 それぞれの立方体をある1つの平面で切断したときの切断面としてありえる場合には、その切断面の形として最もふさわしい図形の名前を答えなさい。切断面としてありえない場合には、「×」と答えなさい。
この動画を見る
下の図1から図5の立体は、すべて立方体です。図の辺上にある・は、すべてそれぞれの辺を4等分する点のうちの1つです。図1から図5の斜線部分について、 それぞれの立方体をある1つの平面で切断したときの切断面としてありえる場合には、その切断面の形として最もふさわしい図形の名前を答えなさい。切断面としてありえない場合には、「×」と答えなさい。
