 京都大学
京都大学
 京都大学
京都大学
福田の数学〜京都大学2023年理系第5問〜回転体の体積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ Oを原点とするxyz空間において、点Pと点Qは次の3つの条件(a),(b),(c)を満たしている。
(a):点Pはx軸上にある。
(b):点Qはyz平面上にある。
(c):線分OPと線分OQの長さの和は1である。
点Pと点Qが条件(a),(b),(c)を満たしながらくまなく動くとき、線分PQが通過してできる立体の体積を求めよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{5}$ Oを原点とするxyz空間において、点Pと点Qは次の3つの条件(a),(b),(c)を満たしている。
(a):点Pはx軸上にある。
(b):点Qはyz平面上にある。
(c):線分OPと線分OQの長さの和は1である。
点Pと点Qが条件(a),(b),(c)を満たしながらくまなく動くとき、線分PQが通過してできる立体の体積を求めよ。
2023京都大学理系過去問
福田の数学〜京都大学2023年理系第4問〜複雑な関数の最大値と最小値

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 次の関数f(x)の最大値と最小値を求めよ。
f(x)=$e^{-x^2}$+$\frac{1}{4}x^2$+1+$\frac{1}{e^{-x^2}+\frac{1}{4}x^2+1}$ (-1≦x≦1)
ただし、eは自然対数の底であり、その値はe=2.71...である。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{4}$ 次の関数f(x)の最大値と最小値を求めよ。
f(x)=$e^{-x^2}$+$\frac{1}{4}x^2$+1+$\frac{1}{e^{-x^2}+\frac{1}{4}x^2+1}$ (-1≦x≦1)
ただし、eは自然対数の底であり、その値はe=2.71...である。
2023京都大学理系過去問
福田の数学〜京都大学2023年理系第3問〜サイコロの目の積が15で割り切れる確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
nを自然数とする。 1個のさいころをn回投げ、出た目を順に$X_1,X_2,…,X_n$とし、
n個の数の積$X_1X_2…X_n$をYとする。
(1)Yが5で割り切れる確率を求めよ。
(2)Yが15で割り切れる確率を求めよ。
2023京都大学理系過去問
この動画を見る
nを自然数とする。 1個のさいころをn回投げ、出た目を順に$X_1,X_2,…,X_n$とし、
n個の数の積$X_1X_2…X_n$をYとする。
(1)Yが5で割り切れる確率を求めよ。
(2)Yが15で割り切れる確率を求めよ。
2023京都大学理系過去問
福田の数学〜京都大学2023年理系第2問〜空間の位置ベクトルと直線のベクトル方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#空間ベクトル#剰余の定理・因数定理・組み立て除法と高次方程式#空間ベクトル#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 空間内の4点O,A,B,Cは同一平面上にないとする。点D,P,Qを次のように定める。点Dは$\overrightarrow{OD}$=$\overrightarrow{OA}$+$2\overrightarrow{OB}$+$3\overrightarrow{OC}$を満たし、点Pは線分OAを1:2に内分し、点Qは線分OBの中点である。さらに、直線OD上の点Rを、直線QRと直線PCが交点を持つように定める。このとき、線分ORの長さと線分RDの長さの比OR:RDを求めよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{2}$ 空間内の4点O,A,B,Cは同一平面上にないとする。点D,P,Qを次のように定める。点Dは$\overrightarrow{OD}$=$\overrightarrow{OA}$+$2\overrightarrow{OB}$+$3\overrightarrow{OC}$を満たし、点Pは線分OAを1:2に内分し、点Qは線分OBの中点である。さらに、直線OD上の点Rを、直線QRと直線PCが交点を持つように定める。このとき、線分ORの長さと線分RDの長さの比OR:RDを求めよ。
2023京都大学理系過去問
福田の数学〜京都大学2023年理系第1問(2)〜整式の割り算と余り

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 問2 整式$x^{2023}$-1 を整式$x^4$+$x^3$+$x^2$+$x$+1 で割った時の余りを求めよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{1}$ 問2 整式$x^{2023}$-1 を整式$x^4$+$x^3$+$x^2$+$x$+1 で割った時の余りを求めよ。
2023京都大学理系過去問
福田の数学〜京都大学2023年理系第1問(1)〜定積分の計算

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
今回は京都大学2023年理系第1問(1)。定積分の計算の問題。
$\int_1^4 \sqrt{x}\log (x^2)dx$を求めよ
2023京都大学理系過去問
この動画を見る
今回は京都大学2023年理系第1問(1)。定積分の計算の問題。
$\int_1^4 \sqrt{x}\log (x^2)dx$を求めよ
2023京都大学理系過去問
【積分】2023年京大数学!絶対に落としてはいけない問題です【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
定積分 $\displaystyle \int_{1}^{4}\sqrt{x}\log(x^{2})dx$の値を求めよ。
京都大過去問
この動画を見る
定積分 $\displaystyle \int_{1}^{4}\sqrt{x}\log(x^{2})dx$の値を求めよ。
京都大過去問
2023年京大数学!整式の割り算!2通りで解説します【京都大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
整式$x^{2023}-1$を整式$x^{4}+x^{3}+x^{2}+x+1$で割ったときの余りを求めよ。
京都大過去問
この動画を見る
整式$x^{2023}-1$を整式$x^{4}+x^{3}+x^{2}+x+1$で割ったときの余りを求めよ。
京都大過去問
2023年京大の数学!最大値・最小値【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
次の関数$f(x)$の最大値と最小値を求めよ。
$f(x)=e^{-x^{2}}+\dfrac{1}{4}x^{2}+1+\dfrac{1}{e^{-x^{2}}+\dfrac{1}{4}x^{2}+1}$ $(-1≦x≦1)$
ただし、$e$は自然対数の底であり、その値は$e=2.71・・・$である。
2023京都大過去問
この動画を見る
次の関数$f(x)$の最大値と最小値を求めよ。
$f(x)=e^{-x^{2}}+\dfrac{1}{4}x^{2}+1+\dfrac{1}{e^{-x^{2}}+\dfrac{1}{4}x^{2}+1}$ $(-1≦x≦1)$
ただし、$e$は自然対数の底であり、その値は$e=2.71・・・$である。
2023京都大過去問
気持ちいい別解あり!これ解ける?【京都大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a,b,c$を正の数とするとき、不等式
$2\left( -\frac{a+b}{2}-\sqrt{ab}\right)≦3\left(\frac{a+b+c}{2}-\sqrt[3]{abc}\right)$
を証明せよ。
また、等号が成立するのはどんな場合か。
京都大過去問
この動画を見る
$a,b,c$を正の数とするとき、不等式
$2\left( -\frac{a+b}{2}-\sqrt{ab}\right)≦3\left(\frac{a+b+c}{2}-\sqrt[3]{abc}\right)$
を証明せよ。
また、等号が成立するのはどんな場合か。
京都大過去問
【合格体験記】京大法学部に現役合格した篠原塾卒業生と対談

2023京都大学 整式の剰余

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2023}-1$を$x^4+x^3+x^2+x+1$で割ったあまりを求めよ.
2023京都大過去問
この動画を見る
$x^{2023}-1$を$x^4+x^3+x^2+x+1$で割ったあまりを求めよ.
2023京都大過去問
2023京都大学 3乗根の分母の有理化

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
分母を有利化せよ.
$\dfrac{55}{2\sqrt[3]{9}+\sqrt[3]{3}+5}$
2023京都大過去問
この動画を見る
分母を有利化せよ.
$\dfrac{55}{2\sqrt[3]{9}+\sqrt[3]{3}+5}$
2023京都大過去問
福田の1.5倍速演習〜合格する重要問題080〜京都大学2018年度理系第5問〜曲線の長さと極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 曲線y=$\log x$上の点A(t, $\log t$)における法線上に、点BをAB=1となるようにとる。ただしBのx座標はtより大きい。
(1)点Bの座標(u(t), v(t))を求めよ。また$\left(\frac{du}{dt}, \frac{dv}{dt}\right)$を求めよ。
(2)実数rは0<r<1を満たすとし、tがrから1まで動くときに点Aと点Bが描く曲線の長さをそれぞれ$L_1(r)$, $L_2(r)$とする。このとき、極限$\displaystyle\lim_{r \to +0}(L_1(r)-L_2(r))$を求めよ。
2018京都大学理系過去問
この動画を見る
$\Large\boxed{5}$ 曲線y=$\log x$上の点A(t, $\log t$)における法線上に、点BをAB=1となるようにとる。ただしBのx座標はtより大きい。
(1)点Bの座標(u(t), v(t))を求めよ。また$\left(\frac{du}{dt}, \frac{dv}{dt}\right)$を求めよ。
(2)実数rは0<r<1を満たすとし、tがrから1まで動くときに点Aと点Bが描く曲線の長さをそれぞれ$L_1(r)$, $L_2(r)$とする。このとき、極限$\displaystyle\lim_{r \to +0}(L_1(r)-L_2(r))$を求めよ。
2018京都大学理系過去問
福田の1.5倍速演習〜合格する重要問題079〜京都大学2018年度理系第3問〜円に内接する四角形の4辺の積の最大

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次関数とグラフ#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ αは0<α≦$\frac{\pi}{2}$を満たす定数とし、四角形ABCDに関する次の2つの条件を考える。
(i)四角形ABCDは半径1の円に内接する。
(ii)$\angle$ABC=$\angle$DAB=α
条件(i)(ii)を満たす四角形のなかで、4辺の長さの積
k=AB・BC・CD・DA
が最大となるものについて、kの値を求めよ。
2018京都大学理系過去問
この動画を見る
$\Large\boxed{3}$ αは0<α≦$\frac{\pi}{2}$を満たす定数とし、四角形ABCDに関する次の2つの条件を考える。
(i)四角形ABCDは半径1の円に内接する。
(ii)$\angle$ABC=$\angle$DAB=α
条件(i)(ii)を満たす四角形のなかで、4辺の長さの積
k=AB・BC・CD・DA
が最大となるものについて、kの値を求めよ。
2018京都大学理系過去問
福田の1.5倍速演習〜合格する重要問題078〜京都大学2018年度文理共通問題〜素数の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#微分法と積分法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $n^3$-7$n$+9 が素数となるような整数$n$を全て求めよ。
2018京都大学文理過去問
この動画を見る
$\Large\boxed{2}$ $n^3$-7$n$+9 が素数となるような整数$n$を全て求めよ。
2018京都大学文理過去問
福田の1.5倍速演習〜合格する重要問題038〜京都大学2017年度理系第3問〜三角関数と自然数解

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#三角関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$p,q$を自然数,$\alpha,\beta$を
$\tan\alpha=\frac{1}{p}$,$\tan\beta=\frac{1}{q}$
を満たす実数とする。このとき、
$\tan(\alpha+2\beta)=2$
を満たすp,qの組(p,q)を全て求めよ。
2017京都大学理系過去問
この動画を見る
$p,q$を自然数,$\alpha,\beta$を
$\tan\alpha=\frac{1}{p}$,$\tan\beta=\frac{1}{q}$
を満たす実数とする。このとき、
$\tan(\alpha+2\beta)=2$
を満たすp,qの組(p,q)を全て求めよ。
2017京都大学理系過去問
福田の1.5倍速演習〜合格する重要問題036〜京都大学2017年度文系第2問〜特定の素因数を持つ整数の個数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#指数関数と対数関数#対数関数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の問いに答えよ。ただし、$0.3010 \lt \log_{10}2 \lt 0.3011$
であることは用いてよい。
(1)100桁以下の自然数で、2以下の素因数を持たないものの個数を求めよ。
(2)100桁の自然数で、2と5以外の素因巣を持たないものの個数を求めよ。
2017京都大学文系過去問
この動画を見る
次の問いに答えよ。ただし、$0.3010 \lt \log_{10}2 \lt 0.3011$
であることは用いてよい。
(1)100桁以下の自然数で、2以下の素因数を持たないものの個数を求めよ。
(2)100桁の自然数で、2と5以外の素因巣を持たないものの個数を求めよ。
2017京都大学文系過去問
複素数平面!円が1と−1を通るということは・・・【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
複素数$a$に対してその共役な複素数$\bar{ a }$で表す。
$a$を実数でない複素数とする。複素数平面内の円$C$が$1,-1,a$を通るならば,$C$は-$\displaystyle \frac{1}{\bar{ a }}$も通ることを示せ。
京都大過去問
この動画を見る
複素数$a$に対してその共役な複素数$\bar{ a }$で表す。
$a$を実数でない複素数とする。複素数平面内の円$C$が$1,-1,a$を通るならば,$C$は-$\displaystyle \frac{1}{\bar{ a }}$も通ることを示せ。
京都大過去問
頻出!微分のよく見るような問題【京都大学】【数学 入試問題】
単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
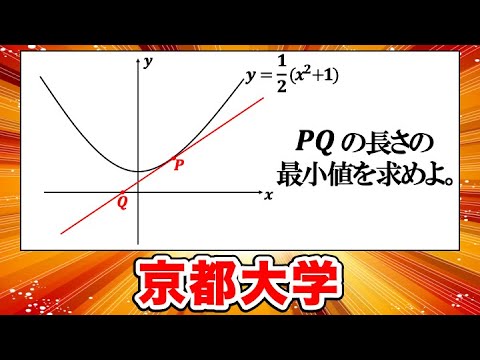
問題文全文(内容文):
曲線$y=\displaystyle \frac{1}{2}(x^2+1)$上の点$P$における接線は$x$軸と交わるとし,その交点を$\varrho$とおく。線分$P\varrho$の長さを$L$とするとき,$L$が取りうる値の最小値を求めよ。
京都大過去問
この動画を見る
曲線$y=\displaystyle \frac{1}{2}(x^2+1)$上の点$P$における接線は$x$軸と交わるとし,その交点を$\varrho$とおく。線分$P\varrho$の長さを$L$とするとき,$L$が取りうる値の最小値を求めよ。
京都大過去問
頻出!微分のよく見るような問題【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
曲線y=-1/2(x²+1)上の点Pにおける接線はx軸と交わるとし,その交点をQとおく。線分PQの長さをLとするとき, Lが取りうる値の最小値を求めよ。
京都大過去問
この動画を見る
曲線y=-1/2(x²+1)上の点Pにおける接線はx軸と交わるとし,その交点をQとおく。線分PQの長さをLとするとき, Lが取りうる値の最小値を求めよ。
京都大過去問
福田の1.5倍速演習〜合格する重要問題016〜京都大学2016年度理系数学第2問〜素数の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学的帰納法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
素数p,qを用いて
$p^q+q^p$
と表される素数を全て求めよ。
2016京都大学理系過去問
この動画を見る
素数p,qを用いて
$p^q+q^p$
と表される素数を全て求めよ。
2016京都大学理系過去問
福田の1.5倍速演習〜合格する重要問題013〜京都大学2015年度理系数学第3問〜極限と追い出しの原理

単元:
#大学入試過去問(数学)#微分とその応用#数列の極限#微分法#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
aを実数とするとき、(a,0)を通り、$y=e^x+1$に接する直線がただ
一つ存在することを示せ。
(2)$a_1=1$として、$n=1,2,\cdots$について、$(a_n, 0)$を通り、$y=e^x+1$に接する
直線の接点のx座標を$a_{n+1}$とする。このとき、$\lim_{n \to \infty}(a_{n+1}-a_n)$を求めよ。
2015京都大学理系過去問
この動画を見る
aを実数とするとき、(a,0)を通り、$y=e^x+1$に接する直線がただ
一つ存在することを示せ。
(2)$a_1=1$として、$n=1,2,\cdots$について、$(a_n, 0)$を通り、$y=e^x+1$に接する
直線の接点のx座標を$a_{n+1}$とする。このとき、$\lim_{n \to \infty}(a_{n+1}-a_n)$を求めよ。
2015京都大学理系過去問
福田の1.5倍速演習〜合格する重要問題012〜京都大学2015年度文系数学第1問〜折れ線と交わらない条件

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#2次関数#一次不等式(不等式・絶対値のある方程式・不等式)#2次関数とグラフ#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#面積、体積#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
直線$y=px+q$が、$y=x^2-x$のグラフとは交わるが、$y=|x|+|x-1|+1$
のグラフとは交わらないような(p,q)の範囲を図示し、その面積を求めよ。
2015京都大学文系過去問
この動画を見る
直線$y=px+q$が、$y=x^2-x$のグラフとは交わるが、$y=|x|+|x-1|+1$
のグラフとは交わらないような(p,q)の範囲を図示し、その面積を求めよ。
2015京都大学文系過去問
大学入試問題#371「少し変わった置換積分」 京都大学 改 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{2}{\sqrt{ 3 }}}^{2}\displaystyle \frac{dx}{x\sqrt{ x^2-1 }}$
出典:京都大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{2}{\sqrt{ 3 }}}^{2}\displaystyle \frac{dx}{x\sqrt{ x^2-1 }}$
出典:京都大学 入試問題
京大の整数問題!〇〇に注目!【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
二つの奇数$a,b$に対して,$m=11a+b,n=3a+b$とおく。$m,n$がともに平方数であることはないことを証明せよ。
京都大過去問
この動画を見る
二つの奇数$a,b$に対して,$m=11a+b,n=3a+b$とおく。$m,n$がともに平方数であることはないことを証明せよ。
京都大過去問
福田の1.5倍速演習〜合格する重要問題002〜京都大学2015年理系数学第1問〜回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
2つの関数$y = \sin(x+\frac{\pi}{8})$と$y=\sin2x$のグラフの$0\leqq x\leqq \frac{\pi}{2}$の部分で囲まれ
る領域を、x軸のまわりに1回転させてできる立体の体積を求めよ。
ただし、$x=0$と$x=\frac{\pi}{2}$は領域を囲む線とは考えない。
2015京都大学理系過去問
この動画を見る
2つの関数$y = \sin(x+\frac{\pi}{8})$と$y=\sin2x$のグラフの$0\leqq x\leqq \frac{\pi}{2}$の部分で囲まれ
る領域を、x軸のまわりに1回転させてできる立体の体積を求めよ。
ただし、$x=0$と$x=\frac{\pi}{2}$は領域を囲む線とは考えない。
2015京都大学理系過去問
京大の整数問題!〇〇に注目!【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
2つの奇数a,bに対して、$m=11a+b,n=3a+b$とおく。
$m,n$が平方数でないことを証明しなさい。
京都大過去問
この動画を見る
2つの奇数a,bに対して、$m=11a+b,n=3a+b$とおく。
$m,n$が平方数でないことを証明しなさい。
京都大過去問
【工夫あり】これが本当に京大の入試問題?絶対値を含んだ積分【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
定積分$\displaystyle \int_{-1}^{1}\left| x^2-\dfrac{1}{2}x-\dfrac{1}{2} \right | dx$を求めよ。
京都大過去問
この動画を見る
定積分$\displaystyle \int_{-1}^{1}\left| x^2-\dfrac{1}{2}x-\dfrac{1}{2} \right | dx$を求めよ。
京都大過去問
ベクトルの簡単すぎる京大の問題【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$\triangle OAB$において$OA=3,OB=2,\angle AOB=90^{ \circ }$とする。$\triangle OAB$の垂心を$H$とするとき,$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
京都大過去問
この動画を見る
$\triangle OAB$において$OA=3,OB=2,\angle AOB=90^{ \circ }$とする。$\triangle OAB$の垂心を$H$とするとき,$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
京都大過去問
