 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
【別解の考え方自身は超大切…!】因数分解:法政大学高等学校~全国入試問題解法

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#法政大学
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学高等学校
$(a^2+2a)^2-2(a^2+2a)-3$
を因数分解しなさい。
この動画を見る
入試問題 法政大学高等学校
$(a^2+2a)^2-2(a^2+2a)-3$
を因数分解しなさい。
大学入試問題#861「初見では苦しいか!?」 #学習院大学(2017) 視聴者の僚太さんの紹介

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#学習院大学
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0,b \gt 0$
$\displaystyle \lim_{ x \to \infty } x \sin(\sqrt{ a^2x^2+b }-ax)$
出典:2017年学習大学
この動画を見る
$a \gt 0,b \gt 0$
$\displaystyle \lim_{ x \to \infty } x \sin(\sqrt{ a^2x^2+b }-ax)$
出典:2017年学習大学
福田の数学〜慶應義塾大学2024年経済学部第1問(2)〜三角関数への置き換えによる分数関数の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$
(2)$\theta$は|$\theta$|<$\displaystyle\frac{\pi}{2}$の範囲の定数とする。$x$=$\tan\theta$とおくと、$\displaystyle\frac{x}{x^2+1}$=$\frac{\boxed{ク}}{\boxed{ケ}}\sin2\theta$かつ$\displaystyle\frac{1}{x^2+1}$=$\frac{\boxed{コ}}{\boxed{サ}}(\cos2\theta$+1)であるので、$\displaystyle y=\frac{x^2+3x+5}{x^2+1}$とすると、
$\displaystyle y=\frac{\boxed{シ}}{\boxed{ス}}\sin(2\theta+\alpha)$+$\boxed{セ}$
と表せる。ただし、$\cos\alpha$=$\frac{\boxed{ソ}}{\boxed{タ}}$, $\sin\alpha$=$\frac{\boxed{チ}}{\boxed{ツ}}$である。また、|$x$|≦1に対応する$\theta$の範囲が|$\theta$|≦$\displaystyle\frac{\pi}{\boxed{テ}}$であることに注意すると、|$x$|≦1における$y$の取りうる値の最大値は$\frac{\boxed{トナ}}{\boxed{ニ}}$、最小値は$\frac{\boxed{ヌ}}{\boxed{ネ}}$ である。
この動画を見る
$\Large\boxed{1}$
(2)$\theta$は|$\theta$|<$\displaystyle\frac{\pi}{2}$の範囲の定数とする。$x$=$\tan\theta$とおくと、$\displaystyle\frac{x}{x^2+1}$=$\frac{\boxed{ク}}{\boxed{ケ}}\sin2\theta$かつ$\displaystyle\frac{1}{x^2+1}$=$\frac{\boxed{コ}}{\boxed{サ}}(\cos2\theta$+1)であるので、$\displaystyle y=\frac{x^2+3x+5}{x^2+1}$とすると、
$\displaystyle y=\frac{\boxed{シ}}{\boxed{ス}}\sin(2\theta+\alpha)$+$\boxed{セ}$
と表せる。ただし、$\cos\alpha$=$\frac{\boxed{ソ}}{\boxed{タ}}$, $\sin\alpha$=$\frac{\boxed{チ}}{\boxed{ツ}}$である。また、|$x$|≦1に対応する$\theta$の範囲が|$\theta$|≦$\displaystyle\frac{\pi}{\boxed{テ}}$であることに注意すると、|$x$|≦1における$y$の取りうる値の最大値は$\frac{\boxed{トナ}}{\boxed{ニ}}$、最小値は$\frac{\boxed{ヌ}}{\boxed{ネ}}$ である。
視聴者の僚太さんの難易度高めの積分です。大事な感覚が盛り込まれてます。

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#大学入試解答速報
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x^2}{(1+x^2)\sqrt{ 1+x^2 }}$
この動画を見る
$\displaystyle \int \displaystyle \frac{x^2}{(1+x^2)\sqrt{ 1+x^2 }}$
福田の数学〜慶應義塾大学2024年経済学部第1問(1)〜2次方程式が整数解をもつ条件

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#ユークリッド互除法と不定方程式・N進法#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)$p$を実数とする。$x$の2次方程式$x^2$-($p$-9)$x$-$p$+1=0 の解は整数$m$<0<$n$が成り立つとする。このとき$mn$+$m$+$n$=$\boxed{\ \ アイ\ \ }$なので、$m$=$\boxed{\ \ ウエ\ \ }$, $n$=$\boxed{\ \ オ\ \ }$, $p$=$\boxed{\ \ カキ\ \ }$ である。
この動画を見る
$\Large\boxed{1}$ (1)$p$を実数とする。$x$の2次方程式$x^2$-($p$-9)$x$-$p$+1=0 の解は整数$m$<0<$n$が成り立つとする。このとき$mn$+$m$+$n$=$\boxed{\ \ アイ\ \ }$なので、$m$=$\boxed{\ \ ウエ\ \ }$, $n$=$\boxed{\ \ オ\ \ }$, $p$=$\boxed{\ \ カキ\ \ }$ である。
大学入試問題#860「これ、ええ問題」 #立教大学 #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin(1-\cos x)}{x^2}$
出典:立教大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{\sin(1-\cos x)}{x^2}$
出典:立教大学 入試問題
福田の数学〜慶應義塾大学2024年医学部第4問〜空間に浮かぶ四面体の平面による切り口の面積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標空間の4点O(0,0,0),A(-3,-1,1),B(2,-2,2),C(3,3,3)を頂点とする四面体OABCの、平面$z$=$t$による切り口を$S_t$とする。
(1)$S_t$は1<$t$<2のとき四角形となり、$t$=1および$t$=2のとき三角形となる。
1<$t$1 となるので、点Eはこの六面体の外にある。
(さ),(し),(す)の選択肢:ABC,ABD,ACD,BCD,OAD,OBD,OCD
(4)1<$t$<2に対して、(3)の六面体を平面$z$=$t$で切った切り口の面積を$U(t)$とすると、$U(t)$は$t$=$\boxed{\ \ (た)\ \ }$(ただし1<$\boxed{\ \ (た)\ \ }$<2)において最大値$\boxed{\ \ (ち)\ \ }$をとる。
この動画を見る
$\Large\boxed{4}$ 座標空間の4点O(0,0,0),A(-3,-1,1),B(2,-2,2),C(3,3,3)を頂点とする四面体OABCの、平面$z$=$t$による切り口を$S_t$とする。
(1)$S_t$は1<$t$<2のとき四角形となり、$t$=1および$t$=2のとき三角形となる。
1<$t$1 となるので、点Eはこの六面体の外にある。
(さ),(し),(す)の選択肢:ABC,ABD,ACD,BCD,OAD,OBD,OCD
(4)1<$t$<2に対して、(3)の六面体を平面$z$=$t$で切った切り口の面積を$U(t)$とすると、$U(t)$は$t$=$\boxed{\ \ (た)\ \ }$(ただし1<$\boxed{\ \ (た)\ \ }$<2)において最大値$\boxed{\ \ (ち)\ \ }$をとる。
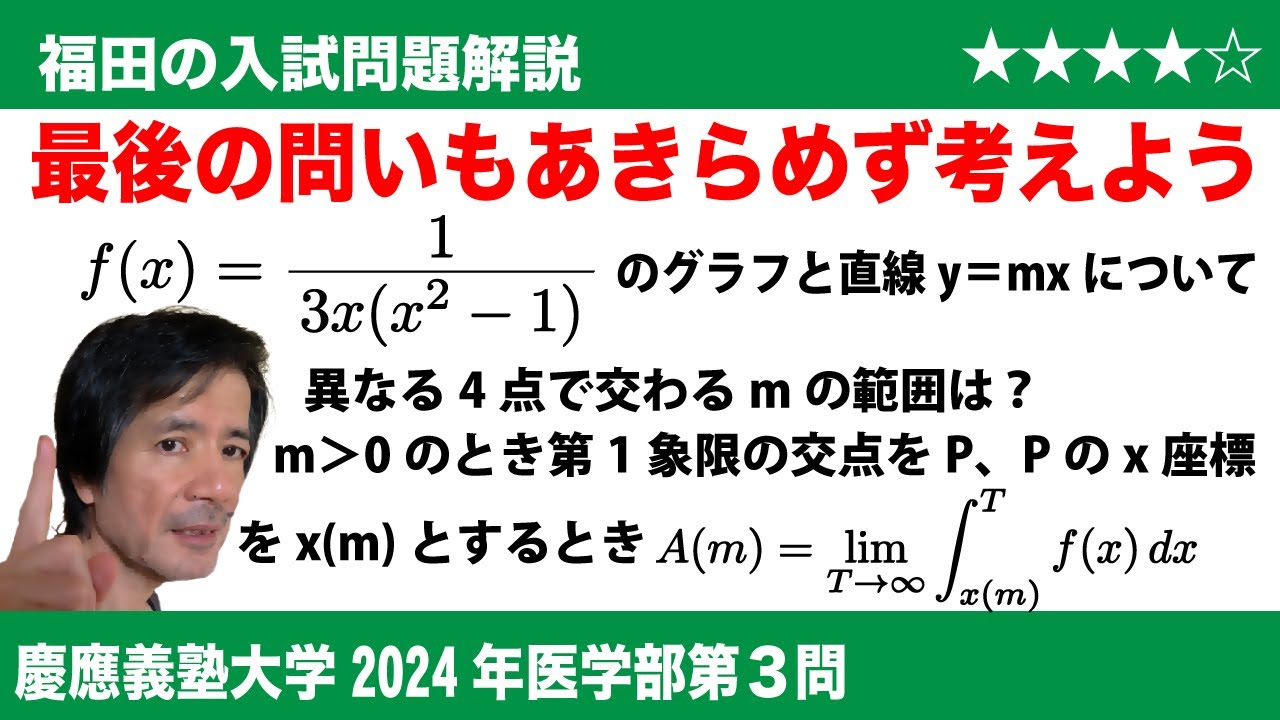
福田の数学〜慶應義塾大学2024年医学部第3問〜四面体の切断面の面積と極限
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ -1,0,1以外のすべての実数$x$に対して定義された関数
$f(x)$=$\displaystyle\frac{1}{3x(x^2-1)}$
を考える。
(1)$f(x)$は$x$=$\boxed{\ \ (あ)\ \ }$において極小値$\boxed{\ \ (い)\ \ }$をとり、$x$=$\boxed{\ \ (う)\ \ }$において極大値$\boxed{\ \ (え)\ \ }$をとる。
(2)曲線$y$=$f(x)$の概形を描きなさい。
(3)直線$y$=$mx$が曲線$y$=$f(x)$とちょうど4点で交わるとき、定数$m$の値の範囲は$\boxed{\ \ (お)\ \ }$である。
(4)$a$=$\boxed{\ \ (か)\ \ }$, $b$=$\boxed{\ \ (き)\ \ }$, $c$=$\boxed{\ \ (く)\ \ }$とすると、つぎの恒等式が成り立つ。
$f(x)$=$\displaystyle\frac{a}{x-1}$+$\displaystyle\frac{b}{x}$+$\displaystyle\frac{c}{x+1}$
(5)直線$y$=$mx$ (ただし$m$>0)が曲線$y$=$f(x)$と第1象限において交わる点Pの$x$座標を$x(m)$とし、
$A(m)$=$\displaystyle\lim_{T \to \infty}\int_{x(m)}^Tf(x)dx$
とおいて、$A(m)$を$m$の式で表すと、$A(m)$=$\boxed{\ \ (け)\ \ }$となる。また、原点をO、$\left(x(m),0\right)$を座標とする点をQとし、三角形OPQの面積を$B(m)$とおくと$\displaystyle\lim_{m \to +0}\frac{A(m)}{B(m)}$=$\boxed{\ \ (こ)\ \ }$ となる。
この動画を見る
$\Large\boxed{3}$ -1,0,1以外のすべての実数$x$に対して定義された関数
$f(x)$=$\displaystyle\frac{1}{3x(x^2-1)}$
を考える。
(1)$f(x)$は$x$=$\boxed{\ \ (あ)\ \ }$において極小値$\boxed{\ \ (い)\ \ }$をとり、$x$=$\boxed{\ \ (う)\ \ }$において極大値$\boxed{\ \ (え)\ \ }$をとる。
(2)曲線$y$=$f(x)$の概形を描きなさい。
(3)直線$y$=$mx$が曲線$y$=$f(x)$とちょうど4点で交わるとき、定数$m$の値の範囲は$\boxed{\ \ (お)\ \ }$である。
(4)$a$=$\boxed{\ \ (か)\ \ }$, $b$=$\boxed{\ \ (き)\ \ }$, $c$=$\boxed{\ \ (く)\ \ }$とすると、つぎの恒等式が成り立つ。
$f(x)$=$\displaystyle\frac{a}{x-1}$+$\displaystyle\frac{b}{x}$+$\displaystyle\frac{c}{x+1}$
(5)直線$y$=$mx$ (ただし$m$>0)が曲線$y$=$f(x)$と第1象限において交わる点Pの$x$座標を$x(m)$とし、
$A(m)$=$\displaystyle\lim_{T \to \infty}\int_{x(m)}^Tf(x)dx$
とおいて、$A(m)$を$m$の式で表すと、$A(m)$=$\boxed{\ \ (け)\ \ }$となる。また、原点をO、$\left(x(m),0\right)$を座標とする点をQとし、三角形OPQの面積を$B(m)$とおくと$\displaystyle\lim_{m \to +0}\frac{A(m)}{B(m)}$=$\boxed{\ \ (こ)\ \ }$ となる。
大学入試問題#862「計算力と根性!」 #京都大学(2023) #数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=3 \\
a_n=\displaystyle \frac{S_n}{n}+(n-1)・2^n
\end{array}
\right.
\end{eqnarray}$
を満たすような数列$\{a_n\}$の一般項を求めよ
出典:2023年京都大学 入試問題
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a_1=3 \\
a_n=\displaystyle \frac{S_n}{n}+(n-1)・2^n
\end{array}
\right.
\end{eqnarray}$
を満たすような数列$\{a_n\}$の一般項を求めよ
出典:2023年京都大学 入試問題
福田の数学〜慶應義塾大学2024年医学部第2問〜確率漸化式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 袋が2つ(袋1と袋2)および赤玉2個、白玉4個が用意されている。それぞれの袋に玉が3個ずつ入った状態として、次の3つがあり得る。
状態A:袋1に入っている赤玉が0個である状態
状態B:袋1に入っている赤玉が1個である状態
状態C:袋1に入っている赤玉が2個である状態
上記の各状態に対して、次の2段階からなる操作Tを考える。
操作T:袋1から玉を1個無作為に取り出し、それを袋2に入れる。次に、袋2から玉を1個無作為に取り出し、それを袋1に入れる。
(1)X,YをそれぞれA,B,Cのいずれかとする。状態Xに対し操作Tを1回施した結果、状態Yになる確率をP(X→Y)で表す。このとき、
P(A→A)=$\boxed{\ \ (あ)\ \ }$, P(A→B)=$\boxed{\ \ (い)\ \ }$, P(B→A)=$\boxed{\ \ (う)\ \ }$,
P(B→B)=$\boxed{\ \ (え)\ \ }$, P(C→A)=$\boxed{\ \ (お)\ \ }$, P(C→B)=$\boxed{\ \ (か)\ \ }$ である。
(2)以下、$n$を自然数とし、状態Bから始めて操作Tを繰り返し施す。操作Tを$n$回施し終えたとき、状態Aである確率を$a_n$、状態Bである確率を$b_n$、状態Cである確率を$c_n$とする。$n$≧2 とするとき、$a_n$,$b_n$,$c_n$と$a_{n-1}$,$b_{n-1}$,$c_{n-1}$の間には次の関係式が成り立つ。
$\left\{\begin{array}{1}
a_n=\boxed{\ \ (あ)\ \ }a_{n-1}+\boxed{\ \ (う)\ \ }b_{n-1}+\boxed{\ \ (お)\ \ }c_{n-1}\\
b_n=\boxed{\ \ (い)\ \ }a_{n-1}+\boxed{\ \ (え)\ \ }b_{n-1}+\boxed{\ \ (か)\ \ }c_{n-1}\\
\end{array}\right.$
したがって$b_n$と$b_{n-1}$の間には次の関係式が成り立つことが分かる。
$b_n$=$\boxed{\ \ (き)\ \ }b_{n-1}$+$\boxed{\ \ (く)\ \ }$
これより、$n$≧1 に対して$b_n$を$n$の式で表すと
$b_n$=$\boxed{\ \ (け)\ \ }$+$\boxed{\ \ (こ)\ \ }(\boxed{\ \ (さ)\ \ })^n$
となる。さらに$d_n$=$\displaystyle\frac{a_n}{(\boxed{\ \ (あ)\ \ })^n}$とおくとき、$d_n$を$n$の式で表すと
$d_n$=$\boxed{\ \ (し)\ \ }\left\{(\boxed{\ \ (す)\ \ })^n-(\boxed{\ \ (せ)\ \ })^n\right\}$
となる。
この動画を見る
$\Large\boxed{2}$ 袋が2つ(袋1と袋2)および赤玉2個、白玉4個が用意されている。それぞれの袋に玉が3個ずつ入った状態として、次の3つがあり得る。
状態A:袋1に入っている赤玉が0個である状態
状態B:袋1に入っている赤玉が1個である状態
状態C:袋1に入っている赤玉が2個である状態
上記の各状態に対して、次の2段階からなる操作Tを考える。
操作T:袋1から玉を1個無作為に取り出し、それを袋2に入れる。次に、袋2から玉を1個無作為に取り出し、それを袋1に入れる。
(1)X,YをそれぞれA,B,Cのいずれかとする。状態Xに対し操作Tを1回施した結果、状態Yになる確率をP(X→Y)で表す。このとき、
P(A→A)=$\boxed{\ \ (あ)\ \ }$, P(A→B)=$\boxed{\ \ (い)\ \ }$, P(B→A)=$\boxed{\ \ (う)\ \ }$,
P(B→B)=$\boxed{\ \ (え)\ \ }$, P(C→A)=$\boxed{\ \ (お)\ \ }$, P(C→B)=$\boxed{\ \ (か)\ \ }$ である。
(2)以下、$n$を自然数とし、状態Bから始めて操作Tを繰り返し施す。操作Tを$n$回施し終えたとき、状態Aである確率を$a_n$、状態Bである確率を$b_n$、状態Cである確率を$c_n$とする。$n$≧2 とするとき、$a_n$,$b_n$,$c_n$と$a_{n-1}$,$b_{n-1}$,$c_{n-1}$の間には次の関係式が成り立つ。
$\left\{\begin{array}{1}
a_n=\boxed{\ \ (あ)\ \ }a_{n-1}+\boxed{\ \ (う)\ \ }b_{n-1}+\boxed{\ \ (お)\ \ }c_{n-1}\\
b_n=\boxed{\ \ (い)\ \ }a_{n-1}+\boxed{\ \ (え)\ \ }b_{n-1}+\boxed{\ \ (か)\ \ }c_{n-1}\\
\end{array}\right.$
したがって$b_n$と$b_{n-1}$の間には次の関係式が成り立つことが分かる。
$b_n$=$\boxed{\ \ (き)\ \ }b_{n-1}$+$\boxed{\ \ (く)\ \ }$
これより、$n$≧1 に対して$b_n$を$n$の式で表すと
$b_n$=$\boxed{\ \ (け)\ \ }$+$\boxed{\ \ (こ)\ \ }(\boxed{\ \ (さ)\ \ })^n$
となる。さらに$d_n$=$\displaystyle\frac{a_n}{(\boxed{\ \ (あ)\ \ })^n}$とおくとき、$d_n$を$n$の式で表すと
$d_n$=$\boxed{\ \ (し)\ \ }\left\{(\boxed{\ \ (す)\ \ })^n-(\boxed{\ \ (せ)\ \ })^n\right\}$
となる。
大学入試問題#857「スッキリとした解答になるはず」 #大阪市立大学(1998) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} \displaystyle \frac{1}{\mathit{u}^{(\frac{3}{2})}}\{\sin(log\ \mathit{u})+\displaystyle \frac{1}{2}\cos(log\ \mathit{u})\}du$
出典:1998年大阪市立大学
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{1}{\mathit{u}^{(\frac{3}{2})}}\{\sin(log\ \mathit{u})+\displaystyle \frac{1}{2}\cos(log\ \mathit{u})\}du$
出典:1998年大阪市立大学
福田の数学〜慶應義塾大学2024年医学部第1問(3)〜三角関数の増減とグラフと面積

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$
(3) 関数$y$=$\cos x\sin 2x$ $\left(0≦x≦\displaystyle\frac{\pi}{2}\right)$の最大値は$\boxed{\ \ (け)\ \ }$である。また、この関数のグラフと$x$軸で囲まれてできる図形の面積は$\boxed{\ \ (こ)\ \ }$である。
この動画を見る
$\Large\boxed{1}$
(3) 関数$y$=$\cos x\sin 2x$ $\left(0≦x≦\displaystyle\frac{\pi}{2}\right)$の最大値は$\boxed{\ \ (け)\ \ }$である。また、この関数のグラフと$x$軸で囲まれてできる図形の面積は$\boxed{\ \ (こ)\ \ }$である。
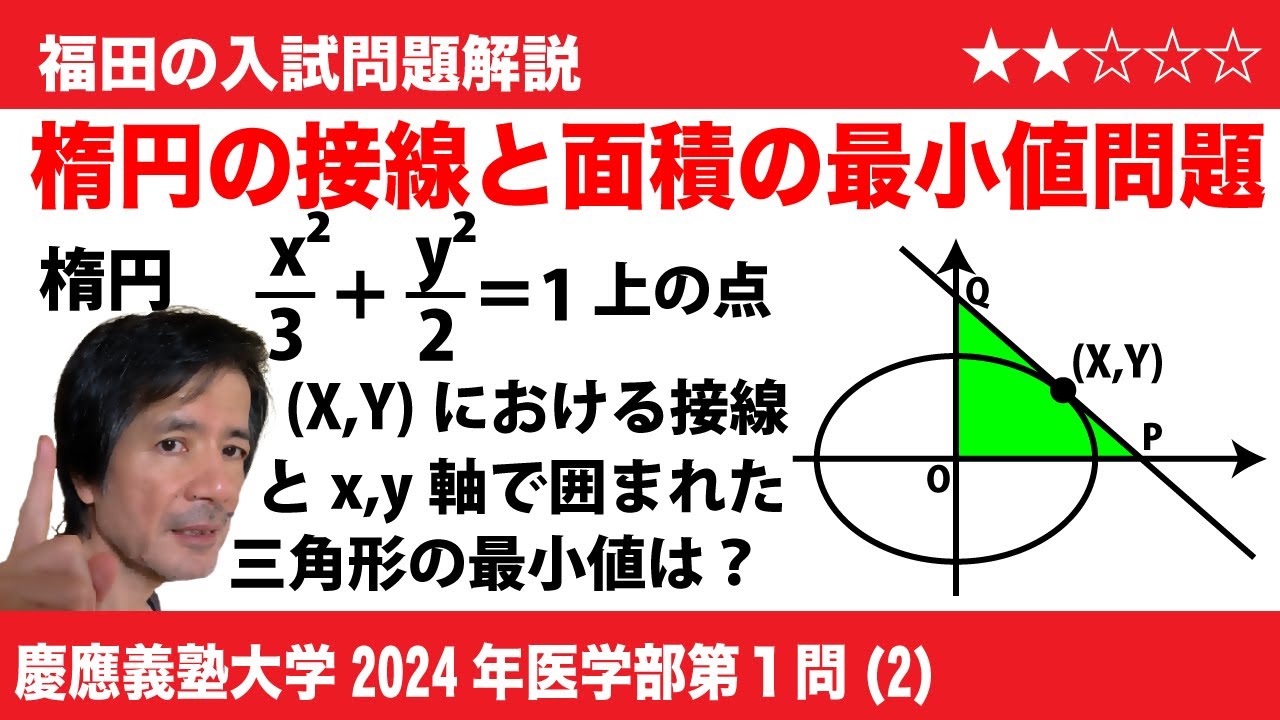
福田の数学〜慶應義塾大学2024年医学部第1問(2)〜楕円の接線とx軸y軸で作る三角形の面積の最小
単元:
#大学入試過去問(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)座標平面の第1象限の点(X,Y)において楕円$\frac{x^2}{3}$+$\frac{y^2}{2}$=1 に接する直線を$l$とすると、$l$の傾きは$\boxed{\ \ (お)\ \ }$である。また、原点をO、$l$と$x$軸, $y$軸との交点をそれぞれP, Qとすると、三角形OPQの面積は(X,Y)=($\boxed{\ \ (か)\ \ }$, $\boxed{\ \ (き)\ \ }$)のときに最小値$\boxed{\ \ (く)\ \ }$をとる。
この動画を見る
$\Large\boxed{1}$ (2)座標平面の第1象限の点(X,Y)において楕円$\frac{x^2}{3}$+$\frac{y^2}{2}$=1 に接する直線を$l$とすると、$l$の傾きは$\boxed{\ \ (お)\ \ }$である。また、原点をO、$l$と$x$軸, $y$軸との交点をそれぞれP, Qとすると、三角形OPQの面積は(X,Y)=($\boxed{\ \ (か)\ \ }$, $\boxed{\ \ (き)\ \ }$)のときに最小値$\boxed{\ \ (く)\ \ }$をとる。
大学入試問題#856「対称性なら余裕!」 #産業医科大学(2012) #高次方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$2x^4+7x^3+4x^2+7x+2=0$の実数解を求めよ
出典:2012年産業医科大学 入試問題
この動画を見る
$2x^4+7x^3+4x^2+7x+2=0$の実数解を求めよ
出典:2012年産業医科大学 入試問題
福田の数学〜慶應義塾大学2024年医学部第1問(1)〜三角形の外心と内心の座標の求め方

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)座標平面の3点O(0,0), A(3,0), B(1, $\sqrt 3$)を頂点とする三角形OABの外心の座標は($\boxed{\ \ (あ)\ \ }$, $\boxed{\ \ (い)\ \ }$)であり、内心の座標は($\boxed{\ \ (う)\ \ }$, $\boxed{\ \ (え)\ \ }$)である。
この動画を見る
$\Large\boxed{1}$ (1)座標平面の3点O(0,0), A(3,0), B(1, $\sqrt 3$)を頂点とする三角形OABの外心の座標は($\boxed{\ \ (あ)\ \ }$, $\boxed{\ \ (い)\ \ }$)であり、内心の座標は($\boxed{\ \ (う)\ \ }$, $\boxed{\ \ (え)\ \ }$)である。
大学入試問題#855「47の主張が強すぎる」 #自治医科大学(2012) #式変形

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$x^{\frac{1}{4}}+x^{-\frac{1}{4}}=3$のとき
$\displaystyle \frac{47}{2}(\displaystyle \frac{x^{\frac{3}{4}}+x^{-\frac{3}{4}}}{x+x^{-1}})$の値を求めよ。
$(0 \lt x:$実数$)$
出典:2012年自治医科大学
この動画を見る
$x^{\frac{1}{4}}+x^{-\frac{1}{4}}=3$のとき
$\displaystyle \frac{47}{2}(\displaystyle \frac{x^{\frac{3}{4}}+x^{-\frac{3}{4}}}{x+x^{-1}})$の値を求めよ。
$(0 \lt x:$実数$)$
出典:2012年自治医科大学
福田の数学〜九州大学2024年文系第2問〜ベクトルの内積計算と三角形の面積

単元:
#大学入試過去問(数学)#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 座標平面上の原点O(0,0)、点A(2,1)を考える。点Bは第1象限にあり、|$\overrightarrow{OB}$|=$\sqrt{10}$, $\overrightarrow{OA}\bot\overrightarrow{AB}$を満たすとする。以下の問いに答えよ。
(1)点Bの座標を求めよ。
(2)$s$,$t$を正の実数とし、$\overrightarrow{OC}$=$s\overrightarrow{OA}$+$t\overrightarrow{OB}$ を満たす点Cを考える。三角形OACと三角形OBCの面積が等しく、|$\overrightarrow{OC}$|=4 が成り立つとき、$s$,$t$の値を求めよ。
この動画を見る
$\Large\boxed{2}$ 座標平面上の原点O(0,0)、点A(2,1)を考える。点Bは第1象限にあり、|$\overrightarrow{OB}$|=$\sqrt{10}$, $\overrightarrow{OA}\bot\overrightarrow{AB}$を満たすとする。以下の問いに答えよ。
(1)点Bの座標を求めよ。
(2)$s$,$t$を正の実数とし、$\overrightarrow{OC}$=$s\overrightarrow{OA}$+$t\overrightarrow{OB}$ を満たす点Cを考える。三角形OACと三角形OBCの面積が等しく、|$\overrightarrow{OC}$|=4 が成り立つとき、$s$,$t$の値を求めよ。
#大学入試問題#853「ファンタスティックな解答求む」 #大阪工業大学(2023) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#大阪工業大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{4} \displaystyle \frac{x-1}{2x-\sqrt{ x }} dx$
出典:2023年大阪工業大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{4} \displaystyle \frac{x-1}{2x-\sqrt{ x }} dx$
出典:2023年大阪工業大学 入試問題
大学入試問題#852「これは、大変・・・グラフでもいけるんかなー」 #小樽商科大学(2018) #整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#小樽商科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{2n-2}{n^2+2n+2}$が整数となるような整数$n$をすべて求めよ
出典:2018年小樽商科大学
この動画を見る
$\displaystyle \frac{2n-2}{n^2+2n+2}$が整数となるような整数$n$をすべて求めよ
出典:2018年小樽商科大学
福田の数学〜九州大学2024年理系第4問〜3個以上の格子点を通る直線の個数

単元:
#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $n$を3以上の整数とする。座標平面上の点のうち、$x$座標と$y$座標がともに1以上$n$以下の整数であるものを考える。これら$n^2$個の点のうち3点以上を通る直線の個数を$L(n)$とする。以下の問いに答えよ。
(1)$L(3)$を求めよ。
(2)$L(4)$を求めよ。
(3)$L(5)$を求めよ。
この動画を見る
$\Large\boxed{4}$ $n$を3以上の整数とする。座標平面上の点のうち、$x$座標と$y$座標がともに1以上$n$以下の整数であるものを考える。これら$n^2$個の点のうち3点以上を通る直線の個数を$L(n)$とする。以下の問いに答えよ。
(1)$L(3)$を求めよ。
(2)$L(4)$を求めよ。
(3)$L(5)$を求めよ。
大学入試問題#851「いやー見た目がきつい」 #自治医科大(2018)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$x$が$0$以上の実数であるとき、関数$f(x)=\displaystyle \frac{x^4-2x^3-x^2+2x+34}{x^2-x+3}$の最小値を求めよ
出典:2018年自治医科大学 入試問題
この動画を見る
$x$が$0$以上の実数であるとき、関数$f(x)=\displaystyle \frac{x^4-2x^3-x^2+2x+34}{x^2-x+3}$の最小値を求めよ
出典:2018年自治医科大学 入試問題
福田の数学〜九州大学2024年理系第3問〜階乗を含む不定方程式の解

単元:
#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 以下の問いに答えよ。
(1)自然数$a$, $b$が$a$<$b$を満たすとき、$\displaystyle\frac{b!}{a!}$≧$b$ が成り立つことを示せ。
(2)2・$a!$=$b!$ を満たす自然数の組($a$, $b$)を全て求めよ。
(3)$a!$+$b!$=2・$c!$ を満たす自然数の組($a$, $b$, $c$)を全て求めよ。
この動画を見る
$\Large\boxed{3}$ 以下の問いに答えよ。
(1)自然数$a$, $b$が$a$<$b$を満たすとき、$\displaystyle\frac{b!}{a!}$≧$b$ が成り立つことを示せ。
(2)2・$a!$=$b!$ を満たす自然数の組($a$, $b$)を全て求めよ。
(3)$a!$+$b!$=2・$c!$ を満たす自然数の組($a$, $b$, $c$)を全て求めよ。
大学入試問題#850「おもろいパズル」 #京都大学(2023) #有理化 #式変形

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{55}{2\sqrt[ 3 ]{ 9 }+\sqrt[ 3 ]{ 3 }+5}$を有利化せよ
出典:2023年京都大学
この動画を見る
$\displaystyle \frac{55}{2\sqrt[ 3 ]{ 9 }+\sqrt[ 3 ]{ 3 }+5}$を有利化せよ
出典:2023年京都大学
福田の数学〜九州大学2024年理系第2問〜複素数平面と高次方程式の解

単元:
#数Ⅱ#複素数と方程式#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 整式$f(z)$=$z^6$+$z^4$+$z^2$+1
について、以下の問いに答えよ。
(1)$f(z)$=0 を満たす全ての複素数$z$に対して、|$z$|=1 が成り立つことを示せ。
(2)次の条件を満たす複素数$w$を全て求めよ。
条件:$f(z)$=0 を満たす全ての複素数$z$に対して
$f(wz)$=0 が成り立つ。
この動画を見る
$\Large\boxed{2}$ 整式$f(z)$=$z^6$+$z^4$+$z^2$+1
について、以下の問いに答えよ。
(1)$f(z)$=0 を満たす全ての複素数$z$に対して、|$z$|=1 が成り立つことを示せ。
(2)次の条件を満たす複素数$w$を全て求めよ。
条件:$f(z)$=0 を満たす全ての複素数$z$に対して
$f(wz)$=0 が成り立つ。
大学入試問題#849「これ得意かも」 #和歌山大学(2017) #式変形

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#和歌山大学
指導講師:
ますただ
問題文全文(内容文):
$\sqrt[ 3 ]{ \sqrt{ 5 }+2 }-\sqrt[ 3 ]{ \sqrt{ 5 }-2 }$が整数であることを示せ
出典:2017年和歌山大学 入試問題
この動画を見る
$\sqrt[ 3 ]{ \sqrt{ 5 }+2 }-\sqrt[ 3 ]{ \sqrt{ 5 }-2 }$が整数であることを示せ
出典:2017年和歌山大学 入試問題
福田の数学〜九州大学2024年理系第1問〜空間における三角形の面積の最大値

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $a$を実数とし、座標空間内の3点P(-1,1,-1), Q(1,1,1), R($a$, $a^2$, $a^3$)を考える。以下の問いに答えよ。
(1)$a$≠-1, $a$≠1 のとき、3点P,Q,Rは一直線上にないことを示せ。
(2)$a$が-1<$a$<1 の範囲を動くとき、三角形PQRの面積の最大値を求めよ。
この動画を見る
$\Large\boxed{1}$ $a$を実数とし、座標空間内の3点P(-1,1,-1), Q(1,1,1), R($a$, $a^2$, $a^3$)を考える。以下の問いに答えよ。
(1)$a$≠-1, $a$≠1 のとき、3点P,Q,Rは一直線上にないことを示せ。
(2)$a$が-1<$a$<1 の範囲を動くとき、三角形PQRの面積の最大値を求めよ。
大学入試問題#848「何種類か解法がありそう」 #宮崎大学(2023) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{1}{\sqrt{ 3 }}}^{\sqrt{ 3 }} \displaystyle \frac{1+x}{x(1+x^2)} dx$
出典:2023年宮崎大学
この動画を見る
$\displaystyle \int_{\frac{1}{\sqrt{ 3 }}}^{\sqrt{ 3 }} \displaystyle \frac{1+x}{x(1+x^2)} dx$
出典:2023年宮崎大学
福田の数学〜神戸大学2024年文系第2問〜さいころの目と約数に関する確率

単元:
#数A#場合の数と確率#整数の性質#確率#約数・倍数・整数の割り算と余り・合同式#神戸大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$で最小のものを求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$で最小のものを求めよ。
(3)1個のサイコロを3回投げて出た目の積が20の約数となる確率を求めよ。
この動画を見る
$\Large\boxed{2}$ $n$を自然数とする。以下の問いに答えよ。
(1)1個のサイコロを投げて出た目が必ず$n$の約数となるような$n$で最小のものを求めよ。
(2)1個のサイコロを投げて出た目が$n$の約数となる確率が$\displaystyle\frac{5}{6}$であるような$n$で最小のものを求めよ。
(3)1個のサイコロを3回投げて出た目の積が20の約数となる確率を求めよ。
大学入試問題#847「もうネタ切れ寸前」 #青山学院大学(2006) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \{log(4-x^2)+2\} dx$
出典:2006年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \{log(4-x^2)+2\} dx$
出典:2006年青山学院大学 入試問題
福田の数学〜神戸大学2024年文系第1問〜3次関数で定義された数列

単元:
#数列#漸化式#神戸大学#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 各項が正である数列$\left\{a_n\right\}$を次のように定める。$a_1$は関数
$y$=$\displaystyle\frac{1}{3}x^3$-10$x$ ($x$≧0)
が最小値をとるときの$x$の値とする。$a_{n+1}$は関数
$y$=$\displaystyle\frac{1}{3}x^3$-100$a_nx$ ($x$≧0)
が最小値をとるときの$x$の値とする。数列$\left\{b_n\right\}$を$b_n$=$\log_{10}a_n$ で定める。以下の問いに答えよ。
(1)$a_1$と$b_1$を求めよ。 (2)$a_{n+1}$を$a_n$を用いて表せ。
(3)$b_{n+1}$を$b_n$を用いて表せ。
(4)数列$\left\{b_n\right\}$の一般項を求めよ。
(5)$\displaystyle\frac{a_1a_2a_3}{100}$ の値を求めよ。
この動画を見る
$\Large\boxed{1}$ 各項が正である数列$\left\{a_n\right\}$を次のように定める。$a_1$は関数
$y$=$\displaystyle\frac{1}{3}x^3$-10$x$ ($x$≧0)
が最小値をとるときの$x$の値とする。$a_{n+1}$は関数
$y$=$\displaystyle\frac{1}{3}x^3$-100$a_nx$ ($x$≧0)
が最小値をとるときの$x$の値とする。数列$\left\{b_n\right\}$を$b_n$=$\log_{10}a_n$ で定める。以下の問いに答えよ。
(1)$a_1$と$b_1$を求めよ。 (2)$a_{n+1}$を$a_n$を用いて表せ。
(3)$b_{n+1}$を$b_n$を用いて表せ。
(4)数列$\left\{b_n\right\}$の一般項を求めよ。
(5)$\displaystyle\frac{a_1a_2a_3}{100}$ の値を求めよ。
