 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
展開だけど、カラクリわかるかな? 慶應義塾

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(x+2y)(2x-y)(3x+y)(x-3y)を展開せよ
慶應義塾高等学校
この動画を見る
(x+2y)(2x-y)(3x+y)(x-3y)を展開せよ
慶應義塾高等学校
福田の数学〜京都大学2023年理系第2問〜空間の位置ベクトルと直線のベクトル方程式

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#空間ベクトル#剰余の定理・因数定理・組み立て除法と高次方程式#空間ベクトル#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 空間内の4点O,A,B,Cは同一平面上にないとする。点D,P,Qを次のように定める。点Dは$\overrightarrow{OD}$=$\overrightarrow{OA}$+$2\overrightarrow{OB}$+$3\overrightarrow{OC}$を満たし、点Pは線分OAを1:2に内分し、点Qは線分OBの中点である。さらに、直線OD上の点Rを、直線QRと直線PCが交点を持つように定める。このとき、線分ORの長さと線分RDの長さの比OR:RDを求めよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{2}$ 空間内の4点O,A,B,Cは同一平面上にないとする。点D,P,Qを次のように定める。点Dは$\overrightarrow{OD}$=$\overrightarrow{OA}$+$2\overrightarrow{OB}$+$3\overrightarrow{OC}$を満たし、点Pは線分OAを1:2に内分し、点Qは線分OBの中点である。さらに、直線OD上の点Rを、直線QRと直線PCが交点を持つように定める。このとき、線分ORの長さと線分RDの長さの比OR:RDを求めよ。
2023京都大学理系過去問
2023年東工大の整数問題!86400!?大きい値をどう扱うか【東京工業大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
方程式 $(x^{3}-x)^{2}(y^{3}-y)$=86400
を満たす整数の組$(x,y)$をすべて求めよ。
この動画を見る
方程式 $(x^{3}-x)^{2}(y^{3}-y)$=86400
を満たす整数の組$(x,y)$をすべて求めよ。
福田の数学〜京都大学2023年理系第1問(2)〜整式の割り算と余り

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 問2 整式$x^{2023}$-1 を整式$x^4$+$x^3$+$x^2$+$x$+1 で割った時の余りを求めよ。
2023京都大学理系過去問
この動画を見る
$\Large\boxed{1}$ 問2 整式$x^{2023}$-1 を整式$x^4$+$x^3$+$x^2$+$x$+1 で割った時の余りを求めよ。
2023京都大学理系過去問
福田の数学〜京都大学2023年理系第1問(1)〜定積分の計算

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
今回は京都大学2023年理系第1問(1)。定積分の計算の問題。
$\int_1^4 \sqrt{x}\log (x^2)dx$を求めよ
2023京都大学理系過去問
この動画を見る
今回は京都大学2023年理系第1問(1)。定積分の計算の問題。
$\int_1^4 \sqrt{x}\log (x^2)dx$を求めよ
2023京都大学理系過去問
【積分】2023年京大数学!絶対に落としてはいけない問題です【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
定積分 $\displaystyle \int_{1}^{4}\sqrt{x}\log(x^{2})dx$の値を求めよ。
京都大過去問
この動画を見る
定積分 $\displaystyle \int_{1}^{4}\sqrt{x}\log(x^{2})dx$の値を求めよ。
京都大過去問
福田の数学〜東京大学2023年文系第4問〜四面体の体積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#図形と方程式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 半径1の球面上の相異なる4点A,B,C,Dが
AB=1, AC=BC, AD=BD, $\cos\angle ACB$=$\cos\angle ADB$=$\displaystyle\frac{4}{5}$
を満たしているとする。
(1)三角形ABCの面積を求めよ。
(2)四角形ABCDの体積を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{4}$ 半径1の球面上の相異なる4点A,B,C,Dが
AB=1, AC=BC, AD=BD, $\cos\angle ACB$=$\cos\angle ADB$=$\displaystyle\frac{4}{5}$
を満たしているとする。
(1)三角形ABCの面積を求めよ。
(2)四角形ABCDの体積を求めよ。
2023東京大学文系過去問
大学入試問題#478「これは落とせない問題でしょう。」 福島大学(2022) #方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師:
ますただ
問題文全文(内容文):
$(x^2+2x+1)(x^2+2x+9)+12=0$を複素数の範囲で解け。
出典:2022年福島大学 入試問題
この動画を見る
$(x^2+2x+1)(x^2+2x+9)+12=0$を複素数の範囲で解け。
出典:2022年福島大学 入試問題
福田の数学〜東京大学2023年理系第6問〜線分の先端の可動範囲と関節を加えたときの可動範囲(PART2)

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ Oを原点とする座標空間において、不等式|x|≦1, |y|≦1, |z|≦1の表す立方体を考える。その立方体の表面のうち、z<1を満たす部分をSとする。
以下、座標空間内の2点A,Bが一致するとき、線分ABは点Aを表すものとし、その長さを0と定める。
(1)座標空間内の点Pが次の条件(i),(ii)をともに満たすとき、点Pが動きうる範囲Vの体積を求めよ。
(i)OP≦$\sqrt 3$
(ii)線分OPとSは、共有点をもたないか、点Pのみを共有点にもつ。
(2)座標空間内の点Nと点Pが次の条件(iii),(iv),(v)をすべて満たすとき、点Pが動きうる範囲Wの体積を求めよ。必要ならば、$\sin\alpha$=$\frac{1}{\sqrt 3}$を満たす実数α(0<α<$\frac{\pi}{2}$)を用いてよい。
(iii)ON+NP≦$\sqrt 3$
(iv)線分ONとSは共有点を持たない。
(v)線分NPとSは、共有点を持たないか、点Pのみを共有点を持つ。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{6}$ Oを原点とする座標空間において、不等式|x|≦1, |y|≦1, |z|≦1の表す立方体を考える。その立方体の表面のうち、z<1を満たす部分をSとする。
以下、座標空間内の2点A,Bが一致するとき、線分ABは点Aを表すものとし、その長さを0と定める。
(1)座標空間内の点Pが次の条件(i),(ii)をともに満たすとき、点Pが動きうる範囲Vの体積を求めよ。
(i)OP≦$\sqrt 3$
(ii)線分OPとSは、共有点をもたないか、点Pのみを共有点にもつ。
(2)座標空間内の点Nと点Pが次の条件(iii),(iv),(v)をすべて満たすとき、点Pが動きうる範囲Wの体積を求めよ。必要ならば、$\sin\alpha$=$\frac{1}{\sqrt 3}$を満たす実数α(0<α<$\frac{\pi}{2}$)を用いてよい。
(iii)ON+NP≦$\sqrt 3$
(iv)線分ONとSは共有点を持たない。
(v)線分NPとSは、共有点を持たないか、点Pのみを共有点を持つ。
2023東京大学理系過去問
大学入試問題#477「もうすこし工夫できそう」 山形大学(2016) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学#数Ⅲ#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{1}{e}}^{1} (1+\displaystyle \frac{1}{x})log\ x\ dx$
出典:2016年山形大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{1}{e}}^{1} (1+\displaystyle \frac{1}{x})log\ x\ dx$
出典:2016年山形大学 入試問題
福田の数学〜東京大学2023年理系第6問〜線分の先端の可動範囲と関節を加えたときの可動範囲(PART1)

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{6}$ Oを原点とする座標空間において、不等式|x|≦1, |y|≦1, |z|≦1の表す立方体を考える。その立方体の表面のうち、z<1を満たす部分をSとする。
以下、座標空間内の2点A,Bが一致するとき、線分ABは点Aを表すものとし、その長さを0と定める。
(1)座標空間内の点Pが次の条件(i),(ii)をともに満たすとき、点Pが動きうる範囲Vの体積を求めよ。
(i)OP≦$\sqrt 3$
(ii)線分OPとSは、共有点をもたないか、点Pのみを共有点にもつ。
(2)座標空間内の点Nと点Pが次の条件(iii),(iv),(v)をすべて満たすとき、点Pが動きうる範囲Wの体積を求めよ。必要ならば、$\sin\alpha$=$\frac{1}{\sqrt 3}$を満たす実数α(0<α<$\frac{\pi}{2}$)を用いてよい。
(iii)ON+NP≦$\sqrt 3$
(iv)線分ONとSは共有点を持たない。
(v)線分NPとSは、共有点を持たないか、点Pのみを共有点を持つ。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{6}$ Oを原点とする座標空間において、不等式|x|≦1, |y|≦1, |z|≦1の表す立方体を考える。その立方体の表面のうち、z<1を満たす部分をSとする。
以下、座標空間内の2点A,Bが一致するとき、線分ABは点Aを表すものとし、その長さを0と定める。
(1)座標空間内の点Pが次の条件(i),(ii)をともに満たすとき、点Pが動きうる範囲Vの体積を求めよ。
(i)OP≦$\sqrt 3$
(ii)線分OPとSは、共有点をもたないか、点Pのみを共有点にもつ。
(2)座標空間内の点Nと点Pが次の条件(iii),(iv),(v)をすべて満たすとき、点Pが動きうる範囲Wの体積を求めよ。必要ならば、$\sin\alpha$=$\frac{1}{\sqrt 3}$を満たす実数α(0<α<$\frac{\pi}{2}$)を用いてよい。
(iii)ON+NP≦$\sqrt 3$
(iv)線分ONとSは共有点を持たない。
(v)線分NPとSは、共有点を持たないか、点Pのみを共有点を持つ。
2023東京大学理系過去問
大学入試問題#476「むむむ!」 信州大学(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \int_{0}^{a} \displaystyle \frac{x}{1+\sqrt{ a^2-x^2 }} dx$
出典:2010年信州大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int_{0}^{a} \displaystyle \frac{x}{1+\sqrt{ a^2-x^2 }} dx$
出典:2010年信州大学 入試問題
福田の数学〜東京大学2023年文系第2問〜定積分で表された関数と最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#不定積分・定積分#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 座標平面上の放物線y=3$x^2$-4xをCとおき、直線y=2xをlとおく。実数tに対し、C上の点P(t, $3t^2-4t$)とlの距離をf(t)とする。
(1)-1≦a≦2の範囲の実数aに対し、定積分
g(a)=$\displaystyle\int_{-1}^af(t)dt$
を求めよ。
(2)aが0≦a≦2の範囲を動くとき、g(a)-f(a)の最大値および最小値を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{2}$ 座標平面上の放物線y=3$x^2$-4xをCとおき、直線y=2xをlとおく。実数tに対し、C上の点P(t, $3t^2-4t$)とlの距離をf(t)とする。
(1)-1≦a≦2の範囲の実数aに対し、定積分
g(a)=$\displaystyle\int_{-1}^af(t)dt$
を求めよ。
(2)aが0≦a≦2の範囲を動くとき、g(a)-f(a)の最大値および最小値を求めよ。
2023東京大学文系過去問
大学入試問題#475「エフ(f)3つ!」 早稲田大学(2004) #逆関数

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
実数$a$に対して
$f(x)=ax+2$とする
$f(f(f(x)))$が$f(x)$の逆関数になるような$a$の値を求めよ。
出典:2004年早稲田大学理工 入試問題
この動画を見る
実数$a$に対して
$f(x)=ax+2$とする
$f(f(f(x)))$が$f(x)$の逆関数になるような$a$の値を求めよ。
出典:2004年早稲田大学理工 入試問題
2023久留米大(医)確率漸化式

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
無作為に1個取り出して戻すを繰り返す.
n回取り出したときの数の合計が3の倍数になる確率$P_{n}$を求めよ.
久留米大(医)過去問
この動画を見る
無作為に1個取り出して戻すを繰り返す.
n回取り出したときの数の合計が3の倍数になる確率$P_{n}$を求めよ.
久留米大(医)過去問
2023年京大数学!整式の割り算!2通りで解説します【京都大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
整式$x^{2023}-1$を整式$x^{4}+x^{3}+x^{2}+x+1$で割ったときの余りを求めよ。
京都大過去問
この動画を見る
整式$x^{2023}-1$を整式$x^{4}+x^{3}+x^{2}+x+1$で割ったときの余りを求めよ。
京都大過去問
福田の数学〜東京大学2023年理系第5問〜整式の割り算と2重因子をもつ条件

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#剰余の定理・因数定理・組み立て除法と高次方程式#微分とその応用#微分法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ 整式f(x)=$(x-1)^2(x-2)$を考える。
(1)g(x)を実数を係数とする整式とし、g(x)をf(x)で割った余りをr(x)とおく。
$g(x)^7$をf(x)で割った余りと$r(x)^7$をf(x)で割った余りが等しいことを示せ。
(2)a,bを実数とし、h(x)=$x^2$+ax+b とおく。$h(x)^7$をf(x)で割った余りを$h_1(x)$とおき、$h_1(x)^7$をf(x)で割った余りを$h_2(x)$とおく。$h_2(x)$がh(x)に等しくなるようなa,bの組を全て求めよ。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{5}$ 整式f(x)=$(x-1)^2(x-2)$を考える。
(1)g(x)を実数を係数とする整式とし、g(x)をf(x)で割った余りをr(x)とおく。
$g(x)^7$をf(x)で割った余りと$r(x)^7$をf(x)で割った余りが等しいことを示せ。
(2)a,bを実数とし、h(x)=$x^2$+ax+b とおく。$h(x)^7$をf(x)で割った余りを$h_1(x)$とおき、$h_1(x)^7$をf(x)で割った余りを$h_2(x)$とおく。$h_2(x)$がh(x)に等しくなるようなa,bの組を全て求めよ。
2023東京大学理系過去問
大学入試問題#474「沼にはまりがち」 信州大学後期(2011) #不定積分
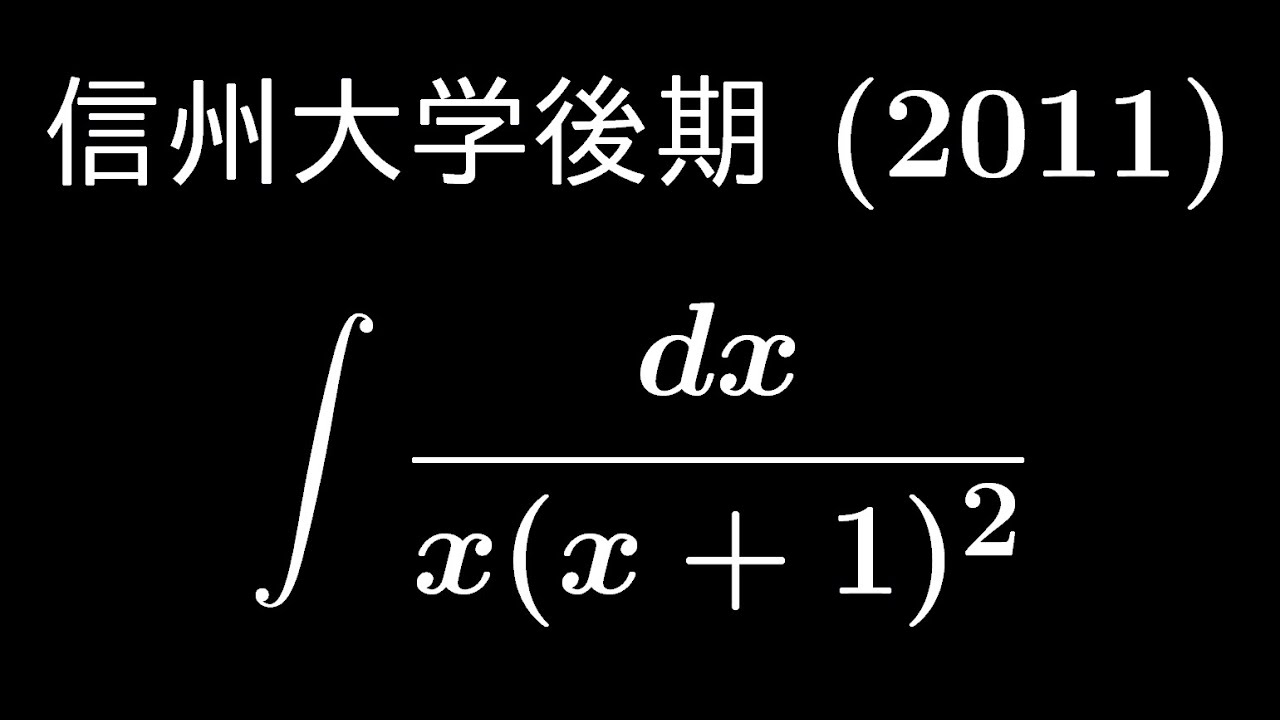
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x(x+1)^2}$
出典:2011年信州大学後期 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x(x+1)^2}$
出典:2011年信州大学後期 入試問題
2023久留米大(医)複素数の計算

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
複素数Zは$\vert Z \vert =1$で$Z^2-2Z+\dfrac{1}{Z}$が純虚数であるZの値を求めよ。
久留米大(医)過去問
この動画を見る
複素数Zは$\vert Z \vert =1$で$Z^2-2Z+\dfrac{1}{Z}$が純虚数であるZの値を求めよ。
久留米大(医)過去問
福田の数学〜東京大学2023年理系第4問〜球面と三角形が共有点をもつ条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#平面上のベクトル#空間ベクトル#集合と命題(集合・命題と条件・背理法)#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標空間内の4点O(0,0,0), A(2,0,0), B(1,1,1), C(1,2,3)を考える。
(1)$\overrightarrow{OP}\bot\overrightarrow{OA}$, $\overrightarrow{OP}\bot\overrightarrow{OB}$, $\overrightarrow{OP}\bot\overrightarrow{OC}$=1 を満たす点Pの座標を求めよ。
(2)点Pから直線ABに垂線を下ろし、その垂線と直線ABの交点をHとする。
$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)点Qを$\overrightarrow{OQ}$=$\frac{3}{4}\overrightarrow{OA}$+$\overrightarrow{OP}$により定め、Qを中心とする半径rの球面Sを考える。Sが三角形OHBと共有点を持つようなrの範囲を求めよ。ただし、三角形OHBは3点O, H, Bを含む平面内にあり、周とその内部からなるものとする。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{4}$ 座標空間内の4点O(0,0,0), A(2,0,0), B(1,1,1), C(1,2,3)を考える。
(1)$\overrightarrow{OP}\bot\overrightarrow{OA}$, $\overrightarrow{OP}\bot\overrightarrow{OB}$, $\overrightarrow{OP}\bot\overrightarrow{OC}$=1 を満たす点Pの座標を求めよ。
(2)点Pから直線ABに垂線を下ろし、その垂線と直線ABの交点をHとする。
$\overrightarrow{OH}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)点Qを$\overrightarrow{OQ}$=$\frac{3}{4}\overrightarrow{OA}$+$\overrightarrow{OP}$により定め、Qを中心とする半径rの球面Sを考える。Sが三角形OHBと共有点を持つようなrの範囲を求めよ。ただし、三角形OHBは3点O, H, Bを含む平面内にあり、周とその内部からなるものとする。
2023東京大学理系過去問
大学入試問題#473「計算は大変かもしれない」 信州大学 理・医 (2011) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int log(1+\sqrt{ x }) dx$
出典:2011年信州大学 入試問題
この動画を見る
$\displaystyle \int log(1+\sqrt{ x }) dx$
出典:2011年信州大学 入試問題
福田の数学〜東京工業大学2023年理系第5問(PART2)〜4直線に接する球面の決定

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
大学入試問題#472「最後の計算量を減らすには?」 弘前大学(2012) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{e^{4x}}{e^x+1} dx$
出典:2012年弘前大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{e^{4x}}{e^x+1} dx$
出典:2012年弘前大学 入試問題
2023早稲田(社)三乗根の計算

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}$とする.
(1)$a^3$をaの一次式で表せ.
(2)aは整数であることを示せ.
(3)$b=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}$とするとき,bを越えない最大の整数を求めよ.
2023早稲田大(社)過去問
この動画を見る
$a=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}$とする.
(1)$a^3$をaの一次式で表せ.
(2)aは整数であることを示せ.
(3)$b=\sqrt[3]{5\sqrt2+7}-\sqrt[3]{5\sqrt2-7}$とするとき,bを越えない最大の整数を求めよ.
2023早稲田大(社)過去問
福田の数学〜東京工業大学2023年理系第5問(PART1)〜4直線に接する球面の決定

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#図形と方程式#点と直線#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{5}$ xyz空間の4点A(1,0,0), B(1,1,1), C(-1,1,-1), D(-1,0,0)を考える。
(1)2直線AB,BCから等距離にある点全体のなす図形を求めよ。
(2)4直線AB, BC, CD, DAに共に接する球面の中心と半径の組を全て求めよ。
2023東京工業大学理系過去問
2023年京大の数学!最大値・最小値【京都大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
次の関数$f(x)$の最大値と最小値を求めよ。
$f(x)=e^{-x^{2}}+\dfrac{1}{4}x^{2}+1+\dfrac{1}{e^{-x^{2}}+\dfrac{1}{4}x^{2}+1}$ $(-1≦x≦1)$
ただし、$e$は自然対数の底であり、その値は$e=2.71・・・$である。
2023京都大過去問
この動画を見る
次の関数$f(x)$の最大値と最小値を求めよ。
$f(x)=e^{-x^{2}}+\dfrac{1}{4}x^{2}+1+\dfrac{1}{e^{-x^{2}}+\dfrac{1}{4}x^{2}+1}$ $(-1≦x≦1)$
ただし、$e$は自然対数の底であり、その値は$e=2.71・・・$である。
2023京都大過去問
大学入試問題#471「深夜1時でストック0」 信州大学後期(2013) 不定積分
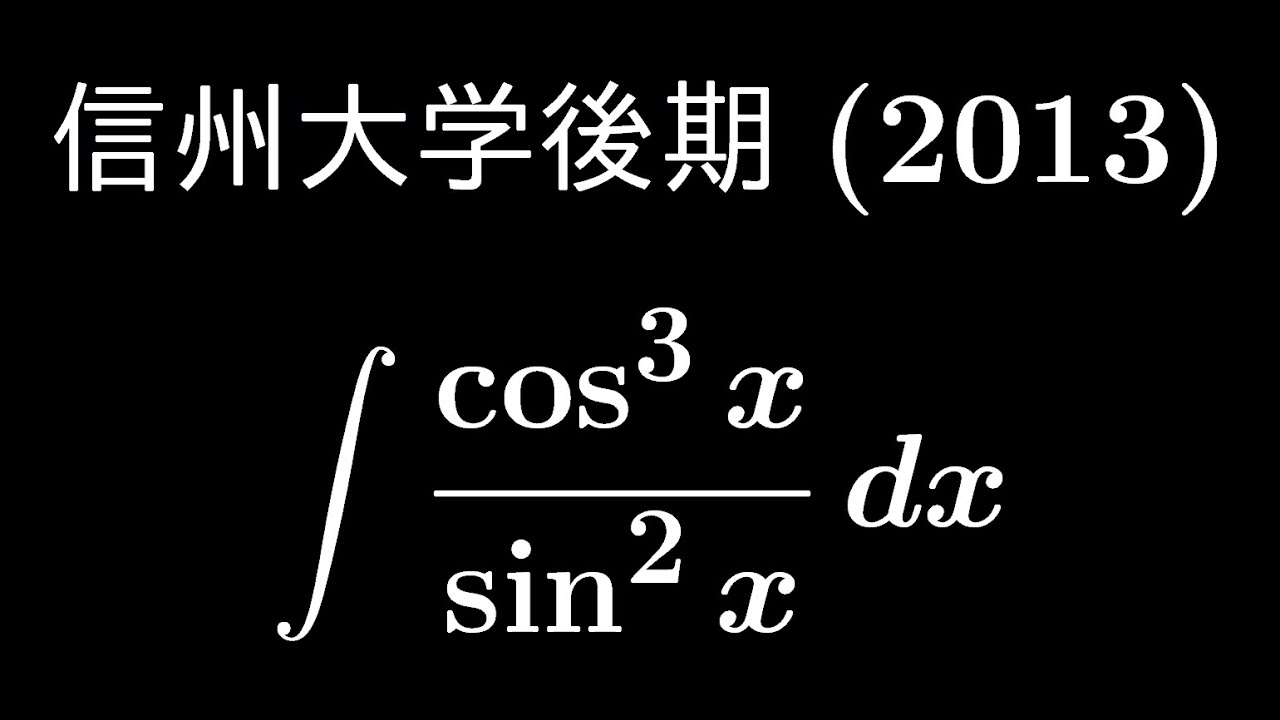
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典:2013年信州大学後期 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos^3\ x}{\sin^2\ x} dx$
出典:2013年信州大学後期 入試問題
2023昭和大(医)漸化式の基本問題

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#昭和大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=4$
$\displaystyle \sum_{k=1}^{n+1} a_k=4,a_n+8$
一般項$a_n$を求めよ.
昭和大(医)過去問
この動画を見る
$a_1=4$
$\displaystyle \sum_{k=1}^{n+1} a_k=4,a_n+8$
一般項$a_n$を求めよ.
昭和大(医)過去問
福田の数学〜東京慈恵会医科大学2023年医学部第2問〜定積分で表された関数と極限

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ nを自然数、aを正の定数とする。関数f(x)は等式
$f(x)=x+\displaystyle\frac{1}{n}\int_0^xf(t)dt$
を満たし、関数g(x)は$g(x)$=$ae^{-\frac{x}{n}}+a$とする。2つの曲線y=f(x)とy=g(x)はある1点を共有し、その点における2つの接線が直交するとき、次の問いに答えよ。ただし、eは自然対数の底とする。
(1)h(x)=$e^{-\frac{x}{n}}f(x)$とおくとき、導関数h'(x)とh(x)を求めよ。
(2)aをnを用いて表せ。
(3)2つの曲線y=f(x), y=g(x)とy軸で囲まれた部分の面積を$S_n$とするとき、
極限値$\displaystyle\lim_{n \to \infty}\frac{S_1+S_2+\cdots+S_n}{n^3}$ を求めよ。
2023東京慈恵会医科大学医学部過去問
この動画を見る
$\Large\boxed{2}$ nを自然数、aを正の定数とする。関数f(x)は等式
$f(x)=x+\displaystyle\frac{1}{n}\int_0^xf(t)dt$
を満たし、関数g(x)は$g(x)$=$ae^{-\frac{x}{n}}+a$とする。2つの曲線y=f(x)とy=g(x)はある1点を共有し、その点における2つの接線が直交するとき、次の問いに答えよ。ただし、eは自然対数の底とする。
(1)h(x)=$e^{-\frac{x}{n}}f(x)$とおくとき、導関数h'(x)とh(x)を求めよ。
(2)aをnを用いて表せ。
(3)2つの曲線y=f(x), y=g(x)とy軸で囲まれた部分の面積を$S_n$とするとき、
極限値$\displaystyle\lim_{n \to \infty}\frac{S_1+S_2+\cdots+S_n}{n^3}$ を求めよ。
2023東京慈恵会医科大学医学部過去問
大学入試問題#470「誘導なくてもどうにかできそう」 信州大学 理・医学部(2021) #微積の応用

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#色々な関数の導関数#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\forall\ a,b$
$f(a+b)=f(a)+f(b)+4ab$
$f'(0)=2$
(1)
$f(0)$を求めよ
(2)
$f(x)$は微分可能を示せ
$f(x)$を求めよ
(3)
$\displaystyle \lim_{ x \to \infty } \displaystyle \int_{1}^{x} \displaystyle \frac{1}{f(t)}dt(x \gt 1)$
出典:2021年信州大学 入試問題
この動画を見る
$\forall\ a,b$
$f(a+b)=f(a)+f(b)+4ab$
$f'(0)=2$
(1)
$f(0)$を求めよ
(2)
$f(x)$は微分可能を示せ
$f(x)$を求めよ
(3)
$\displaystyle \lim_{ x \to \infty } \displaystyle \int_{1}^{x} \displaystyle \frac{1}{f(t)}dt(x \gt 1)$
出典:2021年信州大学 入試問題
