 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
福田の数学〜立教大学2022年理学部第1問(1)〜対数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(1)$実数$x$に関する方程式
$2\log(1-x)-\log(5-x)=\log 2$
を解くと$x=\boxed{ア}$である.
立教大学2022年理学部過去問
この動画を見る
$\boxed{1}(1)$実数$x$に関する方程式
$2\log(1-x)-\log(5-x)=\log 2$
を解くと$x=\boxed{ア}$である.
立教大学2022年理学部過去問
大学入試問題#306 早稲田大学2013 #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{\sqrt{ 1-x^2 }}{1+x}dx$
出典:2013年早稲田大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{\sqrt{ 1-x^2 }}{1+x}dx$
出典:2013年早稲田大学 入試問題
福田の数学〜明治大学2022年理工学部第3問〜平行六面体の対角線を軸とした回転体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#微分法と積分法#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
右の図(※動画参照)のような平行六面体OABC-DEFGにおいて、
すべての辺の長さは1であり、$\overrightarrow{ OA },\ \overrightarrow{ OC },\ \overrightarrow{ OD }$のどの
2つのなす角も$\frac{\pi}{3}$であるとする。
(1)$\overrightarrow{ OF }$を$\overrightarrow{ OA },\ \overrightarrow{ OC },\ \overrightarrow{ OD }$を用いて表すと、
$\overrightarrow{ OF }= \boxed{き}$である。
(2)$|\overrightarrow{ OF }|,\ \cos \angle AOF$を求めると$|\overrightarrow{ OF }|= \boxed{く},$
$\ \cos \angle AOF=\boxed{け}$である。
(3)三角形ACDを底面とする三角錐OACDを、直線OFの周りに1回転して
できる円錐の体積は$\boxed{こ}$である。
(4)対角線OF上に点Pをとり、$|\overrightarrow{ OP }|=t$とおく。点Pを通り、$\overrightarrow{ OF }$に垂直な平面
をHとする。平行六面体$OABC-DEFG$を平面Hで切った時の断面が六角形
となるようなtの範囲は$\boxed{さ}$である。このとき、平面Hと辺AEの交点をQ
として、$|\overrightarrow{ AQ }|$をtの式で表すと$|\overrightarrow{ AQ }|=\boxed{し}$である。
また、$|\overrightarrow{ PQ }|^2$を$t$の式で表すと
$|\overrightarrow{ PQ }|^2=|\overrightarrow{ OQ }|^2-|\overrightarrow{ OP }|^2=\boxed{す}$
である。
(5)平行六面体$OABC-DEFG$を、直線OFの周りに1回転してできる回転体
の体積は$\boxed{こ}$である。
2022明治大学理工学部過去問
この動画を見る
右の図(※動画参照)のような平行六面体OABC-DEFGにおいて、
すべての辺の長さは1であり、$\overrightarrow{ OA },\ \overrightarrow{ OC },\ \overrightarrow{ OD }$のどの
2つのなす角も$\frac{\pi}{3}$であるとする。
(1)$\overrightarrow{ OF }$を$\overrightarrow{ OA },\ \overrightarrow{ OC },\ \overrightarrow{ OD }$を用いて表すと、
$\overrightarrow{ OF }= \boxed{き}$である。
(2)$|\overrightarrow{ OF }|,\ \cos \angle AOF$を求めると$|\overrightarrow{ OF }|= \boxed{く},$
$\ \cos \angle AOF=\boxed{け}$である。
(3)三角形ACDを底面とする三角錐OACDを、直線OFの周りに1回転して
できる円錐の体積は$\boxed{こ}$である。
(4)対角線OF上に点Pをとり、$|\overrightarrow{ OP }|=t$とおく。点Pを通り、$\overrightarrow{ OF }$に垂直な平面
をHとする。平行六面体$OABC-DEFG$を平面Hで切った時の断面が六角形
となるようなtの範囲は$\boxed{さ}$である。このとき、平面Hと辺AEの交点をQ
として、$|\overrightarrow{ AQ }|$をtの式で表すと$|\overrightarrow{ AQ }|=\boxed{し}$である。
また、$|\overrightarrow{ PQ }|^2$を$t$の式で表すと
$|\overrightarrow{ PQ }|^2=|\overrightarrow{ OQ }|^2-|\overrightarrow{ OP }|^2=\boxed{す}$
である。
(5)平行六面体$OABC-DEFG$を、直線OFの周りに1回転してできる回転体
の体積は$\boxed{こ}$である。
2022明治大学理工学部過去問
大学入試問題#305 明治大学(2013) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ h \to \infty }\displaystyle \frac{log(1+5h+6h^2)}{h}$
出典:2013年明治大学 入試問題
この動画を見る
$\displaystyle \lim_{ h \to \infty }\displaystyle \frac{log(1+5h+6h^2)}{h}$
出典:2013年明治大学 入試問題
福田の数学〜明治大学2022年理工学部第2問〜平面図形の計量

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#英語(高校生)#平面図形#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#明治大学#数学(高校生)#明治大学
指導講師:
福田次郎
問題文全文(内容文):
平面上の長さ3の線分AB上に、$AP=t\ (0 \lt t \lt 3)$を満たす点Pをとる。
中心を$O$とする半径1の円Oが、線分ABと点Pで接しているとする。
$\alpha=\angle OAB,\ \beta=\angle OBA$
とおく。$\tan\alpha,\ \tan\beta,\tan(\alpha+\beta)$を$t$で表すと、
$\tan\alpha=\boxed{あ},\ \tan\beta=\boxed{い},$
$\ \tan(\alpha+\beta)=\boxed{う}$である。
$0 \lt \alpha+\beta \lt \frac{\pi}{2}$であるようなtの範囲は$\boxed{え}$である。
tは$\boxed{え}$の範囲にあるとする。点$A,\ B$から円Oに引いた接線の接点のうち、
Pでないものをそれぞれ$Q,\ R$とすると、$\angle QAB+\angle RBA \lt \pi$である。
したがって、線分AQのQの方への延長と線分BRのRの方への延長は交わり、
その交点をCとすると、円Oは三角形ABCの内接円である。
このとき、線分CQの長さをtで表すと$\ \boxed{お}$である。
また、$t$が$\boxed{え}$の範囲を動くとき、三角形ABCの面積Sの取り得る値の範囲は$\boxed{か}$である。
2022明治大学理工学部過去問
この動画を見る
平面上の長さ3の線分AB上に、$AP=t\ (0 \lt t \lt 3)$を満たす点Pをとる。
中心を$O$とする半径1の円Oが、線分ABと点Pで接しているとする。
$\alpha=\angle OAB,\ \beta=\angle OBA$
とおく。$\tan\alpha,\ \tan\beta,\tan(\alpha+\beta)$を$t$で表すと、
$\tan\alpha=\boxed{あ},\ \tan\beta=\boxed{い},$
$\ \tan(\alpha+\beta)=\boxed{う}$である。
$0 \lt \alpha+\beta \lt \frac{\pi}{2}$であるようなtの範囲は$\boxed{え}$である。
tは$\boxed{え}$の範囲にあるとする。点$A,\ B$から円Oに引いた接線の接点のうち、
Pでないものをそれぞれ$Q,\ R$とすると、$\angle QAB+\angle RBA \lt \pi$である。
したがって、線分AQのQの方への延長と線分BRのRの方への延長は交わり、
その交点をCとすると、円Oは三角形ABCの内接円である。
このとき、線分CQの長さをtで表すと$\ \boxed{お}$である。
また、$t$が$\boxed{え}$の範囲を動くとき、三角形ABCの面積Sの取り得る値の範囲は$\boxed{か}$である。
2022明治大学理工学部過去問
大学入試問題#304 早稲田大学2010 #区分求積法 #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ (n+1)(n+2)-(n+n) }$
出典:2010年早稲田大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ (n+1)(n+2)-(n+n) }$
出典:2010年早稲田大学 入試問題
福田の数学〜明治大学2022年理工学部第1問(3)〜接線の本数と接点の個数

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#接線と法線・平均値の定理#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(3)$f(x)=(\log x)^2+2\log x+3$として、座標平面上の曲線$y=f(x)$を$C$とする。
ただし、$\log x$は$x$の自然対数を表し、$e$を自然対数の底とする。
$(\textrm{a})$関数$f(x)$は$x=\frac{\boxed{ソ}}{e}$のとき最小値$\boxed{タ}$をとる。
$(\textrm{b})$曲線Cの変曲点の座標は$(\boxed{チ},\ \boxed{ツ})$である。
$(\textrm{c})$直線$y=\boxed{ツ}$と曲線Cで囲まれた図形の面積は
$\frac{\boxed{テ}}{e^2}$である。
$(\textrm{d})a$を実数とする。曲線$C$の接線で、点$(0,\ a)$を通るものがちょうど1本あるとき、
aの値は$\boxed{ト}$である。
$(\textrm{e})b$を実数とする。曲線Cの2本の接線が点$(0,\ b)$で垂直に交わるとき、
bの値は$\frac{\boxed{ナ}}{\boxed{ニ}}$である。
2022明治大学理工学部過去問
この動画を見る
(3)$f(x)=(\log x)^2+2\log x+3$として、座標平面上の曲線$y=f(x)$を$C$とする。
ただし、$\log x$は$x$の自然対数を表し、$e$を自然対数の底とする。
$(\textrm{a})$関数$f(x)$は$x=\frac{\boxed{ソ}}{e}$のとき最小値$\boxed{タ}$をとる。
$(\textrm{b})$曲線Cの変曲点の座標は$(\boxed{チ},\ \boxed{ツ})$である。
$(\textrm{c})$直線$y=\boxed{ツ}$と曲線Cで囲まれた図形の面積は
$\frac{\boxed{テ}}{e^2}$である。
$(\textrm{d})a$を実数とする。曲線$C$の接線で、点$(0,\ a)$を通るものがちょうど1本あるとき、
aの値は$\boxed{ト}$である。
$(\textrm{e})b$を実数とする。曲線Cの2本の接線が点$(0,\ b)$で垂直に交わるとき、
bの値は$\frac{\boxed{ナ}}{\boxed{ニ}}$である。
2022明治大学理工学部過去問
大学入試問題#303 横浜市立大学医学部(2011) #積分の応用 #微分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)$微分可能
$f(x)+\displaystyle \int_{0}^{x}f(t)e^{x-t}dt=\sin\ x$をみたす
$f(0),f'(x),f(x)$を求めよ
出典:2011年横浜市立大学医学部 入試問題
この動画を見る
$f(x)$微分可能
$f(x)+\displaystyle \int_{0}^{x}f(t)e^{x-t}dt=\sin\ x$をみたす
$f(0),f'(x),f(x)$を求めよ
出典:2011年横浜市立大学医学部 入試問題
福田の数学〜明治大学2022年理工学部第1問(2)〜2次方程式の解の存在範囲

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#複素数と方程式#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)座標平面上の曲線$x^2+2xy+2y^2=5$を$C$とする。
$(\textrm{a})$直線$2x+y=t$が曲線$C$と共有点をもつとき、実数$t$の取り得る値の範囲は
$\boxed{コ}\leqq t \leqq \boxed{サ}$である。
$(\textrm{b})$直線$2x+y=1$が曲線$C$と$x \geqq 0$の範囲で共有点を少なくとも1個もつとき、
実数$t$ の取り得る値の範囲は$-\frac{1}{2}\sqrt{\boxed{シス}} \leqq t \leqq \boxed{セ}$である。
2022明治大学理工学部過去問
この動画を見る
(2)座標平面上の曲線$x^2+2xy+2y^2=5$を$C$とする。
$(\textrm{a})$直線$2x+y=t$が曲線$C$と共有点をもつとき、実数$t$の取り得る値の範囲は
$\boxed{コ}\leqq t \leqq \boxed{サ}$である。
$(\textrm{b})$直線$2x+y=1$が曲線$C$と$x \geqq 0$の範囲で共有点を少なくとも1個もつとき、
実数$t$ の取り得る値の範囲は$-\frac{1}{2}\sqrt{\boxed{シス}} \leqq t \leqq \boxed{セ}$である。
2022明治大学理工学部過去問
大学入試問題#302 青山学院大学(2010) #定積分
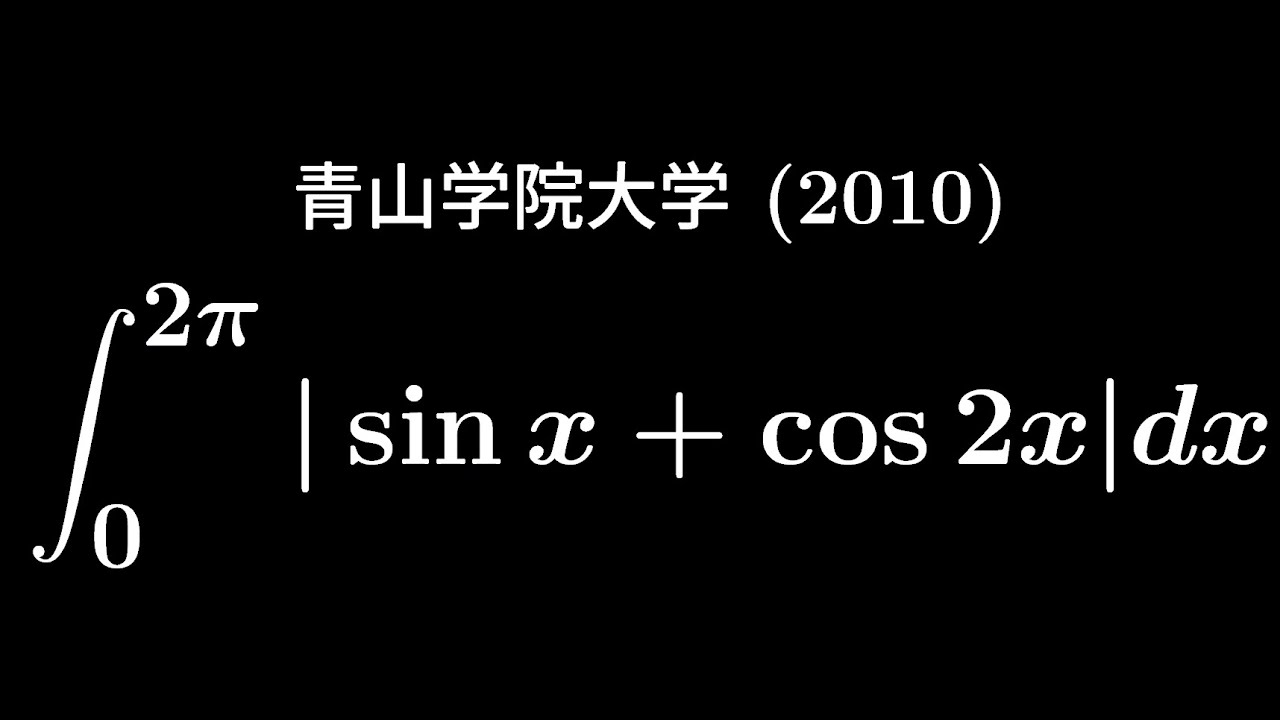
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi}|\sin\ x+\cos2x|dx$
出典:2010年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi}|\sin\ x+\cos2x|dx$
出典:2010年青山学院大学 入試問題
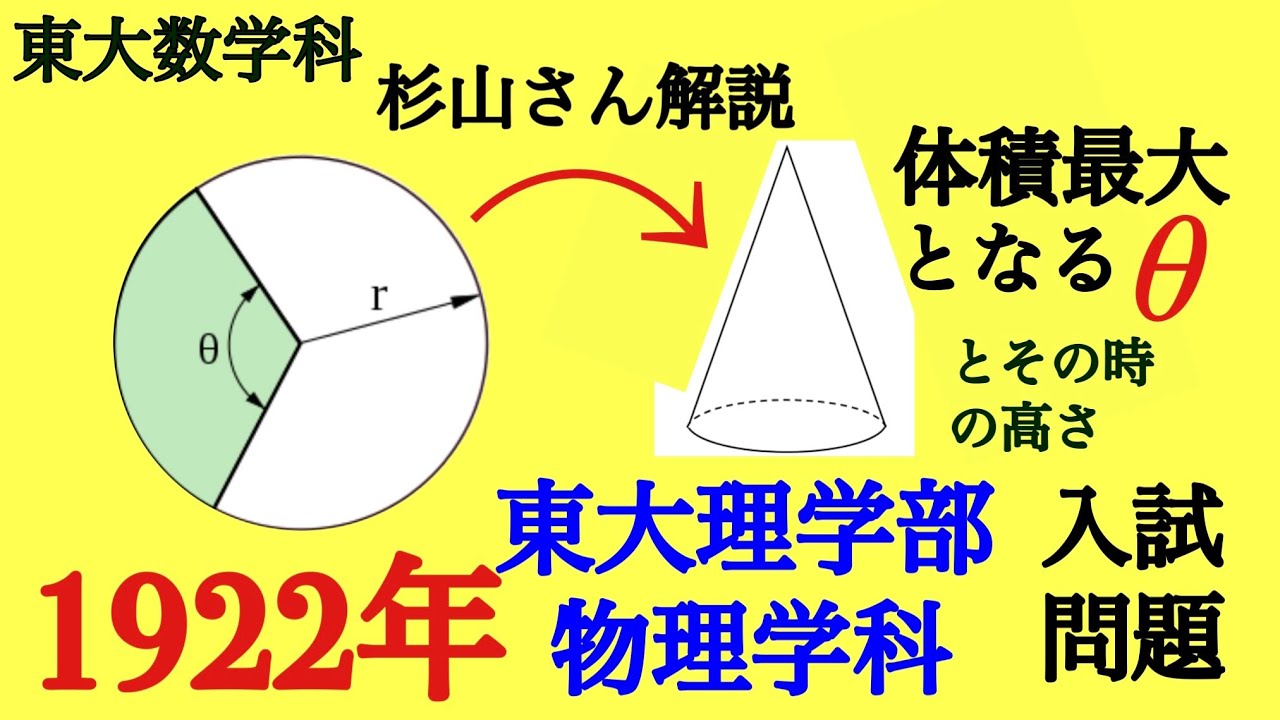
100年前の東大入試問題を東大数学科の杉山さんが解説
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
体積最大となる$\theta$とその時の高さを求めよ.
100年前の東大入試問題に関して解説します.
1922東大理物理学科入試問題
この動画を見る
体積最大となる$\theta$とその時の高さを求めよ.
100年前の東大入試問題に関して解説します.
1922東大理物理学科入試問題
福田の数学〜明治大学2022年理工学部第1問(1)〜整式と二項定理とドモアブルの定理

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数平面#整式の除法・分数式・二項定理#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
(1)$f(x)=(x+2)(x-1)^{10}$とし、この式を展開して
$f(x)=a_0+a_1x+a_2x^2+...+a_{11}x^{11}$
と表す。ただし、$a_0,a_1,...,a_{11}$は定数である。
$(\textrm{a})$多項式$f(x)$を$x-2$で割った時の余りは$\boxed{ア}$である。
$(\textrm{b})a_{10}=-\ \boxed{イ}$である。
$(\textrm{c})a_0+a_2+a_4+a_6+a_8+a_{10}=\boxed{ウエオ}$である。
$(\textrm{d})\ \ \ \ f(i)=\boxed{カキ}-\boxed{クケ}\ i \ $である。ただし、$i$は虚数単位である。
2022明治大学理工学部過去問
この動画を見る
(1)$f(x)=(x+2)(x-1)^{10}$とし、この式を展開して
$f(x)=a_0+a_1x+a_2x^2+...+a_{11}x^{11}$
と表す。ただし、$a_0,a_1,...,a_{11}$は定数である。
$(\textrm{a})$多項式$f(x)$を$x-2$で割った時の余りは$\boxed{ア}$である。
$(\textrm{b})a_{10}=-\ \boxed{イ}$である。
$(\textrm{c})a_0+a_2+a_4+a_6+a_8+a_{10}=\boxed{ウエオ}$である。
$(\textrm{d})\ \ \ \ f(i)=\boxed{カキ}-\boxed{クケ}\ i \ $である。ただし、$i$は虚数単位である。
2022明治大学理工学部過去問
大学入試問題#301 旭川医科大学(2011) #定積分
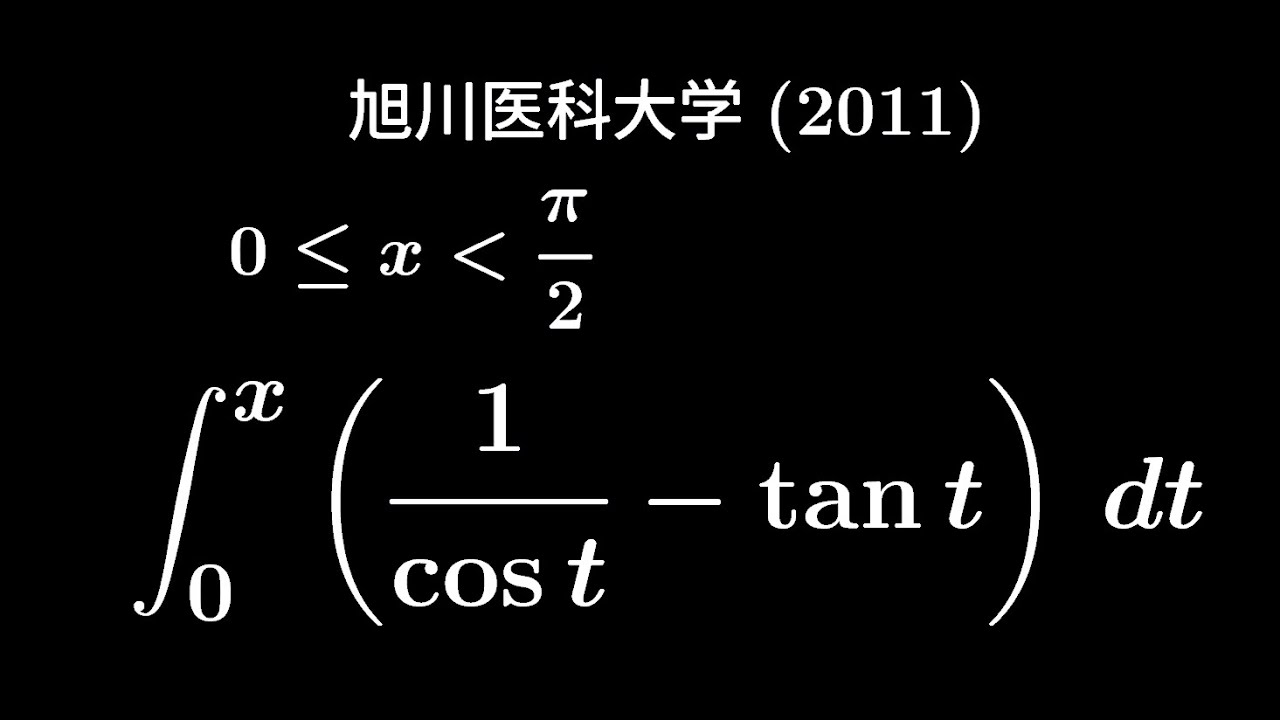
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq x \lt \displaystyle \frac{\pi}{2}$
$\displaystyle \int_{0}^{x}(\displaystyle \frac{1}{\cos\ t}-\tan\ t)dt$
出典:2011年旭川医科大学 入試問題
この動画を見る
$0 \leqq x \lt \displaystyle \frac{\pi}{2}$
$\displaystyle \int_{0}^{x}(\displaystyle \frac{1}{\cos\ t}-\tan\ t)dt$
出典:2011年旭川医科大学 入試問題
素数であることの証明【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を2以上の整数とする。$3^n-2^n$が素数ならば$n$も素数であることを示せ。
京都大過去問
この動画を見る
$n$を2以上の整数とする。$3^n-2^n$が素数ならば$n$も素数であることを示せ。
京都大過去問
福田の数学〜明治大学2022年全学部統一入試理系第4問〜サイコロの目で決まる複素数の値に関する確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#複素数平面#確率#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$i$を虚数単位とし、$z=\frac{1}{2}+\frac{\sqrt3}{2}\ i\$とおく。
さいころを3回ふり、出た目を順に$a,\ b,\ c$とする。
このとき、積$\ abc$が3の倍数となる確率は$\frac{\boxed{アイ}}{\boxed{ウエ}}$である。
また、$z^{abc}=-1$となる確率は$\frac{\boxed{オカ}}{\boxed{キクケ}}$であり、
$z^{abc}=1$となる確率は$\frac{\boxed{コサシ}}{\boxed{スセソ}}$である。
2022明治大学全統理系過去問
この動画を見る
$i$を虚数単位とし、$z=\frac{1}{2}+\frac{\sqrt3}{2}\ i\$とおく。
さいころを3回ふり、出た目を順に$a,\ b,\ c$とする。
このとき、積$\ abc$が3の倍数となる確率は$\frac{\boxed{アイ}}{\boxed{ウエ}}$である。
また、$z^{abc}=-1$となる確率は$\frac{\boxed{オカ}}{\boxed{キクケ}}$であり、
$z^{abc}=1$となる確率は$\frac{\boxed{コサシ}}{\boxed{スセソ}}$である。
2022明治大学全統理系過去問
大学入試問題#300 新潟大学2010 #定積分 #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学
指導講師:
ますただ
問題文全文(内容文):
$F(x)=\displaystyle \int_{0}^{x}\sqrt{ 1+e^{2t} }\ dt$のとき
$\displaystyle \lim_{ x \to \infty }\{F(x)-e^x\}$を求めよ
出典:2010年新潟大学 入試問題
この動画を見る
$F(x)=\displaystyle \int_{0}^{x}\sqrt{ 1+e^{2t} }\ dt$のとき
$\displaystyle \lim_{ x \to \infty }\{F(x)-e^x\}$を求めよ
出典:2010年新潟大学 入試問題
福田の数学〜明治大学2022年全学部統一入試理系第3問〜2次曲線の極方程式と置換積分

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#2次曲線#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#明治大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a,\ h$を正の実数とする。座標平面において、原点Oからの距離が
直線$x=h$からの距離の$a$倍であるような点$P$の軌跡を考える。点$P$の座標を$(x,\ y)$とする
と、$x,\ y$は次の方程式を満たす。
$(1-\boxed{ア})\ x^2+2\ \boxed{イ}\ x+y^2=\boxed{ウ}...(1)$
$\boxed{ア},\ \boxed{イ},\ \boxed{ウ}$の解答群
$⓪a^2 ①h^2 ②a^3 ③a^2h ④ah^2$
$⑤h^3 ⑥b^4 ⑦a^2h^2 ⑧ah^3 ⑨h^4$
次に、座標平面の原点$O$を極、$x$軸の正の部分を始線とする極座標を考える。
点$P$の極座標を$(r\ \theta)$とする。$r \leqq h$を満たすとき、
点$P$の直交座標$(x,\ y)$を$a,\ h,\ θ$を用いて表すと
$(x,\ y)=(\frac{\boxed{エ}}{\boxed{オ}}\ \cos θ,\ \frac{\boxed{エ}}{\boxed{オ}}\ \sin θ)...(2) $
$\boxed{エ},\ \boxed{オ}$の解答群
$⓪h①ah②h^2③ah^2④1+a\cos θ$
$⑤1+a\sin θ ⑥a\cos θ-1⑦a\sin θ-1⑧1-a\cos θ ⑨1-a\sin θ$
(1)から、$a=\boxed{カ}$のとき、点$P$の軌跡は放物線$x=\boxed{キ}\ y^2+\boxed{ク}$となる。
この放物線とy軸で囲まれた図形の面積$S$は
$S=2\int_0^{\boxed{ケ}}xdy=2\int_0^{\boxed{ケ}}(\boxed{キ}\ y^2+\boxed{ク})dy=$
$\frac{\boxed{コ}}{\boxed{サ}}\ h^2$
である。したがって、(2)を利用すれば、置換積分法により次の等式が成り立つことが分かる。
$\int_0^{\frac{\pi}{2}}\frac{\cos θ}{(1+\cos θ)^2}dθ=\frac{\boxed{シ}}{\boxed{ス}}$
$\boxed{キ},\ \boxed{ク},\ \boxed{ケ}$の解答群
$⓪h ①2h ②\frac{h}{2} ③-\frac{h}{2} ④\frac{1}{h}$
$⑤-\frac{1}{h} ⑥\frac{1}{2h} ⑦-\frac{1}{2h} ⑧h^2 ⑨-h^2$
2022明治大学全統理系過去問
この動画を見る
$a,\ h$を正の実数とする。座標平面において、原点Oからの距離が
直線$x=h$からの距離の$a$倍であるような点$P$の軌跡を考える。点$P$の座標を$(x,\ y)$とする
と、$x,\ y$は次の方程式を満たす。
$(1-\boxed{ア})\ x^2+2\ \boxed{イ}\ x+y^2=\boxed{ウ}...(1)$
$\boxed{ア},\ \boxed{イ},\ \boxed{ウ}$の解答群
$⓪a^2 ①h^2 ②a^3 ③a^2h ④ah^2$
$⑤h^3 ⑥b^4 ⑦a^2h^2 ⑧ah^3 ⑨h^4$
次に、座標平面の原点$O$を極、$x$軸の正の部分を始線とする極座標を考える。
点$P$の極座標を$(r\ \theta)$とする。$r \leqq h$を満たすとき、
点$P$の直交座標$(x,\ y)$を$a,\ h,\ θ$を用いて表すと
$(x,\ y)=(\frac{\boxed{エ}}{\boxed{オ}}\ \cos θ,\ \frac{\boxed{エ}}{\boxed{オ}}\ \sin θ)...(2) $
$\boxed{エ},\ \boxed{オ}$の解答群
$⓪h①ah②h^2③ah^2④1+a\cos θ$
$⑤1+a\sin θ ⑥a\cos θ-1⑦a\sin θ-1⑧1-a\cos θ ⑨1-a\sin θ$
(1)から、$a=\boxed{カ}$のとき、点$P$の軌跡は放物線$x=\boxed{キ}\ y^2+\boxed{ク}$となる。
この放物線とy軸で囲まれた図形の面積$S$は
$S=2\int_0^{\boxed{ケ}}xdy=2\int_0^{\boxed{ケ}}(\boxed{キ}\ y^2+\boxed{ク})dy=$
$\frac{\boxed{コ}}{\boxed{サ}}\ h^2$
である。したがって、(2)を利用すれば、置換積分法により次の等式が成り立つことが分かる。
$\int_0^{\frac{\pi}{2}}\frac{\cos θ}{(1+\cos θ)^2}dθ=\frac{\boxed{シ}}{\boxed{ス}}$
$\boxed{キ},\ \boxed{ク},\ \boxed{ケ}$の解答群
$⓪h ①2h ②\frac{h}{2} ③-\frac{h}{2} ④\frac{1}{h}$
$⑤-\frac{1}{h} ⑥\frac{1}{2h} ⑦-\frac{1}{2h} ⑧h^2 ⑨-h^2$
2022明治大学全統理系過去問
大学入試問題#299 信州大学(2001 類題②) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{3}\displaystyle \frac{\sqrt{ x }}{\sqrt{ x+1 }-1}dx$
出典:2001年信州大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{3}\displaystyle \frac{\sqrt{ x }}{\sqrt{ x+1 }-1}dx$
出典:2001年信州大学 入試問題
福田の数学〜明治大学2022年全学部統一入試理系第2問〜方程式の実数解の個数

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a$は$0<a<1$を満たす定数とする。 次の方程式の異なる実数解の個数を求めよう。
$x^2=a^-x$
$f(x) = x^2a^x$ とおけば、
$f(x)$ は $x = [ア]$で極小値$[イ]$をとり、$x= [ウ]$で極大値$[エ]$をとる。
また、$lim(x→-∞) f(x)= [オ]$であり、$ lim(x→∞) f(x)=0$ である。
2022明治大学全統理系過去問
この動画を見る
$a$は$0<a<1$を満たす定数とする。 次の方程式の異なる実数解の個数を求めよう。
$x^2=a^-x$
$f(x) = x^2a^x$ とおけば、
$f(x)$ は $x = [ア]$で極小値$[イ]$をとり、$x= [ウ]$で極大値$[エ]$をとる。
また、$lim(x→-∞) f(x)= [オ]$であり、$ lim(x→∞) f(x)=0$ である。
2022明治大学全統理系過去問
大学入試問題#298 信州大学(2001 類題①) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
(1)
$\displaystyle \int_{1}^{3}\displaystyle \frac{x}{\sqrt{ x+1 }-1}dx$
(2)
$\displaystyle \int_{1}^{3}\displaystyle \frac{1}{\sqrt{ x+1 }-1}dx$
出典:2001年信州大学 入試問題
この動画を見る
(1)
$\displaystyle \int_{1}^{3}\displaystyle \frac{x}{\sqrt{ x+1 }-1}dx$
(2)
$\displaystyle \int_{1}^{3}\displaystyle \frac{1}{\sqrt{ x+1 }-1}dx$
出典:2001年信州大学 入試問題
【良問】素数を扱え!考え方をきっちり理解したい整数問題です【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$p$が素数ならば,$p^4+14$は素数でないことを示せ。
京都大過去問
この動画を見る
$p$が素数ならば,$p^4+14$は素数でないことを示せ。
京都大過去問
福田の数学〜明治大学2022年全学部統一入試理系第1問(3)〜無限級数と極限

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(3)$k$を自然数として、
$f(x)=\sum_{n=1}^{\infty}\frac{x^{2k}}{(1+4x^{2k})^{n-1}}$
とおく。このとき、$\lim_{x \to 0}f(x)=\boxed{カ}$となる。
$\boxed{カ}$の解答群
$⓪0 ①1 ②2 ③\frac{1}{2} ④4$
$⑤\frac{1}{4} ⑥2^k ⑦\frac{1}{2^k} ⑧4^k ⑨\frac{1}{4^k}$
2022明治大学全統理系過去問
この動画を見る
(3)$k$を自然数として、
$f(x)=\sum_{n=1}^{\infty}\frac{x^{2k}}{(1+4x^{2k})^{n-1}}$
とおく。このとき、$\lim_{x \to 0}f(x)=\boxed{カ}$となる。
$\boxed{カ}$の解答群
$⓪0 ①1 ②2 ③\frac{1}{2} ④4$
$⑤\frac{1}{4} ⑥2^k ⑦\frac{1}{2^k} ⑧4^k ⑨\frac{1}{4^k}$
2022明治大学全統理系過去問
大学入試問題#297 産業医科大学(2010) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\cos\ x-x^2-1}{x^2}$
出典:2010年産業医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\cos\ x-x^2-1}{x^2}$
出典:2010年産業医科大学 入試問題
福田の数学〜明治大学2022年全学部統一入試理系第1問(2)〜定積分と極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(2)$\log$を自然対数とするとき、次の等式が成り立つ。
$\lim_{h \to 0}\int_{\frac{\pi}{3}}^{\frac{\pi}{3}+h}\log(|\sin t|^{\frac{1}{h}})dt=$
$\frac{1}{\boxed{ウ}}\log\frac{\boxed{エ}}{\boxed{オ}}$
2022明治大学全統理系過去問
この動画を見る
(2)$\log$を自然対数とするとき、次の等式が成り立つ。
$\lim_{h \to 0}\int_{\frac{\pi}{3}}^{\frac{\pi}{3}+h}\log(|\sin t|^{\frac{1}{h}})dt=$
$\frac{1}{\boxed{ウ}}\log\frac{\boxed{エ}}{\boxed{オ}}$
2022明治大学全統理系過去問
大学入試問題#296 電気通信大学(2012) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{4}\displaystyle \frac{dx}{x^2+x-2}$
出典:2012年電気通信大学 入試問題
この動画を見る
$\displaystyle \int_{2}^{4}\displaystyle \frac{dx}{x^2+x-2}$
出典:2012年電気通信大学 入試問題
福田の数学〜明治大学2022年全学部統一入試理系第1問(1)〜面積計算

単元:
#大学入試過去問(数学)#積分とその応用#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(1)曲線$y=1+\sin^2 x$と$x$軸、$y$軸、
および直線$x=\pi$で囲まれた図形の面積は
$\frac{\boxed{ア}}{\boxed{イ}}\ \pi$となる。
2022明治大学全統理系過去問
この動画を見る
(1)曲線$y=1+\sin^2 x$と$x$軸、$y$軸、
および直線$x=\pi$で囲まれた図形の面積は
$\frac{\boxed{ア}}{\boxed{イ}}\ \pi$となる。
2022明治大学全統理系過去問
大学入試問題#295 防衛大学校(2009) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#防衛大学校#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log2}^{log4}\displaystyle \frac{2e^x-2e^{-x}}{e^{2x}+e^{-2x}+1}dx$
出典:2009年防衛大学校
この動画を見る
$\displaystyle \int_{log2}^{log4}\displaystyle \frac{2e^x-2e^{-x}}{e^{2x}+e^{-2x}+1}dx$
出典:2009年防衛大学校
福田の数学〜明治大学2022年全学部統一入試12AB第3問〜漸化式の図形への応用

単元:
#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数列#漸化式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
(1)三角形$ABC$の内接円が辺$AB$と接する点をPとし、
辺$BC$と接する点を$Q$とし、辺$CA$と接する点をRとする。
$\angle A$の大きさを$θ$とすると、$\angle APR=\boxed{ア}$であり、
$\angle PQR=\boxed{ア}$である。
$\boxed{ア}$の解答群
$⓪0 ①\frac{\pi}{2} ②θ ③\frac{θ}{2} ④\frac{\pi}{2}-θ ⑤\frac{\pi-θ}{2}$
$⑥\pi-\frac{θ}{2} ⑦\pi-θ ⑧\frac{\pi-3θ}{2} ⑨\frac{\pi}{2}-3θ$
(2)三角形$T_1$の3つの角のうち、角の大きさが最小のものは$\frac{\pi}{6}$で、
最大のものは$\frac{\pi}{2}$であるとする。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の内接円を$O_n$とし、
$T_n$と$O_n$とが接する3つの点を頂点とするような三角形を$T_{n+1}$とする。
このとき、三角形$T_2$の3つの角のうち、
角の大きさが最小のものは$\frac{\pi}{\boxed{イ}}$で、
最大のものは$\frac{\boxed{ウ}\ \pi}{\boxed{エオ}}$である。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の3つの角のうち、
角の大きさが最小のものを$a_n$とし、最大のものを$b_n$とする。三角形$T_{n+1}$について、
$a_{n+1}=\boxed{カ},\ \ \ b_{n+1}=\boxed{キ}$
と表せる。この式より
$a_n+b_n=\frac{\boxed{ク}}{\boxed{ケ}}\pi,$
$b_n-a_n=\frac{\pi}{\boxed{コ}・\boxed{サ}^{n-1}}$
であり、$a_n=\frac{\pi}{\boxed{シ}}(1-\frac{1}{\boxed{ス}^n}) $である。
$\boxed{カ}、\boxed{キ}$の解答群
$⓪\frac{a_n}{2} ①\frac{b_n}{2} ②\frac{\pi}{2}-a_n ③\frac{\pi}{2}-b_n ④\frac{\pi-a_n}{2}$
$⑤\frac{\pi-b_n}{2} ⑥\pi-\frac{a_n}{2} ⑦\pi-\frac{b_n}{2} ⑧\pi-a_n ⑨\pi-b_n$
2022明治大学全統過去問
この動画を見る
(1)三角形$ABC$の内接円が辺$AB$と接する点をPとし、
辺$BC$と接する点を$Q$とし、辺$CA$と接する点をRとする。
$\angle A$の大きさを$θ$とすると、$\angle APR=\boxed{ア}$であり、
$\angle PQR=\boxed{ア}$である。
$\boxed{ア}$の解答群
$⓪0 ①\frac{\pi}{2} ②θ ③\frac{θ}{2} ④\frac{\pi}{2}-θ ⑤\frac{\pi-θ}{2}$
$⑥\pi-\frac{θ}{2} ⑦\pi-θ ⑧\frac{\pi-3θ}{2} ⑨\frac{\pi}{2}-3θ$
(2)三角形$T_1$の3つの角のうち、角の大きさが最小のものは$\frac{\pi}{6}$で、
最大のものは$\frac{\pi}{2}$であるとする。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の内接円を$O_n$とし、
$T_n$と$O_n$とが接する3つの点を頂点とするような三角形を$T_{n+1}$とする。
このとき、三角形$T_2$の3つの角のうち、
角の大きさが最小のものは$\frac{\pi}{\boxed{イ}}$で、
最大のものは$\frac{\boxed{ウ}\ \pi}{\boxed{エオ}}$である。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の3つの角のうち、
角の大きさが最小のものを$a_n$とし、最大のものを$b_n$とする。三角形$T_{n+1}$について、
$a_{n+1}=\boxed{カ},\ \ \ b_{n+1}=\boxed{キ}$
と表せる。この式より
$a_n+b_n=\frac{\boxed{ク}}{\boxed{ケ}}\pi,$
$b_n-a_n=\frac{\pi}{\boxed{コ}・\boxed{サ}^{n-1}}$
であり、$a_n=\frac{\pi}{\boxed{シ}}(1-\frac{1}{\boxed{ス}^n}) $である。
$\boxed{カ}、\boxed{キ}$の解答群
$⓪\frac{a_n}{2} ①\frac{b_n}{2} ②\frac{\pi}{2}-a_n ③\frac{\pi}{2}-b_n ④\frac{\pi-a_n}{2}$
$⑤\frac{\pi-b_n}{2} ⑥\pi-\frac{a_n}{2} ⑦\pi-\frac{b_n}{2} ⑧\pi-a_n ⑨\pi-b_n$
2022明治大学全統過去問
【誘導は概要欄のリンクから】大学入試問題#294 東北大学工学部AO II期(2021) #整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
等差数列
$a,a+1,a+2,・・・,a+n$の和が1000となるような自然数の組$(a,n)$をすべて求めよ。
出典:2021年東北大学工学部AOⅡ期 入試問題
この動画を見る
等差数列
$a,a+1,a+2,・・・,a+n$の和が1000となるような自然数の組$(a,n)$をすべて求めよ。
出典:2021年東北大学工学部AOⅡ期 入試問題
福田の数学〜明治大学2022年全学部統一入試12AB第2問〜定積分で表された関数と面積の2等分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
xの関数$f(x)$を$f(x)=x^3$とする。
(1)xの関数$g(x)$を$g(x)=x^3-2x^2-x+3$とする。曲線$y=f(x)$と$y=g(x)$は
3個の交点をもつ。それら交点を$\ x \ $座標が小さい順にA,B,Cとすると、
点$A,B,C$の$\ x\ $座標はそれぞれ$ \boxed{ア},\ \boxed{イ},\ \boxed{ウ}$ である。
曲線$y=g(x)$の接線の傾きが最小となるのは、
接点の$\ x\ $座標が$\frac{\boxed{エ}}{\boxed{オ}}$のときで、
その最小値は$-\frac{\boxed{カ}}{\boxed{\ \ キ\ \ }}$である。
また、点Bを通る$y=g(x)$の接線の傾きの最小値は$-\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$である。
(2)$x$ の関数$h(x)$が
$h(x)=-x^2+\frac{x}{6}\int_0^3h(t)dt+4$
を満たすとき、$h(x)=-x^2+\boxed{\ \ コ\ \ }\ x+4$である。
曲線$y=f(x)$と$y=h(x)$の交点の中点は$(\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }},\ \frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }})$であり、
$y=f(x)$と$y=h(x)$で囲まれる図形の面積は
原点を通る直線$y=\boxed{\ \ コ\ \ }x$で2等分される。
2022明治大学全統過去問
この動画を見る
xの関数$f(x)$を$f(x)=x^3$とする。
(1)xの関数$g(x)$を$g(x)=x^3-2x^2-x+3$とする。曲線$y=f(x)$と$y=g(x)$は
3個の交点をもつ。それら交点を$\ x \ $座標が小さい順にA,B,Cとすると、
点$A,B,C$の$\ x\ $座標はそれぞれ$ \boxed{ア},\ \boxed{イ},\ \boxed{ウ}$ である。
曲線$y=g(x)$の接線の傾きが最小となるのは、
接点の$\ x\ $座標が$\frac{\boxed{エ}}{\boxed{オ}}$のときで、
その最小値は$-\frac{\boxed{カ}}{\boxed{\ \ キ\ \ }}$である。
また、点Bを通る$y=g(x)$の接線の傾きの最小値は$-\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }}$である。
(2)$x$ の関数$h(x)$が
$h(x)=-x^2+\frac{x}{6}\int_0^3h(t)dt+4$
を満たすとき、$h(x)=-x^2+\boxed{\ \ コ\ \ }\ x+4$である。
曲線$y=f(x)$と$y=h(x)$の交点の中点は$(\frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }},\ \frac{\boxed{\ \ ク\ \ }}{\boxed{\ \ ケ\ \ }})$であり、
$y=f(x)$と$y=h(x)$で囲まれる図形の面積は
原点を通る直線$y=\boxed{\ \ コ\ \ }x$で2等分される。
2022明治大学全統過去問
