 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
数学「大学入試良問集」【16−2 複素数平面と三角形の形との関係】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
複素数平面上に三角形$ABC$があり、その頂点$A,B,C$を表す複素数をそれぞれ$z_1,z_2,z_3$とする。
複素数$\omega$に対して、$z_1=\omega z_3,z_2=\omega z_1,z_3=\omega z_2$が成り立つとき、次の各問いに答えよ。
(1)$1+\omega+\omega^2$の値を求めよ。
(2)三角形$ABC$はどんな形の三角形か。
(3)$z=z_1+2z_2+3z_3$の表す点を$D$とすると、三角形$OBD$はどんな形の三角形か。ただし、$O$は原点である。
この動画を見る
複素数平面上に三角形$ABC$があり、その頂点$A,B,C$を表す複素数をそれぞれ$z_1,z_2,z_3$とする。
複素数$\omega$に対して、$z_1=\omega z_3,z_2=\omega z_1,z_3=\omega z_2$が成り立つとき、次の各問いに答えよ。
(1)$1+\omega+\omega^2$の値を求めよ。
(2)三角形$ABC$はどんな形の三角形か。
(3)$z=z_1+2z_2+3z_3$の表す点を$D$とすると、三角形$OBD$はどんな形の三角形か。ただし、$O$は原点である。
大学入試問題#44 明治大学(2021) 複素数

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数C
指導講師:
ますただ
問題文全文(内容文):
$|z|=2$のとき
$|z^2+iz-1|$のとりうる値の範囲を求めよ。
出典:2021年明治大学 入試問題
この動画を見る
$|z|=2$のとき
$|z^2+iz-1|$のとりうる値の範囲を求めよ。
出典:2021年明治大学 入試問題
大学入試問題#43 津田塾大学(2021) 複素数

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#津田塾大学
指導講師:
ますただ
問題文全文(内容文):
$|z-5|=|z+5i|$
$|z-2i|=2$を満たす複素数$z$に対して$z^4$を求めよ。
出典:2021年津田塾大学 入試問題
この動画を見る
$|z-5|=|z+5i|$
$|z-2i|=2$を満たす複素数$z$に対して$z^4$を求めよ。
出典:2021年津田塾大学 入試問題
大学入試問題#42 慶應義塾大学(2021) 絶対値の定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a:$実数
$f(x)=|x|+a$に対して$\displaystyle \int_{-5}^{5}|f(x)|dx$が最小となる$a$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
この動画を見る
$a:$実数
$f(x)=|x|+a$に対して$\displaystyle \int_{-5}^{5}|f(x)|dx$が最小となる$a$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
数学「大学入試良問集」【14−15 折れ線の最小値と空間ベクトル】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
点$A(1,2,4)$を通り、ベクトル$\vec{ n }=(-3,1,2)$に垂直な平面を$\alpha$とする。
平面$\alpha$に関して同じ側に2点$P(-2,1,7),Q(1,3,7)$がある。
次の問いに答えよ。
(1)
平面$\alpha$に関して点$P$と対称な点$R$の座標を求めよ。
(2)
平面$\alpha$上の点で、$PS+QS$を最小にする点$S$の座標とそのときの最小値を求めよ。
この動画を見る
点$A(1,2,4)$を通り、ベクトル$\vec{ n }=(-3,1,2)$に垂直な平面を$\alpha$とする。
平面$\alpha$に関して同じ側に2点$P(-2,1,7),Q(1,3,7)$がある。
次の問いに答えよ。
(1)
平面$\alpha$に関して点$P$と対称な点$R$の座標を求めよ。
(2)
平面$\alpha$上の点で、$PS+QS$を最小にする点$S$の座標とそのときの最小値を求めよ。
大学入試問題#41 東海大学医学部(2021) 因数分解

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
ますただ
問題文全文(内容文):
$(a+b+c)^3-a^3-b^3-c^3$を因数分解せよ。
出典:2021年東海大学医学部 入試問題
この動画を見る
$(a+b+c)^3-a^3-b^3-c^3$を因数分解せよ。
出典:2021年東海大学医学部 入試問題
大学入試問題#40 東京理科大学(2021) 数列と極限
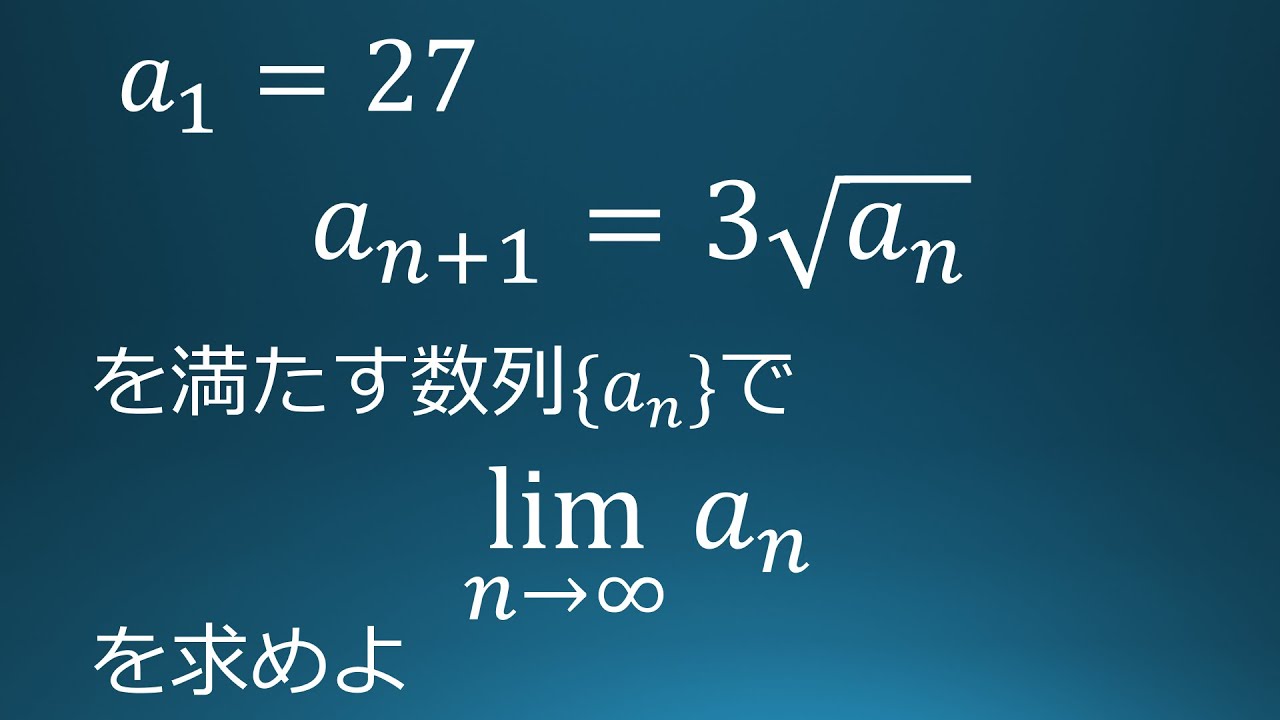
単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a_1=27$
$a_{n+1}=3\sqrt{ a_n }$を満たす数列$\{a_n\}$において
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典:2021年東京理科大学 入試問題
この動画を見る
$a_1=27$
$a_{n+1}=3\sqrt{ a_n }$を満たす数列$\{a_n\}$において
$\displaystyle \lim_{ n \to \infty }a_n$を求めよ。
出典:2021年東京理科大学 入試問題
大学入試問題#39 東海大学医学部(2021) 整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
ますただ
問題文全文(内容文):
$n:$自然数
$n^3+100$が$n+10$で割り切れるような最大の$n$の値を求めよ。
出典:2021年東海大学医学部 入試問題
この動画を見る
$n:$自然数
$n^3+100$が$n+10$で割り切れるような最大の$n$の値を求めよ。
出典:2021年東海大学医学部 入試問題
数学「大学入試良問集」【14−14四面体の体積•平面と垂直な直線】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#大分大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
空間内に4点$A(0,0,0),B(2,1,1),C(-2,2,-4),D(1,2,-4)$がある。
(1)
$\angle BAC=\theta$とおくとき、$\cos\theta$の値と$\triangle ABC$の面積を求めよ。
(2)
$\overrightarrow{ AB }$と$\overrightarrow{ AC }$の両方に垂直なベクトルを1つ求めよ。
(3)
点$D$から、3点$A,B,C$を含む平面に垂直な直線を引き、その交点を$E$とするとき、線分$DE$の長さを求めよ。
(4)
四面体$ABCD$の体積を求めよ。
この動画を見る
空間内に4点$A(0,0,0),B(2,1,1),C(-2,2,-4),D(1,2,-4)$がある。
(1)
$\angle BAC=\theta$とおくとき、$\cos\theta$の値と$\triangle ABC$の面積を求めよ。
(2)
$\overrightarrow{ AB }$と$\overrightarrow{ AC }$の両方に垂直なベクトルを1つ求めよ。
(3)
点$D$から、3点$A,B,C$を含む平面に垂直な直線を引き、その交点を$E$とするとき、線分$DE$の長さを求めよ。
(4)
四面体$ABCD$の体積を求めよ。
数学「大学入試良問集」【14−13線分の長さの最小値】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
座標空間内で点$(3,4,0)$を通り、ベクトル$\vec{ a }=(1,1,1)$に平行な直線$l$、点$(2,-1,0)$を通り、ベクトル$\vec{ b }=(1,-2,0)$に平行な直線$m$とする。
点$P$は直線$l$上を、点$Q$は直線$m$上をそれぞれ勝手に動くとき、線分$PQ$の長さの最小値を求めよ。
この動画を見る
座標空間内で点$(3,4,0)$を通り、ベクトル$\vec{ a }=(1,1,1)$に平行な直線$l$、点$(2,-1,0)$を通り、ベクトル$\vec{ b }=(1,-2,0)$に平行な直線$m$とする。
点$P$は直線$l$上を、点$Q$は直線$m$上をそれぞれ勝手に動くとき、線分$PQ$の長さの最小値を求めよ。
数学「大学入試良問集」【14−12空間ベクトルと平面上の点】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#帯広畜産大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
四面体$OABC$において、$\overrightarrow{ OA }=\vec{ a },\ \overrightarrow{ OB }=\vec{ b },\ \overrightarrow{ OC }=\vec{ c }$とする。
また、線分$OA$を$1:2$に内分する点を$P$、線分$AC$を$1:2$に内分する点を$Q$、線分$BC$を$2:3$に内分する点を$R$、線分$OB$を$t:(1-t)$に内分する点を$S$とする。
ただし、$0 \lt t \lt 1$とする。
(1)
$\overrightarrow{ PQ },\ \overrightarrow{ PR }$を$\vec{ a },\vec{ b },\vec{ c }$を用いて表しなさい。
(2)
適当な実数$k,l$を用いて$\overrightarrow{ PS }=k\overrightarrow{ PQ }+l\overrightarrow{ PR }$と表されるように、$t$の値を定めなさい。
この動画を見る
四面体$OABC$において、$\overrightarrow{ OA }=\vec{ a },\ \overrightarrow{ OB }=\vec{ b },\ \overrightarrow{ OC }=\vec{ c }$とする。
また、線分$OA$を$1:2$に内分する点を$P$、線分$AC$を$1:2$に内分する点を$Q$、線分$BC$を$2:3$に内分する点を$R$、線分$OB$を$t:(1-t)$に内分する点を$S$とする。
ただし、$0 \lt t \lt 1$とする。
(1)
$\overrightarrow{ PQ },\ \overrightarrow{ PR }$を$\vec{ a },\vec{ b },\vec{ c }$を用いて表しなさい。
(2)
適当な実数$k,l$を用いて$\overrightarrow{ PS }=k\overrightarrow{ PQ }+l\overrightarrow{ PR }$と表されるように、$t$の値を定めなさい。
大学入試問題#39 旭川医科大学改(2020) 定積分を利用した不等式の証明

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n$は2以上の整数
$n\ log\ n-(n-1) \lt log2+log\ 3+・・・+log\ n$を示せ
出典:2020年旭川医科大学 入試問題
この動画を見る
$n$は2以上の整数
$n\ log\ n-(n-1) \lt log2+log\ 3+・・・+log\ n$を示せ
出典:2020年旭川医科大学 入試問題
数学「大学入試良問集」【14−11空間ベクトルと正四面体】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
四面体$OABC$の辺$AB$を$4:5$に内分する点を$D$、辺$OC$を$2:1$に内分する点を$E$とし、線分$DE$の中点を$P$、直線$OP$が平面$ABC$と交わる点を$Q$とする。
次の各問いに答えよ。
(1)
$\overrightarrow{ OA }=\vec{ a },\ \overrightarrow{ OB }=\vec{ b },\ \overrightarrow{ OC }=\vec{ c }$とおくとき、$\overrightarrow{ OP }$を$\vec{ a },\ \vec{ b },\ \vec{ c }$で表せ。
また、$\overrightarrow{ OP }$と$\overrightarrow{ OQ }$の大きさの比$|\overrightarrow{ OP }|:|\overrightarrow{ OQ }|$を最も簡単な整数比で表せ。
(2)
$\triangle ABQ$と$\triangle ABC$の面積比$\triangle ABQ:\triangle ABC$を最も簡単な整数比で表せ。
この動画を見る
四面体$OABC$の辺$AB$を$4:5$に内分する点を$D$、辺$OC$を$2:1$に内分する点を$E$とし、線分$DE$の中点を$P$、直線$OP$が平面$ABC$と交わる点を$Q$とする。
次の各問いに答えよ。
(1)
$\overrightarrow{ OA }=\vec{ a },\ \overrightarrow{ OB }=\vec{ b },\ \overrightarrow{ OC }=\vec{ c }$とおくとき、$\overrightarrow{ OP }$を$\vec{ a },\ \vec{ b },\ \vec{ c }$で表せ。
また、$\overrightarrow{ OP }$と$\overrightarrow{ OQ }$の大きさの比$|\overrightarrow{ OP }|:|\overrightarrow{ OQ }|$を最も簡単な整数比で表せ。
(2)
$\triangle ABQ$と$\triangle ABC$の面積比$\triangle ABQ:\triangle ABC$を最も簡単な整数比で表せ。
数学「大学入試良問集」【14−10空間ベクトルと正四面体】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
各辺の長さが1の正四面体$OABC$に対し、$OB$を$2:1$に内分する点を$D,OC$を2等分する点を$E,BC$を2等分にする点を$F$とする。
$DE$と$OF$の交点を$G$とするとき、以下の各問いに答えよ。
(1)$OG$の長さを求めよ。
(2)$AG$の長さを求めよ。
この動画を見る
各辺の長さが1の正四面体$OABC$に対し、$OB$を$2:1$に内分する点を$D,OC$を2等分する点を$E,BC$を2等分にする点を$F$とする。
$DE$と$OF$の交点を$G$とするとき、以下の各問いに答えよ。
(1)$OG$の長さを求めよ。
(2)$AG$の長さを求めよ。
大学入試問題#38 日本大学(2021) 三角関数
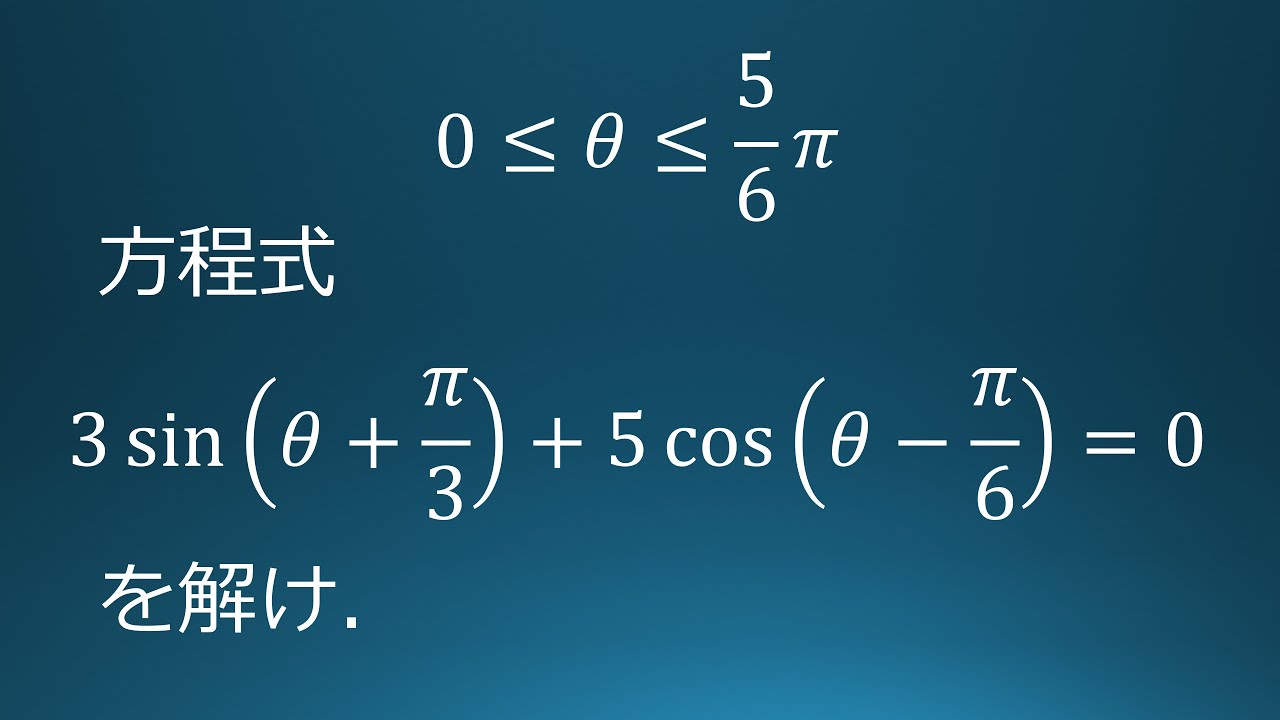
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq \theta \leqq \displaystyle \frac{5}{6}\pi$において
方程式
$3\sin(\theta+\displaystyle \frac{\pi}{3})+5\ \cos(\theta-\displaystyle \frac{\pi}{6})=0$を解け。
出典:2021年日本大学 入試問題
この動画を見る
$0 \leqq \theta \leqq \displaystyle \frac{5}{6}\pi$において
方程式
$3\sin(\theta+\displaystyle \frac{\pi}{3})+5\ \cos(\theta-\displaystyle \frac{\pi}{6})=0$を解け。
出典:2021年日本大学 入試問題
大学入試問題#37 早稲田大学(2021) 整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a,b,c:$実数
$0 \leqq a \leqq b \leqq c$
$a+b+c=7$を満たすとき
$ab,bc,ca$の最大値を求めよ。
出典:2021年早稲田大学 入試問題
この動画を見る
$a,b,c:$実数
$0 \leqq a \leqq b \leqq c$
$a+b+c=7$を満たすとき
$ab,bc,ca$の最大値を求めよ。
出典:2021年早稲田大学 入試問題
数学「大学入試良問集」【14−9ベクトルと反転】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$xy$平面において、原点$O$を通る半径$r(r \gt 0)$の円を$C$とし、その中心を$A$とする。
$O$を除く$C$上の点$P$に対し、次の2つの条件$(a),(b)$で定まる点$Q$を考える。
(a)$\overrightarrow{ OP }$と$\overrightarrow{ OQ }$の向きが同じ。
(b)$|\overrightarrow{ OP }||\overrightarrow{ OQ }|=1$
以下の問いに答えよ。
(1)
点$P$が$O$を除く$C$上を動くとき、点$Q$は$\overrightarrow{ OA }$に直交する直線状を動くことを示せ。
(2)
(1)の直線を$l$とする。
$l$が$C$と2点で交わるとき、$r$のとり得る値の範囲を求めよ。
この動画を見る
$xy$平面において、原点$O$を通る半径$r(r \gt 0)$の円を$C$とし、その中心を$A$とする。
$O$を除く$C$上の点$P$に対し、次の2つの条件$(a),(b)$で定まる点$Q$を考える。
(a)$\overrightarrow{ OP }$と$\overrightarrow{ OQ }$の向きが同じ。
(b)$|\overrightarrow{ OP }||\overrightarrow{ OQ }|=1$
以下の問いに答えよ。
(1)
点$P$が$O$を除く$C$上を動くとき、点$Q$は$\overrightarrow{ OA }$に直交する直線状を動くことを示せ。
(2)
(1)の直線を$l$とする。
$l$が$C$と2点で交わるとき、$r$のとり得る値の範囲を求めよ。
数学「大学入試良問集」【14−8ベクトルと軌跡と等式・不等式】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
平面上において同一直線上にない3点$A,B,C$があるとき、次の各問いに対して、それぞれの式をみたす点$P$の集合を求めよ。
(1)$\overrightarrow{ AP }+\overrightarrow{ BP }+\overrightarrow{ CP }=\overrightarrow{ AC }$
(2)$\overrightarrow{ AB }・\overrightarrow{ AP }=\overrightarrow{ AB }・\overrightarrow{ AB }$
(3)$\overrightarrow{ AB }・\overrightarrow{ AC }+\overrightarrow{ AP }・\overrightarrow{ AP } \leqq \overrightarrow{ AB }・\overrightarrow{ AP }+\overrightarrow{ AC }・\overrightarrow{ AP }$
この動画を見る
平面上において同一直線上にない3点$A,B,C$があるとき、次の各問いに対して、それぞれの式をみたす点$P$の集合を求めよ。
(1)$\overrightarrow{ AP }+\overrightarrow{ BP }+\overrightarrow{ CP }=\overrightarrow{ AC }$
(2)$\overrightarrow{ AB }・\overrightarrow{ AP }=\overrightarrow{ AB }・\overrightarrow{ AB }$
(3)$\overrightarrow{ AB }・\overrightarrow{ AC }+\overrightarrow{ AP }・\overrightarrow{ AP } \leqq \overrightarrow{ AB }・\overrightarrow{ AP }+\overrightarrow{ AC }・\overrightarrow{ AP }$
福田の数学〜立教大学2021年経済学部第3問〜直線の傾きと放物線との接線

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$aを実数の定数とする。座標平面上の放物線$C:y=-x^2+ax-\frac{(a-2-\sqrt3)^2}{4}$,
直線$l:y=(2+\sqrt3)x$がある。$l$と$x$軸のなす角を\$theta$とする。ただし$0 \lt \theta \lt \frac{\pi}{2}$とする。
このとき、次の各問いに答えよ。
(1)$C$と$l$の共有点のx座標をaを用いて表せ。
(2)$\tan\theta, \tan(\theta+\frac{\pi}{4}), \tan(\theta-\frac{\pi}{4})$の値をそれぞれ求めよ。
(3)y切片が2であり、lとのなす角が$\frac{\pi}{4}$である直線の方程式を全て求めよ。
(4)(3)で求めた直線のうち、傾きが負であるものを$m$とする。
$C$と$m$が接するときのaの値を求めよ。
また、そのとき、Cとmの接点の座標を求めよ。
(5)aを(4)で求めた値とするとき、$C,m$および$y$軸で囲まれた図形の面積を求めよ。
2021立教大学経済学部過去問
この動画を見る
${\Large\boxed{3}}$aを実数の定数とする。座標平面上の放物線$C:y=-x^2+ax-\frac{(a-2-\sqrt3)^2}{4}$,
直線$l:y=(2+\sqrt3)x$がある。$l$と$x$軸のなす角を\$theta$とする。ただし$0 \lt \theta \lt \frac{\pi}{2}$とする。
このとき、次の各問いに答えよ。
(1)$C$と$l$の共有点のx座標をaを用いて表せ。
(2)$\tan\theta, \tan(\theta+\frac{\pi}{4}), \tan(\theta-\frac{\pi}{4})$の値をそれぞれ求めよ。
(3)y切片が2であり、lとのなす角が$\frac{\pi}{4}$である直線の方程式を全て求めよ。
(4)(3)で求めた直線のうち、傾きが負であるものを$m$とする。
$C$と$m$が接するときのaの値を求めよ。
また、そのとき、Cとmの接点の座標を求めよ。
(5)aを(4)で求めた値とするとき、$C,m$および$y$軸で囲まれた図形の面積を求めよ。
2021立教大学経済学部過去問
大学入試問題#36 旭川医科大学(2020) 数列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
数列$\{p_n\},\{q_n\}$は
$\begin{eqnarray}
\left\{
\begin{array}{l}
p_{n+1}=\displaystyle \frac{1}{2}p_n+\displaystyle \frac{1}{4}q_n-\displaystyle \frac{1}{4} \\
q_{n+1}=\displaystyle \frac{1}{2}p_n+\displaystyle \frac{3}{4}q_n+\displaystyle \frac{1}{4}
\end{array}
\right.
\end{eqnarray}$ を満たす。
(1)
$p_n+q_n=p_1+q_1$を示せ
(2)
一般項$p_n$を$p_1,q_1$を用いて表せ
(3)
$\displaystyle \sum_{n=1}^\infty p_n=1$のとき、$p_1,q_1$の値を求めよ。
出典:2020年旭川医科大学 入試問題
この動画を見る
数列$\{p_n\},\{q_n\}$は
$\begin{eqnarray}
\left\{
\begin{array}{l}
p_{n+1}=\displaystyle \frac{1}{2}p_n+\displaystyle \frac{1}{4}q_n-\displaystyle \frac{1}{4} \\
q_{n+1}=\displaystyle \frac{1}{2}p_n+\displaystyle \frac{3}{4}q_n+\displaystyle \frac{1}{4}
\end{array}
\right.
\end{eqnarray}$ を満たす。
(1)
$p_n+q_n=p_1+q_1$を示せ
(2)
一般項$p_n$を$p_1,q_1$を用いて表せ
(3)
$\displaystyle \sum_{n=1}^\infty p_n=1$のとき、$p_1,q_1$の値を求めよ。
出典:2020年旭川医科大学 入試問題
数学「大学入試良問集」【14−7ベクトルの等式と円】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$\triangle ABC$の外接円の中心を$O$とし、半径を1とする。
$13\overrightarrow{ OA }+12\overrightarrow{ OB }+5\overrightarrow{ OC }=\vec{ 0 }$であるとき、次の問いに答えよ。
(1)内積$\overrightarrow{ OA }・\overrightarrow{ OB }$を求めよ。
(2)$\triangle OAB,\triangle OBC,\triangle OCA$の面積を求めよ。
この動画を見る
$\triangle ABC$の外接円の中心を$O$とし、半径を1とする。
$13\overrightarrow{ OA }+12\overrightarrow{ OB }+5\overrightarrow{ OC }=\vec{ 0 }$であるとき、次の問いに答えよ。
(1)内積$\overrightarrow{ OA }・\overrightarrow{ OB }$を求めよ。
(2)$\triangle OAB,\triangle OBC,\triangle OCA$の面積を求めよ。
福田の数学〜立教大学2021年経済学部第2問〜2項間の漸化式の解法

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{3}}$次の条件によって定められる数列$\left\{a_n\right\}$がある。
$a_1=1, a_{n+1}=3a_n+4n (n=1,2,3,\ldots)$
また、$n$に無関係な定数$p,q$に対し、
$b_n=a_n+pn+q (n=1,2,3,\ldots)$
とおく。このとき次の問いに答えよ。
(1)$n,p,q$に無関係な定数$A,B,C,D,E$が
$b_{n+1}=Ab_n+(Bp+C)n+(Dp+Eq) (n=1,2,3,\ldots)$
を満たすとき、A,B,C,D,Eの値をそれぞれ求めよ。
(2)Aを(1)で求めた値とする。数列$\left\{b_n\right\}$が公比$A$の等比数列となるような
$p,q$の値をそれぞれ求めよ。
(3)(2)で求めた$p,q$の値に対して、数列$\left\{b_n\right\}$の一般項を求めよ。
2021立教大学経済学部過去問
この動画を見る
${\Large\boxed{3}}$次の条件によって定められる数列$\left\{a_n\right\}$がある。
$a_1=1, a_{n+1}=3a_n+4n (n=1,2,3,\ldots)$
また、$n$に無関係な定数$p,q$に対し、
$b_n=a_n+pn+q (n=1,2,3,\ldots)$
とおく。このとき次の問いに答えよ。
(1)$n,p,q$に無関係な定数$A,B,C,D,E$が
$b_{n+1}=Ab_n+(Bp+C)n+(Dp+Eq) (n=1,2,3,\ldots)$
を満たすとき、A,B,C,D,Eの値をそれぞれ求めよ。
(2)Aを(1)で求めた値とする。数列$\left\{b_n\right\}$が公比$A$の等比数列となるような
$p,q$の値をそれぞれ求めよ。
(3)(2)で求めた$p,q$の値に対して、数列$\left\{b_n\right\}$の一般項を求めよ。
2021立教大学経済学部過去問
大学入試問題#35 秋田大学(2020) 整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#秋田大学
指導講師:
ますただ
問題文全文(内容文):
自然数$n$の各位の数の和を$S(n)$とする。
例:$S(2019)=2+0+1+9$
(1)
$n+S(n)=100$をみたす$n$を求めよ。
(2)
$S(n)=100$をみたす最小の$n$を求めよ。
出典:2020年秋田大学 入試問題
この動画を見る
自然数$n$の各位の数の和を$S(n)$とする。
例:$S(2019)=2+0+1+9$
(1)
$n+S(n)=100$をみたす$n$を求めよ。
(2)
$S(n)=100$をみたす最小の$n$を求めよ。
出典:2020年秋田大学 入試問題
【理数個別の過去問解説】2020年度横浜国立大学 数学 第5問(4)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大学2020年度大問5(4)
aを正の実数とする。$n=1,2,3,…$に対して、
$I_n=\displaystyle \int_{0}^{1}x^{n+a-1}e^{-x}dx$
と定める。次の問に答えよ。
(1)$n=1,2,3,…$に対して、$I_n\leqq \dfrac{1}{n+a}$を示せ。
(2)$n=1,2,3,…$に対して、$I_{n+1}-(n+a)I_n$を求めよ。
(3)極限値$\displaystyle \lim_{n\to\infty}nI_n$を求めよ。
(4)実数b,cに対して、$J_n=n^3\left(I_n+\dfrac{b}{n}+\dfrac{c}{n^2}\right)(n=1,2,3,…)$と定める。数列{$J_n$}が収束するとき、次の問いに答えよ。
(ア)bを求めよ。
(イ)cをaの式で表せ。
(ウ)極限値$\displaystyle \lim_{n\to\infty}J_n$をaの式で表せ。
この動画を見る
横浜国立大学2020年度大問5(4)
aを正の実数とする。$n=1,2,3,…$に対して、
$I_n=\displaystyle \int_{0}^{1}x^{n+a-1}e^{-x}dx$
と定める。次の問に答えよ。
(1)$n=1,2,3,…$に対して、$I_n\leqq \dfrac{1}{n+a}$を示せ。
(2)$n=1,2,3,…$に対して、$I_{n+1}-(n+a)I_n$を求めよ。
(3)極限値$\displaystyle \lim_{n\to\infty}nI_n$を求めよ。
(4)実数b,cに対して、$J_n=n^3\left(I_n+\dfrac{b}{n}+\dfrac{c}{n^2}\right)(n=1,2,3,…)$と定める。数列{$J_n$}が収束するとき、次の問いに答えよ。
(ア)bを求めよ。
(イ)cをaの式で表せ。
(ウ)極限値$\displaystyle \lim_{n\to\infty}J_n$をaの式で表せ。
福田の数学〜立教大学2021年経済学部第1問(6)〜平均と分散の関係

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(6)10個の正三角形がある。それらの辺の長さからなるデータの平均は9である。
また、それらの面積からなるデータの平均値は$\frac{118\sqrt3}{5}$である。このとき、
辺の長さからなるデータの分散は$\ \boxed{ク}$である。
2021立教大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$(6)10個の正三角形がある。それらの辺の長さからなるデータの平均は9である。
また、それらの面積からなるデータの平均値は$\frac{118\sqrt3}{5}$である。このとき、
辺の長さからなるデータの分散は$\ \boxed{ク}$である。
2021立教大学経済学部過去問
微分方程式 高専数学 p 106-1番

単元:
#大学入試過去問(数学)#微分とその応用#微分法#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#高専(高等専門学校)
指導講師:
ますただ
問題文全文(内容文):
微分方程式
$\displaystyle \frac{dx}{dt}=\sqrt{ 2t+x+4 }$の一般解を求めよ。
この動画を見る
微分方程式
$\displaystyle \frac{dx}{dt}=\sqrt{ 2t+x+4 }$の一般解を求めよ。
【理数個別の過去問解説】2020年度横浜国立大学 数学 第5問(3)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大学2020年度大問5(3)
aを正の実数とする。$n=1,2,3,…$に対して、
$I_n=\displaystyle \int_{0}^{1}x^{n+a-1}e^{-x}dx$
と定める。次の問に答えよ。
(1)$n=1,2,3,…$に対して、$I_n\leqq \dfrac{1}{n+a}$を示せ。
(2)$n=1,2,3,…$に対して、$I_{n+1}-(n+a)I_n$を求めよ。
(3)極限値$\displaystyle \lim_{n\to\infty}nI_n$を求めよ。
(4)実数b,cに対して、$J_n=n^3\left(I_n+\dfrac{b}{n}+\dfrac{c}{n^2}\right)(n=1,2,3,…)$と定める。数列{$J_n$}が収束するとき、次の問いに答えよ。
(ア)bを求めよ。
(イ)cをaの式で表せ。
(ウ)極限値$\displaystyle \lim_{n\to\infty}J_n$をaの式で表せ。
この動画を見る
横浜国立大学2020年度大問5(3)
aを正の実数とする。$n=1,2,3,…$に対して、
$I_n=\displaystyle \int_{0}^{1}x^{n+a-1}e^{-x}dx$
と定める。次の問に答えよ。
(1)$n=1,2,3,…$に対して、$I_n\leqq \dfrac{1}{n+a}$を示せ。
(2)$n=1,2,3,…$に対して、$I_{n+1}-(n+a)I_n$を求めよ。
(3)極限値$\displaystyle \lim_{n\to\infty}nI_n$を求めよ。
(4)実数b,cに対して、$J_n=n^3\left(I_n+\dfrac{b}{n}+\dfrac{c}{n^2}\right)(n=1,2,3,…)$と定める。数列{$J_n$}が収束するとき、次の問いに答えよ。
(ア)bを求めよ。
(イ)cをaの式で表せ。
(ウ)極限値$\displaystyle \lim_{n\to\infty}J_n$をaの式で表せ。
数学「大学入試良問集」【14−6ベクトル方程式と領域図示】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$\triangle ABC$において$\overrightarrow{ CA }=\vec{ a },\overrightarrow{ CB }=\vec{ b }$とする。
次の問いに答えよ。
(1)
実数$s,t$が$0 \leqq s+t \leqq 1,s \geqq 0,t \geqq 0$の範囲を動くとき、次の各条件を満たす点$P$の存在する範囲をそれぞれ図示せよ。
(a)$\overrightarrow{ CP }=s\vec{ a }+t(\vec{ a }+\vec{ b })$
(b)$\overrightarrow{ CP }=(2s+t)\vec{ a }+(s-t)\vec{ b }$
(2)
(1)の各場合に、点$P$の存在する範囲の面積は$\triangle ABC$の面積の何倍か。
この動画を見る
$\triangle ABC$において$\overrightarrow{ CA }=\vec{ a },\overrightarrow{ CB }=\vec{ b }$とする。
次の問いに答えよ。
(1)
実数$s,t$が$0 \leqq s+t \leqq 1,s \geqq 0,t \geqq 0$の範囲を動くとき、次の各条件を満たす点$P$の存在する範囲をそれぞれ図示せよ。
(a)$\overrightarrow{ CP }=s\vec{ a }+t(\vec{ a }+\vec{ b })$
(b)$\overrightarrow{ CP }=(2s+t)\vec{ a }+(s-t)\vec{ b }$
(2)
(1)の各場合に、点$P$の存在する範囲の面積は$\triangle ABC$の面積の何倍か。
【理数個別の過去問解説】2020年度横浜国立大学 数学 第5問(2)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大学2020年度大問5(2)
aを正の実数とする。$n=1,2,3,…$に対して、
$I_n=\displaystyle \int_{0}^{1}x^{n+a-1}e^{-x}dx$
と定める。次の問に答えよ。
(1)$n=1,2,3,…$に対して、$I_n\leqq \dfrac{1}{n+a}$を示せ。
(2)$n=1,2,3,…$に対して、$I_{n+1}-(n+a)I_n$を求めよ。
(3)極限値$\displaystyle \lim_{n\to\infty}nI_n$を求めよ。
(4)実数b,cに対して、$J_n=n^3\left(I_n+\dfrac{b}{n}+\dfrac{c}{n^2}\right)(n=1,2,3,…)$と定める。数列{$J_n$}が収束するとき、次の問いに答えよ。
(ア)bを求めよ。
(イ)cをaの式で表せ。
(ウ)極限値$\displaystyle \lim_{n\to\infty}J_n$をaの式で表せ。
この動画を見る
横浜国立大学2020年度大問5(2)
aを正の実数とする。$n=1,2,3,…$に対して、
$I_n=\displaystyle \int_{0}^{1}x^{n+a-1}e^{-x}dx$
と定める。次の問に答えよ。
(1)$n=1,2,3,…$に対して、$I_n\leqq \dfrac{1}{n+a}$を示せ。
(2)$n=1,2,3,…$に対して、$I_{n+1}-(n+a)I_n$を求めよ。
(3)極限値$\displaystyle \lim_{n\to\infty}nI_n$を求めよ。
(4)実数b,cに対して、$J_n=n^3\left(I_n+\dfrac{b}{n}+\dfrac{c}{n^2}\right)(n=1,2,3,…)$と定める。数列{$J_n$}が収束するとき、次の問いに答えよ。
(ア)bを求めよ。
(イ)cをaの式で表せ。
(ウ)極限値$\displaystyle \lim_{n\to\infty}J_n$をaの式で表せ。
福田の数学〜立教大学2021年経済学部第1問(5)〜対数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(5)$x$についての方程式
$(\log_2x)^2+5\log_2x+2=0$
の2つの解を$\alpha,\beta$とおくと、$\alpha\beta=\boxed{キ}$である。
2021立教大学経済学部過去問
この動画を見る
${\Large\boxed{1}}$(5)$x$についての方程式
$(\log_2x)^2+5\log_2x+2=0$
の2つの解を$\alpha,\beta$とおくと、$\alpha\beta=\boxed{キ}$である。
2021立教大学経済学部過去問
