 大学入試過去問(数学)
大学入試過去問(数学)
 大学入試過去問(数学)
大学入試過去問(数学)
福田の数学〜早稲田大学2022年人間科学部第1問(2)〜2次関数のグラフの位置から係数決定

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(2)2次関数$y=ax^2+bx+c$の係数$a,b,c$は次の条件をともに満たすとする。
条件1.$a,b,c$は互いに異なる。
条件2. -3以上5以下の整数である。
この2次関数のグラフが、原点を通り、かつ、頂点が第1象限または第3象限
にあるような$a,b,c$の組は全部で$\boxed{\ \ イ\ \ }$組ある。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{1}}$(2)2次関数$y=ax^2+bx+c$の係数$a,b,c$は次の条件をともに満たすとする。
条件1.$a,b,c$は互いに異なる。
条件2. -3以上5以下の整数である。
この2次関数のグラフが、原点を通り、かつ、頂点が第1象限または第3象限
にあるような$a,b,c$の組は全部で$\boxed{\ \ イ\ \ }$組ある。
2022早稲田大学人間科学部過去問
大学入試問題#267 奈良県立医科大学 改 (2011) #不定積分 【難】
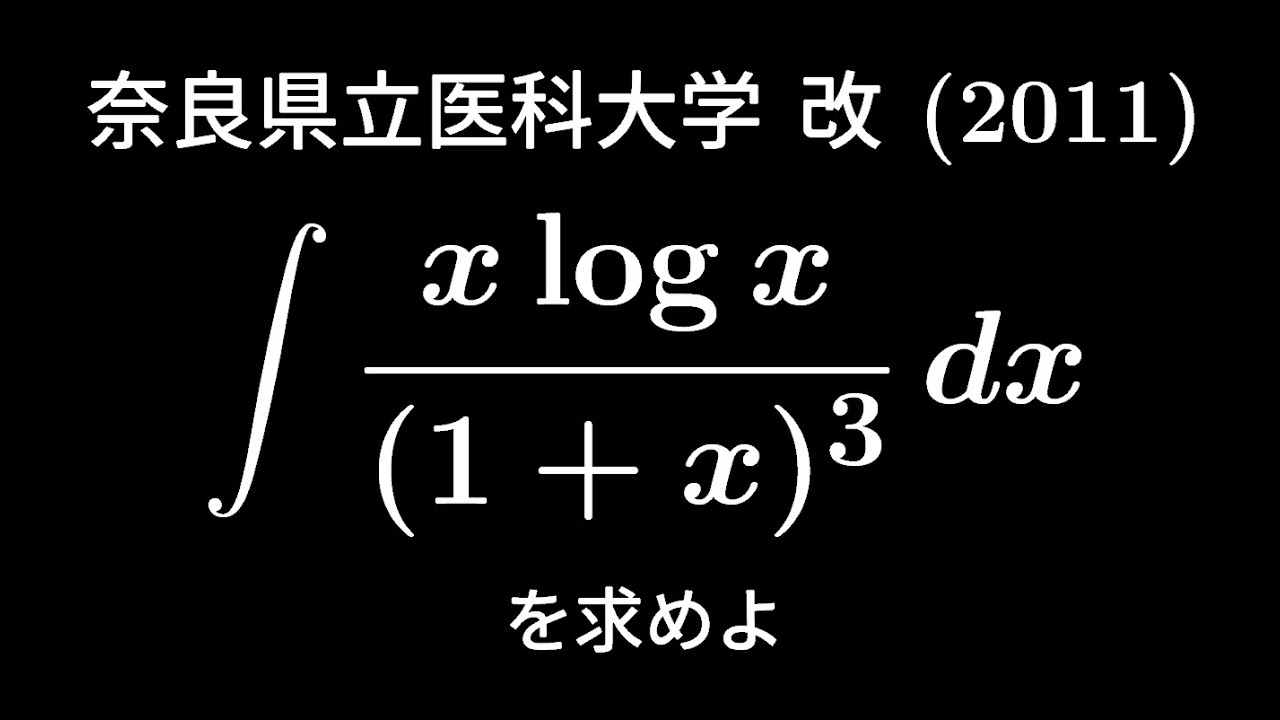
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#奈良県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x\ log\ x}{(1+x)^3}dx$を計算せよ
出典:2011年奈良県立医科大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x\ log\ x}{(1+x)^3}dx$を計算せよ
出典:2011年奈良県立医科大学 入試問題
整数問題!無限降下法を用いた証明!【数学 入試問題】【千葉大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$が3以上の整数のとき,$x^n+2y^n=4z^n$を満たす自然数$x,y,z$は存在しないことを証明せよ。
千葉大過去問
この動画を見る
$n$が3以上の整数のとき,$x^n+2y^n=4z^n$を満たす自然数$x,y,z$は存在しないことを証明せよ。
千葉大過去問
福田の数学〜早稲田大学2022年人間科学部第1問(1)〜命題の真偽とカードの裏表

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(1)表面にアルファベットが、裏面には自然数が書かれている5枚のカードが、
次のように置かれている。
${\large\boxed{P}}\hspace{45pt}{\large\boxed{Q}}\hspace{45pt}{\large\boxed{1}}\hspace{45pt}{\large\boxed{3}}\hspace{45pt}{\large\boxed{6}}$
これら5枚のカードに対する命題「表面がアルファベットPならば、裏面は
素数である」の審議を調べるために、できるだけ少ない枚数のカードを裏返
して確認したい。左からn番目の位置にあるカードを裏返す必要があるとき
には$a_n=1$、必要のないときには$a_n=0$とするとき
$\sum_{k=1}^5 a_k2^{k-1}=\boxed{\ \ ア\ \ }$
である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{1}}$(1)表面にアルファベットが、裏面には自然数が書かれている5枚のカードが、
次のように置かれている。
${\large\boxed{P}}\hspace{45pt}{\large\boxed{Q}}\hspace{45pt}{\large\boxed{1}}\hspace{45pt}{\large\boxed{3}}\hspace{45pt}{\large\boxed{6}}$
これら5枚のカードに対する命題「表面がアルファベットPならば、裏面は
素数である」の審議を調べるために、できるだけ少ない枚数のカードを裏返
して確認したい。左からn番目の位置にあるカードを裏返す必要があるとき
には$a_n=1$、必要のないときには$a_n=0$とするとき
$\sum_{k=1}^5 a_k2^{k-1}=\boxed{\ \ ア\ \ }$
である。
2022早稲田大学人間科学部過去問
福田の数学〜早稲田大学2022年理工学部第5問〜対数関数の極限と変曲点とグラフの接線

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#微分法#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{5}}\ a \gt 0$を定数とし、
$f(x)=x^a\log x$とする。以下の問いに答えよ。
(1)$\lim_{x \to +0}f(x)$を求めよ。必要ならば$\lim_{s \to \infty}se^{-s}=0$が成り立つことは
証明なしに用いてよい。
(2)曲線$y=f(x)$の変曲点がx軸上に存在するときのaの値を求めよ。
さらにそのとき$y=f(x)$のグラフの概形を描け。
(3)$t \gt 0$に対して、曲線$y=f(x)$上の点(t,f(t))における接線をlとする。
lがy軸の負の部分と交わるための$(a,t)$の条件を求め、その条件の表す領域を
a-t平面上に図示せよ。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{5}}\ a \gt 0$を定数とし、
$f(x)=x^a\log x$とする。以下の問いに答えよ。
(1)$\lim_{x \to +0}f(x)$を求めよ。必要ならば$\lim_{s \to \infty}se^{-s}=0$が成り立つことは
証明なしに用いてよい。
(2)曲線$y=f(x)$の変曲点がx軸上に存在するときのaの値を求めよ。
さらにそのとき$y=f(x)$のグラフの概形を描け。
(3)$t \gt 0$に対して、曲線$y=f(x)$上の点(t,f(t))における接線をlとする。
lがy軸の負の部分と交わるための$(a,t)$の条件を求め、その条件の表す領域を
a-t平面上に図示せよ。
2022早稲田大学人間科学部過去問
大学入試問題#266 兵庫医科大学(2011) #対称式
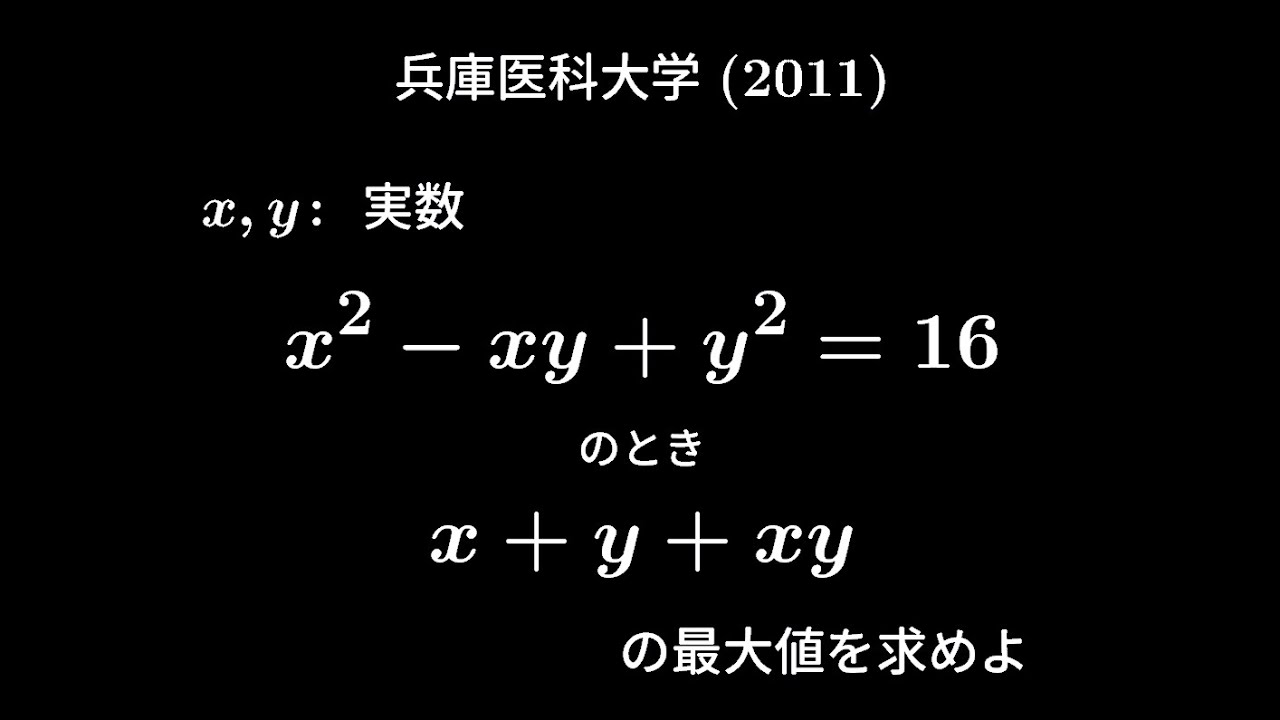
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫医科大学
指導講師:
ますただ
問題文全文(内容文):
$x,y$:実数
$x^2-xy+y^2=16$のとき
$x+y+xy$の最大値を求めよ。
出典:2011年兵庫医科大学 入試問題
この動画を見る
$x,y$:実数
$x^2-xy+y^2=16$のとき
$x+y+xy$の最大値を求めよ。
出典:2011年兵庫医科大学 入試問題
福田の数学〜早稲田大学2022年理工学部第4問〜正八面体の内部に配置した6個の球の和集合の体積と共通部分の体積

単元:
#数A#大学入試過去問(数学)#図形の性質#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$一辺の長さが$\sqrt3+1$である正八面体の頂点を右図(※動画参照)
のように$P_1,P_2,P_3,P_4,P_5,P_6$とする。$i=1,2,\ldots,6$に対して
$P_i$以外の5点を頂点とする四角錐のすべての面に
内接する球(内部含む)を$B_i$とする。$B_1$の体積をXとし、$B_1$と
$B_2$の共通部分の体積をYとし、$B_1,B_2,B_3$の共通部分の体積をZ
とする。さらに$B_1,B_2,\ldots,B_n$を合わせて得られる立体の体積を
$V_n\ \ (n=2,3,\ldots,6)$とする。以下の問いに答えよ。
(1)$V_n=aX+bY+cZ$となる整数a,b,cを$n=2,3,6$の場合
について求めよ。
(2)Xの値を求めよ。
(3)$V_2$の値を求めよ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{4}}$一辺の長さが$\sqrt3+1$である正八面体の頂点を右図(※動画参照)
のように$P_1,P_2,P_3,P_4,P_5,P_6$とする。$i=1,2,\ldots,6$に対して
$P_i$以外の5点を頂点とする四角錐のすべての面に
内接する球(内部含む)を$B_i$とする。$B_1$の体積をXとし、$B_1$と
$B_2$の共通部分の体積をYとし、$B_1,B_2,B_3$の共通部分の体積をZ
とする。さらに$B_1,B_2,\ldots,B_n$を合わせて得られる立体の体積を
$V_n\ \ (n=2,3,\ldots,6)$とする。以下の問いに答えよ。
(1)$V_n=aX+bY+cZ$となる整数a,b,cを$n=2,3,6$の場合
について求めよ。
(2)Xの値を求めよ。
(3)$V_2$の値を求めよ。
2022早稲田大学理工学部過去問
大学入試問題#265 熊本大学2011 #定積分 #Kingproperty

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}log_4(1+\tan\ x)dx$を求めよ
出典:2011年熊本大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}log_4(1+\tan\ x)dx$を求めよ
出典:2011年熊本大学 入試問題
【数Ⅲ】東大の基礎問題!絶対に落としてはいけない!【数学 入試問題】

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
関数
$f(x)=\dfrac{x}{sin x}+cos x$ ($ 0<x<\pi $)
の増減表を作り,$ x→+0,x→\pi-0$のときの極限を調べよ。
東大過去問
この動画を見る
関数
$f(x)=\dfrac{x}{sin x}+cos x$ ($ 0<x<\pi $)
の増減表を作り,$ x→+0,x→\pi-0$のときの極限を調べよ。
東大過去問
福田の数学〜早稲田大学2022年理工学部第3問〜漸化式と数列の極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}\ r$を実数とする。
次の条件によって定められる数列$\left\{a_n\right\},\left\{b_n\right\},\left\{c_n\right\}$を考える。
$a_1=r,a_{n+1}=\frac{[a_n]}{4}+\frac{a_n}{4}+\frac{5}{6}(n=1,2,3,\ldots)$
$b_1=r,b_{n+1}=\frac{b_n}{2}+\frac{7}{12}(n=1,2,3,\ldots)$
$c_1=r,c_{n+1}=\frac{c_n}{2}+\frac{5}{6}(n=1,2,3,\ldots)$
ただし、$[x]$はxを超えない最大の整数とする。以下の問いに答えよ。
(1)$\lim_{n \to \infty}b_n$と$\lim_{n \to \infty}c_n$を求めよ。
(2)$b_n \leqq a_n \leqq c_n (n=1,2,3,\ldots)$を示せ。
(3)$\lim_{n \to \infty}a_n$を求めよ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{3}}\ r$を実数とする。
次の条件によって定められる数列$\left\{a_n\right\},\left\{b_n\right\},\left\{c_n\right\}$を考える。
$a_1=r,a_{n+1}=\frac{[a_n]}{4}+\frac{a_n}{4}+\frac{5}{6}(n=1,2,3,\ldots)$
$b_1=r,b_{n+1}=\frac{b_n}{2}+\frac{7}{12}(n=1,2,3,\ldots)$
$c_1=r,c_{n+1}=\frac{c_n}{2}+\frac{5}{6}(n=1,2,3,\ldots)$
ただし、$[x]$はxを超えない最大の整数とする。以下の問いに答えよ。
(1)$\lim_{n \to \infty}b_n$と$\lim_{n \to \infty}c_n$を求めよ。
(2)$b_n \leqq a_n \leqq c_n (n=1,2,3,\ldots)$を示せ。
(3)$\lim_{n \to \infty}a_n$を求めよ。
2022早稲田大学理工学部過去問
福田の数学〜早稲田大学2022年理工学部第2問〜条件を満たすm個の2次関数の積でできる2m次方程式の異なる解の総和

単元:
#数Ⅰ#数A#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}\ p,q$を相異なる素数とする。次の3条件を満たすxの2次式f(x)を考える。
・係数はすべて整数1で$x^2$の係数は1である。
・$f(1)=pq$である。
・方程式$f(x)=0$は整数解をもつ。
以下の問いに答えよ。
(1)$f(x)$をすべて求めよ。
(2)(1)で求めたものを$f_1(x),f_2(x),\ldots,f_m(x)$とする。2m次方程式
$f_1(x)×f_2(x)×\ldots×f_m(x)=0$
の相異なる解の総和は$p,q$によらないことを示せ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{2}}\ p,q$を相異なる素数とする。次の3条件を満たすxの2次式f(x)を考える。
・係数はすべて整数1で$x^2$の係数は1である。
・$f(1)=pq$である。
・方程式$f(x)=0$は整数解をもつ。
以下の問いに答えよ。
(1)$f(x)$をすべて求めよ。
(2)(1)で求めたものを$f_1(x),f_2(x),\ldots,f_m(x)$とする。2m次方程式
$f_1(x)×f_2(x)×\ldots×f_m(x)=0$
の相異なる解の総和は$p,q$によらないことを示せ。
2022早稲田大学理工学部過去問
大学入試問題#264 芝浦工業大学(2011) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#芝浦工業大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{dt}{1+t^2}$のとき
$\displaystyle \int_{0}^{\sqrt{ 3 }}x\ f(x)dx$を求めよ。
出典:2011年芝浦工業大学 入試問題
この動画を見る
$f(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{dt}{1+t^2}$のとき
$\displaystyle \int_{0}^{\sqrt{ 3 }}x\ f(x)dx$を求めよ。
出典:2011年芝浦工業大学 入試問題
福田の数学〜早稲田大学2022年理工学部第1問〜2つの指数関数に囲まれた部分の面積と回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}\ f(x)=3e^x-6,g(x)=e^{2x}-4e^x$とおく。
xy平面上の曲線$y=f(x)$をC、曲線$y=g(x)$をDとする。
以下の問いに答えよ。
(1)CとDの概形を一つのxy平面上に描け。
(2)CとDによって囲まれた部分の面積Sを求めよ。
(3)CとDによって囲まれた部分を、x軸の周りに1回転させてできる
立体の体積Vを求めよ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{1}}\ f(x)=3e^x-6,g(x)=e^{2x}-4e^x$とおく。
xy平面上の曲線$y=f(x)$をC、曲線$y=g(x)$をDとする。
以下の問いに答えよ。
(1)CとDの概形を一つのxy平面上に描け。
(2)CとDによって囲まれた部分の面積Sを求めよ。
(3)CとDによって囲まれた部分を、x軸の周りに1回転させてできる
立体の体積Vを求めよ。
2022早稲田大学理工学部過去問
大学入試問題#263 山形大学(2011) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi}x\sin^2x\ dx$を求めよ。
出典:2011年山形大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi}x\sin^2x\ dx$を求めよ。
出典:2011年山形大学 入試問題
福田の数学〜慶應義塾大学2022年看護医療学部第5問〜定積分で表された関数の最小値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#不定積分・定積分#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{5}}$関数$f(x)$を$f(x)=(x+1)(|x-1|-1)+2$で定める。
(1)$y=f(x)$のグラフをかきなさい。
(2)kを実数とする。このとき、方程式$f(x)=k$が異なる3つの実数解
をもつようなkの値の範囲は$\boxed{\ \ ア\ \ }$である。
(3)曲線$y=f(x)$上の点$P(0,f(0))$における接線lの方程式は$y=\boxed{\ \ イ\ \ }$である。
また、曲線$y=f(x)$と直線lは2つの共有点をもつが、点Pとは異なる共有点を
Qとするとき、点Qのx座標は$\boxed{\ \ ウ\ \ }$である。さらに、曲線$y=f(x)$と直線lで
囲まれた図形の面積は$\boxed{\ \ エ\ \ }$である。
(4)関数$F(x)$を$F(x)=\int_0^xf(t)dt$で定める。このとき、$F'(x)=0$を満たすxを
すべて求めると$x=\boxed{\ \ オ\ \ }$である。これより、関数$F(x)$は
$x=\boxed{\ \ カ\ \ }$で最小値$\boxed{\ \ キ\ \ }$をとることがわかる。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{5}}$関数$f(x)$を$f(x)=(x+1)(|x-1|-1)+2$で定める。
(1)$y=f(x)$のグラフをかきなさい。
(2)kを実数とする。このとき、方程式$f(x)=k$が異なる3つの実数解
をもつようなkの値の範囲は$\boxed{\ \ ア\ \ }$である。
(3)曲線$y=f(x)$上の点$P(0,f(0))$における接線lの方程式は$y=\boxed{\ \ イ\ \ }$である。
また、曲線$y=f(x)$と直線lは2つの共有点をもつが、点Pとは異なる共有点を
Qとするとき、点Qのx座標は$\boxed{\ \ ウ\ \ }$である。さらに、曲線$y=f(x)$と直線lで
囲まれた図形の面積は$\boxed{\ \ エ\ \ }$である。
(4)関数$F(x)$を$F(x)=\int_0^xf(t)dt$で定める。このとき、$F'(x)=0$を満たすxを
すべて求めると$x=\boxed{\ \ オ\ \ }$である。これより、関数$F(x)$は
$x=\boxed{\ \ カ\ \ }$で最小値$\boxed{\ \ キ\ \ }$をとることがわかる。
2022慶應義塾大学看護医療学科過去問
大学入試問題#262 信州大学(2022) #定積分 #Kingproperty

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\pi}^{\pi}\displaystyle \frac{dx}{1+e^{-2\sin\ x}}$
出典:2022年信州大学 入試問題
この動画を見る
$\displaystyle \int_{-\pi}^{\pi}\displaystyle \frac{dx}{1+e^{-2\sin\ x}}$
出典:2022年信州大学 入試問題
東大の整数問題!かなり良問です【数学 入試問題】【東京大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を1以上の整数とする。
(1)$n^2+1$と$5n^2+9$の最大公約数$d_n$を求めよ。
(2)$(n^2+1)(5n^2+9)$は整数の2乗にならないことを示せ。
東大過去問
この動画を見る
$n$を1以上の整数とする。
(1)$n^2+1$と$5n^2+9$の最大公約数$d_n$を求めよ。
(2)$(n^2+1)(5n^2+9)$は整数の2乗にならないことを示せ。
東大過去問
福田の数学〜慶應義塾大学2022年看護医療学部第4問〜空間図形とベクトル

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$aを1以上の実数とし、$AB=BC=CA=1$および$AD=BD=CD=a$
を満たす四面体ABCDを考える。このとき、$\cos\angle BAD=\boxed{\ \ ア\ \ }$である。
また、ADの中点をEとしたとき、$\overrightarrow{ EB }$を$\overrightarrow{ AB },\overrightarrow{ AC },\overrightarrow{ AD }$を用いて表すと
$\overrightarrow{ EB }=\boxed{\ \ イ\ \ }$となるので、$|\overrightarrow{ EB }|=\boxed{\ \ ウ\ \ }$で、
$\overrightarrow{ EB }・\overrightarrow{ EC }=\boxed{\ \ エ\ \ }$
である。よって、$a=1$のとき、$\cos\angle BEC=\boxed{\ \ オ\ \ }$であり、
$\angle BEC=60°$となるのは$a=\boxed{\ \ カ\ \ }$のときである。
2022慶応義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{4}}$aを1以上の実数とし、$AB=BC=CA=1$および$AD=BD=CD=a$
を満たす四面体ABCDを考える。このとき、$\cos\angle BAD=\boxed{\ \ ア\ \ }$である。
また、ADの中点をEとしたとき、$\overrightarrow{ EB }$を$\overrightarrow{ AB },\overrightarrow{ AC },\overrightarrow{ AD }$を用いて表すと
$\overrightarrow{ EB }=\boxed{\ \ イ\ \ }$となるので、$|\overrightarrow{ EB }|=\boxed{\ \ ウ\ \ }$で、
$\overrightarrow{ EB }・\overrightarrow{ EC }=\boxed{\ \ エ\ \ }$
である。よって、$a=1$のとき、$\cos\angle BEC=\boxed{\ \ オ\ \ }$であり、
$\angle BEC=60°$となるのは$a=\boxed{\ \ カ\ \ }$のときである。
2022慶応義塾大学看護医療学科過去問
大学入試問題#261 山形大学(2011) #数列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学
指導講師:
ますただ
問題文全文(内容文):
$x_1=1$
$x_{n+1}=3x_n+\displaystyle \frac{1}{2^{n+1}}$
一般項$x_n$を求めよ。
出典:2011年山形大学 入試問題
この動画を見る
$x_1=1$
$x_{n+1}=3x_n+\displaystyle \frac{1}{2^{n+1}}$
一般項$x_n$を求めよ。
出典:2011年山形大学 入試問題
福田の数学〜慶應義塾大学2022年看護医療学部第3問〜平均と分散の変換

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}$(1)ある学校で100点満点のテストを行うことになった。
まず10人の教員で解いてみたところ、その得点のヒストグラムは
右図(※動画参照)のようになった。ただし、得点は整数値とする。
このデータの平均値は$\boxed{\ \ ア\ \ }$点、中央値は$\boxed{\ \ イ\ \ }$点、
最頻値は$\boxed{\ \ ウ\ \ }$点、分散は$\boxed{\ \ エ\ \ }$点である。
(2)A組とB組の2つのクラスで数学のテストを行ったところ、A組の得点の平均
値が$\overline{x}_A$、分散が$s_A^2$、B組の得点の平均値が$\overline{x}_B$、分散が$s_B^2$となった。
ただし、$\overline{x}_A,\overline{x}_B,s_A^2,s_B^2$はいずれも0ではなかった。このとき、B組の各生徒
の得点$x$に対して、正の実数aと実数bを用いて$y=ax+b$と変換し、
yの平均値と分散をA組の平均値と分散に一致させるためには、
$a=\boxed{\ \ オ\ \ }、b=\boxed{\ \ カ\ \ }$とすればよい。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{3}}$(1)ある学校で100点満点のテストを行うことになった。
まず10人の教員で解いてみたところ、その得点のヒストグラムは
右図(※動画参照)のようになった。ただし、得点は整数値とする。
このデータの平均値は$\boxed{\ \ ア\ \ }$点、中央値は$\boxed{\ \ イ\ \ }$点、
最頻値は$\boxed{\ \ ウ\ \ }$点、分散は$\boxed{\ \ エ\ \ }$点である。
(2)A組とB組の2つのクラスで数学のテストを行ったところ、A組の得点の平均
値が$\overline{x}_A$、分散が$s_A^2$、B組の得点の平均値が$\overline{x}_B$、分散が$s_B^2$となった。
ただし、$\overline{x}_A,\overline{x}_B,s_A^2,s_B^2$はいずれも0ではなかった。このとき、B組の各生徒
の得点$x$に対して、正の実数aと実数bを用いて$y=ax+b$と変換し、
yの平均値と分散をA組の平均値と分散に一致させるためには、
$a=\boxed{\ \ オ\ \ }、b=\boxed{\ \ カ\ \ }$とすればよい。
2022慶應義塾大学看護医療学科過去問
大学入試問題#260 慶應義塾大学 改 (2011) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2}8(x+1)\sqrt{ 4x+1 }\ dx$を計算せよ。
出典:2011年慶應義塾大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2}8(x+1)\sqrt{ 4x+1 }\ dx$を計算せよ。
出典:2011年慶應義塾大学 入試問題
福田の数学〜慶應義塾大学2022年看護医療学部第2問(3)〜平方数を3で割った余りに関する論証

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#推理と論証#推理と論証#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$(3)次の2つの命題を証明せよ。
$(\textrm{i})$整数nが3の倍数でないならば、$n^2$を3で割った時の余りは1である。
$(\textrm{ii})$3つの整数$x,y,z$が等式$x^2+y^2=z^2$を満たすならば、
xとyの少なくとも一方は3の倍数である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{2}}$(3)次の2つの命題を証明せよ。
$(\textrm{i})$整数nが3の倍数でないならば、$n^2$を3で割った時の余りは1である。
$(\textrm{ii})$3つの整数$x,y,z$が等式$x^2+y^2=z^2$を満たすならば、
xとyの少なくとも一方は3の倍数である。
2022慶應義塾大学看護医療学科過去問
大学入試問題#259 島根大学(2012) #微分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#島根大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=|x|\sin\ x$の$x=0$における微分可能性を調べよ。
出典:2012年島根大学 入試問題
この動画を見る
$f(x)=|x|\sin\ x$の$x=0$における微分可能性を調べよ。
出典:2012年島根大学 入試問題
無限降下法って知ってる?整数問題の難問です【数学 入試問題】【九州大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$a^2+b^2=3c^2$を満たす自然数$a,b,c$は存在しないことを証明せよ。
九州大過去問
この動画を見る
$a^2+b^2=3c^2$を満たす自然数$a,b,c$は存在しないことを証明せよ。
九州大過去問
福田の数学〜慶應義塾大学2022年看護医療学部第2問(2)〜漸化式と和に関する不等式

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$(2)$a_1=4,\ \ \ 4a_{n+1}=2a_n+3(n=1,2,3,\ldots)$で与えられる
数列$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ ア\ \ }$である。
また$\sum_{n=1}^la_n \geqq 20$
を満たす最小の自然数lは$\boxed{\ \ イ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{2}}$(2)$a_1=4,\ \ \ 4a_{n+1}=2a_n+3(n=1,2,3,\ldots)$で与えられる
数列$\left\{a_n\right\}$の一般項は$a_n=\boxed{\ \ ア\ \ }$である。
また$\sum_{n=1}^la_n \geqq 20$
を満たす最小の自然数lは$\boxed{\ \ イ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
大学入試問題#258 東京理科大学(2011) #定積分 #面積

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$y-\tan\ x(0 \leqq x \lt \displaystyle \frac{\pi}{2})$
$y-\cos\ x(0 \leqq x \leqq \displaystyle \frac{\pi}{2})$
$x$軸で囲まれた部分の面積を求めよ。
出典:2011年東京理科大学 入試問題
この動画を見る
$y-\tan\ x(0 \leqq x \lt \displaystyle \frac{\pi}{2})$
$y-\cos\ x(0 \leqq x \leqq \displaystyle \frac{\pi}{2})$
$x$軸で囲まれた部分の面積を求めよ。
出典:2011年東京理科大学 入試問題
福田の数学〜慶應義塾大学2022年看護医療学部第2問(1)〜円が直線から切り取る弦の長さ

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$(1)円$x^2+y^2-2x+6y=0$をCとするとき、
円Cの中心の座標は$\boxed{\ \ ア\ \ }$であり、
半径は$\boxed{\ \ イ\ \ }$である。また、円Cと直線$y=3x-1$の2つの共有点をA,Bとする
とき、線分ABの長さは$\boxed{\ \ ウ\ \ }$であり、線分ABの垂直二等分線の方程式は
$y=\boxed{\ \ エ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{2}}$(1)円$x^2+y^2-2x+6y=0$をCとするとき、
円Cの中心の座標は$\boxed{\ \ ア\ \ }$であり、
半径は$\boxed{\ \ イ\ \ }$である。また、円Cと直線$y=3x-1$の2つの共有点をA,Bとする
とき、線分ABの長さは$\boxed{\ \ ウ\ \ }$であり、線分ABの垂直二等分線の方程式は
$y=\boxed{\ \ エ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
福田の数学〜慶應義塾大学2022年看護医療学部第1問(5)〜解と係数の関係と式の値の計算

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(5)iを虚数単位とし、$\alpha=\frac{1-\sqrt3i}{4}$とする。このとき、
$a,b$を実数とする2次方程式$x^2+ax+b=0$の解の1つが$\alpha$であるならば、
$a=\boxed{\ \ ア\ \ },\ b=\boxed{\ \ イ\ \ }$である。
また、$f(x)=4x^4-3x^3+2x^2$とするとき、$f(\alpha)$の値は$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(5)iを虚数単位とし、$\alpha=\frac{1-\sqrt3i}{4}$とする。このとき、
$a,b$を実数とする2次方程式$x^2+ax+b=0$の解の1つが$\alpha$であるならば、
$a=\boxed{\ \ ア\ \ },\ b=\boxed{\ \ イ\ \ }$である。
また、$f(x)=4x^4-3x^3+2x^2$とするとき、$f(\alpha)$の値は$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
大学入試問題#257 東京理科大学(2011) #極限 #区分求積法

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{k}{n^2}log(\displaystyle \frac{n+k}{n})$を求めよ。
出典:2011年東京理科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{k}{n^2}log(\displaystyle \frac{n+k}{n})$を求めよ。
出典:2011年東京理科大学 入試問題
福田の数学〜慶應義塾大学2022年看護医療学部第1問(4)〜サイコロの目の最小値が2である確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(4)3個のさいころを同時に投げるとき、出た目の最小値が2以上となる確率は
$\boxed{\ \ ア\ \ }$であり、最小値がちょうど2となる確率は$\boxed{\ \ イ\ \ }$である。また、
出た目の最小値が2であったとき、どの2つの目も互いに素である条件付き確率は
$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(4)3個のさいころを同時に投げるとき、出た目の最小値が2以上となる確率は
$\boxed{\ \ ア\ \ }$であり、最小値がちょうど2となる確率は$\boxed{\ \ イ\ \ }$である。また、
出た目の最小値が2であったとき、どの2つの目も互いに素である条件付き確率は
$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
