 式の計算(整式・展開・因数分解)
式の計算(整式・展開・因数分解)
 式の計算(整式・展開・因数分解)
式の計算(整式・展開・因数分解)
x3乗=1
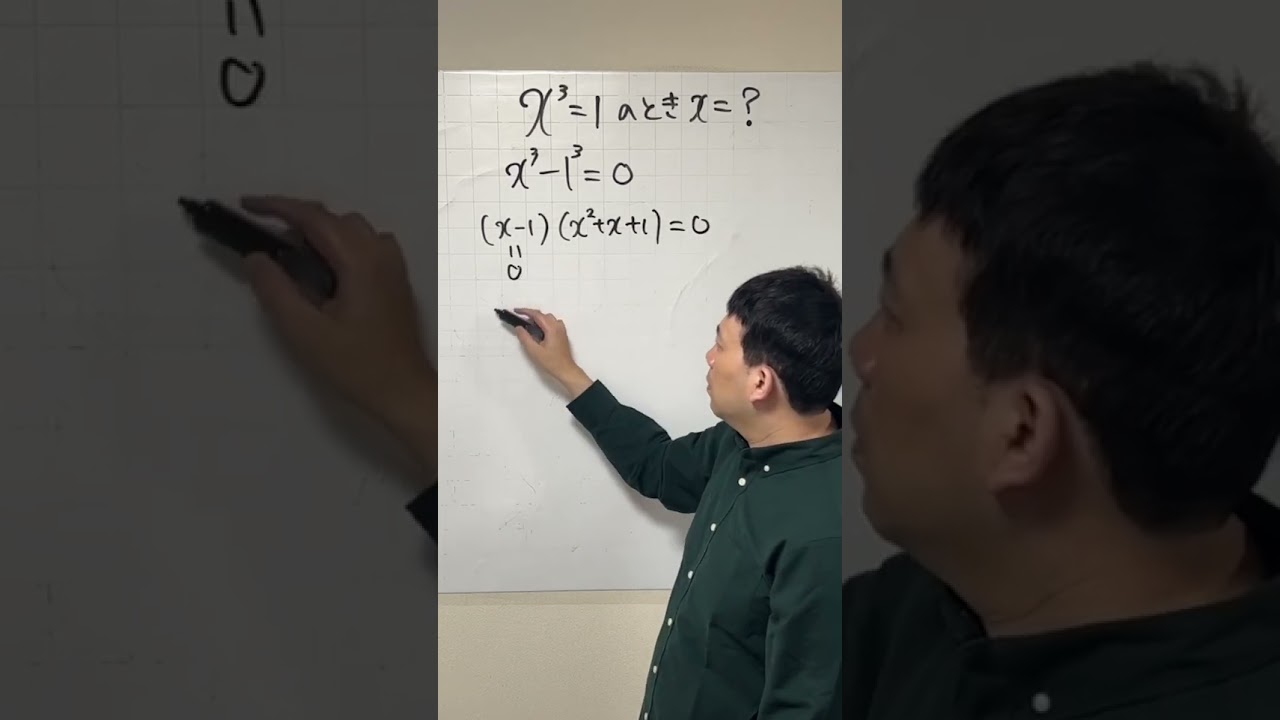
マイナス乗とは?2分の1乗とは?基本から丁寧に解説
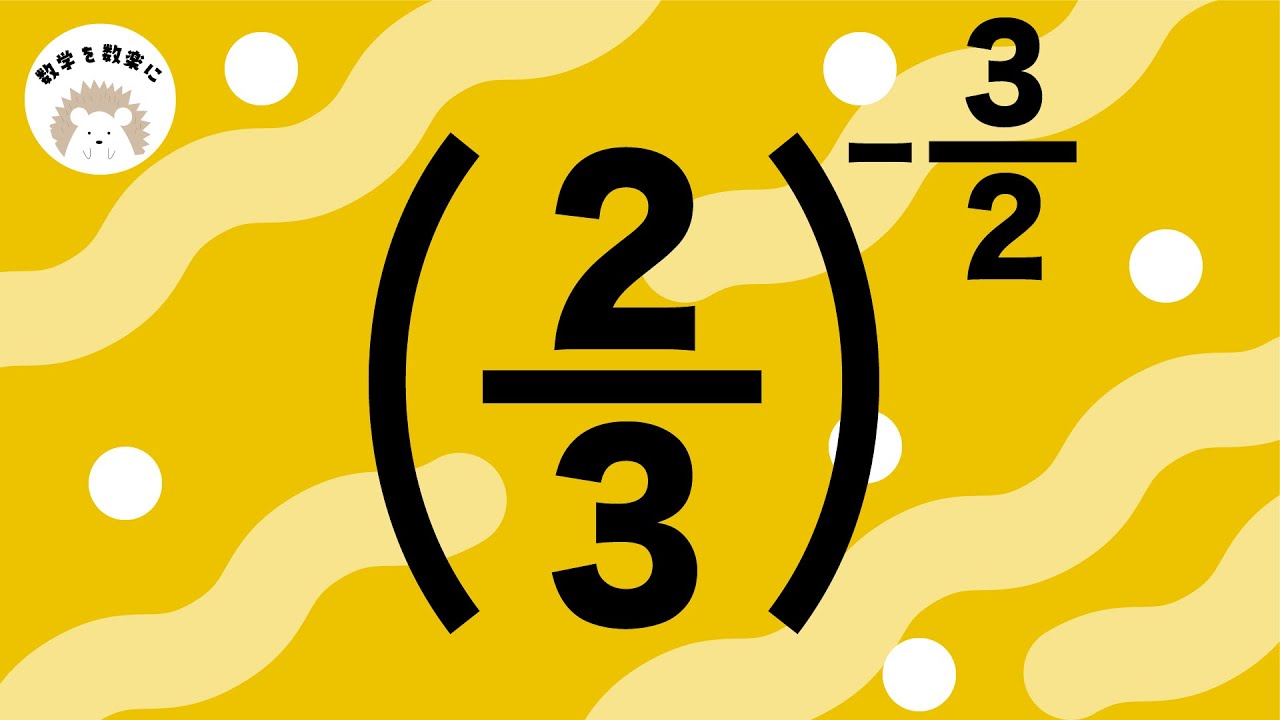
2乗➖2乗は○と○の積を使ってもいいけどさ 大阪教育大附属平野

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$340^2-337^2-3^2$
大阪教育大学附属高等学校平野校舎
2022
この動画を見る
$340^2-337^2-3^2$
大阪教育大学附属高等学校平野校舎
2022
部分分数分解

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} +\frac{1}{20}$
この動画を見る
$\frac{1}{2} + \frac{1}{6} + \frac{1}{12} +\frac{1}{20}$
難しい因数分解やろうぜ【高校数学】

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
難しい因数分解
(1)$a(l^2-c^2)+l(c^2-a^2)+c(a^2-l^2)$
(2)$a^2(b+c)+b^2(c+a)+c^2(a+b)+2abc$
(3)$2x^2+5xy+2y^2-x+y-1$
(4)$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$
(5)$x^2-y^2-zx+yz$
(6)$a(b+c)^2+b(c+a)^2+c(a+b)^2-4abc$
この動画を見る
難しい因数分解
(1)$a(l^2-c^2)+l(c^2-a^2)+c(a^2-l^2)$
(2)$a^2(b+c)+b^2(c+a)+c^2(a+b)+2abc$
(3)$2x^2+5xy+2y^2-x+y-1$
(4)$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$
(5)$x^2-y^2-zx+yz$
(6)$a(b+c)^2+b(c+a)^2+c(a+b)^2-4abc$
式の値 早稲田実業

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
この動画を見る
$a^2 - b^2 -a -b = 0$のとき
$a^2+b^2-2ab-a+b=?$
(a>0,b>0)
早稲田実業学校
6乗−6乗の因数分解

ハートで分けろ 高校数学 式の値
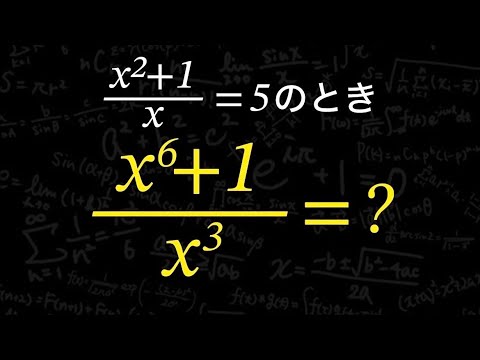
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{x^2+1}{x}=5$のとき
$\frac{x^6+1}{x^3}=?$
この動画を見る
$\frac{x^2+1}{x}=5$のとき
$\frac{x^6+1}{x^3}=?$
2024を素因数分解

2=3
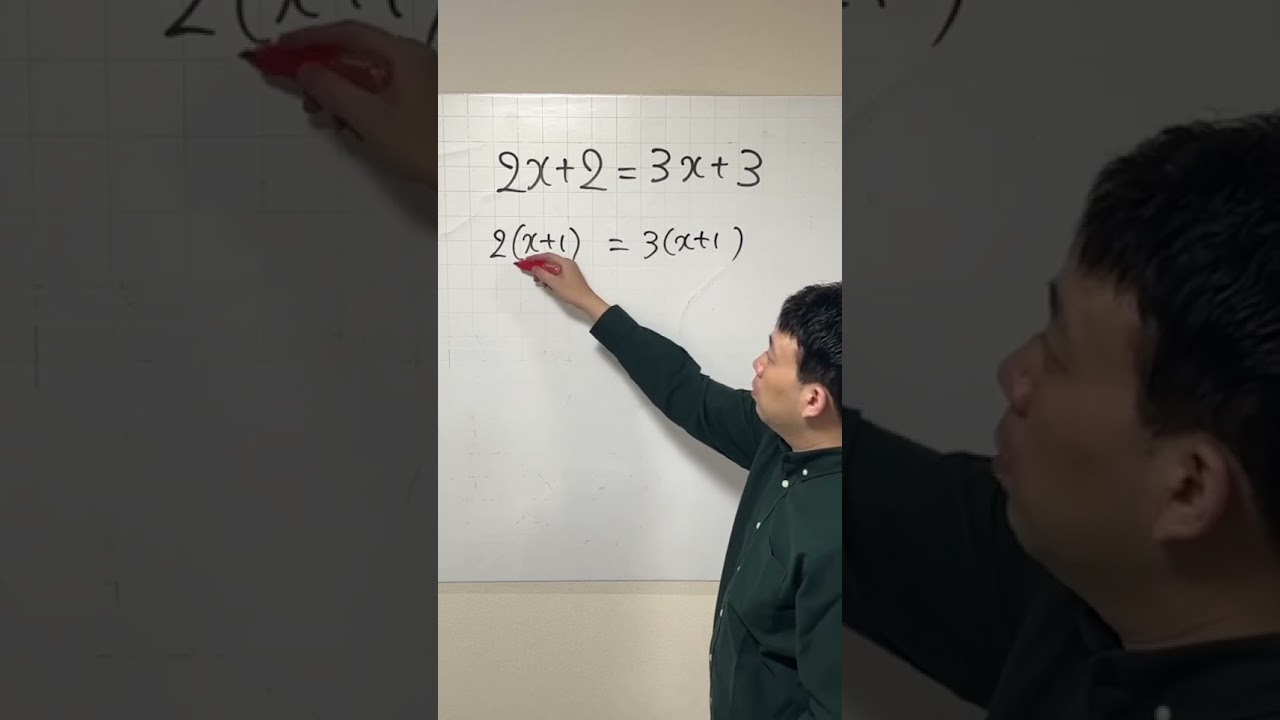
シンガポール数学オリンピック整数問題の基本
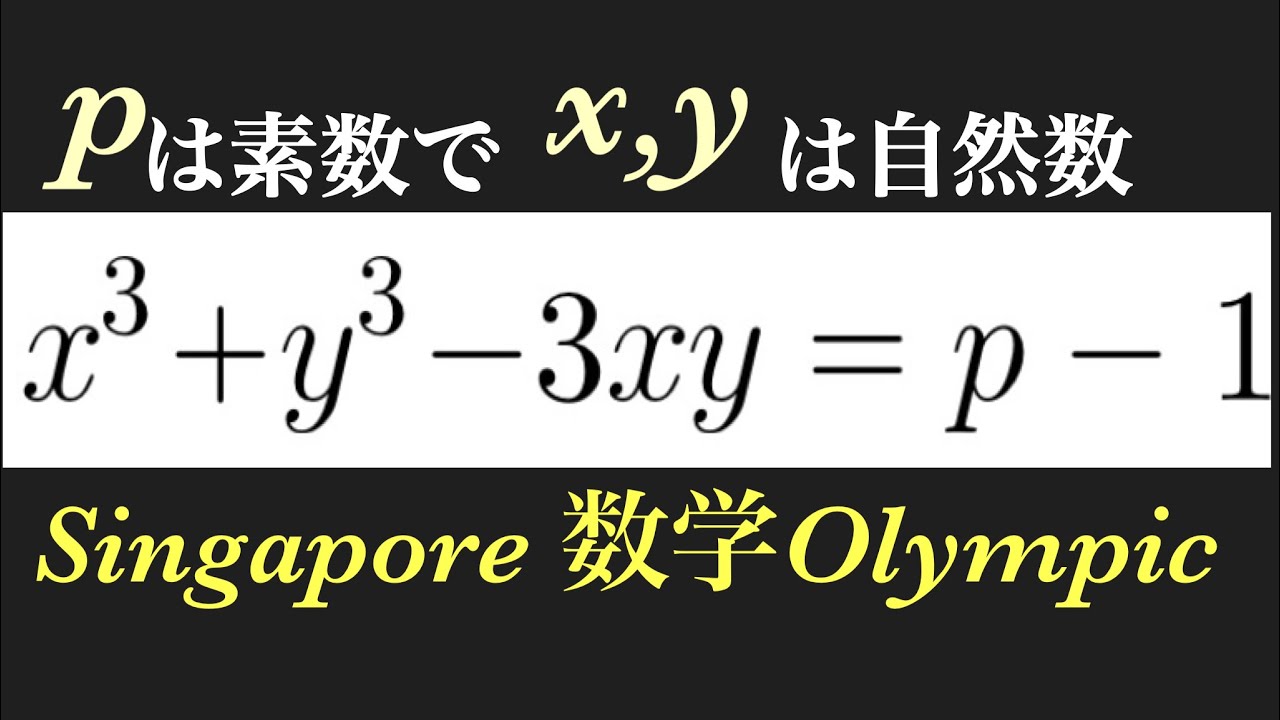
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$P$は素数であり,$x,y$を自然数としたとき,
$x^3+y^3-3xy=p-1$をみたす$(x,y)$をすべて求めよ.
シンガポール数学オリンピック過去問
この動画を見る
$P$は素数であり,$x,y$を自然数としたとき,
$x^3+y^3-3xy=p-1$をみたす$(x,y)$をすべて求めよ.
シンガポール数学オリンピック過去問
ただの因数分解だよ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の式は整数の範囲で因数分解できることが分かっています.
$2x^2-2519376x-3^10$
$(2^{\Box}x-3^{\Box})(2^{\Box}x+3^{\Box})
\Box$ に0以上の整数を入れなさい.
この動画を見る
次の式は整数の範囲で因数分解できることが分かっています.
$2x^2-2519376x-3^10$
$(2^{\Box}x-3^{\Box})(2^{\Box}x+3^{\Box})
\Box$ に0以上の整数を入れなさい.
これって高校範囲なのでは? 埼玉県
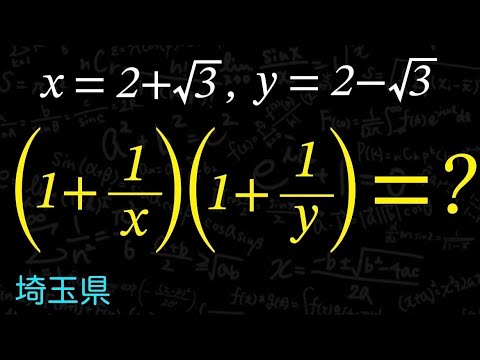
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2+\sqrt 3,y=2- \sqrt 3$
$(1+\frac{1}{x})(1+\frac{1}{y})=?$
埼玉県
この動画を見る
$x=2+\sqrt 3,y=2- \sqrt 3$
$(1+\frac{1}{x})(1+\frac{1}{y})=?$
埼玉県
因数分解

単元:
#数Ⅰ#数Ⅱ#数と式#式の計算(整式・展開・因数分解)#指数関数と対数関数#指数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$9x^2+4168x+2^{15}$
この動画を見る
因数分解せよ.
$9x^2+4168x+2^{15}$
すべて○けろ!!式の値
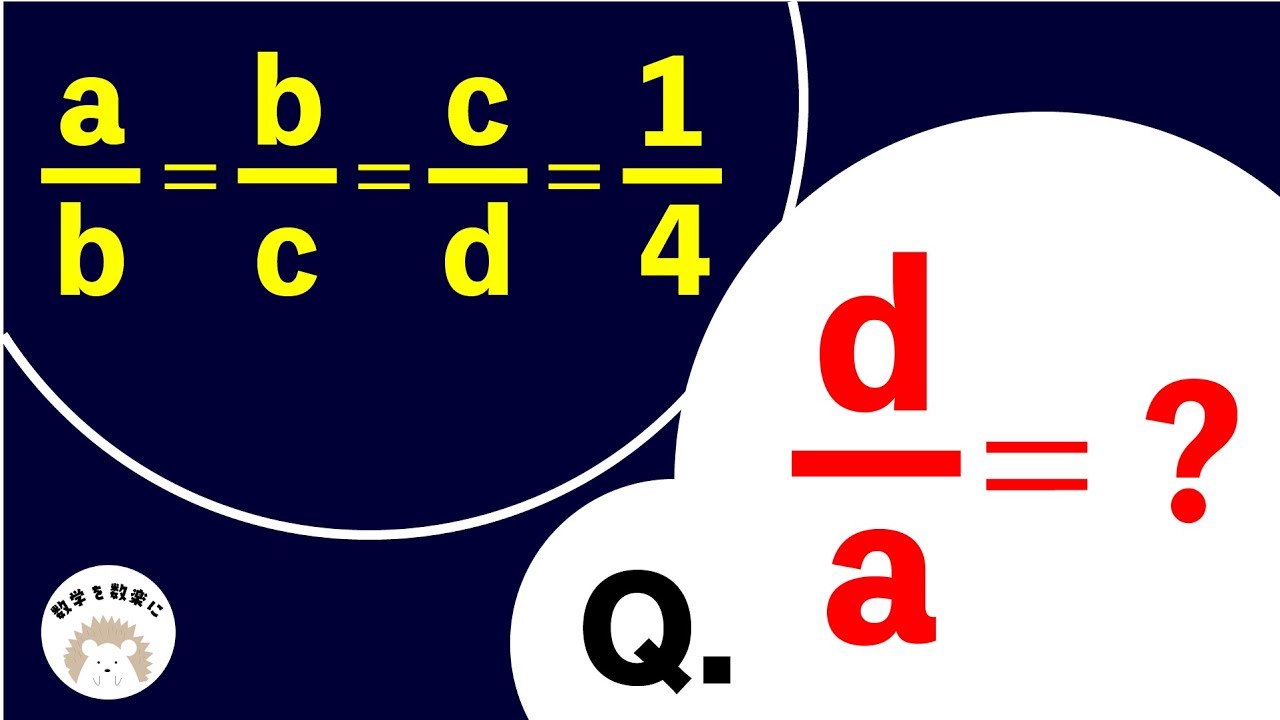
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{a}{b} = \frac{b}{c} = \frac{c}{d} = \frac{1}{4}$
$\frac{d}{a} =?$
この動画を見る
$\frac{a}{b} = \frac{b}{c} = \frac{c}{d} = \frac{1}{4}$
$\frac{d}{a} =?$
志木の展開
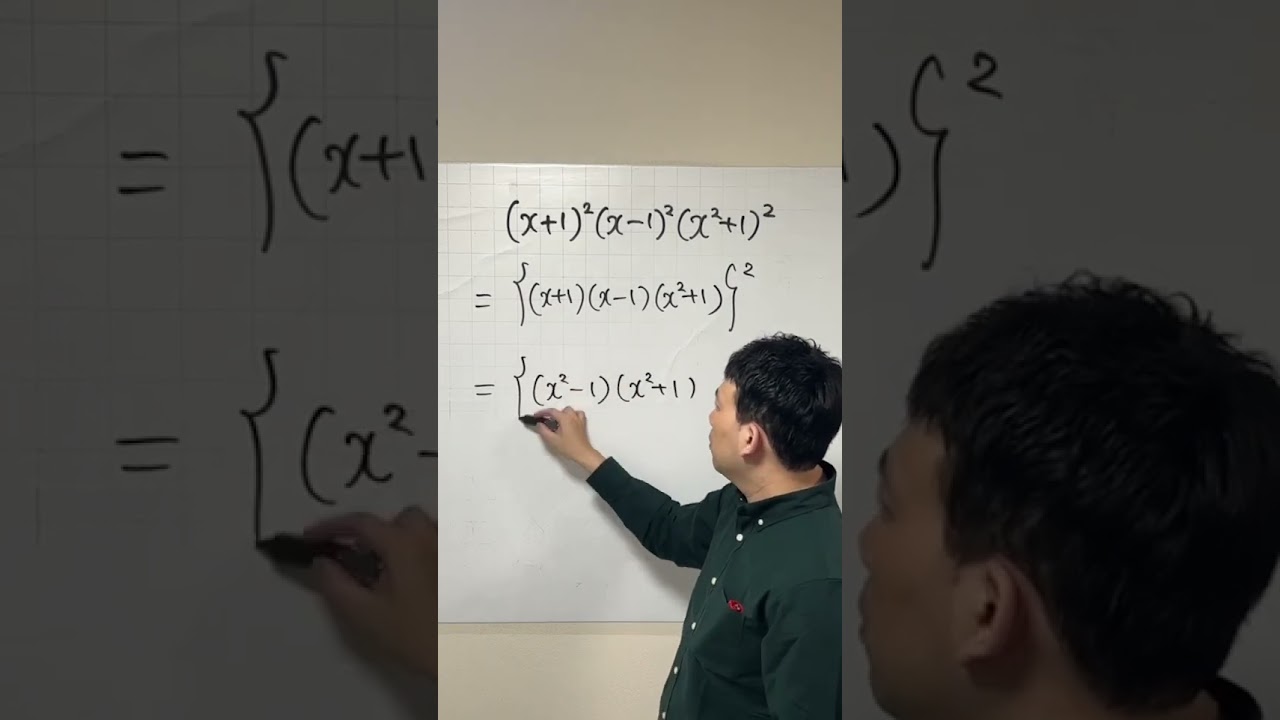
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
展開せよ
$(x+1)^2(x-1)^2(x^2+1)^2$
慶應義塾志木高等学校
この動画を見る
展開せよ
$(x+1)^2(x-1)^2(x^2+1)^2$
慶應義塾志木高等学校
すべてを○けろ!!久留米大附設

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a,b,c,d,e$は正の数
$ab=1,bc=2,cd=3,de=4,ea=5$のとき
$a=?$
久留米大学付設高等学校
この動画を見る
$a,b,c,d,e$は正の数
$ab=1,bc=2,cd=3,de=4,ea=5$のとき
$a=?$
久留米大学付設高等学校
答えはあれじゃないよ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^7=1,x \neq 1$のとき、
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x}+$
$\dfrac{x^5}{1+x^3}+\dfrac{x^6}{1+x^5}$の値を求めよ.
この動画を見る
$x^7=1,x \neq 1$のとき、
$\dfrac{x}{1+x^2}+\dfrac{x^2}{1+x^4}+\dfrac{x^3}{1+x^6}+\dfrac{x^4}{1+x}+$
$\dfrac{x^5}{1+x^3}+\dfrac{x^6}{1+x^5}$の値を求めよ.
解を出さなくても解ける! 難関高校受験するのなら絶対に知って欲しい 解と〇〇の関係 明大明治

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-4x+1=0$の2つの解をa,bとするとき
$a^{10}b^8 + a^6b^8 - 3a^5b^5 =?$
明治大学付属明治高等学校
この動画を見る
$x^2-4x+1=0$の2つの解をa,bとするとき
$a^{10}b^8 + a^6b^8 - 3a^5b^5 =?$
明治大学付属明治高等学校
地道に因数分解?一瞬で因数分解?

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
次の式を因数分解せよ.
$(x-y)^3+(y-z)^3+(z-x)^3$
この動画を見る
次の式を因数分解せよ.
$(x-y)^3+(y-z)^3+(z-x)^3$
ナイスな連立三元2次方程式

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2-yz=1 \\\
y^2-zx=2\\\
z^2-xy=3
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2-yz=1 \\\
y^2-zx=2\\\
z^2-xy=3
\end{array}
\right.
\end{eqnarray}$
誘導にのれるか、のれないか。弘学館

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$45^2 = ?$
$x^2 - 2 \sqrt2x -2023 = 0$を解け
弘学館高等学校
この動画を見る
$45^2 = ?$
$x^2 - 2 \sqrt2x -2023 = 0$を解け
弘学館高等学校
ただの因数分解

ただの因数分解と整数問題

単元:
#数Ⅰ#数A#数と式#場合の数と確率#式の計算(整式・展開・因数分解)#整数の性質#場合の数#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
①因数分解せよ.
$(x-2)(x-1)(x+1)(x+2)+2$
②$n^5-5n^3+5n+7$が120の倍数となる自然数nを一つ求めよ.
この動画を見る
①因数分解せよ.
$(x-2)(x-1)(x+1)(x+2)+2$
②$n^5-5n^3+5n+7$が120の倍数となる自然数nを一つ求めよ.
気付けば一瞬だが、意外と難しいのよ。因数分解

福田の数学〜慶應義塾大学2023年薬学部第1問(1)〜素因数分解と変数の値

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)整式X=6$a^3bc$+11$a^2b^2c$+3$ab^3c$がある。
(i)Xを因数分解するとX=$\boxed{\ \ ア\ \ }$である。
(ii)X=6270 を満たす(a,b,c)の組を全て求めると、(a,b,c)=$\boxed{\ \ イ\ \ }$である。ただし、a,b,cはそれぞれ2以上の整数とする。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (1)整式X=6$a^3bc$+11$a^2b^2c$+3$ab^3c$がある。
(i)Xを因数分解するとX=$\boxed{\ \ ア\ \ }$である。
(ii)X=6270 を満たす(a,b,c)の組を全て求めると、(a,b,c)=$\boxed{\ \ イ\ \ }$である。ただし、a,b,cはそれぞれ2以上の整数とする。
2023慶應義塾大学薬学部過去問
式の値と平方根
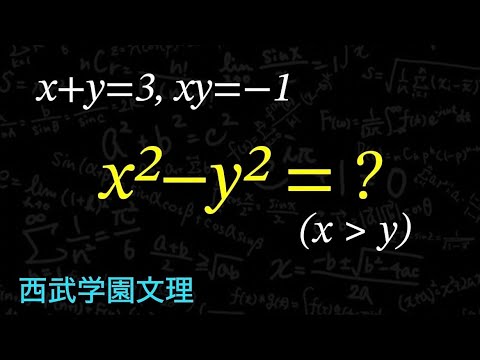
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x + y = 3 , xy = -1$
$x^2 -y^2 = ?$
($x>y$)
西部学園文理高等学校
この動画を見る
$x + y = 3 , xy = -1$
$x^2 -y^2 = ?$
($x>y$)
西部学園文理高等学校
慶應志木 式の値

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=\frac{7}{3+ \sqrt 2}$のとき
$(x-1)(x-2)(x-4)(x-5) = ?$
2023慶應義塾志木高等学校
この動画を見る
$x=\frac{7}{3+ \sqrt 2}$のとき
$(x-1)(x-2)(x-4)(x-5) = ?$
2023慶應義塾志木高等学校
因数分解(難)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$x^3y-xy^3-x^2+y^2+2xy-1$
この動画を見る
因数分解せよ.
$x^3y-xy^3-x^2+y^2+2xy-1$
関西医科大

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#関西医科大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$3x^2+xy-2y^2-x+4y=4$をみたす整数(x,y)を求めよ.
関西医科大過去問
この動画を見る
$3x^2+xy-2y^2-x+4y=4$をみたす整数(x,y)を求めよ.
関西医科大過去問
