 内心・外心・重心とチェバ・メネラウス
内心・外心・重心とチェバ・メネラウス
 内心・外心・重心とチェバ・メネラウス
内心・外心・重心とチェバ・メネラウス
【数A】【図形の性質】円に内接する図形 ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
円oにおいて、平行な2つの弦をAA´、BB´とし、AB´とA´Bが円の内部の点Pで交わっている。このとき、∠APB=∠AOBであることを証明せよ。
鋭角三角形ABCの垂心をHとし、AHがBCと交わる点をD、△ABCの外接円と交わる点をEとする。このとき、Dは線分HEの中点であることを証明せよ。
下の図において、角θを求めよ。
この動画を見る
円oにおいて、平行な2つの弦をAA´、BB´とし、AB´とA´Bが円の内部の点Pで交わっている。このとき、∠APB=∠AOBであることを証明せよ。
鋭角三角形ABCの垂心をHとし、AHがBCと交わる点をD、△ABCの外接円と交わる点をEとする。このとき、Dは線分HEの中点であることを証明せよ。
下の図において、角θを求めよ。
【数A】【図形の性質】三角形の関係証明 ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
△ABCの内部の1点をPとするとき、AP+BP+CP>1/2(AB+BC+CA)を証明せよ。
上の図において、点Pが線分CD上を動くとき、線分の和AP+PBの最小値とそのときの点Pの位置を求めよ。
この動画を見る
△ABCの内部の1点をPとするとき、AP+BP+CP>1/2(AB+BC+CA)を証明せよ。
上の図において、点Pが線分CD上を動くとき、線分の和AP+PBの最小値とそのときの点Pの位置を求めよ。
【数A】【図形の性質】三角形の辺と角 ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
∠B=90度の直角三角形ABCの辺BC上に頂点と異なる点Pを取る時、AB<AP<ACであることを証明せよ。
△ABCにおいて、AB>ACとする。∠Aの二等分線と辺BCの交点をPとする時、次の①~④のうちで常に成り立つものを全て選べ。
①BP=PC ②AB>AP ③AC>AP ④AC>CP
次の長さの線分を3辺とする三角形が存在するようなXの値の範囲を求めよ。
(1)X、2、6 (2)3X、X+4、X+2
この動画を見る
∠B=90度の直角三角形ABCの辺BC上に頂点と異なる点Pを取る時、AB<AP<ACであることを証明せよ。
△ABCにおいて、AB>ACとする。∠Aの二等分線と辺BCの交点をPとする時、次の①~④のうちで常に成り立つものを全て選べ。
①BP=PC ②AB>AP ③AC>AP ④AC>CP
次の長さの線分を3辺とする三角形が存在するようなXの値の範囲を求めよ。
(1)X、2、6 (2)3X、X+4、X+2
【数A】【図形の性質】チェバメネラウス ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
(1):△ABCの辺AB、AC上に、それぞれ頂点と異なる点D、Eを取る時、等式【△ADE/△ABC】=【AD/AB】×【AE/AC】が成り立つことを証明せよ。
(2):△ABCの辺BCを2:3、辺CAを3:1、辺ABを1:2に内分する点をそれぞれD、E、Fとする時、次の値を求めよ。
(ア)△AFE/△ABC (イ)△DEF/△ABC
△ABCの辺ABを2:3に内分する点をR、辺ACを5:6に内分する点をQとする。線分BQと線分CRの交点をOとする。直線AOと辺BCの交点をPとする。
(1)BP:PCを求めよ。 (2)△OBC:△ABCを求めよ。
△ABCの辺ABを2:1に内分する点をD、辺ACを3:1に内分する点をEとする。直線DEとBCの交点をPとする。
(1)BP:PCを求めよ。 (2)DP:PEを求めよ。
この動画を見る
(1):△ABCの辺AB、AC上に、それぞれ頂点と異なる点D、Eを取る時、等式【△ADE/△ABC】=【AD/AB】×【AE/AC】が成り立つことを証明せよ。
(2):△ABCの辺BCを2:3、辺CAを3:1、辺ABを1:2に内分する点をそれぞれD、E、Fとする時、次の値を求めよ。
(ア)△AFE/△ABC (イ)△DEF/△ABC
△ABCの辺ABを2:3に内分する点をR、辺ACを5:6に内分する点をQとする。線分BQと線分CRの交点をOとする。直線AOと辺BCの交点をPとする。
(1)BP:PCを求めよ。 (2)△OBC:△ABCを求めよ。
△ABCの辺ABを2:1に内分する点をD、辺ACを3:1に内分する点をEとする。直線DEとBCの交点をPとする。
(1)BP:PCを求めよ。 (2)DP:PEを求めよ。
【数A】【図形の性質】図形の性質の基本2 ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か?
三角形ABCの内心をI、角Aの内部の傍心をI₁とする時、次の問いに答えよ。
(1)角IBI₁の大きさを求めよ。
(2)三角形ABCの外接円は線分II₁を二等分することを証明せよ。
AB=ACである二等辺三角形ABCの頂点Aから辺BCに下ろした垂線をADとする。
角Bの内部の傍接円IBの半径はADに等しいことを証明せよ。
この動画を見る
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か?
三角形ABCの内心をI、角Aの内部の傍心をI₁とする時、次の問いに答えよ。
(1)角IBI₁の大きさを求めよ。
(2)三角形ABCの外接円は線分II₁を二等分することを証明せよ。
AB=ACである二等辺三角形ABCの頂点Aから辺BCに下ろした垂線をADとする。
角Bの内部の傍接円IBの半径はADに等しいことを証明せよ。
【数A】【図形の性質】図形の性質の基本1 ※問題文は概要欄

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形の性質#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
外心と内心が一致する三角形は正三角形である。このことを証明せよ。
図の三角形ABCは角B=90度の直角三角形であり、3点D、E、Fは三角形ABCの外心・内心・重心のいずれかであるとする。このとき、三角形ABCの外心・内心・重心は3点D、E、Fのいずれであるか?
三角形ABCにおいて、AB=AC=3、BC=2である。三角形ABCの重心をG、内心をIとするとき、線分GIの長さを求めよ。
図において、点Hは三角形ABCの垂心である。角α、βを求めよ。
この動画を見る
外心と内心が一致する三角形は正三角形である。このことを証明せよ。
図の三角形ABCは角B=90度の直角三角形であり、3点D、E、Fは三角形ABCの外心・内心・重心のいずれかであるとする。このとき、三角形ABCの外心・内心・重心は3点D、E、Fのいずれであるか?
三角形ABCにおいて、AB=AC=3、BC=2である。三角形ABCの重心をG、内心をIとするとき、線分GIの長さを求めよ。
図において、点Hは三角形ABCの垂心である。角α、βを求めよ。
これなに?

東大生のワイヤレスイヤホンの見付け方が凄すぎた
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ワイヤレスイヤホンを落としたときの見つけ方
三角形の外心の話です
この動画を見る
ワイヤレスイヤホンを落としたときの見つけ方
三角形の外心の話です
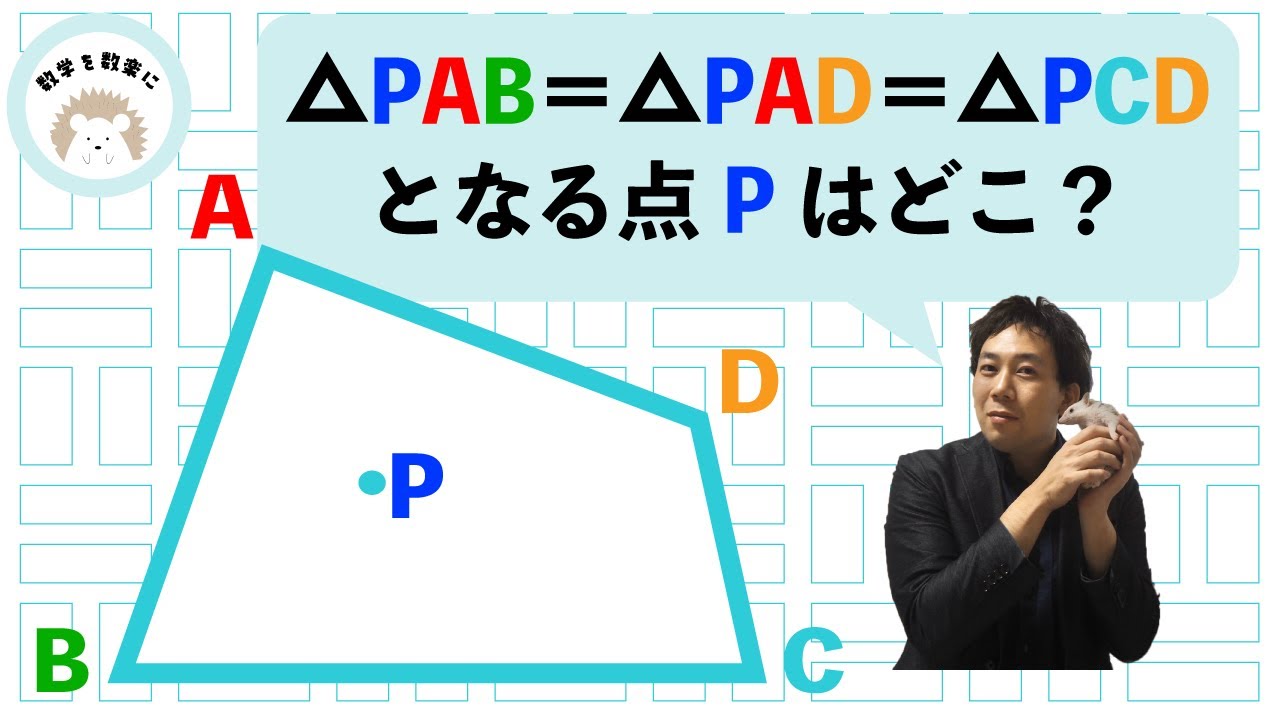
点Pはどこ?
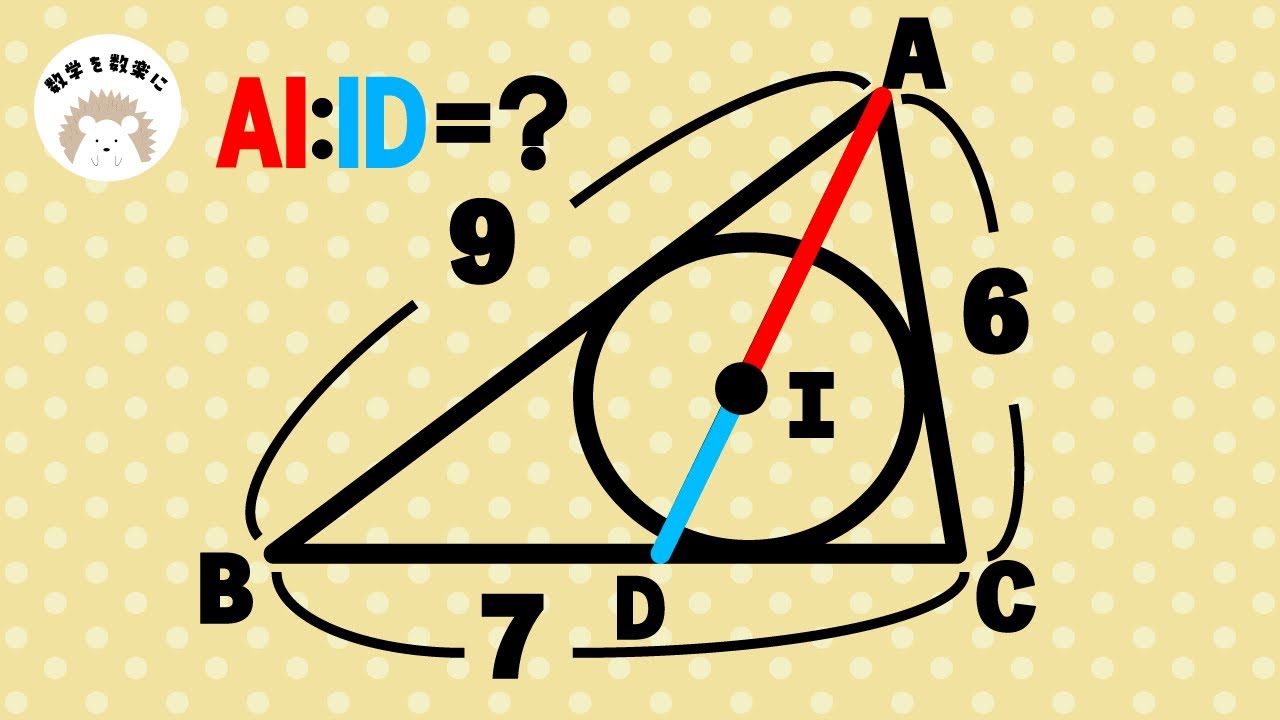
内心と比
2024年共通テスト徹底解説〜数学ⅠA第5問図形の性質〜福田の入試問題解説

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#方べきの定理と2つの円の関係#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
第5 問(1) $\triangle AQD$と直線CEに着目すると$\dfrac{QR}{RD}・\dfrac{DS}{SA}・\dfrac{ア}{CQ}=1$が成り立つのでQR:RD=イ:ウ となる。また、$\triangle AQD$と直線BEに着目するとQB:BD=エ:オ となる。
したがって、BQ:QR:RD=エ:イ:ウとなる個tが分かる。
(2)5点P,Q,R,S,Tが同一演習場にあるとし、AC=8とする。
(i)5点A,P,Q,S,Tに着目すると、AT:ST=1:2より、AT=$\sqrt{ カ }$となる。さらに5点D,Q,R,S,Tに着目すると$DR=4\sqrt{ 3 }$となることがわかる。
( 2 ) 3 点 A , B, C を通る円と点 D の位置関係を次の構想に基づいて調べよう。
構想:線分 AC と BD の交点 Q に着目し、 AQ $\cdot$ CQ と BQ $\cdot$ DQ の大小を比べる。
まず AQ $\cdot$ CQ = 5 $\cdot$ 3 = 15 かっ BQ $\cdot$ DQ =キクであるから
AQ$\cdot$CQ ケ BQ$\cdot$DQ $\cdots$①
が成り立つ。また、3点A,B,Cを通る\と直線BDとの交点のうち、Bと異なる点をXとするとAQ$\cdot$CQ ケ BQ$\cdot$XQ $\cdots$②
①②の左辺は同じなので①②の右辺と比べることによりXQ サ DQが得られる。したがって点DはA,B,Cを通る円の シ にある。
(2)3 点 C , D , E を通る円と 2 点 A , B の位置関係について調べよう。この星形の図形において、さらにCR = RS = SE = 3 となることがわかる。したがって、点 A は 3 点 C, E, D を通る円の ス にあり、点 B は 3 点 C, E, D を通る円の セ にある。
2024共通テスト過去問
この動画を見る
第5 問(1) $\triangle AQD$と直線CEに着目すると$\dfrac{QR}{RD}・\dfrac{DS}{SA}・\dfrac{ア}{CQ}=1$が成り立つのでQR:RD=イ:ウ となる。また、$\triangle AQD$と直線BEに着目するとQB:BD=エ:オ となる。
したがって、BQ:QR:RD=エ:イ:ウとなる個tが分かる。
(2)5点P,Q,R,S,Tが同一演習場にあるとし、AC=8とする。
(i)5点A,P,Q,S,Tに着目すると、AT:ST=1:2より、AT=$\sqrt{ カ }$となる。さらに5点D,Q,R,S,Tに着目すると$DR=4\sqrt{ 3 }$となることがわかる。
( 2 ) 3 点 A , B, C を通る円と点 D の位置関係を次の構想に基づいて調べよう。
構想:線分 AC と BD の交点 Q に着目し、 AQ $\cdot$ CQ と BQ $\cdot$ DQ の大小を比べる。
まず AQ $\cdot$ CQ = 5 $\cdot$ 3 = 15 かっ BQ $\cdot$ DQ =キクであるから
AQ$\cdot$CQ ケ BQ$\cdot$DQ $\cdots$①
が成り立つ。また、3点A,B,Cを通る\と直線BDとの交点のうち、Bと異なる点をXとするとAQ$\cdot$CQ ケ BQ$\cdot$XQ $\cdots$②
①②の左辺は同じなので①②の右辺と比べることによりXQ サ DQが得られる。したがって点DはA,B,Cを通る円の シ にある。
(2)3 点 C , D , E を通る円と 2 点 A , B の位置関係について調べよう。この星形の図形において、さらにCR = RS = SE = 3 となることがわかる。したがって、点 A は 3 点 C, E, D を通る円の ス にあり、点 B は 3 点 C, E, D を通る円の セ にある。
2024共通テスト過去問
福田のおもしろ数学012〜10秒チャレンジ〜重心によって分割される3つの三角形の面積が等しい証明

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
三角形において、その重心 G で分割された 3 つの三角形の面積は等しいことを証明せよ.
※図は動画内参照
この動画を見る
三角形において、その重心 G で分割された 3 つの三角形の面積は等しいことを証明せよ.
※図は動画内参照
重心ではありませんよ。
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
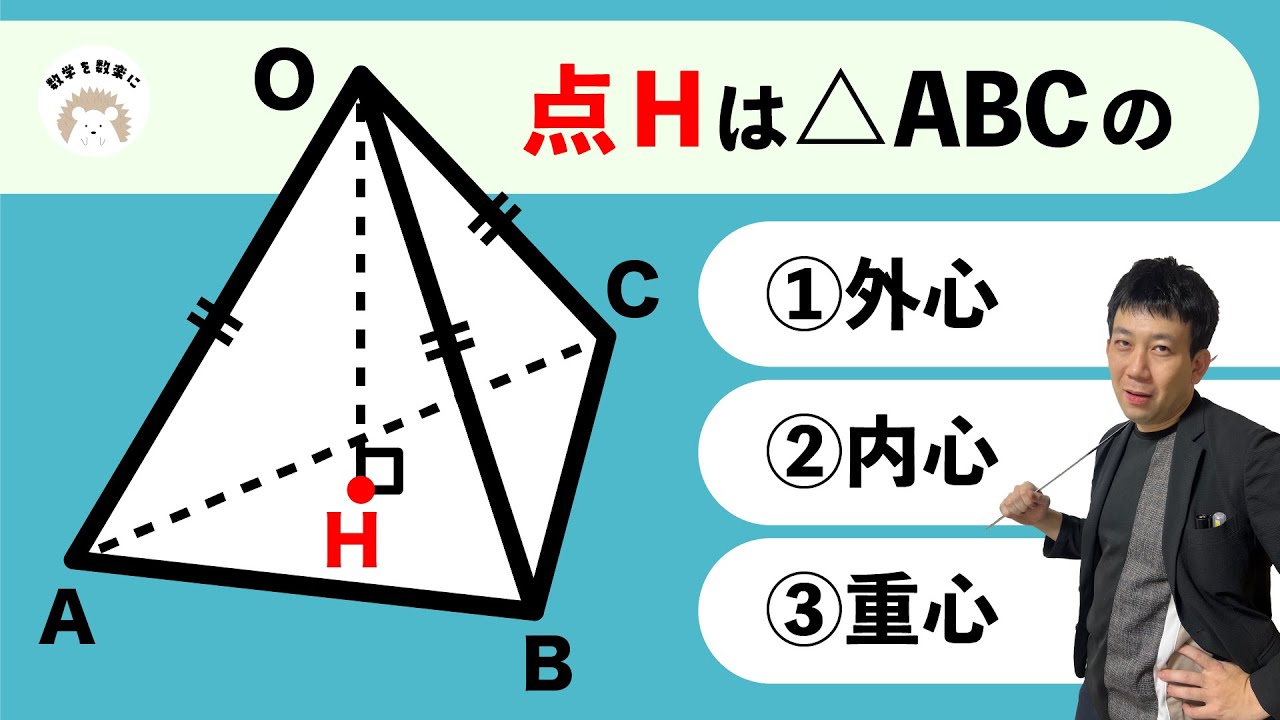
点Hは△ABCの
①外心
②内心
③重心
*図は動画内参照
この動画を見る
点Hは△ABCの
①外心
②内心
③重心
*図は動画内参照
数学どうにかしたい人へ

単元:
#数Ⅰ#数A#数Ⅱ#数と式#2次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#一次不等式(不等式・絶対値のある方程式・不等式)#集合と命題(集合・命題と条件・背理法)#2次方程式と2次不等式#2次関数とグラフ#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#データの分析#整数の性質#場合の数#確率#三角形の辺の比(内分・外分・二等分線)#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と2つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和(等差・等比・階差・Σ)#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数(分数関数・無理関数・逆関数と合成関数)#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体(オイラーの法則)#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
【短時間でポイントチェック!!】内接円や外接円の三角形の面積〔現役講師解説、数学〕

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
※図は動画内参照
①Aは?
②CDは?
③四角形ABCDの面積は?
※図は動画内参照
①$\cos A$
②△ABCの面積$S$
③△ABCの内接円の半径$r$
この動画を見る
※図は動画内参照
①Aは?
②CDは?
③四角形ABCDの面積は?
※図は動画内参照
①$\cos A$
②△ABCの面積$S$
③△ABCの内接円の半径$r$
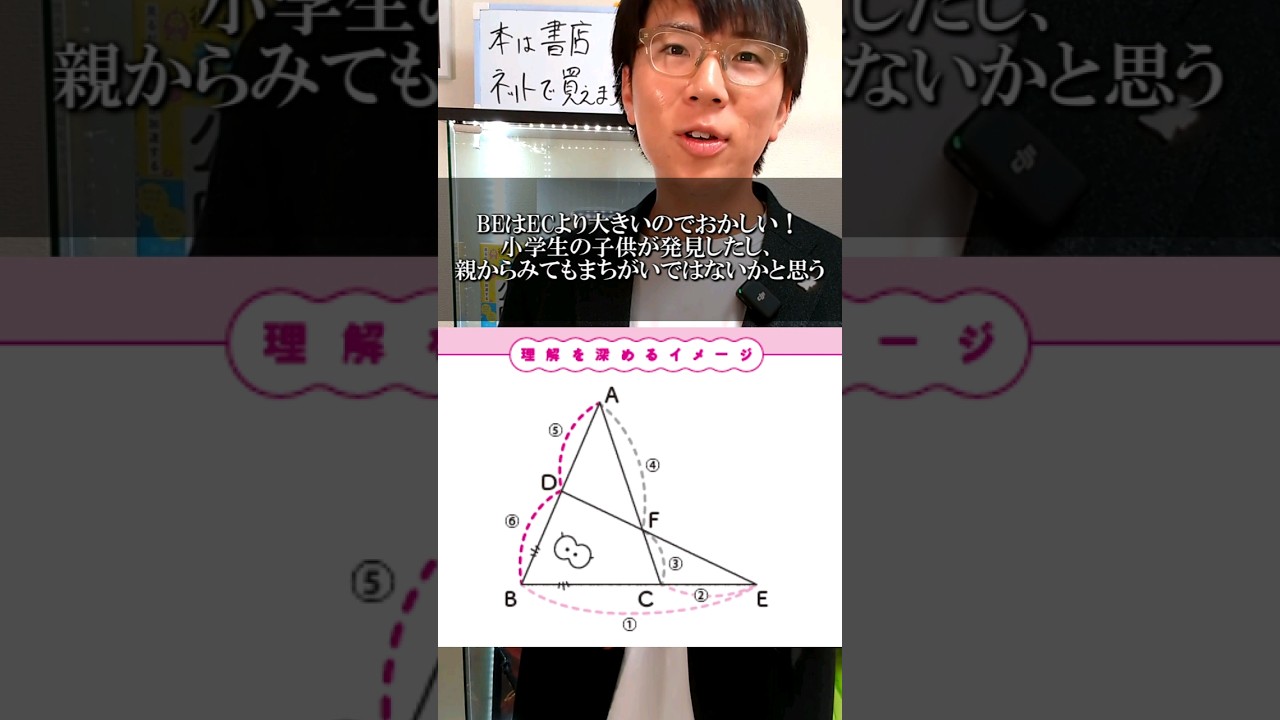
メネラウスの定理が間違ってる?との指摘について
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
あきとんとんの本「見るだけで理解が加速する 数学公式図鑑」についての問い合わせの回答です。他にも疑問に思ってそうだったので動画にしました.
この動画を見る
あきとんとんの本「見るだけで理解が加速する 数学公式図鑑」についての問い合わせの回答です。他にも疑問に思ってそうだったので動画にしました.
福田の数学〜九州大学2023年文系第2問〜2直線のなす角と外接円の半径

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ xy平面上の曲線C:$y$=$x^3$-$x$ を考える。変数$t$>0に対して、曲線C上の点A($t$, $t^3$-$t$)における接線を$l$とする。直線$l$と直線$y$=-$x$の交点をB、三角形OABの外接円の中心をPとする。以下の問いに答えよ。
(1)点Bの座標を$t$を用いて表せ。
(2)θ=$\angle$OBAとする。$\sin^2\theta$を$t$を用いて表せ。
(3)$f(t)$=$\frac{OP}{OA}$とする。$t$>0のとき、$f(t)$を最小にする$t$の値と$f(t)$の最小値を求めよ。
2023九州大学文系過去問
この動画を見る
$\Large\boxed{2}$ xy平面上の曲線C:$y$=$x^3$-$x$ を考える。変数$t$>0に対して、曲線C上の点A($t$, $t^3$-$t$)における接線を$l$とする。直線$l$と直線$y$=-$x$の交点をB、三角形OABの外接円の中心をPとする。以下の問いに答えよ。
(1)点Bの座標を$t$を用いて表せ。
(2)θ=$\angle$OBAとする。$\sin^2\theta$を$t$を用いて表せ。
(3)$f(t)$=$\frac{OP}{OA}$とする。$t$>0のとき、$f(t)$を最小にする$t$の値と$f(t)$の最小値を求めよ。
2023九州大学文系過去問
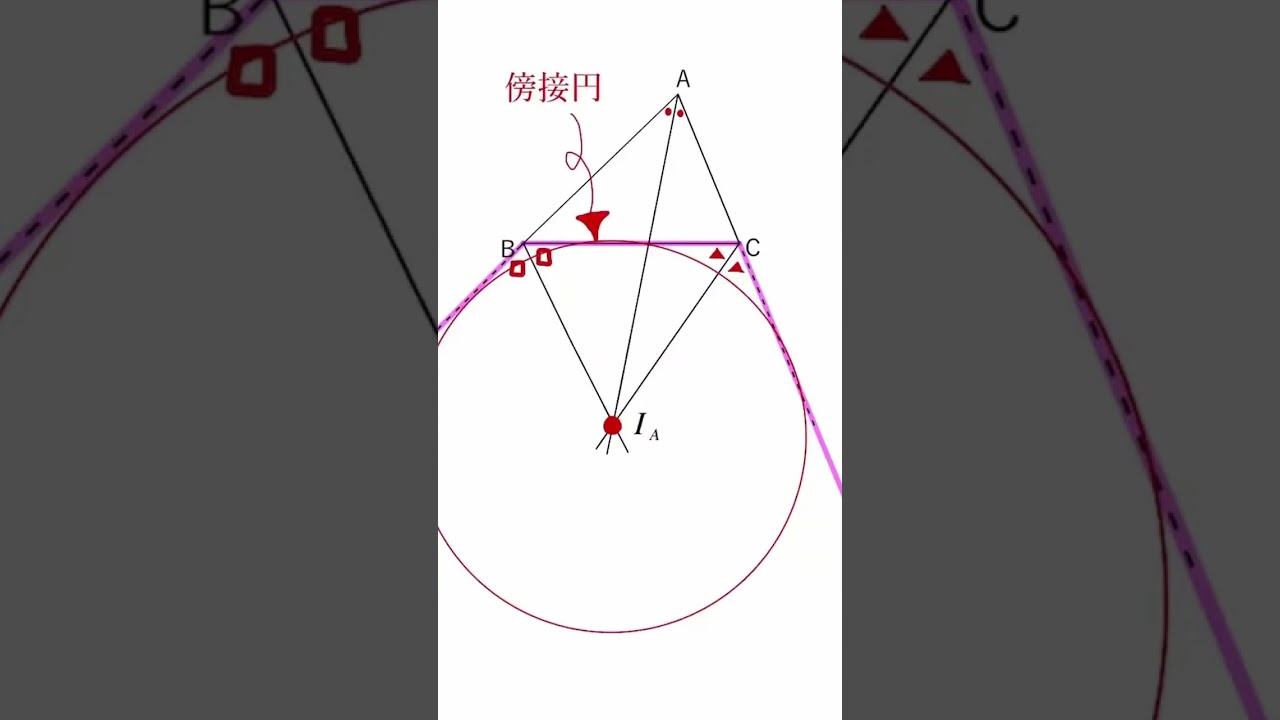
忘れがち!?三角形の傍心ってなに? #Shorts
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形の傍心に関して解説していきます。
この動画を見る
三角形の傍心に関して解説していきます。
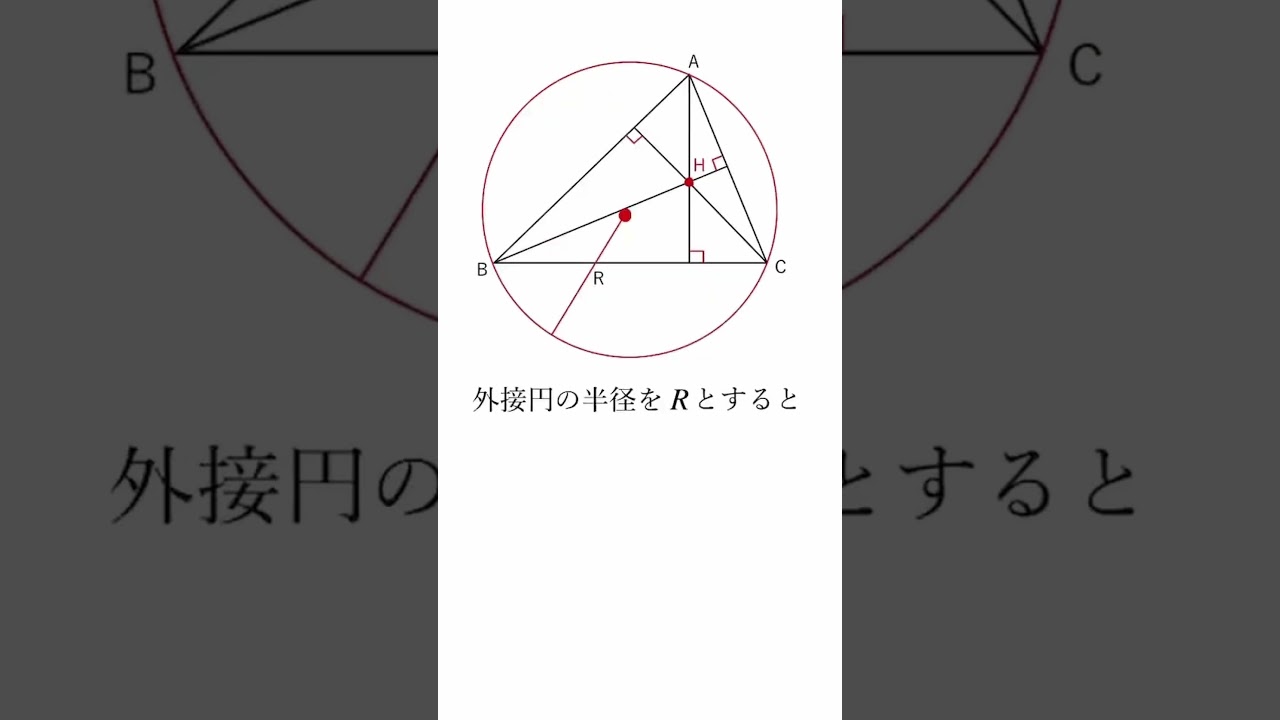
【まとめ】三角形の垂心の特徴をまとめてみた! #Shorts
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形の垂心の特徴について解説していきます。
この動画を見る
三角形の垂心の特徴について解説していきます。
【重要】頻出の三角形の内心の特徴をまとめてみた #Shorts

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形の内心に関して解説していきます。
この動画を見る
三角形の内心に関して解説していきます。
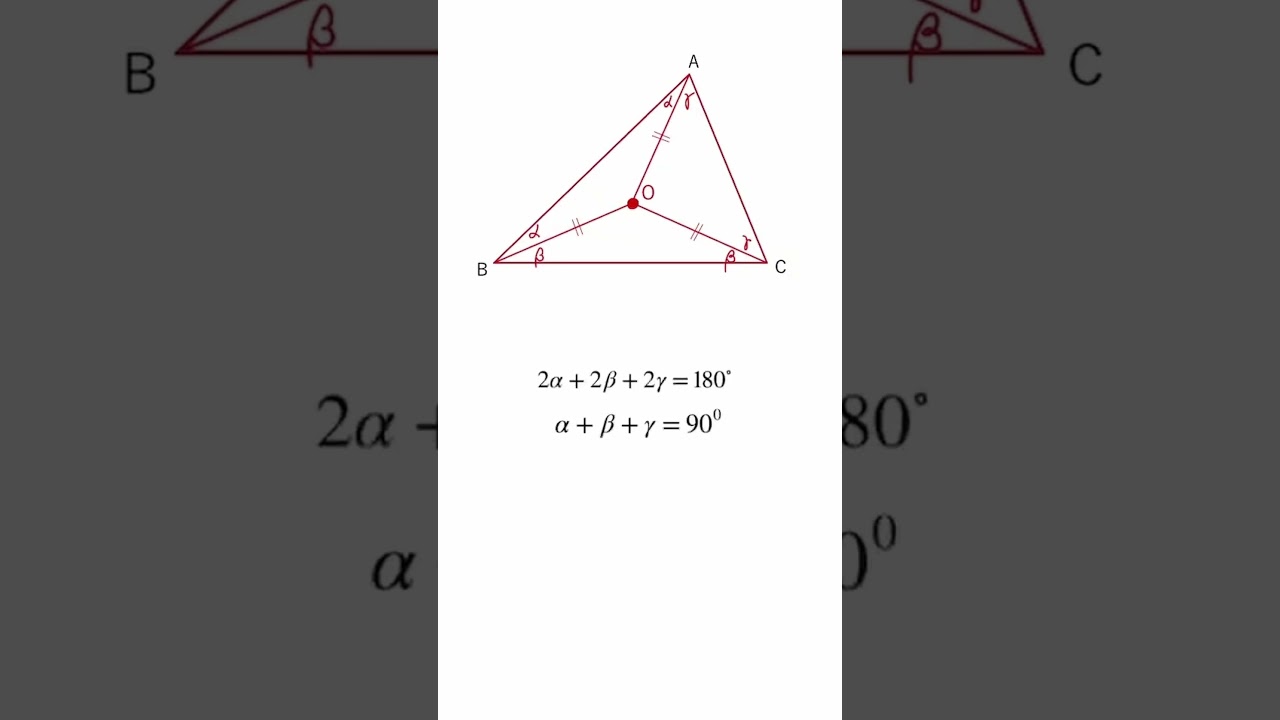
【重要】三角形の外心!特徴をまとめてみた #Shorts
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形の外心の特徴について解説していきます。
この動画を見る
三角形の外心の特徴について解説していきます。
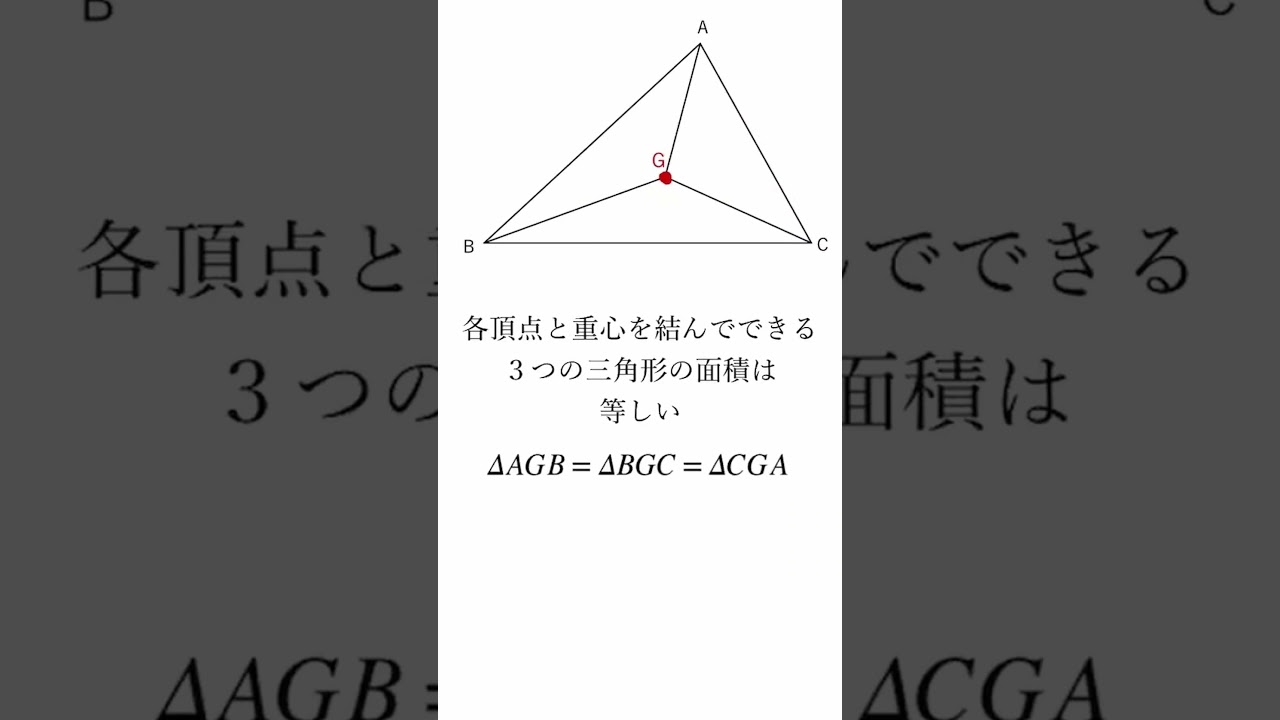
【数学】三角形の五心!特徴をまとめてみた(重心 編) #Shorts
単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形の五心(重心)に関して解説していきます。
この動画を見る
三角形の五心(重心)に関して解説していきます。
【数B】ベクトル:ベクトルの基本⑭係数比較、メネラウスの定理でベクトルを求める

単元:
#数A#図形の性質#平面上のベクトル#内心・外心・重心とチェバ・メネラウス#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ.
この動画を見る
三角形ABCにおいて、辺ABを1:2に内分する点をD、辺ACを3:1に内分する点をEとし、線分CD,BEの交点をPとする。ABをb,ACをcとするとき、APをb,cを用いて表せ.
福田の数学〜早稲田大学2022年社会科学部第2問〜平面幾何と3次関数の増減

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$AB=AC=1,\ BC=a$の二等辺三角形$ABC$の内接円を$I$、外接円を$O$とする。
ただし、$0 \lt a \lt \sqrt2$ である。また、三角形$ABC$と円$I$の3つの接点を頂点とする
三角形を$T$、3点$A,\ B,\ C$で円$O$に外接する三角形を$U$とする。次の問いに答えよ。
(1)三角形$T$の、$BC$に平行な辺の長さ$t$を$a$で表せ。
(2)三角形$U$の、$BC$に平行な辺の長さ$u$を$a$で表せ。
(3)$\frac{t}{u}=p$とする。$p$が最大となる$a$の値と、そのときの$p$の値を求めよ。
2022早稲田大学社会科学部過去問
この動画を見る
$AB=AC=1,\ BC=a$の二等辺三角形$ABC$の内接円を$I$、外接円を$O$とする。
ただし、$0 \lt a \lt \sqrt2$ である。また、三角形$ABC$と円$I$の3つの接点を頂点とする
三角形を$T$、3点$A,\ B,\ C$で円$O$に外接する三角形を$U$とする。次の問いに答えよ。
(1)三角形$T$の、$BC$に平行な辺の長さ$t$を$a$で表せ。
(2)三角形$U$の、$BC$に平行な辺の長さ$u$を$a$で表せ。
(3)$\frac{t}{u}=p$とする。$p$が最大となる$a$の値と、そのときの$p$の値を求めよ。
2022早稲田大学社会科学部過去問
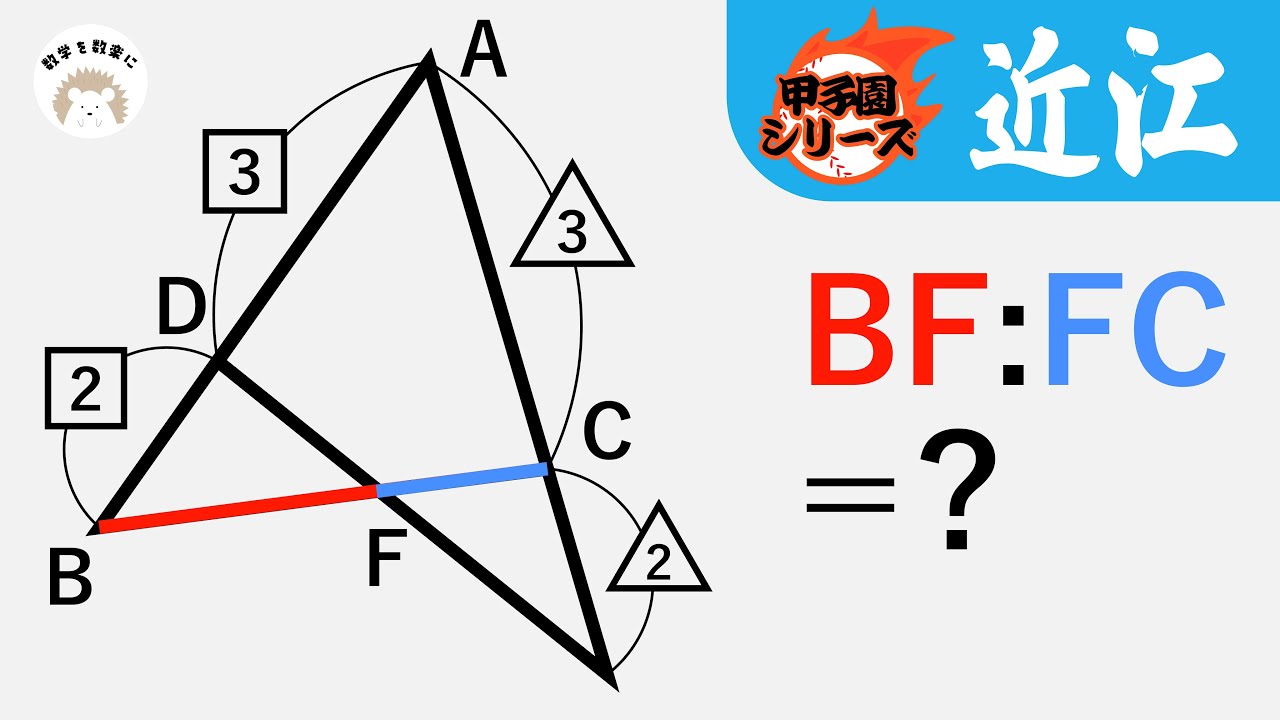
メネラウスの定理でも良いと思います。近江高校(滋賀)
単元:
#数学(中学生)#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BF:FC=?
*図は動画内参照
近江高等学校
この動画を見る
BF:FC=?
*図は動画内参照
近江高等学校
チェバの定理を使いますか?
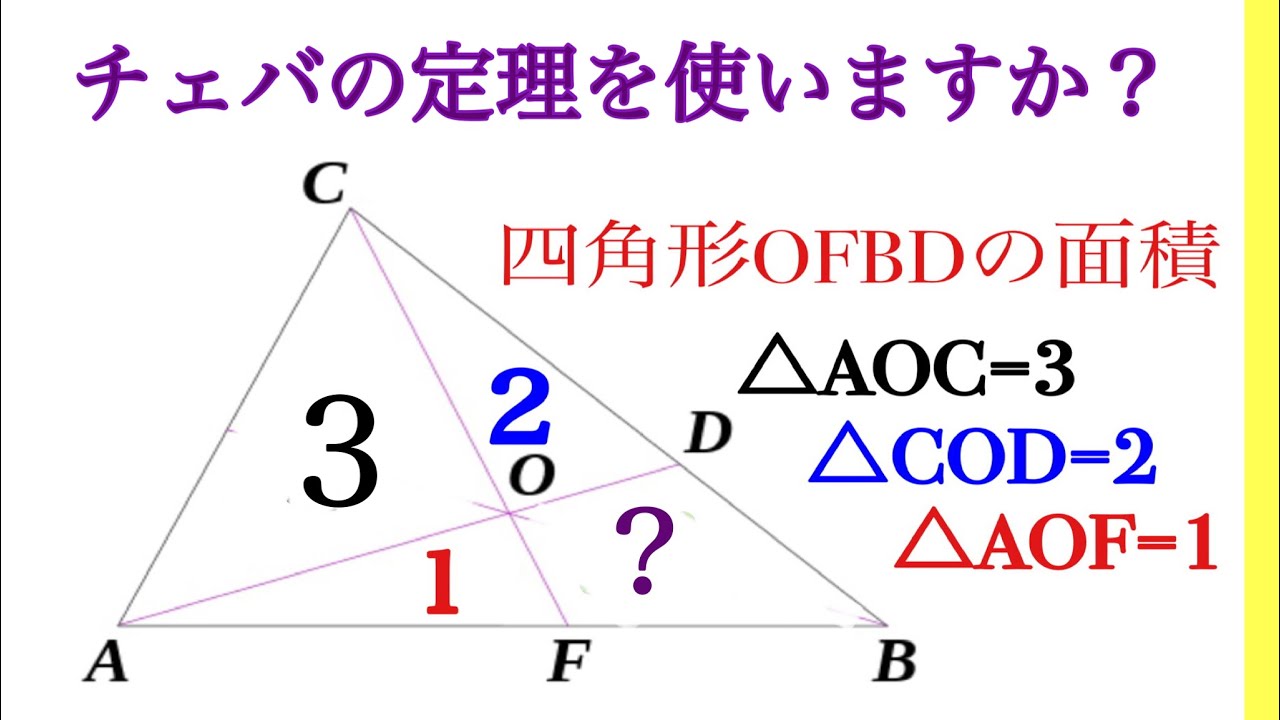
【数A】図形の性質:<これを見て思い出そう>三角形の重心の性質 ~何対何?~

単元:
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
この動画を見る
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
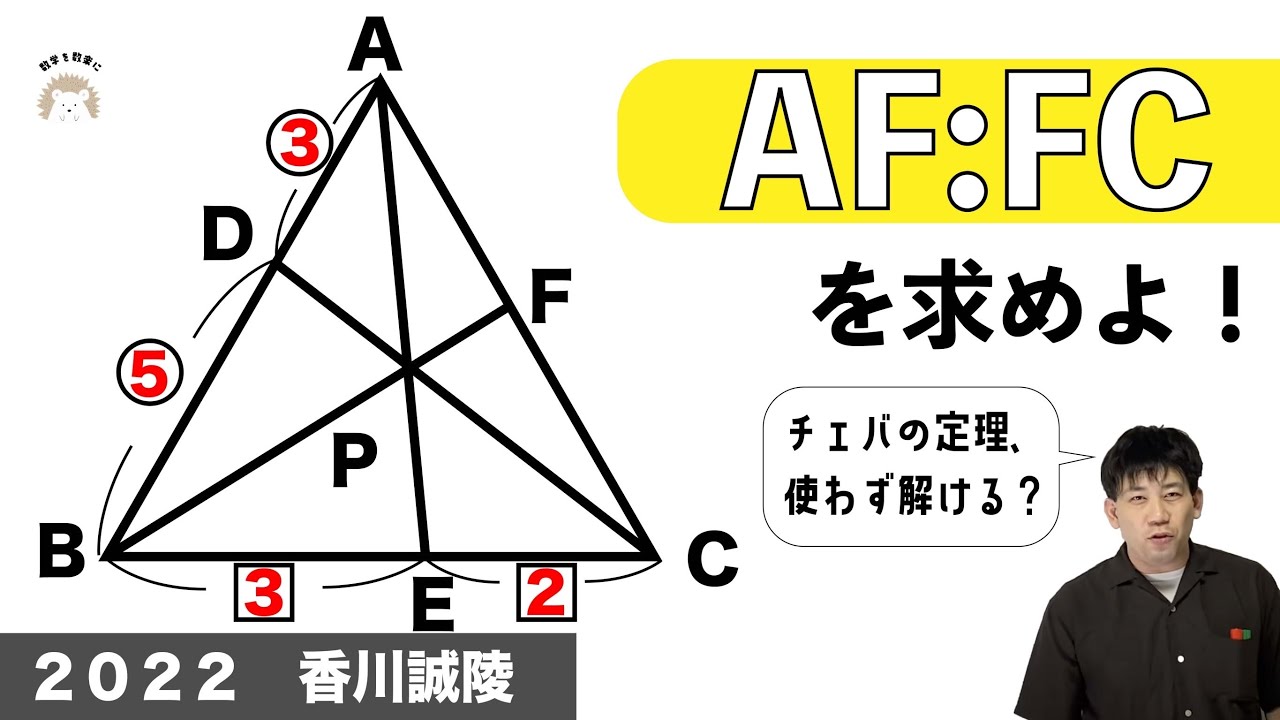
チェバの定理使わずに解ける? 香川誠陵 2022入試問題解説23問目
単元:
#数学(中学生)#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
チェバの定理は使わない
AF:FCを求めよ
*図は動画内参照
2022香川誠陵高等学校
この動画を見る
チェバの定理は使わない
AF:FCを求めよ
*図は動画内参照
2022香川誠陵高等学校
福田の共通テスト解答速報〜2022年共通テスト数学IA問題5。平面幾何の問題。

単元:
#数A#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#方べきの定理と2つの円の関係#センター試験・共通テスト関連#共通テスト#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
第5問 $\triangle ABC$の重心をGとし、線分AG上で点Aとは異なる位置に点Dをとる。
直線AGと辺BCの交点をEとする。また、直線BC上で辺BC上にはない位置に点Fをとる。
直線DFと辺ABの交点をP、直線DFと辺ACの交点をQとする。
(1)点Dは線分AGの中点であるとする。
このとき、$\triangle ABC$の形状に関係なく$\frac{AD}{DE}=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。また、点Fの位置に関係なく$\frac{BP}{AP}=\boxed{\ \ ウ\ \ }×\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }},$
$\frac{CQ}{AQ}=\boxed{\ \ カ\ \ }×\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$であるので、常に$\frac{BP}{AP}+\frac{CQ}{AQ}=\boxed{\ \ ケ\ \ }$
$\boxed{\ \ エ\ \ }~\boxed{\ \ ケ\ \ }$の解答群
⓪BC ①BF ②CF ③EF ④FP ⑤FQ ⑥PQ
(2)$AB=9, BC=8, AC=6$とし、(1)と同様に、点Dは線分AGの中点であるとする。
ここで、4点B,C,Q,Pが同一円周上にあるように点Fをとる。このとき、
$AQ=\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\ AP$であるから
$AP=\frac{\boxed{\ \ シス\ \ }}{\boxed{\ \ セ\ \ }}, AQ=\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チ\ \ }}$であり、
$CF=\frac{\boxed{\ \ ツテ\ \ }}{\boxed{\ \ トナ\ \ }}$である。
(3)$\triangle ABC$の形状や点Fの位置に関係なく、常に$\frac{BP}{AP}+\frac{CQ}{AQ}=10$となるのは
$\frac{AD}{DG}=\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$のときである。
2022共通テスト数学過去問
この動画を見る
第5問 $\triangle ABC$の重心をGとし、線分AG上で点Aとは異なる位置に点Dをとる。
直線AGと辺BCの交点をEとする。また、直線BC上で辺BC上にはない位置に点Fをとる。
直線DFと辺ABの交点をP、直線DFと辺ACの交点をQとする。
(1)点Dは線分AGの中点であるとする。
このとき、$\triangle ABC$の形状に関係なく$\frac{AD}{DE}=\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}$
である。また、点Fの位置に関係なく$\frac{BP}{AP}=\boxed{\ \ ウ\ \ }×\frac{\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }},$
$\frac{CQ}{AQ}=\boxed{\ \ カ\ \ }×\frac{\boxed{\ \ キ\ \ }}{\boxed{\ \ ク\ \ }}$であるので、常に$\frac{BP}{AP}+\frac{CQ}{AQ}=\boxed{\ \ ケ\ \ }$
$\boxed{\ \ エ\ \ }~\boxed{\ \ ケ\ \ }$の解答群
⓪BC ①BF ②CF ③EF ④FP ⑤FQ ⑥PQ
(2)$AB=9, BC=8, AC=6$とし、(1)と同様に、点Dは線分AGの中点であるとする。
ここで、4点B,C,Q,Pが同一円周上にあるように点Fをとる。このとき、
$AQ=\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\ AP$であるから
$AP=\frac{\boxed{\ \ シス\ \ }}{\boxed{\ \ セ\ \ }}, AQ=\frac{\boxed{\ \ ソタ\ \ }}{\boxed{\ \ チ\ \ }}$であり、
$CF=\frac{\boxed{\ \ ツテ\ \ }}{\boxed{\ \ トナ\ \ }}$である。
(3)$\triangle ABC$の形状や点Fの位置に関係なく、常に$\frac{BP}{AP}+\frac{CQ}{AQ}=10$となるのは
$\frac{AD}{DG}=\frac{\boxed{\ \ ニ\ \ }}{\boxed{\ \ ヌ\ \ }}$のときである。
2022共通テスト数学過去問
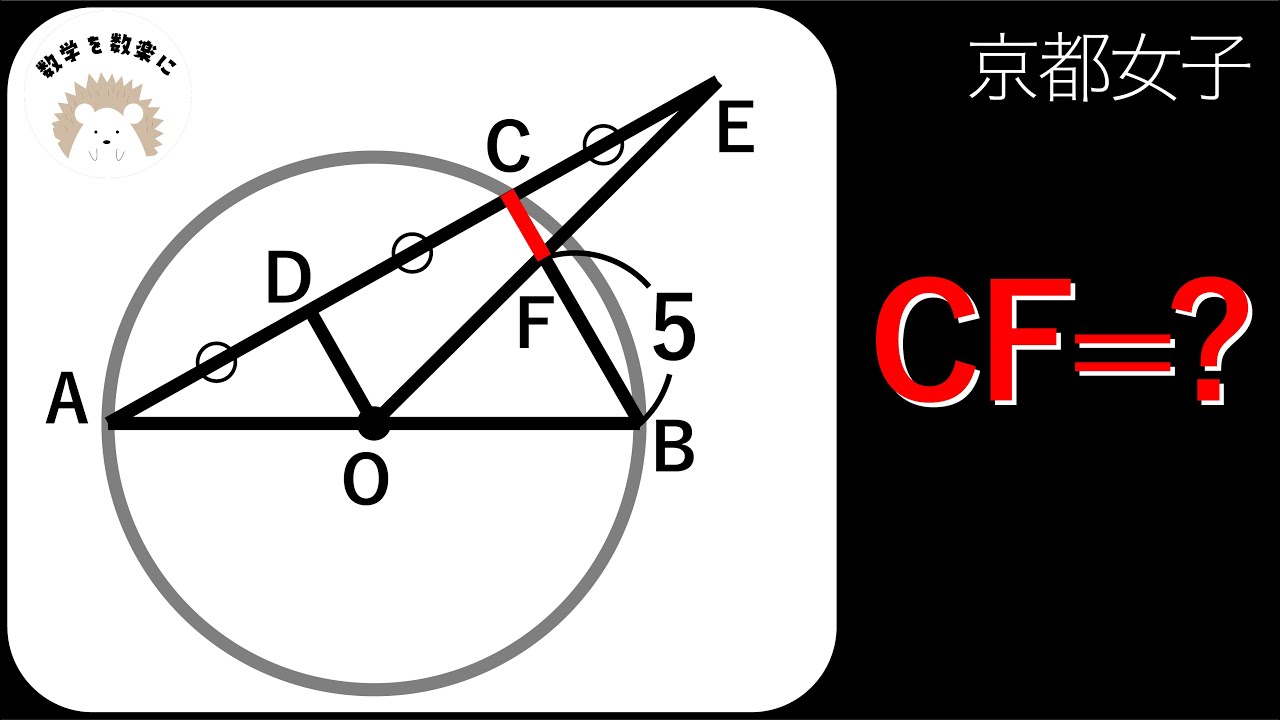
2通りで解説!!京都女子
単元:
#数学(中学生)#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
CF=?
*図は動画内参照
京都女子高等学校
この動画を見る
CF=?
*図は動画内参照
京都女子高等学校
