 整数の性質
整数の性質
 整数の性質
整数の性質
筆算するな! 開成中

単元:
#算数(中学受験)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#過去問解説(学校別)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{array}{r}
1234567 \\[-3pt]
2345671 \\[-3pt]
3456712 \\[-3pt]
4567123 \\[-3pt]
\underline{+\phantom{0}5671234}\\[-3pt]
\end{array}
$
9で割ったあまりは?
開成中学校
この動画を見る
$
\begin{array}{r}
1234567 \\[-3pt]
2345671 \\[-3pt]
3456712 \\[-3pt]
4567123 \\[-3pt]
\underline{+\phantom{0}5671234}\\[-3pt]
\end{array}
$
9で割ったあまりは?
開成中学校
AkiyaMath様の作成問題① 初コラボ #整数問題 #3次方程式の応用

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$k$:整数
3次方程式
$4x^3-(k+3)x+2k+1=0$の解になる2以上の有理数の総和を求めよ。
この動画を見る
$k$:整数
3次方程式
$4x^3-(k+3)x+2k+1=0$の解になる2以上の有理数の総和を求めよ。
大学入試問題#248 慶應義塾大学(2014) #方程式

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x,y,z:0$でない整数
$\displaystyle \frac{1}{xy}+\displaystyle \frac{1}{yz}+\displaystyle \frac{1}{zx}=\displaystyle \frac{1}{xy+yz+zx}$
$2^{x+1}=\displaystyle \frac{5^{2y}}{10^{z+1}}$
をみたすとき$x,y,z$の値を求めよ。
出典:2014年慶應義塾大学 入試問題
この動画を見る
$x,y,z:0$でない整数
$\displaystyle \frac{1}{xy}+\displaystyle \frac{1}{yz}+\displaystyle \frac{1}{zx}=\displaystyle \frac{1}{xy+yz+zx}$
$2^{x+1}=\displaystyle \frac{5^{2y}}{10^{z+1}}$
をみたすとき$x,y,z$の値を求めよ。
出典:2014年慶應義塾大学 入試問題
整数問題やや難

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
m,nを自然数とする.
$2^n+17=m^4$
,これを解け.
この動画を見る
m,nを自然数とする.
$2^n+17=m^4$
,これを解け.
【裏技】約分できますか?

解けるように選ばれた数字で作られた問題
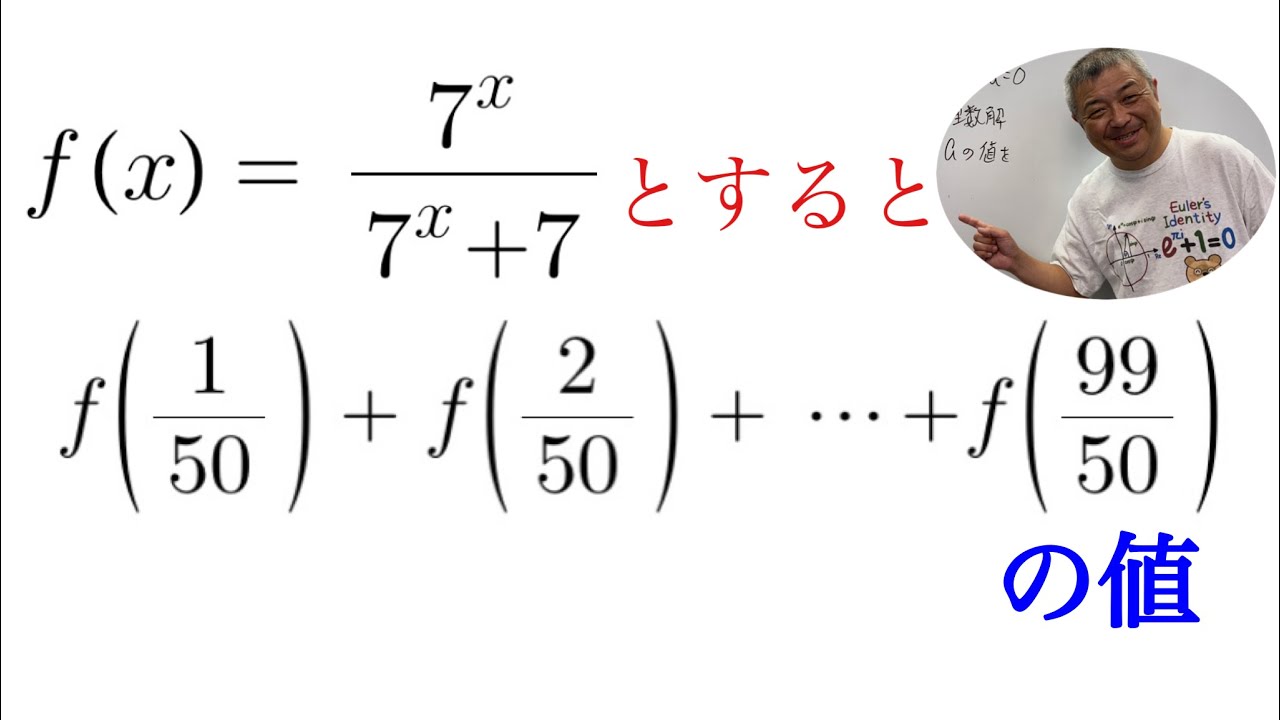
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ f(x)=\dfrac{7^x}{7^x+7}$とする.
$f\left(\frac{1}{50} \right)+f\left(\frac{2}{50} \right)+……f\left(\frac{98}{50} \right)+f\left(\frac{99}{50} \right)$
の値を求めよ.
この動画を見る
$ f(x)=\dfrac{7^x}{7^x+7}$とする.
$f\left(\frac{1}{50} \right)+f\left(\frac{2}{50} \right)+……f\left(\frac{98}{50} \right)+f\left(\frac{99}{50} \right)$
の値を求めよ.
大学入試だけど、中学生も解ける!!(東京理科大)

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
ある2桁の正の整数mを2乗すると下2桁が36になるとき、
m=?
東京理科大学
この動画を見る
ある2桁の正の整数mを2乗すると下2桁が36になるとき、
m=?
東京理科大学
N進法

【整数の性質】見終わったら整数の性質が得意になる動画【前編】(数学A)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
(1)
最大公約数が15で、最小公倍数が390えある。
2つの自然数をすべて求めよ
(2)
等式$5m+2n=25$を満たす自然数の組をすべて求めよ
(3)
$(m-4)n=12$を満たす自然数の組$(m.n)$をすべて求めよ。
この動画を見る
(1)
最大公約数が15で、最小公倍数が390えある。
2つの自然数をすべて求めよ
(2)
等式$5m+2n=25$を満たす自然数の組をすべて求めよ
(3)
$(m-4)n=12$を満たす自然数の組$(m.n)$をすべて求めよ。
約分の裏技をまとめました

単元:
#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次の数を約分せよ
(1) $\displaystyle \frac{3007}{3201}$
(2) $\displaystyle \frac{10033}{12877}$
この動画を見る
次の数を約分せよ
(1) $\displaystyle \frac{3007}{3201}$
(2) $\displaystyle \frac{10033}{12877}$
ナイスな不定二次方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
x,yは自然数とする.
$x^2(2-y)+y^2(2-x)=-12$を満たす$(x,y)$をすべて求めよ.
この動画を見る
x,yは自然数とする.
$x^2(2-y)+y^2(2-x)=-12$を満たす$(x,y)$をすべて求めよ.
1の三乗根 ω

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1の3乗根のうち虚数であるものの1つをωとすると
$ω^4+ω^3 + 3ω^2 + 2ω +1 =?$
名城大学
この動画を見る
1の3乗根のうち虚数であるものの1つをωとすると
$ω^4+ω^3 + 3ω^2 + 2ω +1 =?$
名城大学
負の数の余りを求めよ!~余りについて~

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
\begin{eqnarray}
(1) -15 \div 3 \,の商と余りを求めよ
\end{eqnarray}
この動画を見る
\begin{eqnarray}
(1) -15 \div 3 \,の商と余りを求めよ
\end{eqnarray}
5乗数を平方の和で
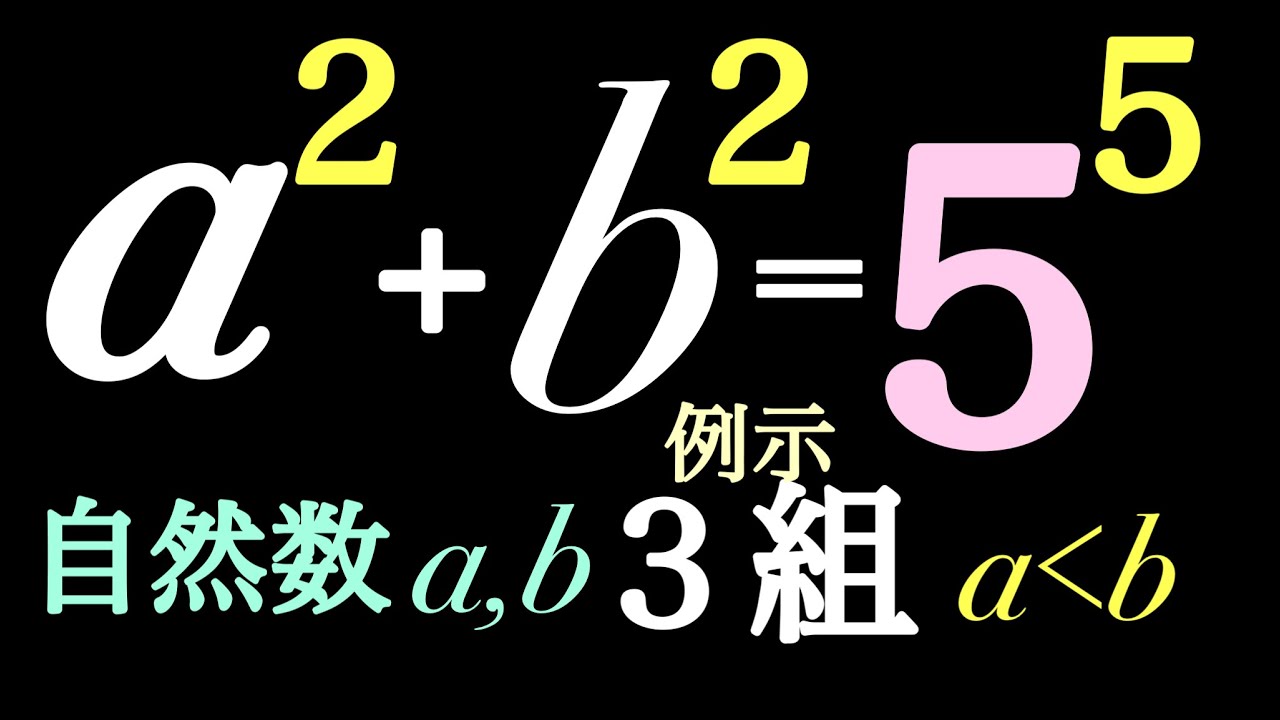
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a^2+b^2=5^5,a \lt b$とする.
自然数(a,b)を3組例示せよ.
この動画を見る
$ a^2+b^2=5^5,a \lt b$とする.
自然数(a,b)を3組例示せよ.
福田の数学〜慶應義塾大学2022年商学部第1問(1)〜倍数の個数を数える

単元:
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)1から1000までの整数のうち、2,3,5の少なくとも2つで割り切れる数
は$\boxed{\ \ アイウ\ \ }$個あり、2,3,5の少なくとも1つで割り切れ、
かつ6で割り切れない数は$\boxed{\ \ エオカ\ \ }$個ある。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{1}}$(1)1から1000までの整数のうち、2,3,5の少なくとも2つで割り切れる数
は$\boxed{\ \ アイウ\ \ }$個あり、2,3,5の少なくとも1つで割り切れ、
かつ6で割り切れない数は$\boxed{\ \ エオカ\ \ }$個ある。
2022慶應義塾大学商学部過去問
不定三次方程式
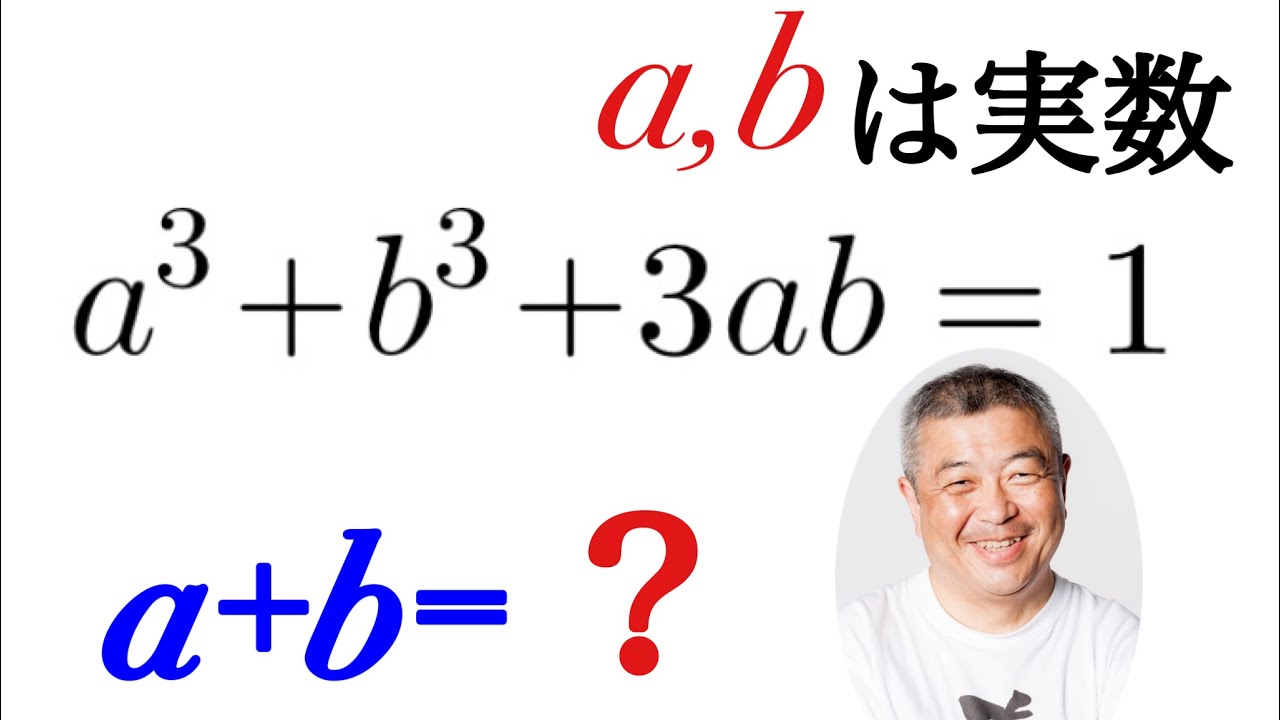
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
a,bを実数とする.
$a^3+b^3+3ab=1,a+b=?$これを解け.
この動画を見る
a,bを実数とする.
$a^3+b^3+3ab=1,a+b=?$これを解け.
大学入試問題#236 富山県立大学(2012) #背理法

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#富山県立大学
指導講師:
ますただ
問題文全文(内容文):
$x^3-x^2+2x-1=0$の実数解は無理数であることを背理法を用いて示せ
出典:2012年富山県立大学 入試問題
この動画を見る
$x^3-x^2+2x-1=0$の実数解は無理数であることを背理法を用いて示せ
出典:2012年富山県立大学 入試問題
【小学校の学習範囲から始まって】整数:市川高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$A-2B-2G+L=2021$のとき,自然数の組$(A,B)$をすべて求めよ.
※$G$は1でない自然数とする.
市川高校過去問
この動画を見る
$A-2B-2G+L=2021$のとき,自然数の組$(A,B)$をすべて求めよ.
※$G$は1でない自然数とする.
市川高校過去問
高校の宿題をアレンジしてみたその2

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
5Nを7で割ると3余り,6Nを11で割ると4余るようなNで3桁で最小のものを求めよ.
この動画を見る
5Nを7で割ると3余り,6Nを11で割ると4余るようなNで3桁で最小のものを求めよ.
【数学オリンピックに挑戦】下3桁じゃなく上3桁!?【数学】

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学オリンピック#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
6桁の平方数の上3桁として考えられるものは全部でいくつあるか。
数学オリンピック過去問
この動画を見る
6桁の平方数の上3桁として考えられるものは全部でいくつあるか。
数学オリンピック過去問
高校の宿題をアレンジしてみた(合同式)

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)4Nを5で割ると2余り,3Nを7で割ると3余る.Nを35で割った余りを求めよ.
(2)3Nを5で割ると4余り,3N+1は7で割り切れる.Nを35で割った余りを求めよ.
この動画を見る
(1)4Nを5で割ると2余り,3Nを7で割ると3余る.Nを35で割った余りを求めよ.
(2)3Nを5で割ると4余り,3N+1は7で割り切れる.Nを35で割った余りを求めよ.
筆算した人いる?いないか。四天王寺高校

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
N=1234×17+35
Nを17で割ったときの商と余りを求めよ。
四天王寺高等学校
この動画を見る
N=1234×17+35
Nを17で割ったときの商と余りを求めよ。
四天王寺高等学校
大学入試問題#229 大阪府立大学(2020) #整数問題

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#大阪府立大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$m,n$:整数
$0 \leqq n \leqq m$
$3m^2+mn-2n^2$が素数となるような組$(m,n)$を全て求めよ。
出典:2020年大阪府立大学 入試問題
この動画を見る
$m,n$:整数
$0 \leqq n \leqq m$
$3m^2+mn-2n^2$が素数となるような組$(m,n)$を全て求めよ。
出典:2020年大阪府立大学 入試問題
数A 整数問題 不定方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$3x-5y=1$を満たす整数の組(x,y)を求めよ
この動画を見る
$3x-5y=1$を満たす整数の組(x,y)を求めよ
【良問】京大の整数問題!2つの解法で解きます!【数学 入試問題】【京都大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n^3-7n+9$が素数となるような整数$n$を全て求めよ。
京都大過去問
この動画を見る
$n^3-7n+9$が素数となるような整数$n$を全て求めよ。
京都大過去問
福田の入試問題解説〜慶應義塾大学2022年理工学部第1問(2)〜ガウス記号と倍数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)$n$を奇数とする。nと$[\frac{3n+2}{2}]$の積が6の倍数であるための必要十分条件は、
nを$\boxed{\ \ エ\ \ }$で割った時の余りが$\boxed{\ \ オ\ \ }$となるときである。ただし、
実数xに対しxを超えない最大の整数を[x]と表す。
また、$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$は$0 \leqq \boxed{\ \ オ\ \ } \lt \boxed{\ \ エ\ \ }$
を満たす整数である。$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$を求める過程を解答欄に記述しなさい。
2022慶應義塾大学理工学部過去問
この動画を見る
(2)$n$を奇数とする。nと$[\frac{3n+2}{2}]$の積が6の倍数であるための必要十分条件は、
nを$\boxed{\ \ エ\ \ }$で割った時の余りが$\boxed{\ \ オ\ \ }$となるときである。ただし、
実数xに対しxを超えない最大の整数を[x]と表す。
また、$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$は$0 \leqq \boxed{\ \ オ\ \ } \lt \boxed{\ \ エ\ \ }$
を満たす整数である。$\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ }$を求める過程を解答欄に記述しなさい。
2022慶應義塾大学理工学部過去問
京大の整数問題!落としてはいけない問題です!【数学 入試問題】【京都大学】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
2以上の自然数$n$に対し、$n$と$n^2+2$がともに素数になるのは、$n=3$の場合に限ることを示せ。
京都大過去問
この動画を見る
2以上の自然数$n$に対し、$n$と$n^2+2$がともに素数になるのは、$n=3$の場合に限ることを示せ。
京都大過去問
【その場で「考える力」を身に付ける!】整数:大阪星光学院高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2数$a,b$の最大公約数を$[a\odot b]$と表すと・・・
$[1\odot 2]+[2\odot 3]+[3\odot 4]+・・・+[100\odot 101]=\Box$であり,
$[1\odot 3]+[2\odot 4]+[3\dot 5]+・・・+[99\odot 101]+[100\odot 102]=\box$である.
大阪星光高校過去問
この動画を見る
2数$a,b$の最大公約数を$[a\odot b]$と表すと・・・
$[1\odot 2]+[2\odot 3]+[3\odot 4]+・・・+[100\odot 101]=\Box$であり,
$[1\odot 3]+[2\odot 4]+[3\dot 5]+・・・+[99\odot 101]+[100\odot 102]=\box$である.
大阪星光高校過去問
良問のはずだったんだけどなー
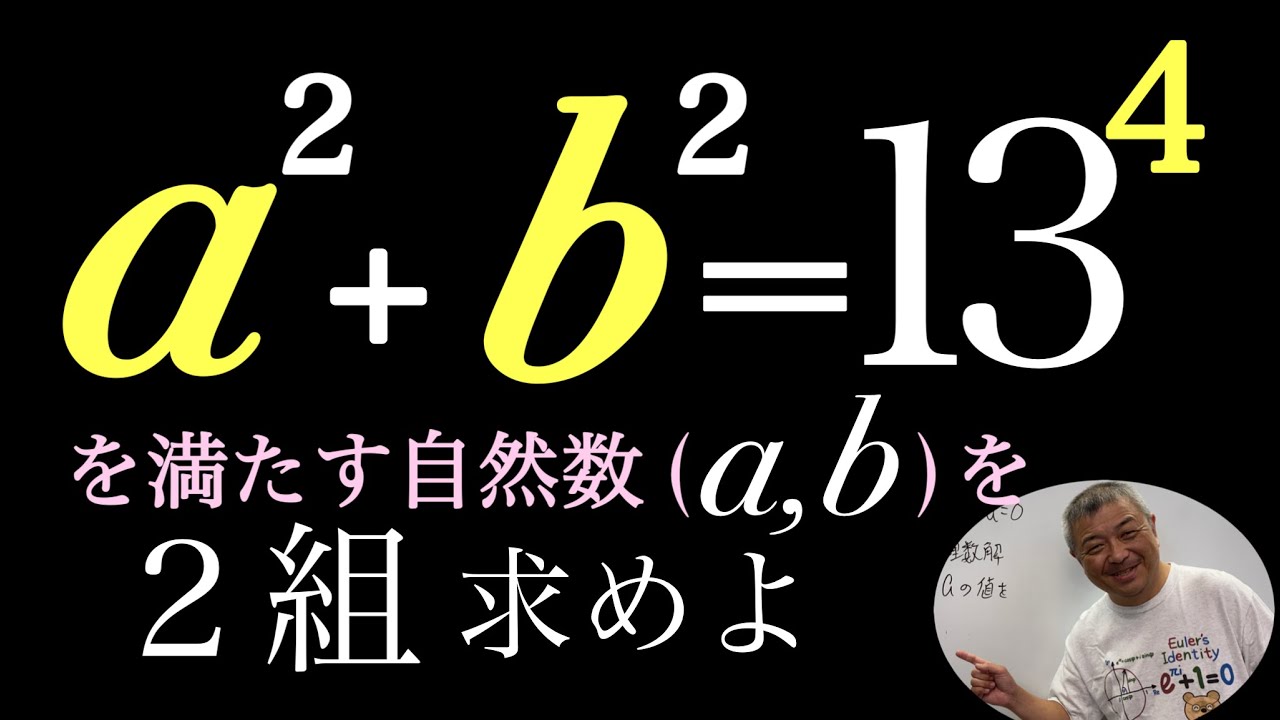
素数問題の良問だよ

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
p,qは素数である.
$p^3-q^5=(p+q)^2$を満たす(p,q)の組をすべて求めよ.
この動画を見る
p,qは素数である.
$p^3-q^5=(p+q)^2$を満たす(p,q)の組をすべて求めよ.
