 式と証明
式と証明
 式と証明
式と証明
いくつでしょうか?

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
この値を求めよ.
$2^{\frac{1}{4}}・4^{\frac{1}{8}}・8^{\frac{1}{16}}・16^{\frac{1}{32}}・・・・・・\infty$
この動画を見る
この値を求めよ.
$2^{\frac{1}{4}}・4^{\frac{1}{8}}・8^{\frac{1}{16}}・16^{\frac{1}{32}}・・・・・・\infty$
【ゼロからわかる】整式の割り算(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の整式$A,B$について、$A$を$B$で割った商と余りを求めよ。
(1)$A=a^2+6a+5,B=a+3$
(2)$A=4x^3-3x+2,B=2x+3$
この動画を見る
次の整式$A,B$について、$A$を$B$で割った商と余りを求めよ。
(1)$A=a^2+6a+5,B=a+3$
(2)$A=4x^3-3x+2,B=2x+3$
雑問

単元:
#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ 25^{63}\times 63^{25}$の下3桁を求めよ.
この動画を見る
$ 25^{63}\times 63^{25}$の下3桁を求めよ.
福田の数学〜京都大学2022年理系第5問〜方程式の解と不等式の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#恒等式・等式・不等式の証明#解と判別式・解と係数の関係#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
曲線$C:y=\cos^3x$ $(0 \leqq x \leqq \frac{\pi}{2})$,x軸およびy軸で囲まれる図形の面s系をS
とする。$0 \lt t \lt \frac{\pi}{2}$とし、C上の点Q$(t,\cos^3t)$と原点O,およびP$(t,o),R(0,\cos^3t)$
を頂点にもつ長方形OPQRの面積をf(t)とする。このとき、次の問いに答えよ。
(1)Sを求めよ。
(2)$f(t)$は最大値をただ一つのtでとることを示せ。そのときのtを$\alpha$とすると、
$f(\alpha)=\frac{\cos^4\alpha}{3\sin\alpha}$ であることを示せ。
(3)$\frac{f(\alpha)}{S} \lt \frac{9}{16}$ を示せ。
2022京都大学理系過去問
この動画を見る
曲線$C:y=\cos^3x$ $(0 \leqq x \leqq \frac{\pi}{2})$,x軸およびy軸で囲まれる図形の面s系をS
とする。$0 \lt t \lt \frac{\pi}{2}$とし、C上の点Q$(t,\cos^3t)$と原点O,およびP$(t,o),R(0,\cos^3t)$
を頂点にもつ長方形OPQRの面積をf(t)とする。このとき、次の問いに答えよ。
(1)Sを求めよ。
(2)$f(t)$は最大値をただ一つのtでとることを示せ。そのときのtを$\alpha$とすると、
$f(\alpha)=\frac{\cos^4\alpha}{3\sin\alpha}$ であることを示せ。
(3)$\frac{f(\alpha)}{S} \lt \frac{9}{16}$ を示せ。
2022京都大学理系過去問
2022藤田医科大の簡単な問題 メインはn個の相加相乗平均の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x\gt 0$において$\dfrac{x}{2}+\dfrac{2}{x^2}$の最小値を求めよ.
2022藤田医科大過去問
この動画を見る
$ x\gt 0$において$\dfrac{x}{2}+\dfrac{2}{x^2}$の最小値を求めよ.
2022藤田医科大過去問
福田の数学〜慶應義塾大学2022年薬学部第2問〜二項定理と数列の部分和

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$\left\{a_n\right\}$の初項から第n項までの和$S_n$、数列$\left\{b_n\right\}$の初項から第n項までの和$T_n$
はそれぞれ
$S_n=\sum_{k=1}^n {}_n \mathrm{ C }_k, T_n=\sum_{k=1}^n k・{}_n \mathrm{ C }_k$
で表される。
(1)$x \gt y \geqq 1$を満たす自然数x,yについて、
${}_x \mathrm{ C }_y={}_{x-1} \mathrm{ C }_y+{}_i \mathrm{ C }_j, y・{}_x \mathrm{ C }_y=x・{}_p \mathrm{ C }_q,$
が成り立つ。i,j,p,qをそれぞれx,yを用いて表すと、$i=\boxed{\ \ ス\ \ },j=\boxed{\ \ セ\ \ },$
$p=\boxed{\ \ ソ\ \ },q=\boxed{\ \ タ\ \ }$である。
(2)$a_2,b_4$の値をそれぞれ求めると$a_2=\boxed{\ \ チ\ \ },b_4=\boxed{\ \ ツ\ \ }$である。
(3)$S_n,a_n$をそれぞれnの式で表すと、$S_n=\boxed{\ \ テ\ \ },a_n=\boxed{\ \ ト\ \ }$である。
(4)$b_n$をnの式で表すと、$b_n=\boxed{\ \ ナ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
数列$\left\{a_n\right\}$の初項から第n項までの和$S_n$、数列$\left\{b_n\right\}$の初項から第n項までの和$T_n$
はそれぞれ
$S_n=\sum_{k=1}^n {}_n \mathrm{ C }_k, T_n=\sum_{k=1}^n k・{}_n \mathrm{ C }_k$
で表される。
(1)$x \gt y \geqq 1$を満たす自然数x,yについて、
${}_x \mathrm{ C }_y={}_{x-1} \mathrm{ C }_y+{}_i \mathrm{ C }_j, y・{}_x \mathrm{ C }_y=x・{}_p \mathrm{ C }_q,$
が成り立つ。i,j,p,qをそれぞれx,yを用いて表すと、$i=\boxed{\ \ ス\ \ },j=\boxed{\ \ セ\ \ },$
$p=\boxed{\ \ ソ\ \ },q=\boxed{\ \ タ\ \ }$である。
(2)$a_2,b_4$の値をそれぞれ求めると$a_2=\boxed{\ \ チ\ \ },b_4=\boxed{\ \ ツ\ \ }$である。
(3)$S_n,a_n$をそれぞれnの式で表すと、$S_n=\boxed{\ \ テ\ \ },a_n=\boxed{\ \ ト\ \ }$である。
(4)$b_n$をnの式で表すと、$b_n=\boxed{\ \ ナ\ \ }$である。
2022慶應義塾大学薬学部過去問
【ゼロからわかる】二項定理を3項で利用する(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式の展開式における、[ ]内の項の係数を求めよ。
$(x+2y-z)^6$ $[x^3y^2z]$
この動画を見る
次の式の展開式における、[ ]内の項の係数を求めよ。
$(x+2y-z)^6$ $[x^3y^2z]$
【わかりやすく解説】数学Ⅱ 二項定理で項の係数を求めよう!

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式の展開式における、[ ]内の項の係数を求めよ。
(1)
$(x+3)^5$ $[x^3]$
(2)
$(2x-3y)^6$ $[x^2y^4]$
この動画を見る
次の式の展開式における、[ ]内の項の係数を求めよ。
(1)
$(x+3)^5$ $[x^3]$
(2)
$(2x-3y)^6$ $[x^2y^4]$
2022北海道大

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-$
$k+1 $
(1)$ f(k-1)$の値を求めよ.
(2)$ \vert k \vert \lt 2$のとき,不等式 $ f(n)\geqq 0$を解け.
2022北海道大過去問
この動画を見る
$ f(x)=x^3-(2k-1)x^2+(k^2-k+1)x-$
$k+1 $
(1)$ f(k-1)$の値を求めよ.
(2)$ \vert k \vert \lt 2$のとき,不等式 $ f(n)\geqq 0$を解け.
2022北海道大過去問
福田の数学〜京都大学2022年理系第4問〜四面体に関する証明と線分の長さの最小

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#微分法と積分法#恒等式・等式・不等式の証明#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
四面体OABCが
$OA=4, OB=AB=BC=3, OC=AC=2\sqrt3$
を満たしているとする。Pを辺BC上の点とし、$\triangle OAP$の重心をGとする。
このとき、次の各問いに答えよ。
(1)$\overrightarrow{ PG } ∟ \overrightarrow{ OA }$を示せ。
(2)Pが辺BC上を動くとき、PGの最小値を求めよ。
2022京都大学理系過去問
この動画を見る
四面体OABCが
$OA=4, OB=AB=BC=3, OC=AC=2\sqrt3$
を満たしているとする。Pを辺BC上の点とし、$\triangle OAP$の重心をGとする。
このとき、次の各問いに答えよ。
(1)$\overrightarrow{ PG } ∟ \overrightarrow{ OA }$を示せ。
(2)Pが辺BC上を動くとき、PGの最小値を求めよ。
2022京都大学理系過去問
【ゼロからわかる】二項定理の基本(高校数学Ⅱ)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式の展開式を求めよ。
(1)
$(x+3)^4$
(2)
$(2a-b)^5$
この動画を見る
次の式の展開式を求めよ。
(1)
$(x+3)^4$
(2)
$(2a-b)^5$
大学入試問題#129 関西学院大学(1991) 二項定理の応用

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$(a+b+\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b})^7$を展開した時の$ab^2$の係数を求めよ。
出典:1991年関西学院大学 入試問題
この動画を見る
$(a+b+\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b})^7$を展開した時の$ab^2$の係数を求めよ。
出典:1991年関西学院大学 入試問題
ざ・見掛け倒しだよ

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+・・・・・・・+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を17で割った余りを求めよ.
この動画を見る
$\dfrac{1}{2}+\dfrac{2}{3}+\dfrac{3}{4}+・・・・・・・+\dfrac{32}{33}=\dfrac{a}{33!}$
$a$を17で割った余りを求めよ.
福田の数学〜東京慈恵会医科大学2022年医学部第3問〜約数と倍数の性質

単元:
#数A#数Ⅱ#大学入試過去問(数学)#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
mは3以上の奇数とし、mの全ての正の約数を$a_1,a_2,\ldots,a_k$と並べる。
ただし、$a_1 \lt a_2 \lt \ldots \lt a_k$とする。
以下の2つの条件$(\textrm{i}),(\textrm{ii})$を満たすmについて考える。
$(\textrm{i})m$は素数ではない。
$(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt k$を満たす全ての整数i,jについて$a_j-a_i \leqq 3$が
成り立つ。
このとき、次の問いに答えよ。
(1)kは3または4であることを示し、mを$a_2$を用いて表せ。
(2)$k=3$となるとき、全ての正の整数nについて$(a_2n+1)^{a_2}-1$は
mの倍数であることを示せ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
mは3以上の奇数とし、mの全ての正の約数を$a_1,a_2,\ldots,a_k$と並べる。
ただし、$a_1 \lt a_2 \lt \ldots \lt a_k$とする。
以下の2つの条件$(\textrm{i}),(\textrm{ii})$を満たすmについて考える。
$(\textrm{i})m$は素数ではない。
$(\textrm{ii})i \leqq j,1 \lt i \lt k ,1 \lt j \lt k$を満たす全ての整数i,jについて$a_j-a_i \leqq 3$が
成り立つ。
このとき、次の問いに答えよ。
(1)kは3または4であることを示し、mを$a_2$を用いて表せ。
(2)$k=3$となるとき、全ての正の整数nについて$(a_2n+1)^{a_2}-1$は
mの倍数であることを示せ。
2022東京慈恵会医科大学医学部過去問
2022都立入試 整数問題証明(11の倍数)

単元:
#数学(中学生)#数A#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数列#数列とその和(等差・等比・階差・Σ)#高校入試過去問(数学)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
2022都立入試 整数問題証明に関して解説していきます.
この動画を見る
2022都立入試 整数問題証明に関して解説していきます.
1=0.999...らしい

大学入試問題#103 東海大学医学部(2017) 二項定理
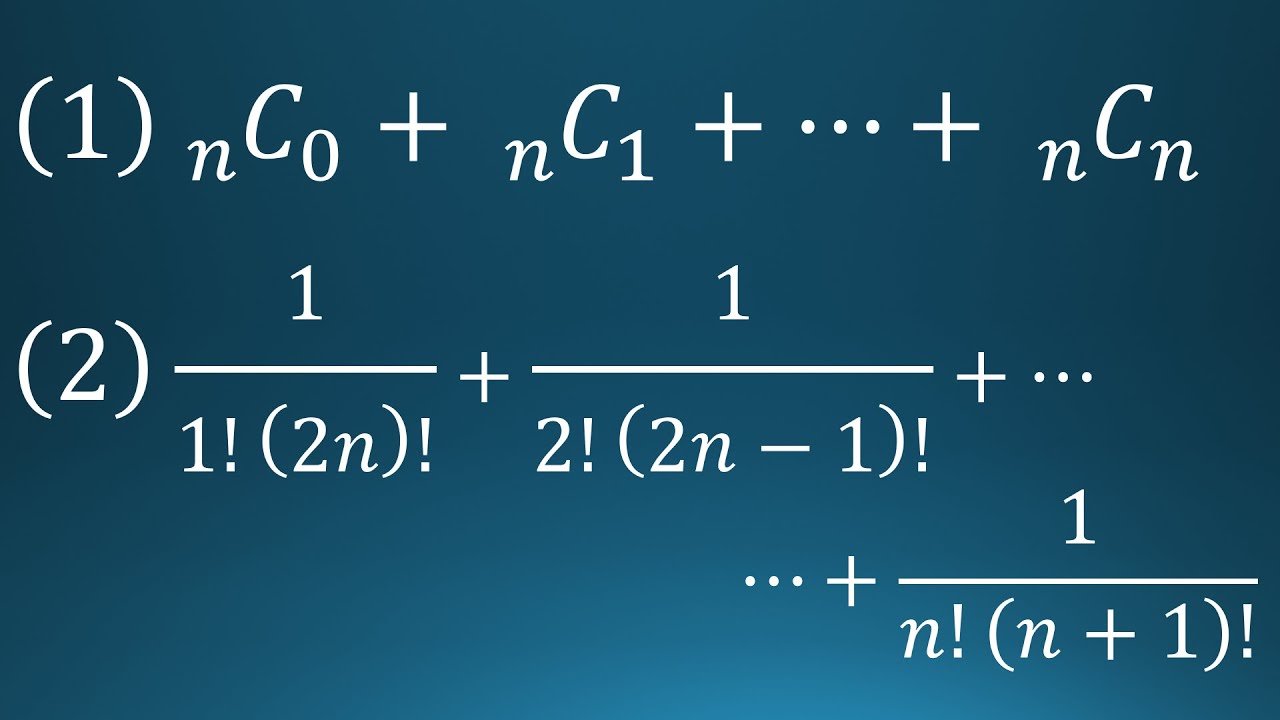
単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#東海大学
指導講師:
ますただ
問題文全文(内容文):
次の和を求めよ。
(1)
${}_{ n }C_0+{}_{ n }C_1+・・・+{}_{ n }C_n$
(2)
$\displaystyle \frac{1}{1!(2n)!}+\displaystyle \frac{1}{2(2n-1)!}+・・・+\displaystyle \frac{1}{n!(n+1)!}$
出典:2017年東海大学医学部 入試問題
この動画を見る
次の和を求めよ。
(1)
${}_{ n }C_0+{}_{ n }C_1+・・・+{}_{ n }C_n$
(2)
$\displaystyle \frac{1}{1!(2n)!}+\displaystyle \frac{1}{2(2n-1)!}+・・・+\displaystyle \frac{1}{n!(n+1)!}$
出典:2017年東海大学医学部 入試問題
🟨にあてはまる数は? 連分数 渋谷教育学園幕張 2022入試問題解説14問目
単元:
#数学(中学生)#数Ⅱ#式と証明#整式の除法・分数式・二項定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
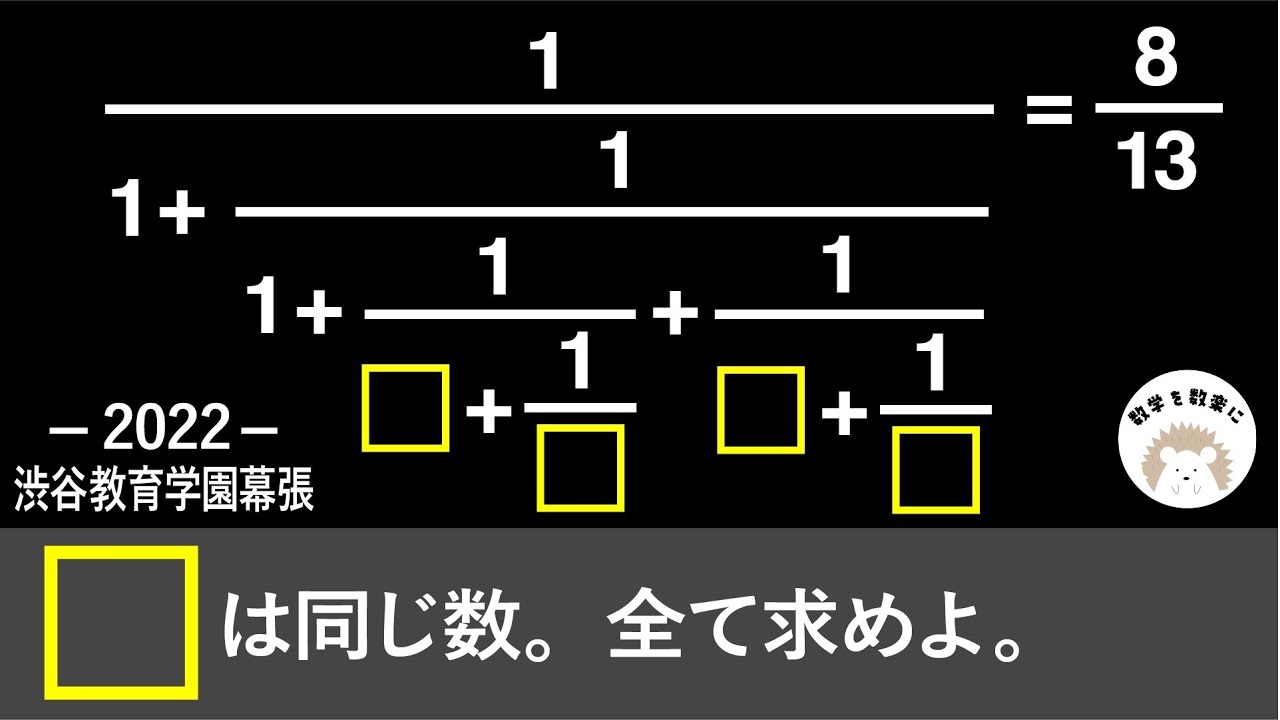
$\frac{1}{1+\frac{1}{1+\frac{1}{▢+\frac{1}{▢}}+\frac{1}{▢+\frac{1}{▢}}}}$=$\frac{8}{13}$
▢は同じ数。全て求めよ。
2022渋谷教育学園幕張
この動画を見る
$\frac{1}{1+\frac{1}{1+\frac{1}{▢+\frac{1}{▢}}+\frac{1}{▢+\frac{1}{▢}}}}$=$\frac{8}{13}$
▢は同じ数。全て求めよ。
2022渋谷教育学園幕張
式の値
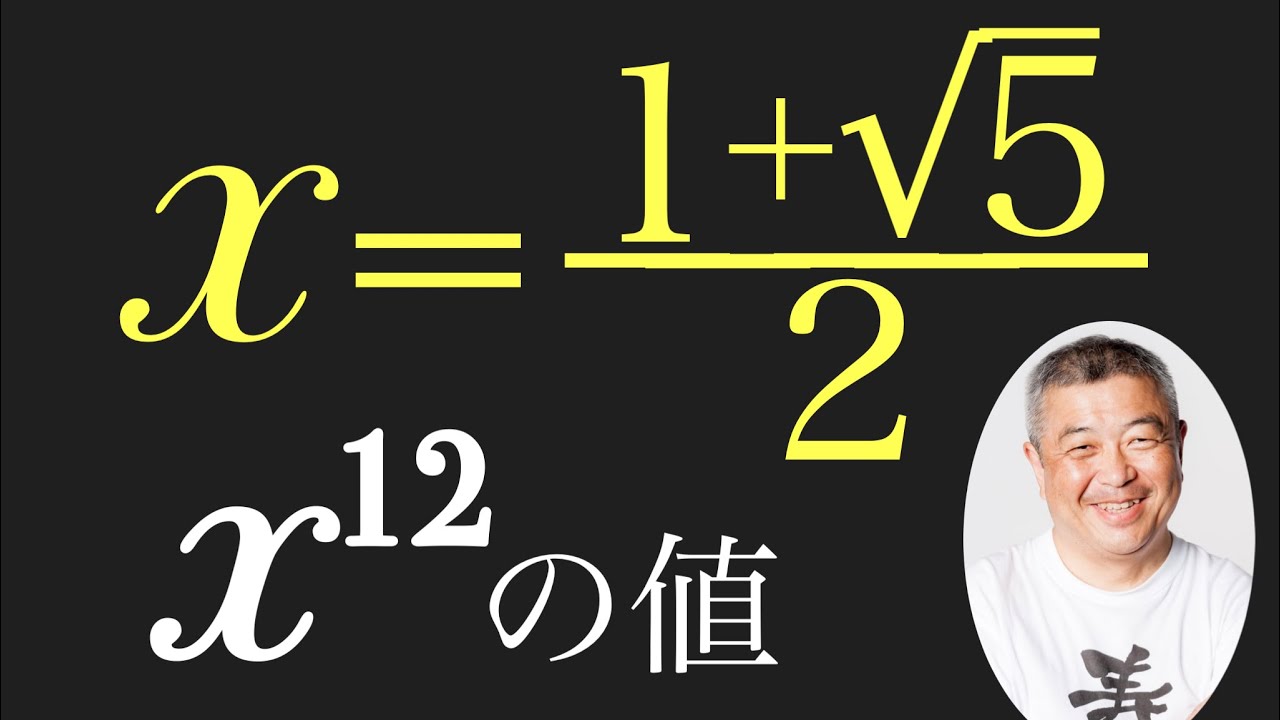
単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x=\dfrac{1+\sqrt5}{2}$
$x^{12}$の値を求めよ.
この動画を見る
$x=\dfrac{1+\sqrt5}{2}$
$x^{12}$の値を求めよ.
分数式

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x\neq 0$であり,$x$は実数であるとする.
$\dfrac{x}{x^2+x+1}=a$
$\dfrac{x^2}{x^4+x^2+1}$の値を$a$で表せ.
この動画を見る
$x\neq 0$であり,$x$は実数であるとする.
$\dfrac{x}{x^2+x+1}=a$
$\dfrac{x^2}{x^4+x^2+1}$の値を$a$で表せ.
分数の中に分数 慶應義塾高校

単元:
#数学(中学生)#数Ⅱ#式と証明#整式の除法・分数式・二項定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{\frac{1}{3} - \frac{2}{5} }
{\frac{1}{3} - \frac{2}{5} + \frac{3}{7}}$
慶應義塾高等学校
この動画を見る
$\frac{\frac{1}{3} - \frac{2}{5} }
{\frac{1}{3} - \frac{2}{5} + \frac{3}{7}}$
慶應義塾高等学校
【不等式はこれを抑えよう!】不等式の証明での注意点をすべてまとめました!〔数学 高校数学〕

#47 数検1級1次 過去問 二項定理
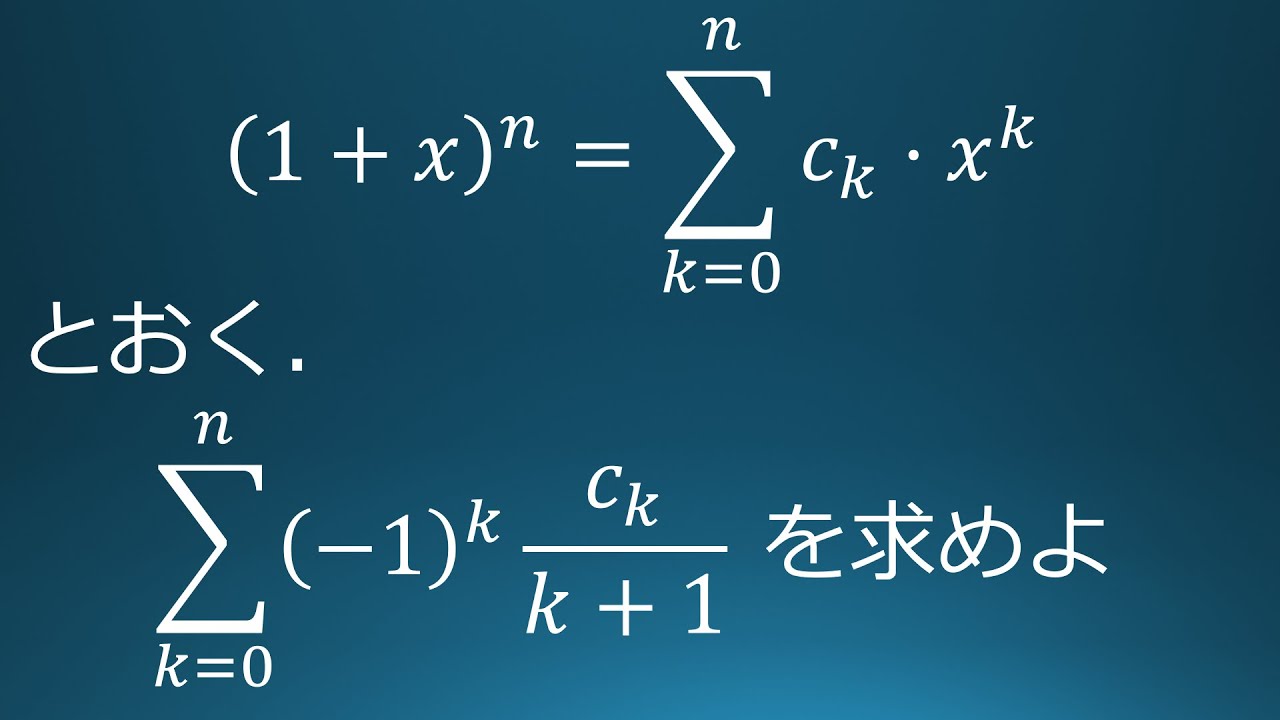
単元:
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#式と証明#微分法と積分法#整式の除法・分数式・二項定理#不定積分・定積分#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$(1+x)^n$を$c_0+c_1x+・・・+c_nx^n$とおく。
$\displaystyle \sum_{k=1}^n(-1)^k\displaystyle \frac{c_k}{k+1}$の値を求めよ。
この動画を見る
$(1+x)^n$を$c_0+c_1x+・・・+c_nx^n$とおく。
$\displaystyle \sum_{k=1}^n(-1)^k\displaystyle \frac{c_k}{k+1}$の値を求めよ。
福田のわかった数学〜高校3年生理系100〜不等式の証明(7)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 不等式の証明(7)
$e^a(b-a) \lt e^b-e^a \lt e^b(b-a)$
(ただし、$a \lt b$)
この動画を見る
数学$\textrm{III}$ 不等式の証明(7)
$e^a(b-a) \lt e^b-e^a \lt e^b(b-a)$
(ただし、$a \lt b$)
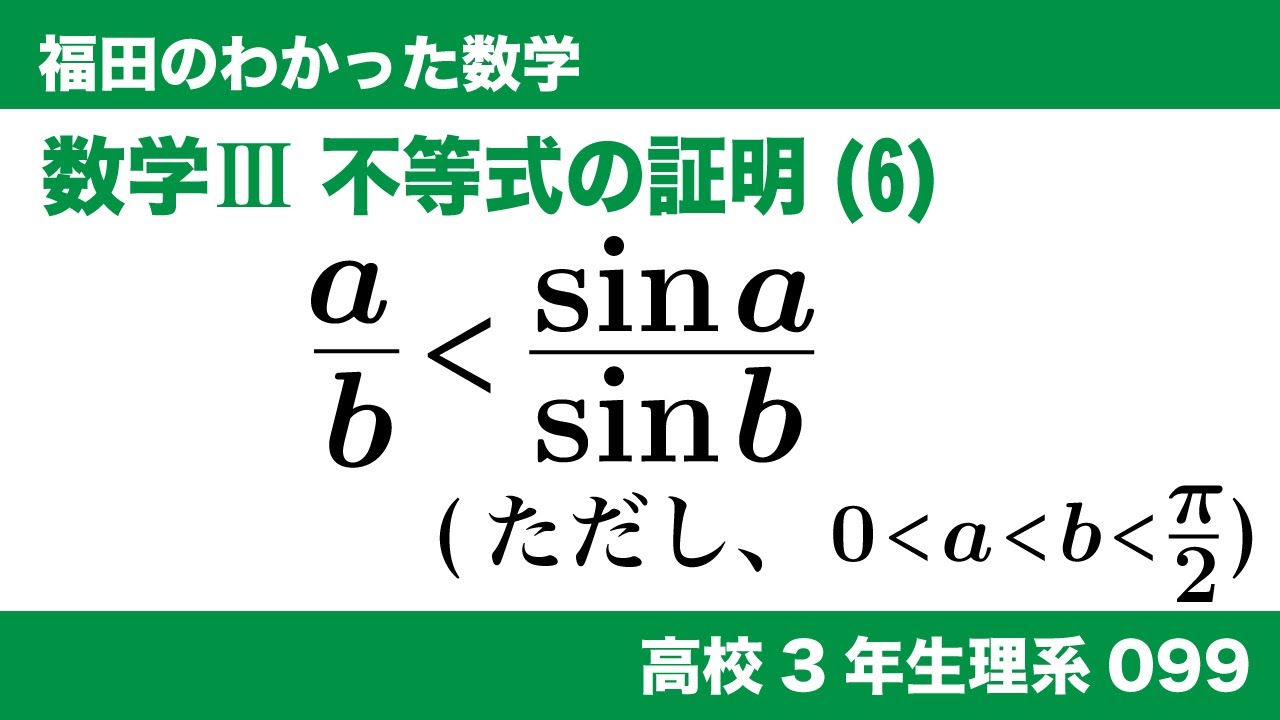
福田のわかった数学〜高校3年生理系099〜不等式の証明(6)
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 不等式の証明(6)
$0 \lt a \lt b \lt \frac{\pi}{2}$のとき、
$\frac{a}{b} \lt \frac{\sin a}{\sin b}$が成り立つことを証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(6)
$0 \lt a \lt b \lt \frac{\pi}{2}$のとき、
$\frac{a}{b} \lt \frac{\sin a}{\sin b}$が成り立つことを証明せよ。
福田のわかった数学〜高校3年生理系098〜不等式の証明(5)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 不等式の証明(5)
$b(\log a-\log b) \leqq a-b (a \gt 0, b \gt 0)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(5)
$b(\log a-\log b) \leqq a-b (a \gt 0, b \gt 0)$を証明せよ。
【数Ⅱ】相加平均・相乗平均の関係を正しく使いこなそう【よくある間違え方とは】

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ (1)x \gt 0のとき,x+\dfrac{9}{x}\geqq 6を示せ.
(2)x \gt 0のとき,x+\dfrac{9}{x}の最小値を求めよ.
(3)x \gt 0のとき,x+\dfrac{6}{x+1}の最小値を求めよ.
(4)x \gt 0のとき,\dfrac{x^2;5x+15}{x+2}の最小値を求めよ.
(5)a \gt 0,b \gt 0のとき\left(a+\frac{1}{b} \right)\left(\frac{16}{a}+b \right)の最小値
を求めよ.$
この動画を見る
$ (1)x \gt 0のとき,x+\dfrac{9}{x}\geqq 6を示せ.
(2)x \gt 0のとき,x+\dfrac{9}{x}の最小値を求めよ.
(3)x \gt 0のとき,x+\dfrac{6}{x+1}の最小値を求めよ.
(4)x \gt 0のとき,\dfrac{x^2;5x+15}{x+2}の最小値を求めよ.
(5)a \gt 0,b \gt 0のとき\left(a+\frac{1}{b} \right)\left(\frac{16}{a}+b \right)の最小値
を求めよ.$
福田のわかった数学〜高校3年生理系097〜不等式の証明(4)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 不等式の証明(4)
$(x+2)\log(x+1) \geqq 2x (x \geqq 0)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(4)
$(x+2)\log(x+1) \geqq 2x (x \geqq 0)$を証明せよ。
【数Ⅱ】不等式の証明・基本パターン【書き出しに注意!】

高校範囲だけど中3生も解けるし

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{x^2-2}{x-1} + \frac{1}{x-1}$
この動画を見る
$\frac{x^2-2}{x-1} + \frac{1}{x-1}$
