解と判別式・解と係数の関係
解と判別式・解と係数の関係
福田の数学〜神戸大学2023年文系第1問〜2次方程式の解の存在範囲
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ $a$, $b$を実数とする。整式$f(x)$を$f(x)$=$x^2$+$ax$+$b$で定める。以下の問いに答えよ。
(1)2次方程式$f(x)$=0 が異なる2つの正の解をもつための$a$と$b$が満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0 が異なる2つの実数解をもち、それらが共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。
(3)2次方程式$f(x)$=0 の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。ただし、2次方程式の重解は2つと数える。
2023神戸大学文系過去問
この動画を見る
$\Large\boxed{1}$ $a$, $b$を実数とする。整式$f(x)$を$f(x)$=$x^2$+$ax$+$b$で定める。以下の問いに答えよ。
(1)2次方程式$f(x)$=0 が異なる2つの正の解をもつための$a$と$b$が満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0 が異なる2つの実数解をもち、それらが共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。
(3)2次方程式$f(x)$=0 の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲を$ab$平面上に図示せよ。ただし、2次方程式の重解は2つと数える。
2023神戸大学文系過去問
福田の数学〜神戸大学2023年理系第2問〜２次方程式の解の存在範囲
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ a,bを実数とする。整式$f(x)$=$x^2$+$ax$+$b$ で定める。以下の問いに答えよ。ただし、2次方程式の重解は2つと数える。
(1)2次方程式$f(x)$=0が異なる2つの正の解をもつためのaとbが満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0の2つの解の実部が共に0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
(3)2次方程式$f(x)$=0の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
2023神戸大学理系過去問
この動画を見る
$\Large\boxed{2}$ a,bを実数とする。整式$f(x)$=$x^2$+$ax$+$b$ で定める。以下の問いに答えよ。ただし、2次方程式の重解は2つと数える。
(1)2次方程式$f(x)$=0が異なる2つの正の解をもつためのaとbが満たすべき必要十分条件を求めよ。
(2)2次方程式$f(x)$=0の2つの解の実部が共に0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
(3)2次方程式$f(x)$=0の2つの解の実部が共に-1より大きく、0より小さくなるような点(a, b)の存在する範囲をab平面上に図示せよ。
2023神戸大学理系過去問
フツーにやっても出るけどね三次方程式解と係数の関係
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^3+2x^2+3x+4=0$の３つの解を$\alpha,\beta,\delta$としたとき、
次の３つを解にもつ３次方程式を作れ.
(1)$\dfrac{1}{\alpha},\dfrac{1}{\beta},\dfrac{1}{\delta}$
(2)$\dfrac{1}{\alpha^2},\dfrac{1}{\beta^2},\dfrac{1}{\delta^2}$
この動画を見る
$x^3+2x^2+3x+4=0$の３つの解を$\alpha,\beta,\delta$としたとき、
次の３つを解にもつ３次方程式を作れ.
(1)$\dfrac{1}{\alpha},\dfrac{1}{\beta},\dfrac{1}{\delta}$
(2)$\dfrac{1}{\alpha^2},\dfrac{1}{\beta^2},\dfrac{1}{\delta^2}$
４次方程式の解と係数の関係？
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(x+1)(x+2)(x+3)(x+4)=4$の4つの解を$\alpha,\beta,\delta,\zeta$とするとき,
$\alpha^3+\beta^3+\delta^3+\zeta^3$の値を求めよ.
この動画を見る
$(x+1)(x+2)(x+3)(x+4)=4$の4つの解を$\alpha,\beta,\delta,\zeta$とするとき,
$\alpha^3+\beta^3+\delta^3+\zeta^3$の値を求めよ.
福田の数学〜慶應義塾大学2023年看護医療学部第１問(3)〜解と係数の関係
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ (3)2次方程式$x^2$+$x$+3=0 の2つの解を$\alpha$、$\beta$とするとき、
$\frac{\beta}{\alpha}$+$\frac{\alpha}{\beta}$=$\boxed{\ \ オ\ \ }$であり、$\frac{\beta^2}{\alpha}$+$\frac{\alpha^2}{\beta}$=$\boxed{\ \ カ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{1}$ (3)2次方程式$x^2$+$x$+3=0 の2つの解を$\alpha$、$\beta$とするとき、
$\frac{\beta}{\alpha}$+$\frac{\alpha}{\beta}$=$\boxed{\ \ オ\ \ }$であり、$\frac{\beta^2}{\alpha}$+$\frac{\alpha^2}{\beta}$=$\boxed{\ \ カ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
意外と差がつく？しっかりと取りたい問題です【大阪大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#三角関数#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
a,bを実数とする。θについての方程式$\cos 2θ=a\ sin θ+b$が実数解をもつような点(a,b)の存在範囲を座標平面上に図示せよ。
大阪大過去問
この動画を見る
a,bを実数とする。θについての方程式$\cos 2θ=a\ sin θ+b$が実数解をもつような点(a,b)の存在範囲を座標平面上に図示せよ。
大阪大過去問
ざ・解と係数の関係
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^3+2x^2-2x-1=0$の3つの解を$\alpha,\beta,\delta$とする.
$\dfrac{1}{(\delta-3)(\beta-3)},\dfrac{1}{(\delta-3)(\delta-3)},\dfrac{1}{(\delta-3)(\alpha-3)}$を解にもつ3次方程式を求めよ.
この動画を見る
$x^3+2x^2-2x-1=0$の3つの解を$\alpha,\beta,\delta$とする.
$\dfrac{1}{(\delta-3)(\beta-3)},\dfrac{1}{(\delta-3)(\delta-3)},\dfrac{1}{(\delta-3)(\alpha-3)}$を解にもつ3次方程式を求めよ.
大学入試問題#483「作成時間がありませんでした」 近畿大学医学部(2023) #解と係数の関係
単元：
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係#数列#漸化式#数B
指導講師：
ますただ
問題文全文(内容文)：
$x^2-x+1=0$の解を$\alpha,\beta$とする
$\alpha^9+\beta^9$の値を求めよ
出典：2023年近畿大学医学 入試問題
この動画を見る
$x^2-x+1=0$の解を$\alpha,\beta$とする
$\alpha^9+\beta^9$の値を求めよ
出典：2023年近畿大学医学 入試問題
福田の数学〜東京大学2023年文系数学第１問〜解と係数の関係と最小値
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ kを正の実数とし、2次方程式$x^2+x-k$=0 の2つの実数解をα,βとする。
kがk＞2の範囲を動くとき、
$\displaystyle\frac{\alpha^3}{1-\beta}$+$\displaystyle\frac{\beta^3}{1-\alpha}$
の最小値を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{1}$ kを正の実数とし、2次方程式$x^2+x-k$=0 の2つの実数解をα,βとする。
kがk＞2の範囲を動くとき、
$\displaystyle\frac{\alpha^3}{1-\beta}$+$\displaystyle\frac{\beta^3}{1-\alpha}$
の最小値を求めよ。
2023東京大学文系過去問
基本対称式 あれで出そうよ
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha+\beta+\delta=1 \\
\alpha\beta+\beta\delta+\delta\alpha=2,
\alpha\beta\delta=3
\end{array}
\right.
\end{eqnarray}$
を満たすとき,
①$\dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2}+\dfrac{1}{\delta^2}$
②$\dfrac{1}{\alpha^3}+\dfrac{1}{\beta^3}+\dfrac{1}{\delta^3}$の値を求めよ.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
\alpha+\beta+\delta=1 \\
\alpha\beta+\beta\delta+\delta\alpha=2,
\alpha\beta\delta=3
\end{array}
\right.
\end{eqnarray}$
を満たすとき,
①$\dfrac{1}{\alpha^2}+\dfrac{1}{\beta^2}+\dfrac{1}{\delta^2}$
②$\dfrac{1}{\alpha^3}+\dfrac{1}{\beta^3}+\dfrac{1}{\delta^3}$の値を求めよ.
福田の1.5倍速演習〜合格する重要問題045〜東北大学2017年度理系第1問〜絶対値の付いた２次関数のグラフと直線の共有点の個数
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次関数とグラフ#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a,b$を実数とする。$y=|x^2-4|$で表される曲線をCとし、
$y=ax+b$で表される直線をlとする。
(1)lが点(-2,0)を通り、lとCがちょうど3つの共有点をもつような
a,bの条件を求めよ。
(2)lとCがちょうど3つの共有点をもつような点(a,b)の軌跡を
ab平面上に図示せよ。
2017東北大学理系過去問
この動画を見る
$a,b$を実数とする。$y=|x^2-4|$で表される曲線をCとし、
$y=ax+b$で表される直線をlとする。
(1)lが点(-2,0)を通り、lとCがちょうど3つの共有点をもつような
a,bの条件を求めよ。
(2)lとCがちょうど3つの共有点をもつような点(a,b)の軌跡を
ab平面上に図示せよ。
2017東北大学理系過去問
４次方程式の解と係数の関係？
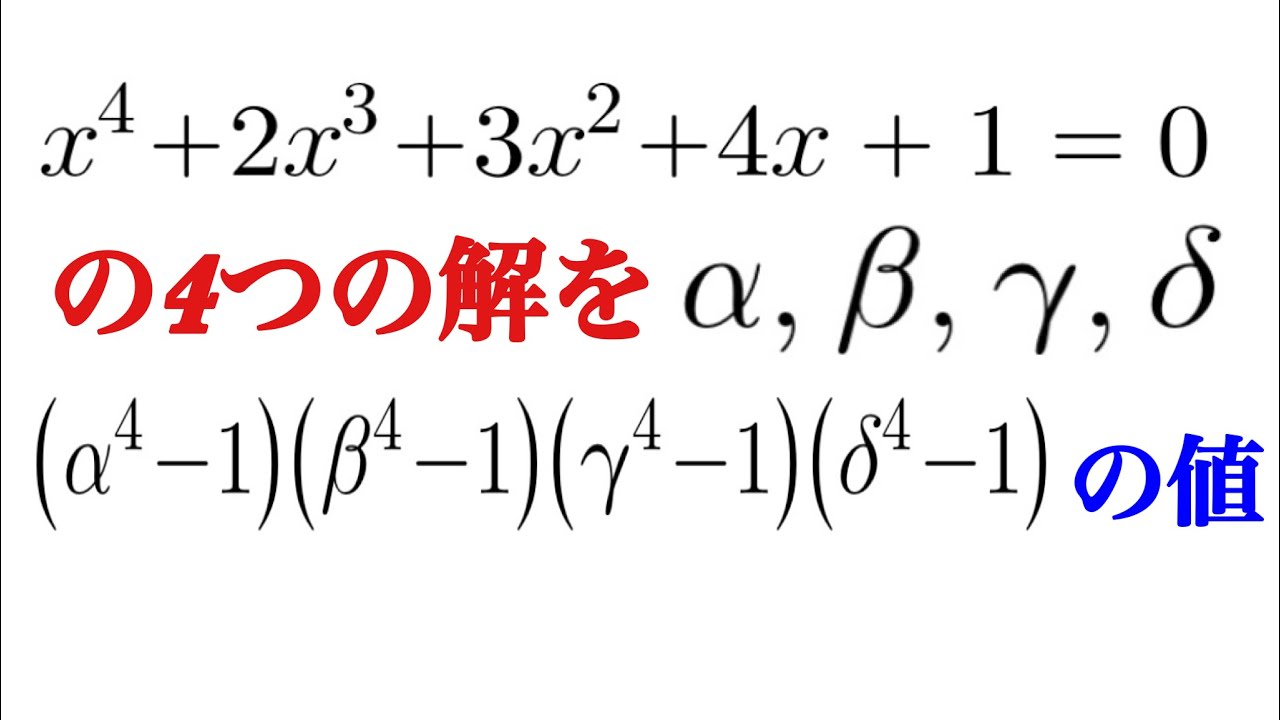
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^4+2x^3+3x^2+4x+1=0$の4つの解を
$α,β,γ,δ$とおくとき,
$(α^4-1)(β^4-1)(γ^4-1)(δ^4-1)$の値を求めよ.
この動画を見る
$x^4+2x^3+3x^2+4x+1=0$の4つの解を
$α,β,γ,δ$とおくとき,
$(α^4-1)(β^4-1)(γ^4-1)(δ^4-1)$の値を求めよ.
【数Ⅱ】複素数と方程式：解と係数の関係：「解と係数の関係」の基本を10分でマスター！
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
解と係数の関係の基本を10分でマスター！例題も4問解説！
この動画を見る
解と係数の関係の基本を10分でマスター！例題も4問解説！
福田の1.5倍速演習〜合格する重要問題022〜一橋大学2016年度文系数学第５問〜ベクトルの絶対値の比の範囲
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#平面上のベクトル#解と判別式・解と係数の関係#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
平面上の2つのベクトル$\overrightarrow{ a }$と$\overrightarrow{ b }$は零ベクトルではなく、$\overrightarrow{ a }$と$\overrightarrow{ b }$のなす角度は
60°である。このとき
$r=\frac{|\overrightarrow{ a }+2\overrightarrow{ b }|}{|2\overrightarrow{ a }+\overrightarrow{ b }}$
のとりうる値の範囲を求めよ。
2016一橋大学文系過去問
この動画を見る
平面上の2つのベクトル$\overrightarrow{ a }$と$\overrightarrow{ b }$は零ベクトルではなく、$\overrightarrow{ a }$と$\overrightarrow{ b }$のなす角度は
60°である。このとき
$r=\frac{|\overrightarrow{ a }+2\overrightarrow{ b }|}{|2\overrightarrow{ a }+\overrightarrow{ b }}$
のとりうる値の範囲を求めよ。
2016一橋大学文系過去問
連立二元二次方程式2023
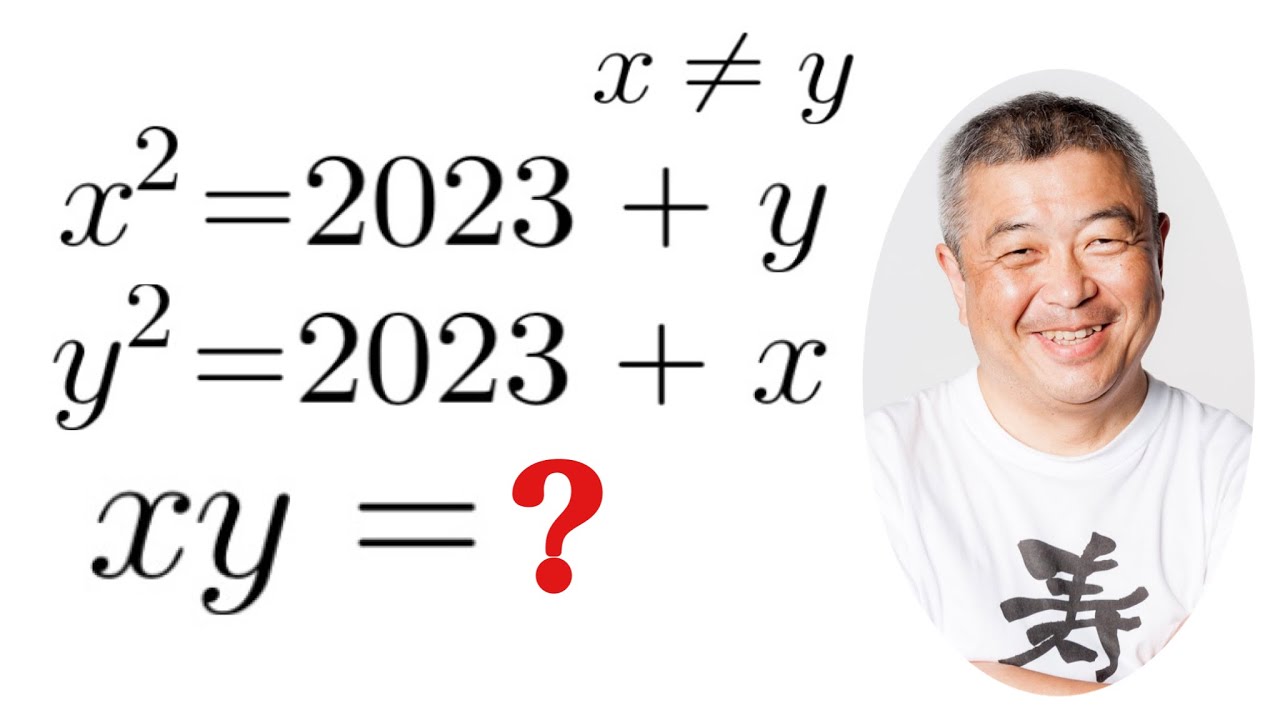
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^2=2023+y$
$y^2=2023+x$
このときxyの値を求めよ.
この動画を見る
$x^2=2023+y$
$y^2=2023+x$
このときxyの値を求めよ.
福田の1.5倍速演習〜合格する重要問題008〜神戸大学文系数学第１問〜対称式と軌跡
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#平面上のベクトル#図形と方程式#解と判別式・解と係数の関係#軌跡と領域#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
s,tを$s \lt t$をみたす実数とする。座標平面上の3点$A(1,2),B(s,s^2),C(t,t^2)$が一直線上にあるとする。以下の問いに答えよ。
(1)sとtの関係式を求めよ。
(2)線分BCの中点をM(u,v)とする。uとvの間の関係式を求めよ。
(3)s,tが変化するとき、vの最小値と、その時のu,s,tの値を求めよ。
神戸大学文系過去問
この動画を見る
s,tを$s \lt t$をみたす実数とする。座標平面上の3点$A(1,2),B(s,s^2),C(t,t^2)$が一直線上にあるとする。以下の問いに答えよ。
(1)sとtの関係式を求めよ。
(2)線分BCの中点をM(u,v)とする。uとvの間の関係式を求めよ。
(3)s,tが変化するとき、vの最小値と、その時のu,s,tの値を求めよ。
神戸大学文系過去問
福田の数学〜東京理科大学2022年理工学部第１問(1)〜解と係数の関係と３次関数の最大最小
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#解と判別式・解と係数の関係#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
(1)mを実数とする。xについての2次方程式$x^2-(m+3)x+m^2-9=0$の
二つの解を$α,β$とする。$α,β$が実数であるための必要十分条件は$- \boxed{ア} \leqq m \leqq \boxed{イ}$である。
mが$- \boxed{ア} \leqq m \leqq \boxed{イ}$の範囲を動くときの
$α^3+β^3$の最小値は$\boxed{ウ}$、最大値は$\boxed{エオカ}$である。
この動画を見る
(1)mを実数とする。xについての2次方程式$x^2-(m+3)x+m^2-9=0$の
二つの解を$α,β$とする。$α,β$が実数であるための必要十分条件は$- \boxed{ア} \leqq m \leqq \boxed{イ}$である。
mが$- \boxed{ア} \leqq m \leqq \boxed{イ}$の範囲を動くときの
$α^3+β^3$の最小値は$\boxed{ウ}$、最大値は$\boxed{エオカ}$である。
普通に計算すれば出るけどね
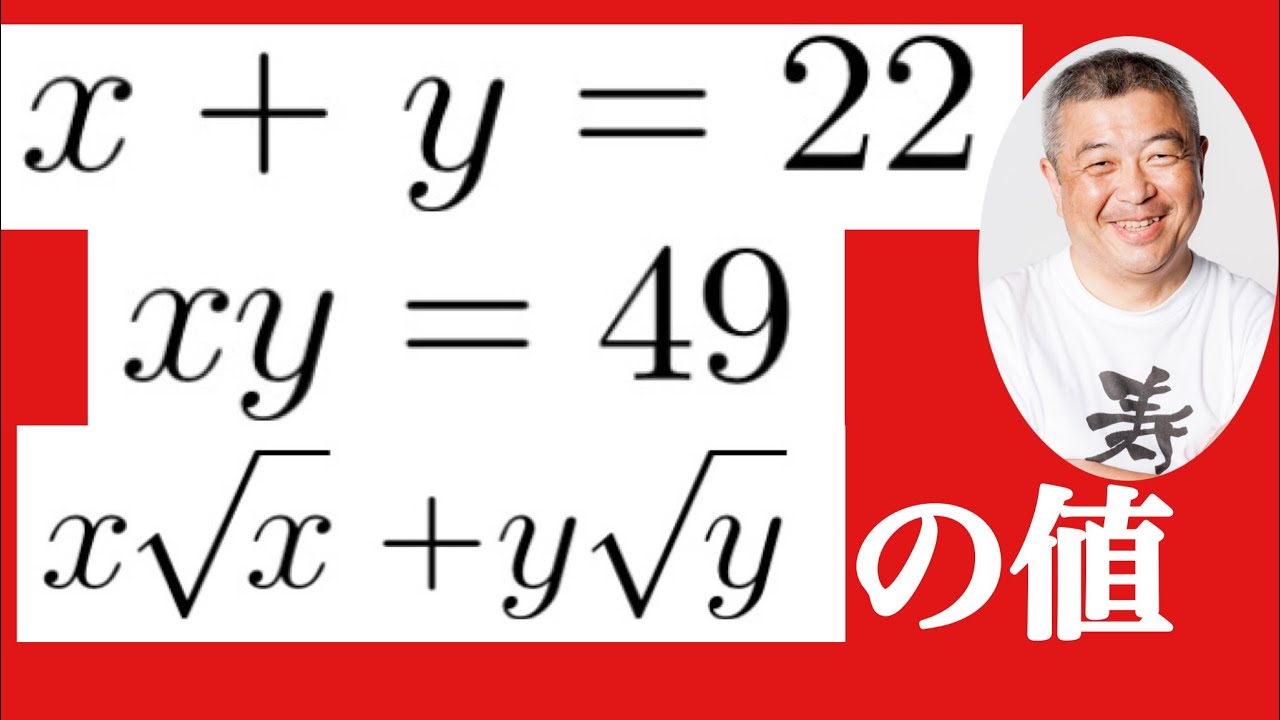
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x+y=22,xy=49,x\sqrt x+y\sqrt y$の値を求めよ.
この動画を見る
$ x+y=22,xy=49,x\sqrt x+y\sqrt y$の値を求めよ.
瞬殺！地道に頑張りたくないよね！３次方程式解と係数の関係
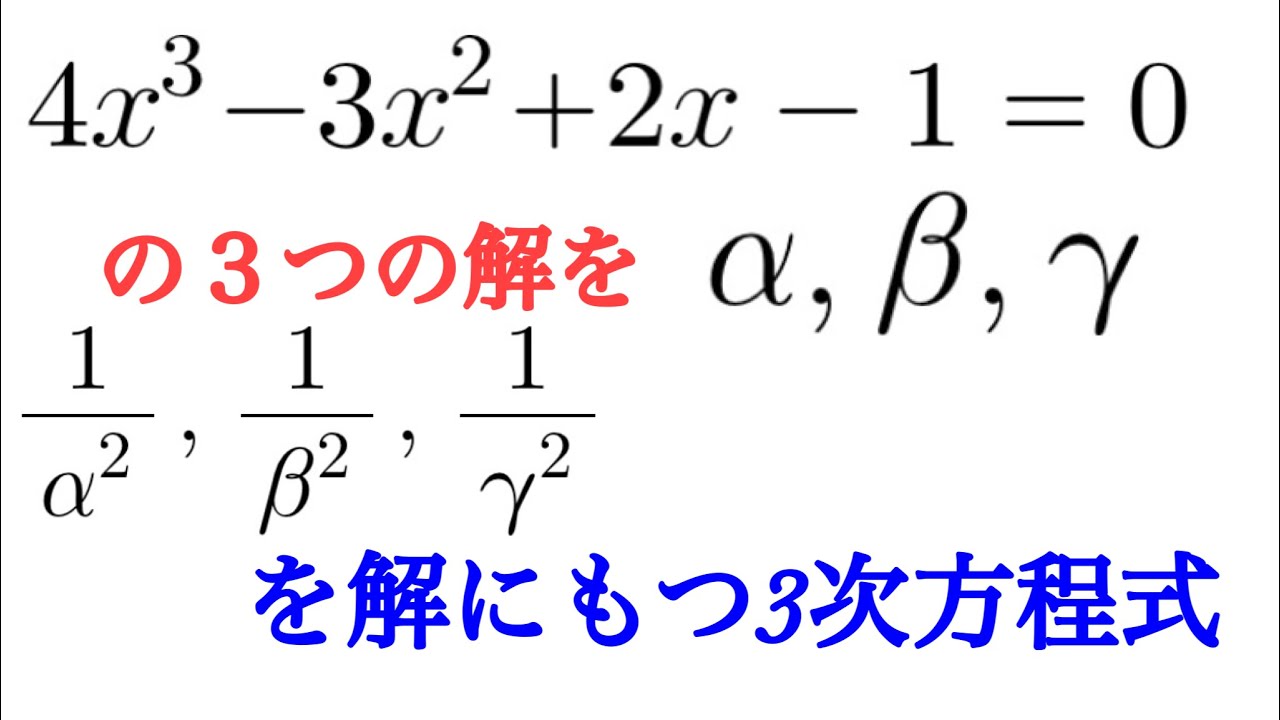
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ 4x^3-3x^2+2x-1=0$の3つの解を,$\alpha,\beta,\delta$とする.
$\dfrac{1}{\alpha^2},\dfrac{1}{\beta^2},\dfrac{1}{\delta^2}$を解にもつ三次方程式を求めよ.
この動画を見る
$ 4x^3-3x^2+2x-1=0$の3つの解を,$\alpha,\beta,\delta$とする.
$\dfrac{1}{\alpha^2},\dfrac{1}{\beta^2},\dfrac{1}{\delta^2}$を解にもつ三次方程式を求めよ.
３次方程式の解と係数の関係 あっという間に出す方法もあるよ
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x^3-2x^2+3x+4=0$の3つの解を$\alpha,\beta,\delta$とする.
$\alpha^2,\beta^2,\delta^2$を解にもつ方程式を1つ例示せよ.
この動画を見る
$ x^3-2x^2+3x+4=0$の3つの解を$\alpha,\beta,\delta$とする.
$\alpha^2,\beta^2,\delta^2$を解にもつ方程式を1つ例示せよ.
福田の数学〜立教大学2022年理学部第１問(4)〜解と係数の関係
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
2次方程式$2x^2+4x+1=0$の解を$\alpha,\ \beta(\alpha\lt \beta)$とする。実数$p,q$に対して、
2次方程式$x^2+px+q=0$の解が$\alpha^3,\ \beta^3$であるならば、
$p=\boxed{オ},\ q=\boxed{カ}$である。
2022立教大学理学部過去問
この動画を見る
2次方程式$2x^2+4x+1=0$の解を$\alpha,\ \beta(\alpha\lt \beta)$とする。実数$p,q$に対して、
2次方程式$x^2+px+q=0$の解が$\alpha^3,\ \beta^3$であるならば、
$p=\boxed{オ},\ q=\boxed{カ}$である。
2022立教大学理学部過去問
福田の数学〜明治大学2022年理工学部第１問(2)〜2次方程式の解の存在範囲
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#複素数と方程式#2次方程式と2次不等式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(2)座標平面上の曲線$x^2+2xy+2y^2=5$を$C$とする。
$(\textrm{a})$直線$2x+y=t$が曲線$C$と共有点をもつとき、実数$t$の取り得る値の範囲は
$\boxed{コ}\leqq t \leqq \boxed{サ}$である。
$(\textrm{b})$直線$2x+y=1$が曲線$C$と$x \geqq 0$の範囲で共有点を少なくとも1個もつとき、
実数$t$ の取り得る値の範囲は$-\frac{1}{2}\sqrt{\boxed{シス}} \leqq t \leqq \boxed{セ}$である。
2022明治大学理工学部過去問
この動画を見る
(2)座標平面上の曲線$x^2+2xy+2y^2=5$を$C$とする。
$(\textrm{a})$直線$2x+y=t$が曲線$C$と共有点をもつとき、実数$t$の取り得る値の範囲は
$\boxed{コ}\leqq t \leqq \boxed{サ}$である。
$(\textrm{b})$直線$2x+y=1$が曲線$C$と$x \geqq 0$の範囲で共有点を少なくとも1個もつとき、
実数$t$ の取り得る値の範囲は$-\frac{1}{2}\sqrt{\boxed{シス}} \leqq t \leqq \boxed{セ}$である。
2022明治大学理工学部過去問
福田の数学〜早稲田大学2022年人間科学部第４問〜3変数の基本対称式と解と係数の関係
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#複素数#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\large\boxed{4}}$互いに異なる実数$a,b,c$について、
$a+b+c=0,\ bc+ca+ab=-3$であるとき、
$abc$のとりうる値の範囲は、$\boxed{\ \ ア\ \ } \lt abc \lt \boxed{\ \ イ\ \ }$である。
さらに$a \lt b \lt c$のとき、$a,b,c$のとりうる値の範囲は
$\boxed{\ \ ウ\ \ } \lt a \lt \boxed{\ \ エ\ \ } \lt b \lt \boxed{\ \ オ\ \ } \lt c \lt \boxed{\ \ カ\ \ }$である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{4}}$互いに異なる実数$a,b,c$について、
$a+b+c=0,\ bc+ca+ab=-3$であるとき、
$abc$のとりうる値の範囲は、$\boxed{\ \ ア\ \ } \lt abc \lt \boxed{\ \ イ\ \ }$である。
さらに$a \lt b \lt c$のとき、$a,b,c$のとりうる値の範囲は
$\boxed{\ \ ウ\ \ } \lt a \lt \boxed{\ \ エ\ \ } \lt b \lt \boxed{\ \ オ\ \ } \lt c \lt \boxed{\ \ カ\ \ }$である。
2022早稲田大学人間科学部過去問
福田の数学〜慶應義塾大学2022年看護医療学部第１問(5)〜解と係数の関係と式の値の計算
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
${\large\boxed{1}}$(5)iを虚数単位とし、$\alpha=\frac{1-\sqrt3i}{4}$とする。このとき、
$a,b$を実数とする2次方程式$x^2+ax+b=0$の解の1つが$\alpha$であるならば、
$a=\boxed{\ \ ア\ \ },\ b=\boxed{\ \ イ\ \ }$である。
また、$f(x)=4x^4-3x^3+2x^2$とするとき、$f(\alpha)$の値は$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{1}}$(5)iを虚数単位とし、$\alpha=\frac{1-\sqrt3i}{4}$とする。このとき、
$a,b$を実数とする2次方程式$x^2+ax+b=0$の解の1つが$\alpha$であるならば、
$a=\boxed{\ \ ア\ \ },\ b=\boxed{\ \ イ\ \ }$である。
また、$f(x)=4x^4-3x^3+2x^2$とするとき、$f(\alpha)$の値は$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
数学オリンピック予選
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#解と判別式・解と係数の関係#数学オリンピック#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
有理数係数の2次方程式
$ x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+$
$･･････+a_{2n-1}x+a_{2n}=0$
の解はすべて$x^2+5x+7=0$の解にもなっている.
$a_1$の値を求めよ.
この動画を見る
有理数係数の2次方程式
$ x^{2n}+a_1x^{2n-1}+a_2x^{2n-2}+$
$･･････+a_{2n-1}x+a_{2n}=0$
の解はすべて$x^2+5x+7=0$の解にもなっている.
$a_1$の値を求めよ.
虚数解の６乗が実数
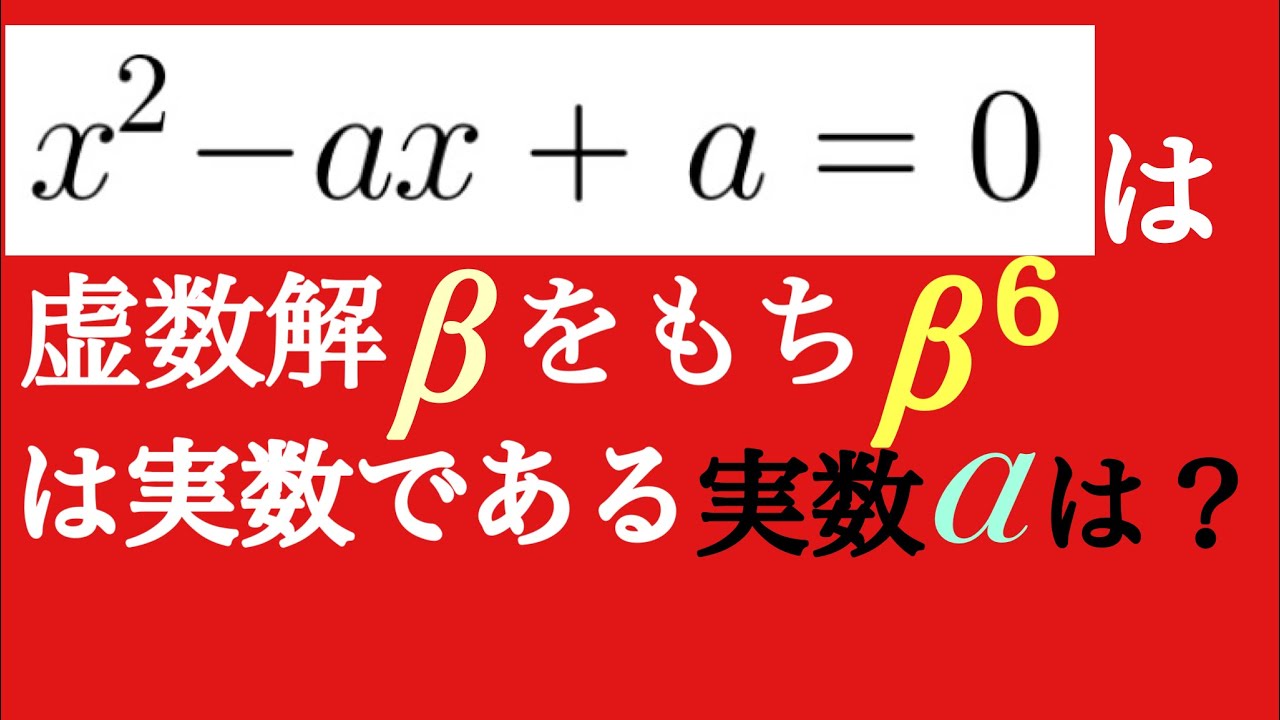
単元：
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x^2-ax+a=0$は虚数解$\beta$をもち$\beta^6$は実数である.
aの値を求めよ.
この動画を見る
$ x^2-ax+a=0$は虚数解$\beta$をもち$\beta^6$は実数である.
aの値を求めよ.
東北大文系 虚数のナイスな問題
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#解と判別式・解と係数の関係#数列#漸化式#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数B
指導講師：
鈴木貫太郎
問題文全文(内容文)：
pは0でない実数である.$x^2-px+5p=0$の解を$\alpha,\beta$とする.
(1)$\alpha^5+\beta^5=p\5$となるpを求めよ.
(2)$\alpha$は虚数で$\alpha^5$が実数となるpを求めよ.
東北大文系過去問
この動画を見る
pは0でない実数である.$x^2-px+5p=0$の解を$\alpha,\beta$とする.
(1)$\alpha^5+\beta^5=p\5$となるpを求めよ.
(2)$\alpha$は虚数で$\alpha^5$が実数となるpを求めよ.
東北大文系過去問
ただの連立方程式
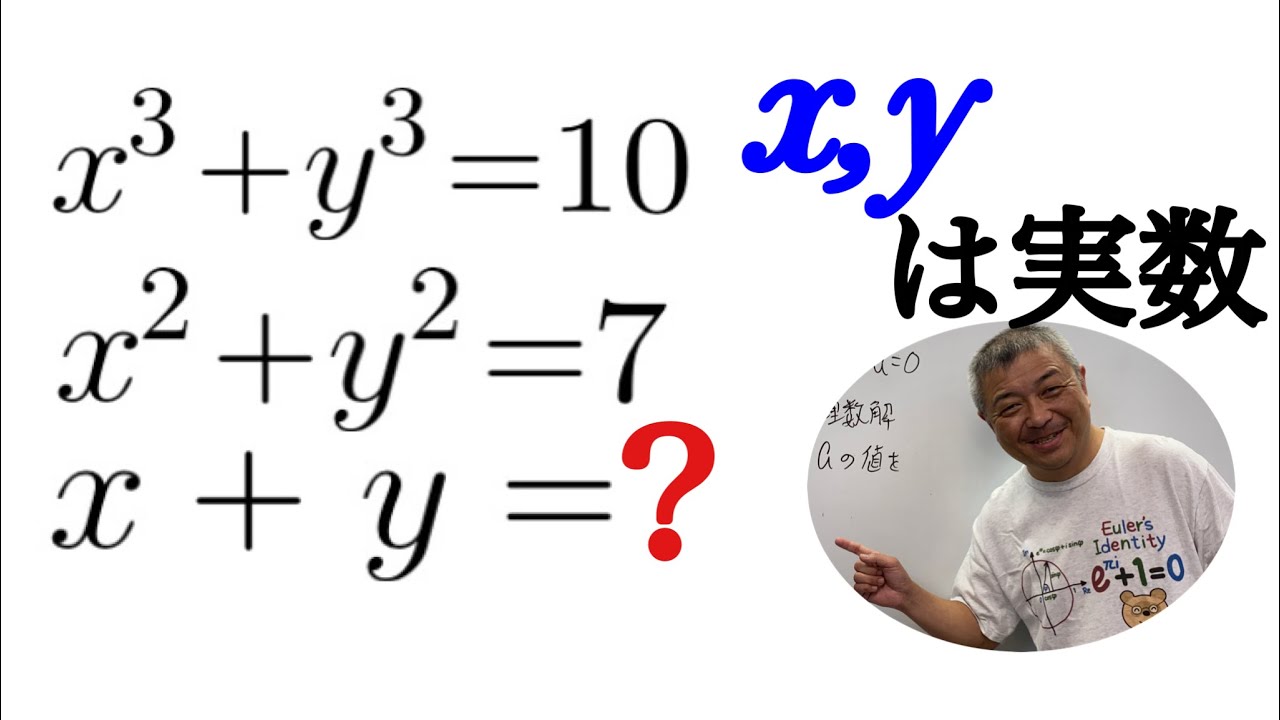
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
x,yは実数とする.
x^3+y^3=10,x^2+y^2=7,x+y=?$
これを解け.
この動画を見る
x,yは実数とする.
x^3+y^3=10,x^2+y^2=7,x+y=?$
これを解け.
式の値 基本
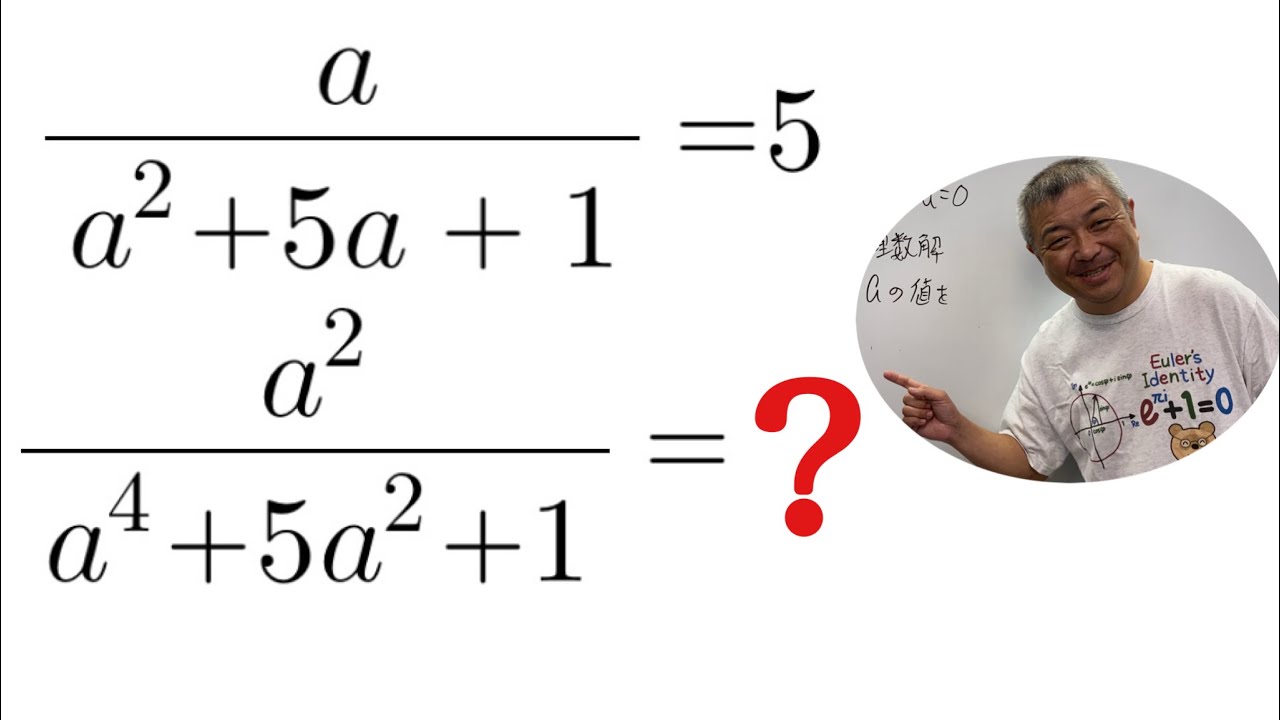
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ \dfrac{a}{a^2+5a+1}=5$のとき,
$\dfrac{a^2}{a^4+5a^2+1}=?$
これを解け.
この動画を見る
$ \dfrac{a}{a^2+5a+1}=5$のとき,
$\dfrac{a^2}{a^4+5a^2+1}=?$
これを解け.
2次方程式の因数分解や解の公式が不要な新しい解き方の証明
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
2次方程式の因数分解や解の公式が不要な新しい解き方の証明
この動画を見る
2次方程式の因数分解や解の公式が不要な新しい解き方の証明