数Ⅱ
数Ⅱ
福田の一夜漬け数学〜平面ベクトル(3)〜受験編・文理共通
単元：
#数Ⅱ#平面上のベクトル#図形と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
点$O$を原点、$A(1,1),B(1,-1)$とする。
(1) $\overrightarrow{ OP }=s\ \overrightarrow{ OA }+t\ \overrightarrow{ OB }$で定められる点Pを考える。$s,t$が $2s+t \leqq 2,$
$s \geqq 0,t \geqq 0$を満たすながら動くとき、点$P$の存在する範囲を図示せよ。
(2) $\overrightarrow{ OQ }=(1-u)\overrightarrow{ QA }+2u\overrightarrow{ QB }$で定められる点$Q$を考える。$u$が$0 \leqq u \leqq 1$を
満たしながら動くとき、点$P$の存在する範囲を図示せよ。
この動画を見る
点$O$を原点、$A(1,1),B(1,-1)$とする。
(1) $\overrightarrow{ OP }=s\ \overrightarrow{ OA }+t\ \overrightarrow{ OB }$で定められる点Pを考える。$s,t$が $2s+t \leqq 2,$
$s \geqq 0,t \geqq 0$を満たすながら動くとき、点$P$の存在する範囲を図示せよ。
(2) $\overrightarrow{ OQ }=(1-u)\overrightarrow{ QA }+2u\overrightarrow{ QB }$で定められる点$Q$を考える。$u$が$0 \leqq u \leqq 1$を
満たしながら動くとき、点$P$の存在する範囲を図示せよ。
大阪大学 対数 不等式 質問への返答「対数微分法」高校数学 Japanese university entrance exam questions
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#微分法#色々な関数の導関数#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
大阪大学過去問題
xの範囲を求めよ
$\log_2(1-x)+\log_4(x+4) \leqq 2$
この動画を見る
大阪大学過去問題
xの範囲を求めよ
$\log_2(1-x)+\log_4(x+4) \leqq 2$
一橋大学（’９４）微分 高校数学 Japanese university entrance exam questions
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
一橋大学'94過去問題
$y=x^3$と$y=x^2+x+c$
との両方に接する直線が4本あるようなcの範囲
この動画を見る
一橋大学'94過去問題
$y=x^3$と$y=x^2+x+c$
との両方に接する直線が4本あるようなcの範囲
福田の一夜漬け数学〜多変数関数１文字固定(3)〜受験編
単元：
#数Ⅱ#図形と方程式#指数関数と対数関数#微分法と積分法#軌跡と領域#指数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
三辺の長さがa,b,cである直方体を長さがbの一辺を回転軸として$90^{ \circ }$
回転させる。直方体が通過する点全体が作る体積をVとする。
(1)$V$を$a,b,c$で表せ。
(2)$a+b+c=1$のとき、$V$の取り得る値の範囲を求めよ。
この動画を見る
三辺の長さがa,b,cである直方体を長さがbの一辺を回転軸として$90^{ \circ }$
回転させる。直方体が通過する点全体が作る体積をVとする。
(1)$V$を$a,b,c$で表せ。
(2)$a+b+c=1$のとき、$V$の取り得る値の範囲を求めよ。
福田の一夜漬け数学〜多変数関数、１文字固定その２（受験編）
単元：
#数Ⅱ#式と証明#三角関数#恒等式・等式・不等式の証明#加法定理とその応用#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\triangle ABC$において次の不等式を示せ。
(1)$\cos A+\cos B+\cos C \leqq \frac{3}{2}$
(2)$\cos A\cos B \cos C \leqq \frac{1}{8}$
この動画を見る
$\triangle ABC$において次の不等式を示せ。
(1)$\cos A+\cos B+\cos C \leqq \frac{3}{2}$
(2)$\cos A\cos B \cos C \leqq \frac{1}{8}$
福田の一夜漬け数学〜多変数関数、１文字固定（受験編）
単元：
#数Ⅱ#式と証明#図形と方程式#微分法と積分法#恒等式・等式・不等式の証明#軌跡と領域#平均変化率・極限・導関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$a+b+c=1$のとき、$a^2+b^2+c^2$の最小値を求めよ。
$xy$平面内の領域$-1 \leqq x \leqq 1,-1 \leqq y \leqq 1$ において、$1-ax-by+axy$
の最小値が正であるような$(a,b)$の存在範囲を図示せよ。
この動画を見る
$a+b+c=1$のとき、$a^2+b^2+c^2$の最小値を求めよ。
$xy$平面内の領域$-1 \leqq x \leqq 1,-1 \leqq y \leqq 1$ において、$1-ax-by+axy$
の最小値が正であるような$(a,b)$の存在範囲を図示せよ。
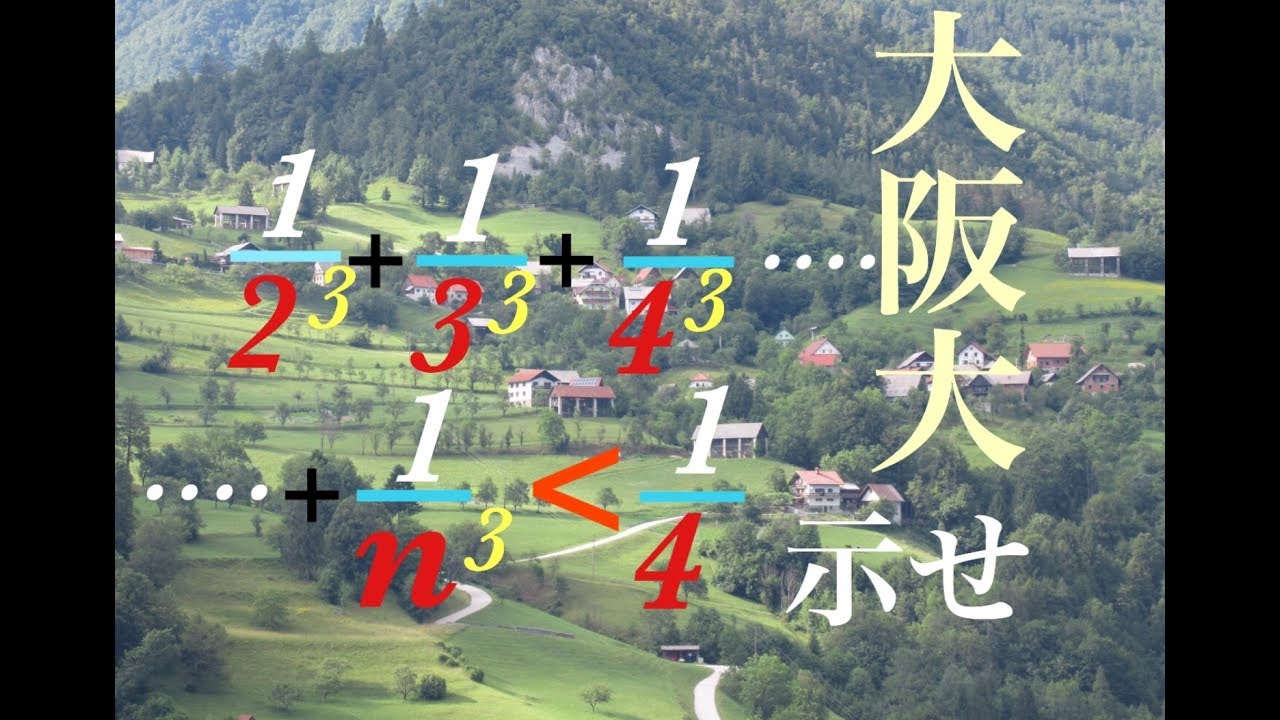
大阪大学 自然数（２以上）の立方の逆数の和 1/4未満 示せ 高校数学 Japanese university entrance exam questions
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
自然数（２以上）の立方の逆数の和 が1/4未満であることを示せ.
大阪大学過去問
この動画を見る
自然数（２以上）の立方の逆数の和 が1/4未満であることを示せ.
大阪大学過去問
【高校数学】数Ⅲ-84 三角関数と極限③
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty} \dfrac{\sin x}{x}$
②$\displaystyle \lim_{x\to 0} x^2 \sin \dfrac{1}{x}$
③$\displaystyle \lim_{x\to \infty} x \sin \dfrac{1}{x}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty} \dfrac{\sin x}{x}$
②$\displaystyle \lim_{x\to 0} x^2 \sin \dfrac{1}{x}$
③$\displaystyle \lim_{x\to \infty} x \sin \dfrac{1}{x}$
組立除法、三角関数の合成、視聴者からの質問への返答
単元：
#複素数と方程式#三角関数#剰余の定理・因数定理・組み立て除法と高次方程式#加法定理とその応用#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
組立除法、三角関数の合成、視聴者からの質問への返答です.
\begin{array}{r}
x-α\enclose{longdiv}{ax^3+bx^2+cx+d\phantom{0}} \\[-3pt]
\end{array}
この動画を見る
組立除法、三角関数の合成、視聴者からの質問への返答です.
\begin{array}{r}
x-α\enclose{longdiv}{ax^3+bx^2+cx+d\phantom{0}} \\[-3pt]
\end{array}
【高校数学】数Ⅲ-83 三角関数と極限②
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0} \dfrac{1-\cos x}{x^2}$
②$\displaystyle \lim_{x\to \frac{\pi}{2}} \dfrac{\cos x}{2x-\pi}$
③$\displaystyle \lim_{x\to 0}\dfrac{\cos 3x-\cos 2x}{x^2}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0} \dfrac{1-\cos x}{x^2}$
②$\displaystyle \lim_{x\to \frac{\pi}{2}} \dfrac{\cos x}{2x-\pi}$
③$\displaystyle \lim_{x\to 0}\dfrac{\cos 3x-\cos 2x}{x^2}$
【高校数学】数Ⅲ-82 三角関数と極限①
単元：
#数Ⅱ#三角関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0}\dfrac{\sin 3x}{x}$
②$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{2x}$
③$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{\sin 2x}$
④$\displaystyle \lim_{x\to 0}\dfrac{\sin x-\sin 5x}{2x}$
⑤$\displaystyle \lim_{x\to 0}\dfrac{1-\cos 2x}{x^2}$
⑥$\displaystyle \lim_{x\to 0}\dfrac{x\sin x}{1-\cos x}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to 0}\dfrac{\sin 3x}{x}$
②$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{2x}$
③$\displaystyle \lim_{x\to 0}\dfrac{\tan 3x}{\sin 2x}$
④$\displaystyle \lim_{x\to 0}\dfrac{\sin x-\sin 5x}{2x}$
⑤$\displaystyle \lim_{x\to 0}\dfrac{1-\cos 2x}{x^2}$
⑥$\displaystyle \lim_{x\to 0}\dfrac{x\sin x}{1-\cos x}$
【高校数学】数Ⅲ-81 関数の極限⑥(対数関数)
単元：
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty}\log_3 x$
②$\displaystyle \lim_{x\to \infty}\log_{\frac{1}{2}} x$
③$\displaystyle \lim_{x\to \infty}\log_{\frac{1}{2}}x$
④$\displaystyle \lim_{x\to \infty}\log_2 \dfrac{1}{2}$
⑤$\displaystyle \lim_{x\to \infty}\{\log_3 (x^2+1)-2\log_3 x\}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{x\to \infty}\log_3 x$
②$\displaystyle \lim_{x\to \infty}\log_{\frac{1}{2}} x$
③$\displaystyle \lim_{x\to \infty}\log_{\frac{1}{2}}x$
④$\displaystyle \lim_{x\to \infty}\log_2 \dfrac{1}{2}$
⑤$\displaystyle \lim_{x\to \infty}\{\log_3 (x^2+1)-2\log_3 x\}$
原点を中心とする円周上には無数に有理点がある。ピタゴラス数と関係が？
単元：
#数A#数Ⅱ#整数の性質#図形と方程式#微分法と積分法#円と方程式#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
原点を中心とする円周上には無数に有理点がある。ピタゴラス数と関係があるのか解説していきます.
この動画を見る
原点を中心とする円周上には無数に有理点がある。ピタゴラス数と関係があるのか解説していきます.
球の体積、表面積 中学生にも納得のいく方法で。 積分でも出します
単元：
#数学(中学生)#中１数学#数Ⅱ#空間図形#微分法と積分法#面積、体積#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
球の表面積、体積の公式がなぜそうなるのかわかりやすく解説します！
この動画を見る
球の表面積、体積の公式がなぜそうなるのかわかりやすく解説します！
二項定理・多項定理を理解する
三倍角の公式を複素数の掛け算（ド・モアブルの定理）で簡単に導く
【数学】３分で和積公式が馬鹿でもわかる考え方
【数学】４分で積和公式が馬鹿でもわかる考え方
２点を通る直線の方程式を求めるのに連立方程式を使うのは卒業しましょう
積の微分、合成関数の微分、商の微分の導出
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
積の微分,合成関数の微分,商の微分の導出に関して解説していきます.
この動画を見る
積の微分,合成関数の微分,商の微分の導出に関して解説していきます.
積分で面積が出る理由
弧度法を使う理由
単元：
#数Ⅱ#三角関数#微分法と積分法#三角関数とグラフ#平均変化率・極限・導関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
弧度法を使う理由を解説していきます.
この動画を見る
弧度法を使う理由を解説していきます.
指数法則 ０乗はなぜ１か
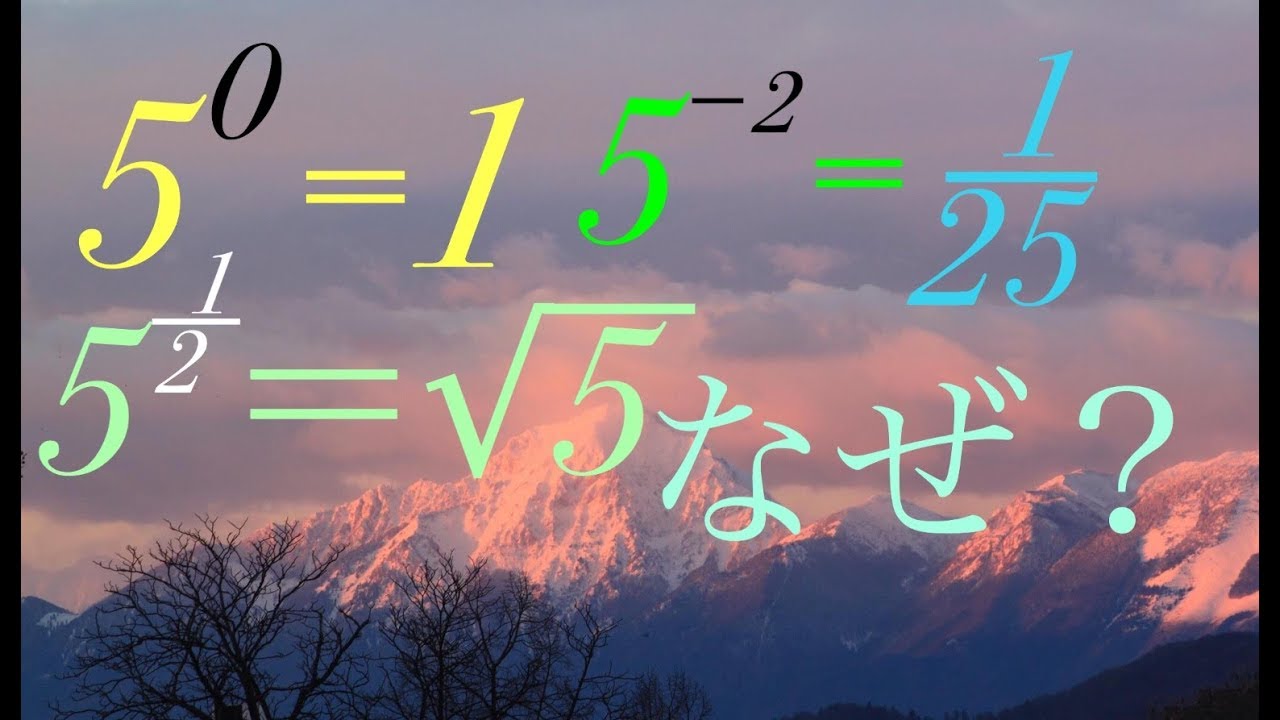
【高校数学】数Ⅲ-57 無理方程式の解の個数
単元：
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①方程式$\sqrt{x+1}=x+k$が異なる2つの実数解をもつように、
実数$k$の値の範囲を求めよ。
この動画を見る
①方程式$\sqrt{x+1}=x+k$が異なる2つの実数解をもつように、
実数$k$の値の範囲を求めよ。
中学生の知識でオイラーの公式を理解しよう VOL ６ e ネイピア数の正体
単元：
#数Ⅱ#指数関数と対数関数#指数関数#関数と極限#微分とその応用#関数の極限#色々な関数の導関数#数学(高校生)#数Ⅲ
指導講師：
鈴木貫太郎
問題文全文(内容文)：
中学生の知識でオイラーの公式を理解しよう VOL ６ e ネイピア数の正体
この動画を見る
中学生の知識でオイラーの公式を理解しよう VOL ６ e ネイピア数の正体
中学生の知識でオイラーの公式を理解しよう Vol 4 微分の定義
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
中学生の知識でオイラーの公式を理解しよう Vol 4 微分の定義を解説
この動画を見る
中学生の知識でオイラーの公式を理解しよう Vol 4 微分の定義を解説
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.3 三角比 余弦定理 加法定理
単元：
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.3 三角比 余弦定理 加法定理
この動画を見る
Euler's formula 中学生の知識でオイラーの公式を理解しよう Vol.3 三角比 余弦定理 加法定理
【高校数学】数Ⅲ－２８ 楕円④
単元：
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
①円$x^2+y^2=36$を$x$軸を基準にして$y$軸方向に
$\dfrac{2}{3}$倍して得られる図形の方程式を求めよ.
②長さ8の線分$PQ$がある.
点$P$が$x$軸上,点$Q$が$y$軸上を動くとき,
$PQ$を$3:5$に内分する点$R$の軌跡を求めよ.
この動画を見る
①円$x^2+y^2=36$を$x$軸を基準にして$y$軸方向に
$\dfrac{2}{3}$倍して得られる図形の方程式を求めよ.
②長さ8の線分$PQ$がある.
点$P$が$x$軸上,点$Q$が$y$軸上を動くとき,
$PQ$を$3:5$に内分する点$R$の軌跡を求めよ.
【高校数学】数Ⅲ－２７ 楕円③
単元：
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の楕円の方程式を求めよ.
①2点$(2,0),(-2,0)$からの距離の和が6
②2点$(0,3),(0,-3)$を焦点とし,短軸の長さが8
③2点$(\sqrt2,0),(-\sqrt2,0)$を焦点とし,点$(\sqrt3,\sqrt2)$を通る
この動画を見る
次の楕円の方程式を求めよ.
①2点$(2,0),(-2,0)$からの距離の和が6
②2点$(0,3),(0,-3)$を焦点とし,短軸の長さが8
③2点$(\sqrt2,0),(-\sqrt2,0)$を焦点とし,点$(\sqrt3,\sqrt2)$を通る
【高校数学】数Ⅲ－２６ 楕円②
単元：
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
次の楕円の頂点と焦点を求めよ.
①$\dfrac{x^2}{9}+\dfrac{y^2}{4}=1$
②$x^2+4y^2=4$
③$9x^2+4y^2=1$
④$9x^2+y^2=16$
この動画を見る
次の楕円の頂点と焦点を求めよ.
①$\dfrac{x^2}{9}+\dfrac{y^2}{4}=1$
②$x^2+4y^2=4$
③$9x^2+4y^2=1$
④$9x^2+y^2=16$