 微分とその応用
微分とその応用
 微分とその応用
微分とその応用
福田の数学〜青山学院大学2022年理工学部第3問〜関数の増減と極値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
関数
$f(x)=\sqrt{1-2\cos x}-\frac{1}{2}x$
について以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$f'(x) \gt 0$ となるxの値の範囲を求めよ。
(3)f(x)の増減を調べ、極値を求めよ。
2022青山学院大学理工学部過去問
この動画を見る
関数
$f(x)=\sqrt{1-2\cos x}-\frac{1}{2}x$
について以下の問いに答えよ。
(1)$f'(x)$を求めよ。
(2)$f'(x) \gt 0$ となるxの値の範囲を求めよ。
(3)f(x)の増減を調べ、極値を求めよ。
2022青山学院大学理工学部過去問
福田の数学〜立教大学2022年理学部第2問〜接線と囲まれた部分の面積と回転体の体積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数xに対し、関数f(x)を
$f(x)=xe^{-x}$
により定める。座標平面上の曲線$C:y=f(x)$に関して、次の問(1)~(5)に答えよ。
(1)f(x)の導関数$f'(x)$を求め、$f(x)$の増減表を書け。ただし、極値も記入すること。
(2)f(x)の第2次導関数$f''(x)$を求め、Cの変曲点の座標を求めよ。
(3)Cの変曲点と、座標平面上の原点を通る直線を$l$とする。
Cとlで囲まれた領域の面積Sを求めよ。
(4)$a,\ b,\ c$を定数とし、関数$g(x)$を$g(x)=(ax^2+bx+c)e^{-2x}$と定める。
$g(x)$の導関数$g'(x)$が$g'(x)=x^2e^{-2x}$を満たすとき、$a,\ b,\ c$の値を求めよ。
(5)Cと(3)で定めたlで囲まれた領域を、x軸の周りに1回転してできる
回転体の体積Vを求めよ。
2022立教大学理学部過去問
この動画を見る
実数xに対し、関数f(x)を
$f(x)=xe^{-x}$
により定める。座標平面上の曲線$C:y=f(x)$に関して、次の問(1)~(5)に答えよ。
(1)f(x)の導関数$f'(x)$を求め、$f(x)$の増減表を書け。ただし、極値も記入すること。
(2)f(x)の第2次導関数$f''(x)$を求め、Cの変曲点の座標を求めよ。
(3)Cの変曲点と、座標平面上の原点を通る直線を$l$とする。
Cとlで囲まれた領域の面積Sを求めよ。
(4)$a,\ b,\ c$を定数とし、関数$g(x)$を$g(x)=(ax^2+bx+c)e^{-2x}$と定める。
$g(x)$の導関数$g'(x)$が$g'(x)=x^2e^{-2x}$を満たすとき、$a,\ b,\ c$の値を求めよ。
(5)Cと(3)で定めたlで囲まれた領域を、x軸の周りに1回転してできる
回転体の体積Vを求めよ。
2022立教大学理学部過去問
答えが出ればいいか!?
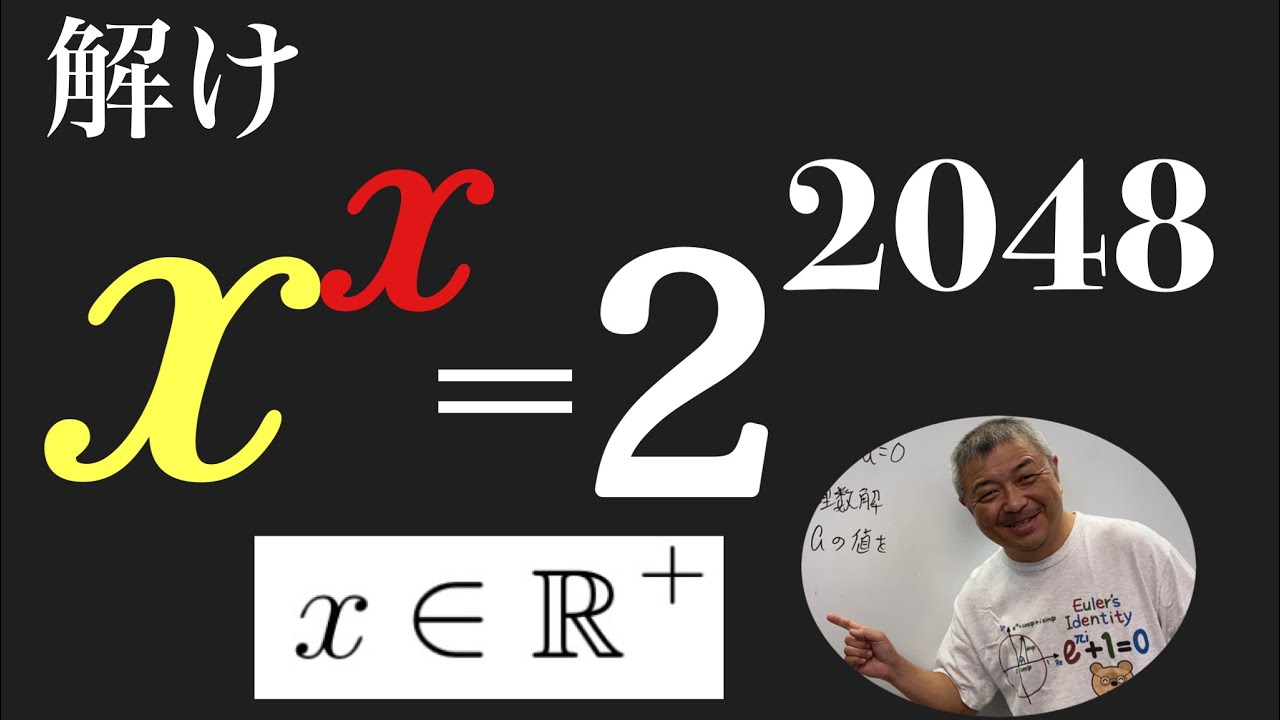
単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x\gt 0$とする.
$x^x=2^{2048}$のxを求めよ.
この動画を見る
$ x\gt 0$とする.
$x^x=2^{2048}$のxを求めよ.
福田の数学〜立教大学2022年理学部第1問(1)〜対数方程式

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(1)$実数$x$に関する方程式
$2\log(1-x)-\log(5-x)=\log 2$
を解くと$x=\boxed{ア}$である.
立教大学2022年理学部過去問
この動画を見る
$\boxed{1}(1)$実数$x$に関する方程式
$2\log(1-x)-\log(5-x)=\log 2$
を解くと$x=\boxed{ア}$である.
立教大学2022年理学部過去問
東大数学科が解説!球の体積の公式を微分すると面積公式になるのはなぜ?

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
球の体積の公式を微分すると面積公式になるのはなぜか解説します
この動画を見る
球の体積の公式を微分すると面積公式になるのはなぜか解説します
福田の数学〜明治大学2022年理工学部第1問(3)〜接線の本数と接点の個数

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#接線と法線・平均値の定理#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(3)$f(x)=(\log x)^2+2\log x+3$として、座標平面上の曲線$y=f(x)$を$C$とする。
ただし、$\log x$は$x$の自然対数を表し、$e$を自然対数の底とする。
$(\textrm{a})$関数$f(x)$は$x=\frac{\boxed{ソ}}{e}$のとき最小値$\boxed{タ}$をとる。
$(\textrm{b})$曲線Cの変曲点の座標は$(\boxed{チ},\ \boxed{ツ})$である。
$(\textrm{c})$直線$y=\boxed{ツ}$と曲線Cで囲まれた図形の面積は
$\frac{\boxed{テ}}{e^2}$である。
$(\textrm{d})a$を実数とする。曲線$C$の接線で、点$(0,\ a)$を通るものがちょうど1本あるとき、
aの値は$\boxed{ト}$である。
$(\textrm{e})b$を実数とする。曲線Cの2本の接線が点$(0,\ b)$で垂直に交わるとき、
bの値は$\frac{\boxed{ナ}}{\boxed{ニ}}$である。
2022明治大学理工学部過去問
この動画を見る
(3)$f(x)=(\log x)^2+2\log x+3$として、座標平面上の曲線$y=f(x)$を$C$とする。
ただし、$\log x$は$x$の自然対数を表し、$e$を自然対数の底とする。
$(\textrm{a})$関数$f(x)$は$x=\frac{\boxed{ソ}}{e}$のとき最小値$\boxed{タ}$をとる。
$(\textrm{b})$曲線Cの変曲点の座標は$(\boxed{チ},\ \boxed{ツ})$である。
$(\textrm{c})$直線$y=\boxed{ツ}$と曲線Cで囲まれた図形の面積は
$\frac{\boxed{テ}}{e^2}$である。
$(\textrm{d})a$を実数とする。曲線$C$の接線で、点$(0,\ a)$を通るものがちょうど1本あるとき、
aの値は$\boxed{ト}$である。
$(\textrm{e})b$を実数とする。曲線Cの2本の接線が点$(0,\ b)$で垂直に交わるとき、
bの値は$\frac{\boxed{ナ}}{\boxed{ニ}}$である。
2022明治大学理工学部過去問
福田の数学〜明治大学2022年全学部統一入試理系第3問〜2次曲線の極方程式と置換積分

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#2次曲線#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#明治大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a,\ h$を正の実数とする。座標平面において、原点Oからの距離が
直線$x=h$からの距離の$a$倍であるような点$P$の軌跡を考える。点$P$の座標を$(x,\ y)$とする
と、$x,\ y$は次の方程式を満たす。
$(1-\boxed{ア})\ x^2+2\ \boxed{イ}\ x+y^2=\boxed{ウ}...(1)$
$\boxed{ア},\ \boxed{イ},\ \boxed{ウ}$の解答群
$⓪a^2 ①h^2 ②a^3 ③a^2h ④ah^2$
$⑤h^3 ⑥b^4 ⑦a^2h^2 ⑧ah^3 ⑨h^4$
次に、座標平面の原点$O$を極、$x$軸の正の部分を始線とする極座標を考える。
点$P$の極座標を$(r\ \theta)$とする。$r \leqq h$を満たすとき、
点$P$の直交座標$(x,\ y)$を$a,\ h,\ θ$を用いて表すと
$(x,\ y)=(\frac{\boxed{エ}}{\boxed{オ}}\ \cos θ,\ \frac{\boxed{エ}}{\boxed{オ}}\ \sin θ)...(2) $
$\boxed{エ},\ \boxed{オ}$の解答群
$⓪h①ah②h^2③ah^2④1+a\cos θ$
$⑤1+a\sin θ ⑥a\cos θ-1⑦a\sin θ-1⑧1-a\cos θ ⑨1-a\sin θ$
(1)から、$a=\boxed{カ}$のとき、点$P$の軌跡は放物線$x=\boxed{キ}\ y^2+\boxed{ク}$となる。
この放物線とy軸で囲まれた図形の面積$S$は
$S=2\int_0^{\boxed{ケ}}xdy=2\int_0^{\boxed{ケ}}(\boxed{キ}\ y^2+\boxed{ク})dy=$
$\frac{\boxed{コ}}{\boxed{サ}}\ h^2$
である。したがって、(2)を利用すれば、置換積分法により次の等式が成り立つことが分かる。
$\int_0^{\frac{\pi}{2}}\frac{\cos θ}{(1+\cos θ)^2}dθ=\frac{\boxed{シ}}{\boxed{ス}}$
$\boxed{キ},\ \boxed{ク},\ \boxed{ケ}$の解答群
$⓪h ①2h ②\frac{h}{2} ③-\frac{h}{2} ④\frac{1}{h}$
$⑤-\frac{1}{h} ⑥\frac{1}{2h} ⑦-\frac{1}{2h} ⑧h^2 ⑨-h^2$
2022明治大学全統理系過去問
この動画を見る
$a,\ h$を正の実数とする。座標平面において、原点Oからの距離が
直線$x=h$からの距離の$a$倍であるような点$P$の軌跡を考える。点$P$の座標を$(x,\ y)$とする
と、$x,\ y$は次の方程式を満たす。
$(1-\boxed{ア})\ x^2+2\ \boxed{イ}\ x+y^2=\boxed{ウ}...(1)$
$\boxed{ア},\ \boxed{イ},\ \boxed{ウ}$の解答群
$⓪a^2 ①h^2 ②a^3 ③a^2h ④ah^2$
$⑤h^3 ⑥b^4 ⑦a^2h^2 ⑧ah^3 ⑨h^4$
次に、座標平面の原点$O$を極、$x$軸の正の部分を始線とする極座標を考える。
点$P$の極座標を$(r\ \theta)$とする。$r \leqq h$を満たすとき、
点$P$の直交座標$(x,\ y)$を$a,\ h,\ θ$を用いて表すと
$(x,\ y)=(\frac{\boxed{エ}}{\boxed{オ}}\ \cos θ,\ \frac{\boxed{エ}}{\boxed{オ}}\ \sin θ)...(2) $
$\boxed{エ},\ \boxed{オ}$の解答群
$⓪h①ah②h^2③ah^2④1+a\cos θ$
$⑤1+a\sin θ ⑥a\cos θ-1⑦a\sin θ-1⑧1-a\cos θ ⑨1-a\sin θ$
(1)から、$a=\boxed{カ}$のとき、点$P$の軌跡は放物線$x=\boxed{キ}\ y^2+\boxed{ク}$となる。
この放物線とy軸で囲まれた図形の面積$S$は
$S=2\int_0^{\boxed{ケ}}xdy=2\int_0^{\boxed{ケ}}(\boxed{キ}\ y^2+\boxed{ク})dy=$
$\frac{\boxed{コ}}{\boxed{サ}}\ h^2$
である。したがって、(2)を利用すれば、置換積分法により次の等式が成り立つことが分かる。
$\int_0^{\frac{\pi}{2}}\frac{\cos θ}{(1+\cos θ)^2}dθ=\frac{\boxed{シ}}{\boxed{ス}}$
$\boxed{キ},\ \boxed{ク},\ \boxed{ケ}$の解答群
$⓪h ①2h ②\frac{h}{2} ③-\frac{h}{2} ④\frac{1}{h}$
$⑤-\frac{1}{h} ⑥\frac{1}{2h} ⑦-\frac{1}{2h} ⑧h^2 ⑨-h^2$
2022明治大学全統理系過去問
福田の数学〜早稲田大学2022年人間科学部第6問〜楕円を軸以外の直線で回転させた立体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#積分とその応用#2次曲線#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{6}}$直線$x+y=1$に接する楕円$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a \gt 0,\ b \gt 0)$がある。
このとき、$b^2=\boxed{\ \ ア\ \ }\ a^2+\boxed{\ \ イ\ \ }$である。
この楕円を直線$y=b$のまわりに1回転してできる立体の体積は、
$a=\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$のとき、
最大値$\frac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}\pi^2$をとる。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{6}}$直線$x+y=1$に接する楕円$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a \gt 0,\ b \gt 0)$がある。
このとき、$b^2=\boxed{\ \ ア\ \ }\ a^2+\boxed{\ \ イ\ \ }$である。
この楕円を直線$y=b$のまわりに1回転してできる立体の体積は、
$a=\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$のとき、
最大値$\frac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}\pi^2$をとる。
2022早稲田大学人間科学部過去問
福田の数学〜早稲田大学2022年人間科学部第2問〜三角不等式の解

単元:
#大学入試過去問(数学)#三角関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}2\sin\theta+\sin2\theta+2\sin3\theta-2\sin2\theta\cos\theta \gt 0\hspace{10pt}(0 \lt \theta \lt \pi)$
を満たす$\theta$の範囲は
$0 \lt \theta \lt \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\ \pi,\ \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\ \pi \lt \theta \lt \pi$
である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{2}}2\sin\theta+\sin2\theta+2\sin3\theta-2\sin2\theta\cos\theta \gt 0\hspace{10pt}(0 \lt \theta \lt \pi)$
を満たす$\theta$の範囲は
$0 \lt \theta \lt \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\ \pi,\ \frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\ \pi \lt \theta \lt \pi$
である。
2022早稲田大学人間科学部過去問
福田の数学〜早稲田大学2022年理工学部第5問〜対数関数の極限と変曲点とグラフの接線

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#微分法#接線と法線・平均値の定理#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{5}}\ a \gt 0$を定数とし、
$f(x)=x^a\log x$とする。以下の問いに答えよ。
(1)$\lim_{x \to +0}f(x)$を求めよ。必要ならば$\lim_{s \to \infty}se^{-s}=0$が成り立つことは
証明なしに用いてよい。
(2)曲線$y=f(x)$の変曲点がx軸上に存在するときのaの値を求めよ。
さらにそのとき$y=f(x)$のグラフの概形を描け。
(3)$t \gt 0$に対して、曲線$y=f(x)$上の点(t,f(t))における接線をlとする。
lがy軸の負の部分と交わるための$(a,t)$の条件を求め、その条件の表す領域を
a-t平面上に図示せよ。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{5}}\ a \gt 0$を定数とし、
$f(x)=x^a\log x$とする。以下の問いに答えよ。
(1)$\lim_{x \to +0}f(x)$を求めよ。必要ならば$\lim_{s \to \infty}se^{-s}=0$が成り立つことは
証明なしに用いてよい。
(2)曲線$y=f(x)$の変曲点がx軸上に存在するときのaの値を求めよ。
さらにそのとき$y=f(x)$のグラフの概形を描け。
(3)$t \gt 0$に対して、曲線$y=f(x)$上の点(t,f(t))における接線をlとする。
lがy軸の負の部分と交わるための$(a,t)$の条件を求め、その条件の表す領域を
a-t平面上に図示せよ。
2022早稲田大学人間科学部過去問
【数Ⅲ】東大の基礎問題!絶対に落としてはいけない!【数学 入試問題】

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
関数
$f(x)=\dfrac{x}{sin x}+cos x$ ($ 0<x<\pi $)
の増減表を作り,$ x→+0,x→\pi-0$のときの極限を調べよ。
東大過去問
この動画を見る
関数
$f(x)=\dfrac{x}{sin x}+cos x$ ($ 0<x<\pi $)
の増減表を作り,$ x→+0,x→\pi-0$のときの極限を調べよ。
東大過去問
大学入試問題#240 防衛医科大学(2020) #曲線の長さ

単元:
#大学入試過去問(数学)#微分とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq t \leqq \pi$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=3\cos\ t-\cos\ 3t \\
y=3\sin\ t-\sin\ 3t
\end{array}
\right.
\end{eqnarray}$
で表される曲線の長さを求めよ。
出典:2020年防衛医科大学 入試問題
この動画を見る
$0 \leqq t \leqq \pi$
$\begin{eqnarray}
\left\{
\begin{array}{l}
x=3\cos\ t-\cos\ 3t \\
y=3\sin\ t-\sin\ 3t
\end{array}
\right.
\end{eqnarray}$
で表される曲線の長さを求めよ。
出典:2020年防衛医科大学 入試問題
福田の数学〜慶應義塾大学2022年商学部第1問(2)〜三角不等式の一般解

単元:
#大学入試過去問(数学)#三角関数#三角関数とグラフ#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)xを変数とする2次方程式$x^2+(2\sqrt2\cos\theta)x+\sqrt2\sin\theta=0$が
異なる2つの実数解をもつような実数$\theta$の範囲は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{1}}$(2)xを変数とする2次方程式$x^2+(2\sqrt2\cos\theta)x+\sqrt2\sin\theta=0$が
異なる2つの実数解をもつような実数$\theta$の範囲は$\boxed{\ \ ア\ \ }$である。
2022慶應義塾大学商学部過去問
阪大の証明問題!解けますか?【数学 入試問題】【大阪大学 理系】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$n$を2以上の自然数とする。三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。$ \angle ACB=n \angle ABC$であるとき,$ c<nb $を示せ。
大阪大理系過去問
この動画を見る
$n$を2以上の自然数とする。三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。$ \angle ACB=n \angle ABC$であるとき,$ c<nb $を示せ。
大阪大理系過去問
阪大の証明問題!ぜひとも取りたい問題【数学 入試問題】【大阪大学 文系】

単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比への応用(正弦・余弦・面積)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。
$\angle ACB=3\angle ABC$であるとき,$c<3b$を示せ。
大阪大過去問
この動画を見る
三角形$ABC$において,辺$AB$の長さを$c$,辺$CA$の長さを$b$で表す。
$\angle ACB=3\angle ABC$であるとき,$c<3b$を示せ。
大阪大過去問
福田の入試問題解説〜慶應義塾大学2022年医学部第4問〜4次関数の増減凹凸と曲線の長さ

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面上の点A(a,b)を1つ固定し、曲線$y=x^2$上の点P$(x,x^2)$と点A
との距離の2乗をg(x)とおく。関数$y=g(x)$のグラフが区間$(-\infty,\infty)$において下に凸
となるための条件は$b \leqq \boxed{\ \ ア\ \ }$となることである。$b \gt \boxed{\ \ ア\ \ }$のとき$y=g(x)$のグラフは
2つの変曲点をもち、そのx座標は$\boxed{\ \ イ\ \ }$及び$\boxed{\ \ ウ\ \ }$である。
ただし$\boxed{\ \ イ\ \ }\lt \boxed{\ \ ウ\ \ }$とする。また、関数$y=g(x)$が極小となるxがただ1つであるために
a,bが満たすべき条件を$b \leqq F(a)$と書くと、$F(a)=\boxed{\ \ エ\ \ }$ である。
$b= F(a)$のとき、関数$y=g(x)$は$x=\boxed{\ \ オ\ \ }$において最小値をとる。
さらに、連立不等式$x \geqq 0,\ y \geqq x^2$が表す領域をDとするとき、
曲線$y=F(x)$のDに含まれる部分の長さLを求めると、$L=\boxed{\ \ カ\ \ }$である。
2022慶應義塾大学医学部過去問
この動画を見る
座標平面上の点A(a,b)を1つ固定し、曲線$y=x^2$上の点P$(x,x^2)$と点A
との距離の2乗をg(x)とおく。関数$y=g(x)$のグラフが区間$(-\infty,\infty)$において下に凸
となるための条件は$b \leqq \boxed{\ \ ア\ \ }$となることである。$b \gt \boxed{\ \ ア\ \ }$のとき$y=g(x)$のグラフは
2つの変曲点をもち、そのx座標は$\boxed{\ \ イ\ \ }$及び$\boxed{\ \ ウ\ \ }$である。
ただし$\boxed{\ \ イ\ \ }\lt \boxed{\ \ ウ\ \ }$とする。また、関数$y=g(x)$が極小となるxがただ1つであるために
a,bが満たすべき条件を$b \leqq F(a)$と書くと、$F(a)=\boxed{\ \ エ\ \ }$ である。
$b= F(a)$のとき、関数$y=g(x)$は$x=\boxed{\ \ オ\ \ }$において最小値をとる。
さらに、連立不等式$x \geqq 0,\ y \geqq x^2$が表す領域をDとするとき、
曲線$y=F(x)$のDに含まれる部分の長さLを求めると、$L=\boxed{\ \ カ\ \ }$である。
2022慶應義塾大学医学部過去問
微分のよく出る問題!解けますか?【数学 入試問題】【東京電機大学】

単元:
#微分とその応用#接線と法線・平均値の定理#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
曲線$y=\dfrac{\log(ax)}{x^2}$の傾きが$9e^2$の接線が原点を通るとき、正の定数$a$を求めよ。
東京電機大過去問
この動画を見る
曲線$y=\dfrac{\log(ax)}{x^2}$の傾きが$9e^2$の接線が原点を通るとき、正の定数$a$を求めよ。
東京電機大過去問
福田の入試問題解説〜慶應義塾大学2022年理工学部第4問〜指数関数と直線の位置関係と極限

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#関数と極限#微分とその応用#関数の極限#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
曲線$C:y=e^x$を考える。
(1)$a,b$を実数とし、$a \geqq 0$とする。曲線Cと直線$y=ax+b$が共有点をもつため
のaとbの条件を求めよ。
(2)正の実数tに対し、C上の点$A(t,e^t)$を中心とし、直線$y=x$に接する円Dを
考える。直線$y=x$と円Dの接点Bのx座標は$\boxed{\ \ タ\ \ }$であり、
円Dの半径は$\boxed{\ \ チ\ \ }$である。線分ABを3:2に内分する点をPとし、Pのx座標、y座標
をそれぞれX(t),Y(t)とする。このとき、等式
$\lim_{t \to \infty}\frac{Y(t)-kX(t)}{\sqrt{\left\{X(t)\right\}^2+\left\{Y(t)\right\}^2}}=0$
が成り立つような実数kを定めると$k=\boxed{\ \ ツ\ \ }$である。
ただし、$\lim_{t \to \infty}te^{-t}=0$である。
2022慶應義塾大学理工学部過去問
この動画を見る
曲線$C:y=e^x$を考える。
(1)$a,b$を実数とし、$a \geqq 0$とする。曲線Cと直線$y=ax+b$が共有点をもつため
のaとbの条件を求めよ。
(2)正の実数tに対し、C上の点$A(t,e^t)$を中心とし、直線$y=x$に接する円Dを
考える。直線$y=x$と円Dの接点Bのx座標は$\boxed{\ \ タ\ \ }$であり、
円Dの半径は$\boxed{\ \ チ\ \ }$である。線分ABを3:2に内分する点をPとし、Pのx座標、y座標
をそれぞれX(t),Y(t)とする。このとき、等式
$\lim_{t \to \infty}\frac{Y(t)-kX(t)}{\sqrt{\left\{X(t)\right\}^2+\left\{Y(t)\right\}^2}}=0$
が成り立つような実数kを定めると$k=\boxed{\ \ ツ\ \ }$である。
ただし、$\lim_{t \to \infty}te^{-t}=0$である。
2022慶應義塾大学理工学部過去問
福田の入試問題解説〜慶應義塾大学2022年理工学部第2問〜連立不等式の表す領域の面積と回転体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$r$を正の実数とし、円$C_1:(x-2)^2+y^2=r^2$、楕円$C_2:\frac{x^2}{9}+y^2=1$を考える。
(1)円$C_1$と楕円$C_2$の共有点が存在するようなrの値の範囲は$\boxed{\ \ カ\ \ } \leqq r \leqq \boxed{\ \ キ\ \ }$である。
(2)$r=1$のとき、$C_1$と$C_2$の共有点の座標を全て求めると$\boxed{\ \ ク\ \ }$である。
これらの共有点のうちy座標が正となる点のy座標を$y_0$とする。連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
0 \leqq y \leqq y_0\\
\end{array}\right.$
の表す領域の面積は$\boxed{\ \ ケ\ \ }$である。
(3)連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
\displaystyle\frac{x^2}{9}+y^2 \geqq 1\\
y \geqq 0\\
\end{array}\right.$
の表す領域をDとする。Dをy軸のまわりに
1回転させてできる立体の体積は$\boxed{\ \ コ\ \ }$である。
2022慶應義塾大学理工学部過去問
この動画を見る
$r$を正の実数とし、円$C_1:(x-2)^2+y^2=r^2$、楕円$C_2:\frac{x^2}{9}+y^2=1$を考える。
(1)円$C_1$と楕円$C_2$の共有点が存在するようなrの値の範囲は$\boxed{\ \ カ\ \ } \leqq r \leqq \boxed{\ \ キ\ \ }$である。
(2)$r=1$のとき、$C_1$と$C_2$の共有点の座標を全て求めると$\boxed{\ \ ク\ \ }$である。
これらの共有点のうちy座標が正となる点のy座標を$y_0$とする。連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
0 \leqq y \leqq y_0\\
\end{array}\right.$
の表す領域の面積は$\boxed{\ \ ケ\ \ }$である。
(3)連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
\displaystyle\frac{x^2}{9}+y^2 \geqq 1\\
y \geqq 0\\
\end{array}\right.$
の表す領域をDとする。Dをy軸のまわりに
1回転させてできる立体の体積は$\boxed{\ \ コ\ \ }$である。
2022慶應義塾大学理工学部過去問
福田の数学〜筑波大学2022年理系第5問〜関数の増減と最大値

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
曲線$C:y=(x+1)e^{-x} (x \gt -1)$上の点Pにおける法線とx軸との交点をQとする。
点Pのx座標をtとし、点Qと点R(t,0)との距離をd(t)とする。
(1) d(t)をtを用いて表せ。
(2) $x \geqq 0$のとき $e^x \geqq 1+x+\frac{x^2}{2}$であることを示せ。
(3) 点Pが曲線C上を動くとき、d(t)の最大値を求めよ。
2022筑波大学理系過去問
この動画を見る
曲線$C:y=(x+1)e^{-x} (x \gt -1)$上の点Pにおける法線とx軸との交点をQとする。
点Pのx座標をtとし、点Qと点R(t,0)との距離をd(t)とする。
(1) d(t)をtを用いて表せ。
(2) $x \geqq 0$のとき $e^x \geqq 1+x+\frac{x^2}{2}$であることを示せ。
(3) 点Pが曲線C上を動くとき、d(t)の最大値を求めよ。
2022筑波大学理系過去問
【数Ⅲ】絶対に落としてはいけない微分!ポイントがぎゅっと詰まった問題【数学 入試問題】

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
関数$ f(x)=x sin(\log x) (1≦x≦e^\pi)$の最大値を求めよ。
数学入試問題過去問
この動画を見る
関数$ f(x)=x sin(\log x) (1≦x≦e^\pi)$の最大値を求めよ。
数学入試問題過去問
【数Ⅲ】うまく式変形できる?【数学 入試問題】

単元:
#大学入試過去問(数学)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$ f(x)=x sin^2x(0≦x≦\pi)$
の最大値を与える$ x$を$a$とするとき、$f(a)$を$a$の分数式で表せ。
横浜市大過去問
この動画を見る
$ f(x)=x sin^2x(0≦x≦\pi)$
の最大値を与える$ x$を$a$とするとき、$f(a)$を$a$の分数式で表せ。
横浜市大過去問
福田の数学〜東京医科歯科大学2022年理系第2問〜放物線に反射する直線の方程式と面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#微分法と積分法#点と直線#円と方程式#微分とその応用#積分とその応用#接線と法線・平均値の定理#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#数Ⅲ#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
$xy$平面上の放物線$P:y^2=4x$上に異なる2点A,Bをとり、A,Bそれぞれに
おいてPへの接線と直交する直線を$n_A,\ n_B$とする。aを正の数として、点Aの座標
を$(a,\ \sqrt{4a})$とするとき、以下の各問いに答えよ。
(1)$\ n_A$の方程式を求めよ。
(2)直線ABと直線$y=\sqrt{4a}$とがなす角の2等分線の一つが、$n_A$に一致する
とき、直線ABの方程式をaを用いて表せ。
(3)(2)のとき、点Bを通る直線$r_B$を考える。$r_B$と直線ABとがなす角の
2等分線の一つが、$n_B$に一致するとき、$r_B$の方程式をaを用いて表せ。
(4)(3)のとき、直線ABと放物線Pで囲まれた図形の面積をS_1とし、Pと直線\\
$y=\sqrt{4a}$、直線$x=-1$および(3)の$r_B$で囲まれた図形の面積を$S_2$とする。
aを変化させたとき、$\frac{S_1}{S_2}$の最大値を求めよ。
2022東京医科歯科大学理系過去問
この動画を見る
$xy$平面上の放物線$P:y^2=4x$上に異なる2点A,Bをとり、A,Bそれぞれに
おいてPへの接線と直交する直線を$n_A,\ n_B$とする。aを正の数として、点Aの座標
を$(a,\ \sqrt{4a})$とするとき、以下の各問いに答えよ。
(1)$\ n_A$の方程式を求めよ。
(2)直線ABと直線$y=\sqrt{4a}$とがなす角の2等分線の一つが、$n_A$に一致する
とき、直線ABの方程式をaを用いて表せ。
(3)(2)のとき、点Bを通る直線$r_B$を考える。$r_B$と直線ABとがなす角の
2等分線の一つが、$n_B$に一致するとき、$r_B$の方程式をaを用いて表せ。
(4)(3)のとき、直線ABと放物線Pで囲まれた図形の面積をS_1とし、Pと直線\\
$y=\sqrt{4a}$、直線$x=-1$および(3)の$r_B$で囲まれた図形の面積を$S_2$とする。
aを変化させたとき、$\frac{S_1}{S_2}$の最大値を求めよ。
2022東京医科歯科大学理系過去問
福田の数学〜千葉大学2022年理系第9問〜関数が常に増加する条件

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
rを正の実数とし、関数
$f(x)=x+\frac{r}{\sqrt{1+\sin^2x}}$
を考える。
(1)$r=1$のとき、f$(x)$は常に増加することを示せ。
(2)次の条件を満たす最大の正の実数cを求めよ。
条件:$0 \lt r \lt c$のときは$f(x)$が常に増加する。
2022千葉大学理系過去問
この動画を見る
rを正の実数とし、関数
$f(x)=x+\frac{r}{\sqrt{1+\sin^2x}}$
を考える。
(1)$r=1$のとき、f$(x)$は常に増加することを示せ。
(2)次の条件を満たす最大の正の実数cを求めよ。
条件:$0 \lt r \lt c$のときは$f(x)$が常に増加する。
2022千葉大学理系過去問
福田の数学〜千葉大学2022年理系第6問〜独立に動く空間上の2点の距離の最小

単元:
#大学入試過去問(数学)#空間ベクトル#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標空間において、原点Oと点A(1,0,-1)と点B(0,5,0)がある。
実数$t$を用いて$t\ \overrightarrow{ OA }+\overrightarrow{ OB }$と表される点全体をlとする。また、平面xy平面上
の$y=x^2$を満たす点全体からなる曲線をCとする。
(1)曲線$C$上の点$P(a,a^2,0)$を固定する。l上の点Qを、$\overrightarrow{ OA }$と$\overrightarrow{ PQ }$
が垂直であるようにとる。このとき、点Qの座標をaを用いて表せ。
(2)曲線C上の点Rとl上の点Sのうち、$|\overrightarrow{ RS }|$を最小にする点Rと点Sの
組み合わせを全て求めよ。また、そのときの$|\overrightarrow{ RS }|$の値を求めよ。
2022千葉大学理系過去問
この動画を見る
座標空間において、原点Oと点A(1,0,-1)と点B(0,5,0)がある。
実数$t$を用いて$t\ \overrightarrow{ OA }+\overrightarrow{ OB }$と表される点全体をlとする。また、平面xy平面上
の$y=x^2$を満たす点全体からなる曲線をCとする。
(1)曲線$C$上の点$P(a,a^2,0)$を固定する。l上の点Qを、$\overrightarrow{ OA }$と$\overrightarrow{ PQ }$
が垂直であるようにとる。このとき、点Qの座標をaを用いて表せ。
(2)曲線C上の点Rとl上の点Sのうち、$|\overrightarrow{ RS }|$を最小にする点Rと点Sの
組み合わせを全て求めよ。また、そのときの$|\overrightarrow{ RS }|$の値を求めよ。
2022千葉大学理系過去問
福田の数学〜九州大学2022年理系第5問の背景を考える〜内サイクロイド曲線(ハイポサイクロイド、アステロイド)の媒介変数表示

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上の曲線#ベクトルと平面図形、ベクトル方程式#微分とその応用#微分法#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#数学(高校生)#九州大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
xy平面上の曲線Cを、媒介変数tを用いて次のように定める。
$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
この動画を見る
xy平面上の曲線Cを、媒介変数tを用いて次のように定める。
$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
福田の数学〜九州大学2022年理系第5問〜媒介変数表示のグラフの対称性とグラフの追跡

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#数学(高校生)#九州大学#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$xy$平面上の曲線Cを、媒介変数tを用いて次のように定める。$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
この動画を見る
$xy$平面上の曲線Cを、媒介変数tを用いて次のように定める。$x=5\cos t+\cos5t, y=5\sin t-\sin5t (-\pi \leqq t \lt \pi)$
以下の問いに答えよ。
(1)区間$0 \lt t \lt \frac{\pi}{6}$において、$\frac{dx}{dt} \lt 0, \frac{dy}{dx} \lt 0$であることを示せ。
(2)曲線Cの$0 \leqq t \leqq \frac{\pi}{6}$の部分、x軸、直線$y=\frac{1}{\sqrt3}x$で囲まれた
図形の面積を求めよ。
(3)曲線Cはx軸に関して対称であることを示せ。また、C上の点を
原点を中心として反時計回りに$\frac{\pi}{3}$だけ回転させた点はC上
にあることを示せ。
(4)曲線Cの概形を図示せよ。
2022九州大学理系過去問
福田の数学〜九州大学2022年理系第4問〜定積分の定義から性質を証明する

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#恒等式・等式・不等式の証明#微分とその応用#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
定積分について述べた次の文章を読んで、後の問いに答えよ。
区間$a \leqq x \leqq b$で連続な関数f(x)に対して$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$\int_a^bf(x)dx=F(b)-F(a) \ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$ a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、$f(x),g(x),h(x)$は区間$a \leqq x \leqq b$で連続な関数、$k,l$は定数である。
以下、$f(x)$を区間$0 \leqq x \leqq 1$で連続な増加関数とし、
nを自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、はさみうちの原理より$\lim_{n \to \infty}S_n=\int_0^1f(x)dx$が成り立つ。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことを、導関数の定義に従って示せ。
また、この等式と定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と平均値の定理を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学理系過去問
この動画を見る
定積分について述べた次の文章を読んで、後の問いに答えよ。
区間$a \leqq x \leqq b$で連続な関数f(x)に対して$F'(x)=f(x)$となる$F(x)$を1つ選び、
$f(x)$のaからbまでの定積分を
$\int_a^bf(x)dx=F(b)-F(a) \ldots①$
で定義する。定積分の値はF(x)の選び方によらずに定まる。
定積分は次の性質(A),(B),(C)をもつ。
(A)$\int_a^b\left\{kf(x)+lg(x)\right\}dx=k\int_a^bf(x)dx+l\int_a^bg(x)dx$
(B)$ a \leqq c \leqq b$のとき、$\int_a^cf(x)dx+\int_c^bf(x)dx=\int_a^bf(x)dx$
(C)区間$a \leqq x \leqq b$において$g(x) \geqq h(x)$ならば、$\int_a^bg(x)dx \geqq \int_a^bh(x)dx$
ただし、$f(x),g(x),h(x)$は区間$a \leqq x \leqq b$で連続な関数、$k,l$は定数である。
以下、$f(x)$を区間$0 \leqq x \leqq 1$で連続な増加関数とし、
nを自然数とする。定積分の性質$\boxed{\ \ ア\ \ }$を用い、定数関数に対する定積分の計算を行うと、
$\frac{1}{n}f(\frac{i-1}{n}) \leqq \int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx \leqq \frac{1}{n}f(\frac{i}{n}) (i = 1,2,\ldots,n) \ldots②$
が成り立つことがわかる。$S_n=\frac{1}{n}\sum_{i=1}^nf(\frac{i-1}{n})$とおくと、
不等式②と定積分の性質$\boxed{\ \ イ\ \ }$より次の不等式が成り立つ。
$0 \leqq \int_0^1f(x)dx-S_n \leqq \frac{f(1)-f(0)}{n} \ldots③$
よって、はさみうちの原理より$\lim_{n \to \infty}S_n=\int_0^1f(x)dx$が成り立つ。
(1)関数F(x),G(x)が微分可能であるとき、$\left\{F(x)+G(x)\right\}'=F'(x)+G'(x)$が
成り立つことを、導関数の定義に従って示せ。
また、この等式と定積分の定義①を用いて、性質(A)で$k=l=1$とした場合の等式
$\int_a^b\left\{f(x)+g(x)\right\}dx=\int_a^bf(x)dx+\int_a^bg(x)dx$ を示せ。
(2)定積分の定義①と平均値の定理を用いて、次を示せ。
$a \lt b$のとき、区間$a \leqq x \leqq b$において$g(x) \gt 0$ならば、$\int_a^bg(x)dx \gt 0$
(3)(A),(B),(C)のうち、空欄$\boxed{\ \ ア\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、文章中の下線部の内容を詳しく説明することで、
不等式②を示せ。
(4)(A),(B),(C)のうち、空欄$\boxed{\ \ イ\ \ }$に入る記号として最もふさわしいものを
1つ選び答えよ。また、不等式③を示せ。
2022九州大学理系過去問
福田の数学〜神戸大学2022年理系第3問〜関数の増減と面積

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
aを実数、$0 \lt a \lt 1$とし、$f(x)=\log(1+x^2)-ax^2$とする。以下の問いに答えよ.
(1)関数f(x)の極値を求めよ。
(2)$f(1)=0$とする。曲線$y=f(x)$とx軸で囲まれた図形の面積を求めよ。
2022神戸大学理系過去問
この動画を見る
aを実数、$0 \lt a \lt 1$とし、$f(x)=\log(1+x^2)-ax^2$とする。以下の問いに答えよ.
(1)関数f(x)の極値を求めよ。
(2)$f(1)=0$とする。曲線$y=f(x)$とx軸で囲まれた図形の面積を求めよ。
2022神戸大学理系過去問
【良問】数IIの知識で解けます【山形大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#点と直線#円と方程式#加法定理とその応用#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
$T=\dfrac{sin\theta cos\theta}{1+sin^2\theta}$とする。
$\theta$が$0<\theta<\dfrac{\pi}{2}$の範囲を動くとき、$T$の最大値を求めよ。
山形大過去問
この動画を見る
$T=\dfrac{sin\theta cos\theta}{1+sin^2\theta}$とする。
$\theta$が$0<\theta<\dfrac{\pi}{2}$の範囲を動くとき、$T$の最大値を求めよ。
山形大過去問
