 積分とその応用
積分とその応用
 積分とその応用
積分とその応用
AkiyaMathさんと学ぶ積分計算Level 3
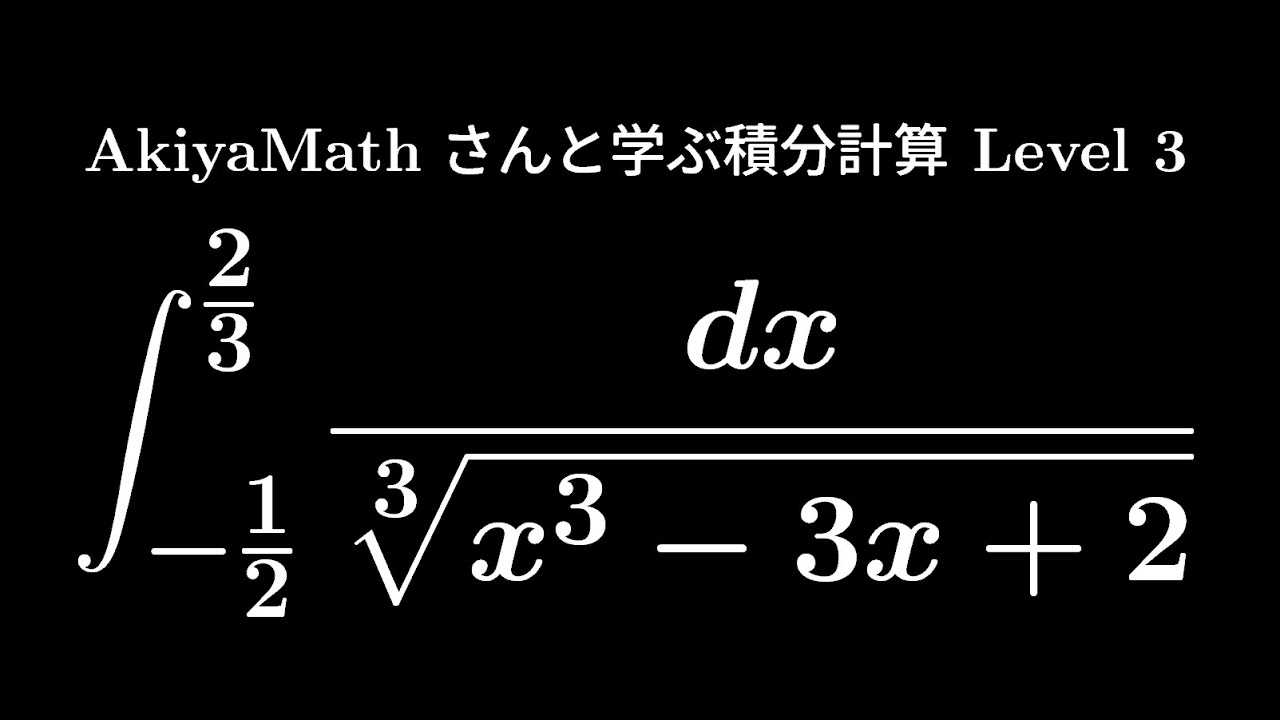
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{1}{2}}^{\frac{2}{3}}\displaystyle \frac{dx}{\sqrt[ 3 ]{ x^3-3x+2 }}$
この動画を見る
$\displaystyle \int_{-\frac{1}{2}}^{\frac{2}{3}}\displaystyle \frac{dx}{\sqrt[ 3 ]{ x^3-3x+2 }}$
福田の数学〜早稲田大学2022年教育学部第1問(2)〜定積分で表された関数

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}\ (2)t \geqq 0$に対して
$f(t)=2\pi\int_0^{2t}|x-t|\cos(2\pi x)dx-t\sin(4\pi t)$
と定義する。このとき、
$f(t)=0$
を満たすtのうち、閉区間[0,1]に属する相異なるものはいくつあるか
早稲田大学教育学部過去問
この動画を見る
${\large\boxed{1}}\ (2)t \geqq 0$に対して
$f(t)=2\pi\int_0^{2t}|x-t|\cos(2\pi x)dx-t\sin(4\pi t)$
と定義する。このとき、
$f(t)=0$
を満たすtのうち、閉区間[0,1]に属する相異なるものはいくつあるか
早稲田大学教育学部過去問
福田の数学〜早稲田大学2022年人間科学部第6問〜楕円を軸以外の直線で回転させた立体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#積分とその応用#2次曲線#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{6}}$直線$x+y=1$に接する楕円$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a \gt 0,\ b \gt 0)$がある。
このとき、$b^2=\boxed{\ \ ア\ \ }\ a^2+\boxed{\ \ イ\ \ }$である。
この楕円を直線$y=b$のまわりに1回転してできる立体の体積は、
$a=\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$のとき、
最大値$\frac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}\pi^2$をとる。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{6}}$直線$x+y=1$に接する楕円$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a \gt 0,\ b \gt 0)$がある。
このとき、$b^2=\boxed{\ \ ア\ \ }\ a^2+\boxed{\ \ イ\ \ }$である。
この楕円を直線$y=b$のまわりに1回転してできる立体の体積は、
$a=\frac{\sqrt{\boxed{\ \ ウ\ \ }}}{\boxed{\ \ エ\ \ }}$のとき、
最大値$\frac{\boxed{\ \ オ\ \ }\sqrt{\boxed{\ \ カ\ \ }}}{\boxed{\ \ キ\ \ }}\pi^2$をとる。
2022早稲田大学人間科学部過去問
AkiyaMathさんと学ぶ積分計算 Level 2 【難】#定積分
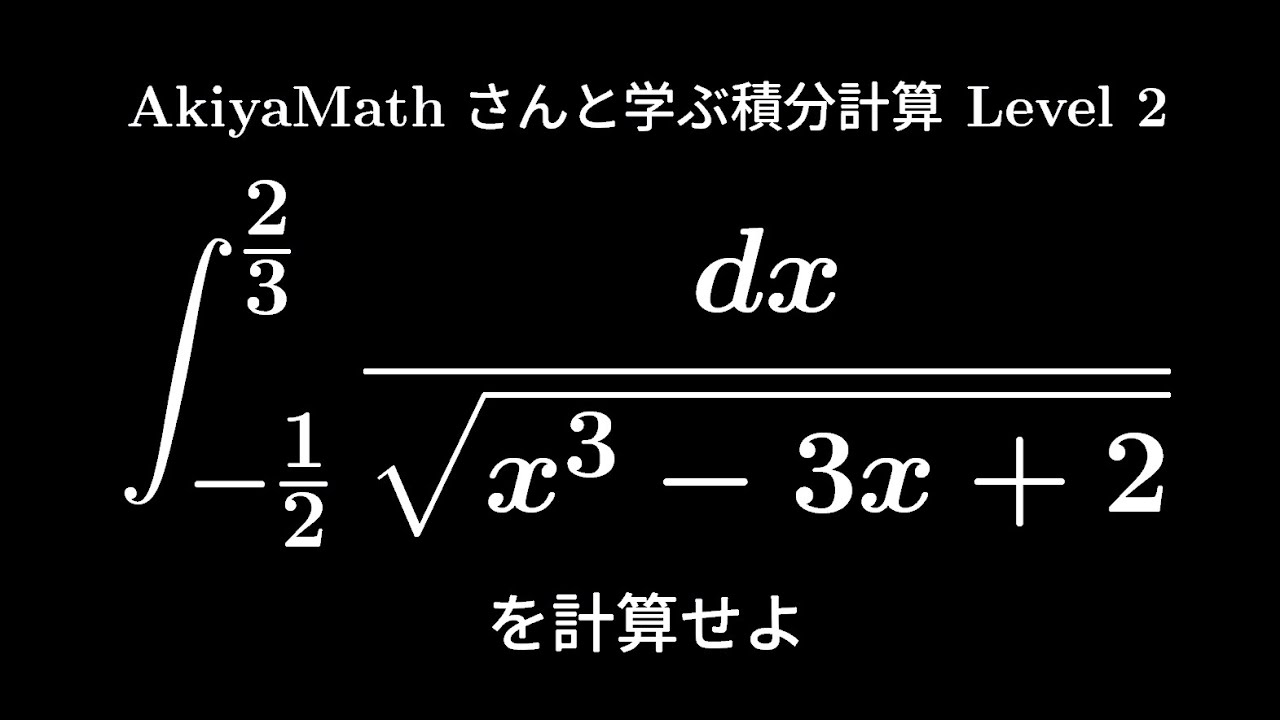
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{1}{2}}^{\frac{2}{3}}\displaystyle \frac{dx}{\sqrt{ x^3-3x+2 }}$を求めよ。
この動画を見る
$\displaystyle \int_{-\frac{1}{2}}^{\frac{2}{3}}\displaystyle \frac{dx}{\sqrt{ x^3-3x+2 }}$を求めよ。
福田の数学〜早稲田大学2022年理工学部第4問〜正八面体の内部に配置した6個の球の和集合の体積と共通部分の体積

単元:
#数A#大学入試過去問(数学)#図形の性質#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{4}}$一辺の長さが$\sqrt3+1$である正八面体の頂点を右図(※動画参照)
のように$P_1,P_2,P_3,P_4,P_5,P_6$とする。$i=1,2,\ldots,6$に対して
$P_i$以外の5点を頂点とする四角錐のすべての面に
内接する球(内部含む)を$B_i$とする。$B_1$の体積をXとし、$B_1$と
$B_2$の共通部分の体積をYとし、$B_1,B_2,B_3$の共通部分の体積をZ
とする。さらに$B_1,B_2,\ldots,B_n$を合わせて得られる立体の体積を
$V_n\ \ (n=2,3,\ldots,6)$とする。以下の問いに答えよ。
(1)$V_n=aX+bY+cZ$となる整数a,b,cを$n=2,3,6$の場合
について求めよ。
(2)Xの値を求めよ。
(3)$V_2$の値を求めよ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{4}}$一辺の長さが$\sqrt3+1$である正八面体の頂点を右図(※動画参照)
のように$P_1,P_2,P_3,P_4,P_5,P_6$とする。$i=1,2,\ldots,6$に対して
$P_i$以外の5点を頂点とする四角錐のすべての面に
内接する球(内部含む)を$B_i$とする。$B_1$の体積をXとし、$B_1$と
$B_2$の共通部分の体積をYとし、$B_1,B_2,B_3$の共通部分の体積をZ
とする。さらに$B_1,B_2,\ldots,B_n$を合わせて得られる立体の体積を
$V_n\ \ (n=2,3,\ldots,6)$とする。以下の問いに答えよ。
(1)$V_n=aX+bY+cZ$となる整数a,b,cを$n=2,3,6$の場合
について求めよ。
(2)Xの値を求めよ。
(3)$V_2$の値を求めよ。
2022早稲田大学理工学部過去問
福田の数学〜早稲田大学2022年理工学部第1問〜2つの指数関数に囲まれた部分の面積と回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}\ f(x)=3e^x-6,g(x)=e^{2x}-4e^x$とおく。
xy平面上の曲線$y=f(x)$をC、曲線$y=g(x)$をDとする。
以下の問いに答えよ。
(1)CとDの概形を一つのxy平面上に描け。
(2)CとDによって囲まれた部分の面積Sを求めよ。
(3)CとDによって囲まれた部分を、x軸の周りに1回転させてできる
立体の体積Vを求めよ。
2022早稲田大学理工学部過去問
この動画を見る
${\large\boxed{1}}\ f(x)=3e^x-6,g(x)=e^{2x}-4e^x$とおく。
xy平面上の曲線$y=f(x)$をC、曲線$y=g(x)$をDとする。
以下の問いに答えよ。
(1)CとDの概形を一つのxy平面上に描け。
(2)CとDによって囲まれた部分の面積Sを求めよ。
(3)CとDによって囲まれた部分を、x軸の周りに1回転させてできる
立体の体積Vを求めよ。
2022早稲田大学理工学部過去問
AkiyaMathさんと学ぶ積分計算 Level 1 #定積分

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{1}{2}}^{\frac{3}{2}}\displaystyle \frac{dx}{x^3-3x+2}$を計算せよ
この動画を見る
$\displaystyle \int_{-\frac{1}{2}}^{\frac{3}{2}}\displaystyle \frac{dx}{x^3-3x+2}$を計算せよ
大学入試問題#254 神戸大学2012 #定積分
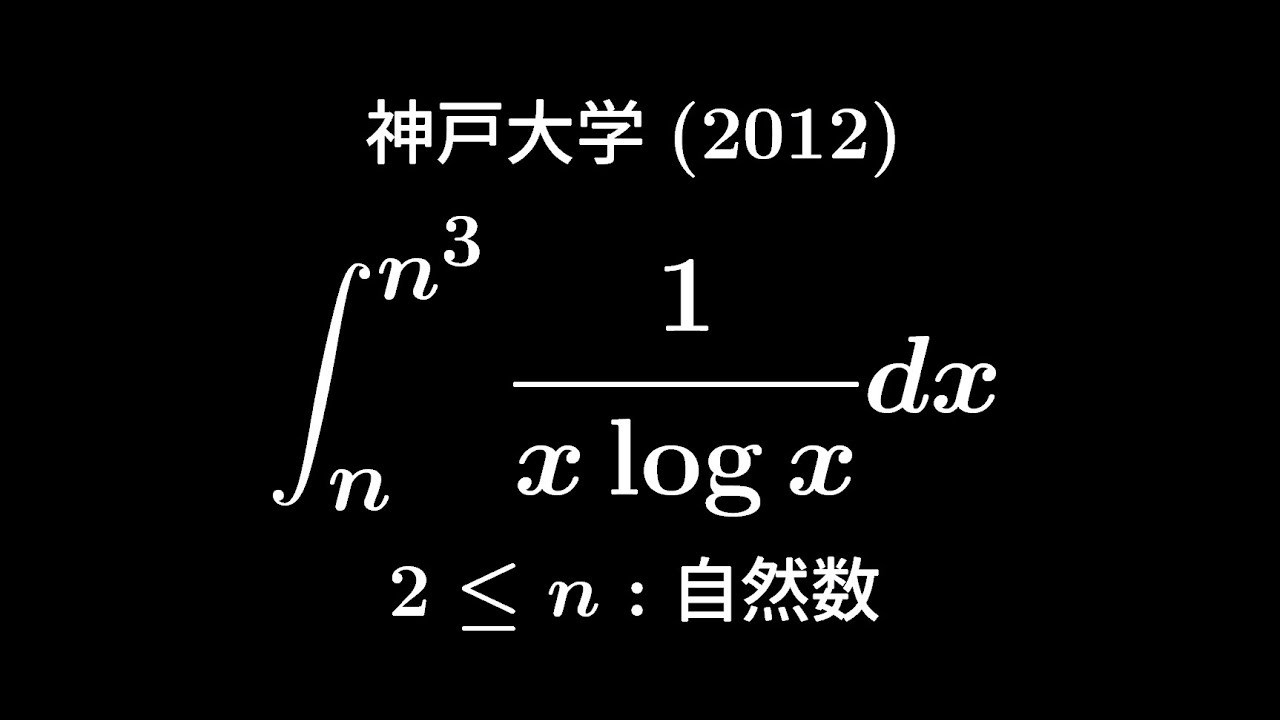
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典:2012年神戸大学 入試問題
この動画を見る
$2 \leqq n$自然数
$\displaystyle \int_{n}^{n^3}\displaystyle \frac{dx}{x\ log\ x}$を計算せよ。
出典:2012年神戸大学 入試問題
大学入試問題#253 青山学院大学(2011) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典:2011年青山学院大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2\pi}x(\sin\ x+\cos\ 2x)dx$を計算せよ。
出典:2011年青山学院大学 入試問題
大学入試問題#252 茨城大学(2012) #定積分

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#対数関数#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{log2}e^{|x|}e^xdx$を計算せよ。
出典:2012年茨城大学 入試問題
大学入試問題#250 福井大学(2012) #定積分
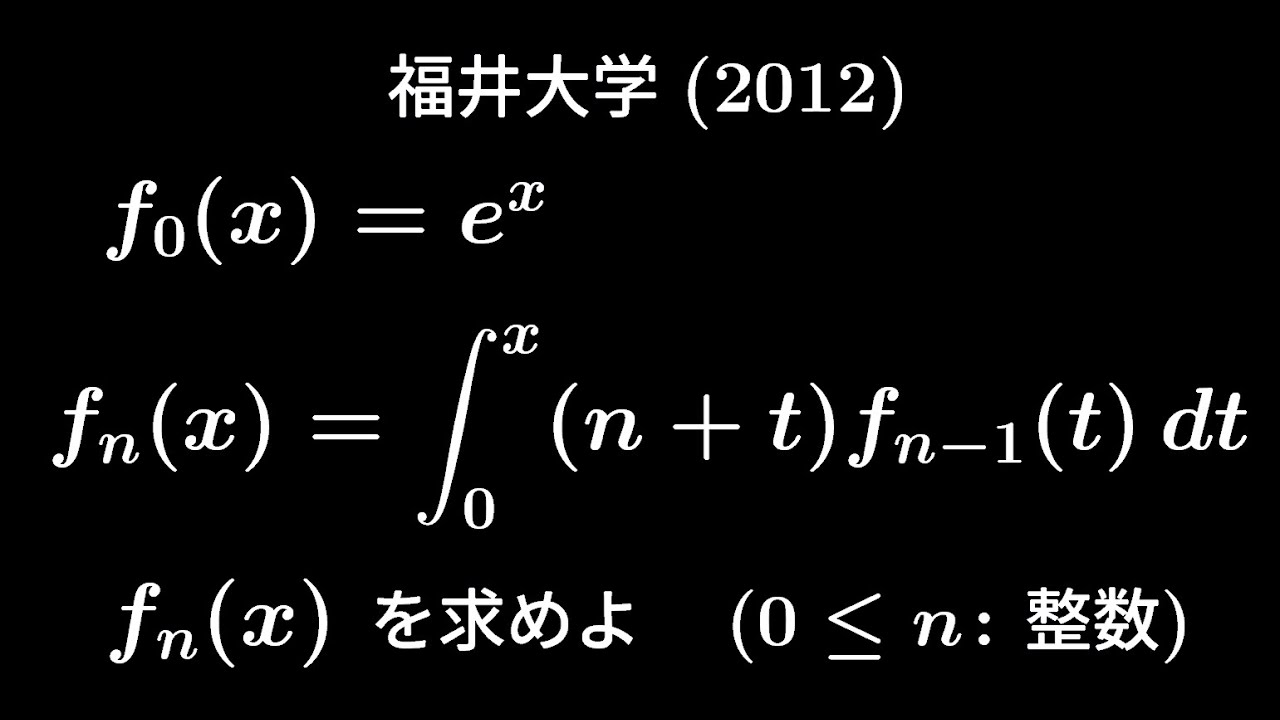
単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#数列#漸化式#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数B#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
この動画を見る
$n$を0以上の整数とする。
次の2つの条件をみたす関数$f_n(x)$を求めよ。
(ⅰ)$f_0(x)=e^x$
(ⅱ)$f_n(x)=\displaystyle \int_{0}^{x}(n+t)f_{n-1}(t)dt$
出典:2012年福井大学 入試問題
大学入試問題#249 早稲田大学(2014) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典:2014年早稲田大学 入試問題
この動画を見る
$a,b$を正の定数
$\displaystyle \int_{0}^{2\pi}|a\ \sin\ x+b\ \cos\ x|dx$を求めよ。
出典:2014年早稲田大学 入試問題
大学入試問題#244 南山大学(2014) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#南山大学
指導講師:
ますただ
問題文全文(内容文):
$a$:正の定数
$\displaystyle \int_{-a}^{a}\displaystyle \frac{|x|e^x}{(1+e^x)^2}dx$を計算せよ
出典:2014年南山大学 入試問題
この動画を見る
$a$:正の定数
$\displaystyle \int_{-a}^{a}\displaystyle \frac{|x|e^x}{(1+e^x)^2}dx$を計算せよ
出典:2014年南山大学 入試問題
大学入試問題#242 神戸大学(2015) 改 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ \sin\ x}{\cos^2x}$dxを計算せよ。
出典:2015年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ \sin\ x}{\cos^2x}$dxを計算せよ。
出典:2015年神戸大学 入試問題
大学入試問題#239 弘前大学(2012) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{3}(x-\displaystyle \frac{1}{x})(log\ x)^2dx$を計算せよ。
出典:2012年
この動画を見る
$\displaystyle \int_{1}^{3}(x-\displaystyle \frac{1}{x})(log\ x)^2dx$を計算せよ。
出典:2012年
【誘導有:概要欄】大学入試問題#238 首都大学東京(2012) #定積分
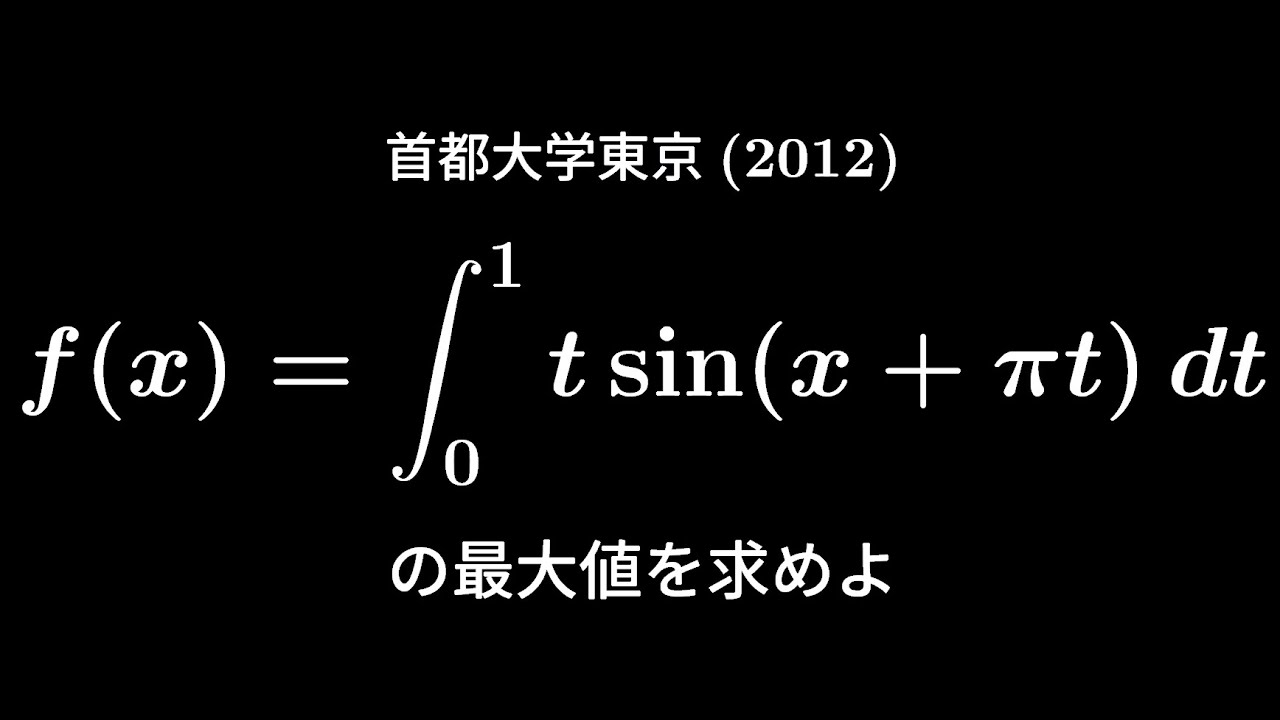
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
実数$x$に対して定積分$f(x)=\displaystyle \int_{0}^{1}t\ \sin(x+\pi t)dt$を求めよ。
(2)
関数$f(x)$の最大値を求めよ。
出典:2012年首都大学東京 入試問題
この動画を見る
(1)
実数$x$に対して定積分$f(x)=\displaystyle \int_{0}^{1}t\ \sin(x+\pi t)dt$を求めよ。
(2)
関数$f(x)$の最大値を求めよ。
出典:2012年首都大学東京 入試問題
大学入試問題#236 茨城大学(2012) 改 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#茨城大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{x^2}(1+\displaystyle \frac{2}{x})^4dx$を計算せよ。
出典:2012年茨城大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{x^2}(1+\displaystyle \frac{2}{x})^4dx$を計算せよ。
出典:2012年茨城大学 入試問題
大学入試問題#234 東京理科大学 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{3}{4}\pi}\sqrt{ 1-\cos\ 4x }\ dx$
出典:2012年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{3}{4}\pi}\sqrt{ 1-\cos\ 4x }\ dx$
出典:2012年東京理科大学 入試問題
大学入試問題#231 電気通信大学(2012) #不定積分

単元:
#大学入試過去問(数学)#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典:2012年電気通信大学 入試問題
この動画を見る
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典:2012年電気通信大学 入試問題
#53 数検1級1次 過去問 #微分方程式

単元:
#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dx}{dt}=2x+4y ・・・① \\
\displaystyle \frac{dy}{dt}=x-y ・・・②
\end{array}
\right.
\end{eqnarray}$
$x(0)=3,\ y(0=-1)$を満たす解を求めよ。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{dx}{dt}=2x+4y ・・・① \\
\displaystyle \frac{dy}{dt}=x-y ・・・②
\end{array}
\right.
\end{eqnarray}$
$x(0)=3,\ y(0=-1)$を満たす解を求めよ。
#52 数検1級1次試験 過去問 #微分方程式

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x\displaystyle \frac{dy}{dx}+y=(log\ x)^2$
$y(1)=1$をみたす解を$y=y(x)$で表せ
この動画を見る
$x\displaystyle \frac{dy}{dx}+y=(log\ x)^2$
$y(1)=1$をみたす解を$y=y(x)$で表せ
大学入試問題#230 首都大学東京(2020) #定積分

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{1}{(x^2+1)^3}dx$
出典:2020年首都大学東京 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{1}{(x^2+1)^3}dx$
出典:2020年首都大学東京 入試問題
大学入試問題#226 信州大学(2012) #不定積分
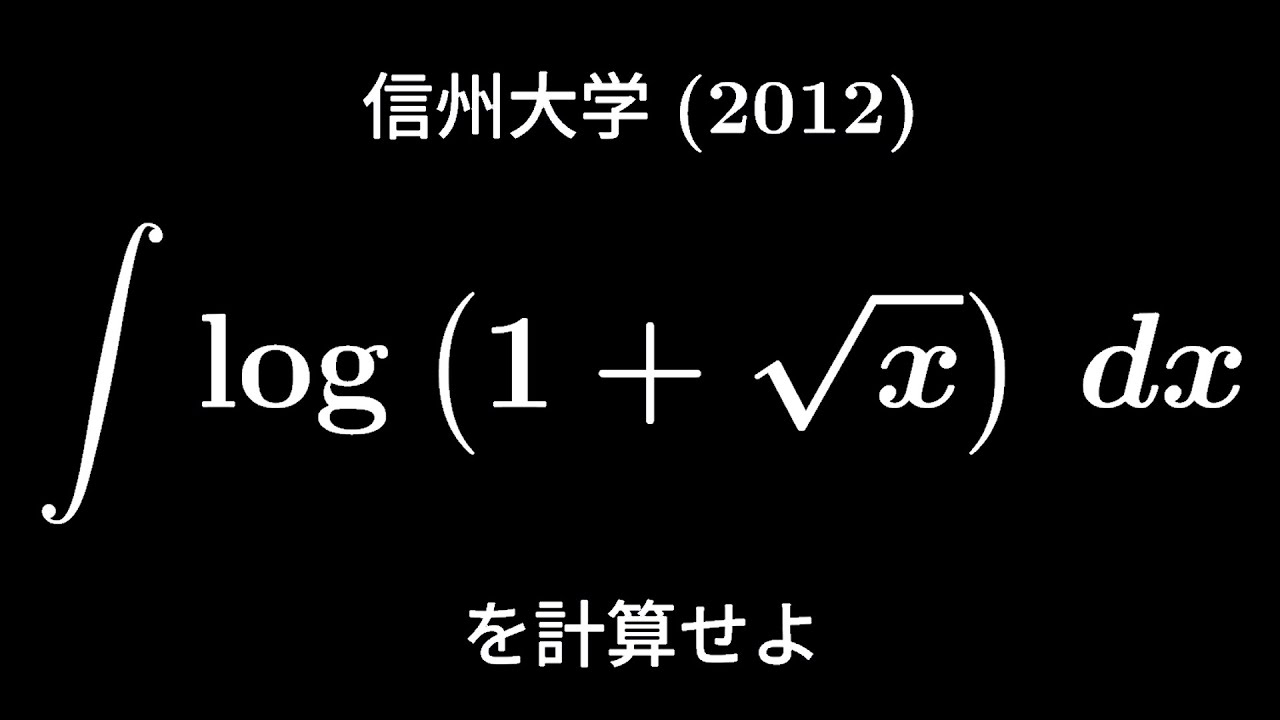
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int log(1+\sqrt{ x })dx$を計算せよ
出典:2012年信州大学 入試問題
この動画を見る
$\displaystyle \int log(1+\sqrt{ x })dx$を計算せよ
出典:2012年信州大学 入試問題
大学入試問題#225 埼玉大学 #定積分
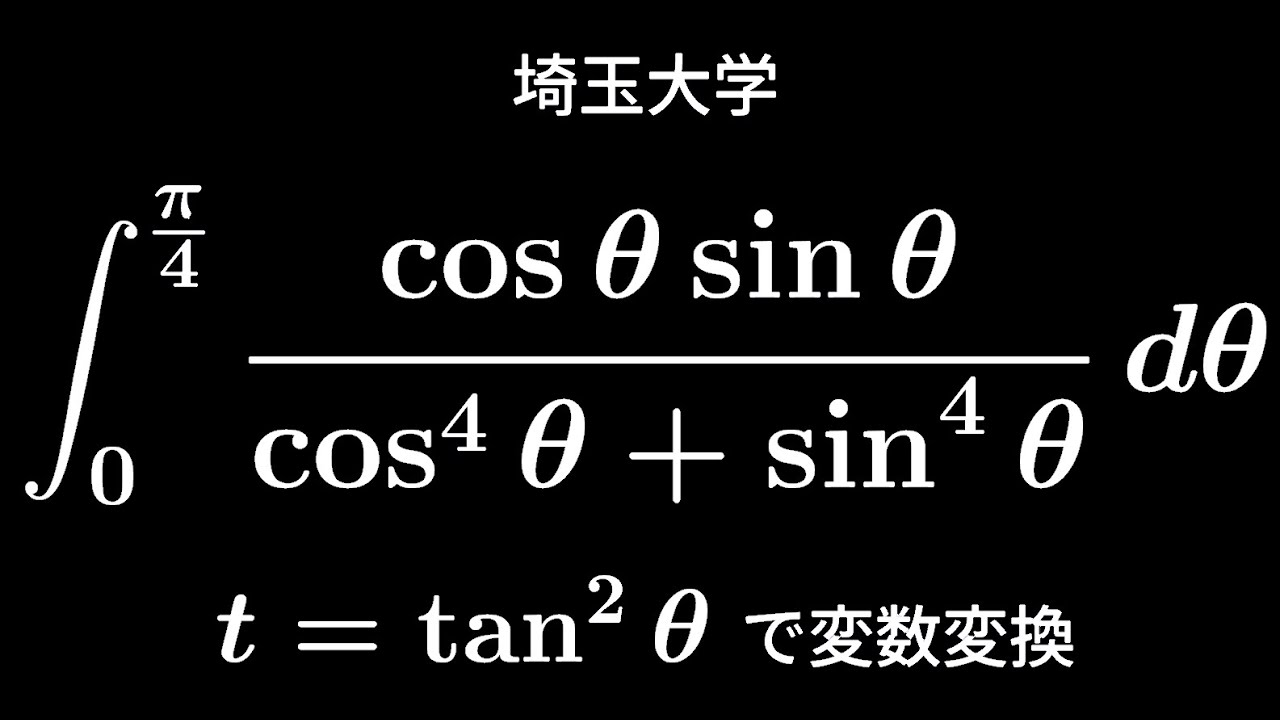
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{\cos\theta\sin\theta}{\cos^4\theta+\sin^4\theta}d\theta$
$t=\tan^2\theta$で変数変換
出典:埼玉大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{\cos\theta\sin\theta}{\cos^4\theta+\sin^4\theta}d\theta$
$t=\tan^2\theta$で変数変換
出典:埼玉大学 入試問題
大学入試問題#224 防衛医科大学(2015) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$を計算せよ
出典:2015年防衛医科大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$を計算せよ
出典:2015年防衛医科大学 入試問題
福田の入試問題解説〜慶應義塾大学2022年理工学部第2問〜連立不等式の表す領域の面積と回転体の体積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$r$を正の実数とし、円$C_1:(x-2)^2+y^2=r^2$、楕円$C_2:\frac{x^2}{9}+y^2=1$を考える。
(1)円$C_1$と楕円$C_2$の共有点が存在するようなrの値の範囲は$\boxed{\ \ カ\ \ } \leqq r \leqq \boxed{\ \ キ\ \ }$である。
(2)$r=1$のとき、$C_1$と$C_2$の共有点の座標を全て求めると$\boxed{\ \ ク\ \ }$である。
これらの共有点のうちy座標が正となる点のy座標を$y_0$とする。連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
0 \leqq y \leqq y_0\\
\end{array}\right.$
の表す領域の面積は$\boxed{\ \ ケ\ \ }$である。
(3)連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
\displaystyle\frac{x^2}{9}+y^2 \geqq 1\\
y \geqq 0\\
\end{array}\right.$
の表す領域をDとする。Dをy軸のまわりに
1回転させてできる立体の体積は$\boxed{\ \ コ\ \ }$である。
2022慶應義塾大学理工学部過去問
この動画を見る
$r$を正の実数とし、円$C_1:(x-2)^2+y^2=r^2$、楕円$C_2:\frac{x^2}{9}+y^2=1$を考える。
(1)円$C_1$と楕円$C_2$の共有点が存在するようなrの値の範囲は$\boxed{\ \ カ\ \ } \leqq r \leqq \boxed{\ \ キ\ \ }$である。
(2)$r=1$のとき、$C_1$と$C_2$の共有点の座標を全て求めると$\boxed{\ \ ク\ \ }$である。
これらの共有点のうちy座標が正となる点のy座標を$y_0$とする。連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
0 \leqq y \leqq y_0\\
\end{array}\right.$
の表す領域の面積は$\boxed{\ \ ケ\ \ }$である。
(3)連立不等式
$\left\{\begin{array}{1}
(x-2)^2+y^2 \leqq 1\\
\displaystyle\frac{x^2}{9}+y^2 \geqq 1\\
y \geqq 0\\
\end{array}\right.$
の表す領域をDとする。Dをy軸のまわりに
1回転させてできる立体の体積は$\boxed{\ \ コ\ \ }$である。
2022慶應義塾大学理工学部過去問
大学入試問題#223 宮崎大学(2015) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}\ dx$
出典:2015年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}\ dx$
出典:2015年宮崎大学 入試問題
大学入試問題#222 広島市立大学2015 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$を計算せよ
出典:2015年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$を計算せよ
出典:2015年広島市立大学 入試問題
大学入試問題#221 横浜国立大学(2015) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$を計算せよ
出典:2015年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$を計算せよ
出典:2015年横浜国立大学 入試問題
大学入試問題#220 東海大学医学部【再投稿】 #定積分 #King property

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東海大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi}x(\cos^2x)(\sin\ x)dx$
出典:東海大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi}x(\cos^2x)(\sin\ x)dx$
出典:東海大学医学部 入試問題
