 積分とその応用
積分とその応用
 積分とその応用
積分とその応用
福田の数学〜名古屋大学2022年理系第4問〜定積分の極限と方程式の解

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数f(x)は区間$x \geqq 0$において連続な増加関数で$f(0)=1$を満たすとする。
ただしf(x)が区間$x \geqq 0$における増加関数であるとは、区間内の任意の実数$x_1,x_2$に対し
$x_1 \lt x_2$ならば$f(x_1) \lt f(x_2)$が成り立つ時をいう。以下、nは正の整数とする。
(1)$\lim_{n \to \infty}\int_0^{2-\frac{1}{n}}\frac{f(x)}{2-x}dx=\infty$ を示せ。
(2)区間$y \gt 2$ において関数$F_n(y)$を$F_n(y)=\int_{2+\frac{1}{n}}^y\frac{f(x)}{2-x}dx$と定めるとき、
$\lim_{y \to \infty}F_n(y)=\infty$を示せ。また$2+\frac{1}{n}$より大きい実数$a_n$で
$\int_0^{2-\frac{1}{n}}\frac{f(x)}{2-x}dx+\int_{{2+\frac{1}{n}}}^{a_n}\frac{f(x)}{2-x}dx=0$
を満たすものがただ1つ存在することを示せ。
(3)(2)の$a_n$について、不等式$a_n \lt 4$がすべてのnに対して成り立つことを示せ。
2022名古屋大学理系過去問
この動画を見る
関数f(x)は区間$x \geqq 0$において連続な増加関数で$f(0)=1$を満たすとする。
ただしf(x)が区間$x \geqq 0$における増加関数であるとは、区間内の任意の実数$x_1,x_2$に対し
$x_1 \lt x_2$ならば$f(x_1) \lt f(x_2)$が成り立つ時をいう。以下、nは正の整数とする。
(1)$\lim_{n \to \infty}\int_0^{2-\frac{1}{n}}\frac{f(x)}{2-x}dx=\infty$ を示せ。
(2)区間$y \gt 2$ において関数$F_n(y)$を$F_n(y)=\int_{2+\frac{1}{n}}^y\frac{f(x)}{2-x}dx$と定めるとき、
$\lim_{y \to \infty}F_n(y)=\infty$を示せ。また$2+\frac{1}{n}$より大きい実数$a_n$で
$\int_0^{2-\frac{1}{n}}\frac{f(x)}{2-x}dx+\int_{{2+\frac{1}{n}}}^{a_n}\frac{f(x)}{2-x}dx=0$
を満たすものがただ1つ存在することを示せ。
(3)(2)の$a_n$について、不等式$a_n \lt 4$がすべてのnに対して成り立つことを示せ。
2022名古屋大学理系過去問
大学入試問題#166 東京大学 改 (2022) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\cos\ x\ log(\cos\ x)dx$を求めよ。
出典:2022年東京大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\cos\ x\ log(\cos\ x)dx$を求めよ。
出典:2022年東京大学 入試問題
大学入試問題#165 神戸大学(2021) ウォリス積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}x^2\sqrt{ 1-x^2 }\ dx$を求めよ。
(ウォリス積分)
出典:2021年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^2\sqrt{ 1-x^2 }\ dx$を求めよ。
(ウォリス積分)
出典:2021年神戸大学 入試問題
大学入試問題#163 信州大学(2004) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2}\displaystyle \frac{log\ x}{x^3}\ dx$
出典:2004年信州大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2}\displaystyle \frac{log\ x}{x^3}\ dx$
出典:2004年信州大学 入試問題
大学入試問題#161 大阪市立大学(1999) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}(\displaystyle \frac{x\ \sin\ x}{1+\cos\ x}+\displaystyle \frac{x\ \cos\ x}{1+\sin\ x})dx$を計算せよ。
出典:1999年大阪市立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}(\displaystyle \frac{x\ \sin\ x}{1+\cos\ x}+\displaystyle \frac{x\ \cos\ x}{1+\sin\ x})dx$を計算せよ。
出典:1999年大阪市立大学 入試問題
福田の数学〜東京工業大学2022年理系第5問〜定積分と不等式と区分求積

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
aは$0 \lt a \leqq \frac{\pi}{4}$を満たす実数とし、
$f(x)=\frac{4}{3}\sin(\frac{\pi}{4}+ax)\cos(\frac{\pi}{4}-ax)$
とする。このとき、次の問いに答えよ。
(1)次の等式(*)を満たすaがただ1つ存在することを示せ。
(*) $\int_0^1f(x)dx=1$
(2)$0 \leqq b \lt c \leqq 1$を満たす実数b,cについて、不等式
$f(b)(c-b) \leqq \int_b^cf(x)dx \leqq f(c)(c-b)$
が成り立つことを示せ。
(3)次の試行を考える。\\
[試行]n個の数$1,2,\ldots\ldots,n$を出目とする、あるルーレットをk回まわす。
この試行において、各$i=1,2,\ldots\ldots,n$についてiが出た回数を$S_{n,k,i}$とし、
(**)$\lim_{k \to \infty}\frac{S_{n,k,i}}{k}=\int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx$
が成り立つとする。このとき、(1)の等式(*)が成り立つことを示せ。
(4)(3)の[試行]において出た数の平均値を$A_{n,k}$とし、$A_n=\lim_{k \to \infty}A_{n,k}$とする。
(**)が成り立つとき、極限$\lim_{n \to \infty}\frac{A_n}{n}$をaを用いて表せ。
2022東京工業大学理系過去問
この動画を見る
aは$0 \lt a \leqq \frac{\pi}{4}$を満たす実数とし、
$f(x)=\frac{4}{3}\sin(\frac{\pi}{4}+ax)\cos(\frac{\pi}{4}-ax)$
とする。このとき、次の問いに答えよ。
(1)次の等式(*)を満たすaがただ1つ存在することを示せ。
(*) $\int_0^1f(x)dx=1$
(2)$0 \leqq b \lt c \leqq 1$を満たす実数b,cについて、不等式
$f(b)(c-b) \leqq \int_b^cf(x)dx \leqq f(c)(c-b)$
が成り立つことを示せ。
(3)次の試行を考える。\\
[試行]n個の数$1,2,\ldots\ldots,n$を出目とする、あるルーレットをk回まわす。
この試行において、各$i=1,2,\ldots\ldots,n$についてiが出た回数を$S_{n,k,i}$とし、
(**)$\lim_{k \to \infty}\frac{S_{n,k,i}}{k}=\int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx$
が成り立つとする。このとき、(1)の等式(*)が成り立つことを示せ。
(4)(3)の[試行]において出た数の平均値を$A_{n,k}$とし、$A_n=\lim_{k \to \infty}A_{n,k}$とする。
(**)が成り立つとき、極限$\lim_{n \to \infty}\frac{A_n}{n}$をaを用いて表せ。
2022東京工業大学理系過去問
大学入試問題#159 横浜国立大学 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{4}\displaystyle \frac{dx}{\sqrt{ 3-\sqrt{ x } }}$を計算せよ
出典:横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{4}\displaystyle \frac{dx}{\sqrt{ 3-\sqrt{ x } }}$を計算せよ
出典:横浜国立大学 入試問題
大学入試問題#157 旭川医科大学(2014) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}log(1+x^2)dx$を求めよ。
出典:2014年旭川医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}log(1+x^2)dx$を求めよ。
出典:2014年旭川医科大学 入試問題
大学入試問題#156 昭和大学(2019) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#昭和大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2}\displaystyle \frac{dx}{x^2-2x+2}$を求めよ。
出典:2019年昭和大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2}\displaystyle \frac{dx}{x^2-2x+2}$を求めよ。
出典:2019年昭和大学 入試問題
大学入試問題#154 横浜市立大学医学部(2017) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{\cos\ 2x}\ dx$を求めよ。
出典:2017年横浜市立大学医学部 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{\cos\ 2x}\ dx$を求めよ。
出典:2017年横浜市立大学医学部 入試問題
大学入試問題#153 東京医科大学(2017) 微積の応用

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科大学#東京医科大学
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$
$f(x)=\displaystyle \int_{1}^{x}\displaystyle \frac{x+4t}{\sqrt{ 3x^4+t^4 }}\ dt$において$f'(x)$を求めよ。
出典:2017年東京医科大学 入試問題
この動画を見る
$x \gt 0$
$f(x)=\displaystyle \int_{1}^{x}\displaystyle \frac{x+4t}{\sqrt{ 3x^4+t^4 }}\ dt$において$f'(x)$を求めよ。
出典:2017年東京医科大学 入試問題
福田の数学・入試問題解説〜東北大学2022年理系第6問〜円柱と球の共通部分の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
半径1の円を底面とする高さが$\sqrt3$の直円柱と、半径がrの球を考える。
直円柱の底面の中心と球の中心が一致するとき、直円柱の内部と球の内部の
共通部分の体積V(r)を求めよ。
2022東北大学理系過去問
この動画を見る
半径1の円を底面とする高さが$\sqrt3$の直円柱と、半径がrの球を考える。
直円柱の底面の中心と球の中心が一致するとき、直円柱の内部と球の内部の
共通部分の体積V(r)を求めよ。
2022東北大学理系過去問
大学入試問題#151 東北大学2020 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{(1+x^2)^3}$を計算せよ。
出典:2020年東北大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{(1+x^2)^3}$を計算せよ。
出典:2020年東北大学 入試問題
大学入試問題#150 京都大学(1991) 積分の応用

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$a$実数
$e^x \geqq e^a+(x-1)e^a$を示せ
(2)
$\displaystyle \int_{0}^{1}e^{\sin\ \pi\ x}dx \geqq e^{\frac{2}{x}}$を示せ
出典:1991年京都大学 入試問題
この動画を見る
(1)
$a$実数
$e^x \geqq e^a+(x-1)e^a$を示せ
(2)
$\displaystyle \int_{0}^{1}e^{\sin\ \pi\ x}dx \geqq e^{\frac{2}{x}}$を示せ
出典:1991年京都大学 入試問題
大学入試問題#149 岩手大学(2019) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{3}\displaystyle \frac{x}{(4-x)^3}\ dx$を計算せよ。
出典:2019年岩手大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{3}\displaystyle \frac{x}{(4-x)^3}\ dx$を計算せよ。
出典:2019年岩手大学 入試問題
大学入試問題#148 京都大学(1972) 積分と極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$
$F(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{t}{(t+1)(t+3)}dt$のとき
$\displaystyle \lim_{ x \to \infty }(F(x)-log\ x)$を求めよ。
出典:1972年京都大学 入試問題
この動画を見る
$x \gt 0$
$F(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{t}{(t+1)(t+3)}dt$のとき
$\displaystyle \lim_{ x \to \infty }(F(x)-log\ x)$を求めよ。
出典:1972年京都大学 入試問題
大学入試問題#147 三重大学(2020) 積分の応用

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#三重大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$x \geqq 1$のとき
$x \geqq 1+log\ x$を示せ
(2)
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{1+log\ x}dx \geqq \displaystyle \frac{1}{2}$を示せ
出典:2020年三重大学 入試問題
この動画を見る
(1)
$x \geqq 1$のとき
$x \geqq 1+log\ x$を示せ
(2)
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{1+log\ x}dx \geqq \displaystyle \frac{1}{2}$を示せ
出典:2020年三重大学 入試問題
大学入試問題#146 東京工業大学(1966) 定積分
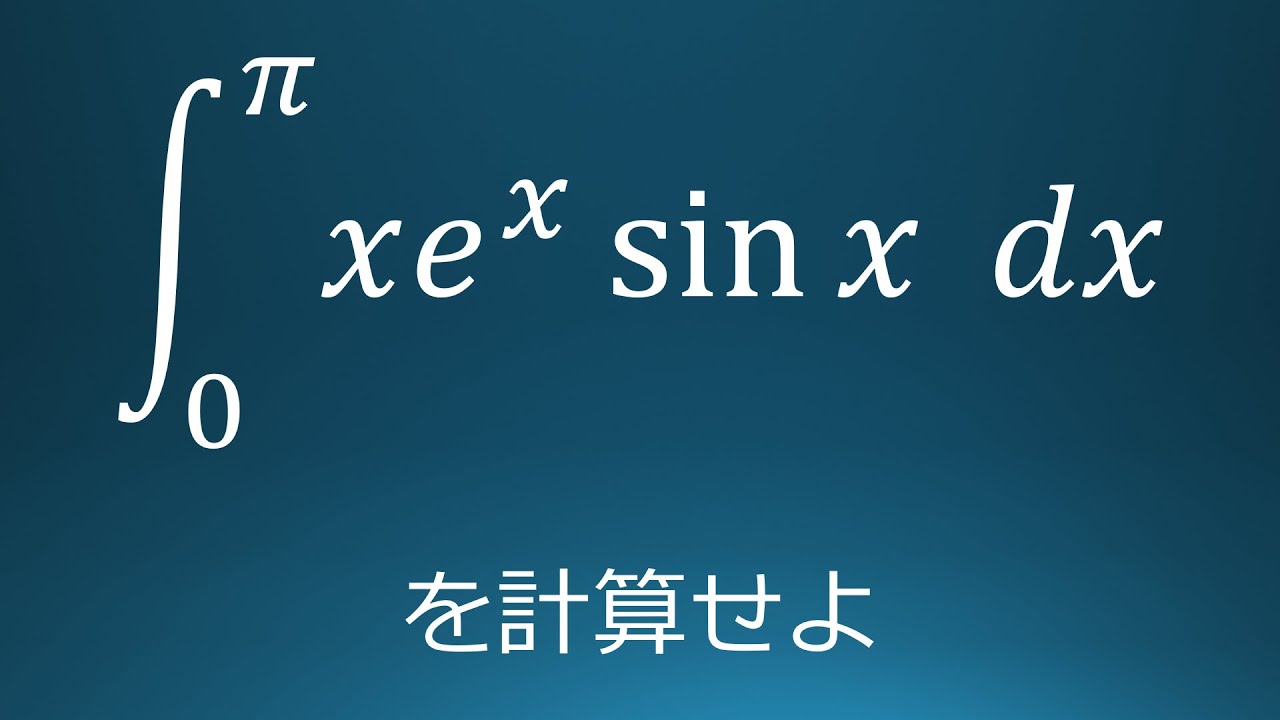
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi}xe^x\sin\ x\ dx$を計算せよ。
出典:1966年東京工業大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi}xe^x\sin\ x\ dx$を計算せよ。
出典:1966年東京工業大学 入試問題
大学入試問題#144 東京理科大学(2006) 定積分
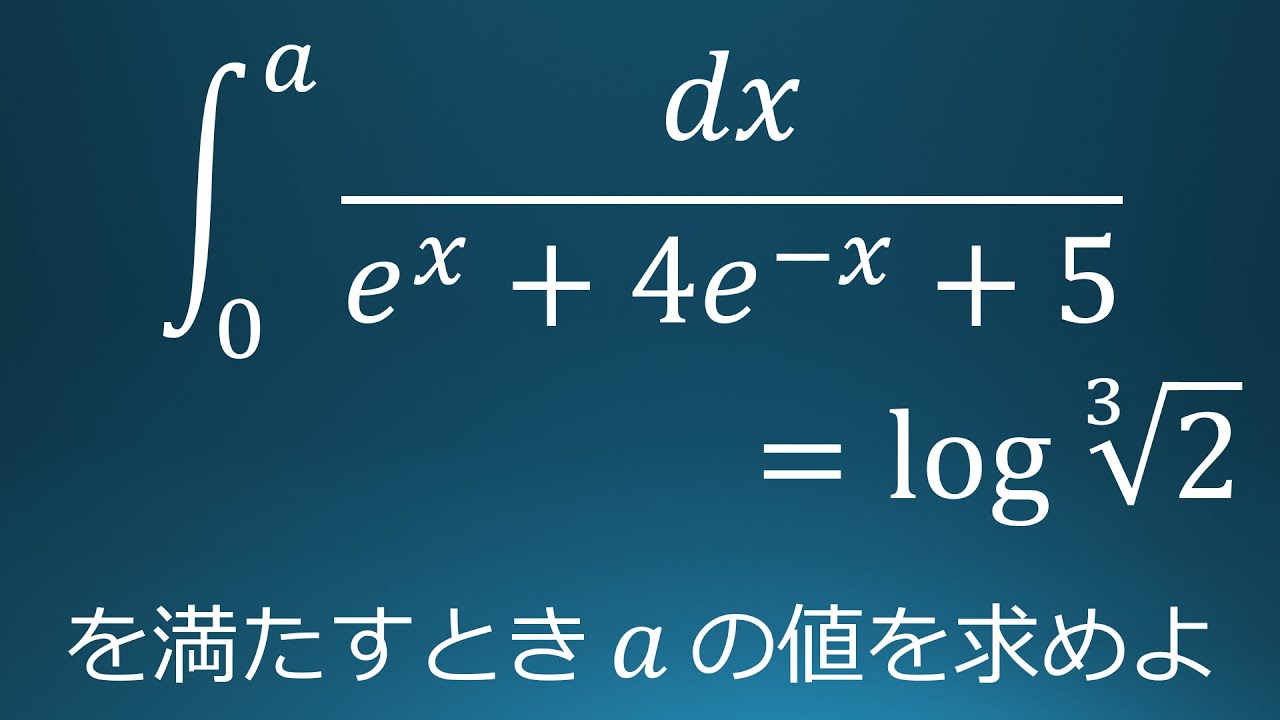
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{a}\displaystyle \frac{dx}{e^x+4e^{-x}+5}=log\sqrt[ 3 ]{ 2 }$が成り立つとき$a$の値を求めよ。
出典:2006年東京理科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{a}\displaystyle \frac{dx}{e^x+4e^{-x}+5}=log\sqrt[ 3 ]{ 2 }$が成り立つとき$a$の値を求めよ。
出典:2006年東京理科大学 入試問題
大学入試問題#142 広島市立大学(2014) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \cos\sqrt{ x }\ dx$を計算せよ。
出典:2014年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \cos\sqrt{ x }\ dx$を計算せよ。
出典:2014年広島市立大学 入試問題
大学入試問題#140 横浜市立大学医学部(2008) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-2}^{2}x^4\sqrt{ 4-x^2 }\ dx$を計算せよ。
出典:2008年横浜市立大学医学部 入試問題
この動画を見る
$\displaystyle \int_{-2}^{2}x^4\sqrt{ 4-x^2 }\ dx$を計算せよ。
出典:2008年横浜市立大学医学部 入試問題
大学入試問題#139 佐賀大学(2014) 定積分
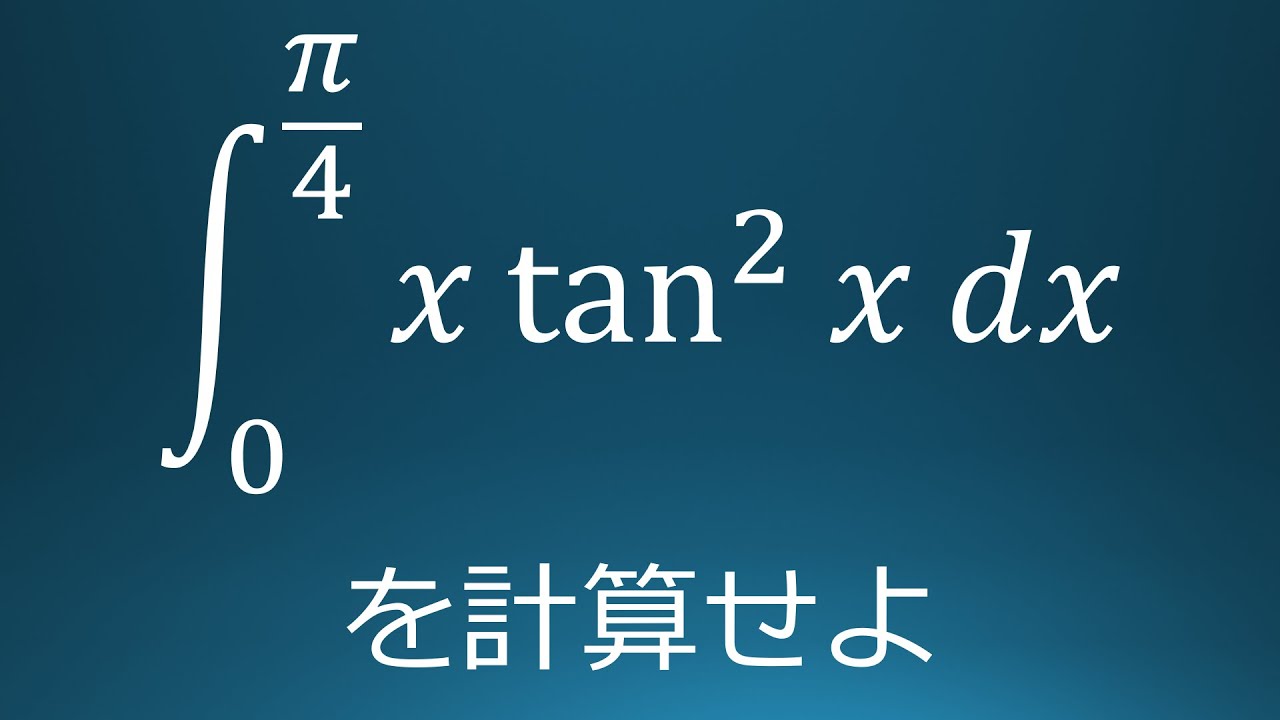
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}x\ \tan^2x\ dx$を計算せよ。
出典:2014年佐賀大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}x\ \tan^2x\ dx$を計算せよ。
出典:2014年佐賀大学 入試問題
大学入試問題#138 静岡県立大学(2021) 定積分
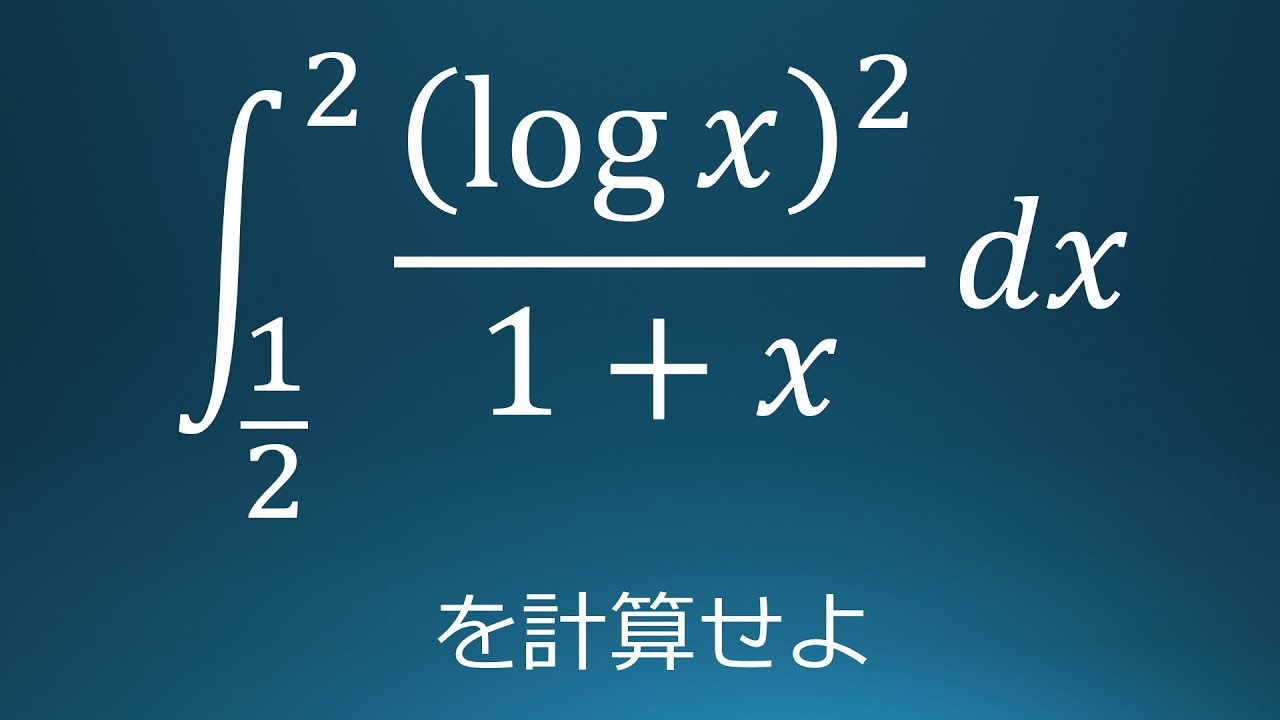
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{1}{2}}^{2}\displaystyle \frac{(log\ x)^2}{1+x}\ dx$を計算せよ。
出典:2019年静岡県立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{1}{2}}^{2}\displaystyle \frac{(log\ x)^2}{1+x}\ dx$を計算せよ。
出典:2019年静岡県立大学 入試問題
大学入試問題#137 京都大学(2021) 曲線の長さ
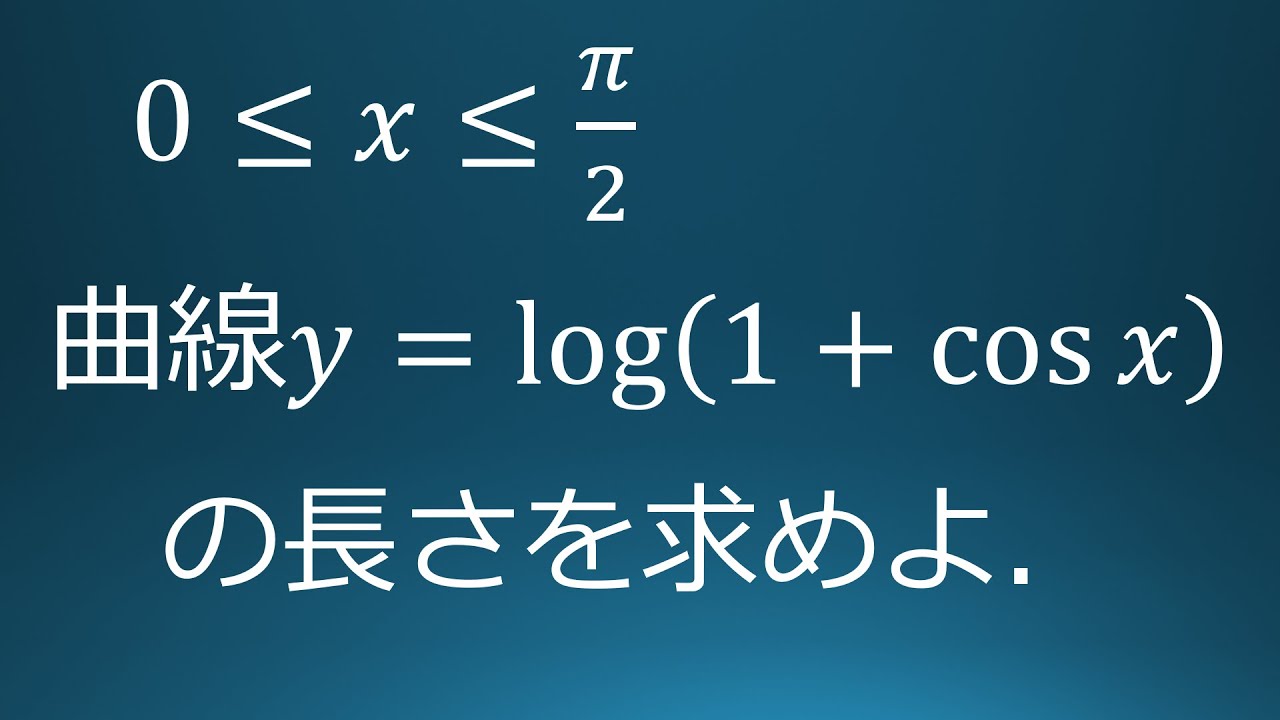
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq x \leqq \displaystyle \frac{\pi}{2}$
曲線$y=log(1+\cos\ x)$の長さ$l$を求めよ。
出典:2021年京都大学 入試問題
この動画を見る
$0 \leqq x \leqq \displaystyle \frac{\pi}{2}$
曲線$y=log(1+\cos\ x)$の長さ$l$を求めよ。
出典:2021年京都大学 入試問題
福田の数学〜京都大学2022年理系第5問〜方程式の解と不等式の証明

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数と方程式#恒等式・等式・不等式の証明#解と判別式・解と係数の関係#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
曲線$C:y=\cos^3x$ $(0 \leqq x \leqq \frac{\pi}{2})$,x軸およびy軸で囲まれる図形の面s系をS
とする。$0 \lt t \lt \frac{\pi}{2}$とし、C上の点Q$(t,\cos^3t)$と原点O,およびP$(t,o),R(0,\cos^3t)$
を頂点にもつ長方形OPQRの面積をf(t)とする。このとき、次の問いに答えよ。
(1)Sを求めよ。
(2)$f(t)$は最大値をただ一つのtでとることを示せ。そのときのtを$\alpha$とすると、
$f(\alpha)=\frac{\cos^4\alpha}{3\sin\alpha}$ であることを示せ。
(3)$\frac{f(\alpha)}{S} \lt \frac{9}{16}$ を示せ。
2022京都大学理系過去問
この動画を見る
曲線$C:y=\cos^3x$ $(0 \leqq x \leqq \frac{\pi}{2})$,x軸およびy軸で囲まれる図形の面s系をS
とする。$0 \lt t \lt \frac{\pi}{2}$とし、C上の点Q$(t,\cos^3t)$と原点O,およびP$(t,o),R(0,\cos^3t)$
を頂点にもつ長方形OPQRの面積をf(t)とする。このとき、次の問いに答えよ。
(1)Sを求めよ。
(2)$f(t)$は最大値をただ一つのtでとることを示せ。そのときのtを$\alpha$とすると、
$f(\alpha)=\frac{\cos^4\alpha}{3\sin\alpha}$ であることを示せ。
(3)$\frac{f(\alpha)}{S} \lt \frac{9}{16}$ を示せ。
2022京都大学理系過去問
大学入試問題#136 南山大学(2021) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#南山大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1}|2x(1-x^2)e^{-x^2}|dx$を計算せよ。
出典:2021年南山大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1}|2x(1-x^2)e^{-x^2}|dx$を計算せよ。
出典:2021年南山大学 入試問題
大学入試問題#135 横浜市立大学(2020) 定積分 個人的には難
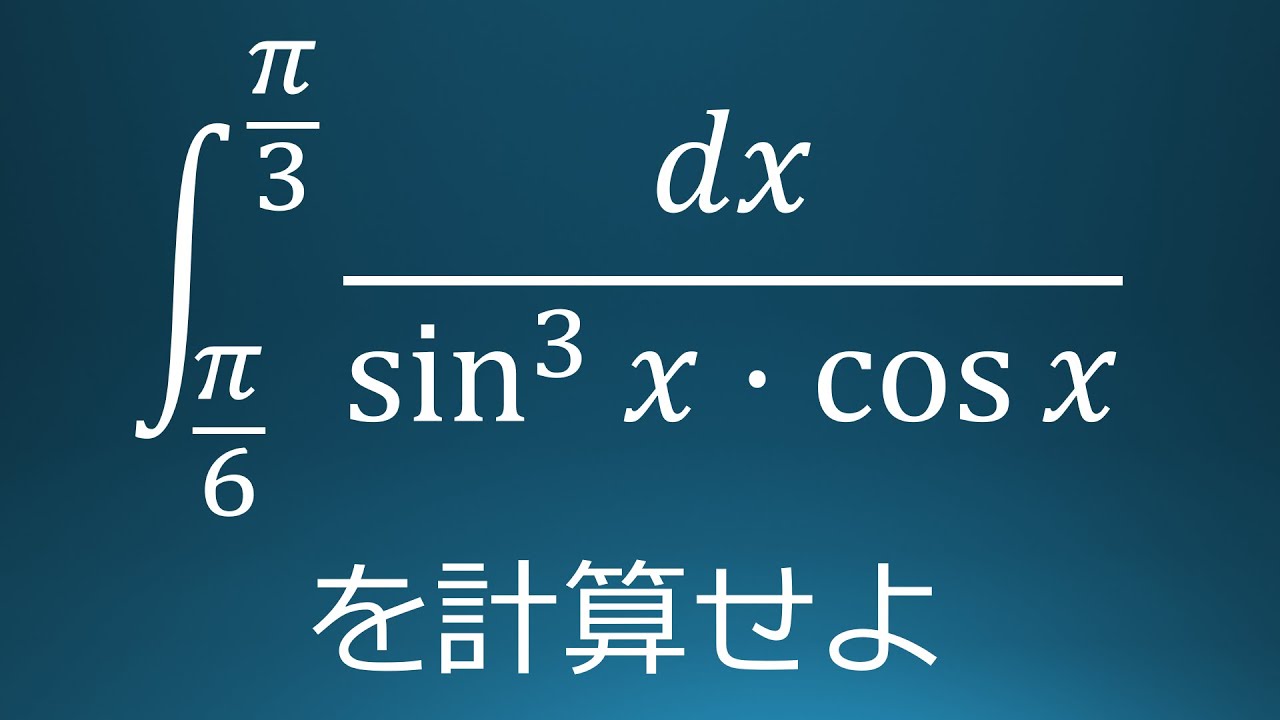
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\displaystyle \frac{dx}{\sin^3x\ \cos\ x}$
出典:2020年横浜市立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}}\displaystyle \frac{dx}{\sin^3x\ \cos\ x}$
出典:2020年横浜市立大学 入試問題
大学入試問題#134 京都工芸繊維大学(2018) 不定積分

単元:
#積分とその応用#不定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \{log(3+\cos^2\theta)\}\cos\theta d \theta$を計算せよ。
出典:2018年京都工芸繊維大学 入試問題
この動画を見る
$\displaystyle \int \{log(3+\cos^2\theta)\}\cos\theta d \theta$を計算せよ。
出典:2018年京都工芸繊維大学 入試問題
福田の入試問題解説〜東京大学2022年理系第5問〜立体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標空間内の点A(0,0,2)と点B(1,0,1)を結ぶ線分ABをz軸の周りに
1回転させて得られる局面をSとする。S上の点Pとxy平面上の点Qが$PQ=2$を
満たしながら動くとき、線分PQの中点Mが通過しうる範囲をKとする。
Kの体積を求めよ。
2022東京大学理系過去問
この動画を見る
座標空間内の点A(0,0,2)と点B(1,0,1)を結ぶ線分ABをz軸の周りに
1回転させて得られる局面をSとする。S上の点Pとxy平面上の点Qが$PQ=2$を
満たしながら動くとき、線分PQの中点Mが通過しうる範囲をKとする。
Kの体積を求めよ。
2022東京大学理系過去問
大学入試問題#132 横浜国立大学(2007) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{4}{3}}^{2}\displaystyle \frac{1}{x^2\sqrt{ x-1 }}\ dx$を計算せよ。
出典:2007年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{4}{3}}^{2}\displaystyle \frac{1}{x^2\sqrt{ x-1 }}\ dx$を計算せよ。
出典:2007年横浜国立大学 入試問題
