複素数平面
複素数平面
大阪大の問題の背景 特に文系の人見てください
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#図形と計量#三角比（三角比・拡張・相互関係・単位円）#複素数平面#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
(1)$ \cos\dfrac{2}{7}\pi, \cos\dfrac{4}{7}\pi, \cos\dfrac{6}{7}\pi$を解にもつ
$3$次方程式$ x^3+ax^2+bx+c=0$を求めよ.＊$ z^7=1$
(2)$ f(x)=8x^3+4x^2-4x-1$,$f\left(\cos\dfrac{2}{7}\pi \right)=0$を示せ.
この動画を見る
(1)$ \cos\dfrac{2}{7}\pi, \cos\dfrac{4}{7}\pi, \cos\dfrac{6}{7}\pi$を解にもつ
$3$次方程式$ x^3+ax^2+bx+c=0$を求めよ.＊$ z^7=1$
(2)$ f(x)=8x^3+4x^2-4x-1$,$f\left(\cos\dfrac{2}{7}\pi \right)=0$を示せ.
福田の数学〜慶應義塾大学2022年薬学部第１問(1)〜複素数の計算とド・モアブルの定理
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
(1)整数a,bは等式$(a+bi)^3=-16+16i$を満たす。ただし、iは虚数単位とする。
$(\textrm{i})a=\boxed{\ \ ア\ \ }, b=\boxed{\ \ イ\ \ }$である。
$(\textrm{ii})\frac{i}{a+bi}-\frac{1+5i}{4}$を計算すると$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学薬学部過去問
この動画を見る
(1)整数a,bは等式$(a+bi)^3=-16+16i$を満たす。ただし、iは虚数単位とする。
$(\textrm{i})a=\boxed{\ \ ア\ \ }, b=\boxed{\ \ イ\ \ }$である。
$(\textrm{ii})\frac{i}{a+bi}-\frac{1+5i}{4}$を計算すると$\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学薬学部過去問
福田の数学〜東京慈恵会医科大学2022年医学部第４問〜複素数平面と図形
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#平面上の曲線#複素数平面#方べきの定理と２つの円の関係#図形と方程式#点と直線#2次曲線#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学
指導講師：
福田次郎
問題文全文(内容文)：
複素数平面上の点zが原点を中心とする半径1の円周上を動くとき、$w=z+\frac{2}{z}$
で表される点wの描く図形をCとする。Cで囲まれた部分の内部(ただし、
境界線は含まない)に定点$\alpha$をとり、$\alpha$を通る直線lがCと交わる2点を$\beta_1,\beta_2$とする。
(1)$w=u+vi$(u,vは実数)とするとき、uとvの間に成り立つ関係式を求めよ。
(2)点$\alpha$を固定したままlを動かすとき、積$|\beta_1-\alpha|・|\beta_2-\alpha|$が最大となる
ようなlはどのような直線のときか調べよ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
複素数平面上の点zが原点を中心とする半径1の円周上を動くとき、$w=z+\frac{2}{z}$
で表される点wの描く図形をCとする。Cで囲まれた部分の内部(ただし、
境界線は含まない)に定点$\alpha$をとり、$\alpha$を通る直線lがCと交わる2点を$\beta_1,\beta_2$とする。
(1)$w=u+vi$(u,vは実数)とするとき、uとvの間に成り立つ関係式を求めよ。
(2)点$\alpha$を固定したままlを動かすとき、積$|\beta_1-\alpha|・|\beta_2-\alpha|$が最大となる
ようなlはどのような直線のときか調べよ。
2022東京慈恵会医科大学医学部過去問
2022東海大（医）ドモアブルの定理の基本
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東海大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ (\sqrt{2+\sqrt2}+\sqrt{2-\sqrt2i})^8$
これを解け.
2022東海大(医)過去問
この動画を見る
$ (\sqrt{2+\sqrt2}+\sqrt{2-\sqrt2i})^8$
これを解け.
2022東海大(医)過去問
大学入試問題#52 防衛医科大学(2020) 複素数
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#防衛医科大学
指導講師：
ますただ
問題文全文(内容文)：
$z^3=8$の虚数解の1つを$\alpha$とする。
$\alpha^4+6\alpha^3+8\alpha^2+8\alpha$の値を求めよ。
出典：2020年防衛医科大学 入試問題
この動画を見る
$z^3=8$の虚数解の1つを$\alpha$とする。
$\alpha^4+6\alpha^3+8\alpha^2+8\alpha$の値を求めよ。
出典：2020年防衛医科大学 入試問題
数学「大学入試良問集」【16−3 ド・モアブルの定理と累乗の取り扱い】を宇宙一わかりやすく
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$z$を絶対値が1の複素数とする。
このとき以下の問いに答えよ。
（1）$z^3-z$の実部が$0$となるような$z$をすべて求めよ。
（2）$z^5+z$の絶対値が1となるような$z$をすべて求めよ。
（3）$n$を自然数とする。$z^n+1$の絶対値が1となるような$z$となるような$z$をすべてかけ合わせて得られる複素数を求めよ。
この動画を見る
$z$を絶対値が1の複素数とする。
このとき以下の問いに答えよ。
（1）$z^3-z$の実部が$0$となるような$z$をすべて求めよ。
（2）$z^5+z$の絶対値が1となるような$z$をすべて求めよ。
（3）$n$を自然数とする。$z^n+1$の絶対値が1となるような$z$となるような$z$をすべてかけ合わせて得られる複素数を求めよ。
数学「大学入試良問集」【16−2 複素数平面と三角形の形との関係】を宇宙一わかりやすく
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
複素数平面上に三角形$ABC$があり、その頂点$A,B,C$を表す複素数をそれぞれ$z_1,z_2,z_3$とする。
複素数$\omega$に対して、$z_1=\omega z_3,z_2=\omega z_1,z_3=\omega z_2$が成り立つとき、次の各問いに答えよ。
（1）$1+\omega+\omega^2$の値を求めよ。
（2）三角形$ABC$はどんな形の三角形か。
（3）$z=z_1+2z_2+3z_3$の表す点を$D$とすると、三角形$OBD$はどんな形の三角形か。ただし、$O$は原点である。
この動画を見る
複素数平面上に三角形$ABC$があり、その頂点$A,B,C$を表す複素数をそれぞれ$z_1,z_2,z_3$とする。
複素数$\omega$に対して、$z_1=\omega z_3,z_2=\omega z_1,z_3=\omega z_2$が成り立つとき、次の各問いに答えよ。
（1）$1+\omega+\omega^2$の値を求めよ。
（2）三角形$ABC$はどんな形の三角形か。
（3）$z=z_1+2z_2+3z_3$の表す点を$D$とすると、三角形$OBD$はどんな形の三角形か。ただし、$O$は原点である。
数学「大学入試良問集」【16−1 複素数平面と解と係数の関係】を宇宙一わかりやすく
単元：
#複素数平面#複素数平面#英語(高校生)#大学入試過去問(英語)#学校別大学入試過去問解説(英語)#数学(高校生)#数C#京都大学
指導講師：
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文)：
$c$を実数とする。$x$についての2次方程式
$x^2+(3-2c)x+c^2+5=0$が2つの解$\alpha,\ \beta$を持つとする。
複素平面上の3点$\alpha,\beta,c^2$が三角形の3頂点になり、その三角形の重心は$0$であるという。
$c$を求めよ。
この動画を見る
$c$を実数とする。$x$についての2次方程式
$x^2+(3-2c)x+c^2+5=0$が2つの解$\alpha,\ \beta$を持つとする。
複素平面上の3点$\alpha,\beta,c^2$が三角形の3頂点になり、その三角形の重心は$0$であるという。
$c$を求めよ。
福田の数学〜立教大学2021年理学部第４問〜極形式で与えられたzの計算
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{4}}$複素数$z$を$z=\cos\frac{2\pi}{7}+i\sin\frac{2\pi}{7}$とする。ただし、iは虚数単位とする。また、
$a=z+\frac{1}{z}, b=z^2+\frac{1}{z^2}, c=z^3+\frac{1}{z^3}$ とおく。次の問いに答えよ。
(1)$z^7$は有理数になる。その値を求めよ。
(2)$z+z^2+z^3+z^4+z^5+z^6$ は有理数になる。その値を求めよ。
(3)$A=a+b+c$ は有理数になる。その値を求めよ。
(4)$B=a^2+b^2+c^2$ は有理数になる。その値を求めよ。
(5)$C=ab+bc+ca$ は有理数になる。その値を求めよ。
(6)$D=a^3+b^3+c^3-3abc$ は有理数になる。その値を求めよ。
2021立教大学理工学部過去問
この動画を見る
${\Large\boxed{4}}$複素数$z$を$z=\cos\frac{2\pi}{7}+i\sin\frac{2\pi}{7}$とする。ただし、iは虚数単位とする。また、
$a=z+\frac{1}{z}, b=z^2+\frac{1}{z^2}, c=z^3+\frac{1}{z^3}$ とおく。次の問いに答えよ。
(1)$z^7$は有理数になる。その値を求めよ。
(2)$z+z^2+z^3+z^4+z^5+z^6$ は有理数になる。その値を求めよ。
(3)$A=a+b+c$ は有理数になる。その値を求めよ。
(4)$B=a^2+b^2+c^2$ は有理数になる。その値を求めよ。
(5)$C=ab+bc+ca$ は有理数になる。その値を求めよ。
(6)$D=a^3+b^3+c^3-3abc$ は有理数になる。その値を求めよ。
2021立教大学理工学部過去問
福田の数学〜明治大学2021年理工学部第１問(3)〜複素数平面と図形
単元：
#数A#図形の性質#複素数平面#複素数平面#数学(高校生)#大学入試解答速報#数学#明治大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$(3)複素数$z$と正の実数rは、等式
$z^4=r(\cos\frac{2}{3}\pi+i\sin\frac{2}{3}\pi) \ldots(*)$
を満たしている。ただし、$i$は虚数単位である。
$(\textrm{i})z$の偏角$\thetaを0 \leqq \theta \lt 2\pi$の範囲にとるとき、$\theta$のとりうる値の
うち最小のものは$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}\pi$であり、最大のものは$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}\pi$である。
$(\textrm{ii})$等式(*)と等式
$|z-i|=1$
が共に成り立つとき、$r$の値は$r=\boxed{\ \ ナ\ \ }$または$r=\boxed{\ \ ニ\ \ }$である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$(3)複素数$z$と正の実数rは、等式
$z^4=r(\cos\frac{2}{3}\pi+i\sin\frac{2}{3}\pi) \ldots(*)$
を満たしている。ただし、$i$は虚数単位である。
$(\textrm{i})z$の偏角$\thetaを0 \leqq \theta \lt 2\pi$の範囲にとるとき、$\theta$のとりうる値の
うち最小のものは$\frac{\boxed{\ \ チ\ \ }}{\boxed{\ \ ツ\ \ }}\pi$であり、最大のものは$\frac{\boxed{\ \ テ\ \ }}{\boxed{\ \ ト\ \ }}\pi$である。
$(\textrm{ii})$等式(*)と等式
$|z-i|=1$
が共に成り立つとき、$r$の値は$r=\boxed{\ \ ナ\ \ }$または$r=\boxed{\ \ ニ\ \ }$である。
2021明治大学理工学部過去問
福田の数学〜明治大学2021年全学部統一入試Ⅲ第２問(2)〜２次方程式の解が同一円周上にある条件
単元：
#数Ⅱ#２次関数#図形の性質#複素数平面#2次方程式と2次不等式#周角と円に内接する四角形・円と接線・接弦定理#複素数平面#数学(高校生)#大学入試解答速報#数学#明治大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{2}}$(2)方程式$x^2+x+1=0$の2つの解を$\alpha,\ \beta$とする。またbを実数として、
方程式$x^2+x+1=0$の2つの解を$\gamma,\ \delta$とする。複素数平面上で、4点$A(\alpha),$
$B(\beta),C(\gamma),D(\delta)$が同じ円上にあるとき、bの値は$±\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$となる。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$(2)方程式$x^2+x+1=0$の2つの解を$\alpha,\ \beta$とする。またbを実数として、
方程式$x^2+x+1=0$の2つの解を$\gamma,\ \delta$とする。複素数平面上で、4点$A(\alpha),$
$B(\beta),C(\gamma),D(\delta)$が同じ円上にあるとき、bの値は$±\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$となる。
2021明治大学全統過去問
福田の数学〜明治大学2021年全学部統一入試Ⅲ第２問(1)〜楕円と複素数平面
単元：
#平面上の曲線#複素数平面#図形と計量#三角比（三角比・拡張・相互関係・単位円）#2次曲線#複素数平面#大学入試解答速報#数学#明治大学#数C
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{2}}$(1)座標平面において、点$(-1,\ 0)$からの距離と点$(1,\ 0)$からの距離の和が4
である点は方程式$\frac{x^2}{\boxed{\ \ ア\ \ }}+\frac{y^2}{\boxed{\ \ イ\ \ }}=1$で表される曲線C上にある。点$(x,\ y)$
が曲線C上を動くとき、点$(x,\ y)$と点$(-1,\ 0)$の距離をdとおけば、dの最小値
は$\boxed{\ \ ウ\ \ }$、最大値は$\boxed{\ \ エ\ \ }$となる。複素数$z$が$|z|+|z-4|=8$を満たすとき、
$|z|$のとりうる範囲は$\boxed{\ \ オ\ \ } \leqq |z| \leqq \boxed{\ \ カ\ \ }$である。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$(1)座標平面において、点$(-1,\ 0)$からの距離と点$(1,\ 0)$からの距離の和が4
である点は方程式$\frac{x^2}{\boxed{\ \ ア\ \ }}+\frac{y^2}{\boxed{\ \ イ\ \ }}=1$で表される曲線C上にある。点$(x,\ y)$
が曲線C上を動くとき、点$(x,\ y)$と点$(-1,\ 0)$の距離をdとおけば、dの最小値
は$\boxed{\ \ ウ\ \ }$、最大値は$\boxed{\ \ エ\ \ }$となる。複素数$z$が$|z|+|z-4|=8$を満たすとき、
$|z|$のとりうる範囲は$\boxed{\ \ オ\ \ } \leqq |z| \leqq \boxed{\ \ カ\ \ }$である。
2021明治大学全統過去問
福田の数学〜青山学院大学2021年理工学部第４問〜複素数平面上の点の軌跡
単元：
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#青山学院大学
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{4}}$複素数平面上の点zが$z+\bar{ z }=2$を満たしながら動くとき、以下の問いに答えよ。
(1)点z全体が描く図形を複素数平面上に図示せよ。
(2)$w=(2+i)z$ で定まる点w全体が描く図形を調べよう。
$(\textrm{a})w$の実部をu、虚部をvとして$w=u+vi$と表すとき、u,vが満たす方程式
を求めよ。
$(\textrm{b})$点w全体が描く図形を複素数平面上に図示せよ。
(3)$w=z^2$で定まる点w全体が描く図形を複素数平面上に図示せよ。
2021青山学院大学理工学部過去問
この動画を見る
${\Large\boxed{4}}$複素数平面上の点zが$z+\bar{ z }=2$を満たしながら動くとき、以下の問いに答えよ。
(1)点z全体が描く図形を複素数平面上に図示せよ。
(2)$w=(2+i)z$ で定まる点w全体が描く図形を調べよう。
$(\textrm{a})w$の実部をu、虚部をvとして$w=u+vi$と表すとき、u,vが満たす方程式
を求めよ。
$(\textrm{b})$点w全体が描く図形を複素数平面上に図示せよ。
(3)$w=z^2$で定まる点w全体が描く図形を複素数平面上に図示せよ。
2021青山学院大学理工学部過去問
福田の数学〜上智大学2021年理工学部第３問〜複素数平面と図形
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{3}}$ $i$を虚数単位とする。複素数zの絶対値を$|z|$と表す。
$w=\cos\frac{2\pi}{5}+i\sin\frac{2\pi}{5}$ とし、$\alpha=w+w^4$ とする。
(1)$\alpha^2=\boxed{\ \ お\ \ }$である。これより、$\alpha=\frac{\boxed{\ \ ソ\ \ }+\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$である。
(2)複素数平面上の2点$\frac{i}{2}$,-1間の距離は$\boxed{\ \ か\ \ }$である。
(3)複素数平面上の2点$w^2,$ -1間の距離は$\boxed{\ \ き\ \ }$である。
(4)$\frac{w^2+1}{w+1}=r(\cos\theta+i\sin\theta)$ (ただし、$r \gt 0,\ 0 \leqq \theta \lt 2\pi$)
とおくとき、$r=\boxed{\ \ く\ \ }$であり、$\theta=\frac{\boxed{\ \ ツ\ \ }}{\boxed{\ \ テ\ \ }}\pi$である。
(5)複素数平面上で、-1を中心都市$w^2$を通る円上をzが動くとする。
$x=\frac{1}{z}$とするとき、$x$は$|1+x|=\boxed{\ \ け\ \ }|x|$を満たし、$\boxed{\ \ こ\ \ }$を
中心とする半径$\boxed{\ \ さ\ \ }$の円を描く。
$\boxed{\ \ お\ \ }～\ \boxed{\ \ さ\ \ }$の選択肢
$(\textrm{a})1 (\textrm{b})2 (\textrm{c})\alpha (\textrm{d})2\alpha$
$(\textrm{e})\frac{\alpha}{2}+1 (\textrm{f})\frac{\alpha}{2}-1 (\textrm{g})-\frac{\alpha}{2}+1 (\textrm{h})-\frac{\alpha}{2}-1$
$(\textrm{i})\alpha+1 (\textrm{j})\alpha-1 (\textrm{k})-\alpha+1 (\textrm{l})-\alpha-1$
$(\textrm{m})\alpha+\frac{1}{2} (\textrm{n})\alpha-\frac{1}{2} (\textrm{o})-\alpha+\frac{1}{2} (\textrm{p})-\alpha-\frac{1}{2}$
2021上智大学理工学部過去問
この動画を見る
${\Large\boxed{3}}$ $i$を虚数単位とする。複素数zの絶対値を$|z|$と表す。
$w=\cos\frac{2\pi}{5}+i\sin\frac{2\pi}{5}$ とし、$\alpha=w+w^4$ とする。
(1)$\alpha^2=\boxed{\ \ お\ \ }$である。これより、$\alpha=\frac{\boxed{\ \ ソ\ \ }+\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}$である。
(2)複素数平面上の2点$\frac{i}{2}$,-1間の距離は$\boxed{\ \ か\ \ }$である。
(3)複素数平面上の2点$w^2,$ -1間の距離は$\boxed{\ \ き\ \ }$である。
(4)$\frac{w^2+1}{w+1}=r(\cos\theta+i\sin\theta)$ (ただし、$r \gt 0,\ 0 \leqq \theta \lt 2\pi$)
とおくとき、$r=\boxed{\ \ く\ \ }$であり、$\theta=\frac{\boxed{\ \ ツ\ \ }}{\boxed{\ \ テ\ \ }}\pi$である。
(5)複素数平面上で、-1を中心都市$w^2$を通る円上をzが動くとする。
$x=\frac{1}{z}$とするとき、$x$は$|1+x|=\boxed{\ \ け\ \ }|x|$を満たし、$\boxed{\ \ こ\ \ }$を
中心とする半径$\boxed{\ \ さ\ \ }$の円を描く。
$\boxed{\ \ お\ \ }～\ \boxed{\ \ さ\ \ }$の選択肢
$(\textrm{a})1 (\textrm{b})2 (\textrm{c})\alpha (\textrm{d})2\alpha$
$(\textrm{e})\frac{\alpha}{2}+1 (\textrm{f})\frac{\alpha}{2}-1 (\textrm{g})-\frac{\alpha}{2}+1 (\textrm{h})-\frac{\alpha}{2}-1$
$(\textrm{i})\alpha+1 (\textrm{j})\alpha-1 (\textrm{k})-\alpha+1 (\textrm{l})-\alpha-1$
$(\textrm{m})\alpha+\frac{1}{2} (\textrm{n})\alpha-\frac{1}{2} (\textrm{o})-\alpha+\frac{1}{2} (\textrm{p})-\alpha-\frac{1}{2}$
2021上智大学理工学部過去問
福田の数学〜慶應義塾大学2021年薬学部第１問(1)〜ド･モアブルの定理
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{1}}$
$(1)\ (1+i)^{10}$を展開して得られる複素数は$\boxed{\ \ ア\ \ }$である。ただし、iは虚数単位とする。
2021慶應義塾大学薬学部過去問
この動画を見る
${\Large\boxed{1}}$
$(1)\ (1+i)^{10}$を展開して得られる複素数は$\boxed{\ \ ア\ \ }$である。ただし、iは虚数単位とする。
2021慶應義塾大学薬学部過去問
福田の数学〜早稲田大学2021年人間科学部第６問〜回転で定義された点列の極限
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
\begin{eqnarray}
{\Large\boxed{6}} 点M_1(0,0)を中心に点(1,0)を、時計の針の回転と逆の向きを正として、\thetaだけ\\
回転させた点をP_1とする。次に線分M_1P_1の中点M_2とし、このM_2を中心に点P_1\\
を\thetaだけ回転させた点をP_2とする。同様に自然数nに対して、線分M_nP_nの中点\\
M_{n+1}を中心に点P_nを\thetaだけ回転させた点をP_{n+1}とする。P_nの座標を(x_n,y_n)と\\
する。\\
\\
(1)\theta=\frac{\pi}{4}のとき、x_2=\frac{\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}, y_2=\frac{\boxed{\ \ ツ\ \ }+\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }} である。\\
\\
(2)\theta=\frac{\pi}{3}のとき、\lim_{n \to \infty}x_n=\boxed{\ \ ナ\ \ }, \lim_{n \to \infty}y_n=\frac{\sqrt{\boxed{\ \ ニ\ \ }}}{\boxed{\ \ ヌ\ \ }} である。
\end{eqnarray}
2021早稲田大学人間科学部過去問
この動画を見る
\begin{eqnarray}
{\Large\boxed{6}} 点M_1(0,0)を中心に点(1,0)を、時計の針の回転と逆の向きを正として、\thetaだけ\\
回転させた点をP_1とする。次に線分M_1P_1の中点M_2とし、このM_2を中心に点P_1\\
を\thetaだけ回転させた点をP_2とする。同様に自然数nに対して、線分M_nP_nの中点\\
M_{n+1}を中心に点P_nを\thetaだけ回転させた点をP_{n+1}とする。P_nの座標を(x_n,y_n)と\\
する。\\
\\
(1)\theta=\frac{\pi}{4}のとき、x_2=\frac{\sqrt{\boxed{\ \ タ\ \ }}}{\boxed{\ \ チ\ \ }}, y_2=\frac{\boxed{\ \ ツ\ \ }+\sqrt{\boxed{\ \ テ\ \ }}}{\boxed{\ \ ト\ \ }} である。\\
\\
(2)\theta=\frac{\pi}{3}のとき、\lim_{n \to \infty}x_n=\boxed{\ \ ナ\ \ }, \lim_{n \to \infty}y_n=\frac{\sqrt{\boxed{\ \ ニ\ \ }}}{\boxed{\ \ ヌ\ \ }} である。
\end{eqnarray}
2021早稲田大学人間科学部過去問
福田の数学〜早稲田大学2021年理工学部第３問〜複素数平面上の点の軌跡
単元：
#大学入試過去問(数学)#複素数平面#積分とその応用#複素数平面#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{3}}$ 複素数$\alpha=2+i,$ $\beta=-\displaystyle \frac{1}{2}+i$に対応する複素数平面上の点を$A(\alpha),\ B(\beta)$とする。
このとき、以下の問いに答えよ。
(1)複素数平面上の点$C(\alpha^2),\ D(\beta^2)$と原点$O$の3点は一直線上にあることを示せ。
(2)点$P(z)$が直線$AB$上を動くとき、$z^2$の実部を$x$、虚部を$y$として、点$Q(z^2)$の軌跡
を$x,y$の方程式で表せ。
(3)点$P(z)$が三角形$OAB$の周および内部にあるとき、点$Q(z^2)$全体のなす図形をK
とする。$K$を複素数平面上に図示せよ。
(4)(3)の図形$K$の面積を求めよ。
2021早稲田大学理工学部過去問
この動画を見る
${\Large\boxed{3}}$ 複素数$\alpha=2+i,$ $\beta=-\displaystyle \frac{1}{2}+i$に対応する複素数平面上の点を$A(\alpha),\ B(\beta)$とする。
このとき、以下の問いに答えよ。
(1)複素数平面上の点$C(\alpha^2),\ D(\beta^2)$と原点$O$の3点は一直線上にあることを示せ。
(2)点$P(z)$が直線$AB$上を動くとき、$z^2$の実部を$x$、虚部を$y$として、点$Q(z^2)$の軌跡
を$x,y$の方程式で表せ。
(3)点$P(z)$が三角形$OAB$の周および内部にあるとき、点$Q(z^2)$全体のなす図形をK
とする。$K$を複素数平面上に図示せよ。
(4)(3)の図形$K$の面積を求めよ。
2021早稲田大学理工学部過去問
数学Ⅲが１時間で分かる動画！極限、微分積分をメインに！複素数平面を添えて【篠原好】
単元：
#数Ⅱ#複素数平面#微分法と積分法#平均変化率・極限・導関数#複素数平面#数学(高校生)#数C
指導講師：
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文)：
極限、微分積分をメインに！複素数平面を添えて
「数学Ⅲが１時間で分かる」動画です。
この動画を見る
極限、微分積分をメインに！複素数平面を添えて
「数学Ⅲが１時間で分かる」動画です。
【理数個別の過去問解説】2021年度東京大学 数学 理科第2問(1)解説
単元：
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師：
理数個別チャンネル
問題文全文(内容文)：
複素数a,b,cに対して整式$f(z)=az^2+bz+c$を考える。iを虚数単位とする。$\alpha,\beta,y$を複素数とする。
$f(0)=α,f(1)=β,f(i)=(γ)$が成り立つとき、$a,b,c$をそれぞれ$\alpha,\beta,y$で表せ。
この動画を見る
複素数a,b,cに対して整式$f(z)=az^2+bz+c$を考える。iを虚数単位とする。$\alpha,\beta,y$を複素数とする。
$f(0)=α,f(1)=β,f(i)=(γ)$が成り立つとき、$a,b,c$をそれぞれ$\alpha,\beta,y$で表せ。
福田の数学〜慶應義塾大学2021年理工学部第２問〜複素数と多項式の商と余り
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
${\Large\boxed{2}}$ (1)複素数$\alpha$は$\alpha^2+3\alpha+3=0$ を満たすとする。このとき、$(\alpha+1)^2(\alpha+2)^5=\boxed{\ \ キ\ \ }$
である。また、$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組を全て求めよ。
(2)多項式$(x+1)^3(x+2)^2$を$x^2+3x+3$で割った時の商は$\boxed{\ \ ク\ \ }$、余りは$\boxed{\ \ ケ\ \ }$である。
また、$(x+1)^{2021}$を$x^2+3x+3$で割った時の余りは$\boxed{\ \ コ\ \ }$である。
2021慶應義塾大学理工学部過去問
この動画を見る
${\Large\boxed{2}}$ (1)複素数$\alpha$は$\alpha^2+3\alpha+3=0$ を満たすとする。このとき、$(\alpha+1)^2(\alpha+2)^5=\boxed{\ \ キ\ \ }$
である。また、$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組を全て求めよ。
(2)多項式$(x+1)^3(x+2)^2$を$x^2+3x+3$で割った時の商は$\boxed{\ \ ク\ \ }$、余りは$\boxed{\ \ ケ\ \ }$である。
また、$(x+1)^{2021}$を$x^2+3x+3$で割った時の余りは$\boxed{\ \ コ\ \ }$である。
2021慶應義塾大学理工学部過去問
2021久留米大（医）三次方程式と複素平面
単元：
#数Ⅱ#複素数と方程式#複素数平面#複素数#剰余の定理・因数定理・組み立て除法と高次方程式#複素数平面#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a\lt 0,a,b$は実数である.
$x^3-2(a+1)x^2+(5a^2+1)x+b-0$の3つの解は$2,z,\omega$である.
複素平面上で3点,$2,z,\omega$を結ぶと直角二等辺三角形になる.
$a,b,z,\omega$を求めよ.
2021久留米(医)
この動画を見る
$a\lt 0,a,b$は実数である.
$x^3-2(a+1)x^2+(5a^2+1)x+b-0$の3つの解は$2,z,\omega$である.
複素平面上で3点,$2,z,\omega$を結ぶと直角二等辺三角形になる.
$a,b,z,\omega$を求めよ.
2021久留米(医)
13東京都教員採用試験（数学：6番 複素数）
単元：
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
6⃣$argZ=\frac{4}{3} \pi$ , $arg(1-z)=\frac{\pi}{4}$
$arg \frac{z}{(1-z)^2}$ , |z|を求めよ。
この動画を見る
6⃣$argZ=\frac{4}{3} \pi$ , $arg(1-z)=\frac{\pi}{4}$
$arg \frac{z}{(1-z)^2}$ , |z|を求めよ。
18愛知県教員採用試験（数学：10番 複素数）
単元：
#複素数平面#複素数平面#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$\boxed{10}$ $w=\frac{z-2i}{z+i},|z|=2$
(1)wはどのような図形か
(2)|w-i|の最大値
この動画を見る
$\boxed{10}$ $w=\frac{z-2i}{z+i},|z|=2$
(1)wはどのような図形か
(2)|w-i|の最大値
15東京都教員採用試験（数学：1-3 複素数）
単元：
#複素数平面#複素数平面#その他#数学(高校生)#数C#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
1⃣-(3)
$α、β \in \mathbb{ C }$
$α^2+αβ+β^2=0$ (α,β≠0)
$arg \frac{α}{β}$
この動画を見る
1⃣-(3)
$α、β \in \mathbb{ C }$
$α^2+αβ+β^2=0$ (α,β≠0)
$arg \frac{α}{β}$
一橋大 整式の剰余
単元：
#数Ⅱ#大学入試過去問(数学)#式と証明#複素数平面#整式の除法・分数式・二項定理#複素数平面#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$f(z)=z^{2n}+z^n+1$を
$z^2+z+1$で割ったあまり
$z^2-z+1$で割ったあまり
を求めよ.$n$は自然数である.
一橋大学過去問
この動画を見る
$f(z)=z^{2n}+z^n+1$を
$z^2+z+1$で割ったあまり
$z^2-z+1$で割ったあまり
を求めよ.$n$は自然数である.
一橋大学過去問
北里大 複素数の総和
単元：
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$z=-1+i$
$\displaystyle \sum_{n=1}^{12} z^n$
出典：2014年北里大学 過去問
この動画を見る
$z=-1+i$
$\displaystyle \sum_{n=1}^{12} z^n$
出典：2014年北里大学 過去問
神戸大 複素数の2次方程式
単元：
#数Ⅱ#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^2+i=0$を解け
出典：1971年神戸大学 過去問
この動画を見る
$x^2+i=0$を解け
出典：1971年神戸大学 過去問
福井大 ２次方程式と複素平面
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#複素数平面#2次方程式と2次不等式#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#福井大学#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$(k \gt 0)$
$x^2-2kx+2k^2=0$の解のうち虚部が正の方を$\alpha$
複素平面上で$0,\alpha,\alpha^2$が二等辺三角形になる。
$k$の値を求めよ
出典：2000年福井大学 過去問
この動画を見る
$(k \gt 0)$
$x^2-2kx+2k^2=0$の解のうち虚部が正の方を$\alpha$
複素平面上で$0,\alpha,\alpha^2$が二等辺三角形になる。
$k$の値を求めよ
出典：2000年福井大学 過去問
山梨大 ２次方程式と複素数平面
単元：
#数Ⅰ#大学入試過去問(数学)#２次関数#複素数平面#2次方程式と2次不等式#複素数平面#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)#数C
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$x^2-2kx+k=0$は実数解なし
2つの解$\alpha,\beta$と1を複素中面で結ぶと正三角形となる。
$k$の値を求めよ
出典：2000年山梨大学 過去問
この動画を見る
$x^2-2kx+k=0$は実数解なし
2つの解$\alpha,\beta$と1を複素中面で結ぶと正三角形となる。
$k$の値を求めよ
出典：2000年山梨大学 過去問
【数学III】複素数平面のイメージ・ニュアンスが30分で丸わかり動画
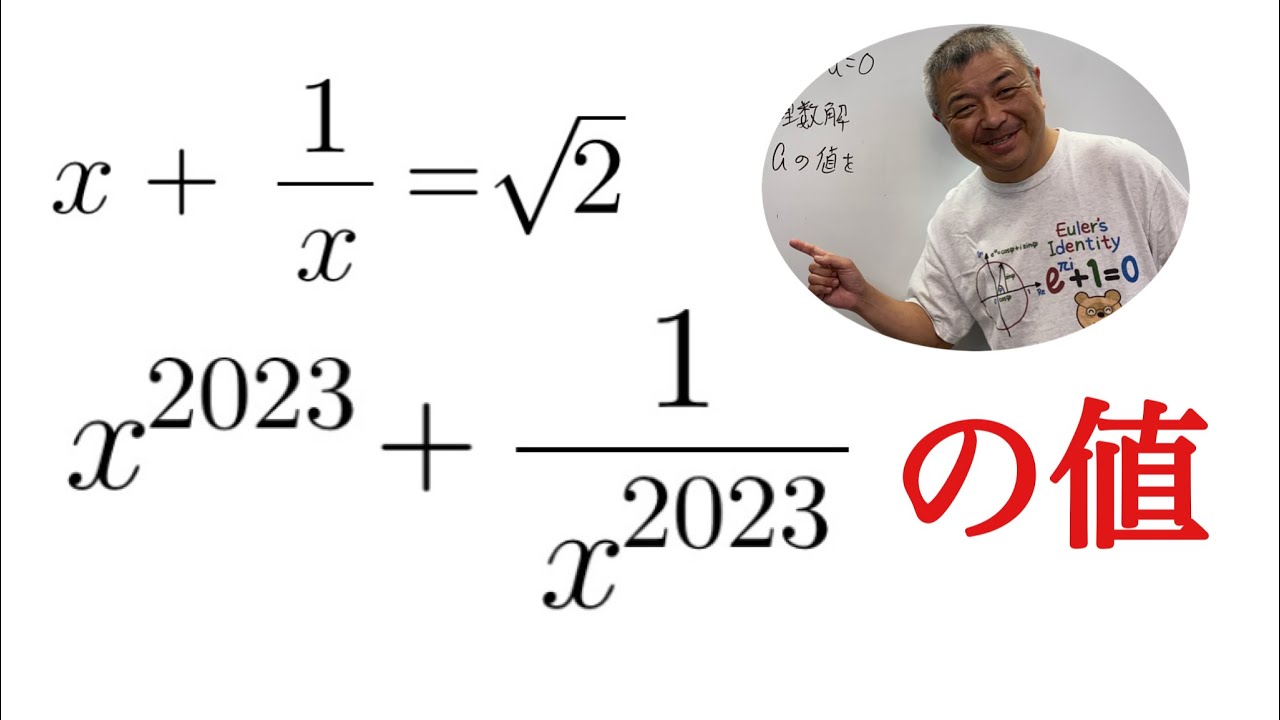
単元：
#複素数平面#複素数平面#数学(高校生)#数C
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
【数学III】複素数平面のイメージ・ニュアンス解説動画です
この動画を見る
【数学III】複素数平面のイメージ・ニュアンス解説動画です