 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数C】【複素数平面】複素数と図形1 ※問題文は概要欄

単元:
#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形の各辺の中点が$\alpha=-1+i,\beta=1+2i,\gamma=2$であるとき、この三角形の3つの頂点を表す複素数を求めよ。
この動画を見る
三角形の各辺の中点が$\alpha=-1+i,\beta=1+2i,\gamma=2$であるとき、この三角形の3つの頂点を表す複素数を求めよ。
【数C】【複素数平面】高次方程式3 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式$z^6+z^3+1=0$の解を求めよ。ただし、解は 極形式のままでよい。
この動画を見る
方程式$z^6+z^3+1=0$の解を求めよ。ただし、解は 極形式のままでよい。
【数C】【複素数平面】高次方程式2 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数$z$が、$z+\dfrac 1z=2\cos\theta$を満たすとき、次の問いに答えよ。
(1)$z$を$\theta$を用いて表せ。
(2)$n$が自然数のとき、等式、$z^n+\dfrac{1}{z^n}=2\cos n\theta$が成り立つことを示せ。
この動画を見る
複素数$z$が、$z+\dfrac 1z=2\cos\theta$を満たすとき、次の問いに答えよ。
(1)$z$を$\theta$を用いて表せ。
(2)$n$が自然数のとき、等式、$z^n+\dfrac{1}{z^n}=2\cos n\theta$が成り立つことを示せ。
【数C】【複素数平面】高次方程式1 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$を自然数とし、$\displaystyle \alpha = \cos \frac{\pi}{n}+i\sin \frac{\pi}{n}$とする。次の問いに答えよ。
(1) $1+ \alpha +\alpha^2 + \cdots\cdots +\alpha^{2n-1}$の値を求めよ。
(2) $z^{2n}=1$の解は$1, \alpha, \alpha^2, \cdots\cdots, \alpha^{2n-1}$であることを示せ。
この動画を見る
$n$を自然数とし、$\displaystyle \alpha = \cos \frac{\pi}{n}+i\sin \frac{\pi}{n}$とする。次の問いに答えよ。
(1) $1+ \alpha +\alpha^2 + \cdots\cdots +\alpha^{2n-1}$の値を求めよ。
(2) $z^{2n}=1$の解は$1, \alpha, \alpha^2, \cdots\cdots, \alpha^{2n-1}$であることを示せ。
福田のおもしろ数学431〜sin^318°+sin^218°の値を求める

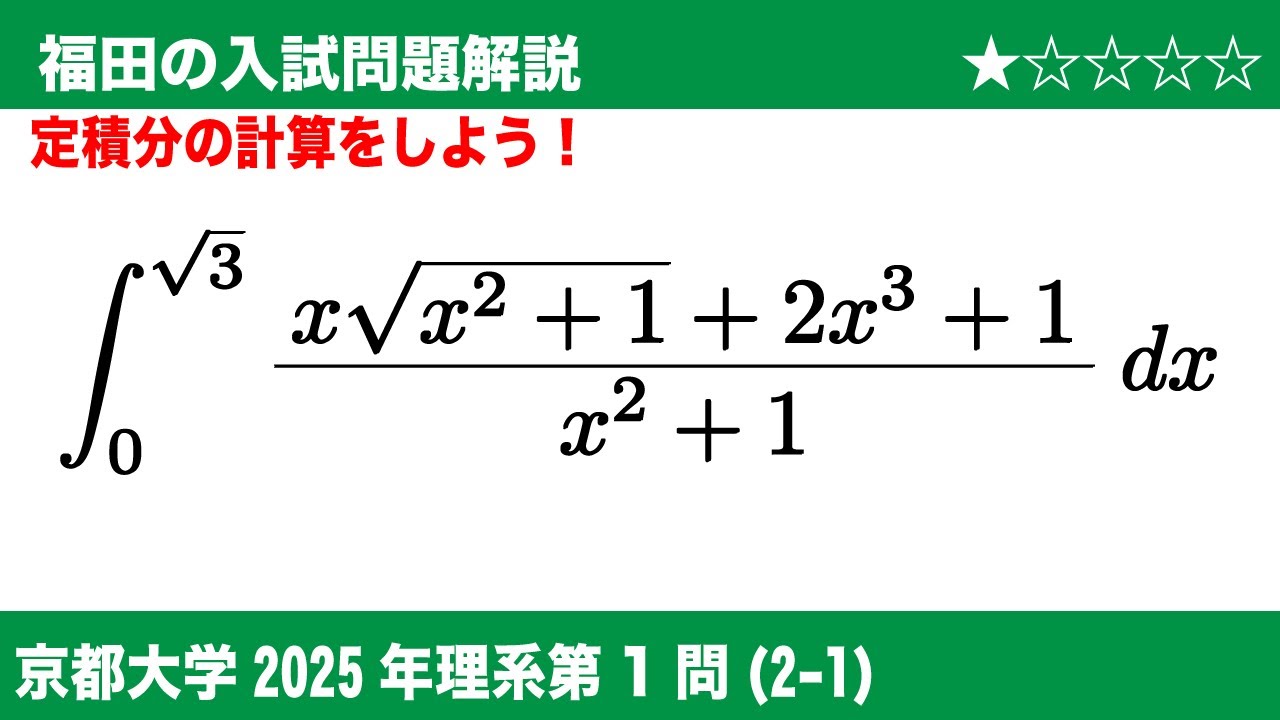
福田の数学〜京都大学2025理系第1問(2−1)〜定積分の計算
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2-1)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\sqrt3} \dfrac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(2-1)次の定積分の値を求めよ。
$\displaystyle \int_{0}^{\sqrt3} \dfrac{x\sqrt{x^2+1}+2x^3+1}{x^2+1}dx$
$2025$年京都大学理系過去問題
【数C】【複素数平面】ド・モアブルの定理2 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$が、$ \displaystyle a_n=(\frac{\sqrt{3}+1}{2} +\frac{\sqrt{3}-1}{2})^{2n}$ が実数となる最小の自然数であるとき、$a_n$の値を求めよ。
この動画を見る
$n$が、$ \displaystyle a_n=(\frac{\sqrt{3}+1}{2} +\frac{\sqrt{3}-1}{2})^{2n}$ が実数となる最小の自然数であるとき、$a_n$の値を求めよ。
【数C】【複素数平面】ド・モアブルの定理1 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$が自然数のとき、$\displaystyle (\frac{1+i}{\sqrt{2}})^n-(\frac{1-i}{\sqrt{2}})^n$ の値を求めよ。
この動画を見る
$n$が自然数のとき、$\displaystyle (\frac{1+i}{\sqrt{2}})^n-(\frac{1-i}{\sqrt{2}})^n$ の値を求めよ。
【数C】【複素数平面】複素数平面の対称移動 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上で$\mathrm{O}(0)、\mathrm{A}(-1+\sqrt{3}i)$とする。点$z$を直線$\mathrm{OA}$に関して対称移動した点を$w$とするとき、$w$を$z$を用いて表せ。
この動画を見る
複素数平面上で$\mathrm{O}(0)、\mathrm{A}(-1+\sqrt{3}i)$とする。点$z$を直線$\mathrm{OA}$に関して対称移動した点を$w$とするとき、$w$を$z$を用いて表せ。
【数C】【複素数平面】複素数平面の回転 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面上の点 $\mathrm{P}(x,y)$ を原点を中心として $\theta$ だけ回転した点を $\mathrm{Q}$ とするとき、 $\mathrm{Q}$ の座標を求めよ。
この動画を見る
座標平面上の点 $\mathrm{P}(x,y)$ を原点を中心として $\theta$ だけ回転した点を $\mathrm{Q}$ とするとき、 $\mathrm{Q}$ の座標を求めよ。
【数B】【確率分布と統計的な推測】仮説検定 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
テニス選手 A、B の年間の対戦成績は、Aの 23 勝 13 敗であった。両選手の力に差があると判断してよいか。有意水準 5% で検定せよ。
ある政党の 5 年間の支持率は 20% であった。無作為に 900 人を選んで調査したところ、 151 人が支持しているという結果であった。支持率は 5 年前から下がったと判断してよいか。有意水準 1% で検定せよ。
ある高校で、生徒会の会員に A、B の 2 人が立候補した。選挙の直前に、全生徒の中から 48 人を無作為抽出し、どちらを支持するかを調査したところ 30 人がAを支持し、 18 人が日を支持した。全生徒 1000 人が投票するものとして、次の問いに答えよ。ただし、白票や無効票はないものとする。
(1) Aの得票数を信頼度 95% で推定せよ。
(2) Aの支持率の方が高いと判断してよいか。有意水準 5% で検定せよ。
この動画を見る
テニス選手 A、B の年間の対戦成績は、Aの 23 勝 13 敗であった。両選手の力に差があると判断してよいか。有意水準 5% で検定せよ。
ある政党の 5 年間の支持率は 20% であった。無作為に 900 人を選んで調査したところ、 151 人が支持しているという結果であった。支持率は 5 年前から下がったと判断してよいか。有意水準 1% で検定せよ。
ある高校で、生徒会の会員に A、B の 2 人が立候補した。選挙の直前に、全生徒の中から 48 人を無作為抽出し、どちらを支持するかを調査したところ 30 人がAを支持し、 18 人が日を支持した。全生徒 1000 人が投票するものとして、次の問いに答えよ。ただし、白票や無効票はないものとする。
(1) Aの得票数を信頼度 95% で推定せよ。
(2) Aの支持率の方が高いと判断してよいか。有意水準 5% で検定せよ。
【数B】【確率分布と統計的な推測】推定 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある町で、 1 つの政策に対する賛否を調べる世論調査を、任意に抽出した有権者 400 人に対して行ったところ、政策支持者は 216 人であった。この町の有権者 1 万人のうち、この政策の支持者は何人ぐらいいると推定されるか。95% の信頼度で推定せよ。
数千枚の答案の採点をした。信頼度 95% 、信頼区間の幅 4 点以下でその平均点を推定したいとすると、少なくとも何枚以上の答案を抜き出さなければならないか。また、信頼区間の幅 2 点以下で推定するとすればどうか。ただし、従来の経験で点数の標準偏差は 15 点としてよいことはわかっているものとする。
(1) 確率変数 $Z$ が標準正規分布に従うとき、$P(|Z|≦\square)=0.99$ が成り立つ。 $\square$ に当てはまる最も適切な値を、次の$①〜④$のうちから1つ選べ。
$①1.75 ②1.96 ③2.33 ④2.58$
(2) ある試験を受けた高校生の中から、100 人を任意に選んだところ、平均点は 58.3 点であった。母標準偏差を 13.0 点として、母平均を信頼度 99% で推定せよ。
この動画を見る
ある町で、 1 つの政策に対する賛否を調べる世論調査を、任意に抽出した有権者 400 人に対して行ったところ、政策支持者は 216 人であった。この町の有権者 1 万人のうち、この政策の支持者は何人ぐらいいると推定されるか。95% の信頼度で推定せよ。
数千枚の答案の採点をした。信頼度 95% 、信頼区間の幅 4 点以下でその平均点を推定したいとすると、少なくとも何枚以上の答案を抜き出さなければならないか。また、信頼区間の幅 2 点以下で推定するとすればどうか。ただし、従来の経験で点数の標準偏差は 15 点としてよいことはわかっているものとする。
(1) 確率変数 $Z$ が標準正規分布に従うとき、$P(|Z|≦\square)=0.99$ が成り立つ。 $\square$ に当てはまる最も適切な値を、次の$①〜④$のうちから1つ選べ。
$①1.75 ②1.96 ③2.33 ④2.58$
(2) ある試験を受けた高校生の中から、100 人を任意に選んだところ、平均点は 58.3 点であった。母標準偏差を 13.0 点として、母平均を信頼度 99% で推定せよ。
【数B】【確率分布と統計的な推測】母集団と標本 ※問題文は概要欄

単元:
#確率分布と統計的な推測#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
1,1,2,3,3の数字を記入した5枚のカードが袋の中にある。これを母集団とし、無作為に大きさ2の標本$X_{1},X_{2}$を抽出する。
(1) 母集団分布と母平均を求めよ。
(2) 標本平均$\bar{X}$の確率分布を、復元抽出、非復元抽出の各場合について求めよ。
1,2,3,4,5の数字を書いた5枚のカードが袋の中にある。これを母集団とし、書かれた数字が奇数であるという特性をAとするとき、次の問いに答えよ。
(1) 特性Aの母比率を求めよ。
(2) この母集団から、大きさ1の無作為標本を抽出するとき、特性Aの標本比率の確率分布を求めよ。
(3) この母集団から、大きさ2の無作為標本を抽出するとき、復元抽出,非復元抽出の各場合について、特性Aの標本比率の確率分布を求めよ。
1枚の硬貨をn回投げて、表の出る回数をXとするとき、$|\frac{X}{n}-\frac{1}{2}|\leq0.01$となる確率が0.95以上になるためには、nをどのくらい大きくすればよいか。 100未満を切り上げて答えよ。
この動画を見る
1,1,2,3,3の数字を記入した5枚のカードが袋の中にある。これを母集団とし、無作為に大きさ2の標本$X_{1},X_{2}$を抽出する。
(1) 母集団分布と母平均を求めよ。
(2) 標本平均$\bar{X}$の確率分布を、復元抽出、非復元抽出の各場合について求めよ。
1,2,3,4,5の数字を書いた5枚のカードが袋の中にある。これを母集団とし、書かれた数字が奇数であるという特性をAとするとき、次の問いに答えよ。
(1) 特性Aの母比率を求めよ。
(2) この母集団から、大きさ1の無作為標本を抽出するとき、特性Aの標本比率の確率分布を求めよ。
(3) この母集団から、大きさ2の無作為標本を抽出するとき、復元抽出,非復元抽出の各場合について、特性Aの標本比率の確率分布を求めよ。
1枚の硬貨をn回投げて、表の出る回数をXとするとき、$|\frac{X}{n}-\frac{1}{2}|\leq0.01$となる確率が0.95以上になるためには、nをどのくらい大きくすればよいか。 100未満を切り上げて答えよ。
福田のおもしろ数学430〜整式を満たす整数解の性質

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
整数係数の整式$P(x)$に対して
$P(x)=1$と$P(x)=3$がともに整数解をもつとき、
$P(x)=2$
は異なる$2$つの整数解をもてるか?
この動画を見る
整数係数の整式$P(x)$に対して
$P(x)=1$と$P(x)=3$がともに整数解をもつとき、
$P(x)=2$
は異なる$2$つの整数解をもてるか?
福田の数学〜京都大学2025理系第1問(1)〜複素数の絶対値の取り得る値の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)$i$は虚数単位とする。
複素数$z$が、
絶対値が$2$である複素数全体を動くとき、
$\left \vert z-\dfrac{i}{z}\right \vert$
の最大値と最小値を求めよ。
$2025$年京都大学理系過去問題
この動画を見る
$\boxed{1}$
(1)$i$は虚数単位とする。
複素数$z$が、
絶対値が$2$である複素数全体を動くとき、
$\left \vert z-\dfrac{i}{z}\right \vert$
の最大値と最小値を求めよ。
$2025$年京都大学理系過去問題
【数Ⅱ】【図形と方程式】2直線の関係4 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような三角形の面積を求めよ。
(1)3点(-1,1),(3,2),(1,4)を頂点とする三角形
(2)3直線$x-3y=-5,4x+3y=-5,2x-y=5$で作られる三角形
平面上の2点をA(1,1),B(2,3)とする。
点Pが放物線$y=x^{2}+4x+11$を動くとき、$\triangle$PABの面積の最小値を求めよ。
この動画を見る
次のような三角形の面積を求めよ。
(1)3点(-1,1),(3,2),(1,4)を頂点とする三角形
(2)3直線$x-3y=-5,4x+3y=-5,2x-y=5$で作られる三角形
平面上の2点をA(1,1),B(2,3)とする。
点Pが放物線$y=x^{2}+4x+11$を動くとき、$\triangle$PABの面積の最小値を求めよ。
【数Ⅱ】【図形と方程式】2直線の関係3 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
問1
直線$y=2x$を$l$とするとき、次のものを求めよ。
(1)$l$に関して、点$\rm A(5,0)$と対称な点Bの座標
(2) $l$に関して、直線$3x+y=15$と対称な直線の方程式
問2
$k$を定数とする。直線$(k+2)x+(2k-3)y=5k-4$は$k$の値に関係なく定点を通る。その定点の座標を求めよ。
問3
$x-y=1,2x-3y=1,ax+by=1$が1点で交わらなければ、3点$(1,ー1),(2,ー3),(a,b)$は一直線上にあることを証明せよ。
この動画を見る
問1
直線$y=2x$を$l$とするとき、次のものを求めよ。
(1)$l$に関して、点$\rm A(5,0)$と対称な点Bの座標
(2) $l$に関して、直線$3x+y=15$と対称な直線の方程式
問2
$k$を定数とする。直線$(k+2)x+(2k-3)y=5k-4$は$k$の値に関係なく定点を通る。その定点の座標を求めよ。
問3
$x-y=1,2x-3y=1,ax+by=1$が1点で交わらなければ、3点$(1,ー1),(2,ー3),(a,b)$は一直線上にあることを証明せよ。
【数Ⅱ】【図形と方程式】2直線の関係2 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$3x-2y+3=0,2x-4y+k=0,x-ky+5=0$が1点で交わるように、定数$k$の値を求めよ。
$x+3y=2,x+y=0,ax+2y=-4$が三角形を作らないような定数$a$の値を求めよ。
2直線$x-y+1=0,3x+2y-12=0$の交点を通り、次の条件を満たす直線の方程式を、それぞれ求めよ。
(1)直線$5xー6yー8=0$に平行である。
(2)直線$5xー6yー8=0$に垂直である。
この動画を見る
$3x-2y+3=0,2x-4y+k=0,x-ky+5=0$が1点で交わるように、定数$k$の値を求めよ。
$x+3y=2,x+y=0,ax+2y=-4$が三角形を作らないような定数$a$の値を求めよ。
2直線$x-y+1=0,3x+2y-12=0$の交点を通り、次の条件を満たす直線の方程式を、それぞれ求めよ。
(1)直線$5xー6yー8=0$に平行である。
(2)直線$5xー6yー8=0$に垂直である。
【数Ⅱ】【図形と方程式】2直線の関係1 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形$\rm ABC$について次の三直線の方程式を求めよ。またそれらが1点で交わることを示し、その点の座標を求めよ。
(1) 各辺の垂直二等分線
(2) 各頂点から対辺に下した垂線
$x+ay+1=0, ax+(a+2)y+3=0$ が次の条件を満たすとき定数$a$の値をそれぞれ求めよ。
(1) 平行である
(2) 垂直である
この動画を見る
三角形$\rm ABC$について次の三直線の方程式を求めよ。またそれらが1点で交わることを示し、その点の座標を求めよ。
(1) 各辺の垂直二等分線
(2) 各頂点から対辺に下した垂線
$x+ay+1=0, ax+(a+2)y+3=0$ が次の条件を満たすとき定数$a$の値をそれぞれ求めよ。
(1) 平行である
(2) 垂直である
【数Ⅱ】【図形と方程式】内分外分の利用 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
3点$(2,-2),(-1,1),\rm C$を頂点とする三角形が正三角形になるとき、点$\rm C$の座標を求めよ。
3点$(3,5),(2,-2),-(6,2)$から等距離にある点の座標を求めよ。
(1) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形$\rm ABCD$ がある。対角線$\rm AC,BD$の交点及び、頂点$\rm D$の座標を求めよ。
(2) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形について、頂点$\rm D$となりうる点の座標をすべて答えよ。
この動画を見る
3点$(2,-2),(-1,1),\rm C$を頂点とする三角形が正三角形になるとき、点$\rm C$の座標を求めよ。
3点$(3,5),(2,-2),-(6,2)$から等距離にある点の座標を求めよ。
(1) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形$\rm ABCD$ がある。対角線$\rm AC,BD$の交点及び、頂点$\rm D$の座標を求めよ。
(2) 4点$\rm A(-2,3),B(5,4),C(-3,1),D$を頂点とする平行四辺形について、頂点$\rm D$となりうる点の座標をすべて答えよ。
【数Ⅱ】【図形と方程式】内分と外分の基本、点と直線 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2点$\rm A(-5),B(11)$に対して、線分$\rm AB$を$5:3$に内分する点を$\rm P$、$7:11$に外分する点を$\rm Q$とする。線分$\rm PQ$の中点の座標を求めよ。
次の3点が一直線上にあるとき、$t$の値を求めよ。
(1) $(-2,6),(0,3),(4,t)$
(2) $(1,4),(-1,t),(t,2)$
この動画を見る
2点$\rm A(-5),B(11)$に対して、線分$\rm AB$を$5:3$に内分する点を$\rm P$、$7:11$に外分する点を$\rm Q$とする。線分$\rm PQ$の中点の座標を求めよ。
次の3点が一直線上にあるとき、$t$の値を求めよ。
(1) $(-2,6),(0,3),(4,t)$
(2) $(1,4),(-1,t),(t,2)$
【数Ⅱ】【図形と方程式】内分外分重心 ※問題文は概要欄

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形の各辺の中点の座標を$(-1,-1),(-0,-1),(2,-2)$であるとき、この三角形の3つの頂点の座標を求めよ。
$\triangle \rm ABC$の重心を$\rm G$とするとき、次の等式を証明せよ。$\rm AB^2+AC^2=BG^2+CG^2+4AG^2$
$\triangle \rm ABC$において辺$\rm AB,BC,CA$を$3:2$に内分する点を、それぞれ$\rm D,E,F$とするとき、$\triangle \rm ABC$と$\triangle \rm DEF$の重心は一致することを証明せよ。
この動画を見る
三角形の各辺の中点の座標を$(-1,-1),(-0,-1),(2,-2)$であるとき、この三角形の3つの頂点の座標を求めよ。
$\triangle \rm ABC$の重心を$\rm G$とするとき、次の等式を証明せよ。$\rm AB^2+AC^2=BG^2+CG^2+4AG^2$
$\triangle \rm ABC$において辺$\rm AB,BC,CA$を$3:2$に内分する点を、それぞれ$\rm D,E,F$とするとき、$\triangle \rm ABC$と$\triangle \rm DEF$の重心は一致することを証明せよ。
【高校数学】東京大学2025年度理系数学第2問 積分と極限の問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
■【東京大学 2025】
(1)$x>1$のとき、不等式$logx≦x-1$を示せ。
(2)次の極限を求めよ。
$\displaystyle\lim_{n\to \infty}n\displaystyle \int_1^2log\displaystyle(\frac{1+x^{\frac{1}{n}}}{2})dx$
この動画を見る
■【東京大学 2025】
(1)$x>1$のとき、不等式$logx≦x-1$を示せ。
(2)次の極限を求めよ。
$\displaystyle\lim_{n\to \infty}n\displaystyle \int_1^2log\displaystyle(\frac{1+x^{\frac{1}{n}}}{2})dx$
福田のおもしろ数学429〜複雑な無理関数の最大値

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$xy+x\sqrt{1-y^2}+y\sqrt{1-x^2}$
$\qquad -\sqrt{(1-x^2)(1-y^2)}$
の最大値を求めよ。
この動画を見る
$xy+x\sqrt{1-y^2}+y\sqrt{1-x^2}$
$\qquad -\sqrt{(1-x^2)(1-y^2)}$
の最大値を求めよ。
福田の数学〜東京大学2025文系第4問〜放物線で囲まれた面積の最大値

単元:
#連立方程式#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$a$は実数とする。
座標平面において、次の連立不等式の表す領域の
面積を$S(a)$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \leqq -\dfrac{1}{2}x^2+2 \\
y \geqq \vert x^2+a \vert \\\
-1 \leqq x \leqq 1
\end{array}
\right.
\end{eqnarray}$
$a$が$ 2\leqq a \leqq 2$の範囲を動くとき、
$S(a)$の最大値を求めよ。
$2025$年東京大学文系過去問
この動画を見る
$\boxed{4}$
$a$は実数とする。
座標平面において、次の連立不等式の表す領域の
面積を$S(a)$とする。
$\begin{eqnarray}
\left\{
\begin{array}{l}
y \leqq -\dfrac{1}{2}x^2+2 \\
y \geqq \vert x^2+a \vert \\\
-1 \leqq x \leqq 1
\end{array}
\right.
\end{eqnarray}$
$a$が$ 2\leqq a \leqq 2$の範囲を動くとき、
$S(a)$の最大値を求めよ。
$2025$年東京大学文系過去問
【数A】【場合の数と確率】期待値、このゲームは得?損? ※問題文は概要欄

単元:
#数A#場合の数と確率#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
白玉2個、黒玉5個、赤玉3個が入っている袋から玉を1個取り出し、白玉が出たら1000円、黒玉が出たら100円もらえ、赤玉が出たら800円を支払うゲームがある。ゲームの参加料が0円であるとき、このゲームに参加することは得であるといえるか。
この動画を見る
白玉2個、黒玉5個、赤玉3個が入っている袋から玉を1個取り出し、白玉が出たら1000円、黒玉が出たら100円もらえ、赤玉が出たら800円を支払うゲームがある。ゲームの参加料が0円であるとき、このゲームに参加することは得であるといえるか。
【数A】【場合の数と確率】コインを投げたときの得点の期待値 ※問題文は概要欄

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
3枚の硬貨を同時に投げて、表が3枚出たら100点、2枚出たら50点を獲得し、1枚のときは60点を、1枚も出ていないときは70点を失うものとする。1回硬貨を投げるときの得点の期待値を求めよ。
この動画を見る
3枚の硬貨を同時に投げて、表が3枚出たら100点、2枚出たら50点を獲得し、1枚のときは60点を、1枚も出ていないときは70点を失うものとする。1回硬貨を投げるときの得点の期待値を求めよ。
【数A】【場合の数と確率】さいころ2個の目の積の期待値 ※問題文は概要欄

【数A】【場合の数と確率】条件付き確率、帽子を忘れてくる確率 ※問題文は概要欄

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
5回に1回の割合で帽子を忘れるくせのあるK君が、正月A、B、C3軒を順に年始回りをして家に帰ったところ、帽子を忘れてきたことに気がついた。2番目の家Bに忘れてきた確率を求めよ。
この動画を見る
5回に1回の割合で帽子を忘れるくせのあるK君が、正月A、B、C3軒を順に年始回りをして家に帰ったところ、帽子を忘れてきたことに気がついた。2番目の家Bに忘れてきた確率を求めよ。
【数A】【場合の数と確率】条件付き確率、原因の確率 ※問題文は概要欄

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある電器店が、A社、B社、C社から同じ製品を仕入れた。A社、B社、C社から仕入れた比率は4:3:2であり、製品が不良品である比率はそれぞれ3%、4%、5%であるという。いま、大量にある3社の製品をよく混ぜ、その中から1個抜き取って調べたところ、不良品であった。これがA社から仕入れたものである確率を求めよ。
この動画を見る
ある電器店が、A社、B社、C社から同じ製品を仕入れた。A社、B社、C社から仕入れた比率は4:3:2であり、製品が不良品である比率はそれぞれ3%、4%、5%であるという。いま、大量にある3社の製品をよく混ぜ、その中から1個抜き取って調べたところ、不良品であった。これがA社から仕入れたものである確率を求めよ。
