 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
【「定石」の前に…!】因数分解:自由が丘学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
(a+2b)²-3(a+2b)+2(a+b)-2(1-b)を因数分解しなさい
この動画を見る
(a+2b)²-3(a+2b)+2(a+b)-2(1-b)を因数分解しなさい
【いかに解くのか…!】計算:大東文化大学第一高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中2数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)#大東文化大学第一高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1001×999-101×99
この動画を見る
1001×999-101×99
【トケイ問題…!?】方程式:精華女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#方程式#高校入試過去問(数学)#精華女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
時計で6時と7時の間で短針と長針がちょうど重なる時刻を求めなさい。u
この動画を見る
時計で6時と7時の間で短針と長針がちょうど重なる時刻を求めなさい。u
calculation : Shirotan's cute kawaii math show #数学 #高校入試 #京大数学 #小学生テスト

単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
(30²+37²+44²+…+79²)-(1²+8²+15²+…+50²)=?
この動画を見る
(30²+37²+44²+…+79²)-(1²+8²+15²+…+50²)=?
【2つの不等式…!】不等式:興南高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#興南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
興南高等学校の入試から、不等式の問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
この動画を見る
興南高等学校の入試から、不等式の問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
【応用の効く…!】整数:函館白百合学園高等学校~全国入試問題解法

【その場で導け…!】図形:開智高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#円#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
開智高等学校の入試から、図形問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
このコンテンツの作成手段
この動画を見る
開智高等学校の入試から、図形問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
このコンテンツの作成手段
【別解付きで解きたい…!】図形:函館白百合学園高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#函館白百合学園高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
函館白百合学園高等学校の入試から、図形問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
この動画を見る
函館白百合学園高等学校の入試から、図形問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
【解法のテクニック…!】二次方程式:同志社国際高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#同志社国際高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
同志社国際高等学校の入試から、二次方程式の問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
この動画を見る
同志社国際高等学校の入試から、二次方程式の問題です。
全国の入試問題から、意図が分かりやすい大切な問題に絞って、ひたすら解きまくっていきます。
傾向と対策のために、軽い頭の体操のために、あるいは、時間つぶしのためにどうぞ。
チャンネル登録は、こちらで。
/ @math_shirotan
X、tik tok、Instagramのフォローもお願いします!
#高校受験 #高校入試 #数学
音楽素材:
音楽 → 「たうろんの!成りあ音楽!」
FREE BGM DOVA-SYNDROME
フリー音楽素材 魔王魂
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
integer problems : Shirotan's cute kawaii math show #数学 #高校入試 #京大数学 #小学生テスト

単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
Let's enjoy oriental mathematics for just a little while.
You will discover a cute world from mathematics.
Everyone in the world should love and be good at mathematics.
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
この動画を見る
Let's enjoy oriental mathematics for just a little while.
You will discover a cute world from mathematics.
Everyone in the world should love and be good at mathematics.
We are introducing the entrance exam questions for Japanese high schools.
It's an important issue for you to understand the basics of mathematics.
Would you like to solve this math problem and check out our commentary?
【手を付けることが大切…!】因数分解:同志社国際高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の式を因数分解せよ。3(a-3c)(a-c)+(a+4b)(a-4b)
この動画を見る
次の式を因数分解せよ。3(a-3c)(a-c)+(a+4b)(a-4b)
【十分な理解がないと…!】文字式:國學院大學久我山高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)#國學院大學久我山高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の文字式を計算しなさい。(-2x/y)^4×(3y/-z^2)^3×(z/2x)^2
この動画を見る
次の文字式を計算しなさい。(-2x/y)^4×(3y/-z^2)^3×(z/2x)^2
東大寺学園が書類送検される #shorts

単元:
#算数(中学受験)#数学(中学生)#英語(中学生)#過去問解説(学校別)#高校入試過去問(英語)#高校入試過去問(数学)#東大寺学園中学#東大寺学園高等学校#東大寺学園高等学校
指導講師:
Morite2 English Channel
問題文全文(内容文):
あの**超有名進学校**がまさかの事態に!
高校生クイズでもおなじみの**東大寺学園**と校長たちが、労働基準法違反の容疑で**書類送検**されたぞ。
奈良労働基準監督署の調べによると、2024年10月、教員36人に対し、時間外労働や休日労働をさせたにもかかわらず、**割増賃金約130万円を支払わなかった**疑いが持たれている。
この未払いのほとんどは、**部活動**に関わるものだったという。
しかも、もっとヤバいのは、実は2023年12月に是正勧告が出ていたにもかかわらず、翌年2024年11月の立ち入り調査で**再び不払いが確認された**という事実!どうなってんだ!?
この問題は、残業代がまともに支払われず、**働かせ放題**になっている公立学校の先生たちの労働環境にもつながる、**日本の教育現場の闇**を象徴しているぞ。
この動画を見る
あの**超有名進学校**がまさかの事態に!
高校生クイズでもおなじみの**東大寺学園**と校長たちが、労働基準法違反の容疑で**書類送検**されたぞ。
奈良労働基準監督署の調べによると、2024年10月、教員36人に対し、時間外労働や休日労働をさせたにもかかわらず、**割増賃金約130万円を支払わなかった**疑いが持たれている。
この未払いのほとんどは、**部活動**に関わるものだったという。
しかも、もっとヤバいのは、実は2023年12月に是正勧告が出ていたにもかかわらず、翌年2024年11月の立ち入り調査で**再び不払いが確認された**という事実!どうなってんだ!?
この問題は、残業代がまともに支払われず、**働かせ放題**になっている公立学校の先生たちの労働環境にもつながる、**日本の教育現場の闇**を象徴しているぞ。
Shirotan's cute kawaii math show #数学 #高校入試 #勉強 #チャンネル登録をお願いします

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#巣鴨高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
3つの二次方程式:x^2+ax+b=0, 2x^2+3ax+9b=0, x^2-2x-3=0が同じ正の解をもつとする。このとき、定数a,bの値を求めよ。
この動画を見る
3つの二次方程式:x^2+ax+b=0, 2x^2+3ax+9b=0, x^2-2x-3=0が同じ正の解をもつとする。このとき、定数a,bの値を求めよ。
【戸惑う人も多い…!】平方根:秋田県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sqrt{32}$$-$$\sqrt{50}$$+$$\sqrt{27}$
この動画を見る
$\sqrt{32}$$-$$\sqrt{50}$$+$$\sqrt{27}$
【少しでも上手く…!】文字式:明治大学付属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x =\sqrt{1103} + \sqrt{1101}$
$ y = \sqrt{1103} - \sqrt{1101}$
のとき
$\left( \frac{1}{2} x^2 y \right)^5 \div \left( \frac{1}{4} x^3 y^2 \right)^3 + x^3 y^7 \cdot xy \div x^4 y^6
$の値は$\boxed{ }$である
この動画を見る
$x =\sqrt{1103} + \sqrt{1101}$
$ y = \sqrt{1103} - \sqrt{1101}$
のとき
$\left( \frac{1}{2} x^2 y \right)^5 \div \left( \frac{1}{4} x^3 y^2 \right)^3 + x^3 y^7 \cdot xy \div x^4 y^6
$の値は$\boxed{ }$である
factorization : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study

単元:
#数学(中学生)#相似な図形#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x^2-\boxed{ }x+14$が$(x-a)(x-b)$の形に因数分解できる。
$\boxed{ }$に当てはまる自然数を二つ書け。
この動画を見る
$x^2-\boxed{ }x+14$が$(x-a)(x-b)$の形に因数分解できる。
$\boxed{ }$に当てはまる自然数を二つ書け。
さぁどうやって計算する?2025堀川高校最初の一問
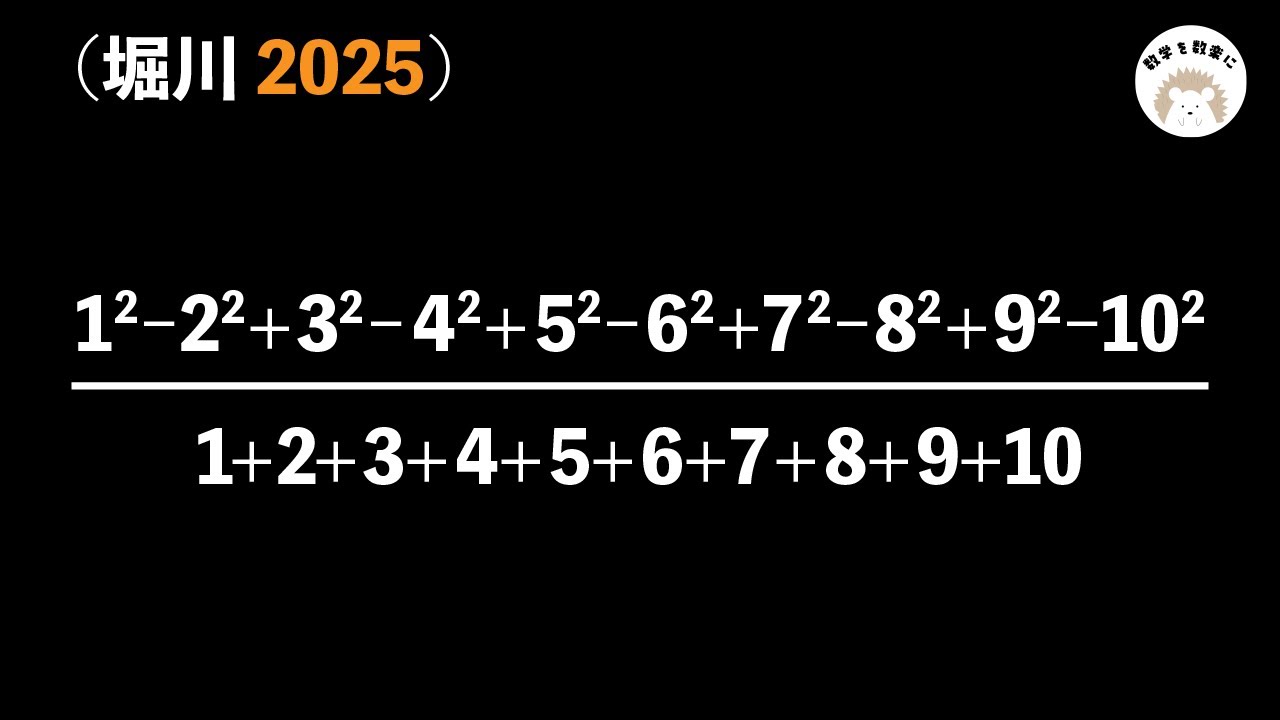
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \frac{1^2-2^2+3^2-4^2+5^2-6^2+7^2-8^2+9^2-10^2}{1+2+3+4+5+6+7+8+9+10}$
この動画を見る
$\displaystyle \frac{1^2-2^2+3^2-4^2+5^2-6^2+7^2-8^2+9^2-10^2}{1+2+3+4+5+6+7+8+9+10}$
【中学数学】箱ひげ図の問題~2024年度北海道公立高校入試大問1~【高校受験】
単元:
#数学(中学生)#中1数学#中2数学#中3数学#高校入試過去問(数学)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
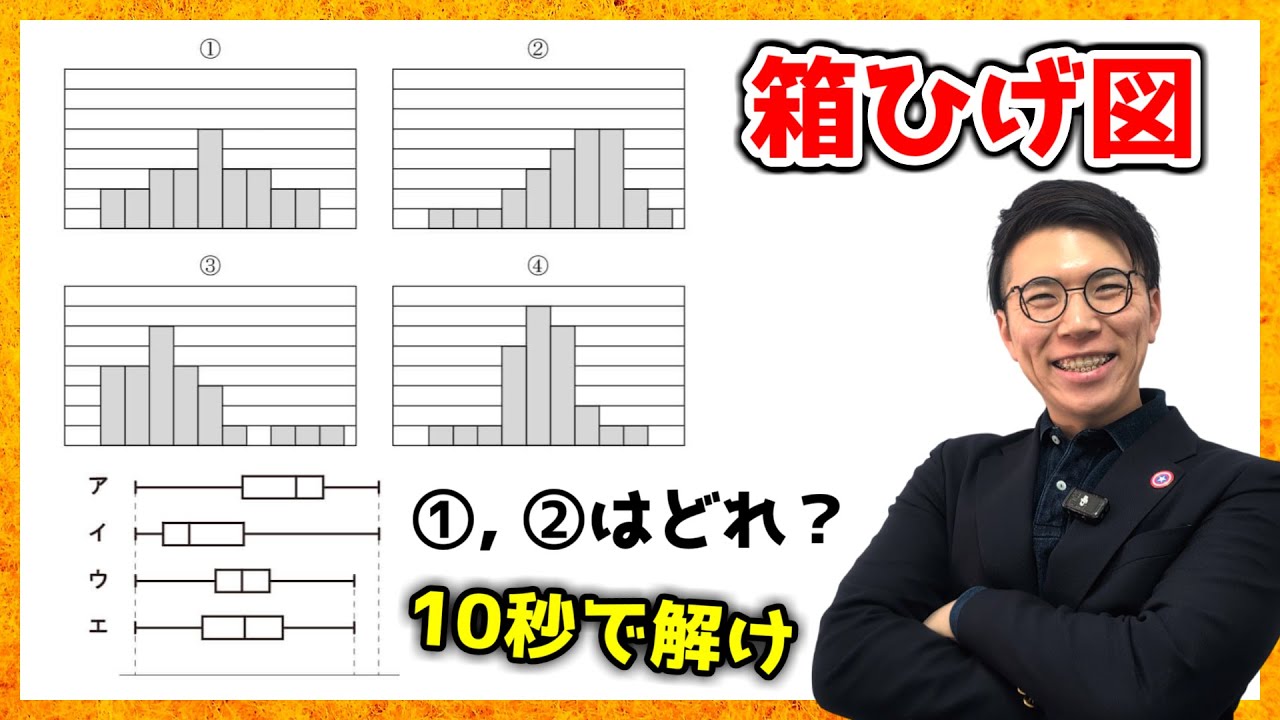
【中学数学】箱ひげ図の問題~2024年度北海道公立高校入試大問1~【高校受験】①~④のヒストグラムは、それぞれア~エのいずれかの箱ひげ図と同じデータを使ってまとめたものです。①、②のヒストグラムは、どの箱ひげ図と同じデータを使ってまとめたものですか。最も適当なものを、それぞれア~エから選びなさい。
この動画を見る
【中学数学】箱ひげ図の問題~2024年度北海道公立高校入試大問1~【高校受験】①~④のヒストグラムは、それぞれア~エのいずれかの箱ひげ図と同じデータを使ってまとめたものです。①、②のヒストグラムは、どの箱ひげ図と同じデータを使ってまとめたものですか。最も適当なものを、それぞれア~エから選びなさい。
【初めの一手は…!】二次方程式:中央大学杉並高等学校~全国入試問題解法

単元:
#数学(中学生)#数Ⅰ#高校入試過去問(数学)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$4(x - 7)(x - 16)+56 = (x-8)(x-9)$を解きなさい
この動画を見る
$4(x - 7)(x - 16)+56 = (x-8)(x-9)$を解きなさい
2つの二次方程式 2025立教新座

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#立教新座高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
立教新座高等学校過去問
2つの2次方程式
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 - kx - 10&=& 0 \\
x^2 + 5x + 2k&=& 0
\end{array}
\right.
\end{eqnarray}
が共通解を1つだけ持つ。
この共通解と定数$k$の値を求めよ。ただし$k\ne5$
この動画を見る
立教新座高等学校過去問
2つの2次方程式
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 - kx - 10&=& 0 \\
x^2 + 5x + 2k&=& 0
\end{array}
\right.
\end{eqnarray}
が共通解を1つだけ持つ。
この共通解と定数$k$の値を求めよ。ただし$k\ne5$
【ストーリーを読め…!】整数:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#数A#高校入試過去問(数学)#数学(高校生)#慶應義塾高等学校
指導講師:
問題文全文(内容文):
$x^2 + (3y - 9)x + y(2y - 9)が素数の平方数となるような$
$9以下の正の整数x,yの組を全て求めよ$
この動画を見る
$x^2 + (3y - 9)x + y(2y - 9)が素数の平方数となるような$
$9以下の正の整数x,yの組を全て求めよ$
【解法は1つでない…!】連立方程式:東京工業大学附属科学技術高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\begin{cases}
(2a-1)x+(b+1)y =-3 \\
(2b+1)x+(a-1)y =11
\end{cases}
\end{eqnarray}$
の解が$x=-1, y=2であるとき定数a,bの値をそれぞれ求めなさい$
この動画を見る
$\begin{eqnarray}
\begin{cases}
(2a-1)x+(b+1)y =-3 \\
(2b+1)x+(a-1)y =11
\end{cases}
\end{eqnarray}$
の解が$x=-1, y=2であるとき定数a,bの値をそれぞれ求めなさい$
灘高の大問1が難しすぎると話題?

【最終兵器…!?】因数分解:ラ・サール高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\frac{x}{12}(9+x)+(19-\frac{5}{3}x)×(1-\frac{x}{4})-\frac{1}{6}(42-x)$を因数分解せよ
この動画を見る
$\frac{x}{12}(9+x)+(19-\frac{5}{3}x)×(1-\frac{x}{4})-\frac{1}{6}(42-x)$を因数分解せよ
【最終兵器…!?】因数分解:ラ・サール高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\frac{x}{12}(9+x)+(19-\frac{5}{3}x)×(1-\frac{x}{4})-\frac{1}{6}(42-x)$
この動画を見る
$\frac{x}{12}(9+x)+(19-\frac{5}{3}x)×(1-\frac{x}{4})-\frac{1}{6}(42-x)$
【理解度が試される…!】平方根:同志社高等学校~全国入試問題解法

単元:
#数学(中学生)#数と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\frac{(1+\sqrt{2}+\sqrt{3})(1+\sqrt{2}-\sqrt{3})}{\sqrt{(-2)^2}}$
この動画を見る
$\frac{(1+\sqrt{2}+\sqrt{3})(1+\sqrt{2}-\sqrt{3})}{\sqrt{(-2)^2}}$
【よく出る…!】図形:和洋国府台女子高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
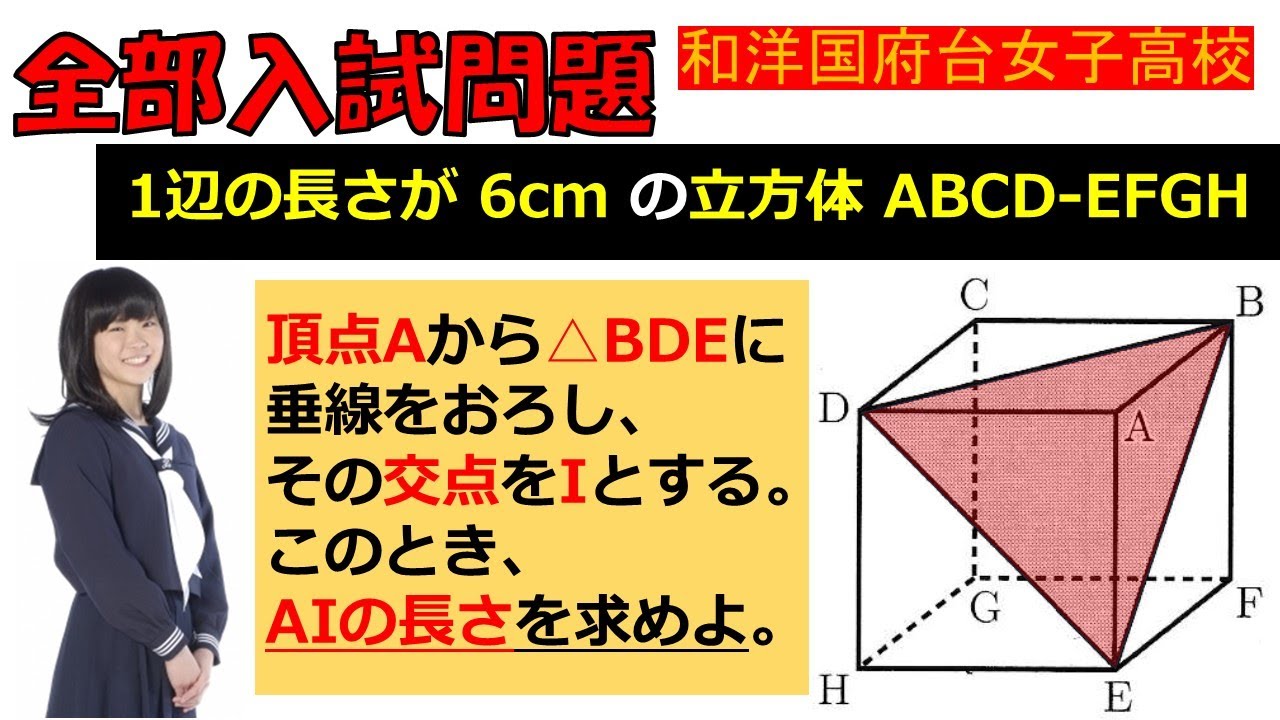
$頂点Aから\triangle{BDE}に垂線をおろし、その交点をIとする。$$このとき、AIの長さを求めよ。$
この動画を見る
$頂点Aから\triangle{BDE}に垂線をおろし、その交点をIとする。$$このとき、AIの長さを求めよ。$
【入試らしい1問…!】因数分解:法政大学国際高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#高校入試過去問(数学)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(x^2+3x)^2-38(x^2+3x)+280$$を因数分解せよ$
この動画を見る
$(x^2+3x)^2-38(x^2+3x)+280$$を因数分解せよ$
平方根 最大の整数 香川誠陵

単元:
#数学(中学生)#中3数学#平方根#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
${3\sqrt{2} }$以下の実数のうち、最大の整数を求めよ
この動画を見る
${3\sqrt{2} }$以下の実数のうち、最大の整数を求めよ
