 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
気づけば爽快!!平方根の計算 中央大学附属

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)#中央大学附属高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
${(\sqrt{5}+\sqrt{3})^2}-{\sqrt{2}(\sqrt{10}+\sqrt{6})(\sqrt{5}-\sqrt{3})}+{(\sqrt{5}-\sqrt{3})^2}$
この動画を見る
${(\sqrt{5}+\sqrt{3})^2}-{\sqrt{2}(\sqrt{10}+\sqrt{6})(\sqrt{5}-\sqrt{3})}+{(\sqrt{5}-\sqrt{3})^2}$
ガウス記号 2025渋谷幕張
【入試数学との接し方…!】整数:城北高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$xを超えない最大の整数を[x]と表す$
$[\sqrt{m+10}]×[\sqrt{n}]=6となるような自然数の組はいくつあるか$
この動画を見る
$xを超えない最大の整数を[x]と表す$
$[\sqrt{m+10}]×[\sqrt{n}]=6となるような自然数の組はいくつあるか$
ガウス記号 2025渋谷幕張

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
正の数$x$に対して、$x$以下の最大の整数を$[x]$と表す。
\begin{eqnarray}
\left\{
\begin{array}{l}
[x] + [2x] = 7 \\
3x^2 - 4[2x]x + 16[x] = 0
\end{array}
\right.
\end{eqnarray}
$[x]$=? $x$=?
この動画を見る
正の数$x$に対して、$x$以下の最大の整数を$[x]$と表す。
\begin{eqnarray}
\left\{
\begin{array}{l}
[x] + [2x] = 7 \\
3x^2 - 4[2x]x + 16[x] = 0
\end{array}
\right.
\end{eqnarray}
$[x]$=? $x$=?
これが入試問題の現実か。。。連立方程式 渋谷幕張2025
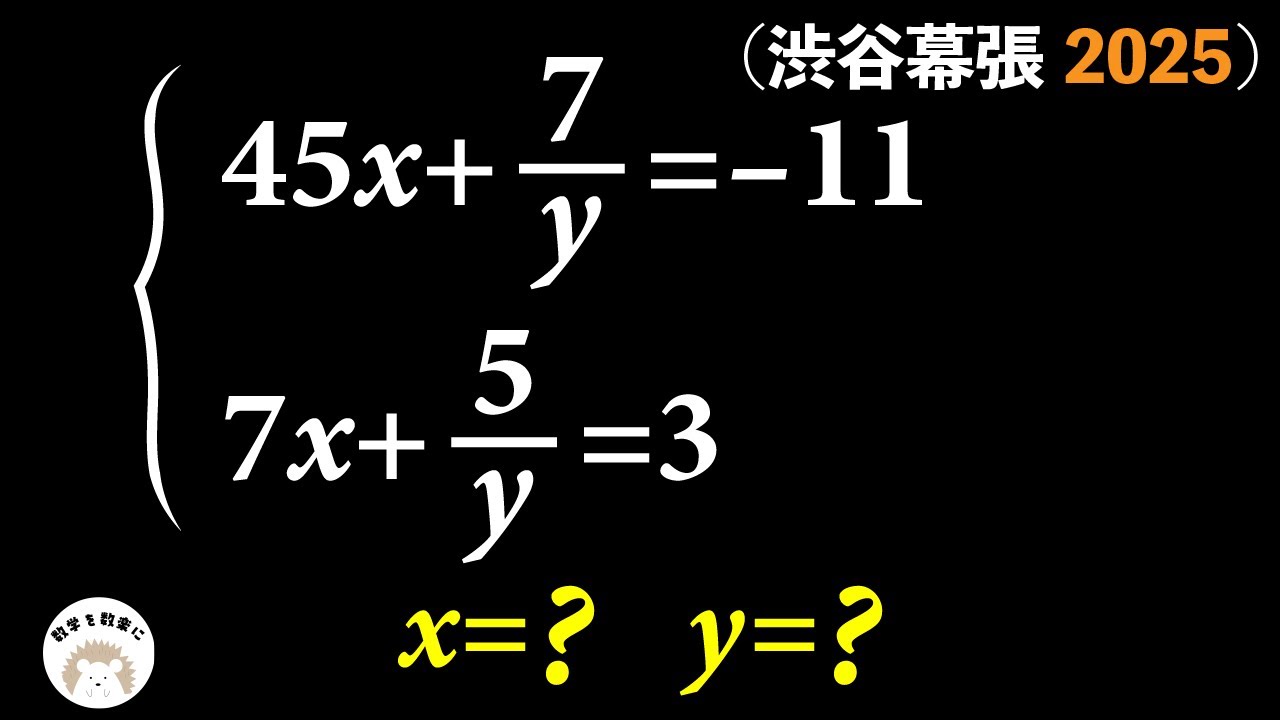
これが入試問題の現実か。。。連立方程式 渋谷幕張2025
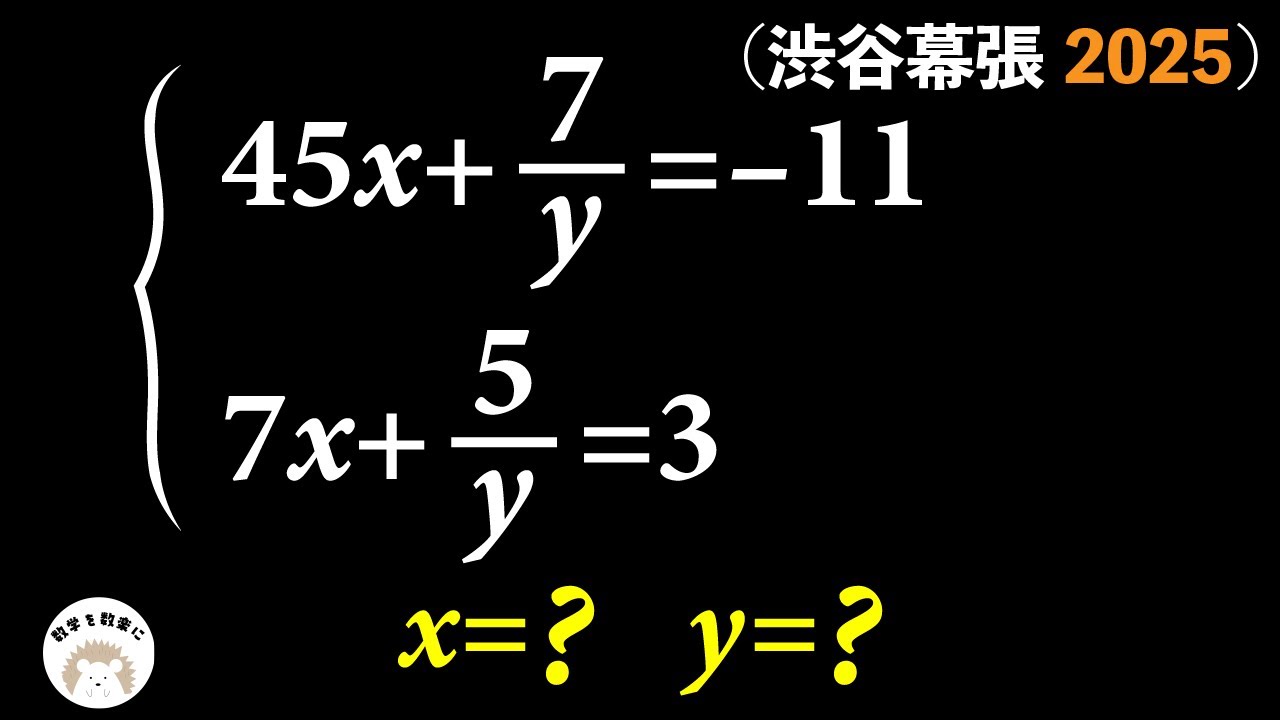
単元:
#数学(中学生)#中2数学#連立方程式#1次関数#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
45x + \displaystyle \frac{7}{y} = -11 \\
7x + \displaystyle \frac{5}{y} = 3
\end{array}
\right.
\end{eqnarray}
$x$=? $y$=?
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
45x + \displaystyle \frac{7}{y} = -11 \\
7x + \displaystyle \frac{5}{y} = 3
\end{array}
\right.
\end{eqnarray}
$x$=? $y$=?
【とても大切…!】図形:国立高等専門学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#立体図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
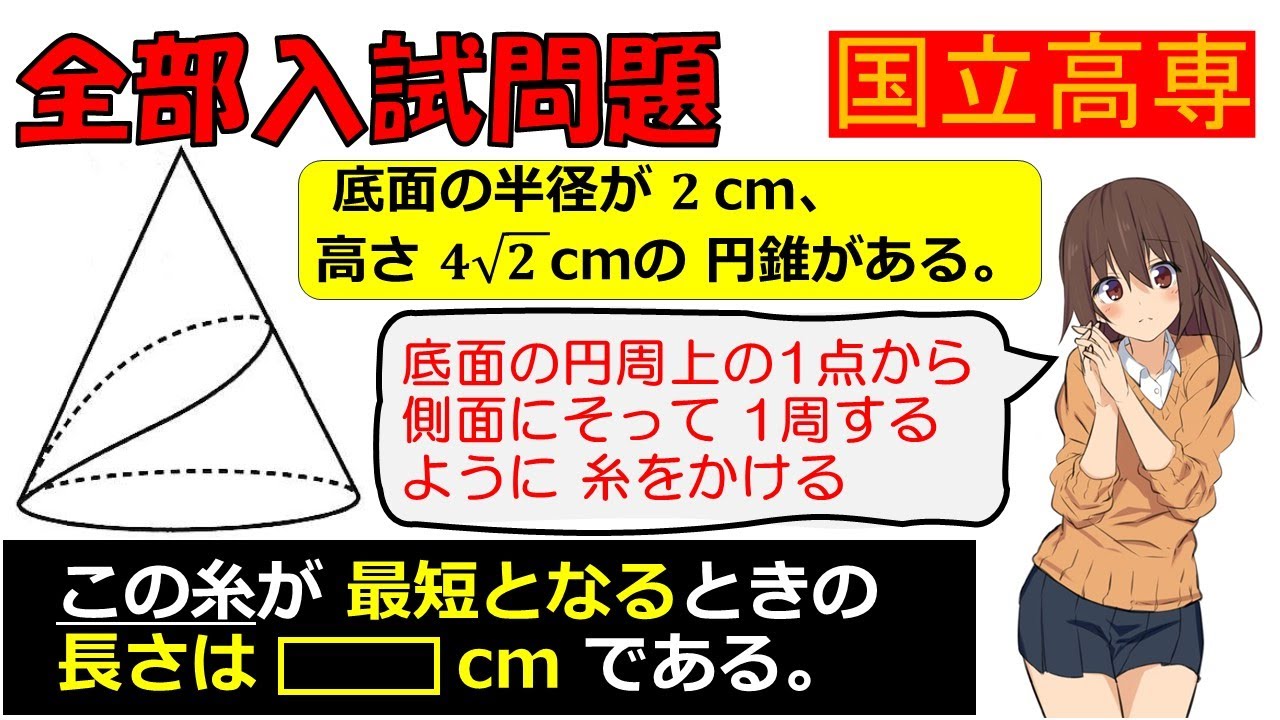
$底面の半径が2cm、高さ4\sqrt{2}cmの円錐がある。$
$底面の円周上の一点から側面に沿って一周するように糸を書ける$
$この糸が最短となるときの長さは\boxed{ }cmである。$
この動画を見る
$底面の半径が2cm、高さ4\sqrt{2}cmの円錐がある。$
$底面の円周上の一点から側面に沿って一周するように糸を書ける$
$この糸が最短となるときの長さは\boxed{ }cmである。$
因数分解 2025 渋谷幕張

【式をよく見て…!】二次方程式:灘高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#灘高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$3(x+a)^2=(2a^2-1)(x+a)+x^2-2ax-3a^2が解を1つしか持たないようなaの値を全て求めると$$a=\boxed{ }である$
この動画を見る
$3(x+a)^2=(2a^2-1)(x+a)+x^2-2ax-3a^2が解を1つしか持たないようなaの値を全て求めると$$a=\boxed{ }である$
平方根の式の値 3通りで解説
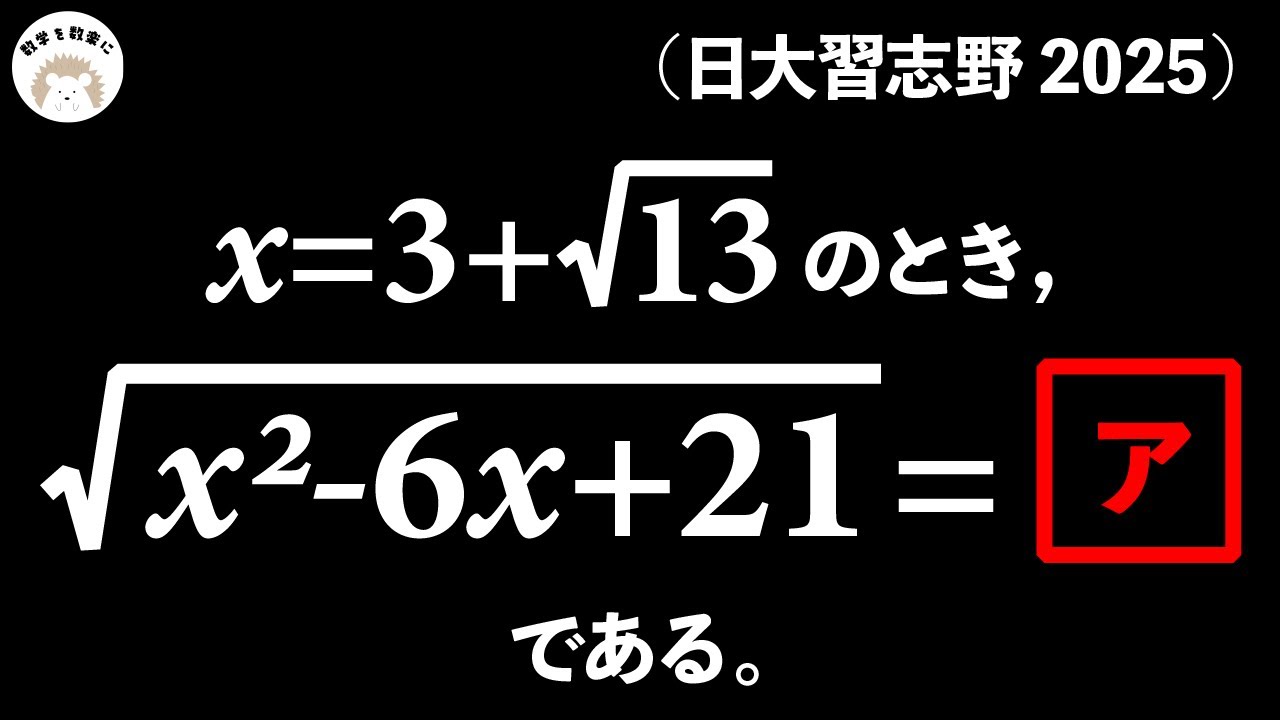
整数部分 小数部分

【分数だと…!?】因数分解:関西学院高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#関西学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\frac{1}{2}a^3+a^2b-4ab^2を因数分解せよ$
この動画を見る
$\frac{1}{2}a^3+a^2b-4ab^2を因数分解せよ$
【正体を見たり…!】方程式:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(x-y+1)(x+y-1)=0 ... が成り立つことを「x★y」と表す。$$「x★y」が成り立つxが1つだけになるようなyの値を求めなさい。$
この動画を見る
$(x-y+1)(x+y-1)=0 ... が成り立つことを「x★y」と表す。$$「x★y」が成り立つxが1つだけになるようなyの値を求めなさい。$
【類題がよく出る…!】整数:八代白百合学園高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#鳥取県公立高校入試#八代白百合学園高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\frac{56}{5}との積がある整数の2乗になるような自然数nのうち、できるだけ小さいnを求めよ。$
この動画を見る
$\frac{56}{5}との積がある整数の2乗になるような自然数nのうち、できるだけ小さいnを求めよ。$
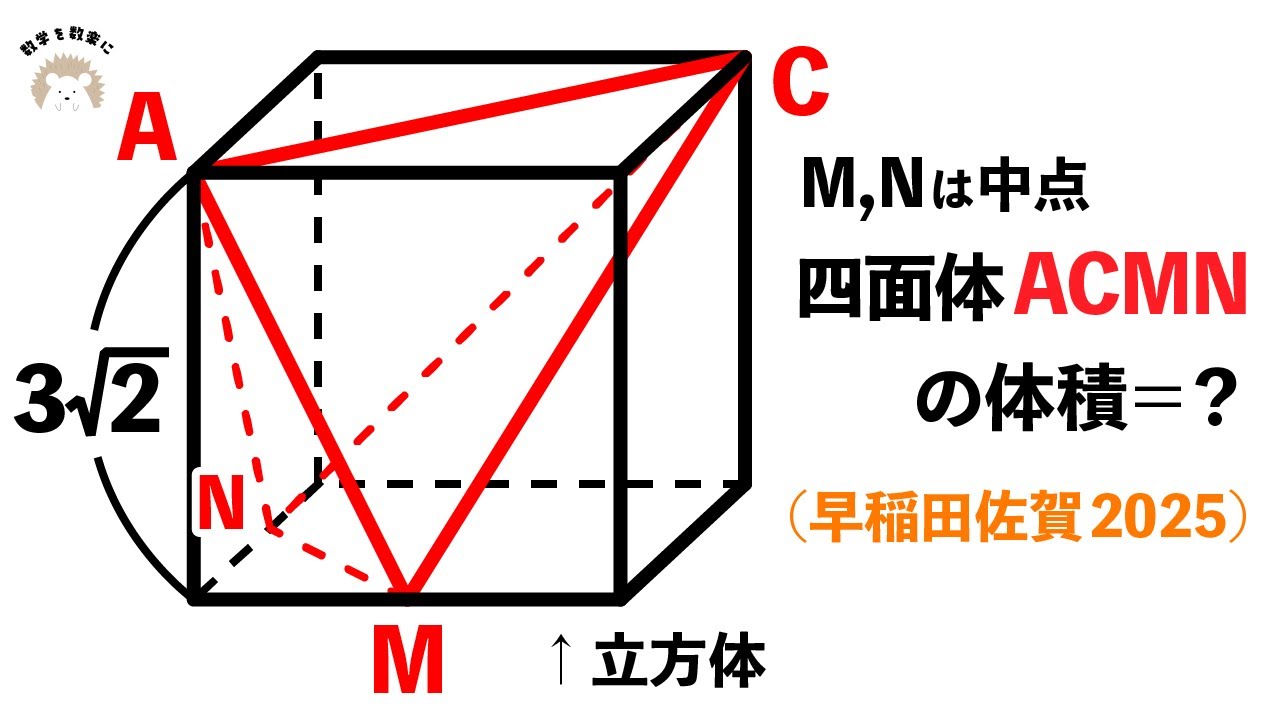
立方体の中にある四面体の体積
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)#早稲田大学系属早稲田佐賀高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
M、Nは中点。四面体ACMNの体積=?
*図は動画内参照
この動画を見る
M、Nは中点。四面体ACMNの体積=?
*図は動画内参照
【入試らしい1問…!】図形:岐阜県~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#岐阜県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$図1: 1辺9cmの立方体状の容器に水を入れる。→水面が頂点ABCを通る平面
$$図2: この容器を水平な台の上に置く。→底面から水面までの高さがxcmになった。$
この動画を見る
$図1: 1辺9cmの立方体状の容器に水を入れる。→水面が頂点ABCを通る平面
$$図2: この容器を水平な台の上に置く。→底面から水面までの高さがxcmになった。$
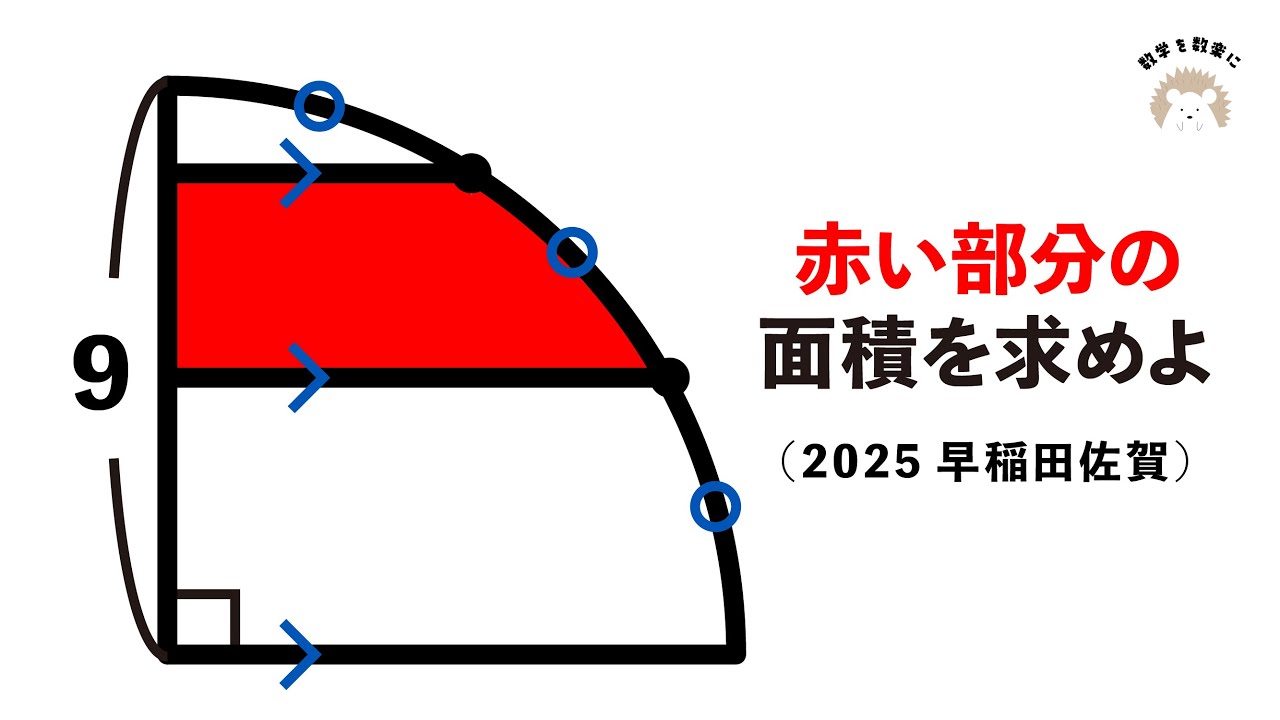
4分の1円の中の面積 2025早稲田佐賀
単元:
#数学(中学生)#中2数学#平行と合同#高校入試過去問(数学)#早稲田大学系属早稲田佐賀高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
図の赤い部分の面積を求めよ(図は動画参照)
この動画を見る
図の赤い部分の面積を求めよ(図は動画参照)
【中学数学】面積は何倍か?~2024年度埼玉県公立高校入試大問1(11)~【高校受験】
単元:
#数学(中学生)#中3数学#高校入試過去問(数学)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【中学数学】面積は何倍か?~2024年度埼玉県公立高校入試大問1(11)~【高校受験】
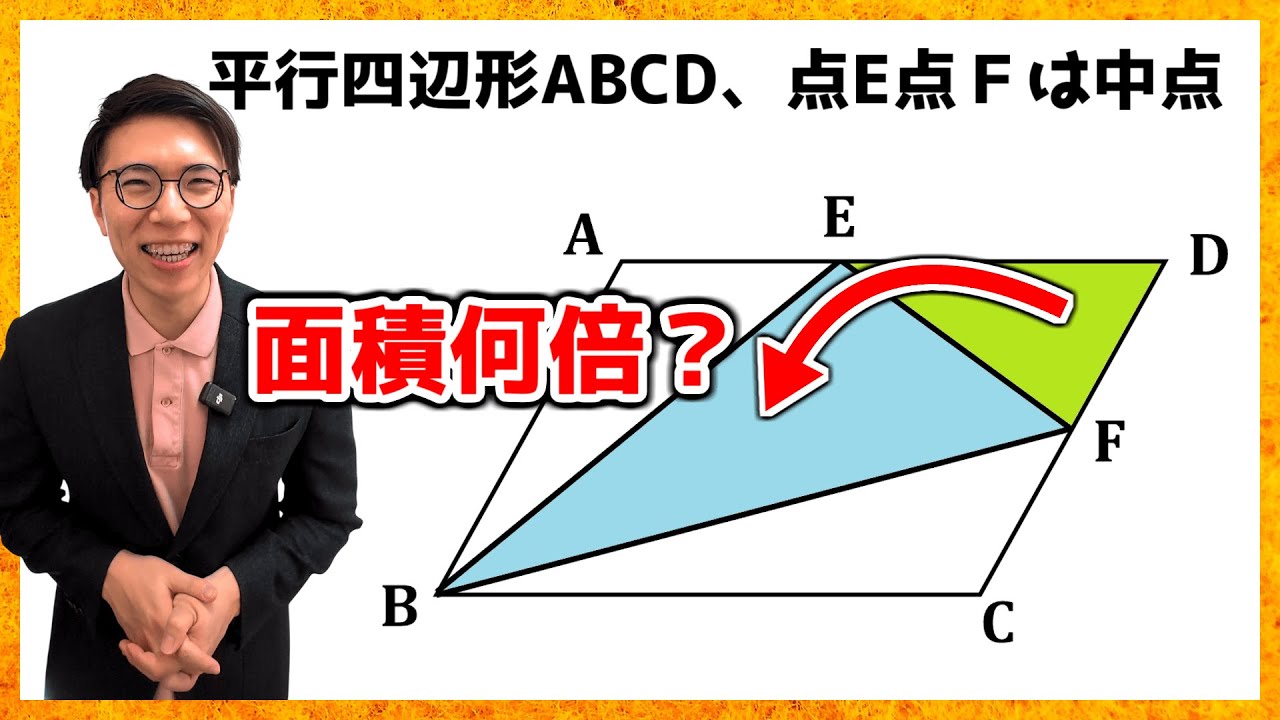
図のように平行四辺形ABCDがあり、辺AD、CDの中点をそれぞれE、Fとします。
このとき、△EBFの面積は△DEFの面積の何倍になるか求めなさい。
この動画を見る
【中学数学】面積は何倍か?~2024年度埼玉県公立高校入試大問1(11)~【高校受験】
図のように平行四辺形ABCDがあり、辺AD、CDの中点をそれぞれE、Fとします。
このとき、△EBFの面積は△DEFの面積の何倍になるか求めなさい。
【中学数学】円周角の定理の問題~2024年度埼玉県公立高校入試大問1(10)~【高校受験】

単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#埼玉県高等学校
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
図のように、円周の長さを10等分する点A~Jがあります。
△AEHと△BEHをつくり、辺AEと辺BEとの交点をKとするとき、
∠AKHの大きさxを求めよ。
※図は動画内参照
この動画を見る
図のように、円周の長さを10等分する点A~Jがあります。
△AEHと△BEHをつくり、辺AEと辺BEとの交点をKとするとき、
∠AKHの大きさxを求めよ。
※図は動画内参照
【試される思考…!】整数:日本大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#日本大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$【a】は自然数aを5で割った余りを表す。$
$このとき次の値を求めよ$
$【1^2】+【2^2】+【3^2】+...+【100^2】$
この動画を見る
$【a】は自然数aを5で割った余りを表す。$
$このとき次の値を求めよ$
$【1^2】+【2^2】+【3^2】+...+【100^2】$
【問題文が全て…!】二次方程式:桐朋高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#桐朋高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ax^2+2a^2x-6=0$
$x=3が解であるとき、定数aの値を全て求めよ$
この動画を見る
$ax^2+2a^2x-6=0$
$x=3が解であるとき、定数aの値を全て求めよ$
【どちらで解く…!】平方根:巣鴨高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#巣鴨高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(\frac{\sqrt{5}+\sqrt{2}}{\sqrt{7}})^2+(\frac{\sqrt{5}-\sqrt{2}}{\sqrt{7}})^2$を計算しなさい
この動画を見る
$(\frac{\sqrt{5}+\sqrt{2}}{\sqrt{7}})^2+(\frac{\sqrt{5}-\sqrt{2}}{\sqrt{7}})^2$を計算しなさい
2次方程式のこれ解ける?

単元:
#数学(中学生)#中3数学#2次方程式#数Ⅰ#2次関数#2次方程式と2次不等式#高校入試過去問(数学)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
aを定数とする。xの2次方程式
$3(x+a)^2 = (2a^2+1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値を全て求めよ。(灘高校 2024)
この動画を見る
aを定数とする。xの2次方程式
$3(x+a)^2 = (2a^2+1)(x+a)+x^2-2ax-3a^2$
が解を1つしかもたないようなaの値を全て求めよ。(灘高校 2024)
【重要な図形…!】図形:岐阜県~全国入試問題解法
単元:
#数学(中学生)#中1数学#中3数学#相似な図形#平面図形#高校入試過去問(数学)#岐阜県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
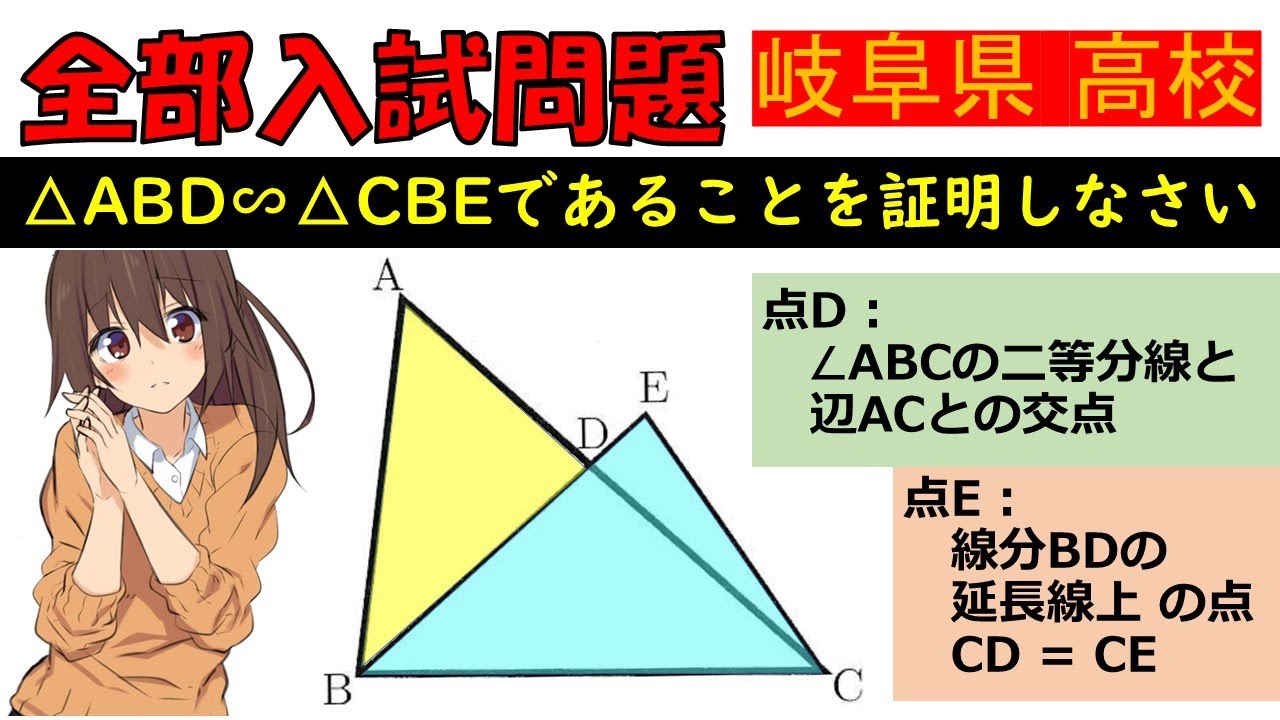
$\triangle ABD \backsim \triangle CBE であることを証明しなさい$
$点D : \angle ABCの二等分線と辺ACとの交点$
$点E : 線分BDの延長線上の点CD =CE$
この動画を見る
$\triangle ABD \backsim \triangle CBE であることを証明しなさい$
$点D : \angle ABCの二等分線と辺ACとの交点$
$点E : 線分BDの延長線上の点CD =CE$
【さらに発展的解法…!】整数:東京都立産業技術高等専門学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#東京都立産業技術高等専門学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a^2bcの約数は何個あるか。$
$a,b,cは素数で a \lt b \lt cである$
この動画を見る
$a^2bcの約数は何個あるか。$
$a,b,cは素数で a \lt b \lt cである$
integer problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study

単元:
#高校入試過去問(数学)#立命館高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$2104^2を11で割った余りを求めなさい$
この動画を見る
$2104^2を11で割った余りを求めなさい$
【数式に翻訳せよ…!】整数:新潟県~全国入試問題解法
【会話文形式が楽しい…!】図形:早稲田大学系属早稲田実業学校高等部~全国入試問題解法
【会話文形式が楽しい…!】図形:早稲田大学系属早稲田実業学校高等部~全国入試問題解法
【正解を導くことが第一…!】連立方程式:東京都立新宿高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#東京都立新宿高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
0.25x + y = 0.75 \\
\frac{x-2y}{5} = \frac{21}{25}
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
0.25x + y = 0.75 \\
\frac{x-2y}{5} = \frac{21}{25}
\end{array}
\right.
\end{eqnarray}$
